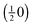Role of RuO2(100) in surface oxidation and CO oxidation catalysis on Ru(0001)
Jan Ingo
Flege
*a,
Jan
Lachnitt
b,
Daniel
Mazur
b,
Peter
Sutter†
c and
Jens
Falta
ad
aInstitute of Solid State Physics, University of Bremen, Otto-Hahn-Allee 1, 28359 Bremen, Germany. E-mail: flege@ifp.uni-bremen.de; Fax: +49 421 218 62251; Tel: +49 421 218 62243
bFaculty of Mathematics and Physics, Department of Surface and Plasma Science, Charles University in Prague, V Holešovičkách 2, 18000 Prague 8, Czech Republic
cCenter for Functional Nanomaterials, Brookhaven National Laboratory, Upton, NY 11973, USA
dMAPEX Center for Materials and Processes, University of Bremen, 28359 Bremen, Germany
First published on 19th November 2015
Abstract
We have studied the oxidation of the Ru(0001) surface by in situ microscopy during exposure to NO2, an efficient source of atomic oxygen, at elevated temperatures. In a previous investigation [Flege et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 165407], at O coverages exceeding 1 monolayer, using the combination of intensity–voltage (I(V)) low-energy electron microscopy (LEEM) and multiple scattering calculations for the (00) beam in the very-low-energy range (E ≤ 50 eV) we identified three surface components during the initial Ru oxidation: a (1 × 1)-O chemisorption phase, the RuO2(110) oxide phase, and a surface oxide structure characterized by a trilayer O–Ru–O stacking. Here, we use dark-field LEEM imaging and micro-illumination low-energy electron diffraction in the range of 100 to 400 eV to show that this trilayer phase is actually a RuO2(100)-(1 × 1) phase with possibly mixed O and Ru surface terminations. This identification rationalizes the thermodynamic stability of this phase at elevated temperatures and is consistent with the observation of catalytic activity of the phase in CO oxidation.
1 Introduction
The oxidation and surface chemistry of the late transition metals has attracted persistent interest in the last decades due to their widespread use in a variety of technological areas as, e.g., in corrosion protection and heterogeneous catalysis.1,2 One of the most prominent examples for the so-called pressure gap in catalysis research is the oxidation of CO over metallic ruthenium, which manifests itself in a very high catalytic activity at high (near-ambient) pressures and a very low catalytic activity at ultrahigh-vacuum (UHV) conditions. In model studies on Ru(0001) single crystals, this behavior has been traced back to the emergence of ruthenium oxide phases, and specifically the growth of RuO2(110) islands that were shown to efficiently catalyze the formation of CO2.3 This seminal result, proving that the metal oxide may be catalytically much more efficient than its metallic counterpart, stimulated numerous studies that have been dedicated to unraveling the oxidation characteristics and the oxidation pathway of ruthenium, from the metallic surface to the growth of the thin film oxide. An important realization is that this oxide phase does not occur at near-UHV O2 pressures, but appears after dosing at significantly elevated pressures only; the critical O2 pressure has recently been determined to 10−5 mbar.4 Consequently, to enable the use of surface science tools, many experiments have been devoted to understanding the static atomic and mesoscale structure of the oxygen-rich Ru(0001) surface after oxidation, partly also by using more effective and hence more UHV-compatible means of oxidation, e.g., suitable precursors to atomic oxygen or atomic O directly.5On the basis of a large number of studies, the following general picture of the oxidation pathway has evolved: after the initial oxygen uptake of the pristine Ru(0001) surface up to about one monolayer (ML) coverage, which can be accommodated in the outermost layer via an oxygen adlayer with (1 × 1) periodicity,6 further oxygen may only be incorporated in subsurface layers, which has been argued to occur in several ways. Malik and Hrbek brought forward the notion of a disordered incorporation in the near-surface region of the crystal without the formation of an ordered oxide structure.7 Based on density functional theory (DFT) calculations, Reuter and co-workers presented a scenario for a transformation with increasing oxygen coverage, from the (1 × 1)-O chemisorbed adlayer to a RuO2(110) surface oxide that was predicted to proceed via the formation of a metastable trilayer precursor phase.8 Experimental evidence, however, for this particular O–Ru–O trilayer structure has been quite elusive while similar intermediate trilayer structures have indeed been observed in the oxidation pathway of other late transition metals as, e.g., for Rh(111),9 Ir(111),10 and Pd(100).11,12
Previously, we presented an in situ study of the oxidation of the Ru(0001) surface by exposure to NO2, an efficient source of atomic oxygen,7 using intensity–voltage low-energy electron microscopy (I(V)-LEEM)13 carried out dynamically during exposure in combination with multiple scattering calculations.14 A key result was the identification of a “trilayerlike” surface oxide with O–Ru–O stacking that was found to coexist with the established (1 × 1)-O and RuO2(110) phases, which had previously been observed in a large number of investigations,5 over a wide range of gas-phase conditions. Yet, this trilayer-like oxide was never observed to transform into the RuO2(110) bulk-like oxide, quite in contrast to the scenario predicted by Reuter et al.8 Intriguingly, in subsequent experiments on CO oxidation the trilayerlike surface oxide was found to take part in the overall surface-catalyzed reaction by direct and spillover-mediated processes,14 adding an additional level of complexity to the hotly debated question regarding the nature of the active phase in CO oxidation.15–19 However, despite extensive efforts to address the nature of its apparent (2 × 2)-like lateral ordering, the atomic structure of the trilayerlike oxide was never completely resolved.
Here, we address the structure by the analysis of an extended I(V)-LEED data set within the framework of multiple scattering calculations and additional dark-field LEEM experiments, which directly link objects in real-space to crystallographic information from electron diffraction. We demonstrate that all available experimental data are consistently explained by the formation of a RuO2(100)-(1 × 1) thin-film oxide, which is found to be both intrinsically and extrinsically active in CO oxidation. This result is in contrast to the purely intrinsic activity of the RuO2(110) phase14 and sheds new light on the complex origin of the high activity of oxidized ruthenium surfaces in CO oxidation catalysis.
2 Experimental and computational details
The experiments have been performed in a commercial low-energy electron microscope (LEEM III, Elmitec) including an energy filter, formerly installed at beamline U5UA at the National Synchrotron Light Source (NSLS) at Brookhaven National Laboratory (BNL).20 The Ru(0001) crystal (Mateck) was cleaned by established procedures,14 essentially comprising repeated cycles of oxidation and subsequent flash-annealing. The oxidation experiments were performed at temperatures of 750 and 790 K; the sample was exposed to NO2 at partial pressures of 5 × 10−7 to 1 × 10−6 mbar, with total doses in the 1000 L range (a dose of 1 Langmuir (L) amounts to 1.33 × 10−6 mbar s). Simultaneously, the evolution of the surface structure and morphology was followed in situ using LEEM, which is able to record “live” images of the surface transformations at video rates. After completing the oxidation process, i.e., after pumping down to UHV conditions and considerably reducing the sample temperature, local structural information was obtained from micro-illumination low-energy electron diffraction (μLEED) acquired by confining the incident beam to an area of 1 μm in diameter. This μLEED capability is especially useful if, as in the case presented here, the surface composition is structurally inhomogeneous on the mesoscale, allowing independent determination of surface structure by diffraction techniques. Both LEEM and LEED data were processed with the GXSM software package developed by Zahl and co-workers.21The multiple scattering I(V)-LEED calculations have been performed using the newly developed AQuaLEED package22 that is based on existing Barbieri/Van Hove packages,23 which include the phase shift calculation package and the symmetrized automated tensor LEED (SATLEED) package. The layer doubling extension by Materer24 is also employed.
3 Results and discussion
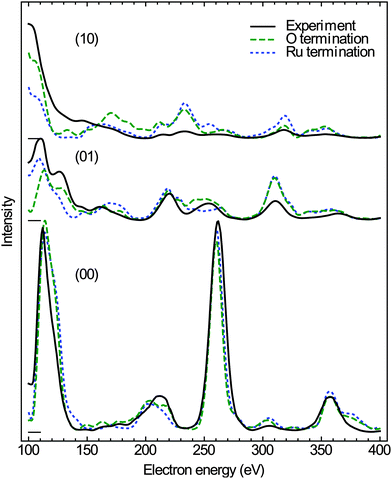
The evolution of the Ru(0001) surface upon exposure to NO2 is illustrated by the time-lapse LEEM sequence displayed in Fig. 1. Two RuOx phases are seen to independently grow from the (1 × 1)-O adlayer phase (light gray contrast), one consisting of anisotropic, needle-like islands and appearing in dark contrast while the other manifests itself as round, dark gray islands that first decorate the substrate step edges before nucleating on the terraces (Fig. 1b). After a NO2 dose of 760 L, virtually the whole O adlayer has been consumed by the growing RuOx phases (Fig. 1c). The needle-like islands have already been unambiguously identified14,25 as RuO2(110), whose characteristic integral LEED pattern (Fig. 2a) is a mixture of three single-domain, rectangular μLEED patterns as the one shown in Fig. 2b, which has been recorded by solely illuminating the encircled region “A” in Fig. 1c. | ||
| Fig. 1 (a)–(c) LEEM time-lapse sequence acquired during exposure of the Ru(0001) surface to NO2 at 750 K and p(NO2) = 1 × 10−6 Torr. The electron energy is 8.4 eV. In (c), the areas illuminated in the LEED experiments (Fig. 2b and c) are indicated by dashed yellow circles labeled “A” and “B”, respectively. | ||
 | ||
| Fig. 2 (a) Integral LEED pattern (55 eV) of the oxidized Ru(0001) surface after exposure to 760 L of NO2 at 750 K. (b) Single-domain LEED pattern (55 eV) of RuO2(110) recorded from the single dark island labeled “A” in Fig. 1c. The sharp LEED spots in (a) are the result of a superposition of three single-domain patterns rotated by 0 and ± 120°, respectively. (c) LEED pattern (55 eV) of the surface region labeled “B” in Fig. 1c. The (10) and (01) reflections of one rotational domain are marked exemplarily. (d) Schematic LEED pattern of the epitaxially grown RuO2(100) phase on Ru(0001) including 3 rotational domains (red, green, blue). The positions where the (1 × 1) substrate LEED spots would show up are marked by white circles. | ||
Comparing the μLEED pattern shown in Fig. 2c, which has been collected from region “B” in Fig. 1c, with the integral pattern displayed in Fig. 2a directly proves that the blurry diffraction spots must be attributed to the second, dark gray RuOx phase. In our previous publication,14 this hexagonal pattern was attributed to a (2 × 2)-ordered phase with a slightly stretched lattice constant, compatible with a trilayerlike, strain-relaxed surface oxide. In the following, we will show that this pattern actually originates from the coexistence of six rotational domains of epitaxial RuO2(100). A schematic LEED pattern for epitaxially grown RuO2(100) with the [001] direction oriented along the 〈2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0〉 high symmetry directions of the substrate is displayed in Fig. 2(d). From the comparison with the experimental pattern (Fig. 2c), it becomes clear that the azimuthally strongly broadened spots near the position of the (01) spots of Ru(0001) (not visible) are actually comprised of two diffuse, yet distinct (11) spots belonging to different rotational domains of RuO2(100).
0〉 high symmetry directions of the substrate is displayed in Fig. 2(d). From the comparison with the experimental pattern (Fig. 2c), it becomes clear that the azimuthally strongly broadened spots near the position of the (01) spots of Ru(0001) (not visible) are actually comprised of two diffuse, yet distinct (11) spots belonging to different rotational domains of RuO2(100).
The spatial distribution of the different rotational domains can very elegantly be visualized by dark-field LEEM when selectively employing three azimuthally rotated (01) LEED reflections (Fig. 2c) for imaging. Typically, dark-field imaging is performed by tilting the incident electron beam such that the desired LEED beam with non-vanishing parallel momentum transfer is reflected along the optical axis of the imaging column of the LEEM instrument. By introducing a suitable aperture into the beam path, only this beam is employed for image creation, and only those parts of the surface that contribute to this spatial frequency will show up bright in this dark-field image.26 In Ru oxidation, we have successfully used this approach to analyze the grain structure of the RuO2(110) islands,25,27 which yield stronger and sharper reflections than the RuO2(100) phase observed here.
The result of the dark-field experiment following oxidation by exposure to NO2 at 790 K is shown in Fig. 3. In the bright-field reference image (Fig. 3a), the chemisorbed O adlayer appears bright while the RuO2(110) and RuO2(100) phases are gray and black, respectively. Independent of the electron kinetic energy (4–100 eV), no contrast is observed within the (100) patches. Strikingly, however, in dark-field mode employing three azimuthally rotated (01) LEED reflections (Fig. 3b–d) a distinct contrast is observed within the islands, directly proving that they are composed of a “wheel-like” mixture of distinct rotational domains that all seem to originate from the center where the initial nucleation of the oxygen-rich phase took place. This is better visible in the zoomed images presented in Fig. 4.
The alternating contrast within the chemisorbed O adlayer evidences partial thermal reduction of the (1 × 1)-O phase and is rationalized as follows: the creation of O vacancies and their subsequent ordering induces the formation of the (2 × 2)-3O phase,28 which on individual Ru(0001) terraces may appear in three rotational domains rotated by ±120°. In LEED, this process leads to the emergence of additional half-order LEED spots so close to the (01) reflections of RuO2(100) that both beams may pass the contrast aperture unperturbed in a dark-field experiment. Due to the A/B stacking of hexagonally close-packed ruthenium, the substrate surface has only threefold rotational symmetry, and (2 × 2)-3O domains on adjacent terraces that are separated by monatomic steps will additionally be rotated by another 60°. At certain diffraction conditions, i.e., electron kinetic energies, this broken symmetry will cause the appearance of clearly threefold symmetric LEED patterns from individual terraces,29 consequently causing an alternating contrast on the adlayer terraces in dark-field LEEM if the individual terraces are predominantly covered by a single rotational domain. We also note that this (2 × 2)-3O phase can independently be identified by I(V)-LEEM analysis.30
After this re-assignment of the LEED spots of oxidized Ru(0001), we turn to the atomic structure of the RuO2(100) islands. For this purpose, we have performed an intensity–voltage (I(V)) LEED analysis, i.e., we have measured the variations in LEED spot intensities with electron energy and compared them to simulations for the RuO2(100) phase based on multiple scattering theory.31,32 The model surface structures have been optimized to fit the experimental I(V) data.
The experimental I(V)-LEED dataset, consisting of the (00), (01), and (10) diffracted beams of the surface oxide in the range of 100 to 400 eV, was acquired from area “B” of the oxidized surface with a diameter of about 1 μm (see Fig. 1c). For this purpose, the incident electron beam was confined to the selected region of interest by using an illumination aperture in the LEEM apparatus, thereby avoiding problems related to spherical aberrations of the objective lens in non-corrected low-energy electron microscopes.33
In the I(V) calculations, all the three possible surface terminations of truncated bulk RuO2(100), i.e., termination with a ruthenium layer, single oxygen layer, and a double oxygen layer, have been considered to account for potential surface reduction due to the elevated temperature during the measurements directly after oxidation. As the anticipated thickness of the oxide layer is about 2 nm, the calculations have been simplified by assuming an infinite depth of the RuO2 crystal, i.e., the influence of the ruthenium substrate has been neglected. The lattice parameters, measured from the composite diffraction pattern (Fig. 2a) using the known values of the RuO2(110) phase34 for calibration of reciprocal space, are c = 3.11 ± 0.01 Å and a∥ = 4.60 ± 0.03 Å, indicating that the oxide layer is slightly stretched along the y-direction with respect to bulk rutile RuO2 (space group P42/mnm), which exhibits lattice parameters of c0 = 3.106 Å and a0 = 4.493 Å.35 The distortion of the tetragonal lattice was accounted for by adjusting the vertical lattice parameter a⊥ = 4.42 Å according to the published Poisson ratio of 0.3236 in the calculations. Furthermore, the vibrational parameters (Debye temperatures) of RuO2 were estimated on the basis of literature data.37
The experimental data and the best-fit calculated I(V) curves using the experimental lattice parameters are compared in Fig. 5; the surface models and the best-fit surface relaxations are presented in Fig. 6 and 7, and the adjusted structural parameters are reproduced in Table 1. Interestingly, the ruthenium and the single O layer terminated surface structures yield almost the same Pendry R-factor38 of 0.23 ± 0.05, indicating a satisfactory match between theory and experiment in either case; the alternative oxygen-rich termination (O double layer) produced a significantly worse R-factor of 0.30 ± 0.06, from which we conclude that the actual structure, characterized after oxidation (i.e., at elevated temperature and thus reducing conditions) does not show such an oxygen-rich termination.
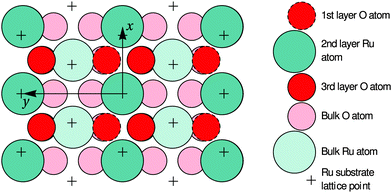 | ||
| Fig. 6 Top view of the optimized O-terminated RuO2(100) phase. The x and y axes are pointing along the [10] and [01] directions of the RuO2(100) surface, which are parallel to the [001] and [010] directions of bulk RuO2, respectively. The arrows demark the size of the surface unit cell. The first-layer O atoms are not present in the Ru-terminated phase; details regarding the slightly different surface relaxations are given in Table 1. | ||
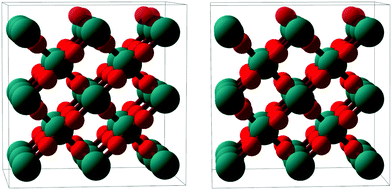 | ||
| Fig. 7 Stereoscopic image enabling a quasi-three dimensional view of a ball-and-stick model of the RuO2(100) phase (side view, roughly along the x axis). Ru atoms: larger teal balls; O atoms: smaller red balls. The top-most oxygen atoms, which are present only in the O-termination model, are rendered semi-transparent. The depicted surface relaxation corresponds to the optimized O-termination model; details regarding the Ru-terminated model are given in Table 1. | ||
| Atom | Initial position | O termination | Ru termination | ||||
|---|---|---|---|---|---|---|---|
| x | y | z | Δy | Δz | Δy | Δz | |
| O | 1.555 | 0.89 | 0.86 | −0.16 ± 0.36 | +0.10 ± 0.07 | — | — |
| Ru | 0 | 0 | 0 | +0.01 ± 0.12 | −0.01 ± 0.02 | +0.02 ± 0.14 | −0.02 ± 0.02 |
| O | 1.555 | 3.71 | −0.86 | +0.04 ± 0.17 | +0.05 ± 0.10 | +0.10 ± 0.16 | +0.10 ± 0.11 |
| O | 0 | 1.41 | −1.35 | — | — | +0.05 ± 0.25 | +0.05 ± 0.11 |
While our I(V) analysis does not allow a distinction between the Ru and the single-layer O terminations, it provides strong evidence that the assumption of a bulk-like RuO2(100) structure is indeed correct. The indistinguishability of the two terminations may simply result from the relatively small I(V) data base (cumulative range 900 eV) due to the limited number of diffraction spots accessible in the LEEM instrument. The small data base is also reflected by the relatively large uncertainties of the R-factors and structural (i.e. relaxation) parameters. It is also possible, however, that both terminations coexist, either in ordered subdomains or a disordered manner, reflecting the reducibility of this oxide phase. The azimuthal smearing of the LEED spots indicates the presence of different registries to the substrate, which might likely induce different levels of strain in the thin-film oxide depending on azimuthal orientation, potentially further affecting its reducibility.
The identification of the surface oxide as RuO2(100)-(1 × 1) also serves to elucidate and reconcile its previously stated catalytic behavior14 with the present state of knowledge. In oxidation catalysis involving reducible oxides, a likely scenario is the Mars–van Krevelen type mechanism in which the substrate is repeatedly reduced by the reactant and sequentially reoxidized by the oxygen supplied from the gas phase.39 Our I(V)-LEED results suggest that the reducibility of the RuO2(100)-(1 × 1) phase is directly linked to the facile removal (and replenishment) of the top-most oxygen layers, very similar to the stripping of the bridging O atoms on the RuO2(110) surface found upon reduction by CO.40,41 Thus, our present identification of the RuO2(100)-(1 × 1) phase and our previous14 observation of reduction of the surface oxide during CO exposure and subsequent re-oxidation by O2 exposure are consistent and indicate a surface Mars–van Krevelen type mechanism in which the oxygen vacancies in the near-surface layers are healed upon reoxidation in the second catalytic half-cycle. Furthermore, this interpretation is also in agreement with other findings from the literature since the unreconstructed RuO2(100) phase is actually known to exhibit a similar catalytic activity as the (110) phase.5 It is very interesting, however, to realize that the previously identified cooperative effect14 in the oxidation of CO is now clearly identified as oxygen spillover from the RuO2(100) patches to the O chemisorption phase. So far, no such evidence has been presented for the existence of a similar effect of the RuO2(110) phase, rendering this study the first observation that the occurrence of spillover may critically depend on the particular surface orientation of the oxide and the structure of the inter-phase boundary.
In the following paragraphs, we address the structural implications when using O2 or NO2 as oxidants in Ru(0001) oxidation experiments. During both O2 and NO2 exposure, the RuO2(100) phase is found to nucleate first among the oxygen-rich phases and preferentially at step bunches or other line defects whereas the growth of other RuO2 orientations is subsequently found following secondary nucleation events in adjacent areas.14,42 This similarity in oxidation behavior for O2 and NO2 indicates that the initial nucleation step is not significantly influenced by the oxidation kinetics, which is largely governed by the need to overcome the activation barrier for dissociation of the O2 molecule, but by thermodynamics instead: the enhanced stability of the RuO2(100) orientation is very likely due to the formation of a coincidence lattice at the metal–oxide interface in which the [010] direction of the oxide roughly matches twice the row spacing (2.34 Å) in the 〈1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 00〉 directions of the underlying Ru(0001) substrate, as revealed by closer analysis of Fig. 6. The enhanced stability of the (100) oriented RuO2 surface oxide is also consistent with observations that show a transformation of RuO2(110) into RuO2(100) once the O adlayer phase has been completely consumed.14 This transformation process, which was not easily understandable in the trilayer model, results in an apparent roughening of the lateral shape of the RuO2(110) needle-like islands already at 750 K, which is apparent when comparing their boundaries in Fig. 1b and c: whereas the edges between the (110) oxide islands and the O adlayer phase are smooth, they become increasingly jagged and ill-defined with further NO2 exposure once the adlayer has vanished locally. As the changes in the oxide morphology are less pronounced at 750 K than at 810 K, the extent of this transition from the (110) to the (100) phase clearly depends on temperature, rendering this phase transformation a thermally activated process.
00〉 directions of the underlying Ru(0001) substrate, as revealed by closer analysis of Fig. 6. The enhanced stability of the (100) oriented RuO2 surface oxide is also consistent with observations that show a transformation of RuO2(110) into RuO2(100) once the O adlayer phase has been completely consumed.14 This transformation process, which was not easily understandable in the trilayer model, results in an apparent roughening of the lateral shape of the RuO2(110) needle-like islands already at 750 K, which is apparent when comparing their boundaries in Fig. 1b and c: whereas the edges between the (110) oxide islands and the O adlayer phase are smooth, they become increasingly jagged and ill-defined with further NO2 exposure once the adlayer has vanished locally. As the changes in the oxide morphology are less pronounced at 750 K than at 810 K, the extent of this transition from the (110) to the (100) phase clearly depends on temperature, rendering this phase transformation a thermally activated process.
Lastly, we address the influence of the oxidant on the oxide morphology. At the same oxidation temperature, the relative surface coverage of the (100) versus the (110) orientation is considerably higher for oxidation by NO2. The strong preference for the RuO2(110) orientation when oxidizing with O2 in a temperature range of about 600 to 700 K is most probably related to the previously identified autocatalytic growth of RuO2(110) due to the strongly enhanced probability of O2 dissociation at the growing oxide surface,34 which has been estimated to be around 70%.43 Such a strongly enhanced dissociative sticking coefficient for O2 has not yet been identified for RuO2(100), whose nucleation therefore is limited by the local amount of atomic oxygen. This qualitative picture is consistent with the observation that for oxidation by O2 the nucleation and growth of the RuO2(100) orientation is predominantly found at step bunches or grain boundaries,42 where O2 dissociation and incorporation is known to be more effective. At similar oxidation temperatures, however, this precondition is not necessary in the oxidation from NO2, in which case atomic O is supplied effectively.25 Finally, we note that the depicted scenario is also in qualitative agreement with the findings for electrochemical oxidation of the Ru(0001) surface, which is a rather aggressive form of oxidation and which induces the formation of small RuO2(100) islands already at room temperature.44
4 Conclusions
We have revisited the oxidation of the Ru(0001) surface by exposure to NO2 at elevated temperatures. By close re-examination of previously reported LEED data14 together with new results of additional in situ dark-field LEEM and I(V)-μLEED experiments, the structure and morphology of the previously identified O–Ru–O stacked trilayer phase14 could unambiguously be resolved as an unreconstructed RuO2(100) surface oxide occurring in six rotational domains with possible structural disorder. This finding reconciles the observed growth behavior, notably the lack of transformation between the previously assumed trilayer and the RuO2(110) bulk oxide, and the catalytic activity with results from other authors in the literature. Furthermore, new light is shed on the oxidation pathway and catalytic activity of Ru(0001) in CO oxidation, allowing the following two more far-reaching conclusions: first, in terms of materials design by oxidation routes, our results clearly demonstrate that the choice of oxidant strongly influences the resulting structure and morphology, providing a convenient handle for finetuning the target material. The applicability of this kinetic effect is expected to directly translate to other materials systems and oxidation processes sufficiently governed by kinetics. Incidentally, a similar approach has very recently been followed for improving the catalytic activity of the related Pd(111) system, where surface modification by pre-oxidation at higher temperatures enabled efficient and sustainable CO oxidation at room temperature.45 Second, our results demonstrate an unprecedented structure sensitivity in oxygen spillover from the RuO2 islands to the Ru metal, which for the present RuO2/Ru(0001) system was shown to depend on the specific surface orientation of the oxide, rendering the (100) orientation spillover-active and the (110) orientation spillover-inactive. This finding is a direct manifestation of the importance of precise interfacial structure and control at the (in this case planar) phase boundary in surface chemistry and oxidation catalysis.Acknowledgements
Research carried out in part at the National Synchrotron Light Source and the Center for Functional Nanomaterials, Brookhaven National Laboratory, which are supported by the U. S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-98CH10886. The authors also gratefully acknowledge support from the European COST Action CM1104. The software utility LEEDpat, Version 4.1, (C) K. E. Herrmann (FHI Berlin) and M. A. Van Hove (Baptist University Hong Kong) was used in the evaluation of the data; see also http://www.fhi-berlin.mpg.de/KHsoftware/LEEDpat/index.html. J. L. thanks K. Pussi for helpful suggestions.References
- K. Reuter, Nanometer and Subnanometer Thin Oxide Films at Surfaces of Late Transition Metals, in Nanocatalysis, ed. U. Heiz and U. Landman, Springer, Berlin, Heidelberg, New York, 1st edn, 2007, pp. 343–376 Search PubMed.
- J. F. Weaver, Chem. Rev., 2013, 113, 4164–4215 CrossRef CAS PubMed.
- H. Over, Y. D. Kim, A. P. Seitsonen, S. Wendt, E. Lundgren, M. Schmid, P. Varga, A. Morgante and G. Ertl, Science, 2000, 287, 1474–1476 CrossRef CAS PubMed.
- B. Herd, M. Knapp and H. Over, J. Phys. Chem. C, 2012, 116, 24649–24660 CAS.
- H. Over, Chem. Rev., 2012, 112, 3356–3426 CrossRef CAS PubMed.
- C. Stampfl, S. Schwegmann, H. Over, M. Scheffler and G. Ertl, Phys. Rev. Lett., 1996, 77, 3371 CrossRef CAS PubMed.
- I. J. Malik and J. Hrbek, J. Vac. Sci. Technol., A, 1992, 10, 2565–2569 CAS.
- K. Reuter, M. V. Ganduglia-Pirovano, C. Stampfl and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165403 CrossRef.
- J. Gustafson, A. Mikkelsen, M. Borg, E. Lundgren, L. Köhler, G. Kresse, M. Schmid, P. Varga, J. Yuhara, X. Torrelles, C. Quirós and J. N. Andersen, Phys. Rev. Lett., 2004, 92, 126102 CrossRef CAS PubMed.
- Y. B. He, A. Stierle, W. X. Li, A. Farkas, N. Kasper and H. Over, J. Phys. Chem. C, 2008, 112, 11946–11953 CAS.
- M. Todorova, E. Lundgren, V. Blum, A. Mikkelsen, S. Gray, J. Gustafson, M. Borg, J. Rogal, K. Reuter, J. Andersen and M. Scheffler, Surf. Sci., 2003, 541, 101–112 CrossRef CAS.
- E. Lundgren, J. Gustafson, A. Mikkelsen, J. N. Andersen, A. Stierle, H. Dosch, M. Todorova, J. Rogal, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2004, 92, 046101 CrossRef CAS PubMed.
- J. I. Flege and E. E. Krasovskii, Phys. Status Solidi RRL, 2014, 8, 463–477 CrossRef CAS.
- J. I. Flege, J. Hrbek and P. Sutter, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 165407 CrossRef.
- R. Blume, M. Hävecker, S. Zafeiratos, D. Teschner, E. Kleimenov, A. Knop-Gericke, R. Schlögl, A. Barinov, P. Dudin and M. Kiskinova, J. Catal., 2006, 239, 354–361 CrossRef CAS.
- D. W. Goodman, C. H. F. Peden and M. S. Chen, Surf. Sci., 2007, 601, L124 CrossRef CAS.
- H. Over, M. Muhler and A. P. Seitsonen, Surf. Sci., 2007, 601, 5659–5662 CrossRef CAS.
- Ž. Šljivančanin and B. Hammer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 121413 CrossRef.
- F. Gao and D. W. Goodman, Phys. Chem. Chem. Phys., 2012, 14, 6688–6697 RSC.
- J. I. Flege, E. Vescovo, G. Nintzel, L. H. Lewis, S. Hulbert and P. Sutter, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 261, 855–858 CrossRef CAS.
- P. Zahl, T. Wagner, R. Möller and A. Klust, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 2010, 28, C4E39–C4E47 CAS.
- J. Lachnitt and D. Mazur, in preparation.
- A. Barbieri and M. A. V. Hove, private communication, http://www.icts.hkbu.edu.hk/vanhove/.
- N. F. Materer, Surf. Sci., 2001, 491, 131–139 CrossRef CAS.
- J. I. Flege and P. Sutter, J. Phys.: Condens. Matter, 2009, 21, 314018 CrossRef CAS PubMed.
- J. I. Flege, W. X. Tang and M. S. Altman, in Low-Energy Electron Microscopy, ed. E. N. Kaufmann, John Wiley & Sons, Inc., 2012 Search PubMed.
- J. Goritzka, B. Herd, P. P. T. Krause, J. Falta, J. I. Flege and H. Over, Phys. Chem. Chem. Phys., 2015, 17, 13895–13903 RSC.
- K. L. Kostov, M. Gsell, P. Jakob, T. Moritz, W. Widdra and D. Menzel, Surf. Sci., 1997, 394, L138–L144 CrossRef CAS.
- J. de la Figuera, J. Puerta, J. Cerda, F. E. Gabaly and K. McCarty, Surf. Sci., 2006, 600, L105–L109 CrossRef CAS.
- E. E. Krasovskii, J. Höcker, J. Falta and J. I. Flege, J. Phys.: Condens. Matter, 2015, 27, 035501 CrossRef CAS PubMed.
- J. B. Pendry, Low Energy Electron Diffraction: The Theory and Its Application to Determination of Surface Structure, Academic Press, London, 1974 Search PubMed.
- M. A. Van Hove, W. H. Weinberg and C.-M. Chan, Low-Energy Electron Diffraction, Springer, Berlin, Heidelberg, 1986, vol. 6, pp. 145–204 Search PubMed.
- R. M. Tromp, Ultramicroscopy, 2012, 120, 73–77 CrossRef CAS PubMed.
- Y. B. He, M. Knapp, E. Lundgren and H. Over, J. Phys. Chem. B, 2005, 109, 21825 CrossRef CAS PubMed.
- J. Haines, J. M. Léger, O. Schulte and S. Hull, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1997, 53, 880–884 Search PubMed.
- N. Mehtougui, D. Rached, R. Khenata, H. Rached, M. Rabah and S. Bin-Omran, Mater. Sci. Semicond. Process., 2012, 15, 331–339 CrossRef CAS.
- K.-I. Murai, Y. Akune, Y. Suzuki, T. Moriga and I. Nakabayashi, Int. J. Mod. Phys. B, 2006, 20, 4111–4116 CrossRef CAS.
- J. B. Pendry, J. Phys. C: Solid State Phys., 1980, 13, 937–944 CrossRef CAS.
- P. Mars and D. W. V. Krevelen, Chem. Eng. Sci., 1954, 3, 41–59 CrossRef CAS.
- C. Y. Fan, J. Wang, K. Jacobi and G. Ertl, J. Chem. Phys., 2001, 114, 10058–10062 CrossRef CAS.
- A. P. Seitsonen, Y. D. Kim, M. Knapp, S. Wendt and H. Over, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035413 CrossRef.
- J. I. Flege, B. Herd, J. C. Goritzka, H. Over, E. E. Krasovskii and J. Falta, ACS Nano, 2015, 9, 8468–8473 CrossRef CAS PubMed.
- H. Over and M. Muhler, Prog. Surf. Sci., 2003, 72, 3–17 CrossRef CAS.
- W. F. Lin, M. S. Zei, Y. D. Kim, H. Over and G. Ertl, J. Phys. Chem. B, 2000, 104, 6040–6048 CrossRef CAS.
- C. S. Gopinath, K. Roy and S. Nagarajan, ChemCatChem, 2015, 7, 588–594 CrossRef CAS.
Footnote |
| † Present address: Department of Electrical and Computer Engineering, University of Nebraska-Lincoln, Lincoln, NE 68588, USA. |
| This journal is © the Owner Societies 2016 |