Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural, electronic, magnetic and chemical properties of B-, C- and N-doped MgO(001) surfaces
Igor A.
Pašti
*a and
Natalia V.
Skorodumova
bc
aUniversity of Belgrade, Faculty of Physical Chemistry, Studentski trg 12-16, 11158 Belgrade, Serbia. E-mail: igor@ffh.bg.ac.rs; Fax: +381 11 2187 133; Tel: +381 11 3336 628
bDepartment of Materials Science and Engineering, School of Industrial Engineering and Management, KTH – Royal Institute of Technology, Brinellvägen 23, 100 44 Stockholm, Sweden
cDepartment of Physics and Astronomy, Uppsala University, Box 516, 751 20 Uppsala, Sweden
First published on 20th November 2015
Abstract
Doping of simple oxide materials can give rise to new exciting physical and chemical properties and open new perspectives for a variety of possible applications. Here we use density functional theory calculations to investigate the B-, C- and N-doped MgO(001) surfaces. We have found that the investigated dopants induce magnetization of the system amounting to 3, 2 and 1 μB for B, C and N, respectively. The dopants are found to be in the X2− state and tend to segregate to the surface. These impurity sites also present the centers of altered chemical reactivity. We probe the chemisorption properties of the doped MgO(001) surfaces with the CO molecule and atomic O. The adsorption of CO is much stronger on B- and C-doped MgO(001) compared to pure MgO(001) as the impurity sites serve as potent electron donors. The situation is similar to the case of atomic oxygen, for which we find the adsorption energy of −8.78 eV on B-doped MgO(001). The surface reactivity changes locally around the dopant atom, which is mainly restricted to its first coordination shell. The presented results suggest doped MgO as a versatile multifunctional material with possible use as an adsorbent or a catalyst.
1. Introduction
Constant search for materials with desired properties is one of the tasks of contemporary materials science and the basis for advancement of modern technologies. Tailoring materials properties to applications is one of the strategies for this search, which led to successful development of novel materials over the years. In particular, tuning surfaces by introducing defects,1 surface overlayers2,3 or doping4,5 gave rise to outstanding new properties compared to those of unmodified materials.In general, the variability of the surface properties of metal oxides makes them useful for different research fields and technological areas, such as, energy conversion,6 chemical sensors and environmental monitoring,7 ceramics,8 corrosion,9 catalysis10,11 and others. For example, due to its simple rock salt structure, strong ionic bonding, small surface relaxation, simplicity in preparation and good chemical stability magnesium oxide is widely used in surface science. Moreover, the magnesia surface displays rather poor reactivity even in reactions with atomic species,12 which makes it a good catalyst support for numerous catalytic reactions.10,11,13–15 On the other hand, the properties of the MgO surface can be modified, when required, by introducing defects or impurities,16–19 or an underlying metal substrate.20–23
Recently, d0 magnetism has been demonstrated for N-doped MgO.24,25 Grob et al. produced N-doped MgO films on the Mo substrate and confirmed such a behavior.26 Additionally, theoretical calculations based on density functional theory (DFT) suggest that N tends to exchange places with O in the MgO lattice.26 Pesci et al. provided a detailed theoretical description of N-doped bulk MgO using DFT and suggested that the formation of substitutional and interstitial N sites in MgO depended on oxygen concentration and other conditions during preparation.27 The theoretical work by Shein et al. also predicted the appearance of magnetization in the case of C-doped multi-walled MgO nanotubes assuming C → O substitution.28 In fact, the authors suggested that magnetism will appear if the valence orbitals of a dopant lie above the occupied O 2p band of the matrix, and proposed B, C and N as possible dopants for the production of the MgO-based magnetic materials.28 Also, Kenmochi et al. indeed considered B-, C- and N-doped CaO as a new class of diluted magnetic semiconductors.29
In this paper we report our results on the MgO(001) surface doped with B, C and N. We analyze the electronic properties of such surfaces, tendency to surface segregations and appearance of magnetism in these systems. Moreover, knowing that doping of MgO can significantly alter its reactivity30 we probe the chemisorption properties of the doped MgO(001) surfaces towards molecular and atomic adsorption using the CO molecule and atomic O.
2. Computational details
The calculations were based on DFT within the generalized gradient approximation (Perdew–Burke–Ernzerhof exchange–correlation functional31). The calculations were performed using the Quantum ESPRESSO ab initio package32 using ultrasoft pseudopotentials where only the s- and p-states of all atoms were treated as the valence states. The kinetic energy cutoff for the plane-wave basis set was 28 Ry and the charge density cutoff was 16 times higher, for all the calculations. Spin polarization was taken into account for all the investigated systems. The calculated equilibrium lattice constant was 4.22 Å, in good agreement with the experimental value of 4.21 Å.33 The MgO(001) surface was modeled by a 2 × 2 four layer thick slab, which had eight magnesium and eight oxygen atoms per atomic layer. One dopant atom per simulation cell was introduced, thus giving the total dopant concentration of 1.56 at%. The concentration in the layer was 12.5% and the distance between the dopant and its image was 8.44 Å. All the atoms in the MgO(001) slab were relaxed, except for the first bottom layer which was fixed during geometry optimization. The first irreducible Brillouin zone was integrated using a 4 × 4 × 1 Monkhorst–Pack grid.34 A Gaussian smearing procedure, with the broadening of 0.007 Ry, was applied. The surface slabs were separated by a vacuum region of 18 Å. The dipole correction was added to prevent any interactions along the z direction.35 The charge transfer was analyzed using the Bader algorithm36 on a charge density grid by Henkelman et al.37In order to address the energetics of the replacement of oxygen in the MgO lattice with a dopant X (X = B, C or N; we shall use “X” hereafter to denote the dopant atoms) we define the substitution energy (Esub(X)) as
| Esub(X) = (EX–MgO + EO) − (EMgO + EX) | (1) |
| Eb(X) = EX–MgO − (Ev–MgO + EX) | (2) |
In this work we also address the chemisorption properties of the X-doped MgO(001) surface towards CO and atomic O. The chemisorption of a given adsorbate A is quantified here as the adsorption energy (Eads(A)) defined as
| Eads(A) = EX–MgO+A − (EX–MgO + EA) | (3) |
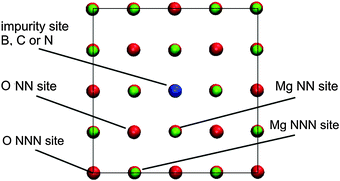 | ||
| Fig. 1 Notation of the adsorption sites at the doped MgO(001) surface within the simulation supercell (NN – Nearest Neighbour, NNN – Next Nearest Neighbor). Graphical presentation was made using the VMD code.38 | ||
3. Results
3.1. Structural, electronic and magnetic properties of X-doped (X = B, C, N) MgO(001)
A surface structure of an oxide can be characterized by relaxation and rumpling parameters. The surface relaxation parameter (δd12, in %) can be defined as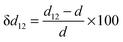 | (4) |
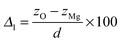 | (5) |
Next we turn to doped MgO(001). We look at the case of substitutional doping when B, C or N replace an O atom in the surface layer or subsurface layer of the MgO(001) slab. By comparing the total energies of doped MgO(001) for the two different dopant positions (Fig. 2, insets A and B), we observe that all the three dopants prefer to be in the surface layer (Fig. 2, inset A). This indicates a tendency of dopants to segregate on the surface, while the energy cost for placing X into the subsurface layer of MgO(001) decays as X approaches oxygen in the Periodic Table of Elements (PTE).
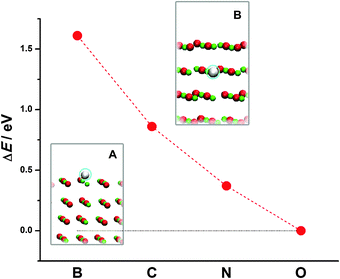 | ||
| Fig. 2 Energy cost for the exchange of X between the surface (structure A) and the subsurface layer of MgO(001) (structure B). | ||
The formation of X-doped MgO(001) can be considered either as the replacement of oxygen with atom X or as the adsorption of atom X at a vacancy site. In the first case, a large energy input is required to replace O with X and it decays as X approaches O in the PTE (Table 1). Hence, healing of the surface vacancy site with oxygen will be preferred over healing with B, C or N. However, if looking at the formation of X–MgO(001) upon the adsorption of X at the O vacancy, this process is followed by deliberation of large amounts of energy (Table 1). As the adsorption of X at an O vacancy site is more exothermic than adsorption on the MgO(001) terrace,12 the investigated dopants are expected to be entrapped by vacancies when no oxygen is available to heal the surface. This agrees with the results of Pesci et al. who suggested that the substitutional doping of MgO with N can be realized under oxygen-poor conditions.26
| Dopant X | E sub(X)a/eV | E b(X)b/eV | Δ X/% | d(X–Mg)/Å | d(X–O)/Å | M/μB | M X/μB | Q X/e |
|---|---|---|---|---|---|---|---|---|
| a Subsitution energy according to eqn (1). b Binding of X at the O vacancy site according to eqn (2). c Corresponds to pristine MgO(001). | ||||||||
| B | 5.91 | −3.46 | 42.2 | 2.37 | 3.17 | 3 | 2.20 | 1.97 |
| C | 4.29 | −5.08 | 19.3 | 2.23 | 3.02 | 2 | 1.62 | 1.98 |
| N | 3.89 | −5.48 | 10.8 | 2.16 | 3.04 | 1 | 0.88 | 1.99 |
| Oc | 0 | −9.37 | 0.05 | 2.11 | 2.99 | 0 | 0 | 1.99 |
Here we can conclude that the adsorption of the investigated elements at the O vacancy site becomes more exothermic as the position of the doping element in the PTE approaches that of oxygen. The adsorption of an O atom at an O vacancy site restores perfect MgO(001) and Eb(O), in this case, equals −9.37 eV. This process is actually reversed to the vacancy formation and its energy balance is in good agreement with the results of Carrasco et al. who found the surface vacancy formation energy to be in the range of 9.31–9.42 eV, depending on the number of MgO layers in the surface model.43 For comparison, we estimate the formation energy of the subsurface vacancy to be 9.87 eV, which is identical to the results of Carrasco et al. for the 3-layer MgO(001) slab.43 The same authors estimated this quantity to be 9.97 eV using the 12 layer model. The preference for the lower coordinated surface sites, observed for the investigated dopants, is in line with the results reported for C-doped MgO nanotubes.28 This preference is not due to the difference between the formation energies of the surface and the subsurface oxygen vacancies. When we calculated the interaction energy between dopant X and the subsurface vacancy, we saw that it was always smaller compared to the interaction with the surface vacancy site.
To characterize the impurity site, we define the vertical shift of atom X as
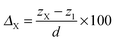 | (6) |
The dopant atoms induce the magnetization of the system mostly at the impurity site. The total magnetization (Table 1) decays from 3 μB (B-doping) to 2 μB (C-doping) and to 1 μB (N-doping). For C and N magnetization matches the one observed in the cases of the adsorption of these atoms on perfect MgO(001).12 For boron the situation is different as the magnetic moment is 3 μB in the case of substitution and 1 μB in the case of adsorption. However, if the magnetization of B-doped MgO(001) is forced to 1 μB the energy of the system increases by 0.44 eV. The difference is even greater (1.59 eV) for subsurface B-doping. Moreover, the magnetic solutions for X-doped MgO(001) are significantly more stable than non-magnetic ones, with the energy difference amounting to 0.66, 0.88 and 0.39 eV for B-, C-, and N-doped MgO, respectively.
The analysis of Bader charges shows that in all the considered cases nearly 2 electrons are transferred to the dopant atoms (Table 1) indicating that the dopants are in the X2− state. Even though B, C and N have lower electronegativity compared to O it is still sufficient to attract the valence electrons of Mg atoms. When a dopant atom receives electrons from neighboring Mg atoms its electron shell expands. As B has a smaller core charge than C and N, for the same amount of donated charge its electron shell will expand more. Considering atoms/ions in MgO as touching spheres the ionic radii of B, C and N in doped MgO(001) can be estimated as 1.675, 1.615 and 1.545 Å, respectively, all of them being larger than that of O2− in MgO (1.499 Å). These considerations offer a simple explanation of the tendency of the dopant atoms to prefer the surface layer of MgO(001). As X2− ions are larger compared to O2−, their introduction into the MgO lattice induces larger strain when placed into subsurface layers, therefore, their migration to the surface layer brings some strain relief. To check this assumption we calculated the deformation energy of the MgO lattice when a dopant is placed into the surface or the subsurface layer (Fig. 3). The deformation energy (ΔE) is calculated here as the difference between the energy of the relaxed X-doped MgO(001) surface when the dopant atom is removed and the corresponding energy when the O atom is removed from pristine MgO(001) (from the surface or subsurface layer). The deformation energy is smaller for the surface doped structures than that for the subsurface ones and it decreases as the ionic radius of the dopant approaches the ionic radius of an O2− ion.
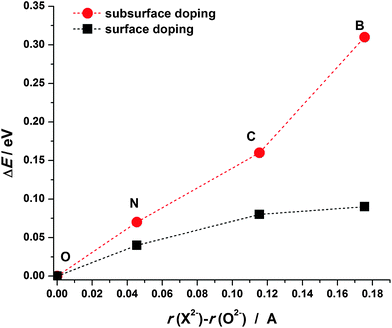 | ||
| Fig. 3 Deformation energy of the MgO lattice (ΔE) upon the incorporation of the investigated dopants into the surface vacancy (squares) and the subsurface vacancy (circles). | ||
The observed charge transfer also provides an intuitive explanation for the observed magnetization. Formally, when boron (which has one unpaired electron) receives 2 electrons, the total number of unpaired electrons becomes 3 that matches the observed magnetization of the system. In the case of nitrogen, the electron transfer induces electron pairing and only one unpaired electron is left (M = 1 μB). This is, of course, a rather simplified view, but it is clear that the magnetic moment is not associated with the charge transfer but the occupancy of the dopant band. The magnetization calculated by us agree well with those provided by Shein et al. for the C-doped triple-walled square-prismatic MgO nanotube28 as well as with the calculations of Grob et al.26 for N-doped MgO. Considering our results and the ones published so far one can conclude that the rise of magnetization is rather localized to the impurity site. For C-doped MgO nanotubes the atomic magnetic moments of the C atoms at the surface are 1.815–1.682 μB,28 while we found 1.62 μB for the carbon dopant using Löwdin population analysis.44,45 The magnetization of the system is then complemented to an integer number by the contributions of dopant neighbors. Such a behavior is clearly evident from the spin density maps (Fig. 4, right), which show that magnetization is localized at the dopant atom. In the case of subsurface doping we also observe that the atomic magnetic moments of the dopants in these systems are slightly smaller than those found for surface doping, which is also in agreement with available reports.28
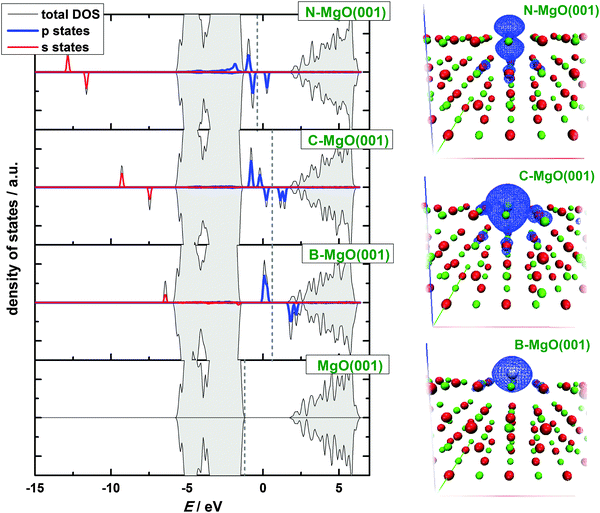
Inspecting the electronic structures of X-doped MgO(001) (Fig. 4), one can see that the magnetization of the systems is due to the partially filled p states of dopants situated in the band gap of MgO(001). The spin up p states of the dopant atoms are filled, while the spin down states are partially unoccupied, giving rise to the magnetization of the system (Fig. 4). This agrees with the observation of ref. 28. The calculated electronic structure of N-doped MgO(001) qualitatively agrees with the results of Grob et al. for N-doped MgO.26 The quantitative differences between our results are due to different levels of theory, which have been applied. Namely, in ref. 26 the DFT+U approach has been used. The calculated electronic structure of N–MgO(001) also qualitatively agrees with the one given in Ref. 27 for the case of substitutional N2− in bulk MgO for the identical concentration of N as considered here. Our results suggest that the investigated substitutionally doped MgO(001) surfaces retain the insulating nature of parental MgO(001), in spite of the fact that the applied GGA-PBE approach underestimates the band gap significantly (calculated value of the band gap is 2.9 eV) compared to experimental values. Namely, electron-energy-loss spectroscopy determined the gap of 6.15–6.2 eV,46 while the value of 7.8 eV was found from the electronic spectrum of single-crystal MgO.47
In order to visualize the 2p band of the dopants we have plotted the Integrated Local Densities of States (ILDOS, Fig. 5). These bands are indeed located mostly at the dopant sites, with a very small contribution of the nearest O atoms. In the case of B and C doping, the 2p states have nearly spherical symmetry around the dopant atom. In the case of N, however, ILDOS has a donut shape oriented in the (001) surface plane. The spherical symmetry of the 2p states for the case of C doping was also observed in ref. 28.
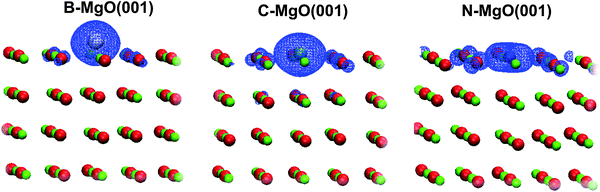 | ||
| Fig. 5 3D ILDOS maps of filled X 2p like bands for the cases of B-doped (left), C-doped (middle) and N-doped MgO(001) (right). The total ILDOS between the MgO valence band and the highest occupied state are given and the width of the energy window chosen for integration depends on the type of X-doped MgO(001) (see Fig. 4). | ||
At the end of this section it is important to address potential ferromagnetic ordering in this class of materials. Pesci et al.27 suggested that a high degree of spin localization may hinder the formation of ferromagnetic order at room temperature. On the other hand, Gross et al.26 demonstrated that the N-doped MgO(001) film on Mo acts as a ferromagnetic d0 insulator.
3.2. Molecular adsorption on X-doped (X = B, C, N) MgO(001): the CO case
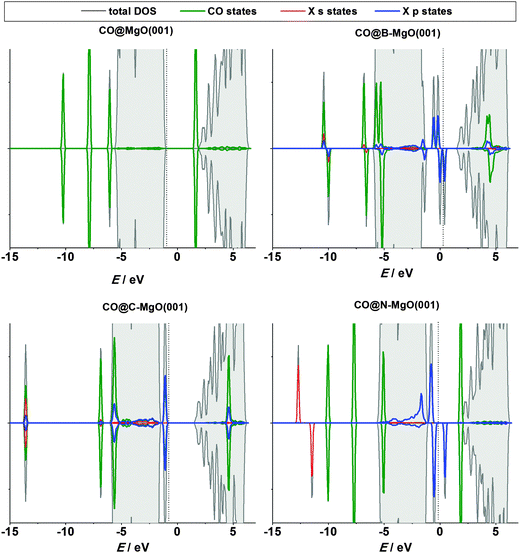
As B, C and N incorporated into the MgO(001) surface have a number of unpaired electrons they can be in a sense regarded as radical species. Hence, these impurity sites can be centers of altered reactivity which might open a possibility of using such doped surfaces as adsorbents, catalysts, and so on. The pure MgO(001) surface is non-magnetic and rather inert. The question we want to answer here is whether the reactivity of the surface can be tuned by the introduction of the investigated impurities.First we consider the CO/MgO(001) system, which attracted a lot of attention as being problematic for conventional DFT, requiring a special treatment and being looked at as a benchmark for the development of advanced theoretical methods.48 Bonding of CO to MgO(001) is rather weak and the dispersion interaction contributes significantly to the adsorption energy.49 Experimentally, it has been found that CO interacts with the Mg sites of the MgO(001) surface with the adsorption energy of −0.13 eV,50 which qualifies the C–MgO(001) interaction as physisorption. Here we found the adsorption energy of −0.16 eV (Table 2), in good agreement with the experimental value, theoretical studies applying a similar level of theory10 as well as the computational study of Civalleri et al.51 who applied modified B3LYP hydrid functionals to account for the dispersion interaction. When CO is bonded to the Mg site the C–O bond remains practically the same as in an isolated CO molecule, while the distance between the Mg center and the C atom is 2.43 Å (Table 2). The latter value is slightly smaller compared to those published previously, 2.489–2.578 Å, varying depending on the level of theory.51 Using the Bader analysis we observed a small charge transfer to the CO molecule (0.09 e). For comparison, in ref. 10 0.10 e was found to be transferred to the CO molecule.
| Ads. site | System | E ads(CO)/eV | d(C–O)/Å | d(C–Su)a/Å | M/μB | ΔQCO/e |
|---|---|---|---|---|---|---|
| a Su denotes surface atom at the CO adsorption site. b Repulsive interaction. c Not stable, relaxes to the impurity site. | ||||||
| Mg site | CO@MgO(001) | −0.16 | 1.14 | 2.43 | 0 | 0.09 |
| Impurity site | CO@B–MgO(001) | −3.40 | 1.19 | 1.43 | 1 | 1.83 |
| CO@C–MgO(001) | −5.08 | 1.20 | 1.31 | 0 | 2.27 | |
| CO@N–MgO(001) | 0b | 1.14 | >3.5 | 1 | 0.00 | |
| Mg NN site | CO@B–MgO(001) | nsc | — | — | — | — |
| CO@C–MgO(001) | nsc | — | — | — | — | |
| CO@N–MgO(001) | −0.17 | 1.15 | 2.43 | 1 | 0.10 | |
| Mg NNN site | CO@B–MgO(001) | −0.19 | 1.14 | 2.47 | 3 | 0.08 |
| CO@C–MgO(001) | −0.16 | 1.14 | 2.44 | 2 | 0.09 | |
| CO@N–MgO(001) | −0.15 | 1.14 | 2.45 | 1 | 0.09 | |
Now, let us turn to the CO chemisorption on X-doped MgO(001). The interaction of the CO molecule with B- and C-doped MgO(001) is mediated by the impurity site, the preferred one for bonding CO (Table 2). The strength of this interaction is remarkable: in the case of C-doped MgO(001) the CO adsorption energy is −5.08 eV. In both cases the total magnetization of the system is reduced by 2 μB. Another striking phenomenon is a tremendous charge transfer to the CO molecule. It results in a significant elongation of the C–O bond (Table 2), suggesting that B and C dopants act as potent electron donors. In contrast to the B and C cases, when MgO(001) is doped with N there is no interaction between the CO molecule and the impurity site. This seems rather unexpected, but can be explained by ILDOS of the N-doped surface (Fig. 4, right), which demonstrates that the N 2p-orbirals are oriented in the surface plane, so the overlap between these states and the CO orbitals cannot be large. In the case of N-doped MgO(001) we have found that the stable adsorption site is the first Mg neighbor of the dopant (Mg NN site, Fig. 1) with the adsorption energy practically the same as for ideal MgO(001) (Table 2). In contrast, these sites are not stable on B- and C-doped MgO(001) and the CO molecule goes to the impurity site during structural relaxation. When moving away from the impurity site, a stable adsorption of the CO molecule is possible at the Mg sites, with the adsorption energies and charge transfer similar to those on defect-free MgO(001). Hence, we conclude that the effects of the dopant atoms on CO adsorption are practically localized to the first coordination shell of the dopant.
The electronic structure of the N-doped surface upon CO adsorption (Fig. 6) demonstrates the absence of surface-molecule interaction, while in the case of pure MgO(001) there is a very small overlap of the CO 2π states with the valence band of MgO(001). However, when MgO(001) is doped with B or C, there is a pronounced interaction between the impurity states and the CO molecule states, while the s and p states of the dopants get hybridized (Fig. 6).
3.3. Atomic adsorption on X-doped (X = B, C, N) MgO(001): O case
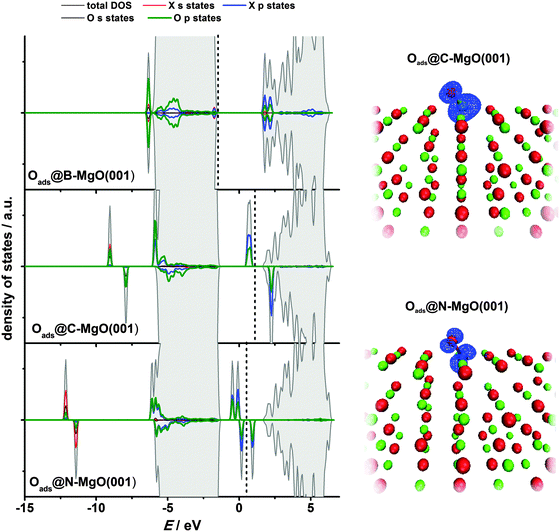
In its ground state, atomic oxygen is a radical with two unpaired 2p-electrons. As a result, it is very reactive but its adsorption on defect-free MgO(001) is relatively weak with Eads(O) calculated to be −2.16 eV (GGA-PBE).12 Using B3LYP a somewhat smaller value, −1.91 eV, was obtained by Di Valentin et al.52 Considering the extreme reactivity of atomic O this is a rather small adsorption energy. For comparison, Eads(O) is −3.7 eV on the low index platinum surface.53 As shown previously by us, Oads@MgO(001) is a non-magnetic system with O attached to the surface oxygen site.12 The O–O bond is tilted towards the other nearest O atom of the MgO(001) surface, most likely due to electrostatic interaction, as Oads receives a certain amount of charge from the substrate.12,52 Upon adsorption a peroxo-like complex is formed. The electronic states of this complex are located below and above the MgO valence band.12Similar to CO adsorption, for Oads we also find an enhanced chemisorption at the impurity site when compared to the Oads formation on the defect-free MgO(001) terrace. The adsorption is extremely strong being strongest for B-doped MgO(001), for which Eads(O) reaches −8.78 eV (Table 3). Considering ideal MgO(001) as the continuation of the given data set one can say that Eads(O) increases linearly as the number of holes in the valence shell of the X2− ions decreases (from B to O). The Oads-dopant bonds are not vertical to the MgO(001) surface plane, and are found to be shifted towards the nearest Mg surface site (in the case of the O adsorption at the B impurity site) or the O surface site (all the other cases). As in the case of molecular CO adsorption, we see a significant charge transfer to Oads, especially in the cases of B- and C-doped MgO(001) (Table 3), indicating once again that these impurities are exceptionally potent electron donors. Although we have shown that the exchange between O and X in the surface layer is significantly endothermic (Section 3.1) spontaneous exchange between X and Oads, which would restore pristine MgO(001) has not been observed. Surface O NN sites to the dopants (Fig. 1) were found to be unstable for O adsorption, as during structural optimization Oads migrated to the impurity sites in all the studied cases. However, a stable adsorption of Oads was found at O NNN sites (Fig. 1) and the adsorption energies were found to be somewhat smaller compared to those on the pure MgO(001) surface.
| Ads. site | System | E ads(O)/eV | d(O–Su)a/Å | d(O–Su1)b/Å | M/μB | ΔQO/e |
|---|---|---|---|---|---|---|
| a Su denotes the surface atom at the CO adsorption site. b Su1 denotes the surface site towards which the O–Su bond is tilted (Mg site in the case of O adsorption at the impurity site of B–MgO(001), O sites in all other cases). | ||||||
| O site | Oads@MgO(001) | −2.18 | 1.53 | 2.72 | 0 | 0.82 |
| Impurity site | Oads@B–MgO(001) | −8.78 | 1.25 | 2.09 | 0 | 1.98 |
| Oads@C–MgO(001) | −7.39 | 1.31 | 2.70 | 2 | 1.94 | |
| Oads@N–MgO(001) | −5.08 | 1.40 | 2.63 | 1 | 0.93 | |
| O NNN site | Oads@B–MgO(001) | −2.42 | 1.53 | 2.73 | 3 | 0.86 |
| Oads@C–MgO(001) | −2.39 | 1.54 | 2.72 | 2 | 0.85 | |
| Oads@N–MgO(001) | −2.50 | 1.54 | 2.73 | 1 | 0.88 | |
The electronic structure of Oads@X–MgO(001) systems reflects the strong interaction of Oads with the impurity sites (Fig. 7, left). The states of the impurities and the adsorbate overlap significantly. For the case of B–MgO(001) we see no states in the band gap and the system is not magnetic. For C- and N-doped MgO(001) the states in the band gap are present and the magnetization of the system has the same value as before oxygen adsorption. The magnetization of the system is mostly due to the p states of Oads and the dopant atom (Fig. 7, right). An interesting observation is that the p states of Oads and the dopants also partially overlap with the MgO valence band, especially with its lower part.
It is also important to outline the difference in the interaction of CO and atomic O with the N-doped MgO(001) surface. In the former case we see no bonding to the impurity site, while in the latter one there is a significant enhancement of chemisorption properties as compared to pure MgO(001). This suggests a possibility of making selective adsorbents and catalysts by a suitable choice of the dopant.
4. Conclusions
We have performed a computational study of the B-, C- and N-doped MgO(001) surfaces, with the concentration of dopants amounting to 1.56 at% (12.5 at% considering only the surface layer). We have found that the investigated dopants induce the appearance of 2p like bands in the band gap of MgO that results in the system magnetization of 3, 2 and 1 μB for B-, C- and N-doping, respectively. The dopants are in the X2− state and the ionic radii of these species are larger than the ionic radius of O2−. As a consequence, all the three dopants prefer the surface sites instead of subsurface ones, as such a placement minimizes the strain of the host MgO lattice. The impurity sites are the centers of altered chemical reactivity. We probed the chemisorption properties of such a doped surface with the CO molecule and atomic O. We have found that CO binds much stronger to B- and C-doped MgO(001) as the impurity sites serve as potent electron donors. The trend is similar for the case of atomic oxygen, for which we find Eads to be −8.78 eV on B-doped MgO(001). The change of local reactivity is seen in the first coordination sphere of the dopant. Our results suggest a possible way of producing a magnetic surface. They also suggest a way of tailoring the properties of the MgO(001) surface by a suitable choice of dopant to produce novel adsorbents and catalysts. This sets doped MgO as a versatile multifunctional material for numerous applications.Acknowledgements
This work was supported by the Swedish Research Links initiative of the Swedish Research Council (348-2012-6196). The computational resources were provided by the Swedish National Infrastructure for Computing (SNIC).References
- H. L. Tuller and S. R. Bishop, Annu. Rev. Mater. Sci., 2011, 41, 369–398 CrossRef CAS.
- F. Calle-Vallejo, M. T. M. Koper and A. S. Bandarenka, Chem. Soc. Rev., 2013, 42, 5210–5230 RSC.
- D. D. Vasić Anićijević, V. M. Nikolić, M. P. Marčeta-Kaninski and I. A. Pašti, Int. J. Hydrogen Energy, 2013, 38, 16071–16079 CrossRef.
- F. Yan, G. Xing, R. Wang and L. Li, Sci. Rep., 2015, 5, 9128, DOI:10.1038/srep09128.
- D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518–3521 CrossRef CAS PubMed.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J.-M. Tarascon, Nature, 2008, 407, 496–499 Search PubMed.
- G. F. Fine, L. M. Cavanagh, A. Afonja and R. Binions, Sensors, 2012, 10, 5469–5502 CrossRef PubMed.
- M. Matsuoka, Jpn. J. Appl. Phys., 1971, 10, 736–746 CrossRef CAS.
- T. Lei, C. Ouyang, W. Tang, L.-F. Li and L.-S. Zhou, Surf. Coat. Technol., 2010, 204, 3798–3803 CrossRef CAS.
- M. Amft and N. V. Skorodumova, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195443 CrossRef.
- B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403–407 CrossRef CAS PubMed.
- I. A. Pašti, M. Baljozović and N. V. Skorodumova, Surf. Sci., 2015, 632, 39–49 CrossRef.
- F. Frusteri, S. Freni, L. Spadaro, V. Chiodo, G. Bonura, S. Donato and S. Cavallaro, Catal. Commun., 2004, 5, 611–615 CrossRef CAS.
- F. Frusteri, S. Freni, V. Chiodo, L. Spadaro, O. Di Blasi, G. Bonura and S. Cavallaro, Appl. Catal., A, 2004, 270, 1–7 CrossRef CAS.
- I. A. Pašti, M. R. Baljozović, L. P. Granda-Marulanda and N. V. Skorodumova, Phys. Chem. Chem. Phys., 2015, 17, 9666–9679 RSC.
- M. J. Stirniman, C. Huang, R. C. Smith, J. A. Joyce and B. D. Kay, J. Chem. Phys., 1996, 105, 1295 CrossRef CAS.
- R. Nada, A. C. Hess and C. Pisani, Surf. Sci., 1995, 336, 353–361 CrossRef CAS.
- C. A. Scamehorn, N. M. Harrison and M. I. McCarthy, J. Chem. Phys., 1994, 101, 1547–1554 CrossRef CAS.
- S. Fernandez, A. Markovits and C. Minot, J. Phys. Chem. C, 2008, 112, 16491–16496 CAS.
- G. Pacchioni and N. Rösch, J. Chem. Phys., 1996, 104, 7329 CrossRef CAS.
- P. A. Žguns, M. Wessel and N. V. Skorodumova, RSC Adv., 2015, 5, 94436–94445 RSC.
- C. Zhang, B. Yoon and U. Landman, J. Am. Chem. Soc., 2007, 129, 2228–2229 CrossRef CAS PubMed.
- H.-J. Freund and G. Pacchioni, Chem. Soc. Rev., 2008, 37, 2224–2242 RSC.
- C. H. Yang, PhD thesis, Stanford University, CA, 2010.
- L. Chun-Ming, G. Hai-Quan, X. Xia, Z. Yan, J. Yong, C. Meng and Z. Xiao-Tao, Chin. Phys. B, 2011, 20, 047505 CrossRef.
- M. Grob, M. Pratzer, M. Morgenstern and M. Ležaić, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075455 CrossRef.
- M. Pesci, F. Gallino, C. Di Valentin and G. Pacchioni, J. Phys. Chem. C, 2010, 114, 1350–1356 CAS.
- I. R. Shein, A. N. Enyashin and A. L. Ivanovskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245404 CrossRef.
- K. Kenmochi, M. Seike, K. Sato, A. Yanase and H. Katayama-Yoshida, Jpn. J. Appl. Phys., 2004, 43, 934–936 CrossRef.
- K. Honkala, Surf. Sci. Rep., 2014, 69, 366–388 CrossRef CAS.
- J. P. Perdev, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. Fabris, G. Fratesi, S. de Gironcoli, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- R. Wyckoff, Crystal Structures, Interscience Publishers, New York, 1963 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- T. Gotoh, S. Murakami, K. Kinosita and Y. Murata, J. Phys. Soc. Jpn., 1981, 50, 2063–2068 CrossRef CAS.
- M. R. Welton-Cook and W. Berndt, J. Phys. C: Solid State Phys., 1982, 15, 5691–5710 CrossRef CAS.
- D. L. Blanchard, D. L. Lessor, J. P. La Femina, D. R. Baer, W. K. Ford and T. Guo, J. Vac. Sci. Technol., A, 1991, 9, 1814–1819 CAS.
- N. V. Skorodumova, K. Hermansson and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125414 CrossRef.
- J. Carrasco, N. Lopez, F. Illas and H.-J. Freund, J. Chem. Phys., 2006, 125, 074711 CrossRef CAS PubMed.
- P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- P.-O. Löwdin, Adv. Quantum Chem., 1970, 5, 185–199 CrossRef.
- V. E. Henrich, G. Dresselhaus and H. J. Zeiger, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 4764–4775 CrossRef CAS.
- D. M. Roessler and W. C. Walker, Phys. Rev., 1967, 159, 733–738 CrossRef CAS.
- R. Valero, J. R. B. Gomes, D. G. Truhlar and F. Illas, J. Chem. Phys., 2008, 129, 124710 CrossRef PubMed.
- P. Ugliengo and A. Damin, Chem. Phys. Lett., 2002, 366, 683–690 CrossRef CAS.
- R. Wichtendahl, M. Rodríguez-Rodrigo, U. Härtel, H. Kuhlenbeck and H.-J. Freund, Surf. Sci., 1999, 423, 90–98 CrossRef CAS.
- B. Civalleri, L. Maschio, P. Ugliengo and C. M. Zicovich-Wilson, Phys. Chem. Chem. Phys., 2010, 12, 6382–6386 RSC.
- C. Di Valentin, R. Ferullo, R. Binda and G. Pacchioni, Surf. Sci., 2006, 600, 1147–1154 CrossRef CAS.
- D. Vasić, Z. Ristanović, I. Pašti and S. Mentus, Russ. J. Phys. Chem. A, 2013, 87, 2214–2218 CrossRef.
| This journal is © the Owner Societies 2016 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) up −
up −