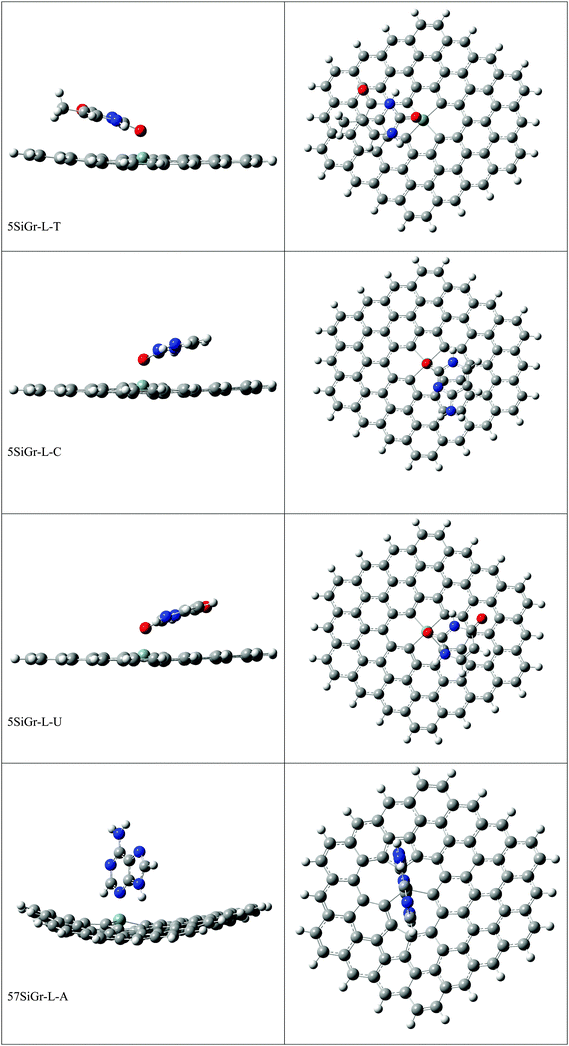
Interaction of nucleobases with silicon doped and defective silicon doped graphene and optical properties†
Sathish Kumar
Mudedla
ab,
Kanagasabai
Balamurugan
a,
Manoharan
Kamaraj
a and
Venkatesan
Subramanian
*ab
aChemical Laboratory, CSIR Central Leather Research Institute, Adyar, Chennai-600 020, India. E-mail: subuchem@hotmail.com; subbu@clri.res.in; Fax: 91 44 24911589; Tel: 91 44 24411630
bAcademy of Scientific and Innovative Research (AcSIR), CSIR-CLRI Campus, Chennai 600 020, India
First published on 6th November 2015
Abstract
The interaction of nucleobases (NBs) with the surface of silicon doped graphene (SiGr) and defective silicon doped graphene (dSiGr) has been studied using electronic structure methods. A systematic comparison of the calculated interaction energies (adsorption strength) of NBs with the surface of SiGr and dSiGr with those of pristine graphene (Gr) has also been made. The doping of graphene with silicon increases the adsorption strength of NBs. The introduction of defects in SiGr further enhances the strength of interaction with NBs. The appreciable stability of complexes (SiGr-NBs and dSiGr-NBs) arises due to the partial electrostatic and covalent (Si⋯O(N)) interaction in addition to π–π stacking. The interaction energy increases with the size of graphene models. The strong interaction between dSiGr-NBs and concomitant charge transfer causes significant changes in the electronic structure of dSiGr in contrast to Gr and SiGr. Further, the calculated optical properties of all the model systems using time dependent density functional theory (TD-DFT) reveal that absorption spectra of SiGr and dSiGr undergo appreciable changes after adsorption of NBs. Thus, the significant variations in the HOMO–LUMO gap and absorption spectra of dSiGr after interaction with the NBs can be exploited for possible applications in the sensing of DNA nucleobases.
1 Introduction
Graphene has a number of unique properties including, electronic, thermal, optical, mechanical and transport properties.1–5 Useful applications of graphene and its derivatives in biosensors, bio-devices, gene delivery systems and cancer therapy have been investigated.6–8 Both covalent and non-covalent functionalization of graphene with DNA and protein have been employed to develop new hybrid materials.9,10 These hybrid materials are highly useful in several fields such as biomolecular sensing, bioengineering and nanoelectronics.11–15 Many studies have been made to understand the interaction of protein motifs with carbon nanomaterials such as graphene and carbon nanotubes.16–20 Understanding the interaction between DNA and graphene is important because of its applications in molecular electronics.21,22 Graphene has potential applications in DNA sequencing, which helps to make personalized medicine.23,24 The genetic information is stored in DNA in terms of its fundamental constituents (guanine (G), adenine (A), thymine (T), cytosine (C) and uracil (U)). Several experimental and theoretical investigations have been conducted to unravel the structure and energetics of NBs with graphene.25–31 Most of the theoretical studies have revealed that the order of binding of NBs varies as G > A > T > C > U and it is in parallel with respective variation in polarizability. NBs interact through dispersion interaction with graphene. DNA sequencing can be performed based on the variations in the conductivity of graphene after the adsorption of NBs. The weak non-covalent interaction is responsible for the change in the conductivity of graphene. In addition, theoretical studies have shown the potential applications of graphene pores, edge hydrogenation of graphene and functionalized graphene nanogaps in DNA sequencing.32–36The doping of graphene with atoms (B, N, P, Si and metals) is an efficient method to enhance its chemical reactivity.37–40 The interaction energy of cytosine with the metal doped graphene is more than that of pristine graphene.41 Recently, distinguishable electrical signals have been observed for NBs (guanine, thymine and cytosine) after interaction with the surface of graphene nanoribbons which are connected to aluminum electrodes through sulphur atoms.42 The same graphene nanoribbon could not detect adenine.42 The graphene nanoribbon doped with boron-nitrogen has exhibited different transmission signals for the NBs.43 In addition to graphene, the theoretical study on the interaction of NBs with silicene (silicon as reactive center) has revealed that it can be useful for DNA sequencing.44 The adsorption strength of NBs with the surface of silicene is governed by Si⋯H (non-covalent) and Si⋯O (partial covalent) interactions.44 The interaction energy of NBs with silicene is higher than that of graphene due to the differences in the structural and electronic properties of silicene when compared to graphene.45 Previous experimental study has been confirmed the presence of silicon impurities in the graphene.46 Recently, Wolfgang et al. have synthesized Si-doped graphene (SiGr). They have also reported that silicon exists in the elemental form.47 A SiGr with large surface area has been synthesized. Further results showed that it has enhanced sensing properties with reference to graphene.48 Silicon atom protrudes from the plane of graphene and it preserves its sp3 character. The presence of silicon in graphene can act as a reactive site for both nucleophiles and electrophile molecules.49 Theoretical studies on SiGr predicted that it can act as metal free catalyst.50 Other theoretical investigations have revealed that SiGr exhibits enhanced capacity to detect the gas molecules such as CO, NH3, NO2, N2O and NO when compared to that of graphene.51,52 The possible sensing of modified NBs by SiGr is evident from a recent DFT study.53 Therefore, silicon atom in SiGr can act as reactive site for the nucleobases of DNA. Theoretical and experimental investigations have shown the presence of defects in SiGr.46–48 The understanding of the interaction of SiGr and defective silicon doped graphene (dSiGr) with NBs would be useful for the design of new nano-bio hybrid systems and DNA sequencing.
In this study, an attempt has been made to investigate the interaction of NBs with SiGr and dSiGr using electronic structure methods. The following points have been addressed in this study:
1. To predict the adsorption strength of NBs on SiGr and dSiGr.
2. To compare the adsorption strength of NBs on SiGr and dSiGr with that of pristine graphene.
3. To unravel the changes in the electronic structure and optical properties of SiGr and dSiGr after adsorption of NBs.
2 Computational details
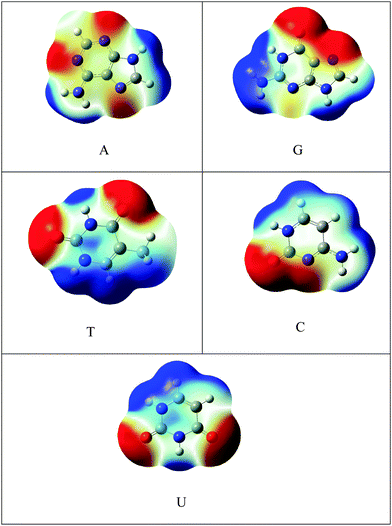
C48H18 was chosen as a model for graphene. The one atom in C48H18 graphene model was doped with silicon and SiC47H18 was taken as the model for SiGr. The selection of the dopant position was made based on the previous studies.53 A previous study has shown the existence of one vacancy and two vacancy defects in SiGr.46–48 Therefore, one vacancy defect was introduced in SiGr by the deletion of one carbon atom. Due to one vacancy defect five membered rings are formed in SiGr and silicon is bonded to two five membered rings. The molecular formula of SiGr with one vacancy defect is SiC46H18. The deletion of two carbon atoms from SiGr introduces the two vacancy defect. In two vacancy defect, the formation of seven membered and five membered rings was observed around silicon. The molecular formula of two vacancy defective silicon doped graphene is SiC45H18. The defects were created based on the previous study.46–48 It has been found from earlier studies that density functionals such as M06-2X, B3LYP-D and ωB97XD, were used to investigate the interaction of NBs with graphene, graphyne and graphdiyne.28,54 We have also explored the suitability of M06-2X in characterizing these interactions using the 6-31+G** basis set.53 Hence, all the calculations were performed at M06-2X/6-31+G** level of theory. The models of graphene, silicon doped graphene and silicon doped graphene with defect are represented as Gr, SiGr, 5SiGr (one vacancy defect) and 57SiGr (two vacancy defect) in the remaining part of the text. In order to explore the effect of size, the models with molecular formulae such as C80H22, SiC79H22, SiC78H22 and SiC77H22 were selected. These models are represented as Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L (L denoting large model) in the remaining part of text. The geometries of these models are optimized using M06-2X/6-31+G** method. The geometry of NBs (guanine (G), adenine (A), thymine (T), cytosine (C) and uracil (U)) were also optimized at the same level of theory. All these calculations were carried out employing the Gaussian 09 suite of programs.55It is well known that the electrostatic potential (ESP) is a highly useful tool to unravel non-covalent interactions and chemical reactivity.56–58 The calculated electrostatic potential surfaces for Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L are shown in Fig. 1. It can be noticed from the figure that the silicon has positive potential in all the models (SiGr-L, 5SiGr-L and 57SiGr-L). The calculated ESP isosurfaces (at 0.001 a.u.) for the NBs are given in Fig. 2. It can be observed that the active centers have negative potential. Hence, the NBs were placed parallel and perpendicular to basal plane of the graphene models. The geometries of all the complexes of Gr, SiGr, 5SiGr and 57SiGr with NBs were optimized using M06-2X/6-31+G** level of theory. Henceforth, the complexes of Gr, SiGr, 5SiGr and 57SiGr with NBs are referred to as Gr-NBs, SiGr-NBs, 5SiGr-NBs and 57SiGr-NBs. The interaction energies (IEs) were calculated at M06-2X/6-31+G** level of theory using optimized geometries of all the complexes with the aid of the supermolecular approach
| IE = EC − (EM1 + EM2) | (1) |
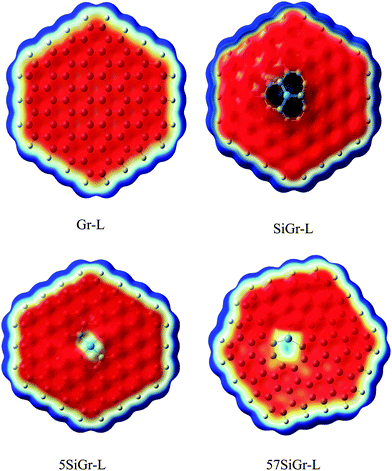 | ||
| Fig. 1 The calculated ESP isosurface of Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L at isovalue 0.001 a.u. (blue and red colors represents positive and negative potentials respectively). | ||
The charge transfer between graphene models (Gr, SiGr, 5SiGr and 57SiGr) and NBs was calculated by using Natural Bond Orbital (NBO) analysis at M06-2X/cc-pVDZ level of theory. The absorption spectra were calculated with the help of TD-DFT using the M06-2X/6-31G** method. The theory of Atoms in Molecules (AIM) was employed to characterize the nature of interaction between graphene models and NBs.60 Energy decomposition analysis (EDA) was carried out by using dispersion corrected Grimme's functional, BLYP-D, available in Amsterdam Density Functional theory (ADF) package.61–63 The density of states were calculated for all the complexes with the help of the program GaussSum.64 The Fukui indices were calculated by employing generalized gradient approximation (GGA-PBE) exchange–correlation functional as proposed by Perdew, Burke, and Ernzerhof with DNP basis set using DMol3 program.65,66
3 Results and discussion
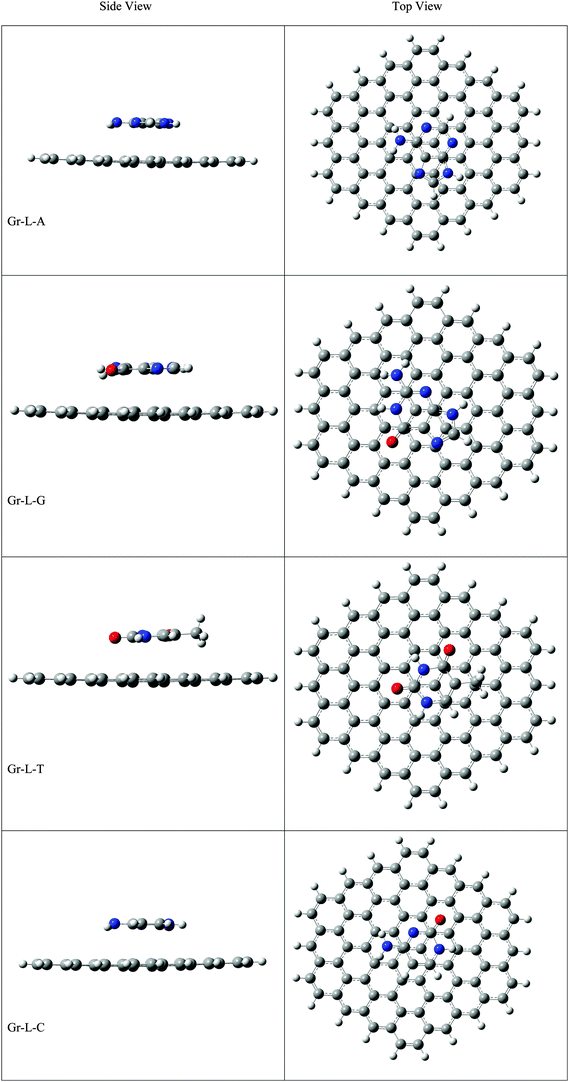
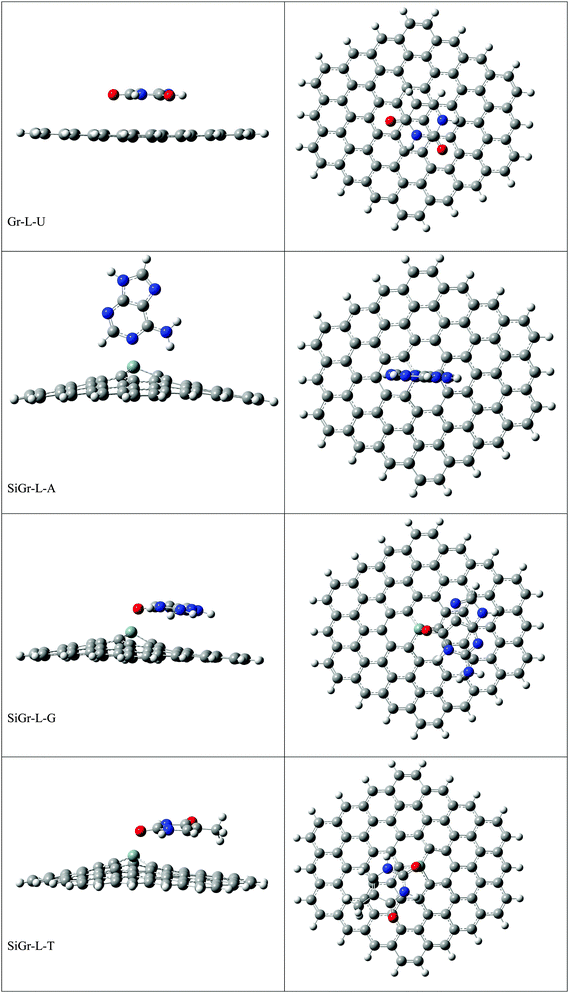
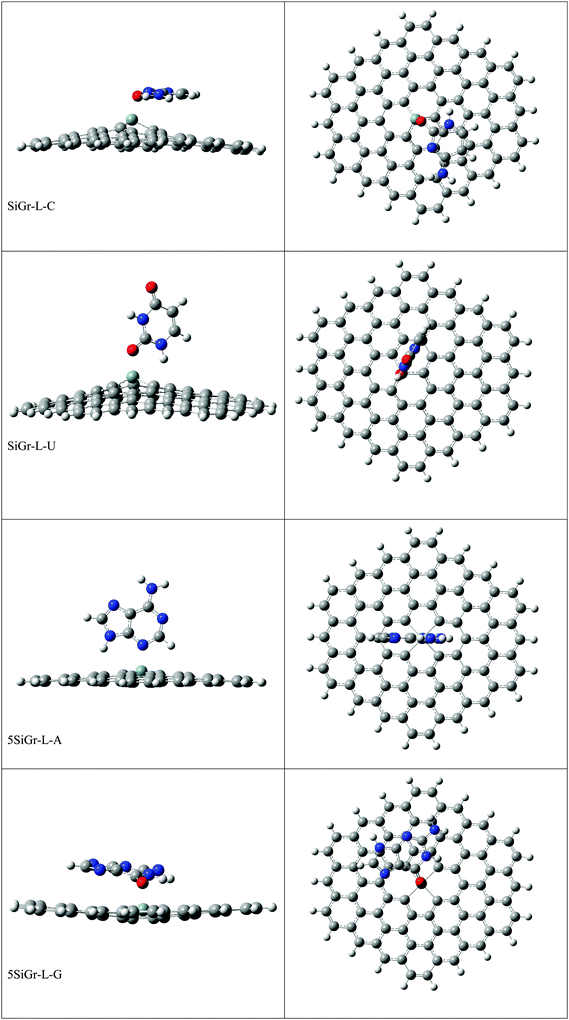
The optimized geometries of Gr, SiGr, 5SiGr and 57SiGr are shown in ESI† (Fig. S1). It is interesting to note that the Si atom is projected out from the plane of graphene due to its large atomic size. As a result, longer Si–C (1.74 Å) bond length is observed when compared to C–C (1.42 Å) bond length. These geometrical changes introduce curvature in the basal plane of graphene around Si atom. These observations are in close agreement with previous studies.53 In one vacancy defective model (5SiGr), the planarity of graphene is retained. The bond length of Si–C (1.88 Å) is different from SiGr model. However, the planarity of 57SiGr is perturbed and it adopts concave shape due to the small size of the graphene model. In 57SiGr, silicon is bonded to the carbon atoms of six, seven and five membered rings and these Si–C bond lengths are 1.85, 1.81 and 1.69 Å. The HOMO–LUMO gap of the Gr model is reduced from 2.4 to 2.3 eV in SiGr. The same is found to be 2.1 eV in the case of 5SiGr and it is less than that of Gr and SiGr models. The HOMO–LUMO gap of 57SiGr is 2.7 eV which is higher than the other models.It is well established that the binding of NBs with graphene is governed by π–π stacking interaction. The NBs can interact through specific atoms (nitrogen (N) and oxygen (O)) by forming anchoring bonds. Particularly, gold clusters form stable complexes with NBs through anchoring bonds between Au and N (O).67,68 The active centers which can form anchoring bonds of NBs are illustrated in Fig. 3. The NBs were interacted with SiGr, 5SiGr and 57SiGr in such geometrical orientations in which the active centers were parallel and perpendicular to basal plane of graphene by facing silicon. In the case of Gr, NBs were placed parallel to basal plane of Gr and then the geometry optimization was performed for all the systems. The optimized geometries of all the complexes are depicted in Fig. S2 (ESI†). These geometries correspond to the minima on the potential energy surface which is confirmed by the frequency calculation. It can be seen from Fig. S2 (ESI†) that the stacking distance of NBs with the π cloud of Gr varies from 3.1–3.3 Å. It is interesting to note that the orientation of NBs in the SiGr complexes is perpendicular to the SiGr surface. Both Si⋯O(N) and N–H⋯π interactions dominate the π–π stacking interaction which are responsible for the stabilization of the SiGr-NBs. The interaction (Si⋯O) is similar to that of NBs with the silicene.44 The shortest distance observed between SiGr and NBs varies from 1.79–1.92 Å which is shorter than those distances in the Gr–NBs complexes. The calculated IEs for all the complexes are presented in Table 1. These values reveal that the IE of guanine (G) with Gr is the highest. For graphene surface the order of IEs is found to be G > A > T > C > U. These results are close in agreement with previous reports.25–31 It is evident from Table 1 that there is a considerable increase in the IE values of SiGr-NBs with reference those values for Gr–NB complexes. Cytosine (C) exhibits the highest binding propensity among the NBs. Analysis of results from previous studies reveals that the IE values are greater than the silicene and less than the silicon nanowires.44,69 The IEs are found to follow the order C > G > A > T > U. This trend is in agreement with that of interaction of NBs with silicene. The IEs vividly illustrate that NBs strongly interact with SiGr.
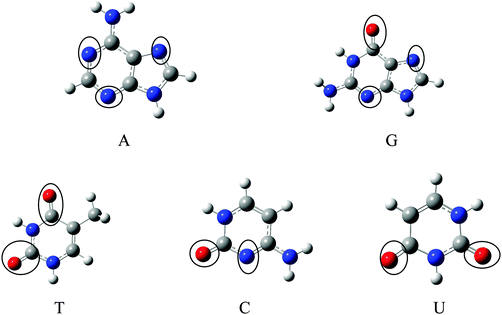 | ||
| Fig. 3 Optimized geometries of A, G, T, C and U at M06-2X/6-31+G** level of theory and the active centers are encircled. | ||
| Model | Interaction energy (kcal mol−1) | ||||
|---|---|---|---|---|---|
| A | G | T | C | U | |
| Gr | −13.92 | −17.84 | −13.97 | −13.73 | −12.02 |
| SiGr | −32.67 | −42.44 | −29.40 | −41.54 | −28.20 |
| 5SiGr | −55.06 | −57.34 | −47.80 | −61.30 | −43.90 |
| 57SiGr | −34.92 | −45.49 | −30.90 | −50.80 | −28.75 |
The optimized geometries of 5SiGr-NBs and 57SiGr-NBs are displayed in ESI† (Fig. S2). It can be seen that the orientation of NBs is parallel to the surface of graphene. Also, defective models interact with NBs through Si⋯O(N) interaction which is akin to that of SiGr in addition to π–π stacking. The silicon atom in 5SiGr and 57SiGr slightly projected out from the plane of surface which facilitates the interaction with NBs. The planarity of 5SiGr is not significantly affected upon adsorption of NBs. However, the structural changes are observed in 57SiGr. The shortest distance between NBs and defective models (5SiGr and 57SiGr) is more than that of SiGr. The shortest distance observed for 5SiGr-NB and 57SiGr-NB complexes ranges from 1.83 to 1.93 Å and 1.82 to 1.95 Å, respectively. It is possible to note from the Table 1 that the calculated IEs are higher than these of Gr and SiGr models. The IEs for the complexes of NBs with 5SiGr are appreciably higher than those values of 57SiGr model. The order of IEs (C > G > A > T > U) is similar to that of SiGr.
The optimized geometries of all the Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L are given in ESI† (depicted in Fig. S3). The projection of silicon atom from the plane is only observed in SiGr-L. Further the planarity of 5SiGr-L and 57SiGr-L is retained. The optimized geometries of complexes of NBs with large graphene models are depicted in Fig. 4. It is interesting to note that the orientation of NBs in all the models is parallel to the plane of graphene except in the case of SiGr-L–U. The orientation of NBs on the surface of SiGr-L is different with respect to that in SiGr model due to the availability of large surface area which in turn facilitate the stacking interaction with NBs. NBs are stabilized by both π–π stacking and Si⋯O(N) interactions in all the models. The bending of graphene is observed in 57SiGr upon adsorption of NBs whereas the same is not observed in the case of SiGr-L and 5SiGr-L. The calculated IEs of these complexes are presented in Table 2. It can be seen that the IEs of these complexes significantly higher than those of small models. The stability of NBs on 5SiGr-L is more than these of other models. The order of interaction energy for these models is found to be 5SiGr-L > 57SiGr-L > SiGr-L > Gr-L. The doping of graphene with silicon increases the strength of interaction of NBs with graphene. The defects in SiGr further enhance the strength of interaction with NBs.
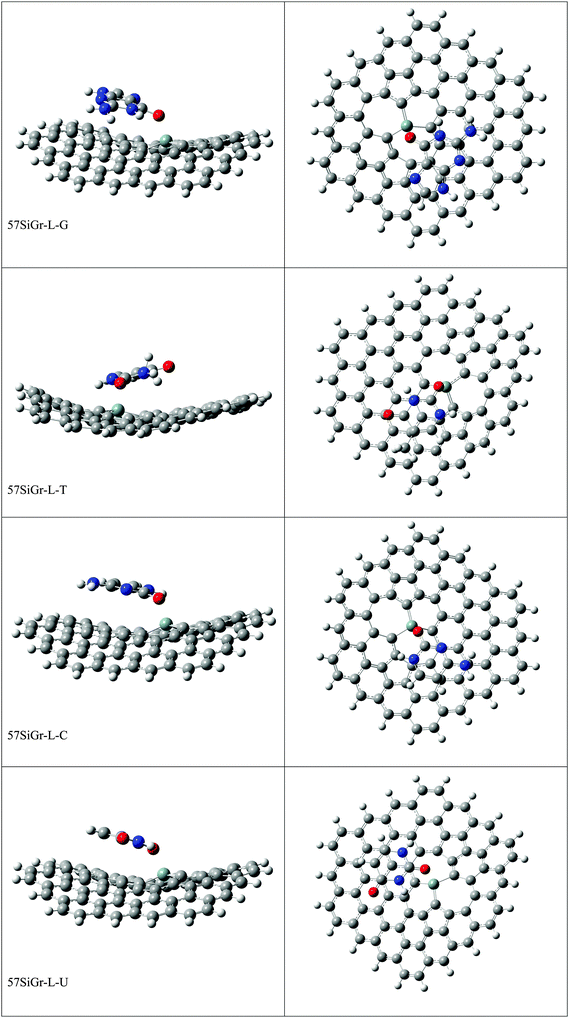 | ||
| Fig. 4 The optimized geometries of the complexes of Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L with NBs at the M06-2X/6-31+G** level. | ||
| Model | Interaction energy (kcal mol−1) | ||||
|---|---|---|---|---|---|
| A | G | T | C | U | |
| Gr-L | −14.41 | −18.07 | −14.33 | −14.10 | −12.36 |
| SiGr-L | −31.47 | −46.72 | −31.12 | −47.28 | −29.00 |
| 5SiGr-L | −57.83 | −63.00 | −50.35 | −65.42 | −50.35 |
| 57SiGr-L | −38.01 | −51.14 | −45.01 | −53.52 | −34.41 |
In order to understand the effect of electric field on the interaction, electric field was applied along the molecular axis (Z-direction) of complexes of 5SiGr with nucleobases. The calculated IEs in the presence of electric field are given in ESI† (Table S1). A marginal increase in the IEs is observed when the electric field is applied in the Z(−) direction, whereas a slight decrease is found in the case of the Z(+) direction. Therefore, the influence of applied electric field on the IEs is marginal with reference to the values observed in the absence of the electric field.
The AIM analysis is used to understand the nature of weak interactions with the help of critical points.70–72 The AIM theory explains the strength of bond in terms of electron density (ρ(rc)) at the bond critical points (BCPs).73 The Laplacian of the electron density (∇2ρ(rc)) at BCPs provides valuable information about the bonding. A negative value of ∇2(ρ(rc)) at the BCP indicates that the formation of covalent bond. On the other hand, the positive value of ∇2(ρ(rc)) reveals the depletion of the electron density along the bond, suggesting a closed shell interaction (ionic interaction, hydrogen bond and π–π stacking). The molecular graphs of various complexes as obtained from the AIM analysis are presented in ESI† (Fig. S4). The presence of BCPs between the two stacked molecules is evident from ESI.† The ∇2ρ(rc) values at BCPs in SiGr-L and Gr-L complexes with NBs are positive. These values indicate the presence of non-covalent interaction between SiGr-L (Gr-L) and NBs. The electron density ρ(rc) at the BCP is of the order of (0.1 a.u.) for covalent bonds while in the case of non-covalent interactions, it is one order lower (0.01 a.u. or even less). The calculated ρ(rc) values (0.07–0.08 a.u.) at BCPs involving Si and O(N) atoms in SiGr-L–NBs, 5SiGr-L–NBs and 57SiGr-L–NBs complexes lie in between the values corresponding to the non-covalent and covalent interactions. Further, to understand the nature of Si⋯O(N) interaction, the total energy density (Hc) at BCP was calculated by using the following equation.
| Hc = Gc + Vc | (2) |
| BCP | ∇2ρ(rc) | H c |
|---|---|---|
| Si⋯N in SiGr-L–A | −0.08 | −0.03 |
| Si⋯O in SiGr-L–G | −0.11 | −0.02 |
| Si⋯O in SiGr-L–T | −0.08 | −0.02 |
| Si⋯O in SiGr-L–C | −0.12 | −0.02 |
| Si⋯O in SiGr-L–U | −0.10 | −0.02 |
| Si⋯N in 5SiGr-L–A | −0.08 | −0.02 |
| Si⋯O in 5SiGr-L–G | −0.10 | −0.02 |
| Si⋯O in 5SiGr-L–T | −0.08 | −0.01 |
| Si⋯O in 5SiGr-L–C | −0.11 | −0.02 |
| Si⋯O in 5SiGr-L–U | −0.09 | −0.01 |
| Si⋯N in 57SiGr-L–A | −0.08 | −0.03 |
| Si⋯O in 57SiGr-L−G | −0.11 | −0.02 |
| Si⋯O in 57SiGr-T | −0.09 | −0.11 |
| Si⋯O in 57SiGr-C | −0.12 | −0.02 |
| Si⋯O in 57SiGr-U | −0.08 | −0.02 |
To understand further the factors which predominantly responsible for the interaction, EDA was performed for the complexes of Gr-L, SiGr-L, 5SiGr-L and 57SiGr-L with NBs. The EDA decomposes the interaction energy between two monomers into several components such as electrostatic energy, orbital energy, Pauli repulsion and dispersion energy. The results from the analysis of EDA are presented in ESI† (Table S2). It can be observed from ESI† (Table S2), that the dispersion interaction stabilizes the NBs on the surface of Gr-L in accordance with previous reports.28–33 The contributions from electrostatic and orbital interactions are high in the stabilization of NBs with the surface of SiGr-L, 5SiGr-L and 57SiGr-L. Therefore, both electrostatic and orbital interactions are primary determinants in the formation of complexes of NBs with SiGr-L, 5SiGr-L and 57SiGr-L. This is in close agreement with previous study which shows that the Si⋯O(N) interaction is partially electrostatic and partially covalent in nature.53 The higher IEs, electrostatic and orbital energies of SiGr-L, 5SiGr-L and 57SiGr-L compared to Gr-L are due to Si⋯O(N) interaction.
Further to understand the orbital interactions, NBO analysis was performed for all the complexes. Second order perturbation theory analysis of Fock matrix was conducted to evaluate the donor–acceptor interactions. The stabilization energies (E(2)) obtained from second order perturbation theory analysis of Fock matrix defines the strength of interaction. The high (E(2)) are observed for the interaction between unoccupied orbitals of silicon (Si) and lone pair occupied orbital of oxygen (O) or nitrogen (N). The values of stabilization energy E(2) for the complexes are listed in Table S3 of ESI.† The E(2) values are directly proportional to IEs of NBs with SiGr-L, 5SiGr-L and 57SiGr-L. Maximum E(2) value is observed for cytosine (C) with doped and defective models. The electrostatic component is responsible for the interaction between models of graphene with NBs.
Further, to understand the reactivity of Si in doped and defective models, Fukui functions were calculated for Si atom in SiGr-L, 5SiGr-L and 57SiGr-L using following expressions
| f(+) = q(N + 1) − q(N) for nucleophilic attack | (3) |
| f(−) = q(N) − q(N − 1) for electrophilic attack | (4) |
The calculated values are presented in Table 4. The f(+) value is high in the case of 5SiGr-L when compared to SiGr-L and 57SiGr-L. The more electrophilic nature of silicon in 5SiGr-L is attributed to the IEs with respect to SiGr-L and 57SiGr-L. The f(−) values of NBs are higher for the atom which is interacting with silicon. These are presented in Table 5. The f(−) value for oxygen in cytosine (C) is more than A(N), G(O), T(O) and U(O). The high nucleophilic nature of cytosine is responsible for the high IEs with SiGr-L, 5SiGr-L and 57SiGr-L.
| Model | f (+) |
|---|---|
| SiGr-L | 0.017 |
| 5SiGr-L | 0.073 |
| 57SiGr-L | 0.010 |
| Nucleobase | f (−) |
|---|---|
| N in adenine | 0.114 |
| O in guanine | 0.131 |
| O in thymine | 0.140 |
| O in cytosine | 0.224 |
| O in uracil | 0.154 |
The calculated NPA charges of all the complexes are given in Table 6. These values indicate that the charge transfer takes place from NBs to graphene models. The magnitude of charge transfer involving complexes of NBs with SiGr-L, 5SiGr-L and 57SiGr-L is appreciably higher whereas the same in the case of Gr is negligible. The strong interaction and considerable charge transfer may affect the electronic structure of the graphene models. Therefore, density of states (DOS) were calculated for all the complexes. The calculated DOS is depicted in ESI† (Fig. S5). It can be observed that the DOS of Gr-L do not change upon the adsorption of NBs and it is due to weak interaction between NBs and Gr-L. There are no significant changes in the HOMO–LUMO gap of Gr-L after the adsorption of NBs. The marginal changes are observed in the pattern of DOS for the SiGr-L after the adsorption of NBs. It can be seen from Fig. S5 (ESI†) that the HOMO and LUMO energy levels of SiGr-L are destabilized after interaction of NBs and thus changes the HOMO–LUMO gap of the SiGr-L–NBs complexes. The values of HOMO–LUMO gap for all the complexes of SiGr-L with NBs are given in Table 7. The adsorption of NBs closes the HOMO–LUMO gap of SiGr-L. However, the variations in the HOMO–LUMO gap of SiGr-L upon adsorption of A, T and U is negligible. The DOS of 5SiGr-L and 57SiGr-L is altered mainly at HOMO and LUMO energy levels upon adsorption of NBs. The adsorption of NBs destabilizes the LUMO level of 5SiGr-L whereas in the case of 57SiGr-L, the HOMO is shifted to higher energy level. The HOMO–LUMO gap for the complexes of 5SiGr-L and 57SiGr-L with NBs is presented in Table 7. The HOMO–LUMO gap of 5SiGr-L and 57SiGr-L undergoes changes upon the adsorption of NBs. The HOMO–LUMO gap of 5SiGr-L increases whereas the same reduces in the case of 57SiGr-L with the interaction of NBs. The HOMO–LUMO gap of 5SiGr-L is increased by 0.19, 0.29, 0.17, 0.26 and 0.17 eV for A, G, C, T and U, respectively. The reduction in the HOMO–LUMO gap of 57SiGr-L is 0.37, 0.31, 0.02, 0.32 and 0.20 eV for A, G, C, T and U, respectively. The change in energy gap of 57SiGr-L after adsorption of T is negligible. The variations in HOMO–LUMO gap of 5SiGr-L and 57SiGr-L are different for each nucleobase. The change in the HOMO–LUMO gap is high for 57SiGr-L compared to 5SiGr-L. The changes in HOMO–LUMO gap is significant in the case of defective models compared to Gr-L and SiGr-L. The reduction in the HOMO–LUMO gap increases the number of electrons in the conduction band and thus enhances the conductivity. The increase in the HOMO–LUMO gap leads to decrease in the conductivity. These variations lead to the change in the conductivity of 5SiGr-L-NBs and 57SiGr-L–NBs compared to 5SiGr-L and 57SiGr-L. These results are beneficial for the chemical sensing of nucleobases and for the development new sensors.
| Model | NB | Charges |
|---|---|---|
| Gr-L | A | 0.003 |
| G | 0.007 | |
| T | 0.000 | |
| C | 0.003 | |
| U | −0.001 | |
| SiGr-L | A | 0.260 |
| G | 0.281 | |
| T | 0.234 | |
| C | 0.282 | |
| U | 0.226 | |
| 5SiGr-L | A | 0.270 |
| G | 0.260 | |
| T | 0.240 | |
| C | 0.270 | |
| U | 0.234 | |
| 57SiGr-L | A | 0.251 |
| G | 0.261 | |
| T | 0.230 | |
| C | 0.270 | |
| U | 0.231 | |
| Model | HOMO–LUMO gap (eV) |
|---|---|
| Gr-L | 3.09 |
| Gr-L–A | 3.08 |
| Gr-L–G | 3.07 |
| Gr-L–T | 3.08 |
| Gr-L–C | 3.07 |
| Gr-L–U | 3.08 |
| SiGr-L | 3.09 |
| SiGr-L–A | 3.06 |
| SiGr-L–G | 2.96 |
| SiGr-L–T | 3.06 |
| SiGr-L–C | 2.94 |
| SiGr-L–U | 3.05 |
| 5SiGr-L | 2.46 |
| 5SiGr-L–A | 2.65 |
| 5SiGr-L–G | 2.75 |
| 5SiGr-L–T | 2.63 |
| 5SiGr-L–C | 2.72 |
| 5SiGr-L–U | 2.63 |
| 57SiGr-L | 3.12 |
| 57SiGr-L–A | 2.75 |
| 57SiGr-L–G | 2.81 |
| 57SiGr-L–T | 3.08 |
| 57SiGr-L–C | 2.67 |
| 57SiGr-L–U | 2.82 |
Cyclic π-delocalization in nucleobases provides an increased stability through the aromatic stabilization energy. Environment of nucleobases significantly influences their aromatic character.74 In order to understand the effect of strong interaction of SiGr and dSiGr on the aromaticity of NBs, the magnetic shielding of a ghost atom located at the ring center of NBs was calculated. The calculated nucleus-independent chemical shifts (NICS(0)) are given in ESI† (Table S4). The calculated values for parent nucleobase are in agreement with the previous results.28 The aromaticity of nucleobases increases after the interaction with Gr-L and it is corroborating with previous study. The same is found in the case of SiGr-L, 5SiGr-L and 57SiGr-L. The NICS(0) values are high for the model 5SiGr-L compared to other models.
Previous studies have shown that finite size of graphene exhibits the absorption in visible region.75,76 To understand the effect of silicon doping and defects on the optical properties of finite size graphene, the absorption spectra were calculated using TD-DFT method with the help of M06-2X/6-31G** method for Gr-L, SiGr-L, 5SIGr-L and 57SiGr-L. The calculated absorption spectrum of Gr-L is shown in Fig. S6 along with SiGr-L. For Gr-L, the peaks are observed at 324 nm (HOMO (H)−7 to LUMO (L)), 358 nm (H to L+5), 384 nm (H−1 to L+1), 428 nm (major peak) (H−1 to L) and 577 nm (H to L) and all these peaks correspond to π–π* transition with in Gr-L. The observed peaks for Gr-L are red shifted and one new peak is found at 520 nm (H to L+2) in the spectrum of SiGr-L. It is possible to note from Fig. S6 (ESI†) that the various peaks in the 5SiGr-L undergo red shifting whereas blue shifting of peaks are seen in the case of 57SiGr-L with reference to the spectrum of SiGr-L. The calculated absorption spectra for the complexes of Gr-L and NBs are presented in Fig. S7 (ESI†). The absorption peaks observed for the Gr-L–NBs complexes is similar to the pristine Gr-L. The adsorption of NBs on Gr-L does not change the pattern of absorption spectrum.
The strong adsorption of NBs on SiGr-L significantly alters the absorption spectrum of SiGr-L. The calculated absorption spectra for SiGr-L–NBs complexes are presented in Fig. S8 (ESI†) and along with SiGr-L spectrum. For SiGr-L–A, the peaks are observed at 364 (H−1 to L+7) (π–π*), 407 (H to L+6) (π–π*(adenine (A))), 449 (H−2 to L) (π–π*), 488 (H to L+1) (π–π*), 592 (H−1 to L) (π–π*) and 720 (H to L) (π–π*) nm. The second peak (407 nm) arises from transition involving adenine (A). The complex SiGr-L–G has the absorption peaks at 369 nm (H−2 to L+2) (π–π*(guanine)), 411 nm (H−1 to L+3) (π–π*), 447 nm (H−2 to L) (π–π*), 492 nm (H to L−1) (π–π*), 596 nm (H−1 to L) (π–π*) and 760 nm (H to L) (π–π*). The orbitals of guanine (G) have been involved in the transition corresponding to the peak at 369 nm. Similar changes are also observed in the absorption spectrum of complexes SiGr-L–C, SiGr-L–T and SiGr-L–U with reference to the spectrum of SiGr-L. The orbitals of NBs involved in the transitions are shown in ESI† (Fig. S9). The oscillator strength of the peaks in the spectrum of SiGr-L decreases after the adsorption of NBs.
The calculated absorption spectra for the complexes of 5SiGr-L with NBs are displayed in Fig. S8 (ESI†) along with 5SiGr-L. It can be seen that the peaks at 430 and 630 nm for 5SiGr-L are blue shifted with respect to the adsorption of NBs. In all 5SiGr-L–NBs complexes, two peaks are observed around 400 and 600 nm. The observed peaks at 411 nm (H to L+3) (π–π*(adenine)), (5SiGr-L–A), 435 nm (H to L+3) (π–π*(guanine)) (5SiGr-L–G), 415 nm (H to L+3) (π–π*(thymine) (5SiGr-L–T), 410 nm (H−1 to L+3, L+4) (π–π*(cytosine)) (5SiGr-L–C) and 418 nm (H to L+2, L+4) (π–π*(uracil)) 5SiGr-L–U) have contributions from the orbitals of NBs. The contour pictures of orbitals involved in the transitions are given in ESI† (Fig. S9).
The calculated absorption spectra of 57SiGr-L–NBs are displayed in Fig. 5 and along with the spectrum of pristine 57SiGr-L. The red shift in the spectrum of 57SiGr-L is observed after the adsorption of NBs. The peaks at 557 nm (H to L+2, H to L+3) (π–π*(guanine)) (57SiGr-L–G), 576 nm (H to L+2) (π–π*(cytosine)) (57SiGr-L–C), and 374 nm (H to L+8) (π–π*) (57SiGr-L–U) arise from the transitions involving the orbitals of NBs. The remaining all transitions are corresponds to π–π* with 57SiGr-L. The red shift in the spectra of SiGr-L and 57SiGr-L is high when compared to blue shift for 5SiGr-L upon adsorption of NBs. The observed spectral changes in the models (SiGr-L, and 57SiGr-L) would be useful in the optical sensing of NBs.
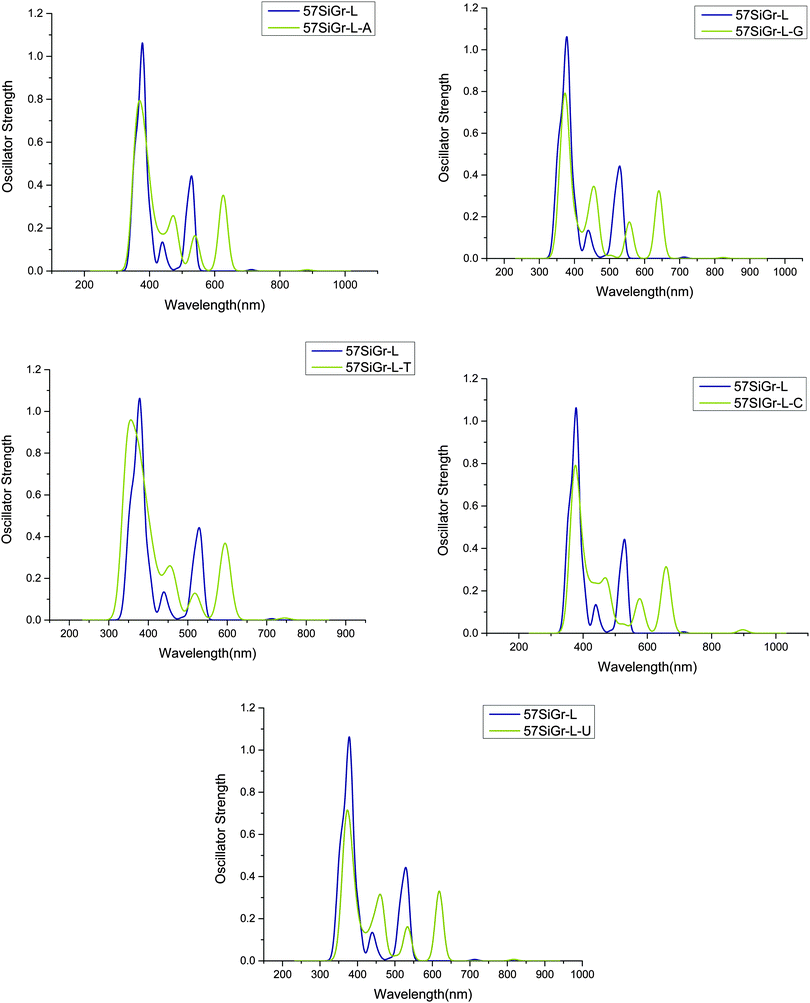 | ||
| Fig. 5 The simulated absorption spectrum of the complexes of nucleobases with 57SiGr-L at M06-2X/6-31G** level of theory. | ||
4 Conclusion
The adsorption of nucleobases on the surface of graphene (Gr), silicon doped graphene (SiGr) and defective silicon doped graphene (dSiGr) and corresponding changes in the electronic structure have been studied using DFT based methods. The doping of silicon in graphene significantly increases the adsorption strength of nucleobases. The defects in SiGr further increase the strength of interaction with nucleobases. The stability of complexes arises due to the partial electrostatic and covalent interaction between lone pair of oxygen or nitrogen (from nucleobase) and unoccupied orbital of silicon (from graphene) in addition to π–π stacking. The size of the graphene model increases the strength of adsorption. The transfer of charge from nucleobases to graphene models is evident from the natural bond orbital analysis. Particularly, the charge transfer is significantly higher in the case of SiGr and dSiGr. The strong adsorption and high charge transfer cause significant changes in the electronic structure of SiGr and dSiGr in contrast to graphene. The HOMO–LUMO gap of dSiGr undergoes significant changes after the adsorption of nucleobase. The observed changes in the HOMO–LUMO gap would be reflected in the conductivity of the inter-molecular complexes and hence dSiGr could be exploited for fast DNA sequencing as well as for the chemical sensing of individual nucleobases. Further, red shifts observed in the absorption spectrum of SiGr and dSiGr after the adsorption of nucleobases would be useful for the optical sensing of individual nucleobases and DNA. A previous experimental study has shown that SiGr enhances the sensing of molecules when compared to graphene.48 Therefore, the current findings may call for further experimental studies in this direction.Acknowledgements
We thank Nanomaterial–Safety, Health and Environment (NanoSHE BSC0112) project funded by Council of Scientific and Industrial Research (CSIR) New Delhi, India, for financial support. S. K. M thanks Department of Science and Technology (DST), New Delhi, India, for providing INSPIRE Fellowship (Senior Research Fellow).References
- K. Geim and K. S. Novosellov, Nat. Mater., 2007, 6, 183 CrossRef PubMed.
- A. K. Geim, Science, 2009, 324, 1530 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- S. Latil and L. Henrard, Phys. Rev. Lett., 2006, 97, 036803 CrossRef PubMed.
- A. A. Balandin, S. Ghosh, W. Z. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902 CrossRef CAS PubMed.
- C. H. Lu, H. H. Yang, C. L. Zhu, X. Chen and G. N. Chen, Angew. Chem., Int. Ed., 2009, 48, 4785 CrossRef CAS PubMed.
- Z. Liu, J. T. Robinson, X. M. Sun and H. J. Dai, J. Am. Chem. Soc., 2008, 130, 10876 CrossRef CAS PubMed.
- X. Sun, Z. Liu, K. Welsher, J. Robinson, A. Goodwin, S. Zaric and H. Dai, Nano Res., 2008, 1, 203 CrossRef CAS PubMed.
- B. S. Husale, S. Sahoo, A. Radenovic, F. Traversi, P. Annibale and A. Kis, Langmuir, 2010, 26, 18078 CrossRef PubMed.
- C. H. Lu, J. Li, X. L. Zhang, A. X. Zheng, H. H. Yang, X. Chen and G. N. Chen, Anal. Chem., 2011, 83, 7276 CrossRef CAS PubMed.
- X. Liu, F. Wang, R. Aizen, O. Yehezkeli and I. Willner, J. Am. Chem. Soc., 2013, 135, 11832 CrossRef CAS PubMed.
- Y. Lu, B. R. Goldsmith, N. J. Kybert and A. T. C. Johnson, Appl. Phys. Lett., 2010, 97, 083107 CrossRef.
- H. Chang, L. Tang, Y. Wang, J. Jiang and J. Li, Anal. Chem., 2010, 82, 2341–2346 CrossRef CAS PubMed.
- S. He, B. Song, D. Li, C. Zhu, W. Qi, Y. Wen, L. Wang, S. Song, H. Fang and C. A Fan, Adv. Funct. Mater., 2010, 20, 453 CrossRef CAS.
- Z. Jin, W. Sun, Y. Ke, C. J. Shih, G. L. Paulus, Q. Hua Wang, B. Mu, P. Yin and M. S. Strano, Nat. Commun., 2013, 4, 1663 CrossRef PubMed.
- K. Balamurugan, E. R. Azhagiya Singam and V. Subramanian, J. Phys. Chem. C, 2011, 115, 8886 CAS.
- K. Balamurugan, R. Gopalakrishnan, S. Sundar Raman and V. Subramanian, J. Phys. Chem. B, 2010, 114, 14048 CrossRef CAS PubMed.
- K. Balamurugan and V. Subramanian, Biopolymers, 2013, 99, 357 CrossRef CAS PubMed.
- L. Baweja, K. Balamurugan, V. Subramanian and A. Dhawan, Langmuir, 2013, 29, 14230 CrossRef CAS PubMed.
- K. Balamurugan and V. Subramanian, J. Biotechnol., 2011, 7, 89–90 CAS.
- Z. S. Siwy and M. Davenport, Nat. Nanotechnol., 2010, 5, 697–698 CrossRef CAS PubMed.
- M. Liu, H. Zhao, S. Chen, H. Yu and X. Quan, Chem. Commun., 2012, 48, 564 RSC.
- S. K. Min, W. Y. Kim, Y. Cho and K. S. Kim, Nat. Nanotechnol., 2011, 6, 162 CrossRef CAS PubMed.
- T. Ahmed, S. Kilina, T. Das, J. T. Haraldsen, J. J. Rehr and A. V. Balatsky, Nano Lett., 2012, 12, 927 CrossRef CAS PubMed.
- N. Varghese, U. Mogera, A. Govindaraj, A. Das, P. K. Maiti, A. K. Sood and C. N. R. Rao, ChemPhysChem, 2009, 10, 206 CrossRef CAS PubMed.
- S. Gowtham, R. H. Scheicher, R. Ahuja, R. Pandey and S. P. Karna, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 033401 CrossRef.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2008, 10, 2722 RSC.
- D. Umadevi and G. N. Sastry, J. Phys. Chem. Lett., 2011, 2, 1572 CrossRef CAS.
- S. Panigrahi, A. Bhattacharya, S. Banerjee and D. Bhattacharyya, J. Phys. Chem. C, 2012, 116, 4374 CAS.
- D. Le, A. Kara, E. Schröder, P. Hyldgaard and T. S. Rahman, J. Phys.: Condens. Matter, 2012, 24, 424210 CrossRef PubMed.
- J. Lee, Y. K. Choi, H. J. Kim, R. H. Scheicher and J. H. Cho, J. Phys. Chem. C, 2013, 117, 13435 CAS.
- T. Nelson, B. Zhang and O. V. Prezhdo, Nano Lett., 2010, 10, 3237 CrossRef CAS PubMed.
- M. A. Stanislav, N. Daijiro, G. R. Claudia, W. G. Jhon, H. Lee, H. Gutierrez and G. Cuniberti, Nano Lett., 2013, 13, 1969 CrossRef PubMed.
- J. Prasongkit, A. Grigoriev, B. Pathak, R. Ahuja and R. H. Scheicher, J. Phys. Chem. C, 2013, 117, 15421 CAS.
- H. W. Postma, Nano Lett., 2010, 10, 420 CrossRef CAS PubMed.
- Y. He, R. H. Scheicher, A. Grigoriev, R. Ahuja, S. Long, Z. Huo and M. Liu, Adv. Funct. Mater., 2011, 21, 2674 CrossRef CAS.
- Y. H. Zhang, Y. B. Chen, K. G. Zhou, C. H. Liu, J. Zeng, H. L. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504 CrossRef PubMed.
- J. Dai, J. Yuan and P. Giannozzi, Appl. Phys. Lett., 2009, 95, 232105 CrossRef.
- Z. Ao, S. Li and Q. Jiang, Solid State Commun., 2010, 150, 680 CrossRef CAS.
- A. Kaniyoor, R. I. Jafri, T. Arokiadoss and S. Ramaprabhu, Nanoscale, 2009, 1, 382 RSC.
- Y. H. Zhang, K. G. Zhou, K. F. Xie, C. H. Liu, H. L. Zhang and Y. Peng, Int. J. Nanosci., 2009, 8, 5 CrossRef CAS.
- B. Song, G. Cuniberti, S. Sanvito and H. Fang, Appl. Phys. Lett., 2012, 100, 063101 Search PubMed.
- B. Bhattacharya, N. B. Singh and U. Sarkar, Soft Nanosci. Lett., 2013, 3, 43 CrossRef CAS.
- G. A. Rodrigo and R. H. Scheicher, cond-mat.mes-hall., 2014, 1 Search PubMed.
- D. Jose and A. Datta, Acc. Chem. Res., 2014, 47, 593 CrossRef CAS PubMed.
- W. Zhou, M. D. Kapetanakis, M. P. Prange, S. T. Pantelides, S. J. Pennycook and J. C. Idrobo, Phys. Rev. Lett., 2012, 109, 206803 CrossRef PubMed.
- M. F. Chishlom, G. Duscher and W. Windl, Nano Lett., 2012, 12, 4651 CrossRef PubMed.
- R. Lv, M. C. dos Santos, C. Antonelli, S. Feng, K. Fujisawa, A. Berkdemir, R. Cruz-Silva, A. L. Elías, N. Perea-Lopez, F. López-Urías, H. Terrones and M. Terrones, Adv. Mater., 2014, 26, 7593 CrossRef CAS PubMed.
- J. X. Zhao, Y. Chen and H. G. Fu, Theor. Chem. Acc., 2012, 131, 1242 CrossRef.
- Y. Chen, Y. J. Liu, H. X. Wang, J. X. Zhao, Q. H. Cai, X. Z. Wang and Y. H. Ding, Mater. Interfaces, 2013, 5, 5994 CrossRef CAS PubMed.
- Y. Zou, F. Li, Z. H. Zhu, M. W. Zhao, X. G. Xu and X. Y. Su, Eur. Phys. J. B, 2011, 81, 475 CrossRef CAS.
- Y. Chen, B. Gao, J. X. Zhao, Q. H. Caii and H. G. Fu, J. Mol. Model., 2012, 18, 2043 CrossRef CAS PubMed.
- S. K. Mudedla, K. Balamurugan and V. Subramanian, J. Phys. Chem. C, 2014, 118, 16165 CAS.
- S. C. Shekar and R. S. Swathi, J. Phys. Chem. C, 2014, 118, 4516 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb and J. R. Cheeseman, et al., Gaussian 09 A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. Neetha, C. H. Suresh, A. Kumar and S. R. Gadre, Phys. Chem. Chem. Phys., 2013, 15, 18401 RSC.
- S. R. Gadre and R. N. Shirsat, In Electrostatics of Atoms and Molecules, Universities Press, Hyderabad, India, 2000 Search PubMed.
- P. Politzer and J. S. Murray, Theor. Chem. Acc., 2002, 108, 134 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- F. Biegler-Konig, J. Schonbohm, R. Derdau, D. Bayles and R. F. W. Bader, AIM2000, Version 1, BielefeldGermany, 2000 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391 Search PubMed.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo and D. P. Chong, et al., ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- N. O'Boyle, A. Tenderholt and K. Langner, J. Comput. Chem., 2008, 29, 839 CrossRef PubMed.
- B. Delley, J. Chem. Phys., 1990, 92, 508 CrossRef CAS.
- B. Delley, J. Chem. Phys., 2000, 113, 7756 CrossRef CAS.
- E. S. Kryachko and F. Remacle, J. Phys. Chem. B, 2005, 109, 22746 CrossRef CAS PubMed.
- A. Kumar, P. C. Mishra and S. Suhai, J. Phys. Chem. A, 2006, 110, 7719 CrossRef CAS PubMed.
- X. Zhong, W. J. Slough, R. Pandey and C. Friedrich, Chem. Phys. Lett., 2012, 553, 55 CrossRef CAS.
- P. L. A. Popelier, Atoms in Molecules: An Introduction, Prentice Hall, New York, 2000 Search PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford UK, 1990 Search PubMed.
- S. J. Grabowski, Hydrogen Bonding – New Insights: Challenges and Advances in Computational Chemistry and Physics, Dordrecht, The Netherlands, 2006, vol. 3 Search PubMed.
- R. Parthasarathi, V. Subramanian and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 3349 CrossRef CAS PubMed.
- C. Piotr and S. Beata, J. Mol. Model., 2010, 16, 1709 CrossRef PubMed.
- V. Hakkim and S. Biplab, RSC Adv., 2015, 5, 4599 RSC.
- V. Hakkim, S. Suparna and S. Biplab, J. Phys. Chem. Lett., 2013, 4, 3710 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–S4 and Fig. S1–S9 are presented in the supporting information. See DOI: 10.1039/c5cp06059a |
| This journal is © the Owner Societies 2016 |