Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory (DFT)†
Peter
Maxwell
ab,
Ángel Martín
Pendás
c and
Paul L. A.
Popelier
*ab
aManchester Institute of Biotechnology (MIB), 131 Princess Street, Manchester M1 7DN, UK. E-mail: paul.popelier@manchester.ac.uk; Tel: +44 (0)161 3064511
bSchool of Chemistry, University of Manchester, Oxford Road, Manchester M13 9PL, UK
cDepartamento de Quimica Fisica y Analitica, Universidad de Oviedo, E-33006 Oviedo, Spain
First published on 25th January 2016
Abstract
An interaction between two atoms, bonded or non-bonded, consists of interatomic contributions: electrostatic energy, exchange energy and electronic correlation energy. Together with the intra-atomic energy of an atom, these contributions are the basic components of the Interacting Quantum Atom (IQA) energy decomposition scheme. Here, we investigate IQA's proper use in conjunction with an explicit implementation of the B3LYP functional. The recovery of the total molecular energy from the IQA components is emphasised, for the first time. A systematic study of three model systems of biological relevance, N-methylacetamide (NMA), the doubly capped tripeptide GlyGlyGly and an alloxan dimer, shows the stabilization effect of B3LYP on most of the interatomic exchange energies (VABX) compared to their Hartree–Fock values. Diagrams of exchange energies versus interatomic distance show the clustering of interactions, one cluster for each 1,n (n = 1 to 6 where the atoms are separated by n − 1 bonds). The positioning of some VABX values outside their expected cluster marks interesting interactions.
1. Introduction
The spatial localization and partitioning of properties of matter is central to Chemistry. Fortunately, matter (at ambient conditions, and excluding metallic systems) allows itself to be described in terms of local features and behaviour, as well as recurring motifs. Indeed, molecular assemblies consist of molecules, which in turn consist of functional groups and largely transferable atoms (e.g.ref. 1–3). This locality and transferability enables Chemistry to classify, systematize and eventually explain and predict the phenomena it observes.There are various alternatives to obtain this local information theoretically and computationally, most popularly by energy and electronic charge. Amongst the most used partitioning schemes are the “energy decomposition analysis” (EDA),4,5 its variant the natural energy decomposition analysis (NEDA),6 the natural bond orbital (NBO) analysis7 or Quantum Chemical Topology (QCT),8 which amongst its various segments incorporates the Quantum Theory of Atoms in Molecules (QTAIM)9 and Interacting Quantum Atoms (IQA).10 The latter approach is conceptually the most minimal of all energy partitioning schemes. IQA is parameter-free although computationally the most expensive method. However, very recently, IQA has gained popularity through its implementation in the efficient computer program AIMAll.11 The IQA method is the subject of this paper, particularly, its use within the context of density functional theory (DFT). We also note again that IQA can operate on non-equilibrium geometries, and can thus go beyond the original QTAIM atomic energies, which are only valid at a stationary point (e.g. an equilibrium geometry).
QCT is a branch of theoretical chemistry that yields a wealth of calculated chemical information from the wavefunction of a molecule, molecular assembly, metallic system or ionic crystal. It uses the (mathematical) language of dynamical systems (e.g. attractor, critical point, separatrix, basin, gradient path) to obtain chemical insight and then ideally make predictions. It defines the so-called topological atom, which is a finite-volume object with a shape, which is specifically determined by the total system that this atom is part of topological atoms do not overlap nor leave gaps: they collectively exhaust space and their properties are additive. In other words, there is no need for corrections due to topological atoms intersecting, or leaving a gap between them (resulting in electron density not belonging to any one atom).
Each topological atom contributes its own intra-atomic energy to the total system's energy.10 In addition to this contribution, and more importantly for this study, IQA also provides all inter-atomic energy contributions. When summed, the intra-atomic and inter-atomic energies (whether attractive or repulsive) account for the complete energy of a molecule or molecular complex. Being able to recover this complete energy is very important but has been ignored in some recent publications applying IQA. A more detailed description of the IQA approach can be found in the Theoretical background section.
IQA has been used to study various bonding patterns such as halogen bonding,12 hydrogen bonding,13,14 interelectronic exchange between electronegative atoms,15 interactions of Zn(II) complexes,16 interactions between organoselenium molecules and diiodine17 and the interactions within halogentrinitromethanes.18 In addition to interaction studies, investigations addressing steric repulsion and binding energies have been reported19–23 including IQA's interpretation of chemical phenomena such as hyperconjugation.24 Finally, charge transfer, chemical potentials and the nature of functional groups,3 as well as the relationship between electronic exchange energy and molecular structure25 have also been reported. Outside of aiding chemical interpretations, IQA has also been used in more technical studies, for example, detailing the relationship between various density partitions, atomic charge and the delocalization index26 but also in rare and direct comparisons20 with non-IQA methods such as EDA and NBO.
A practical limitation of IQA is its potential incompatibility with quantum mechanical methods that solve the Schrödinger equation. Currently, the application of IQA is limited to the following methods: Hartree–Fock (HF), several multiconfigurational expansions including Complete Active Space (CAS), Configuration Interaction with single and double excitations (CISD), and Full Configuration Interaction (FCI), together with Coupled Cluster with single and double excitations (CCSD). Neither perturbation theory nor standard density functional theory (DFT) methods provide well-defined a second-order reduced density matrix, and hence IQA cannot be applied to them. As a consequence, simply adding all IQA energy contributions for a B3LYP wavefunction, for example, does not at all return the original ab initio energy of the molecule or molecular system. However, this fact has not always prevented work18,19,27–30 featuring alternative theory levels such as MP2 or B3LYP from being published. The aim of the current investigation is to identify and clarify what the inter-atomic exchange values represent, and whether they are a cause for concern. This aim will be reached for the most popular density functional to date: B3LYP.31 Being able to recover the total molecular energy from its IQA energy components is important in force field design because energy cannot be spuriously created or suddenly go missing. In this sense, the recent extension of IQA to B3LYP wavefunctions benefits the development of the QCTFF force field.32
In using the B3LYP functional, the Kohn–Sham (KS) second-order density matrix must be estimated from the first-order density matrix and will therefore only be approximate (or “fictitious”33). This fact causes the exchange energy contribution to be incomplete, coming from the use of the KS orbitals for both the intra-atomic and inter-atomic contribution. Overall, here we will explicitly address the interpretation of the interatomic exchange energy produced by an IQA partitioning of a B3LYP wavefunction, compared with that of a Hartree–Fock (HF) wavefunction, for the same molecule.
Note that IQA is not the only method that has identified the use of KS orbitals as a concern before. The same concern surfaces in the calculation and interpretation of delocalization indices (DIs), also denoted δ(A,B). A delocalization index represents the number of electrons delocalized (i.e. exchanged or shared) between atoms A and B. Hence, it is not surprising that there is a relationship between δ(A,B) and the interatomic exchange energy between A and B. Indeed, using a binomial Taylor expansion one can prove34,35 that the interatomic exchange energy is approximately equal to minus δ(A,B) divided by twice the internuclear distance. Thus, a large value for δ(A,B) corresponds to a large absolute value for the interatomic exchange energy, and hence energetic stabilization. In 2002, Poater et al.36 reported the significance of having to use DFT-KS orbitals within a HF-formalism in order to obtain a numerical value at DFT level. They produced δ(A,B) values obtained from a HF treatment of a DFT wavefunction in order to gain useful chemical insight. However, as electron correlation was not fully considered, their values were consistently overestimated. Both δ(A,B) and the interatomic exchange–correlation energies can provide valuable information of chemical significance for polyatomic molecules.25,37,38
We will present a direct comparison of the exchange energies calculated from a HF wavefunction and calculated from a HF treatment of a B3LYP wavefunction, both at exactly the same molecular geometry. In order to examine a range of both intramolecular and intermolecular interactions between atoms, the following biologically relevant molecules are used as case studies: (i) N-methylacetamide (NMA), which serves as a well-studied prototype system for the ubiquitous peptide bond, (ii) triglycine (GlyGlyGly, with a peptide-bond cap at both termini) (TriGly), which is of relevance to the construction of our peptide force field QCTFF given the recent finding39 that single amino acids are not sufficiently transferable towards proteins, and (iii) an alloxan dimer (Cambridge Structural Database (CSD) identifier ALOXAN), which is a remarkable crystal (for a reason explained just below) featuring upfront in an important review40 on intermolecular interactions.
2. Theoretical background
2.1 Interacting quantum atoms (IQA)
Fig. 1 shows an example of a molecular system being partitioned into topological atoms. The picture shows a realm of atoms appearing as malleable boxes, or even “bubbles”, negotiating energies and charges between them, and thereby forming a stable quantum system. As the nuclear positions change, so do these atoms' shapes and properties. It is clear that the topological atoms exhaust space: no overlap and no gaps. A remarkable property of crystalline alloxan (or pyrimidine-2,4,5,6-tetraone) is that hydrogen bonds do not appear in the crystal in spite of the two acidic NH entities for each molecule. Instead, crystalline alloxan features40 an array of short, almost orthogonal intermolecular C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O contacts with distances of about 2.8 Å and C
O contacts with distances of about 2.8 Å and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C angles in the range between 155° and 163°. Two atomic interaction lines, each with a corresponding bond critical point, appear between the two monomeric units.
O⋯C angles in the range between 155° and 163°. Two atomic interaction lines, each with a corresponding bond critical point, appear between the two monomeric units.
The IQA approach10 follows the traditional QTAIM9 formalism by partitioning a molecule into topological atoms. The IQA energies are calculated through the use of the first-order density matrix (non-diagonal) and the second-order (diagonal) density matrix, which allow the complete calculation of the Born–Oppenheimer energy of a molecule. To start, the intra-atomic and inter-atomic energies are given in eqn (1),
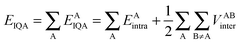 | (1) |
| EAintra = TA + VAAee + VAAen | (2) |
The inter-atomic energy can be subdivided to give
| VABinter = VABnn + VABen + VABne + VABee | (3) |
| VABee = VABCoul + VABX + VABcorr = VABCoul + VABXC | (4) |
The calculation of the electron–electron potential VABee requires integration over atomic volumes of the second-order density matrix, which is computationally very expensive because of the evaluation of a six-dimensional integral, that is, three dimensions for each atom. The VABee energy can be expressed according to Görling–Levy theory41 using perturbation theory as follows:
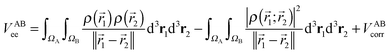 | (5) |
Returning to the conventional HF-compatible IQA, a rearrangement of the inter-atomic energies allows an electrostatic contribution and a covalent contribution to be separated and defined:
| VABelec = VABnn + VABen + VABne + VABCoul | (6) |
| VABXC = VABX + VABcorr | (7) |
| VABinter = VABelec + VABXC | (8) |
First, a technical note is in place here. AIMAll slightly expands the IQA formalism explained above by additionally calculating so-called AA′ inter-atomic energies. Here, A′ represents every other atom in the system with the exclusion of atom A itself. Hence, A′ is equivalent to a summation over all atoms B that are not equal to A,
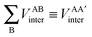 | (9) |
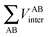 , is more accurately calculated using
, is more accurately calculated using 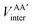 as an intermediate quantity rather than
as an intermediate quantity rather than 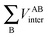 , where VABinter is individually calculated for each atom pair.
, where VABinter is individually calculated for each atom pair.
In theory, summing over B or working with the A′ route should produce equal results but typically there are small differences in the energy values due to the nature of their separate calculation and associated errors (i.e. by grid quadrature or semi-analytical integration). In AIMAll, each of the interaction energy subcomponents (i.e. VABen, VABne or VABee, see eqn (3)) can also be calculated in “AA′ mode”. AIMAll uses the AA′ energies in the calculation of the total molecular energy instead of the summation over every interatomic AB interaction. Using AA′ energies has two advantages: (1) a faster complete calculation of the IQA molecular energy partitioning albeit with reduced chemical insight, and (2) a more accurate recovery of the ab initio energy.
Now we come to the actual incorporation of the explicit B3LYP functional into an IQA energy analysis. The strategy should be made clear upfront. The overall goal is to recover the total energy when using B3LYP, which has been glossed over in the literature so far. This goal is reached in this work by using the explicit functional only within a single atom, i.e. for the total atomic energy only. We will show that the functional cannot be used for an interatomic energy. Thus we have no choice but to adopt the Hartree–Fock-like expression for interatomic exchange energy but then using Kohn–Sham orbitals.
In the development of the B3LYP extension of IQA it is convenient to define energy contributions as total atomic energies,
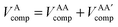 | (10) |
In previous versions of AIMAll, a B3LYP wavefunction would be treated identically to a HF wavefunction, which leads to a huge discrepancy between the total molecular energy and a summation of the various IQA energy components. In the older versions of AIMAll, both the intra-atomic and inter-atomic exchange energy is calculated from the HF exchange energy equation only:
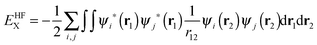 | (11) |
| EB3LYPXC = (1 − a0)ELSDAX + a0EHFX + aXΔEB88X + aCELYPC + (1 − aC)EVWNC | (12) |
Without extra thought or treatment, the introduction of a functional produces incorrect intra-atomic VAAXC and inter-atomic VABXC energies (leading to incorrect VAAee and VABee energies). As a result the total energy of the molecule is incorrectly calculated and one obtains a large energetic discrepancy. In order to obtain a correct result, the exchange–correlation functional needs to be explicitly incorporated. In a later AIMAll version (14.04.17 ref. 11), the total atomic exchange–correlation energy denoted VAXC (see eqn (10)) for the B3LYP functional was implemented. This implementation now allows the well-defined and correct calculation of the total VAXC component of VAee for an atom A:
| VAee = VAXC + VAelec | (13) |
Interatomic exchange energies are chemically meaningful and therefore one must be able to calculate them, again in a DFT context. The division of the total atomic exchange–correlation into intra- (VAAXC) and inter- (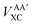 or VABXC) components is actually ambiguous. This ambiguity limits the correct extraction of interatomic terms but a reasonable choice or decision can be made. An “amalgamated” approach has been introduced to tackle this remaining limitation. This approach involves first calculating the inter-atomic exchange–correlation contribution (
or VABXC) components is actually ambiguous. This ambiguity limits the correct extraction of interatomic terms but a reasonable choice or decision can be made. An “amalgamated” approach has been introduced to tackle this remaining limitation. This approach involves first calculating the inter-atomic exchange–correlation contribution (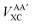 or VABXC) via the pure Hartree–Fock exchange equation only, but by inserting KS orbitals instead of HF orbitals,
or VABXC) via the pure Hartree–Fock exchange equation only, but by inserting KS orbitals instead of HF orbitals,
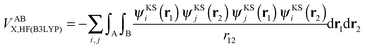 | (14) |
Secondly, this approach calculates the intra-atomic exchange–correlation energy from the well-defined total atomic exchange–correlation, VAXC,B3LYP, and the HF-defined inter-atomic exchange, 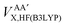 , or
, or
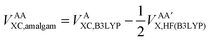 | (15) |
It is pivotal to appreciate the difference in treatment between inter- and intra-atomic exchange–correlation energies. Eqn (14) cannot be rewritten as a function of electron densities, and thus the B3LYP (which is a function of the electron density) cannot be introduced here. Thus, no interatomic exchange(–correlation) energy can be calculated from a 6D integral such as that in eqn (14) but then with the functional appearing in the integrand.
We also point out that a private communication with Dr Keith shows that VAXC,B3LYP is a transferable quantity as demonstrated from a series of tests he conducted on H⋯H interactions in normal alkanes.
Finally, we note that in this proposed scheme, VABX,HF(B3LYP) = VBAX,HF(B3LYP), and that the total molecular exchange–correlation energy can be recovered as follows,
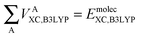 | (16) |
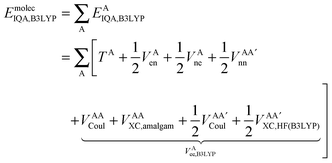 | (17) |
In this investigation we will analyse the effect of only using the HF-defined exchange equation (eqn (11)) in the calculation of interatomic exchange energies derived from KS orbitals. Note that, with the exception of the total atomic B3LYP exchange–correlation functional energy, VAXC, all other intra-atomic and inter-atomic exchange–correlation energies are calculated incorporating only the HF exchange component without correlation. The appropriate notation will be applied throughout the analysis to maintain clarity. Subscript ‘XC’ is used for the total atomic exchange–correlation energy (VAXC) along with the hybrid intra-atomic exchange–correlation energy (VAAXC), and subscript ‘X’ is used for the inter-atomic exchange energy (VABX or 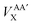 ).
).
2.2 Computational methods
The program GaussView generates sensible geometries for NMA and TriGly, which were subsequently geometry-optimized with the GAUSSIAN0946 program, in order to obtain a local energy minimum for NMA at HF/6-311G(d,p), and for TriGly at HF/6-31+G(d,p) level. The latter level of theory has been recommended47 before for its favourable balance between accuracy and computational demand. Note that no frequency calculations were carried out because this work does not depend on the confirmation of molecular geometries being true minima. Subsequent wavefunctions and ab initio energies were calculated at HF, B3LYP and MP2 levels of theory (with the respective basis set) without re-optimization of the geometry. Note that the MP2 wavefunction did not feature in any IQA energy partitioning but was only used to obtain net atomic charges, necessary for proper quantifying of polarity (see Discussion, Section 4). The latter served in a discussion of bond polarity quantified at HF versus post-HF level. We emphasize that the molecular geometries were those obtained at HF level, and that they were never re-optimized at B3LYP or MP2 level, in order to guarantee a direct comparison of energy components. The geometry of the alloxan dimer was obtained directly from the CSD, without geometry optimization, and the corresponding wavefunctions were again calculated at HF, B3LYP and MP2 levels (with 6-31+G(d,p)).The extensive analysis of NMA and TriGly is preceded by a succinct analysis of H2 and LiH, at HF, B3LYP and full CI level using 6-311G(d,p). The latter level of theory is computationally extremely expensive and hence only possible for the smallest of molecules. Yet, this analysis is useful in setting the scene while making contact with the most advanced non-DFT post-Hartree–Fock method.
The AIMAll11,44 software package (both versions 13.10.19 and 14.04.17) was used to perform the QTAIM analysis and the IQA partitioning calculations for the HF and B3LYP wavefunctions. AIMAll (v 13.10.19) was used for the IQA partitioning of the HF and B3LYP wavefunctions, via a HF-only IQA algorithm, to investigate and compare the VABX values. The B3LYP wavefunctions were then analysed using AIMAll (v 14.04.17) to check if molecular energy is recovered when using the implementation of the B3LYP atomic exchange–correlation functional (VAXC) in the IQA algorithm. Note that both versions produce the same inter-atomic VABX,B3LYP values since both follow the HF exchange-only algorithm.
AIMAll was also used to calculate QTAIM atomic charges. All default parameters (e.g. “auto” quadrature grids “Boaq” and “Briaq”) were used within AIMAll, except the encomp parameter (short for “Energy Components”), which was set to “4” in order to carry out a full IQA partitioning calculation.
AIMStudio, which is a component of the AIMAll package, and in-house software called IRIS were used for visualization.48,49 Within AIMStudio, all default settings were used. Some non-default settings for IRIS were employed, i.e. wireframe for the surface and altered transparency.
Throughout the analysis no interaction energy has been doubly counted. Within the AIMAll format, all interaction energies are split into VAB and VBA, referring to any subscript (e.g. elec, inter, XC, X), and VAB ≡ VBA. Simply adding VABX and VBAX gives the total exchange energy between atoms A and B, or VABX,tot. For clarity, and to condense the data, only the VABX,tot interaction will be reported in the figures. In line with the IQA formalism, VABX,tot will simply be reported as VABX. For each system a table will be presented containing the quantitative analysis of the interaction energies. Within each table, the analysis is divided into sub-sections according to which interatomic exchange energy is more stable, VABX,HF or VABX,B3LYP, where the subscript identifies the nature of the wavefunction used. Within each sub-section, maximum and mean difference percentages between the HF and B3LYP interatomic exchange energies will be presented. The total number of interaction cases for each 1,n interaction type within each sub-section is also included. Percentages were chosen for the analysis to allow a transferable measure that can be analysed, irrespectively of the magnitude of the energy value in question. Across the analysis, the interatomic exchange energies span a range of 10−6 kJ mol−1 to just over 103 kJ mol−1.
3. Results
3.1 Materials
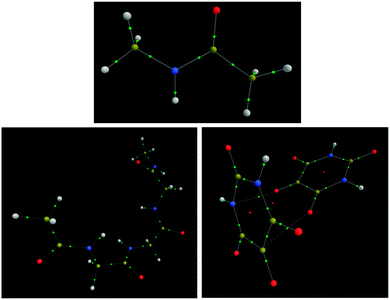
Before the extensive analysis of NMA and TriGly, the scene is set with a brief analysis of H2 and LiH. NMA and TriGly are studied to investigate intra-molecular interactions in small and medium-sized systems. The alloxan dimer system adds another dimension by including intermolecular interactions. Fig. 2 shows the three systems; note that TriGly has 17 H atoms and 22 non-H atoms, while the alloxan dimer has 4 H atoms and 20 non-H atoms. Through individually analyzing every interaction in each of the three systems we aim to rationalize the difference between interatomic HF exchange energies, VABX,HF, and interatomic energies obtained from a HF-treatment of a B3LYP wavefunction, denoted VABX,B3LYP.3.2 IQA molecular energy (EIQA) vs. ab initio (EWFN)
Recent versions of the AIMAll program (version 14.04.17 and later) include the implementation of the explicit B3LYP exchange functional into the IQA partitioning. As a result, the IQA energies accurately recover the ab initio molecular energy (typically within <1 kJ mol−1). Table 1 shows the IQA energy recovery of each system, when using the incorrect HF exchange (AIMAll version 13.10.19) and then the correct B3LYP exchange (14.04.17).| System | Theory level (and AIMAll version) | Energy | ||
|---|---|---|---|---|
| E WFN | E IQA | ΔE = EIQA − EWFN | ||
| NMA | ||||
| HF (v13.10.19) | −648691.11 | −648691.03 | −0.07 | |
| B3LYP (v13.10.19) | −652690.04 | −648588.54 | −4101.50 | |
| B3LYP (v14.04.17) | −652690.04 | −652689.85 | −0.19 | |
| TriGly | ||||
| HF (v13.10.19) | −2277500.00 | −2277500.95 | 0.95 | |
| B3LYP (v13.10.19) | −2290953.80 | −2277187.25 | −13766.55 | |
| B3LYP (v14.04.17) | −2290953.80 | −2290953.39 | −0.41 | |
| Alloxan dimer | ||||
| HF (v13.10.19) | −2946006.19 | −2946010.03 | 3.84 | |
| B3LYP (v13.10.19) | −2961934.04 | −2945606.78 | −16327.26 | |
| B3LYP (v14.04.17) | −2961934.04 | −2961933.37 | −0.67 | |
Clearly, the ab initio energy of each molecular system is not recovered for B3LYP wavefunctions in AIMAll version 13.10.19 because the values for ΔE run in the thousands of kJ mol−1. The ΔE values are also seen to grow with system size. This growing error is due to the increasing number of VAee energies being incorrectly calculated, which we expect to be more dramatic for non-hydrogen atoms. Alloxan has 3 non-hydrogen atoms more than TriGly (in spite of having fewer atoms in total), which probably explains why its energy error is larger than that of TriGly.
When the explicit B3LYP VAXC functional is used in the IQA partitioning, the ab initio molecular energy is accurately recovered. For TriGly and the alloxan dimer, the B3LYP recovery error is much smaller than that of HF. An pitiable IQA energy recovery of ∼3.8 kJ mol−1 was observed for the alloxan dimer, which is caused by poor integration errors (L(Ω) values) for 7 of the 8 carbon atoms in the dimer (see Table S1, ESI†). Extra integrations with non-default quadrature grids show that VABX values are numerically stable, even when L(Ω) is quite large. Hence we deduce that another energy component, most likely the intra-atomic energy, is sensitive to the magnitude of L(Ω). Next, the breakdown of the interatomic exchange energies, VABX, will be investigated for each system.
3.3 Interatomic exchange energies VABX
Fig. S1–S9 (ESI†) contrast the HF and B3LYP HF-calculated VABX energies for each interatomic interaction, together with the VABX,HF = VABX,B3LYP bisector. The figures are grouped into a triplet for each molecular system. Within the grouped figures, the first figure always incorporates all interatomic interactions in the system (66, 528 and 276 for NMA, TriGly and alloxan, respectively). Typically, the first figures of each triplet are dominated by the strongly covalent backbone interactions within the molecule, corresponding to VABX energies in the region of hundreds of kJ mol−1. The second figure of each triplet only identifies VABX energies within the range of −60 to −1 kJ mol−1 (‘medium-range’). The third figure of each triplet only identifies VABX energies within the range of −1 to 0 kJ mol−1 (‘long-range’). These two energy ranges can be loosely translated to strong and weak interatomic interactions. Finally, Fig. 4 and 7 show a direct overlay of |VABX| values obtained at both HF and B3LYP level for the interactions in TriGly and the alloxan dimer, respectively. Fig. 6 is identical to Fig. S9 of the ESI,† and is shown in the main text for convenience and also due to its importance.| Molecule | Measure | HF | B3LYP | FCI |
|---|---|---|---|---|
| H2 | V HHXC | −690.22 | −687.08 | −624.57 |
| δ HH | 1.00 | 1.00 | 0.85 | |
| LiH | V LiHXC | −92.14 | −102.13 | −103.02 |
| δ LiH | 0.19 | 0.22 | 0.21 | |
In general, the results are in line with previously obtained insight. VXC scales proportionally with δ, as expected. In covalent systems (such as H2), the Coulomb correlation localizes the electrons in the atomic basins, which means that δ decreases and that the HF wavefunction is too delocalized. This is a general phenomenon that will be clearly and repeatedly recovered in NMA and TriGly. This exaggerated delocalization by HF is why the |VXC| value of H2 is considerably smaller at the FCI level. In ionic molecules, such as LiH, the situation is reversed (although now the effect is much less pronounced). Here the mean field solution (i.e. HF) returns very well localized ions, while electron correlation transforms them somewhat back into neutral systems. This effect makes both δ and |VXC| increase. The effect of electron correlation on ions is to change their electron density just a little. B3LYP captures this effect nicely, and the B3LYP and FCI results are in very good agreement.
In particular, δHH must be equal to 1, exactly (1.000000), both at the HF and B3LYP levels. This value does only depend on the one-determinant structure of the (pseudo)-wavefunction. This also explains why B3LYP fails to provide a good VXC value. Note that this means that other energy components are greatly affected by this inadequacy (kinetic, electron–nucleus, etc.) because the total B3LYP energy is close to the FCI one. The change in VXC from HF to B3LYP is small since the real change caused by electron correlation in this system (as opposed to that found in LiH) is not in the electron density, but in the second-order density matrix. The HF, B3LYP, and FCI densities in H2 are quite similar but it is the pair behavior that is different. This can only be taken into account using a multi-determinant expansion, which provides smaller δ and |VXC| values.
Fig. S1–S3 (ESI†) compare the HF and B3LYP VABX values in NMA, along with a bisector. The VABX energies are distributed both above and below the bisector, indicating that increased stability may occur at either HF or B3LYP level. Fig. S1 (ESI†) shows all 66 interactions, and at this grand scale, a clear stabilization is perceived for only 3 interactions, which are all 1,2. To see more detail, Fig. S2 and S3 (ESI†) zoom in on smaller energy windows, which are −60 to −1 kJ mol−1 and −1 to 0 kJ mol−1, respectively. Fig. S2 (ESI†) shows the vast majority of 1,3 and 1,4 interactions. Energies are scattered around the bisector, with almost twice as many data points in the |VABX,B3LYP| > |VABX,HF| half (which is hard to see, but clear from Table 3 below).
| |VABX,HF| > |VABX,B3LYP| | |VABX,B3LYP| > |VABX,HF| | |||||
|---|---|---|---|---|---|---|
| Destabilization caused by B3LYP | Stabilization caused by B3LYP | |||||
| 1,n | Maximum | Mean | No. interactions | Maximum | Mean | No. interactions |
| 1,2 | 1.4 | 1.1 | 7 | 15.2 | 9.6 | 4 |
| 1,3 | 14.4 | 6.4 | 12 | 54.8 | 19.9 | 6 |
| 1,4 | 2.8 | 2.8 | 1 | 62.4 | 28.9 | 15 |
| 1,5 | 0.0 | 0.0 | 0 | 57.8 | 34.8 | 12 |
| 1,6 | 16.1 | 10.5 | 2 | 358.1 | 103.8 | 7 |
In Fig. S3 (ESI†), which shows only three 1,4 interactions and all 1,5 and 1,6 interactions, most data points now appear below the bisector, which means that B3LYP stabilizes these interactions compared to HF. This stabilization trend can also be seen as a ‘shift’ in the data points, in going from HF to B3LYP. This analysis benefits from more quantitative information about the distribution of the VABX values at either side of the bisector. This information is provided in Table 3, which groups the VABX values according to which side of the bisector they lie, i.e. either |VABX,HF| > |VABX,B3LYP| (upper half in Fig. S1–S3, ESI†) or |VABX,B3LYP| > |VABX,HF| (lower half).
Table 3 shows only percentages, which characterize the degree to which the introduction of B3LYP changes the HF VABX values. To understand how these percentages (maximum and mean) were calculated, it is instructive to focus on the 4 example interactions (N1–H8, N1–C9, N1–C2 and C2–O3) marked in red in Table S2 (ESI†). These interactions also appear in Fig. S1 (ESI†) where they lie in the |VABX,B3LYP| > |VABX,HF| region, that is, in the lower half, below the bisector. Table S2 (ESI†) makes clear that the largest relative energy shift, going from HF to B3LYP, is −111.8 kJ mol−1 (for N1–C2). Note that negative differences correspond to a stabilization caused by B3LYP. All B3LYP energies in this paper are always referred to HF, so it makes sense to work with the ratio of this energy difference to the original HF. Converting this ratio to a percentage, we define 100 × |VABX,B3LYP − VABX,HF|/VABX,HF as the “absolute difference percentage”. The absolute difference percentage associated with C2–O3 then appears as 15.2% in Table 3 under the 1,2 entry referring to 4 interactions with |VABX,B3LYP| > |VABX,HF|. Table 3 also lists the mean difference percentage (i.e. 9.6%), where the mean represents an average over these 4 interactions.
Table 3 shows that the interactions predominately stabilized by B3LYP are the 1,4 interactions and higher. The 1,2 and 1,3 interactions are mostly destabilized by B3LYP, in a ratio of about 2 to 1. Secondly, when |VABX,B3LYP| > |VABX,HF|, the mean difference percentage increases monotonically with n in 1,n over the whole range of n. However, when |VABX,HF| > |VABX,B3LYP|, there is no apparent trend linking difference percentage to the interaction type.
Fig. 3 shows the shift in VABX energies in going from HF to B3LYP for all 66 interactions in NMA. The logarithmic energy scale brings out the shift in terms of energy ratios. Fig. 3 confirms, at a glance, that the larger n in an 1,n interaction, the more pronounced the relative energy stabilization caused by B3LYP. This effect is consistent with the behaviour of the mean difference percentage in Table 3, for the stabilizing half on the right of this table. This effect may also be related to the fact that B3LYP is not an asymptotically correct functional, so it behaves pathologically at long-range.
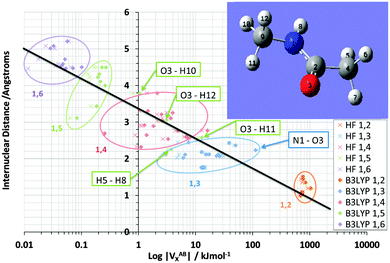
It is pleasing to see that VABX energies broadly fall apart into non-overlapping clusters, each cluster corresponding to an 1,n interaction, where n = 2, 3, 4, 5 or 6. The gap between the 1,2 cluster and the 1,3 cluster is particularly pronounced, while the 1,3 and 1,4 clusters are contiguous. The overall behaviour of VABX energies as a function of internuclear distance is such is that the lowest values occur at the largest distances. The descending line in black captures this behaviour coarsely, with a correlation coefficient r2 of 0.85, referring to the B3LYP data only. This broadly respectable correlation does not attempt to spot any non-linearity in the data, nor does it detect a fine structure emerging by grouping VABX values per interaction pair AB.
Closer inspection of the clusters reveals some energetic anomalies, that is, interactions appearing in unexpected clusters. For example, four 1,5 interactions (green) turn up far outside their cluster. Fig. 3 marks these as O3–H12, O3–H11, O3–H10 and H5–H8. The first two interactions of this set appear near the overall (B3LYP) correlation line (in black). Hence they are not anomalous in terms of how a VABX energy varies with A⋯B distance. On the other hand, O3–H10 is anomalous, not just by connectivity “distance” (i.e. 1,5) but by actual (geometrical) distance. Indeed, this interaction is curiously strong for its relatively large internuclear distance. The reason for this observation is not clear. Inspired by earlier work25 that showed that VH–HX values are anomalously large when part of a planar H–C–C–H arrangement in alkanes, it is tempting to invoke the near-planarity of the H10–C9–N1–C2–O3 fragment (where the H10–C9–N1–C2 dihedral angle is −163° (off by only 17° from 180°) and the C9–N1–C2–O3 dihedral angle is 4°). Finally, note that VN1–O3X is the strongest interaction in the 1,3 cluster, quite far to the right of the black line. This enhanced delocalization across the C–N peptide bond to the oxygen is reminiscent of the resonance canonical imparting double bond character to the CN interaction.
Fig. S4–S6 (ESI†) again compare the HF and B3LYP VABX values, but now in TriGly (counterpart of Fig. S1–S3, ESI†). Fig. S4 (ESI†) shows all 528 interactions, and at this grand scale, clear stabilization materializes for only a dozen or so interactions, which are all 1,2. Fig. S5 (ESI†) (−60 to −1 kJ mol−1) shows the vast majority of 1,3 and 1,4 interactions, along with about a third of the 1,5 interactions. Energies are scattered around the bisector, with 2.6 times as many data points in the |VABX,B3LYP| > |VABX,HF| half. Fig. S6 (ESI†) repeatedly shows a larger shift towards stabilization by B3LYP. The interactions from 1,4 to 1,8 follow trends identical to those observed for NMA, with greater stability favoured in the B3LYP wavefunction.
Table 4 shows that the interactions that B3LYP predominately stabilizes, are the 1,4 interactions and higher, as before for NMA, but this effect tails off at 1,13 and even reverts at 1,14. When lumped together, the 1,2 and 1,3 interactions are neither stabilized nor destabilized by B3LYP. In other words, 46 interactions are less stable under B3LYP while 40 are more so. As in the case of NMA, the mean difference percentage increases monotonically with n (in 1,n) up to 1,8 interactions, again when |VABX,B3LYP| > |VABX,HF|. Thus, in TriGly, the range of the monotonic trend observed up to the 1,6 interactions in NMA, is extended to 1,8. However, at this point, the mean difference percentage decreases (but not monotonically) until the 1,15 interactions are reached. When |VABX,HF| > |VABX,B3LYP|, there is still (as for NMA) no apparent trend linking difference percentage to the interaction type, throughout the whole range of interactions.
| |VABX,HF| > |VABX,B3LYP| | |VABX,B3LYP| > |VABX,HF| | |||||
|---|---|---|---|---|---|---|
| Destabilization caused by B3LYP | Stabilization caused by B3LYP | |||||
| 1,n | Maximum | Mean | No. interactions | Maximum | Mean | No. interactions |
| 1,2 | 1.5 | 1.2 | 12 | 15.2 | 7.7 | 20 |
| 1,3 | 15.2 | 8.9 | 34 | 63.0 | 23.3 | 20 |
| 1,4 | 2.9 | 1.9 | 4 | 72.9 | 27.6 | 59 |
| 1,5 | 0.0 | 0.0 | 0 | 94.2 | 41.7 | 60 |
| 1,6 | 0.0 | 0.0 | 0 | 206.1 | 70.9 | 60 |
| 1,7 | 0.0 | 0.0 | 0 | 194.1 | 99.8 | 49 |
| 1,8 | 0.0 | 0.0 | 0 | 452.1 | 147.8 | 43 |
| 1,9 | 12.2 | 12.2 | 1 | 383.9 | 114.5 | 42 |
| 1,10 | 0.0 | 0.0 | 0 | 295.8 | 100.5 | 33 |
| 1,11 | 4.8 | 4.8 | 1 | 183.0 | 75.7 | 26 |
| 1,12 | 33.8 | 25.5 | 3 | 119.3 | 53.3 | 23 |
| 1,13 | 25.6 | 19.3 | 2 | 228.9 | 76.7 | 14 |
| 1,14 | 64.2 | 43.2 | 4 | 248.4 | 82.4 | 9 |
| 1,15 | 67.6 | 40.3 | 7 | 144.1 | 75.8 | 2 |
On a technical note, such large difference percentages for long-range 1,n interactions could be a cause for concern in the analysis above. However, the reliability of the values for VX should not be called into question, as we now explain. Table S3 (ESI†) shows how a variation in the outer angular integration grid (within AIMAll) affects the VX energies for the very high 1,n interactions for two example interactions in TriGly: C22⋯H27 (1,14) and H24⋯H28 (1,15). A change in the outer angular quadrature integration grid changes the integration error L(Ω) calculated for each atom. A computationally less expensive grid, for example, ‘Low (Lebedev)’ will typically50 result in a higher absolute L(Ω) value for a given atom, compared to that of ‘Sky High (Lebedev)’. Table S3 (ESI†) shows that the variation of the integration grid does cause a significant change in L(Ω) but importantly VX remains very stable throughout. Such small changes in the values of VX, compared to that of L(Ω), allow us to trust the VX values, even for very high n in 1,n. This stability of VX suggests that a large L(Ω) error affects another IQA energy component more, presumably EAintra.
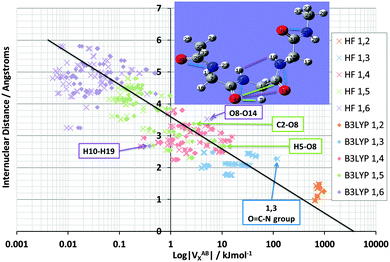
Fig. 4 shows the effect on VABX energies of introducing B3LYP, compared to the original HF values, for all 528 interactions in TriGly computed at the HF/6-31+G(d,p) and B3LYP/6-31+G(d,p) level of theory. As in Fig. 3, it again makes sense to express the overall behaviour of VABX energies as a function of internuclear distance in a coarse, linear way. However, here we draw two lines, one for HF and one for B3LYP, instead of the single black line in Fig. 3. The descending line in black captures this behaviour, admittedly coarsely, with a correlation coefficient r2 of 0.91 for both HF and B3LYP. It is clear that the cloud of B3LYP energies (in red) occurs right of the cloud of HF energies (in blue), which means that most interatomic interactions are indeed more stable at B3LYP level. It is interesting to again analyze anomalies in the same manner as in Fig. 3. It is best to truncate the analysis at 1,6 interactions because energies of about 1 J mol−1 or less are not really significant (unless hundreds of them are considered as a group and their energies simply added, as allowed by the additive nature of VX).
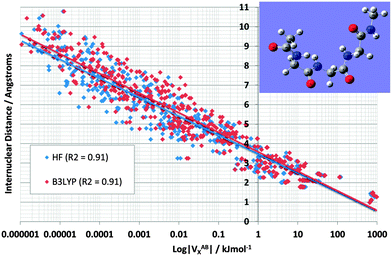 | ||
| Fig. 4 Logarithmic plot of VABXversus interatomic distance for all 528 TriGly interactions at the HF/6-31+G(d,p) and B3LYP/6-31+G(d,p) level of theory. | ||
Fig. 5 shows again the broad behaviour seen before in NMA (Fig. 3): the further two atoms are apart, the less they exchange (i.e. reduced delocalization). In other words, well separated atoms have a small VABX energy. This behaviour is typical for saturated systems, such as this tripeptide, which lacks aromatic amino acids or other extensive electronically delocalized fragments. Secondly, as seen in NMA, the various 1,n interactions do cluster as well, albeit with more overlap compared to NMA. The most substantial overlap takes place between the 1,5 (green) and 1,4 (red) cluster. Such overlap is not surprising because TriGly is a more complex system, which contains a wider variety of interactions than found in NMA. In particular, because TriGly is curled (see inset) there are many instances where the actual (geometrical) distance is smaller than the distance based on bond connectivity (i.e. labelled by 1,n). This mismatch between geometrical and connectivity-based distance shows itself in 1,6 interactions where, for example, the H10⋯H19 distance is only 2.68 Å. The corresponding VABX (B3LYP) energy is a respectable 0.4 kJ mol−1, whereas the mean VABX energy of all 1,6 interactions is at least an order of magnitude smaller.
The next set of interactions of interest is the same as in NMA: chemically meaningful quantities such as VABX are anticipated to be transferable. We expect the N⋯O interactions associated with the peptide bond to be very similar in energy value. QCT is known for providing highly transferable properties. Indeed, the VN⋯OX energy averaged across all four peptide bonds in TriGly and the one peptide bond in NMA, is −113.4 kJ mol−1 with a standard deviation of only 1.0 kJ mol−1 at B3LYP level. The standard deviation at HF level is only 0.2 kJ mol−1, which is a remarkable testimony of transferability. As expected, the VN⋯OX energies again (see NMA, Fig. 3) appear at the strong end of the 1,3 cluster (Fig. 5, at the extreme right of blue data points, marked as “O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N group”). Finally, we mention that the 1,5 interaction H5⋯O8 also appears at the strong extreme of the 1,5 cluster, but energetically this interaction is less anomalous than any O⋯N interaction because VH5⋯O8X lies very near the black line. In contrast, the 1,6 interaction O8⋯O14 lies quite a bit off the black line, and marks an unusually strong stabilization of about 6 kJ mol−1 by “through-space” oxygen⋯oxygen delocalization. This observation sets the scene for exploring another type of interaction that received a great deal of attention in the last decade, called the n → π* interaction.
C–N group”). Finally, we mention that the 1,5 interaction H5⋯O8 also appears at the strong extreme of the 1,5 cluster, but energetically this interaction is less anomalous than any O⋯N interaction because VH5⋯O8X lies very near the black line. In contrast, the 1,6 interaction O8⋯O14 lies quite a bit off the black line, and marks an unusually strong stabilization of about 6 kJ mol−1 by “through-space” oxygen⋯oxygen delocalization. This observation sets the scene for exploring another type of interaction that received a great deal of attention in the last decade, called the n → π* interaction.
TriGly is an ideal system to make contact with the research theme of Raines and co-workers on so-called n → π* interactions in proteins.51 The interaction occurs between protein backbone amides, and is characterized as arising from the delocalization of a lone pair of electrons (n, in fact, the p-rich lone pair) of an amide oxygen, to an antibonding orbital (π*) of the subsequent carbonyl group. This research group has elevated this type of interaction to one that may be as important as hydrogen bonding, which they characterize as an ns → σ* interaction. Here, there is an s-rich lone pair of an amide oxygen delocalizing with the antibonding σ* orbital of the N–H bond of an amide bond, but now four amino residues further down the protein backbone. Although the n → π* interaction can continuously get stronger, Raines et al. propose that the interaction should unmistakably take place if the distance d between OB and CC in CA![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OB⋯CC
OB⋯CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OD is smaller than 3.2 Å, and if the angle θ, defined as OB⋯CC
OD is smaller than 3.2 Å, and if the angle θ, defined as OB⋯CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OD, lies between 99° and 119°. Note that the quantum mechanical interpretation of Raines et al. is couched in the language of Natural Bond Analysis (NBO),7 which suffers from practical issues of computational stability and lack of transparency. However, IQA is alternative candidate to express delocalization effects but now in an orbital invariant way, as well as computationally stable and transparently. In TriGly, the CA
OD, lies between 99° and 119°. Note that the quantum mechanical interpretation of Raines et al. is couched in the language of Natural Bond Analysis (NBO),7 which suffers from practical issues of computational stability and lack of transparency. However, IQA is alternative candidate to express delocalization effects but now in an orbital invariant way, as well as computationally stable and transparently. In TriGly, the CA![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OB⋯CC
OB⋯CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OD system that comes nearest to obeying those geometrical criteria is C6
OD system that comes nearest to obeying those geometrical criteria is C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8⋯C2
O8⋯C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O14, where the distance d is 3.4 Å and θ is 87°. It turns out that that the VC2⋯O8X energy is 2.8 kJ mol−1. This energy is close to a value quoted by Raines et al., still in kcal mol−1, and amounting to 0.5 in that energy unit, obtained after an NBO analysis of an α helix. Having said this, the 1,5 interaction C2⋯O8 (marked in Fig. 5), occupies a rather unremarkable place in the green cluster or with respect to the black line. A likely reason is that the C6
O14, where the distance d is 3.4 Å and θ is 87°. It turns out that that the VC2⋯O8X energy is 2.8 kJ mol−1. This energy is close to a value quoted by Raines et al., still in kcal mol−1, and amounting to 0.5 in that energy unit, obtained after an NBO analysis of an α helix. Having said this, the 1,5 interaction C2⋯O8 (marked in Fig. 5), occupies a rather unremarkable place in the green cluster or with respect to the black line. A likely reason is that the C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O8⋯C2
O8⋯C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O14 fragment falls out of the range proposed by Raines et al., strictly speaking.
O14 fragment falls out of the range proposed by Raines et al., strictly speaking.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/i_char_e001.gif) O type of interaction would seem to play an important part”. Unpublished work from our lab shows that the electrostatics between topological atoms plays an important role in the stability of the complex. Here we only discuss the exchange energy component. The investigation of the intermolecular interactions allows us to compare with the intra-molecular interactions, and present a complete analysis of the VABX energies.
O type of interaction would seem to play an important part”. Unpublished work from our lab shows that the electrostatics between topological atoms plays an important role in the stability of the complex. Here we only discuss the exchange energy component. The investigation of the intermolecular interactions allows us to compare with the intra-molecular interactions, and present a complete analysis of the VABX energies.
The alloxan monomer is a heterocyclic planar system. Within each alloxan monomer, intramolecular interactions only reach to the maximum value of 1,6. When added to the intermolecular interactions, a total interaction count of 24 × (24 − 1) = 276 is obtained, in the knowledge that each alloxan monomer consists of 12 atoms. In the current work, only one of the two known alloxan dimer crystal orientations53 was investigated (see Fig. 2), the other being a dimer held by bifurcated hydrogen bonds. For the purpose of this analysis, a single dimer arrangement is sufficient. The monomers are roughly T-shaped (with a tilt), with two carbonyl groups of one monomer pointing towards the plane of the other monomer, approximately bisecting this plane.
Fig. S7–S9 (ESI†) again compare the HF and B3LYP VABX values, but now in alloxan. Fig. S7 (ESI†) shows all 276 interactions, and at this grand scale, clear stabilization materializes for only a dozen or so interactions, which are all 1,2. The introduction of B3LYP renders the strongest interactions stronger. Fig. S8 (ESI†) (−60 to −1 kJ mol−1) shows the vast majority of 1,3 and all but one of the 1,4 interactions, along with very few 1,5 interactions, as well as up to a quarter of inter-alloxan interactions. Energies are scattered around the bisector, with about 10 times as many data points in the |VABX,B3LYP| > |VABX,HF| half. Fig. S9 (ESI†) repeatedly shows a larger shift towards stabilization by B3LYP. The interactions from 1,4 to 1,8 follow trends identical to those observed for NMA, with greater stability favoured in the B3LYP wavefunction. Fig. 6 (which is identical to Fig. S9, ESI†) covers the range 0 to −1 kJ mol−1, which corresponds to 1,5; 1,6 and the inter-alloxan interactions. Here, 83% interactions are stabilized by B3LYP. Table 5 confirms this observation and quantifies the number of interactions in either the |VABX,B3LYP| > |VABX,HF| half or the |VABX,B3LYP| < |VABX,HF| half.
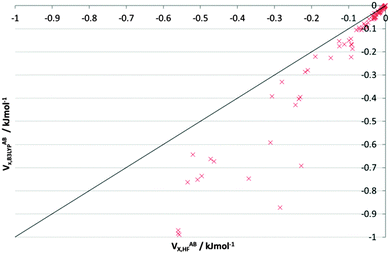 | ||
| Fig. 6 V ABX energies for long-range interactions (0 to −1 kJ mol−1) in the alloxan dimer, from both HF and B3LYP wavefunctions. Note that this figure is repeated in the ESI† as Fig. S9 because there it is part of a triplet of plots on alloxan. | ||
| |VABX,HF| > |VABX,B3LYP| | |VABX,B3LYP| > |VABX,HF| | |||||
|---|---|---|---|---|---|---|
| Destabilization caused by B3LYP | Stabilization caused by B3LYP | |||||
| 1,n | Maximum | Mean | No. interactions | Maximum | Mean | No. interactions |
| 1,2 | 0.3 | 0.2 | 4 | 16.0 | 12.0 | 20 |
| 1,3 | 21.2 | 9.4 | 14 | 56.0 | 26.6 | 22 |
| 1,4 | 0.0 | 0.0 | 0 | 76.3 | 38.3 | 42 |
| 1,5 | 0.0 | 0.0 | 0 | 107.3 | 77.4 | 24 |
| 1,6 | 0.0 | 0.0 | 0 | 206.7 | 136.2 | 6 |
| Intermolecular | 259.4 | 89.7 | 27 | 225.0 | 74.0 | 117 |
The predominately stabilizing trend caused by B3LYP also appears in purely intermolecular (i.e. alloxan⋯alloxan) interactions. In total, there are 144 of these interactions, which amounts to 52% of the complete total of 276 interactions. Table 5 shows these intermolecular interactions as a separate entry. There are now 27 cases for which |VABX,HF| > |VABX,B3LYP| and 117 for which |VABX,B3LYP| > |VABX,HF|. The distribution of cases over these two stabilization regimes can be rationalized as follows. From the TriGly data we learnt that interactions are more stable at HF level if they are (very) long range (or 1,2 and 1,3 but this very short range is not relevant here). Hence, we expect the average internuclear distance for the 27 cases to be large. Indeed, it turns out to be 6.5 Å as shown in Table S6 (ESI†). The value of 6.5 Å falls in between 6.3 Å and 6.8 Å, which are the respective average internuclear distances for 1,8 and 1,9 interactions in TriGly.
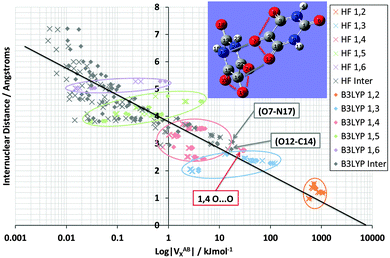
Fig. 7 demonstrates the energetic stability that B3LYP brings to the vast majority of interactions in the alloxan dimer: the red cloud (B3LYP) is indeed predominately shifted to the right compared to the blue cloud (HF). This figure is the counterpart of Fig. 4, and again shows two lines, one for HF and one for B3LYP, with almost identical correlation coefficients r2 of 0.85 and 0.84, respectively. Note that the x-axis is logarithmic hence |VABX| must be used. It is clear that the shift becomes more pronounced as the interatomic distance increases and the exchange energy decreases. The shift is more pronounced here than in TriGly (see Fig. 4).
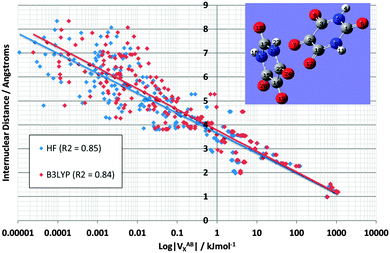 | ||
| Fig. 7 Logarithmic plot of VABXversus interatomic distance for all 276 interactions in the alloxan dimer at HF/6-31+G(d,p) and B3LYP/6-31+G(d,p) level of theory. | ||
Finally, Fig. 8 shows again the broad behaviour seen before in NMA and TriGly (Fig. 3 and 5) but now for the alloxan dimer. The black line represents the overall relationship between VABX and internuclear distance. The corresponding correlation coefficient r2 is 0.84. This time the clusters represents the exchange energy patterns of the alloxan monomers only, and show again minimal overlap. Four intramolecular O⋯O interactions stand out by their unusual strength: O7⋯O8, O7⋯O12 in one alloxan, and O19⋯O2O, O19⋯O24 in the other. The average VOOX B3LYP energy is −30.8 kJ mol−1 with a pleasingly small standard deviation of 0.9 kJ mol−1 (original data in Table S5, ESI†). These four O⋯O interactions appear outside of their 1,4 cluster. This observation is reminiscent of that made in TriGly where the 1,6 interaction O8⋯O14 appeared far outside its cluster.
Fig. 8 also marks inter-alloxan interactions (in grey-brown) having values of |VX,B3LYP| > 0.01 kJ mol−1. These intermolecular interactions mainly populate the weaker end of the energy spectrum: they start in the utmost left region, which is weaker than the intramolecular 1,6 interactions (flat disk), and extend over the 1,5 interactions (green disk) well into the 1,4 interactions (red disk). In fact, two intermolecular interactions even outdo the 1,4 interactions in terms of strength: O7⋯N17 and O12⋯C14 (marked in Fig. 8, and ignoring the 4 intramolecular O⋯O interactions outside the 1,4 disk). They are the strongest intermolecular interactions, and remarkably correspond to the two interatomic interaction lines found between the two monomers. The O12⋯C14 interaction materialises between two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups, and can hence be linked to Dunitz and Schweizer's comment on the important role of C
O groups, and can hence be linked to Dunitz and Schweizer's comment on the important role of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯C
O⋯C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O type interactions played in the stability of the crystal. However, a convincing argument on the stability of the alloxan dimer can only be made when considering all IQA energy contributions.
O type interactions played in the stability of the crystal. However, a convincing argument on the stability of the alloxan dimer can only be made when considering all IQA energy contributions.
4. Discussion
The interatomic exchange energy results provide several points to consider more deeply. These points will be addressed in turn, starting with a brief comment on the comparison between delocalization indices and VABX.A systematic increase in energetic stability is seen between pairwise 1,4 bonded interactions and higher non-bonded interactions. This trend was observed unequivocally until ∼1,14 interactions. However, interactions of 1,6 and higher, in general, had interatomic exchange energies that fell below the integration error of the atoms involved, eventually reaching values as little as ∼1 × 10−6 kJ mol−1 in magnitude. Such interactions would be considered negligible for any application. Hence, up to ∼1,6 interactions, served as an appropriate cut-off for interaction types.
A comparison can be made between the VABX results presented and the trend previously observed in measuring pairwise electron delocalization, via the delocalization index (DI). The consistent overestimation of DI values, which has been observed before, matches the current results for non-bonded interactions (1,5 and higher). This overestimation provides evidence that some Coulomb electron–electron correlation (which is included in the one-electron density) is partly included in the pairwise exchange results, despite the HF-formalism not directly addressing it. This is a well-known phenomenon, which allows a simple explanation in terms of the different behaviour of Kohn–Sham and Hartree–Fock orbitals. KS orbitals are more localized compared to HF orbitals, which is common in largely covalent interactions. This increased localization leads to smaller DIs. Because exchange energies are proportional to DIs, they will be smaller as well (in absolute value). The opposite will be true when KS orbitals become more strongly delocalized than their HF counterparts. In any case, the exact behaviour will never fully be included without the electron-pair density being defined within the HF-formalism.
The 1,2 and 1,3 interactions are neither stabilized nor destabilized by B3LYP. To rationalize this fact, it helps to consider work of Poater et al.36 regarding a similar analysis on δ(A,B) rather than on our VABX values. From their study of ethane and diborane, one concludes that δ(A,B) values of the 1,2 and 1,3 interactions involved can either increase or decrease. Given the proportionality between |VABX| and δ(A,B), mentioned in the Introduction, we can conclude that the results of Poater et al. support our own findings, stated at the beginning of this paragraph. From this parallel behaviour of δ(A,B) and VABX results, we conclude that some first-order density correlation must also being included in VABX.
A more detailed analysis is also possible that allows for a physicochemical interpretation of the systematic differences found in our data beyond the general discussion already presented. Tables S2, S4 and S5 (ESI†) gather all the (1,n) n = 2,3,4 pairs for NMA, TriGly and the alloxan dimer, respectively, listing their VABX,HF and VABX,B3LYP values, their difference, and absolute difference percentages. In order to shed some light on them we take into account the major factors that influence VABX. We will use orbital arguments, which are easier to grasp, although fully orbital invariant insights may also be given. At the HF or KS levels,
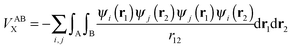 | (18) |
It is useful to introduce net atomic charges (denoted q) into this discussion. Tables S7–S9 (ESI†) provide the net charges of all atoms in NMA, TriGly and the alloxan dimer, respectively. These data show that B3LYP produces net accurate charges that are very close to those generated by MP2, which models correlation effects independently from DFT.
As noticed above, our data favour a clearly biased distribution for 1,4 and higher interactions. When |VABX,B3LYP| > |VABX,HF|, the sum of the net charge on A and on B at the B3LYP level (i.e. q(A) + q(B)) is lower than the sum at the HF level across all 1,n interaction types. In other words, the total electron population contained in the B3LYP (topological) atoms is larger. This is in agreement with the comments on the role of self-interaction posed in the above paragraph, and larger atomic electron populations will be, in general, accompanied by larger |VABX,B3LYP| values, particularly when the implied extra electrons are delocalized between A and B, such that the product ψi2(r1)ψi2(r2) contributes significantly to VX (see eqn (18) and recall that we integrate electron 1 over A and electron 2 over B). Almost all the exceptions to this rule may also be rationalized. For instance, in the C2–C10 interaction in the alloxan dimer, q(A) + q(B) at B3LYP is lower, because these carbon atoms participate in very polar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O interactions at the HF level. However, |VABX,B3LYP| < |VABX,HF|. In this case, the smaller net charge of the B3LYP carbon atoms is due to electrons provided by the neighbouring carbonylic oxygens, which do not affect the electrons participating in the C2–C10 interaction. The latter are still much more delocalized at the HF than at the B3LYP level, giving rise to a larger VX in the former case, as the following paragraph explains.
O interactions at the HF level. However, |VABX,B3LYP| < |VABX,HF|. In this case, the smaller net charge of the B3LYP carbon atoms is due to electrons provided by the neighbouring carbonylic oxygens, which do not affect the electrons participating in the C2–C10 interaction. The latter are still much more delocalized at the HF than at the B3LYP level, giving rise to a larger VX in the former case, as the following paragraph explains.
Similarly, across all 3 systems, all the 1,2 bonded interactions that showed increased stability at the HF level were C–H or C–C interactions. In the case of C–H, the larger HF exchange stems from a spurious polarization giving rise to negatively charged hydrogen atoms, caused by a too delocalized C–H bonding orbital. However, B3LYP recovers the correct polarity by shifting the interatomic surface (or equivalently localizing the bonding orbital) and thereby decreasing the exchange. In the case of C–C, we face the well-known fact that too delocalized HF orbitals lead to exaggerated covalency, counteracted again by localization in the DFT description. We should add that it is a general phenomenon that inclusion of electron correlation considerably decreases both the DI and the exchange–correlation energy in 1,2 homoatomic bonds.
An analysis of the 1,3 interactions along the previous lines also explains the stability of the interactions at each level of theory. The 1,3 interactions that are more stable at HF, consisted of a wider variety of elements (or types of topological atoms, e.g. C⋯N, C⋯O, N⋯H) across the three case studies. Typically, at HF level these interactions typically exhibit a lower sum (not absolute value) of the net charge on A and on B. In some interactions (e.g. N⋯H), the polarity of the H atoms involved, changed according to whether the HF or B3LYP wavefunction was used. At HF, a number of H atoms had exaggerated charges and were often anionic. Some of these atoms exhibited a change in polarity, becoming cationic at B3LYP. The previous anion–anion behaviour would lead to an increase in the |VABX| at HF level. The small number of 1,4 cases that exhibited greater stability at HF were solely due to a decreased sum, q(A) + q(B), at this level. Typically, these cases were limited to N–H, N–N and H–H.
We should add, in passing, that obtaining intermolecular exchange contributions from KS orbitals is not new, because it is actually a standard procedure in the SAPT-DFT method originally proposed by Williams and Chabalowski,54 and later improved by Hesselmann and Jansen.55 This method has become an accurate, yet cheaper alternative to the very expensive symmetry-adapted perturbation-theory calculations.
Overall, this analysis validates the current expansion of IQA to B3LYP level of theory without reason for concern, in spite of the absence of an explicit second order reduced density matrix.
5. Conclusion
To the best of our knowledge, this study is the first to calculate and study interatomic exchange energies VABX by using an explicit density functional, in this case that of B3LYP. As such, the IQA energy decomposition has been satisfactorily extended to DFT. Indeed, we recover the original (unpartitioned) energy of the system from the IQA energy contributions. The correct version (14.04.17 and higher), of the computer program AIMAll contains a pseudo-DFT IQA algorithm that makes this recovery possible within ∼0.7 kJ mol−1 of the original ab initio B3LYP energy.We studied the influence of B3LYP on VABX, compared with the HF values, for three systems of biochemical interest: N-methylacetamide (NMA), doubly capped tripeptide GlyGlyGly (TriGly) and an alloxan dimer. Over the three systems, a grand total of 870 VABX energies for interactions ranging up to 1,15 interactions were carefully analyzed. The 1,6 and higher interactions, with VABX energies corresponding to ∼0.01 kJ mol−1, were disregarded because they are negligible. The introduction of B3LYP invariably stabilized 1,4 and higher interactions, showing a consistent energy shift towards increased exchange energy, in terms of absolute value. Such a shift in stability is almost always due to an decrease in the sum of net atomic charges (q(A) + q(B)) caused by the use of Kohn–Sham orbitals.
However, for 1,2 and 1,3 bonded interactions, the VABX energies were not always shifted in the same direction, i.e. sometimes the HF energies were more stable than the B3LYP energies. The exchange stability for each 1,2 interactions can be understood by considering a combination of the (de)localization of the KS or HF orbitals, the position of the interatomic surface and the sum of net atomic charges (inferring polarity) of the involved atoms. Through the orbital description, DFT methods have some correlation incorporated, resulting in more localized orbitals than HF. Only C–C and C–H interactions are the 1,2 interactions with greater VABX energies using HF orbitals (over KS orbitals). Here, HF over-delocalized their atomic orbitals leading to greater exchange in the interaction. Contrastingly, the increased heteropolarity, experienced by some of the 1,2 interactions (e.g. N–H, N–C, C–O) through a HF orbital description, counteracts the lower sum of net atomic charges, leading to less interatomic exchange at HF but more so at B3LYP. All remaining 1,2 interactions had a reduced sum of net charges at B3LYP, resulting in greater interatomic exchange stability. The 1,3 interactions can be explained similarly to those of the 1,2 interactions.
Plots of VABXversus internuclear distance shows that the vast majority of interactions emerge in well-defined clusters, each associated with a bond-connectivity 1,n. Similar A⋯B pairs yield very similar VABX values, a hallmark of high transferability. Some anomalously strong interactions occur, shedding new light on patterns of exchange stability beyond that of the traditional covalent bonds.
In keeping with previous views and work on delocalization indices, HF-like B3LYP interatomic exchange energies (VABX) also provide chemically relevant values, but now energies. This realization occurs despite only first-order (and not electron-pair) electron density correlation being accounted for. Overall, the extension of IQA to B3LYP can thus be justified.
Acknowledgements
PM thanks the BBSRC for a studentship and PP the EPSRC for an Established Career Fellowship. Gratitude is due to Dr Todd Keith for closely working with him towards an AIMAll code that handles B3LYP functions for the first time, now some time ago. His private communications are much appreciated. It should be clear that Dr Keith has singled-handedly implemented the B3LYP functional in AIMAll, the source code of which he holds. AMP acknowledges funding from MINECO project CTQ2012-31174.References
- R. F. W. Bader and D. Bayles, J. Phys. Chem. A, 2000, 104, 5579–5589 CrossRef CAS.
- P. L. A. Popelier, M. Devereux and M. Rafat, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, A60, 427–433 CrossRef CAS PubMed.
- A. Martín Pendás, E. Francisco and M. A. Blanco, Faraday Discuss., 2007, 135, 423–438 RSC.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–331 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, Rev. Comput. Chem., 2000, 15, 1 CAS.
- E. F. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900 CrossRef CAS.
- F. Weinhold and C. Landis, Valency and Bonding. A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press Cambridge, Great Britain, 2005 Search PubMed.
- P. L. A. Popelier, in Structure and Bonding. Intermolecular Forces and Clusters, ed. D. J. Wales, Springer, Heidelberg, Germany, 2005, vol. 115, pp. 1–56 Search PubMed.
- R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Oxford Univ. Press, Oxford, Great Britain, 1990 Search PubMed.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- T. A. Keith, AIMAll (Version 14.04.17), (http://aim.tkgristmill.com) and T. G. S. Todd A. Keith, Overland Park KS, USA, (http://aim.tkgristmill.com), 2014.
- O. A. Syzgantseva, V. Tognetti and L. Joubert, J. Phys. Chem. A, 2013, 117, 8969–8980 CrossRef CAS PubMed.
- A. Martín Pendás, M. A. Blanco and E. Francisco, J. Chem. Phys., 2006, 125, 184112 CrossRef PubMed.
- J. M. Guevara-Vela, R. Chavez-Calvillo, M. Garcia-Revilla, J. Hernandez-Trujillo, O. Christiansen, E. Francisco, A. Martín Pendás and T. Rocha-Rinza, Chem. – Eur. J., 2013, 19, 14304–14315 CrossRef CAS PubMed.
- V. Tognetti and L. Joubert, J. Chem. Phys., 2013, 138, 024102 CrossRef PubMed.
- I. Cukrowski, J. H. de Lange and M. Mitoraj, J. Phys. Chem. A, 2014, 118, 623–637 CrossRef CAS PubMed.
- T. I. Madzhidov, G. A. Chmutova and A. Martín Pendás, J. Phys. Chem. A, 2011, 115, 10069–10077 CrossRef CAS PubMed.
- T. M. Klapoetke, B. Krumm, R. Moll, S. F. Rest, Y. V. Vishnevskiy, C. Reuter, H.-G. Stammler and N. W. Mitzel, Chem. – Eur. J., 2014, 20, 1–13 CrossRef.
- K. Eskandari and C. Van Alsenoy, J. Comput. Chem., 2014, 35, 1883–1889 CrossRef CAS PubMed.
- A. Martín Pendás, M. A. Blanco and E. Francisco, J. Comput. Chem., 2009, 30, 98–109 CrossRef PubMed.
- E. Francisco, A. Martín Pendás and M. A. Blanco, J. Chem. Theory Comput., 2006, 2, 90–102 CrossRef CAS PubMed.
- J. Dillen, Int. J. Quantum Chem., 2013, 113, 2143–2153 CrossRef CAS.
- A. Martín Pendás, E. Francisco and M. A. Blanco, J. Phys. Chem. A, 2006, 110, 12864–12869 CrossRef PubMed.
- D. Ferro-Costas and R. A. Mosquera, Phys. Chem. Chem. Phys., 2015, 17, 7424–7434 RSC.
- M. Garcia-Revilla, E. Francisco, P. L. A. Popelier and A. Martín Pendás, ChemPhysChem, 2013, 14, 1211–1218 CrossRef CAS PubMed.
- A. Martín Pendás, M. A. Blanco and E. Francisco, J. Comput. Chem., 2007, 28, 161–184 CrossRef PubMed.
- I. Cukrowski, J. H. de Lange, A. S. Adeyinka and P. Mangondo, Comput. Theor. Chem., 2015, 1053, 60–76 CrossRef CAS.
- K. Eskandari and M. Lesani, Chem. – Eur. J., 2015, 21, 4739–4746 CrossRef CAS PubMed.
- P. Matczak, M. Domagała and S. Domagała, Struct. Chem., 2015 DOI:10.1007/s11224-015-0643-3.
- I. Cukrowski, Comput. Theor. Chem., 2016, 1066, 62–75 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. L. A. Popelier, Int. J. Quantum Chem., 2015, 115, 1005–1011 CrossRef CAS.
- V. Tognetti and L. Joubert, Phys. Chem. Chem. Phys., 2014, 16, 14539–14550 RSC.
- M. Rafat and P. L. A. Popelier, in Quantum Theory of Atoms in Molecules, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007, vol. 5, pp. 121–140 Search PubMed.
- P. L. A. Popelier, in The Chemical Bond – 100 years old and getting stronger, ed. M. Mingos, Springer, Germany, 2016 Search PubMed.
- J. Poater, M. Sola, M. Duran and X. Fradera, Theor. Chem. Acc., 2002, 107, 362–371 CrossRef CAS.
- X. Fradera, M. A. Austen and R. F. W. Bader, J. Phys. Chem. A, 1999, 103, 304–314 CrossRef CAS.
- R. F. W. Bader and C. F. Matta, Inorg. Chem., 2001, 40, 5603–5611 CrossRef CAS PubMed.
- P. Maxwell and P. L. A. Popelier, Mol. Phys., 2016 Search PubMed , in press.
- K. Mueller, F. Diederich and R. Paulini, Angew. Chem., Int. Ed., 2005, 44, 1788–1805 CrossRef PubMed.
- A. Goerling and M. Levy, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 50, 196–204 CrossRef CAS.
- W. A. Kohn and L. J. Sham, Phys. Rev. A: At., Mol., Opt. Phys., 1965, 140, 1133–1138 Search PubMed.
- R. Chávez-Calvillo, M. García-Revilla, E. Francisco, A. Martín Pendás and T. Rocha-Rinza, Comput. Theor. Chem., 2015, 1053, 90–95 CrossRef.
- T. A. Keith, AIMAll (Version 13.10.19), (http://aim.tkgristmill.com) and T. G. S. Todd A. Keith, Overland Park KS, USA, (http://aim.tkgristmill.com), 2013.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, 2009.
- Y. Zhao, J. Pu, B. J. Lynch and D. G. Truhlar, Phys. Chem. Chem. Phys., 2004, 6, 673–676 RSC.
- M. Rafat, M. Devereux and P. L. A. Popelier, J. Mol. Graphics Modell., 2005, 24, 111–120 CrossRef CAS PubMed.
- M. Rafat and P. L. A. Popelier, J. Comput. Chem., 2007, 28, 2602–2617 CrossRef CAS PubMed.
- F. M. Aicken and P. L. A. Popelier, Can. J. Chem., 2000, 78, 415–426 CrossRef CAS.
- G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620 CrossRef CAS PubMed.
- W. Bolton, Acta Crystallogr., 1963, 17, 147–152 CrossRef.
- J. D. Dunitz and W. B. Schweizer, CrystEngComm, 2007, 9, 266 RSC.
- H. L. Williams and C. F. Chabalowski, J. Phys. Chem. A, 2001, 105, 646 CrossRef CAS.
- A. Hesselmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp07021j |
| This journal is © the Owner Societies 2016 |