Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of alkali metal cations in the stabilization of guanine quadruplexes: why K+ is the best†‡
F.
Zaccaria
a,
G.
Paragi
ab and
C.
Fonseca Guerra
*a
aDepartment of Theoretical Chemistry and Amsterdam Center for Multiscale Modeling, Vrije Universiteit Amsterdam, De Boelelaan 1083, 1081 HV Amsterdam, The Netherlands. E-mail: c.fonsecaguerra@vu.nl
bMTA-SZTE Supramolecular and Nanostructured Materials Research Group, Dóm tér 8, Szeged, Hungary
First published on 3rd May 2016
Abstract
The alkali metal ion affinity of guanine quadruplexes has been studied using dispersion-corrected density functional theory (DFT-D). We have done computational investigations in aqueous solution that mimics artificial supramolecular conditions where guanine bases assemble into stacked quartets as well as biological environments in which telomeric quadruplexes are formed. In both cases, an alkali metal cation is needed to assist self-assembly. Our quantum chemical computations on these supramolecular systems are able to reproduce the experimental order of affinity of the guanine quadruplexes for the cations Li+, Na+, K+, Rb+, and Cs+. The strongest binding is computed between the potassium cation and the quadruplex as it occurs in nature. The desolvation and the size of alkali metal cations are thought to be responsible for the order of affinity. Until now, the relative importance of these two factors has remained unclear and debated. By assessing the quantum chemical ‘size’ of the cation, determining the amount of deformation of the quadruplex needed to accommodate the cation and through the energy decomposition analysis (EDA) of the interaction energy between the cation and the guanines, we reveal that the desolvation and size of the alkali metal cation are both almost equally responsible for the order of affinity.
1. Introduction
Guanine-rich sequences of DNA, which occur at crucial regulatory hotspots of the human genome, such as telomeres, promoters and immunoglobulin switch regions, can fold into a non-duplex four-stranded type of structure (see Fig. 1).1 These guanine quadruplexes (GQs) are made up of stacked guanine quartets with cations in between the layers. The guanine quartet (G4) consists of four guanines held together by a Hoogsteen-type hydrogen-bonding arrangement. Because of their biological relevance and therapeutic perspective, the GQs have received much attention.2 Furthermore, in supramolecular chemistry the self-assembly of guanosine into quadruplexes driven by molecular recognition and cations has led to different applications.3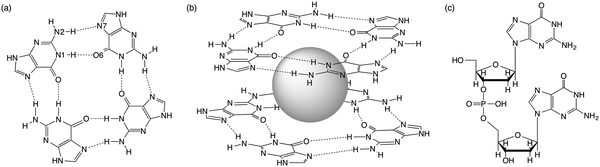 | ||
| Fig. 1 (a) Guanine quartet (G4), (b) G4–M+–G4 and (c) guanine dimer with a sugar-phosphate backbone. | ||
In our previous work on quadruplexes,4 we showed that the hydrogen bonds in G4 experience a large synergetic effect. This cooperativity in G4 originates from charge separation occurring due to donor–acceptor interactions in the σ-electron system, and not, as previously assumed, due to resonance assistance by the π electrons.5 Furthermore, we showed that although alkali metal cations located in the central channel of GQs weaken the hydrogen bonds, the synergy still persists in telomere-like structures.
The general idea on the role of the alkali metal cation is that by being located between two quartets, it generates cation–dipole interactions with eight guanines.6 In that way, it is thought to reduce the repulsion of the eight central oxygen atoms, enhance the hydrogen bond strength and stabilize quartet stacking. This has been rationalized by looking at the electrostatic potential map of a G-tetrad which shows a significant concentration of negative charge in the central area of the G-tetrad.6c Another theoretical work has investigated the cation–quadruplex interaction and revealed polarization of charge towards the cation.7
All existing natural and supramolecular guanine quadruplexes display this locally negative channel in the center of the structure whose most peculiar characteristic is the ability to select over monovalent cations. The experimental consensus8 regarding the overall affinity sequence of alkali metal cations is K+ > Na+, Rb+ ≫ Li+, Cs+ in water, and many studies9 have tried to tackle the question where does this sorting ability come from. An early work by Williamson et al.9a suggested that the observed ion specificity (related to the ability to promote structure formation in solutions containing telomeric oligonucleotides) could be simply explained by the size of the cavity and the relatively snug fit of the concerned cations. Later, Hud et al.,9b treasuring Eisenman's theory10 on equilibrium selectivity of ions and the most up-to-date information about transmembrane ion channels, based their explanation for the competition of the cations for the channel site on the difference in Gibbs free energy of solvation of the alkali metal cations, receiving theoretical support from Gu and Leszczynski.9c Until now, no consensus has been reached on this matter.
In the present paper, we show that the Gibbs free energy of solvation and the ionic radius of the alkali metal cation are both of almost equal importance for the order of affinity for the cavity in the guanine quadruplexes. This follows from extensive computational analyses of double-layer guanine quartets and natural guanine quadruplexes with a sugar-phosphate backbone interacting with the monovalent cations (Li+, Na+, K+, Rb+, and Cs+). The computations are based on dispersion-corrected density functional theory (DFT-D).11 Our investigations cover the situation of quadruplexes under supramolecular and biological conditions in aqueous solution. The deformation energy of the guanine quadruplex for accommodating the cation and the energy decomposition analysis (EDA)12 for the interaction between the cation and the guanines permit us to estimate quantum chemically the size of the cations and to analyze which one fits the best. Furthermore, the destabilization between adjacent oxygen atoms in the quadruplex structure is investigated.
2. Computational methods
2.1. General procedure
All the calculations were performed using the Amsterdam Density Functional (ADF) program13,14 based on dispersion-corrected relativistic density functional theory at the ZORA-BLYP-D3(BJ)/TZ2P level for geometry optimizations and energies.11 No geometrical constraints have been imposed on the quadruplexes without the backbone (129 atoms) and the quadruplexes with the sugar-phosphate backbone (265 atoms), or on the guanine monomers and guanosine dimers. Our quadruplex structures are all parallel-stranded right-handed G-quadruplex structures with anti-glycosidic torsion angles at all guanines. The starting point for every structure was taken from the central G4–G4 layers of a structure from the PDB database with PDB ID: 139D.2iSolvent effects in water have been estimated using the conductor-like screening model (COSMO), as implemented in the ADF program.15 Radii of cations have been computed according to the procedure presented in ref. 15d to reproduce the solvation energy of the cation. Additional information is available in the ESI‡ (Table S1).
The energy of formation, ΔEform, of the guanine quadruplex complexed with the cation is defined as (see also Fig. 2)
| ΔEform = E(G4–M+–G4)aq − 8·E(G)aq − E(M+)aq | (1a) |
The quartet has eight hydrogen bonds pointing in the same direction (see Fig. 1a). If the hydrogen bonds in the two layers are in the same direction, it is called a parallel quadruplex (G4–M+–G4), and if the hydrogen bonds of the lower layer point in an opposite direction to that of the hydrogen bonds in the upper layer, the quadruplex is named anti-parallel, a-G4–M+–G4. The parallel stranded quadruplex is experimentally the prevalent arrangement under physiological conditions.3e–h
The energy of formation for the system with the backbone is formulated as follows:
| ΔEform = E(GQ–M+)aq − 4·E(GG)aq − E(M+)aq | (1b) |
2.2. Bond energy analysis
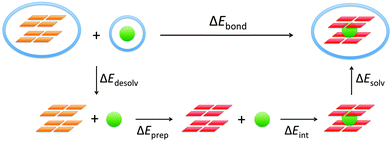
The bond energy between the alkali metal cation and the empty quadruplex scaffold is defined as follows:ΔEbond = E(G4–M+–G4)aq − E(G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)aq − E(M+)aq ]–G4)aq − E(M+)aq | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)aq is the energy of the optimized empty scaffold in water.
]–G4)aq is the energy of the optimized empty scaffold in water.
To understand the different factors that determine the affinity of the cavity of the quadruplex for the alkali metal cations, we have partitioned the bond energy as follows (see Fig. 3):
| ΔEbond = ΔEdesolv + ΔEprep + ΔEint + ΔEsolv | (3) |
The desolvation and solvation energy can be computed as the energy difference between the solvated and the gas phase. The ‘aq’ subscript denotes the COSMO computations in aqueous solution and ‘gas’ the computations in the gas phase.
ΔEdesolv = E(G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)gas − E(G4–[ ]–G4)gas − E(G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)aq + E(M+)gas − E(M+)aq ]–G4)aq + E(M+)gas − E(M+)aq | (4) |
| ΔEsolv = E(G4–M+–G4)aq − E(G4–M+–G4)gas | (5) |
The preparation energy, ΔEprep, is the energy required in the gas phase to deform the empty quadruplex scaffold with the geometry of the solvated state to the geometry it acquires when it is coordinated with the metal cation in the solvated state. (The values of the preparation energy have been checked to be almost phase independent, see Table S2, ESI.‡)
This partitioning of the bond energy allows us to compute the interaction energy:
ΔEint = E(G4–M+–G4)gas − E(G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)gas − E(M+)gas ]–G4)gas − E(M+)gas | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4)gas are computed in the gas phase for the geometries of the solvated state. This approximation is justified as the actual interaction between the alkali metal cation and the guanine bases occurs at the inner center of the quadruplex, which is shielded by the backbone and other bases from the aqueous environment (the relative negative charge of the cavity prevents water from accessing).
]–G4)gas are computed in the gas phase for the geometries of the solvated state. This approximation is justified as the actual interaction between the alkali metal cation and the guanine bases occurs at the inner center of the quadruplex, which is shielded by the backbone and other bases from the aqueous environment (the relative negative charge of the cavity prevents water from accessing).
Eqn (2)–(7) presented for the two parallel layers of guanine quartets, that is without a sugar-phosphate backbone, are also used for the anti-parallel layers and quadruplexes with a backbone, neutralized by H+ or Na+. G4–M+–G4 is replaced by, respectively, a-G4–M+–G4, GQ–M+ or GQ4Na–M+ and the empty scaffold G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4 is replaced by, respectively, a-G4–[
]–G4 is replaced by, respectively, a-G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4, GQ or GQ4Na, where GQ (or GQ4Na) stands for the guanine quadruplex with a sugar-phosphate backbone.
]–G4, GQ or GQ4Na, where GQ (or GQ4Na) stands for the guanine quadruplex with a sugar-phosphate backbone.
The interaction energy in this model is examined in the framework of the Kohn–Sham molecular orbital theory using a quantitative energy decomposition analysis (EDA) which divides the total interaction (ΔEint) into electrostatic interaction, Pauli repulsion, orbital interaction, and dispersion terms:12
| ΔEint = ΔVelstat + ΔEPauli + ΔEoi + ΔEdisp | (7) |
The term ΔVelstat corresponds to the classical electrostatic interactions between the unperturbed charge distributions of the prepared (i.e. deformed) bases and is usually attractive. The Pauli repulsion ΔEPauli comprises the destabilizing interactions between the occupied orbitals and is responsible for any steric repulsion. The orbital interaction ΔEoi accounts for the charge transfer (i.e., donor–acceptor interactions between occupied orbitals on one moiety and unoccupied orbitals on the other moiety, including the HOMO–LUMO interactions) and polarization (empty–occupied orbital mixing on one fragment due to the presence of another fragment). The term ΔEdisp accounts for dispersion corrections.
2.3. Voronoi density deformation analysis
The Voronoi density deformation (VDD) method allows us to analyze the electronic redistributions within polyatomic fragments when a chemical bond is formed between these molecular fragments.16 We have computed the VDD changes in atomic charges for the alkali metal ions in the central cavity. ΔQM+ is computed as the (numerical) integral of the deformation density Δρ(r) associated with the formation of the quadruplex from the empty scaffold and the metal cation in the volume of the Voronoi cell of cation M+ (eqn (8a) and (8b)). The Voronoi cell of M is defined as the compartment of space bounded by the bond midplanes on and perpendicular to all bond axes between nucleus M and its neighboring nuclei.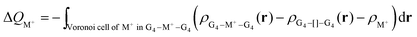 | (8a) |
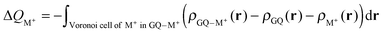 | (8b) |
ΔQM+ monitors how much charge flows out of (ΔQM+ > 0) or into (ΔQM+ < 0) the Voronoi cell of cation M+ as a result of chemical bond formation between fragment M+ and G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4 or GQ in the quadruplex.
]–G4 or GQ in the quadruplex.
3. Results and discussion
3.1. Structure and energy of formation
To study the interaction between the different alkali metal ions and the guanine bases in the naturally occurring quadruplexes, we have investigated computationally four model systems: G4–M+–G4, a-G4–M+–G4, GQ–M+ and GQ4Na–M+ (see Fig. 4). The latter two contain also the sugar-phosphate backbone, and are terminated by H+ or Na+ to compensate the negative charge of the phosphate.17 The geometrical parameters and the energies of formation are presented in Table 1.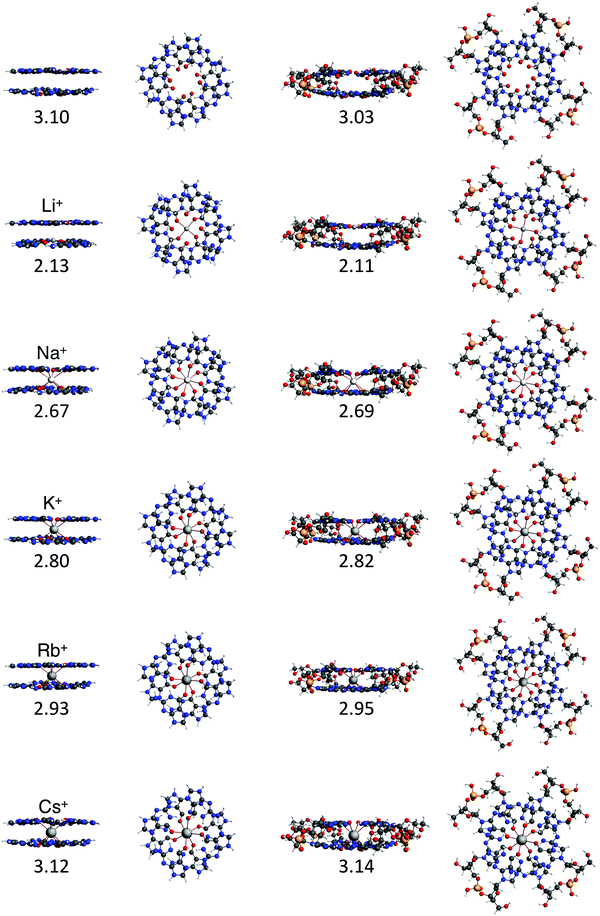 | ||
Fig. 4 Structures of G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4, G4–M+–G4, GQ and GQ–M+ where M+ is an alkali metal cation (optimized at the ZORA-BLYP-D3(BJ)/TZ2P level of theory). ]–G4, G4–M+–G4, GQ and GQ–M+ where M+ is an alkali metal cation (optimized at the ZORA-BLYP-D3(BJ)/TZ2P level of theory). | ||
| System | M+ | d[O–M+]b | R | N2(H)⋯N7d | N1(H)⋯O6e | ΔEform |
|---|---|---|---|---|---|---|
| a Energies and geometries computed at the ZORA-BLYP-D3(BJ)/TZ2P level of theory with COSMO to simulate water. b Average distance between the oxygen atoms and the alkali metal cation. For the empty scaffold the midpoint of the eight oxygen atoms was taken. c Difference in the average z-coordinate of the upper and lower oxygen atoms. d Average outer hydrogen bond distance N2(H)⋯N7. For Li+, this value is not presented, as the quartets are not equal (Li+ lies in the middle of one of the quartets). e Average inner hydrogen bond distance N1(H)⋯O6. | ||||||
| G4–M+–G4 | No metal | 3.10 | 3.60 | 2.88 | 2.80 | −84.4 |
| Li+ | 2.13 | 3.10 | −122.9 | |||
| Na+ | 2.67 | 2.91 | 2.84 | 2.82 | −138.4 | |
| K+ | 2.80 | 3.22 | 2.87 | 2.83 | −138.8 | |
| Rb+ | 2.93 | 3.58 | 2.89 | 2.84 | −132.7 | |
| Cs+ | 3.12 | 4.11 | 2.90 | 2.85 | −124.2 | |
| a-G4–M+–G4 | No metal | 3.14 | 3.60 | 2.90 | 2.82 | −86.2 |
| Na+ | 2.75 | 3.08 | 2.86 | 2.81 | −135.4 | |
| K+ | 2.84 | 3.27 | 2.89 | 2.83 | −137.3 | |
| Rb+ | 2.95 | 3.53 | 2.91 | 2.84 | −131.6 | |
| Cs+ | 3.12 | 4.04 | 2.92 | 2.86 | −123.8 | |
| GQ–M+ | No metal | 3.03 | 3.60 | 2.88 | 2.81 | −62.5 |
| Li+ | 2.11 | 3.34 | −100.2 | |||
| Na+ | 2.69 | 3.00 | 2.84 | 2.81 | −114.5 | |
| K+ | 2.82 | 3.33 | 2.88 | 2.82 | −115.4 | |
| Rb+ | 2.95 | 3.64 | 2.90 | 2.84 | −111.1 | |
| Cs+ | 3.14 | 4.16 | 2.90 | 2.86 | −103.1 | |
| GQ4Na–M+ | No metal | 3.09 | 3.60 | 2.90 | 2.82 | −67.6 |
| Na+ | 2.70 | 3.01 | 2.86 | 2.82 | −119.1 | |
| K+ | 2.83 | 3.33 | 2.89 | 2.84 | −120.4 | |
| Rb+ | 2.95 | 3.60 | 2.91 | 2.85 | −115.1 | |
The most stable complex is obtained in all cases with the potassium cation, fully consistent with the experimental findings. The difference between K+ and Na+ of ∼1 kcal mol−1 (shown in both backbone models) is completely in line with the experiments by Wong and Wu.8a The rest of the order of affinity is also nicely reproduced by our computations. The energies of formation for Na+ and Rb+ are larger than for Cs+ and Li+ cations. Improvement of the computational order of affinity is likely obtained by more realistic systems consisting of three layers and two cations. Cs+, which is too large to fit in the cavity, pulls away the oxygen atoms out of the plane of the quartet (see Fig. 4). Therefore, two Cs+ ions might be as difficult to accommodate as two Li+ ions in a 3-layer quadruplex, resulting in the same computed affinity as expected from the experiments.9
The computed values for the distances between the central cation and the oxygens, d[O–M+], are close to the experimental values. For GQ4Na–Na+, the computed average values are 2.70 Å and 2.65 Å in the crystal structure (see ref. 2h) and for GQ4Na–K+, the computed average value is 2.83 Å and the experimental values are 2.78 Å from a NMR structure (see ref. 2i) and 2.81 Å from a crystal structure (see ref. 2j). The small discrepancies can be attributed to the use of a two layer system in the computations.
Another important finding is that the parallel and the anti-parallel double layers show the same trend of affinity. Furthermore, in the simplified model of the experimental setting, that is without the sugar-phosphate backbone (as in G4–M+–G4), the values for the energy of formation follow the same trend as the values for GQ–M+ and GQ4Na–M+ and are also very close to the experimental order of affinity. This finding justifies the use of the guanine quartets alone in the studies of cation–quadruplex interactions and opens up the possibility to compute quantum chemically stacked systems with many layers.
3.2. Partitioning of the bond energy
To shed light on the obtained order of affinity of the quadruplex for the alkali metal cations, we have partitioned the bond energy (see eqn (2)) into different terms that are often mentioned as the determining factors for the experimental order of affinity: the desolvation of the cation and the size of the cation. In the computations, we can take all factors governing desolvation and solvation of the quadruplex and the cation into account, ΔEdesolv and ΔEsolv (eqn (4) and (5)). Furthermore, we can determine the effect of the size of the cation on the preparation energy ΔEprep and the interaction between the cation and the scaffold, ΔEint (eqn (6)). The preparation energy will be smaller when the size of the cation fits better into the central cavity of the quadruplex and the interaction energy will be larger for the cation with the best coordination with the negatively charged oxygen atoms. The different components of the bond energy are presented in Table 2 and Fig. 5 gives a graphical representation of these results for G4–M+–G4 (quadruplex without the backbone).| System | M+ | ΔEBond | ΔEdesolv | ΔEprep | ΔEprep,Hbondb | ΔEprep,Stack | ΔEint | ΔEsolv | ΔEdesolv + ΔEsolv |
|---|---|---|---|---|---|---|---|---|---|
| a Energies and geometries computed at the ZORA-BLYP-D3(BJ)/TZ2P level of theory. b Preparation energy of the lower and the upper G4 layer. | |||||||||
| G4–M+–G4 | Li+ | −38.5 | 201.3 | 12.9 | 11.4 | 1.5 | −161.5 | −91.1 | 110.1 |
| Na+ | −54.0 | 175.3 | 10.5 | 7.3 | 3.2 | −152.1 | −87.7 | 87.6 | |
| K+ | −54.4 | 157.6 | 5.5 | 3.8 | 1.8 | −128.8 | −88.8 | 68.8 | |
| Rb+ | −48.3 | 153.5 | 4.5 | 2.5 | 2.0 | −115.5 | −90.8 | 62.7 | |
| Cs+ | −39.8 | 147.5 | 6.2 | 2.4 | 3.8 | −99.6 | −94.0 | 53.6 | |
| a-G4–M+–G4 | Na+ | −49.2 | 175.7 | 10.2 | −145.8 | −89.3 | 86.4 | ||
| K+ | −51.1 | 158.0 | 6.6 | −126.6 | −89.2 | 68.2 | |||
| Rb+ | −45.4 | 153.9 | 5.8 | −114.7 | −90.5 | 63.5 | |||
| Cs+ | −37.6 | 148.0 | 8.6 | −99.2 | −95.0 | 53.0 | |||
| GQ–M+ | Li+ | −37.9 | 251.8 | 11.3 | −165.7 | −135.2 | 116.5 | ||
| Na+ | −52.2 | 225.8 | 10.4 | −156.6 | −131.8 | 94.0 | |||
| K+ | −53.2 | 208.1 | 5.7 | −134.7 | −132.2 | 75.9 | |||
| Rb+ | −48.8 | 204.0 | 0.9 | −119.1 | −134.6 | 69.4 | |||
| Cs+ | −40.9 | 198.1 | 1.8 | −104.4 | −136.3 | 61.7 | |||
| GQ4Na–M+ | Na+ | −50.2 | 328.7 | 10.7 | −170.9 | −218.7 | 110.0 | ||
| K+ | −51.4 | 311.0 | 5.1 | −148.8 | −218.8 | 92.2 | |||
| Rb+ | −46.2 | 306.9 | 5.3 | −137.3 | −221.0 | 85.9 | |||
The bond energies obtained for the different simplified systems, G4–M+–G4 with M+ being an alkali metal cation from Li+ to Cs+, match excellently the trend of the bond energies of the guanine quadruplexes that include the sugar-phosphate backbone neutralized by H+ or Na+ (see Table 2). These results permit computational analysis of the coordination of the cations with the guanine quadruplexes excluding the sugar-phosphate backbone.
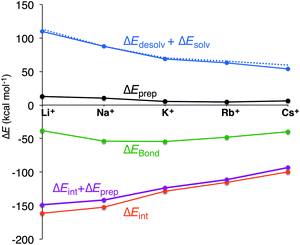
In all cases, the large interaction energy is compensated by the large desolvation energy. Fig. 5 shows that the sum of ΔEdesolv and ΔEsolv follows almost exactly the trend of the experimental desolvation energy of the alkali metal cation (blue dotted line).18 The preparation energy is small compared to the other components of the bond energy and does not change as much as the interaction energy or the desolvation energy going from Li+ to Cs+. The preparation energy becomes smaller as the size of the cation becomes larger, and then increases again for Cs+ as this cation does not fit anymore in the cavity (see the increase of ΔEprep,Stack in Table 2). This result can be understood from cation–oxygen distances d[O–M+] and inter-plane distance R as presented in Table 1. These parameters determine the size of the central cavity. In the empty scaffold, G4–M+–G4, these distances amount to respectively 3.10 Å and 3.60 Å. The sodium cation decreases the size of the central cavity to respectively 2.67 Å and 2.91 Å, whereas cesium enlarges the cavity to 3.12 Å for d[O–M+] and 4.11 Å for R (see also Fig. 4 for the deformation of the central cavity in the quadruplex). For the larger cations, K+ and Rb+, the size of the central cavity is closer to the size of the cavity in the empty scaffold, and thus, these cations give less distortion of the empty scaffold.
For G4–M+–G4, the preparation energy of the quadruplex scaffold can be partitioned in the preparation of the upper and the lower G4 quartet, ΔEprep,Hbond, and the preparation involving the stacking interaction between two G4 units, ΔEprep,Stack. The latter has the smallest value for K+ of 1.8 kcal mol−1, which corresponds to a better fit for K+. However, the energy differences in ΔEprep,Stack are so small compared to the other energy terms that ΔEprep,Stack is not the decisive factor. ΔEprep,Hbond goes from 7.3 kcal mol−1 to 2.4 kcal mol−1 from Na+ to Cs+. (The smallest cation, Li+, cannot be compared to the other ones as it coordinates in the middle of a quartet and not in the middle between two quartets as the other cations.) The outer hydrogen bond distance, N2(H)⋯N7, increases from 2.84 to 2.90 Å and the inner hydrogen bond distance, N1(H)⋯O6, increases from 2.82 Å to 2.85 Å for Na+ to Cs+. Both hydrogen bond distances increase with the size of the cation, as expected. However, the outer hydrogen bond starts for Na+ with a distance of 2.84 Å, which is smaller than for the empty scaffold and for Cs+ it has a distance of 2.90 Å, which is almost the same as for the empty scaffold (2.88 Å). The inner hydrogen bond is always larger for these cationic complexes compared to the empty scaffold.
In the empty scaffold (with no backbone), adjacent oxygen atoms in the same plane are at a distance of 3.33 Å from each other. We have investigated whether these oxygen atoms experience a repulsive interaction between each other as mentioned in the literature.6a For that purpose, we have substituted all the guanines in the empty scaffold by formaldehyde, while keeping C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O6 at the same position in space and for the hydrogen atoms only the x and y coordinates are reoptimized (see Fig. S1 and Table S3, ESI‡). The computed interaction energy between these eight formaldehydes amounts to 0.0 kcal mol−1 (see Table S3, ESI‡). This is due to the cancellation of the small repulsive and attractive energy terms (ΔEPauli = 9.1 kcal mol−1, ΔVelstat = 6.8 kcal mol−1, ΔEoi = −5.7 kcal mol−1 and ΔEdisp = −10.1 kcal mol−1). The alkali metal cation in the central cavity is therefore not needed to relieve electrostatic repulsion between the oxygen atoms. The empty scaffold forms a stable structure. The metal cation is however essential for the much larger energy of formation it provides in aqueous solution (see Table 1). This is in line with experimental findings that the quadruplexes cannot be formed in the absence of metal cations.1b
O6 at the same position in space and for the hydrogen atoms only the x and y coordinates are reoptimized (see Fig. S1 and Table S3, ESI‡). The computed interaction energy between these eight formaldehydes amounts to 0.0 kcal mol−1 (see Table S3, ESI‡). This is due to the cancellation of the small repulsive and attractive energy terms (ΔEPauli = 9.1 kcal mol−1, ΔVelstat = 6.8 kcal mol−1, ΔEoi = −5.7 kcal mol−1 and ΔEdisp = −10.1 kcal mol−1). The alkali metal cation in the central cavity is therefore not needed to relieve electrostatic repulsion between the oxygen atoms. The empty scaffold forms a stable structure. The metal cation is however essential for the much larger energy of formation it provides in aqueous solution (see Table 1). This is in line with experimental findings that the quadruplexes cannot be formed in the absence of metal cations.1b
To completely investigate the effect of size and desolvation of the cation on the affinity of the quadruplexes for the different cations, we have, besides summing up the desolvation and solvation energy terms, also taken the interaction energy and the preparation energy together. Note that the latter sum follows the trend of the interaction energy. Fig. 5 clearly shows that both desolvation (represented by the sum of ΔEdesolv + ΔEsolv) and ‘size’ of the cation (represented by ΔEint + ΔEprep) are of equal importance to determine the affinity. They are almost compensating each other resulting in a very shallow behavior of the bonding energy.
3.3. Energy decomposition analysis
In the previous section, we have pinpointed that the desolvation of the cation and the size of the cation are of equal importance. The latter is represented by the preparation energy of the empty quadruplex scaffold and the interaction energy between the cation and the empty scaffold. To get a better understanding of the interaction between the cation and the quadruplex, we have decomposed ΔEint into physically meaningful energy terms (see Table 3 and Fig. 6). The energy decomposition for all model systems follows exactly the same trend. The interaction energy in all systems (simplified, parallel and anti-parallel and full with H+ or Na+ to compensate for the negatively charged phosphate groups) suddenly drops from Na+ to K+, which counterbalances the smaller desolvation energy of K+. In the parallel simplified models, ΔEint amounts to −152.1 kcal mol−1 for Na+ and to −128.8 kcal mol−1 for K+. This decrease of interaction is not caused by the smaller electrostatic interaction or smaller orbital interaction as they become only 2.7 kcal mol−1 and 1.5 kcal mol−1 less binding in the case of G4–K+–G4 (see Table 3 for all systems). Clearly the Pauli repulsion, which increases by 21.5 kcal mol−1 from Na+ to K+ for G4–M+–G4, is responsible for the decrease in interaction energy from Na+ to K+ (see also Fig. 6). Note that for all model systems this sudden increase only occurs from sodium to potassium, but not from K+ to Rb+ or Rb+ to Cs+.| System | M+ | ΔEint | ΔEPauli | ΔVelstat | ΔEoi | ΔEdisp | ΔQM+ | P virtuals | ε LUMO[M+] |
|---|---|---|---|---|---|---|---|---|---|
| a Energies and geometries computed at the ZORA-BLYP-D3(BJ)/TZ2P level of theory. (Energies in kcal mol−1, population in electrons and orbital energies in eV.) b P virtuals is the sum of the gross Mulliken population of the LUMO till LUMO+9. | |||||||||
| G4–M+–G4 | Li+ | −161.5 | 11.9 | −110.3 | −55.1 | −8.0 | −0.137 | 0.25 | −7.4 |
| Na+ | −152.1 | 10.9 | −107.0 | −43.3 | −12.6 | −0.079 | 0.25 | −7.7 | |
| K+ | −128.8 | 32.4 | −104.3 | −41.8 | −15.0 | −0.058 | 0.13 | −6.3 | |
| Rb+ | −115.5 | 37.4 | −97.4 | −39.3 | −16.2 | −0.054 | 0.15 | −6.2 | |
| Cs+ | −99.6 | 40.8 | −86.7 | −37.1 | −15.9 | −0.060 | 0.12 | −5.7 | |
| a-G4–M+–G4 | Na+ | −145.7 | 8.0 | −99.6 | −40.9 | −13.3 | −0.080 | 0.24 | −7.7 |
| K+ | −126.6 | 28.0 | −99.3 | −40.1 | −15.1 | −0.056 | 0.10 | −6.3 | |
| Rb+ | −114.6 | 35.9 | −95.5 | −38.7 | −16.3 | −0.053 | 0.13 | −6.2 | |
| Cs+ | −99.2 | 41.2 | −86.7 | −37.7 | −15.9 | −0.060 | 0.12 | −5.7 | |
| GQ–M+ | Li+ | −165.7 | 13.2 | −112.8 | −58.3 | −7.7 | −0.142 | 0.27 | −7.4 |
| Na+ | −156.6 | 11.1 | −109.3 | −45.2 | −13.1 | −0.079 | 0.26 | −7.7 | |
| K+ | −134.7 | 29.9 | −106.2 | −43.2 | −15.2 | −0.057 | 0.15 | −6.3 | |
| Rb+ | −119.1 | 35.2 | −97.1 | −40.9 | −16.5 | −0.054 | 0.17 | −6.2 | |
| Cs+ | −104.4 | 39.1 | −88.0 | −39.4 | −16.1 | −0.059 | 0.14 | −5.7 | |
| GQ4Na–M+ | Na+ | −170.9 | 10.1 | −123.1 | −44.8 | −13.0 | −0.079 | 0.25 | −7.7 |
| K+ | −148.7 | 28.9 | −119.5 | −42.9 | −15.2 | −0.057 | 0.12 | −6.3 | |
| Rb+ | −137.2 | 35.0 | −114.9 | −40.9 | −16.5 | −0.054 | 0.14 | −6.2 | |
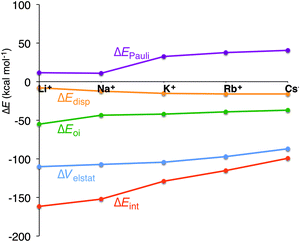 | ||
Fig. 6 Energy decomposition of the interaction energy (kcal mol−1) between the alkali metal cation and the empty scaffold of G4–[![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ]–G4 (see eqn (7)). ]–G4 (see eqn (7)). | ||
The energy decomposition also reveals that the interaction between the cation and the guanines is not a pure electrostatic interaction. The orbital interaction is about half the size of the electrostatic interaction (see Table 3) and together with the dispersion, the three terms account for the bonding components in this coordination. The main contribution to the orbital interaction is the donation of electronic density from the highest occupied orbitals of the guanines (mostly the σ lone pair on the oxygen atoms) to the lowest unoccupied orbitals of the alkali metal cation. The largest donor–acceptor interactions occur for the smaller cations Li+ and Na+, as they have a smaller distance to the oxygens (see d[O–M+] in Table 1). The VDD change in atomic charge, ΔQM+, amounts to −0.137 electrons for Li+ to −0.060 for Cs+ and Pvirtuals (sum of the gross Mulliken population of the LUMO till LUMO+9) equals 0.25 electrons for Li+ to 0.12 electrons for Cs+. Both confirm the charge-transfer interaction between guanines and the cation.
The distance between the metal cation and the oxygen atoms of the guanines increases from Li+ to Cs+. This has a direct effect on the electrostatic and orbital interactions as they are distance dependent. Table 3 shows that the energy of the LUMO of the cation does not correlate with the orbital interaction. However, if K+ is computed in the scaffold of Na+, that is K+ in a smaller cavity (GQNa), and Na+ in the scaffold of K+, that is in a larger cavity (GQK), the orbital interaction follows the trend of the LUMO of the cation. At the same d[O–M+], the orbital interaction is larger for K+ than for Na+. The lower LUMO of K+ gives a stronger donor–acceptor interaction and thus a larger orbital interaction. The differences are however small (see Fig. 7).
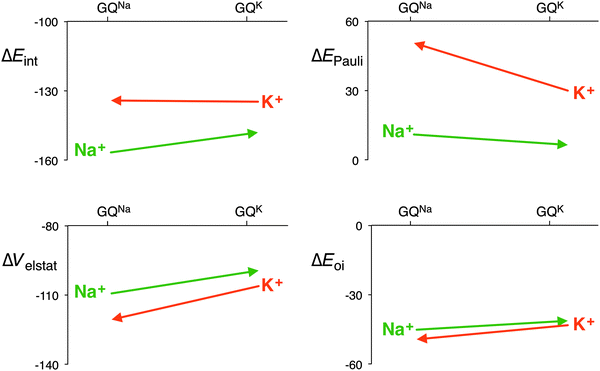 | ||
| Fig. 7 Interaction energy and the different energy terms of the decomposition for Na+ and K+ in each other’s scaffold (GQNa and GQK) with the sugar-phosphate backbone (kcal mol−1). | ||
The effect on the electrostatic interaction is more pronounced. At the shorter d[O–M+] distance, the electrostatic interaction for K+ amounts to −120.6 kcal mol−1, whereas for Na+ it is −109.3 kcal mol−1. The only reason why the potassium cation does not come closer to the oxygen atoms of the guanines is the Pauli repulsion. In the smaller cavity (GQNa), the Pauli repulsion for K+ is 20.6 kcal mol−1 larger than in the bigger cavity (GQK). But for Na+, the Pauli repulsion becomes only 4.7 kcal mol−1 smaller in the bigger cavity. The larger cation, that is the more diffuse cation K+, hits the repulsive wall of the Pauli repulsion between its own electrons and the lone pairs of the oxygen atoms, and thus, in a way, fits worse than the smaller Na+.
4. Conclusions
In this paper, we studied based on dispersion-corrected density functional theory the affinity of guanine quadruplexes for alkali metal ions. The self-assembly of supramolecular model systems, which have a parallel and an anti-parallel double layer of guanine quartets and a short telomeric quadruplex, was studied in aqueous solution. This self-assembly process benefits from the assistance by alkali metal cations. The computational results are very close to the experimental order of affinity and the strongest coordination was computed for K+, which is known to be the preferred alkali metal ion by the supramolecular and telomeric quadruplexes.Partitioning of the bond energy between the cation and the quadruplex into energy terms that can be associated with (de)solvation and with the size of the cation allowed us to shed light on an ongoing debate on the relevance of these two factors for the experimentally observed affinity. The computations revealed that the desolvation and size of the cation are of equal importance. As we descend the first group of the periodic table starting from lithium, the desolvation of the cation gradually becomes smaller; however at the same time, the attractive interaction between the cation and the quadruplexes also diminishes. This translates into a shallow minimum of the bond energy of the cation–quadruplex system, with its stationary point located at K+. The deformation of the quadruplex is small, particularly in the case of K+, Rb+ (and Cs+), for which the central cavity of the empty quadruplex scaffold almost matches the space needed to accommodate the larger cation between the eight oxygen atoms of the guanines.
Furthermore, our computations revealed that the cation in the central cavity is not needed to compensate the electrostatic repulsion between the oxygen atoms of the guanines, as they do not repel each other, but it is needed for extra stabilization of the quadruplex. The stabilizing interaction between the cation and the quadruplex is provided by electrostatic and donor–acceptor interactions. The latter are charge-transfer interactions between mainly the σ lone pair orbitals of the oxygens and the lowest unoccupied orbitals of the cation. Remarkably, the most important reason for the weaker interaction between K+ and the quadruplex than between Na+ and the quadruplex is almost not a reduction of the electrostatic interaction or the orbital interaction, as these two energy terms do not differ much for the two metal cations. It is however the Pauli repulsive wall, which the more diffuse potassium cation hits and does not allow it to go closer to the oxygen atoms. So, in this sense, K+ even fits worse than Na+.
This computational investigation has shown that the combination of large counteracting electronic and solvation effects together with small deformation of the molecular systems involved can determine very subtle phenomena observed in chemistry.
Acknowledgements
C. F. G. gratefully acknowledges the financial support from the Netherlands Organization for Scientific Research NWO (ECHO). G. P. would like to thank for the Marie Curie Intra European Fellowship within the 7th European Community Framework Programme for the financial support.References
- (a) Quadruplex Nucleic Acids, ed. S. Neidle and S. Balasubramanian, RSC Publishing, Cambridge, 2006 Search PubMed; (b) J. T. Davis, Angew. Chem., Int. Ed., 2004, 43, 668 CrossRef CAS PubMed; (c) M. L. Bochman, K. Paeschke and V. A. Zakian, Nat. Rev. Genet., 2012, 13, 770–780 CrossRef CAS PubMed; (d) D. Sen and W. Gilbert, Nature, 1988, 334, 364–366 CrossRef CAS PubMed; (e) E. Henderson, C. C. Hardin, S. K. Walk, I. Tinoco Jr. and E. H. Blackburn, Biochemistry, 1987, 51, 899–908 CAS; (f) W. I. Sundquist and A. Klug, Nature, 1989, 342, 825–829 CrossRef CAS PubMed.
- (a) Guanine Quartets: Structure and Application, ed. W. Fritzsche and L. Spindler, RSC Publishing, Cambridge, 2012 Search PubMed; (b) S. Neidle, Therapeutic Applications of Quadruplex Nucleic Acids, Elsevier, 2012 Search PubMed; (c) S. Balasubramanian, L. H. Hurley and S. Neidle, Nat. Rev. Drug Discovery, 2011, 10, 261–275 CrossRef CAS PubMed; (d) S. N. Georgiades, N. H. AbdKarim, K. Suntharalingam and R. Vilar, Angew. Chem., Int. Ed., 2010, 49, 4020–4034 CrossRef CAS PubMed; (e) D. Rhodes and H. J. Lipps, Nucleic Acids Res., 2015, 43, 8627–8637 CrossRef CAS PubMed; (f) S. Ray, J. N. Bandaria, M. H. Qureshi, A. Yildiz and H. Balci, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(8), 2990–2995 CrossRef CAS PubMed; (g) G. Biffi, M. Di Antonio, D. Tannahill and S. Balasubramanian, Nat. Chem., 2014, 6, 75–80 CrossRef CAS PubMed; (h) C. Creze, B. Rinaldi and P. Gouet, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2007, 63, 682–688 CrossRef CAS PubMed; (i) Y. Wang and D. J. Patel, J. Mol. Biol., 1993, 234, 1171–1183 CrossRef CAS PubMed; (j) G. N. Parkinson, M. P. H. Lee and S. Neidle, Nature, 2002, 417, 876–880 CrossRef CAS PubMed.
- (a) D. González-Rodríguez, J. L. J. van Dongen, M. Lutz, A. L. Spek, A. P. H. J. Schenning and E. W. Meijer, Nat. Chem., 2009, 1, 151 CrossRef PubMed; (b) A. Virgilio, V. Esposito, A. Randazzo, L. Mayol and A. Galeone, Nucleic Acids Res., 2005, 33, 6188–6195 CrossRef CAS PubMed; (c) V. Esposito, A. Virgilio, A. Randazzo, A. Galeone and L. Mayol, Chem. Commun., 2005, 3953–3955 RSC; (d) G. I. Livshits, Nat. Nanotechnol., 2014, 9, 1040–1046 CrossRef CAS PubMed; (e) E. Largy, A. Marchand, S. Amrane, V. Gabelica and J.-L. Mergny, J. Am. Chem. Soc., 2016, 138, 2780–2792 CrossRef CAS PubMed; (f) S. L. Palumbo, S. W. Ebbinghaus and L. H. Hurley, J. Am. Chem. Soc., 2009, 131, 10878–10891 CrossRef CAS PubMed; (g) J. Seenisamy, E. M. Rezler, T. J. Powell, D. Tye, V. Gokhale, C. S. Joshi, A. Siddiqui-Jain and L. H. Hurley, J. Am. Chem. Soc., 2004, 126, 8702–8709 CrossRef CAS PubMed; (h) T. Phan, Y. S. Modi and D. J. Patel, J. Am. Chem. Soc., 2004, 126, 8710–8716 CrossRef PubMed; (i) H. Fernando, A. P. Reszka, J. Huppert, S. Ladame, S. Rankin, A. R. Venkitaraman, S. Neidle and S. Balasubramanian, Biochemistry, 2006, 45, 7854–7860 CrossRef CAS PubMed.
- (a) C. Fonseca Guerra, H. Zijlstra, G. Paragi and F. M. Bickelhaupt, Chem. – Eur. J., 2011, 17, 12612–12622 CrossRef CAS PubMed; (b) L. P. Wolters, N. W. G. Smits and C. Fonseca Guerra, Phys. Chem. Chem. Phys., 2015, 17, 1585–1592 RSC.
- (a) L. Guillaumes, S. Simon and C. Fonseca Guerra, ChemistryOpen, 2015, 4, 318–327 CrossRef CAS PubMed; (b) C. Fonseca Guerra, F. M. Bickelhaupt and E. J. Baerends, ChemPhysChem, 2004, 5, 481–487 CrossRef PubMed; (c) C. Fonseca Guerra, Z. Szekeres and F. M. Bickelhaupt, Chem. – Eur. J., 2011, 17, 8816–8818 CrossRef CAS PubMed; (d) J. Poater, M. Swart, F. M. Bickelhaupt and C. Fonseca Guerra, Org. Biomol. Chem., 2014, 12, 4691–4700 RSC.
- (a) J.-L. Mergny, A. De Cian, A. Ghelab, B. Saccà and L. Lacroix, Nucleic Acids Res., 2005, 33, 81–94 CrossRef CAS PubMed; (b) J. R. Williamson, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 703–730 CrossRef CAS PubMed; (c) J. Gu, J. Leszczynski and M. Bansal, Chem. Phys. Lett., 1999, 311, 209–214 CrossRef CAS; (d) Z. Wang and J.-P. Liu, Clin. Exp. Pharmacol. Physiol., 2015, 42, 902–909 CrossRef CAS PubMed; (e) W. S. Ross and C. C. Hardin, J. Am. Chem. Soc., 1994, 116, 6070–6080 CrossRef CAS; (f) I. V. Smirnov and R. H. Shafer, Biopolymers, 2006, 85, 91–101 CrossRef PubMed; (g) E. Largy, J.-L. Mergny and V. Gabelica, Met. Ions Life Sci., 2016, 16, 203–258 Search PubMed.
- (a) Y. P. Yurenko, J. Novotny, V. Sklenár and R. Marek, Phys. Chem. Chem. Phys., 2014, 16, 2072–2084 RSC; (b) S. Chowdhury and M. Bansal, J. Phys. Chem. B, 2001, 105, 7572–7578 CrossRef CAS; (c) W. Eimer and J. Tohl, J. Mol. Model., 1996, 2, 327–329 CrossRef; (d) K. Gkionis, H. Kruse, J. A. Platts, A. Mládek, J. Koča and J. Šponer, J. Chem. Theory Comput., 2014, 10, 1326–1340 CrossRef CAS PubMed.
- (a) A. Wong and G. Wu, J. Am. Chem. Soc., 2003, 125, 13895–13905 CrossRef CAS PubMed; (b) C. Detellier and P. Laszlo, J. Am. Chem. Soc., 1980, 102, 1135–1141 CrossRef CAS; (c) T. J. Pinnavaia, C. L. Marshall, C. M. Mettler, C. L. Fisk, H. T. Miles and E. D. Becker, J. Am. Chem. Soc., 1978, 100, 3625–3627 CrossRef CAS; (d) R. Ida and G. Wu, J. Am. Chem. Soc., 2008, 130, 3590–3602 CrossRef CAS PubMed.
- (a) J. Williamson, M. Raghuraman and T. Cech, Cell, 1989, 59, 871–880 CrossRef CAS PubMed; (b) N. V. Hud, F. W. Smith, F. A. Anet and J. Feigon, Biochemistry, 1996, 35, 15383–15390 CrossRef PubMed; (c) J. Gu and J. Leszczynski, J. Phys. Chem. A, 2002, 106, 529–532 CrossRef CAS.
- G. Eisenman and R. Horn, J. Membr. Biol., 1983, 225, 197–225 CrossRef.
- (a) S. Grimme, J. Anthony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed; (c) S. Grimme, J. Comput. Chem., 2004, 25, 1463 CrossRef CAS PubMed; (d) S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed; (e) C. Fonseca Guerra, T. van der Wijst, J. Poater, M. Swart and F. M. Bickelhaupt, Theor. Chem. Acc., 2010, 125, 245 CrossRef; (f) T. van der Wijst, C. Fonseca Guerra, M. Swart, F. M. Bickelhaupt and B. Lippert, Angew. Chem., Int. Ed., 2009, 48, 3285 CrossRef CAS PubMed.
- F. M. Bickelhaupt and E. J. Baerends, in Rev. Comput. Chem., ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, S. J. A. van Gisbergen, C. Fonseca Guerra, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, et al., ADF2014.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com Search PubMed.
- (a) A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC; (b) A. Klamt, J. Phys. Chem., 1995, 99, 2224 CrossRef CAS; (c) C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396 CrossRef CAS; (d) T. van der Wijst, C. Fonseca Guerra, M. Swart, F. M. Bickelhaupt and B. Lippert, Angew. Chem., Int. Ed., 2009, 48, 3285–3287 CrossRef CAS PubMed.
- (a) C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210 CrossRef PubMed; (b) O. A. Stasyuk, H. Szatylowicz, T. M. Krygowski and C. Fonseca Guerra, Phys. Chem. Chem. Phys., 2016, 18, 11624–11633 RSC.
- (a) G. Barone, C. Fonseca Guerra and F. M. Bickelhaupt, ChemistryOpen, 2013, 2, 186–193 CrossRef CAS PubMed; (b) C. Fonseca Guerra, F. M. Bickelhaupt, J. G. Snijders and E. J. Baerends, J. Am. Chem. Soc., 2000, 122, 4117–4128 CrossRef.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999 RSC.
Footnotes |
| † Dedicated to Professor Evert Jan Baerends on the occasion of his 70th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp01030j |
| This journal is © the Owner Societies 2016 |