Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First hyperpolarizability of para-aminoaniline induced by a variety of gold nano particles
Stine T.
Olsen
and
Kurt V.
Mikkelsen
*
Department of Chemistry, University of Copenhagen, Copenhagen, Denmark. E-mail: stine.olsen@chem.ku.dk; kmi@chem.ku.dk
First published on 18th August 2016
Abstract
Molecules exposed to an electromagnetic field due to the presence of nearby nanoparticles are known to be affected. The nonlinear response of the molecular system, the first hyperpolarizability, is investigated for 4-nitroaniline (PNA) in a variety of different nanoparticle environments. In order to introduce different molecular environments the quantum mechanical–molecular mechanics DFT/MM response method was utilized for calculating the electromagnetic properties of the molecule interacting with the nanoparticles and the frequency dependent electromagnetic fields. We clearly show that the metal nanoparticles are able to influence the first hyperpolarizability of the molecule, and that the influence strongly depends on the chosen molecular environment. It is found that the first hyperpolarizability of the molecule strongly depends on the distance and orientation to the nanoparticles, whereas the size of the nanoparticles is of little importance when a sufficiently sized nanoparticle is used for representing a bulk metal cluster. Especially, the different orientations of the nanoparticles with respect to the molecule show the chemical effect of different functional groups, since the nonlinear response is significantly larger for the electron withdrawing group pointing towards the nanoparticle.
I. Introduction
The development of methods for optical detection and spectroscopy of nano scale systems has been the focus of numerous research projects and articles. These developments are crucial for investigating and understanding the novel properties that are encountered when working with nanosize systems. Generally the methods involve how the nanosize systems are able to absorb or scatter electromagnetic radiation and the observed effects are either based on whether the interactions with the electromagnetic field are linear or nonlinear with respect to the field strengths of the electromagnetic fields. Based on these methods, it is possible to focus on the key roles that are played by the presence of a molecular compound placed on or within a nanoparticle and it is possible to investigate linear and nonlinear optical responses of the molecular systems and how they are affected by the presence of the nanoparticle.1 Nonlinear effects such as the two-photon absorption of molecules attached to nanoparticles have also been investigated with respect to structure–property relationships and how electron donating and accepting groups have influenced the nonlinear effects.2 Another advantage of non-linear effects and nanoparticles is the possibility of doing up-converted fluorescence emission using organic dyes that undergo two-photon absorption or second-harmonic generation.3 It has also been demonstrated that multicomponent fluorescent organic nanoparticles can display an excitation energy-transfer cascade between the different molecular components within the system. Furthermore, the systems are able to undergo two-photon excitations over a broad spectral range (from 600 nm to 1200 nm) which brings a spectral range inside the biological transparency window. This aspect along with good colloidal stability in aqueous environments indicate that these are promising nanoprobes for bioimaging applications.4 Self-assembly systems forming nanoparticles based on ruthenium phthalocyaninate complexes coordinated by pyrazine have a nonlinear optical response depending on the fabrication of the systems and the study illustrates that self-assembly can be of importance in the future development of nonlinear optical materials.5In this article we will present a powerful and flexible strategy for calculating the optical properties of molecules near or between nanoparticles. Note that the geometries studied in this work are not representative of a fully formed molecular transport junction. Previously, we have utilized a heterogeneous dielectric continuum model for investigating the electrostatic properties of a molecular junction.6,7 In the present investigation we focus on how the environmental nanoparticles and the relative configurations of the molecule nanoparticle structures influence the electromagnetic properties of the attached molecular system. We demonstrate this by the use of a quantum mechanics/molecular mechanics (QM/MM) response model that allows for an atomistic description of the metal nanoparticles or electrodes. We have previously applied this method in order to obtain the linear and nonlinear optical properties of molecules in solution. These calculations have been performed at the Hartree–Fock (HF), coupled cluster (CC) and density functional theory (DFT) levels of electronic structure theory.8–18 We represent the molecular subsystem using a quantum mechanical approach and the molecule is treated fully quantum mechanically and the calculations of the electronic structure are carried out using the chosen electronic structure method. On the other hand the electrodes are treated at a classical level as a structured atomistic environment where each atom is assigned an isotropic atomic polarizability. The electromagnetic response of the electrodes is included as a dynamic electric field in the electronic structure calculations, and the entire problem is solved self-consistently. The electronic structure calculations are performed using density functional theory (DFT)19–32 using the B3LYP19,20 and CAM-B3LYP21 functionals. We perform QM/MM quadratic response calculations in order to determine the frequency dependent first hyperpolarizability of the molecular system interacting with one or two gold nanoparticles in various orientations with respect to the molecule. We are focussing on the first hyperpolarizability in the present investigation since our current research interests are within the non-linear optical properties and how to utilize these properties for interfaces, photon up conversion for information transport, quantum computers, and molecular information technology.
II. Computational strategy
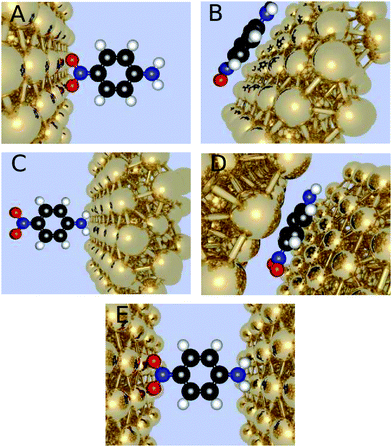
We have considered the frequency-dependent first hyperpolarizability of the molecule 4-nitroaniline (PNA) in the presence of zero, one, or two gold clusters of varying sizes and orientation with respect to the molecule. The orientation with the x-axis connecting the gold nanoparticles through the para connected groups of the amino and nitro substituents is referred to as horizontal positioned, and the one where the gold atoms have been rotated 90 degrees around the center as the vertical positioned. Furthermore, we investigate different molecule-electrode distances (Fig. 1).Initially, the geometry of PNA is optimized in Gaussian0933 utilizing DFT with the CAM-B3LYP functional together with the correlation consistent basis sets34,35 of cc-pVDZ, cc-pVTZ, aug-cc-pVDZ, and aug-cc-pVTZ. These geometries provided the basis for further calculations both for the molecule in a vacuum and in the presence of gold cluster(s).
However, in order to introduce the gold clusters at different distances, orientations, and cluster sizes we have to go beyond the commonly used method of the polarizable continuum model, PCM. We are thus utilizing the QM/MM response method implemented in the Dalton36 electronic structure program. The combined method of QM/MM implies a partitioning of the system into a part treated with the more flexible quantum mechanic approach and the other part treated with the simpler molecular mechanics approach.
The two regions are chosen such that the chemical part of interest is treated with QM and the less interesting part with MM, thus in this investigation it will imply the gold nanoparticles to be treated with MM and the molecule with QM. In the MM region the gold clusters are designed to be half-spheres by choosing a point at the x-axis and including all gold atoms within a finite radius. The binding site on the gold clusters is chosen to be a fcc site on a (111) surface, since previous research has indicated it to be the most likely point of attachment.37,38 In the case of two gold clusters, the second cluster is constructed similarly but inverted and translated along the same axis to the other side of the molecule at the desired distance. The investigated distances for the horizontal orientation of the molecule include 2.2 Å, 2.4 Å, and 2.6 Å when the electrodes face the nitro group, and we use the same electrode molecule distances when the electrodes face the amino group. For the vertical orientation of the molecule the shorter distances of 1.75 Å, 1.95 Å, and 2.15 Å are investigated, due to the shorter van der Waals distances. The gold clusters are geometrically frozen, and the gold atoms are not attributed to permanent electrical poles but assigned to a polarizability of 31.04 au3.
The QM region, i.e. the molecule, is treated as in the vacuum calculations, a DFT description with the functional of CAM-B3LYP together with the same correlation consistent basis sets. Thereby, the vacuum results can be considered as the gold clusters being placed at an infinite distance from the molecule and can be directly compared to the results with the clusters in a finite distance.
The calculations of the frequency-dependent first hyperpolarizability are performed for the following four frequencies (ω) of the external electromagnetic field: 0.0, 0.03, 0.042823, and 0.065625 au. We present the results as the frequency-dependent mean first hyperpolarizability in terms of β||(−2ω;ω,ω):
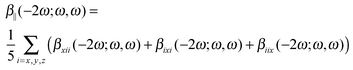 | (1) |
With the established method we are able to investigate both the theoretical as well as the chemical aspect of the first hyperpolarizability of a molecule in the presence of nano particles.
III. Results
The basis set dependence of the hyperpolarizability is depicted in Fig. 2. The relative trends are observed to be independent of the basis set. As is expected, the diffuse functions are observed to have a significant impact on the calculated hyperpolarizability compared to the number of basis functions. We note that the difference in the calculated hyperpolarizability using aug-cc-pVDZ and aug-cc-pVTZ basis sets is negligible, and thus we utilize the aug-cc-pVDZ basis set for further investigations.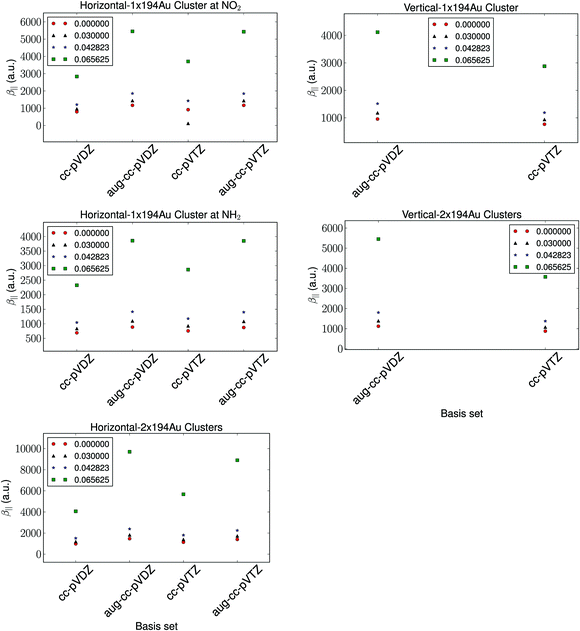 | ||
| Fig. 2 The basis set dependence of the hyperpolarizability with a fixed cluster size of 194 Au atoms and a fixed vertical distance of 1.95 Å and a horizontal distance of 2.4 Å. | ||
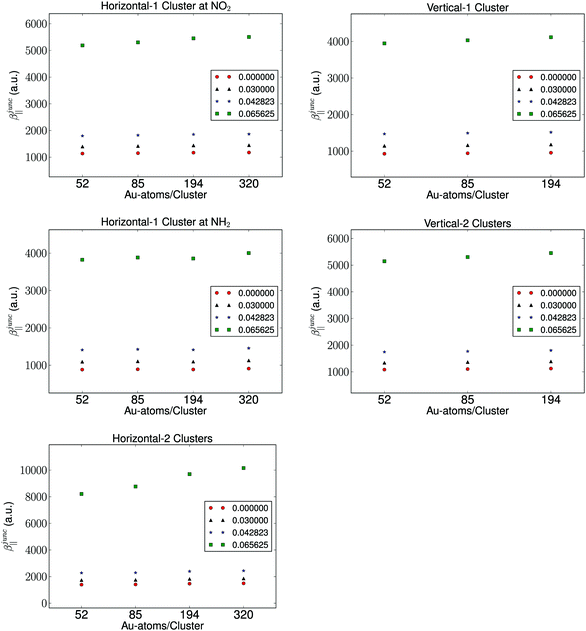
It is well known that the properties of a molecule are affected by a nearby field due to the presence of a metal. Therefore, the molecular hyperpolarizability of the attached molecule depends on the number of metal clusters, the size of the clusters, the orientation of the molecule with respect to the metal cluster(s), and the distance to the clusters. Results from these investigations are depicted in Fig. 3 and 4. We have plotted the difference in hyperpolarizability (βjunc) for the molecule next to the gold clusters and the hyperpolarizability (βvac) of the molecule in a vacuum. From the relative hyperpolarizabilities i.e. βjunc − βvac it is evident that the metal affects the hyperpolarizability of the molecule since the hyperpolarizability is increased significantly compared to the one in a vacuum. We also note that the effect is substantial for the external electromagnetic field of high frequency.
 | ||
| Fig. 3 The cluster size and number dependence of the hyperpolarizability with fixed distance and computational method. | ||
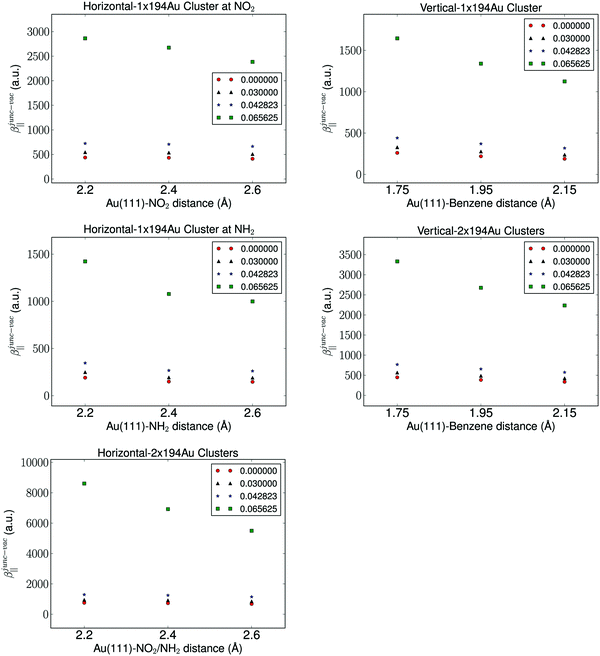 | ||
| Fig. 4 The molecule-electrode distance dependence of the hyperpolarizability with the fixed parameter of a cluster size of 194 Au atoms and the aug-cc-pVDZ basis set. | ||
In the presence of one cluster of gold atoms, we observe that with increasing cluster size of the gold cluster the hyperpolarizability increases, however, the increase is not significant. On the other hand, for the configurations having two gold clusters, we observe a more significant effect on the hyperpolarizabilites as the cluster size is increased. As is expected, the increase in the hyperpolarizabilities is larger for the external electromagnetic fields of higher frequency. However, the effect of increasing the cluster size decreases with increasing cluster size, indicating that we have utilized gold nanoparticles of a sufficient size in order to represent a bulk metal cluster.
We find by varying the distance between the molecule and one cluster with fixed size that the hyperpolarizability decreases with increased distance to the cluster, and this is of course due to the weaker interactions between the molecule and the electrode as the distance between the molecule and the cluster becomes larger. In the case of the molecule placed between two gold clusters, we observe a similar decrease in the effect of the gold clusters on the calculated hyperpolarizabilities. Furthermore, we note that the distance dependence on the hyperpolarizability is larger than the effects related to the size of the gold clusters.
The chemical interpretation of the hyperpolarizability in the context of the orientation of the metal clusters is interesting. It is observed that the hyperpolarizability is significantly larger for one cluster placed horizontally at the nitro group compared to an orientation where the amino group is closest to the gold cluster. The hyperpolarizability depends also on the molecular orientation whether it is placed horizontally or vertically. This effect is due to that large charge separation in the NO2 group and this leads to a larger polarization of the gold cluster. The effect of the type of linker group on the electrodes also manifests in the results of two clusters. The more directly-connected molecule in the horizontal orientation in the junction has a significantly larger hyperpolarizability than the less directly-linked molecule in the vertical position in the junction. We note that the effect of the electron withdrawing group near a metal surface is significant, since the hyperpolarizability of the molecule placed near one cluster facing the nitro group is comparable in magnitude to that of the molecule placed vertically between two clusters.
IV. Conclusion
We have presented a theoretical method and computations of the effects of nanoparticles on frequency dependent first hyperpolarizabilities of molecules. We have utilized quantum mechanical–molecular mechanics (QM/MM) response methods for calculating the electromagnetic properties of molecules interacting with nanoparticles and frequency dependent electromagnetic fields. The frequency dependent first hyperpolarizability of PNA in the presence of zero, one or two gold nanoparticles of varying sizes, orientations and distances is calculated by DFT/MM. The hyperpolarizability of the molecule depends strongly on the distance and orientations between the nanoparticles and the molecule whereas the size of the nanoparticle is of little importance but it could be of interest to perform molecular dynamics simulations of the systems and calculate the macroscopic properties.42 We clearly show that metal nanoparticles are able to influence the first hyperpolarizability of the molecules. Investigations concerning the importance of a quantum description of small metal particles have illustrated the importance of including metal atoms in the quantum mechanical description.41 The plasmon response (the oscillations of free electron density against the fixed positive ions in a metal) of the gold cluster is not included and nevertheless we observe an induced hyperpolarizability in PNA. Recent investigations43 have addressed the importance of introducing models for the classical subsystem where a capacitor model has been used for including the charge redistribution in the metal clusters and this model will be utilized in our future investigations of the nonlinear optical properties of organic molecules attached to metal particles.Acknowledgements
KVM thanks the Danish Research Council, Center for the Exploitation of Solar Energy, and the Danish e-Infrastructure Cooperation for financial support.References
- A. Crut, P. Maioli, N. D. Fatti and F. Vallee, Chem. Soc. Rev., 2014, 43, 3921 RSC.
- I. F. A. Mariz, E. M. S. Macoas, J. M. G. Martinho, L. Zho, P. Zhou, X. Chen and J. Qin, J. Mater. Chem. B, 2013, 1, 2169 RSC.
- Y. Ji and Y. Qian, RSC Adv., 2014, 4, 52485 RSC.
- E. Campioli, D. M. Nikolaidou, V. Hugeus, M. Campanini, L. Nasi, M. Blanchard-Desce and F. Terenziani, J. Mater. Chem. C, 2015, 3, 7483 RSC.
- Y. G. Gorbunova, A. D. Grishina, A. G. Martynov, T. V. Krivenko, A. A. Isakova, V. V. Savelev, S. E. Nefedov, E. V. Abkhalimov, A. V. Vannikov and A. Y. Tsivadze, J. Mater. Chem. C, 2015, 3, 6692 RSC.
- T. Hansen and K. V. Mikkelsen, Theor. Chem. Acc., 2004, 111, 122 CrossRef CAS.
- T. Hansen, T. B. Pedersen and K. V. Mikkelsen, Chem. Phys. Lett., 2005, 405, 118 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Phys. Chem. A, 2003, 107, 2578 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2003, 118, 1620 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2003, 119, 10519 CrossRef CAS.
- J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, J. Chem. Phys., 2004, 120, 3787 CrossRef CAS PubMed.
- K. V. Mikkelsen, Y. Luo, H. Ågren and P. Jørgensen, J. Chem. Phys., 1994, 100, 8240 CrossRef CAS.
- Y. Luo, H. Ågren, P. Jørgensen and K. V. Mikkelsen, Adv. Quantum Chem., 1995, 26, 165 CrossRef CAS.
- P. Norman, Y. Luo, D. Jonsson, K. O. Sylvester-Hvid, K. V. Mikkelsen and H. Agren, J. Chem. Phys., 1997, 107, 9063 CrossRef CAS.
- K. V. Mikkelsen, Annu. Rev. Phys. Chem., 2006, 57, 365 CrossRef CAS PubMed.
- C. B. Nielsen, O. Christiansen, K. V. Mikkelsen and J. Kongsted, J. Chem. Phys., 2007, 126, 154112 CrossRef PubMed.
- T. Hansen, A Molecule Wired, PhD thesis, University of Copenhagen, 2005 Search PubMed.
- S. T. Olsen, T. Hansen and K. V. Mikkelsen, Theor. Chem. Acc., 2011, 130, 839–850 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- F. Jensen, Introduction to Computational Chemistry, Wiley, New York, 2nd edn, 2007 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- O. V. Gritsenko, P. R. T. Schipper and E. J. Baerends, J. Chem. Phys., 1997, 107, 5007 CrossRef CAS.
- L. H. Thomas, Proc. Cambridge Philos. Soc., 1927, 23, 542 CrossRef CAS.
- E. Fermi, Rend. Accad. Naz. Lincei, 1927, 6, 602 CAS.
- R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press Inc., New York, 1989 Search PubMed.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian, Inc., Wallingford, CT, 2004.
- T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- A. K. Wilson, T. van Mourik and T. H. Dunning Jr., J. Mol. Struct., 1996, 388, 339 CrossRef CAS.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- D. M. Ceperly and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566 CrossRef.
- A. Billic, J. R. Reimers and N. S. Hush, J. Chem. Phys., 2005, 122, 094708 CrossRef PubMed.
- R. W. Boyd, Nonlinear Opt., Academic Press, London, 1992 Search PubMed.
- Y. Luo, H. Ågren, K. V. Mikkelsen and P. Jørgensen, Adv. Quantum Chem., 1995, 26, 168 CrossRef.
- Z. Rinkevicius, J. Autschbach, A. Baev, M. Swihart, H. Ågren and P. N. Prasad, J. Phys. Chem. A, 2010, 114, 7590 CrossRef CAS PubMed.
- T. M. Nymand, P.-O. Åstrand and K. V. Mikkelsen, J. Phys. Chem. B, 1997, 101, 4105 CrossRef CAS.
- Z. Rinkevicius, X. Li, J. Sandberg, K. V. Mikkelsen and H. Ågren, J. Chem. Theory Comput., 2014, 10, 989–1003 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2016 |