Magnetic properties with multiwavelets and DFT: the complete basis set limit achieved
Received
25th February 2016
, Accepted 11th April 2016
First published on 11th April 2016
Abstract
Multiwavelets are emerging as an attractive alternative to traditional basis sets such as Gaussian-type orbitals and plane waves. One of their distinctive properties is the ability to reach the basis set limit (often a chimera for traditional approaches) reliably and consistently by fixing the desired precision ε. We present our multiwavelet implementation of the linear response formalism, applied to static magnetic properties, at the self-consistent field level of theory (both for Hartree–Fock and density functional theories). We demonstrate that the multiwavelets consistently improve the accuracy of the results when increasing the desired precision, yielding results that have four to five digits precision, thus providing a very useful benchmark which could otherwise only be estimated by extrapolation methods. Our results show that magnetizabilities obtained with the augmented quadruple-ζ basis (aug-cc-pCVQZ) are practically at the basis set limit, whereas absolute nuclear magnetic resonance shielding tensors are more challenging: even by making use of a standard extrapolation method, the accuracy is not substantially improved. In contrast, our results provide a benchmark that: (1) confirms the validity of the extrapolation ansatz; (2) can be used as a reference to achieve a property-specific extrapolation scheme, thus providing a means to obtain much better extrapolated results; (3) allows us to separate functional-specific errors from basis-set ones and thus to assess the level of cancellation between basis set and functional errors often exploited in density functional theory.
1 Introduction
Density functional theory (DFT) is nowadays the de facto standard for quantum chemistry applications.1,2 There are several reasons for the success of DFT: it is conceptually simple, focussing directly on the observable three-dimensional electron density; its Kohn–Sham formulation3 allows the problem to be recast as the optimization of a single-determinant wavefunction for the fictitious Kohn–Sham system of independent particles, allowing the tools quantum chemists have employed for decades in connection with Hartree–Fock (HF) theory to be straightforwardly applied in the optimization of the Kohn–Sham state. However, the apparent simplicity also comes with a significant challenge: the definition of the (unknown) exchange–correlation (XC) functional.4 To address this shortcoming, a large library of functionals has over the years been developed,5,6 allowing an XC functional to be chosen which is best suited for the problem at hand. This last argument is nevertheless unsatisfactory. Despite attempts at creating hierarchies of XC functionals which could be expected to perform better as the complexity or information content of the functional is increased,7,8 such a universal hierarchy remains elusive: on the one hand improving functionals to yield better results is legitimate and necessary; on the other hand, such a wide choice of XC functionals makes it often possible to achieve the desired result for a specific problem or substrate, though with little to no predictive power when experimental reference data are not available. Avoiding pitfalls arising from spurious error cancellations is not easy, also because scientific literature is often biased towards positive outcomes.†
An important way of assessing and improving the quality of currently available XC functionals is to benchmark their performance for different applications.9,10 The development of most current functionals has focused on energetic aspects through thermochemical data.10–13 The molecular energy is by far the most important quantity, superseding molecular structure, vibrational properties, reactivity, and dynamics. Nevertheless, the interest in molecular properties other than the energy has been steadily growing, both in connection with spectroscopic investigations14–16 and with the development of materials with specific properties.17,18 DFT is for instance often used in connection with response theory to obtain a wide range of molecular properties.19 This asymmetry (functionals optimized/benchmarked with respect to their energetic performance and employed for property calculations) mandates a thorough assessment of the quality of such functionals for molecular properties, and several such studies have already been presented in the literature, see for instance the review by Laurent and Jacquemin of benchmark studies of XC functionals used in time-dependent DFT studies and references therein.20
Another important aspect to be considered is the choice of basis set. For molecular calculations with DFT, a linear combination of atomic orbitals approach have almost exclusively been used. When a given basis is employed, the error on the final result is invariably a combination of a direct basis set error and a functional error, that is, difference between the value obtained with the given functional and the ideal exact one in the limit of a complete basis set. To complicate matters further, most functionals are parametrized against thermochemical data by making use of a given basis set,9,12,13 thus introducing an “indirect” basis set error. As a consequence, the definition and quality of a basis set limit for molecular properties within DFT is still an open question. In particular, in two recent studies, Lutnæs et al.21 and Teale et al.22 have extensively addressed such issues for magnetizabilities and nuclear magnetic resonance (NMR) shielding constants of a set of 28 small, closed-shell molecules.
Low-scaling DFT methods23 combined with modern high-performance computer clusters allow substrates with several thousand atoms to be modelled: ideally, a large basis set should be employed to guarantee convergence in the property value; however, using large basis sets for large systems is challenging due to numerical problems caused by near linear dependencies that will arise in the basis set.24
Another potential problem is given by the integration grids employed in DFT: they are optimized to achieve the best compromise between accuracy and efficiency for energy calculations, but there is no guarantee that such grids will work equally well for the functional derivatives required for the evaluation of molecular properties.
In recent years, real-space numerical methods have emerged as an alternative to atom-centered basis functions,25,26 such as finite difference methods,27,28 finite element methods,29,30 wavelet31 and multiwavelet methods.32–41 The first three groups have been successfully applied in materials modeling, especially in combination with periodic boundary conditions and pseudopotentials. However, for molecular all-electron calculations, the most promising approach so far seems to be the one using multiwavelets, pioneered originally by Harrison and coworkers.32 Several properties make multiwavelets attractive compared to atom-centered bases: they are by construction orthonormal, avoiding linear dependencies; completeness in the basis is achieved by refinement, with a rigorous, predefined error control; function representations can be refined adaptively, limiting the memory footprint; a separated tensorial representation of integral convolution operators is employed,42 coupled with the non-standard form of operators,43 achieving narrow-banded, diagonally dominant matrices that preserve the adaptive refinement.
The multiwavelet formalism provides therefore a reliable route to compute molecular properties with guaranteed precision with respect to the complete basis set (CBS) limit. This has already been illustrated for excitation energies35 and for electric polarizabilities.36,37 In this work, we consider magnetic properties,44 and in particular magnetizabilities and NMR shielding constants.
The rest of this paper is organized as follows: in Section 2 we briefly summarize the theoretical foundation for the calculation of molecular energies and magnetic response properties in a multiwavelet basis. In Section 3 we present the evaluation of second-order molecular magnetic response properties, with special attention to the molecular magnetizability and nuclear magnetic shielding tensor. Section 4 details the computational protocol of our calculations. In Section 5 our results are presented and discussed. We end the paper with a brief summary and outlook.
2 Static linear response equations
The MW formalism has been applied to the ground-state energy32,33 and geometry,34 as well as dynamic polarizabilities36,37 and excitation energies35,38,39 in a linear response formalism. In the present work, we further extend the MW toolbox to include two important second-order magnetic properties: the magnetizability and NMR shielding tensors.44,45 In the following we present the static linear response equations, as our derivation differs slightly from the dynamic equations presented previously in the literature.
In order to solve the SCF problem, the action of the MW representation is required for only two operators, which are of the same form:
| | 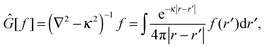 | (1) |
where
κ2 = 0 corresponds to the Poisson operator (used for electrostatic potentials), and
κ2 > 0 is the bound-state Helmholtz (BSH) operator (used in the iterations of the SCF equations). Our MW implementation for functions and operators has been described previously,
40,41 where the parallel performance as well as the inherent linear scaling of the algorithms have been demonstrated in the case of electrostatic Coulomb potentials. A derivative operator is also required for the kinetic energy operator, density gradients for GGA functionals, and angular momentum operators. We have implemented a derivative operator following the work of Alpert
et al.46
2.1 Unperturbed system
The ground-state SCF problem can be written in a general, non-canonical form to allow for localized molecular orbitals (MOs)47,48| | 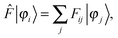 | (2) |
where| | Fij = 〈φi|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) |φj〉, |φj〉, | (3) |
is the Fock matrix, and ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) the Fock operator. The potential operator in Kohn–Sham DFT and HF theory can be written in a general form aswhere 0 ≤ λ ≤ 1 gives the amount of exact exchange. The electron interaction operators
the Fock operator. The potential operator in Kohn–Sham DFT and HF theory can be written in a general form aswhere 0 ≤ λ ≤ 1 gives the amount of exact exchange. The electron interaction operators| | 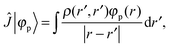 | (5) |
| | 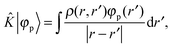 | (6) |
| | 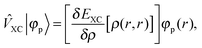 | (7) |
are expressed in terms of the one-particle density matrix ρ(r,r′) which is constructed from the occupied MO| | 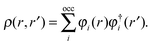 | (8) |
The solution of the unperturbed self-consistent field (SCF) problem follows closely the work of Harrison, Yanai and coworkers,32,33 where the SCF equations are rewritten in integral form49| | 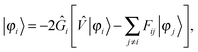 | (9) |
and iterated until convergence, including a Krylov subspace accelerated inexact Newton (KAIN) iterative accelerator.50 The BSH operator Ĝ (eqn (1)) is the inverse of the kinetic energy operator, shifted by the diagonal element of the Fock matrix 2Ĝi = (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − Fii)−1. The second term in the operator argument in eqn (9) corrects for the use of non-canonical (localized) orbitals, and vanishes if the Fock matrix is diagonalized.
− Fii)−1. The second term in the operator argument in eqn (9) corrects for the use of non-canonical (localized) orbitals, and vanishes if the Fock matrix is diagonalized.
2.2 Perturbed system
Adding a small static perturbation ĥ(1) to the unperturbed Hamiltonian ĥ(0)will lead to small changes in the orbitals, and the perturbation in the density can be expressed in terms of the unperturbed {φ(0)} and first-order perturbed {φ(1)} orbitals. Introducing the density operator (the projector onto the occupied orbital space)| | 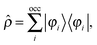 | (11) |
and retaining terms up to first order, we get| | 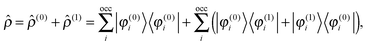 | (12) |
where ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0) is the ground-state density operator and
(0) is the ground-state density operator and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (1) the first-order perturbed density. This change in electron density in turn changes the potential operators in eqn (5–7), and to first order we get
(1) the first-order perturbed density. This change in electron density in turn changes the potential operators in eqn (5–7), and to first order we get| | 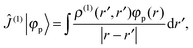 | (13) |
| | 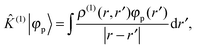 | (14) |
| | 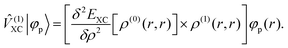 | (15) |
Setting up the SCF problem for the perturbed system to first order leads to the modified Sternheimer equation51| | 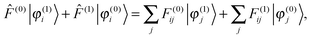 | (16) |
where the perturbed Fock operator contains both the explicit perturbation and the induced perturbations in the potential operator (![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1) = ĥ(1) +
(1) = ĥ(1) + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)). The perturbed Fock matrix elements are obtained by expanding eqn (3) and collecting all the first-order terms:
(1)). The perturbed Fock matrix elements are obtained by expanding eqn (3) and collecting all the first-order terms:| | F(1)ij = 〈φ(1)i|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (0)|φ(0)j〉 + 〈φ(0)i| (0)|φ(0)j〉 + 〈φ(0)i|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1)|φ(0)j〉 + 〈φ(0)i| (1)|φ(0)j〉 + 〈φ(0)i|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (0)|φ(1)j〉. (0)|φ(1)j〉. | (17) |
The orbitals satisfy the following weak orthogonality condition| | | 〈φ(0)i|φ(1)j〉 + 〈φ(1)i|φ(0)j〉 = 0, | (18) |
which is equivalent to the idempotency condition on the density operator ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2 =
2 = ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) to first order. However, in the diagonal terms the orbital phase factors can be chosen arbitrarily, and the off-diagonal terms do not contribute to the density to first-order. Therefore one can in both cases impose the stronger orthogonality condition:
to first order. However, in the diagonal terms the orbital phase factors can be chosen arbitrarily, and the off-diagonal terms do not contribute to the density to first-order. Therefore one can in both cases impose the stronger orthogonality condition:| | | 〈φ(0)i|φ(1)j〉 = 〈φ(1)i|φ(0)j〉 = 0, | (19) |
which has been proposed as a way to speed up convergence.52 On the other hand, for larger systems, the orthogonalization procedure becomes prohibitively expensive, and it would be more efficient to ignore these redundant projections.53 Using the strong orthogonality condition, the first and third terms in eqn (17) will vanish, and we get| | 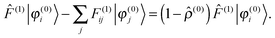 | (20) |
The Sternheimer equation (eqn (16)) can now be written in integral form, in the same way as the unperturbed SCF equation (eqn (9)):| | 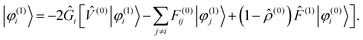 | (21) |
The diagonal element of the unperturbed Fock matrix appears in the BSH operator as 2Ĝi = (![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − F(0)ii)−1. We remark that eqn (21) defines a set of coupled equations which corresponds to the static limit of the response equations of Sekino et al.36,37 and closely resembles the working equations of Yanai et al.35,38 for excitation energies in time-dependent HF/DFT. Kottmann et al.39 recently used the same equations to compute excitation energies in the configuration interaction singles (CIS) approximation.
− F(0)ii)−1. We remark that eqn (21) defines a set of coupled equations which corresponds to the static limit of the response equations of Sekino et al.36,37 and closely resembles the working equations of Yanai et al.35,38 for excitation energies in time-dependent HF/DFT. Kottmann et al.39 recently used the same equations to compute excitation energies in the configuration interaction singles (CIS) approximation.
3 Magnetic properties
A general second-order magnetic property M can be expressed as an energy derivative with respect to two parameters a and b44,45| | 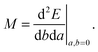 | (22) |
The property will have two contributions, one from a second-order interaction operator ĥ(a,b), and one from a pair of first-order interaction operators ĥ(a) and ĥ(b). The former is known as the diamagnetic contribution, and is computed as an expectation value of the second-order operator and the zeroth-order (unperturbed) density (r = r′ denotes the trace of the density matrix, and will always be assumed in the following)| | 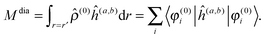 | (23) |
The latter is known as the paramagnetic contribution and is computed by perturbing the system (i.e. solving the response equations) using one of the operators ĥ(a) to get the corresponding perturbed orbitals φ(a) and density ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (a), and computing the expectation value (tracing the density matrix) of the second operator ĥ(b)
(a), and computing the expectation value (tracing the density matrix) of the second operator ĥ(b)| | 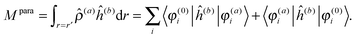 | (24) |
3.1 Magnetizability and NMR shielding
The magnetizability tensor ξ and NMR shielding tensor σ are second-order magnetic properties that can be identified as energy derivatives with respect to the external magnetic field B and the nuclear magnetic moment MK associated with nucleus K| | 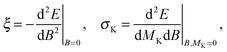 | (25) |
and are thus computed from the following expressions| | 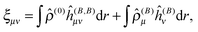 | (26) |
| | 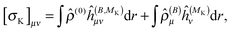 | (27) |
where μ, ν = x, y, z are the components of the perturbing fields and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (B)μ denotes the density perturbed by the μ component of the ĥ(B) operator. The interaction operators are obtained by differentiating the Hamiltonian with respect to B and/or MK and evaluating at zero perturbational strength. For closed-shell systems we get‡44,45
(B)μ denotes the density perturbed by the μ component of the ĥ(B) operator. The interaction operators are obtained by differentiating the Hamiltonian with respect to B and/or MK and evaluating at zero perturbational strength. For closed-shell systems we get‡44,45| | 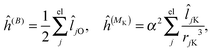 | (28) |
| | 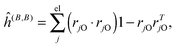 | (29) |
| | 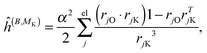 | (30) |
where ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) jO = −irjO × ∇j is the angular momentum operator, rjO is the position of electron j relative to the gauge origin O, rK is the position of nucleus K, and α ≈ 1/137 is the fine-structure constant. The perturbed orbitals φ(B) are obtained by solving the Sternheimer equations (eqn (21)) with the following perturbed Fock operator (there is one for each component μ of the perturbing field)
jO = −irjO × ∇j is the angular momentum operator, rjO is the position of electron j relative to the gauge origin O, rK is the position of nucleus K, and α ≈ 1/137 is the fine-structure constant. The perturbed orbitals φ(B) are obtained by solving the Sternheimer equations (eqn (21)) with the following perturbed Fock operator (there is one for each component μ of the perturbing field)| | ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1) = ĥ(B) + Ĵ(1) − λ (1) = ĥ(B) + Ĵ(1) − λ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (1) + (1) + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)XC. (1)XC. | (31) |
Notice that the perturbed density (in real space) vanishes for pure imaginary perturbations, so Ĵ(1) and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)XC (if there is no explicit current dependence in the functional) can be omitted from this Fock operator. This means that for non-hybrid DFT (λ = 0), we do not get any two-electron contribution in the perturbed Fock operator, which leads to decoupled response equations (at least in the canonical case) that can be solved non-iteratively in a fixed basis of virtual orbitals.54–56 In our case, however, we only have the occupied orbitals, and the equations must still be solved iteratively to sample the (complete) virtual space by application of the BSH Green's function. Notice also that even if the perturbed density vanishes, the paramagnetic expectation value (e.g. with ĥ(MK)) does not
(1)XC (if there is no explicit current dependence in the functional) can be omitted from this Fock operator. This means that for non-hybrid DFT (λ = 0), we do not get any two-electron contribution in the perturbed Fock operator, which leads to decoupled response equations (at least in the canonical case) that can be solved non-iteratively in a fixed basis of virtual orbitals.54–56 In our case, however, we only have the occupied orbitals, and the equations must still be solved iteratively to sample the (complete) virtual space by application of the BSH Green's function. Notice also that even if the perturbed density vanishes, the paramagnetic expectation value (e.g. with ĥ(MK)) does not| | 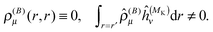 | (32) |
The above expressions can be directly related to others, such as Ramsey's57 original sum-over-states expression for the shielding tensor| | 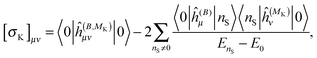 | (33) |
where |0> denotes the ground state and |nS> a singlet-excited state. Whereas such expressions are usually not very useful as they require explicit representations of the excited states of the molecule, some applications have been reported in the literature, in particular in the case of uncoupled density functional theory.54,55 More commonly though, the molecular properties are expressed in terms of the density matrix D in an AO basis| | 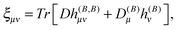 | (34) |
| | 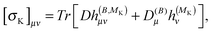 | (35) |
where h(B), h(MK), h(B,B) and h(B,MK) now denote the corresponding matrix representations in the chosen AO basis.
As a side note, we note that in the present formulation, due to the interchange theorem,58,59 the order of the perturbations can be swapped, so that in the case of NMR shielding constants, the response equations are solved using ĥ(MK) as perturbation operator instead of ĥ(B), i.e.
| | 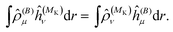 | (36) |
A situation where such a swapping of operators is useful is when computing shielding tensors of selected nuclei in large molecules. Whereas
ĥ(B) is a global operator affecting the entire molecule (plus any explicit solvent molecules), the operator
ĥ(MK) is localized around nucleus K (decays as
r−2 following Biot–Savart's law for induced magnetic fields), leading to localized perturbations that can be treated much more efficiently than the global perturbations arising from
ĥ(B). This approach can also be used in AO-based formulations in combination with gauge-including atomic orbitals (GIAOs), however, when the swap is employed to achieve linear scaling,
60 it requires the implementation of a number of new contributions. By combining this with other linear-scaling techniques for the Coulomb and exchange computations, Ochsenfeld and coworkers have been able to compute NMR shieldings of impressively large molecules.
60–62 However, one has to keep in mind that the number of response equations to be solved increases with the number of selected nuclei, and it eventually becomes beneficial to instead perturb the system with the global
ĥ(B) operator, which requires the solution of only three response equations for all nuclei.
4 Computational details
All Gaussian-type orbital (GTO) calculations were performed with the Dalton program,63 using Dunning's correlation-consistent (cc-pVXZ64) and Jensen's polarization-consistent (pcS-n65) basis sets. The latter was specifically optimized for computing NMR shielding constants using DFT. The calculations were performed using GIAOs unless otherwise specified.
The MW calculations were performed with a development version of the MRChem program package.66 The exchange–correlation functionals and their derivatives to arbitrary order are provided by the XCFun library.67 In the results presented, k denotes the polynomial order of the basis, ε is the overall numerical accuracy used in the calculation (the internal threshold used for truncating the MW representations of all functions and operators) and Δϕ is the convergence threshold in the orbital residuals (both ground-state and response). As starting guess for the ground-state calculations we used converged wave functions in small GTO basis sets (e.g. cc-pVDZ). A zero initial guess was used for the response functions, and the convergence was a bit slower than the corresponding ground-state calculation (for the ground state, typically 2–4 iterations are needed to gain one order of magnitude in accuracy, for the response equations one or two iterations more, but with a larger KAIN iterative history).
5 Results
This section is divided in two parts. In the first we calibrate and benchmark MRChem both for the convergence towards the CBS limit and the origin dependence, through some test calculations of magnetizabilities and NMR shielding constants of the second-row hydrides (geometries given in Table 1). Then we show the MRChem performance on the challenging case of magnesium oxide, which has been shown to “display pathological behaviors with respect to basis set convergence”.65 In the second part, we perform a statistical analysis of a larger set of molecules, originally considered by Lutnæs et al.21 for magnetizabilities and later by Teale et al.22 for shieldings. We will here assess the quality of the density functionals and basis sets that are typically being used for such calculations.
Table 1 Geometries (Bohr) of the second-row hydrides used in the benchmark calculations
| Atom |
x
|
y
|
z
|
| C |
0.000000 |
0.000000 |
0.000000 |
| H |
1.184860 |
−1.184860 |
−1.184860 |
| H |
−1.184860 |
1.184860 |
−1.184860 |
| H |
−1.184860 |
−1.184860 |
1.184860 |
| H |
1.184860 |
1.184860 |
1.184860 |
|
|
| N |
0.000000 |
−0.125000 |
0.000000 |
| H |
1.771618 |
0.594986 |
0.000000 |
| H |
−0.885809 |
0.594986 |
1.534269 |
| H |
−0.885809 |
0.594986 |
−1.534269 |
|
|
| O |
0.000000 |
0.000000 |
−0.125000 |
| H |
1.437500 |
0.000000 |
1.025000 |
| H |
−1.437500 |
0.000000 |
1.025000 |
|
|
| F |
0.000000 |
0.000000 |
0.087300 |
| H |
0.000000 |
0.000000 |
−1.645500 |
5.1 Basis set convergence and parametrization
5.1.1 Magnetizabilities.
Table 2 shows the Hartree–Fock magnetizability of the water molecule computed at two different gauge origins using MW and GTO basis sets of different quality. The MW calculations are grouped in three different overall numerical accuracies with a factor of 100 between them (ε = 10−3, 10−5, 10−7), and for each of these we look at the convergence of the property with respect to the norm of the orbital residuals (Δϕ). The overall precision ε should give the maximum relative accuracy that we are able to obtain as the orbitals converge, which is reflected in the total energies when we compare with the reference value of Yanai et al.33 Even though the convergence of the energy is quadratic in the convergence of the orbitals, the final error in the converged energy will be given by the overall accuracy of the MW calculation.
Table 2 Hartree–Fock magnetizability (a.u.) of water computed using two different gauge origins rO, relative to the molecular geometry given in Table 1. GTO: (0, 0, 0) computed using GIAOs, (5, 5, 5) computed without GIAOs, number of contracted functions in parenthesis. See Section 4 for computational details
|
k
|
ε
|
Δϕ |
E
tot
|
r
O = (0, 0, 0) |
r
O = (5, 5, 5) |
|
ξ
dia
|
ξ
para
|
ξ
tot
|
ξ
dia
|
ξ
para
|
ξ
tot
|
|
Reference energy from Yanai et al.33.
|
| 5 |
10−3 |
10−1 |
−76.058602 |
−3.260207 |
0.218164 |
−3.042043 |
−127.820595 |
124.974478 |
−2.846118 |
|
|
|
10−2 |
−76.058116 |
−3.269608 |
0.325099 |
−2.944509 |
−127.840649 |
124.906519 |
−2.934131 |
|
|
|
10−3 |
−76.058113 |
−3.269318 |
0.320564 |
−2.948754 |
−127.849347 |
124.896921 |
−2.952425 |
|
|
| 7 |
10−5 |
10−3 |
−76.065610 |
−3.269279 |
0.323568 |
−2.945712 |
−127.844963 |
124.889299 |
−2.955665 |
|
|
|
10−4 |
−76.065610 |
−3.269110 |
0.322356 |
−2.946754 |
−127.846582 |
124.900435 |
−2.946147 |
|
|
|
10−5 |
−76.065609 |
−3.269109 |
0.322365 |
−2.946744 |
−127.846562 |
124.900189 |
−2.946373 |
|
|
|
|
|
|
|
|
|
|
|
| 9 |
10−7 |
10−5 |
−76.065595 |
−3.269109 |
0.322362 |
−2.946747 |
−127.846571 |
124.899875 |
−2.946696 |
|
|
|
10−6 |
−76.065595 |
−3.269110 |
0.322364 |
−2.946746 |
−127.846564 |
124.899854 |
−2.946710 |
|
|
|
10−7 |
−76.065595 |
−3.269110 |
0.322364 |
−2.946746 |
−127.846564 |
124.899855 |
−2.946709 |
|
|
| MADNESSa |
|
|
−76.065595 |
|
|
|
|
|
|
|
|
| aug-cc-pV6Z |
(443) |
−76.065569 |
−3.2691 |
0.3224 |
−2.9468 |
−127.8466 |
123.7548 |
−4.0918 |
| aug-cc-pVQZ |
(172) |
−76.064122 |
−3.2701 |
0.3223 |
−2.9479 |
−127.8476 |
120.5026 |
−7.3450 |
| aug-cc-pVDZ |
(41) |
−76.039804 |
−3.2824 |
0.3251 |
−2.9573 |
−127.8713 |
98.7552 |
−29.1161 |
|
|
| cc-pV6Z |
(322) |
−76.065513 |
−3.2659 |
0.3230 |
−2.9429 |
−127.8505 |
123.0783 |
−4.7722 |
| cc-pVQZ |
(115) |
−76.062951 |
−3.2353 |
0.3267 |
−2.9087 |
−127.8299 |
118.0656 |
−9.7643 |
| cc-pVDZ |
(24) |
−76.025444 |
−3.1473 |
0.3571 |
−2.7902 |
−127.7744 |
79.4328 |
−48.3416 |
For magnetizability calculations with a gauge origin within the molecular geometry (rO = (0, 0, 0), close to the center of mass), the error in the diamagnetic contribution is expected to be linear in the error of the ground-state orbitals (Δϕ) and limited by the overall accuracy (ε) of the calculation. This can be seen from the numbers in Table 2, and the error in the last (most accurate) MW value is expected to be around 10−6 atomic units. The paramagnetic contribution depends on both the ground-state and perturbed orbitals, and the absolute error is similar to the error in the corresponding diamagnetic contribution, which means that we get a consistent accuracy in the total magnetizability of the molecule (that is, around 10−6 a.u.). For comparison we see that the cc-pV6Z basis set (including GIAOs) only yields 10−2 a.u. precision for the water magnetizability, while augmenting the basis set with extra diffuse functions increases the accuracy by two orders of magnitude.
5.1.2 Gauge origin dependence.
It is well known that the (arbitrary) placement of the gauge origin will affect the quality of the result whenever an incomplete basis set is used in the calculation of magnetic properties. Several solutions to the problem have been proposed. Nowadays, the most common approach is to use GIAOs, first introduced by London in 1937.68 The method was further developed by Ditchfield in the 1970s,69 but was not made efficiently applicable until 1990, with the work of Wolinski, Hinton and Pulay.70 In the London orbital approach, each AO is made explicitly dependent on the external magnetic field, and a local gauge origin is defined at the center of each AO. In this way, the magnetic properties become gauge-origin independent by construction, though not gauge invariant and current conserving.71,72
The MW basis is in principle complete up to the predefined truncation threshold. Therefore, we expect a much less severe gauge dependence in the computed magnetic properties (effective gauge origin independence as well as gauge invariance to within the accuracy threshold), and very high accuracy is attainable for small molecules by choosing a common gauge origin within the molecular geometry (e.g. center of mass). However, as the accuracy in the response property is relative to the absolute value of the paramagnetic contribution (the diamagnetic contribution is more accurate because it only depends on the unperturbed system), we also expect that it becomes progressively more difficult to attain the same accuracy when the origin is moved out of the molecular framework, as both the diamagnetic and paramagnetic contributions to the magnetizability will increase in magnitude.
Table 2 shows also the same magnetizability computed with a displaced gauge origin (rO = (5, 5, 5)). For the MW calculations, we see that the diamagnetic part is computed with the same absolute accuracy as before (comparing ε = 10−5, Δϕ = 10−5 results with ε = 10−7, Δϕ = 10−7, the variations are on the sixth decimal place in both cases), but for the paramagnetic part, only the relative accuracy is maintained (variations in the fourth digit after the comma). This means that two digits are lost in the total magnetizability in this case, as the magnitude of the paramagnetic part is increased from ∼1 to ∼100. The MW basis still provides reliable and systematically improvable results, but this shows that the origin should not be chosen arbitrarily (and preferably somewhere within the framework of the molecular structure).
For comparison, traditional GTOs are dependent on the GIAO parametrization to yield reasonable results. Whereas the GIAO results would be independent of the choice of gauge origin up to the same numerical issues as observed for the multiwavelet basis,73 without GIAOs, if the gauge origin is moved away from the center of the Gaussians, even the largest basis sets are unable to yield a correct result. This is clearly shown in Table 2, where the magnetizability value for water is correct to ∼10−4 a.u. for the aug-cc-pV6Z basis when London orbitals are employed, but becomes 30% larger with a displaced gauge origin (rO = (5, 5, 5)) without London orbitals.
5.1.3 NMR shielding constants.
Table 3 shows the NMR shielding constants of the second-row hydrides computed using the B3LYP74 functional and MW and GTO basis sets of different quality. As for the magnetizability, the MW calculations are grouped in three different overall accuracies (ε) and we present the convergence of the total NMR shielding constant with respect to the orbital residuals (Δϕ). The gauge origin is chosen close to the center of mass of each molecule (rO = (0, 0, 0) relative to the geometries given in Table 1), whereas the GTO calculations are performed using GIAOs. The final MW shielding constants are expected to be accurate to at least 10−3 ppm for the second row elements, and 10−4 ppm for the hydrogen atoms. For comparison, shielding constants computed with the largest non-augmented Gaussian basis set (pcS-4) are correct to ∼0.1 and ∼0.01 ppm, respectively, and augmenting with extra diffuse functions does not significantly improve the results. The performance of the pcS-n basis sets are thus, as expected, quite good, because they are specifically optimized for NMR shielding calculations.
Table 3 B3LYP nuclear shielding constants (ppm) of second-row hydrides. Geometries given in Table 1. See Section 4 for computational details
|
k
|
ε
|
Δϕ |
CH4 |
NH3 |
H2O |
HF |
|
σ(C) |
σ(H) |
σ(N) |
σ(H) |
σ(O) |
σ(H) |
σ(F) |
σ(H) |
| 5 |
10−3 |
10−1 |
249.8536 |
31.2215 |
321.4904 |
31.4804 |
398.8322 |
29.0981 |
478.5381 |
25.9203 |
|
|
|
10−2 |
189.3407 |
31.3926 |
258.5232 |
31.8928 |
328.1023 |
30.8344 |
415.1414 |
30.2118 |
|
|
|
10−3 |
186.9510 |
31.3978 |
256.0271 |
31.8912 |
314.9383 |
30.8911 |
413.8677 |
30.1005 |
|
|
| 7 |
10−5 |
10−3 |
188.2145 |
31.4860 |
259.0541 |
31.6347 |
318.9669 |
30.4986 |
411.1672 |
29.3182 |
|
|
|
10−4 |
188.1449 |
31.4863 |
259.1961 |
31.6325 |
317.4436 |
30.4973 |
411.1805 |
29.3043 |
|
|
|
10−5 |
188.0891 |
31.4869 |
259.1520 |
31.6326 |
317.4374 |
30.4959 |
411.1565 |
29.3057 |
|
|
| 9 |
10−7 |
10−5 |
188.0877 |
31.4879 |
259.1620 |
31.6317 |
317.4556 |
30.4962 |
411.1777 |
29.3053 |
|
|
|
10−6 |
188.0862 |
31.4879 |
259.1618 |
31.6317 |
317.4707 |
30.4959 |
411.1836 |
29.3053 |
|
|
|
10−7 |
188.0852 |
31.4879 |
259.1619 |
31.6317 |
317.4710 |
30.4959 |
411.1835 |
29.3052 |
|
|
| aug-pcS-4 |
188.0912 |
31.4891 |
259.1699 |
31.6337 |
317.4761 |
30.4994 |
411.1899 |
29.3113 |
| aug-pcS-3 |
188.0779 |
31.4901 |
259.1504 |
31.6359 |
317.4721 |
30.5032 |
411.1675 |
29.3169 |
| aug-pcS-2 |
188.1631 |
31.5072 |
260.0631 |
31.6842 |
319.1405 |
30.5832 |
413.0720 |
29.4299 |
| aug-pcS-1 |
189.8481 |
31.4323 |
259.1238 |
31.6023 |
316.7613 |
30.5556 |
412.8214 |
29.4505 |
| aug-pcS-0 |
195.0982 |
32.3357 |
259.4777 |
32.7576 |
307.5149 |
31.7324 |
403.2127 |
30.7204 |
|
|
| pcS-4 |
188.0906 |
31.4891 |
259.1780 |
31.6344 |
317.4558 |
30.4995 |
411.1456 |
29.3125 |
| pcS-3 |
188.0804 |
31.4916 |
259.1914 |
31.6426 |
317.3621 |
30.5060 |
410.9353 |
29.3237 |
| pcS-2 |
188.8855 |
31.5061 |
261.0480 |
31.7470 |
319.4452 |
30.5726 |
412.1234 |
29.3614 |
| pcS-1 |
188.9008 |
31.4148 |
268.5308 |
31.9186 |
329.2888 |
30.6828 |
412.1724 |
29.4284 |
| pcS-0 |
192.7857 |
32.4843 |
269.1474 |
33.4027 |
332.1143 |
31.9300 |
407.2365 |
30.6812 |
5.1.4 Magnesium oxide.
A molecule which has proven difficult to handle with traditional basis sets is magnesium oxide. In the calibration of the pcS-n basis sets, Jensen decided to remove a handful of molecules from the original test set, as their errors were so large that they would have ruined the statistics.65 The worst of these systems was MgO, and Table 4 shows the shielding constants of this molecule computed with three different functionals (B3LYP, Becke's half-and-half75 functional and Hartree–Fock), using both MW and GTO bases. Whereas B3LYP starts out with a massive overestimation of the shielding constant for the smallest pcS-0 basis set, we do observe a systematic improvement and monotonic convergence for this functional when we increase the cardinal number of the basis. This was also observed and analyzed by Jensen.65 For the BHandH functional, however, the convergence is less systematic and we have to go to the pcS-2 basis and beyond in order to get qualitative agreement between the numbers, and the situation gets even worse for Hartree–Fock, where anything less than pcS-3 gives completely erratic results, and even the biggest basis is only converged to one digit. Again, the augmented basis sets show only slight improvements over the standard pcS-n.
Table 4 Nuclear shielding constants (ppm) of MgO (r = 3.2986a0) using Hartree–Fock and the B3LYP and Becke half-and-half density functionals. Number of contracted basis functions in parenthesis. See Section 4 for computational details
|
k
|
ε
|
Δϕ |
B3LYP |
BHandH |
RHF |
|
σ(Mg) |
σ(O) |
σ(Mg) |
σ(O) |
σ(Mg) |
σ(O) |
| 5 |
10−3 |
10−2 |
964.0904 |
−2051.0527 |
1116.6897 |
−4734.2058 |
1041.2017 |
−6738.2185 |
| 6 |
10−4 |
10−3 |
1002.5959 |
−2454.5817 |
1018.8386 |
−3545.7921 |
1538.9211 |
−16726.3490 |
| 7 |
10−5 |
10−4 |
1006.2229 |
−2484.3481 |
1021.8519 |
−3575.4505 |
1584.1109 |
−17466.4867 |
| 8 |
10−6 |
10−5 |
1007.0809 |
−2492.0231 |
1024.4490 |
−3603.0833 |
1578.7322 |
−17358.6849 |
| 9 |
10−7 |
10−6 |
1007.1533 |
−2491.8762 |
1024.6440 |
−3604.9389 |
1579.4610 |
−17375.4221 |
|
|
| aug-pcS-4 |
(260) |
1007.7858 |
−2498.9207 |
1026.3744 |
−3627.0785 |
1605.7661 |
−17904.0731 |
| aug-pcS-3 |
(162) |
1012.7812 |
−2525.8940 |
1035.6182 |
−3707.6253 |
1719.9701 |
−20055.5992 |
| aug-pcS-2 |
(86) |
1039.0774 |
−2723.3712 |
1088.7973 |
−4244.2865 |
4282.4997 |
−69183.9283 |
| aug-pcS-1 |
(46) |
1080.0457 |
−3018.9200 |
1185.1959 |
−5267.7093 |
−1173.7349 |
10814.1557 |
| aug-pcS-0 |
(27) |
1061.6947 |
−3068.0177 |
1302.9612 |
−7285.5996 |
254.9829 |
36289.8265 |
|
|
| pcS-4 |
(199) |
1007.6675 |
−2498.7484 |
1027.6229 |
−3641.5105 |
1617.5056 |
−18143.8405 |
| pcS-3 |
(121) |
1013.9465 |
−2536.7996 |
1039.3089 |
−3749.0539 |
1757.7204 |
−20822.5428 |
| pcS-2 |
(61) |
1047.5216 |
−2799.5298 |
1130.5457 |
−4694.1604 |
−19388.2423 |
386900.5044 |
| pcS-1 |
(33) |
1513.5862 |
−6292.7417 |
3100.8099 |
−24758.3030 |
94.4529 |
11293.4315 |
| pcS-0 |
(19) |
8890.4390 |
−63570.3234 |
3.6303 |
7411.0254 |
448.6993 |
4880.3077 |
In the MW basis, on the other hand, we see a systematic convergence for all functionals, although a bit slower than for the second-row hydrides presented above. The final MW shielding constants should be accurate to within 1 ppm, except for the Hartree–Fock oxygen value, where the error is on the order of 10 ppm.
5.2 Benchmarking HF and DFT with CBS results
In two recent works, Lutnæs et al.21 and Teale et al.22 investigated the performance of a number of density functionals to assess their ability to reproduce magnetizabilities and shieldings, respectively. In these studies, 28 molecules were considered, comparing the DFT results with coupled cluster results and with experimental data.
In order to minimize basis set errors, they used large basis sets (the largest basis set used was the correlation-consistent, core-valence aug-cc-pCVQZ basis set of Woon and Dunning.76) They also made use of an extrapolation method with a two-point exponential parametrization for HF and a polynomial extrapolation for the correlation part. We report here the extrapolation formula for the HF part:
| | 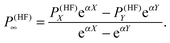 | (37) |
In particular, for the exponential extrapolation of the HF values, they used the same parametrization (
α = 1.63) that is employed for the molecular energy.
77 This choice was justified by the fact that second-order molecular properties are energy derivatives.
With a MW approach, it is possible to provide very accurate benchmark results that can be employed to check the quality of the GTO results, both for HF and for the available density functionals. Additionally, we can determine whether the exponential extrapolation procedure leads to an improvement in the results, as well as investigate to what extent it predicts the correct basis-set limit.
We have therefore considered the same set of molecules and performed calculations at increasing precision (ε = 10−η, η = 3, 4, 5, 6), to compare our MW results with the results obtained using GTOs. We will here summarize our main findings.
Based on the initial test calculations on the first-row hydrides, we will in all the following MW calculations converge the orbitals (both ground-state and perturbed) to 10ε. The reason for this is twofold: firstly, the property is usually converged within the expected error bars at this point, and secondly the convergence might be affected by numerical noise when we approach the limit of the guaranteed accuracy of the computation.
5.2.1 Magnetizabilities.
The HF magnetizabilities computed with MRChem are reported in Table 5, together with the reference values of Lutnæs et al.21 The progression of the MW results clearly show how the results gain consistently in accuracy when η is increased, and our most accurate results are converged to the fifth digit. In more detail, the MW3 results have 1–2 correct digits, MW4 have about three and MW5 four correct digits. The only notable exception is ozone for MW3, which is also qualitatively wrong.
Table 5 Hartree–Fock magnetizabilities (10−30 J T−2) computed with GTO basis sets (aug-cc-pCVXZ, X = T, Q) and MW methods at increasing precision (ε = 10−η, η = 3, 4, 5, 6). All GTO calculations are taken from the ESI of ref. 21
|
|
T
|
Q
|
MW3 |
MW4 |
MW5 |
MW6 |
| HF |
−172.9 |
−172.7 |
−171.63 |
−172.61 |
−172.61 |
−172.62 |
| CO |
−204.9 |
−204.5 |
−200.26 |
−204.61 |
−204.45 |
−204.44 |
| N2 |
−203.3 |
−202.8 |
−196.06 |
−202.56 |
−202.73 |
−202.74 |
| H2O |
−231.4 |
−231.3 |
−231.08 |
−231.27 |
−231.30 |
−231.30 |
| HCN |
−280.5 |
−280.1 |
−251.60 |
−280.04 |
−280.09 |
−280.08 |
| HOF |
−244.9 |
−244.6 |
−246.15 |
−244.36 |
−244.55 |
−244.50 |
| O3 |
580.1 |
580.5 |
−85.51 |
585.06 |
581.98 |
581.94 |
| NH3 |
−287.6 |
−287.4 |
−288.33 |
−287.42 |
−287.53 |
−287.54 |
| CH2O |
−139.8 |
−139.5 |
−107.71 |
−139.40 |
−139.39 |
−139.37 |
| CH4 |
−314.1 |
−313.7 |
−314.13 |
−313.77 |
−313.72 |
−313.75 |
| C2H4 |
−355.1 |
−354.7 |
−348.05 |
−354.53 |
−354.74 |
−354.78 |
| AlF |
−400.4 |
−399.4 |
−395.34 |
−399.16 |
−399.20 |
−399.21 |
| CH3F |
−318.6 |
−318.0 |
−315.81 |
−317.87 |
−317.98 |
−317.97 |
| C3H4 |
−478.4 |
−478.0 |
−411.91 |
−477.96 |
−478.16 |
−478.17 |
| FCCH |
−453.0 |
−452.2 |
−449.10 |
−452.17 |
−452.23 |
−452.24 |
| FCN |
−378.6 |
−378.0 |
−370.80 |
−377.93 |
−378.02 |
−378.00 |
| H2S |
−454.0 |
−452.8 |
−458.85 |
−453.35 |
−452.86 |
−452.84 |
| HCP |
−512.2 |
−511.5 |
−460.27 |
−511.53 |
−511.57 |
−511.57 |
| HFCO |
−312.2 |
−311.5 |
−297.30 |
−311.31 |
−311.38 |
−311.42 |
| H2C2O |
−433.1 |
−432.6 |
−435.55 |
−432.73 |
−432.45 |
−432.63 |
| LiF |
−191.0 |
−190.9 |
−191.30 |
−190.80 |
−190.74 |
−190.74 |
| LiH |
−125.6 |
−125.3 |
−128.08 |
−125.28 |
−125.27 |
−125.26 |
| N2O |
−343.3 |
−342.8 |
−338.38 |
−342.70 |
−342.73 |
−342.73 |
| OCS |
−598.4 |
−597.5 |
−657.92 |
−597.35 |
−597.47 |
−597.45 |
| OF2 |
−272.0 |
−271.6 |
−281.22 |
−271.76 |
−271.58 |
−271.43 |
| H4C2O |
−545.2 |
−544.8 |
−555.68 |
−544.90 |
−545.09 |
−545.05 |
| PN |
−304.0 |
−303.8 |
−305.97 |
−303.00 |
−303.80 |
−303.80 |
| SO2 |
−303.3 |
−301.8 |
−215.00 |
−301.57 |
−301.50 |
−301.50 |
The comparison with the best GTO results shows a very good agreement with differences of about 0.1–0.2 × 10−30 J T−2. Ozone proves to be a challenging system for GTOs with a deviation of 1.4 × 10−30 J T−2. We can therefore conclude that the aug-cc-pCVQZ basis is able to attain very good accuracy for magnetizabilities, yielding results that are comparable to our MW5 values.
A very similar picture is obtained for the density functionals examined, with aug-cc-pCVQZ performing on par with MW5. Our MW6 results are reported in Table 6 together with the aug-cc-pCVQZ results from Lutnæs et al.21
Table 6 Magnetizabilities (10−30 J T−2) computed using a range of density functionals with the aug-cc-pCVQZ basis set and the MW basis at precision ε = 10−6. All GTO calculations are taken from the ESI of ref. 21
| |
LDA |
BLYP |
PBE |
B3LYP |
PBE0 |
|
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
| HF |
−181.1 |
−181.06 |
−181.0 |
−180.99 |
−180.1 |
−180.09 |
−178.5 |
−178.48 |
−177.1 |
−177.05 |
| CO |
−206.6 |
−206.58 |
−209.1 |
−209.11 |
−205.6 |
−205.54 |
−206.8 |
−206.75 |
−202.9 |
−202.91 |
| N2 |
−201.0 |
−200.95 |
−203.6 |
−203.53 |
−199.7 |
−199.63 |
−202.1 |
−201.99 |
−198.1 |
−198.02 |
| H2O |
−241.0 |
−240.99 |
−239.5 |
−239.48 |
−238.5 |
−238.52 |
−236.9 |
−236.89 |
−235.3 |
−235.29 |
| HCN |
−265.1 |
−265.06 |
−268.7 |
−268.65 |
−264.4 |
−264.41 |
−269.6 |
−269.58 |
−266.0 |
−265.94 |
| HOF |
−228.9 |
−228.90 |
−226.6 |
−226.60 |
−227.4 |
−227.33 |
−231.1 |
−231.08 |
−232.8 |
−232.74 |
| O3 |
195.4 |
196.05 |
180.3 |
180.85 |
183.7 |
184.17 |
238.8 |
239.45 |
258.0 |
258.60 |
| NH3 |
−298.2 |
−298.26 |
−293.4 |
−293.48 |
−293.1 |
−293.20 |
−291.5 |
−291.54 |
−290.5 |
−290.54 |
| CH2O |
−95.8 |
−95.73 |
−109.3 |
−109.20 |
−104.9 |
−104.84 |
−114.9 |
−114.74 |
−112.8 |
−112.69 |
| CH4 |
−329.5 |
−329.59 |
−318.2 |
−318.26 |
−320.4 |
−320.42 |
−317.4 |
−317.40 |
−318.5 |
−318.54 |
| C2H4 |
−331.1 |
−331.10 |
−333.4 |
−333.45 |
−330.8 |
−330.82 |
−336.9 |
−336.95 |
−335.3 |
−335.36 |
| AlF |
−396.0 |
−395.86 |
−399.4 |
−399.26 |
−397.1 |
−396.98 |
−397.0 |
−396.92 |
−394.5 |
−394.39 |
| CH3F |
−315.4 |
−315.44 |
−309.6 |
−309.57 |
−311.3 |
−311.26 |
−312.5 |
−312.44 |
−314.4 |
−314.41 |
| C3H4 |
−464.4 |
−464.53 |
−458.4 |
−458.54 |
−459.5 |
−459.65 |
−463.1 |
−463.29 |
−465.1 |
−465.20 |
| FCCH |
−438.6 |
−438.68 |
−438.5 |
−438.58 |
−437.6 |
−437.67 |
−440.2 |
−440.30 |
−439.9 |
−439.93 |
| FCN |
−365.3 |
−365.31 |
−366.4 |
−366.39 |
−365.0 |
−364.97 |
−367.6 |
−367.58 |
−366.6 |
−366.61 |
| H2S |
−466.1 |
−466.22 |
−457.2 |
−457.25 |
−458.8 |
−458.84 |
−455.6 |
−455.70 |
−456.4 |
−456.43 |
| HCP |
−477.5 |
−477.48 |
−485.6 |
−485.63 |
−479.2 |
−479.27 |
−487.8 |
−487.81 |
−482.7 |
−482.74 |
| HFCO |
−296.9 |
−296.84 |
−299.4 |
−299.32 |
−296.9 |
−296.81 |
−300.7 |
−300.62 |
−298.7 |
−298.68 |
| H2C2O |
−427.7 |
−427.75 |
−420.7 |
−420.73 |
−421.9 |
−421.90 |
−422.4 |
−422.39 |
−423.7 |
−423.67 |
| LiF |
−196.4 |
−196.32 |
−196.4 |
−196.30 |
−196.2 |
−196.15 |
−194.9 |
−194.83 |
−194.2 |
−194.13 |
| LiH |
−135.9 |
−135.91 |
−136.6 |
−136.59 |
−135.2 |
−135.15 |
−131.2 |
−131.19 |
−129.1 |
−129.08 |
| N2O |
−334.5 |
−334.41 |
−332.2 |
−332.14 |
−332.0 |
−331.92 |
−334.0 |
−333.97 |
−334.3 |
−334.20 |
| OCS |
−576.7 |
−576.64 |
−576.2 |
−576.14 |
−574.8 |
−574.83 |
−579.9 |
−579.89 |
−579.7 |
−579.63 |
| OF2 |
−220.1 |
−220.01 |
−220.5 |
−220.40 |
−221.4 |
−221.30 |
−233.9 |
−233.86 |
−238.1 |
−237.97 |
| H4C2O |
−529.8 |
−529.97 |
−520.4 |
−520.52 |
−523.9 |
−524.02 |
−527.0 |
−527.19 |
−531.5 |
−531.63 |
| PN |
−284.2 |
−284.06 |
−292.1 |
−291.99 |
−283.9 |
−283.84 |
−292.2 |
−292.07 |
−284.6 |
−284.50 |
| SO2 |
−294.6 |
−294.38 |
−298.0 |
−297.77 |
−293.3 |
−293.10 |
−295.9 |
−295.65 |
−291.0 |
−290.77 |
A detailed error analysis, and the accuracy of the extrapolation formula are not discussed because of the agreement down to the last available digit in the GTO results, and rounding effects would therefore play a major role.
5.2.2 NMR shielding constants.
The NMR shielding constants computed with different basis sets for Hartree–Fock and DFT are presented in Tables 7 and 8, respectively, and the statistical basis set errors of the different methods are reported in Table 9, taking the MW6 values as reference. We begin by considering the progression along the series of MW calculations for Hartree–Fock. The MW3 results yield errors of a few tens of ppm, whereas MW4 are accurate to within 1–2 ppm and MW5 results are on average 0.1–0.2 ppm away from the MW6 values. We can therefore conclude that our best MW results are accurate to within 0.1 ppm or better. It is interesting that ozone, which is completely wrong at MW3, becomes in line with the other cases when MW5 and MW6 are compared. This is a clear indication of the systematic nature of the MW basis, which is able to provide the flexibility required to achieve the CBS result throughout the series.
Table 7 Hartree–Fock shielding constants (ppm) computed with GTO basis sets (aug-cc-pCVXZ, X = T, Q), extrapolation methods (aug-cc-pCV[TQ]Z with α = 1.63 and α = 1.05) and MW methods at increasing precision (ε = 10−η, η = 3, 4, 5, 6). All GTO calculations are taken from the ESI of ref. 22
| |
T
|
Q
|
[TQ1.63] |
[TQ1.05] |
MW3 |
MW4 |
MW5 |
MW6 |
| HF |
H |
28.40 |
28.20 |
28.15 |
28.09 |
29.04 |
28.20 |
28.13 |
28.12 |
|
|
F |
415.00 |
414.70 |
414.63 |
414.54 |
420.63 |
414.26 |
414.59 |
414.56 |
| CO |
C |
−23.30 |
−26.60 |
−27.40 |
−28.38 |
−23.18 |
−27.59 |
−28.43 |
−28.41 |
|
|
O |
−83.50 |
−89.40 |
−90.84 |
−92.58 |
−94.40 |
−95.77 |
−92.70 |
−92.83 |
| N2 |
N |
−108.30 |
−113.20 |
−114.39 |
−115.84 |
−144.94 |
−116.04 |
−116.06 |
−116.07 |
| H2O |
O |
328.80 |
328.10 |
327.93 |
327.72 |
333.39 |
326.59 |
327.83 |
327.78 |
|
|
H |
30.80 |
30.60 |
30.55 |
30.49 |
31.08 |
30.50 |
30.50 |
30.51 |
| HCN |
H |
29.30 |
29.20 |
29.18 |
29.15 |
31.10 |
29.22 |
29.22 |
29.22 |
|
|
C |
72.90 |
70.60 |
70.04 |
69.36 |
68.84 |
69.80 |
69.40 |
69.40 |
|
|
N |
−46.70 |
−51.10 |
−52.17 |
−53.47 |
−111.50 |
−53.47 |
−53.60 |
−53.55 |
| HOF |
O |
−130.60 |
−136.00 |
−137.32 |
−138.91 |
−111.30 |
−139.71 |
−138.79 |
−139.31 |
|
|
H |
19.30 |
19.10 |
19.05 |
18.99 |
19.87 |
19.01 |
19.01 |
19.00 |
|
|
F |
291.60 |
288.90 |
288.24 |
287.45 |
288.14 |
285.09 |
287.53 |
287.65 |
| O3 |
Omidt |
−2669.80 |
−2706.40 |
−2715.32 |
−2726.10 |
38.16 |
−2739.83 |
−2729.98 |
−2730.94 |
|
|
Oterm |
−2739.80 |
−2775.60 |
−2784.32 |
−2794.87 |
−62.57 |
−2808.35 |
−2801.00 |
−2800.06 |
| NH3 |
N |
263.40 |
262.60 |
262.41 |
262.17 |
268.20 |
262.02 |
262.23 |
262.23 |
|
|
H |
31.80 |
31.70 |
31.68 |
31.65 |
31.56 |
31.60 |
31.59 |
31.59 |
| H2CO |
O |
−431.50 |
−441.60 |
−444.06 |
−447.04 |
−673.90 |
−446.42 |
−447.59 |
−447.52 |
|
|
C |
−5.00 |
−7.90 |
−8.61 |
−9.46 |
−22.53 |
−8.94 |
−9.27 |
−9.34 |
|
|
H |
22.50 |
22.50 |
22.50 |
22.50 |
21.80 |
22.48 |
22.48 |
22.48 |
| CH4 |
C |
196.10 |
195.00 |
194.73 |
194.41 |
192.60 |
195.02 |
194.61 |
194.61 |
|
|
H |
31.60 |
31.60 |
31.60 |
31.60 |
31.45 |
31.55 |
31.55 |
31.55 |
| C2H6 |
C |
61.50 |
59.20 |
58.64 |
57.96 |
59.88 |
58.05 |
58.09 |
57.97 |
|
|
H |
26.30 |
26.20 |
26.18 |
26.15 |
25.86 |
26.19 |
26.19 |
26.18 |
| AlF |
Al |
580.40 |
580.20 |
580.15 |
580.09 |
583.44 |
579.61 |
579.61 |
580.03 |
|
|
F |
233.40 |
229.00 |
227.93 |
226.63 |
219.18 |
226.06 |
227.15 |
227.37 |
| CH3F |
C |
126.80 |
125.00 |
124.56 |
124.03 |
131.76 |
124.42 |
124.32 |
124.29 |
|
|
F |
486.90 |
486.70 |
486.65 |
486.59 |
471.85 |
486.07 |
487.02 |
486.93 |
|
|
H |
28.00 |
27.90 |
27.88 |
27.85 |
27.83 |
27.92 |
27.90 |
27.90 |
| C3H4 |
C |
194.40 |
193.30 |
193.03 |
192.71 |
197.60 |
193.25 |
193.03 |
192.97 |
|
|
Cdb |
73.00 |
70.80 |
70.26 |
69.62 |
−21.52 |
69.84 |
69.61 |
69.65 |
|
|
Hdb |
24.20 |
24.10 |
24.08 |
24.05 |
24.92 |
24.07 |
24.05 |
24.05 |
|
|
H |
31.00 |
30.90 |
30.88 |
30.85 |
29.39 |
30.93 |
30.92 |
30.92 |
| HCCF |
C(H) |
177.70 |
176.50 |
176.21 |
175.85 |
183.55 |
175.50 |
175.98 |
175.96 |
|
|
C(F) |
102.80 |
100.80 |
100.31 |
99.72 |
108.91 |
100.45 |
99.91 |
99.89 |
|
|
H |
30.60 |
30.50 |
30.48 |
30.45 |
30.35 |
30.52 |
30.50 |
30.51 |
|
|
F |
428.90 |
428.30 |
428.15 |
427.98 |
415.85 |
427.70 |
428.23 |
428.10 |
| FCN |
F |
378.70 |
377.70 |
377.46 |
377.16 |
360.67 |
378.00 |
377.18 |
377.19 |
|
|
C |
77.70 |
75.30 |
74.72 |
74.01 |
81.39 |
74.51 |
74.19 |
74.11 |
|
|
N |
94.70 |
91.80 |
91.09 |
90.24 |
85.39 |
90.29 |
90.45 |
90.32 |
| H2S |
S |
715.00 |
711.30 |
710.40 |
709.31 |
727.11 |
728.03 |
710.99 |
711.26 |
|
|
H |
30.60 |
30.60 |
30.60 |
30.60 |
32.44 |
30.91 |
30.53 |
30.53 |
| HCP |
H |
30.10 |
30.10 |
30.10 |
30.10 |
31.30 |
30.13 |
30.08 |
30.11 |
|
|
C |
15.80 |
13.30 |
12.69 |
11.95 |
−15.94 |
11.78 |
12.05 |
11.87 |
|
|
P |
338.80 |
339.70 |
339.92 |
340.18 |
123.31 |
339.08 |
339.68 |
339.38 |
| HFCO |
O |
−123.20 |
−129.50 |
−131.04 |
−132.89 |
−193.91 |
−135.04 |
−133.50 |
−133.20 |
|
|
C |
36.10 |
33.40 |
32.74 |
31.95 |
41.58 |
32.31 |
32.13 |
32.09 |
|
|
F |
191.00 |
187.90 |
187.14 |
186.23 |
146.78 |
188.28 |
186.59 |
186.13 |
|
|
H |
24.50 |
24.40 |
24.38 |
24.35 |
24.89 |
24.39 |
24.38 |
24.38 |
| H2C2O |
C(O) |
190.50 |
189.30 |
189.01 |
188.65 |
193.64 |
188.97 |
188.88 |
188.89 |
|
|
C(H) |
−11.70 |
−14.90 |
−15.68 |
−16.62 |
−24.45 |
−16.47 |
−16.57 |
−16.54 |
|
|
O |
−22.30 |
−27.40 |
−28.64 |
−30.15 |
2.46 |
−29.86 |
−30.14 |
−30.41 |
|
|
H |
29.50 |
29.40 |
29.38 |
29.35 |
29.49 |
29.34 |
29.33 |
29.33 |
| LiF |
Li |
90.90 |
90.60 |
90.53 |
90.44 |
90.49 |
90.47 |
90.46 |
90.46 |
|
|
F |
392.10 |
390.80 |
390.48 |
390.10 |
395.36 |
390.28 |
390.16 |
390.17 |
| LiH |
H |
26.60 |
26.60 |
26.60 |
26.60 |
26.51 |
26.61 |
26.61 |
26.61 |
|
|
Li |
89.80 |
89.50 |
89.43 |
89.34 |
90.64 |
89.51 |
89.50 |
89.50 |
| N2O |
Nmidt |
65.70 |
62.70 |
61.97 |
61.09 |
59.78 |
61.40 |
60.92 |
61.04 |
|
|
N |
−29.40 |
−33.40 |
−34.37 |
−35.55 |
−35.66 |
−34.15 |
−35.39 |
−35.73 |
|
|
O |
177.30 |
174.80 |
174.19 |
173.45 |
172.73 |
173.76 |
173.50 |
173.41 |
| OCS |
O |
80.10 |
76.60 |
75.75 |
74.72 |
59.07 |
72.89 |
74.30 |
74.46 |
|
|
C |
10.40 |
7.30 |
6.54 |
5.63 |
0.82 |
5.89 |
5.91 |
5.82 |
|
|
S |
788.80 |
787.60 |
787.31 |
786.95 |
730.46 |
790.81 |
787.98 |
787.70 |
| OF2 |
O |
−435.40 |
−443.80 |
−445.85 |
−448.32 |
−419.25 |
−448.90 |
−448.36 |
−449.10 |
|
|
F |
27.80 |
22.40 |
21.08 |
19.49 |
32.32 |
22.88 |
20.07 |
19.38 |
| H4C2O |
O |
379.10 |
378.80 |
378.73 |
378.64 |
364.09 |
377.84 |
378.82 |
378.80 |
|
|
C |
156.90 |
155.40 |
155.03 |
154.59 |
162.13 |
155.17 |
154.91 |
154.87 |
|
|
H |
29.80 |
29.70 |
29.68 |
29.65 |
29.34 |
29.71 |
29.70 |
29.70 |
| PN |
N |
−498.00 |
−506.50 |
−508.57 |
−511.08 |
−553.60 |
−514.49 |
−511.69 |
−511.80 |
|
|
P |
−110.90 |
−108.40 |
−107.79 |
−107.05 |
−167.61 |
−113.29 |
−108.04 |
−109.37 |
| SO2 |
S |
−393.40 |
−395.20 |
−395.64 |
−396.17 |
−724.14 |
−397.98 |
−395.02 |
−396.57 |
|
|
O |
−330.50 |
−335.60 |
−336.84 |
−338.35 |
−595.92 |
−341.03 |
−340.30 |
−340.38 |
Table 8 Shielding constants (ppm) computed using a range of density functionals with the aug-cc-pCVQZ basis set and the MW basis at precision ε = 10−6. All GTO calculations are taken from the ESI of ref. 22
| |
LDA |
BLYP |
PBE |
B3LYP |
PBE0 |
|
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
Q
|
MW6 |
| HF |
H |
29.20 |
29.13 |
29.90 |
29.82 |
29.90 |
29.78 |
29.50 |
29.35 |
29.40 |
29.26 |
|
|
F |
416.00 |
415.78 |
410.50 |
410.25 |
412.00 |
411.69 |
412.00 |
411.75 |
413.40 |
413.13 |
| CO |
C |
−23.30 |
−25.09 |
−17.70 |
−19.51 |
−15.90 |
−17.58 |
−21.50 |
−23.27 |
−20.00 |
−21.70 |
|
|
O |
−91.70 |
−95.18 |
−81.30 |
−84.69 |
−82.40 |
−85.70 |
−85.50 |
−88.90 |
−86.80 |
−90.21 |
| N2 |
N |
−94.10 |
−96.95 |
−87.20 |
−90.02 |
−85.80 |
−88.58 |
−94.40 |
−97.28 |
−94.20 |
−96.98 |
| H2O |
O |
334.30 |
333.95 |
326.10 |
325.70 |
328.80 |
328.45 |
327.10 |
326.74 |
329.50 |
329.16 |
|
|
H |
30.80 |
30.74 |
31.40 |
31.31 |
31.30 |
31.24 |
31.20 |
31.06 |
31.10 |
30.99 |
| HCN |
H |
28.90 |
28.92 |
29.40 |
29.32 |
29.20 |
29.16 |
29.30 |
29.29 |
29.20 |
29.16 |
|
|
C |
63.70 |
62.48 |
68.90 |
67.63 |
70.20 |
69.02 |
67.90 |
66.63 |
69.40 |
68.20 |
|
|
N |
−59.10 |
−61.65 |
−48.80 |
−51.26 |
−46.60 |
−48.97 |
−51.70 |
−54.23 |
−49.30 |
−51.75 |
| HOF |
O |
−143.40 |
−146.91 |
−138.40 |
−141.89 |
−128.50 |
−131.84 |
−137.30 |
−140.66 |
−125.70 |
−129.05 |
|
|
H |
18.40 |
18.32 |
19.40 |
19.25 |
19.30 |
19.21 |
19.30 |
19.21 |
19.30 |
19.26 |
|
|
F |
160.10 |
157.98 |
145.70 |
143.47 |
150.90 |
148.60 |
175.10 |
173.10 |
185.70 |
183.69 |
| O3 |
Omidt |
−920.70 |
−930.40 |
−902.50 |
−911.95 |
−884.60 |
−893.97 |
−1123.90 |
−1135.21 |
−1164.80 |
−1176.33 |
|
|
Oterm |
−1519.30 |
−1533.59 |
−1461.80 |
−1475.42 |
−1450.80 |
−1464.28 |
−1676.80 |
−1692.22 |
−1719.90 |
−1735.43 |
| NH3 |
N |
266.90 |
266.53 |
259.00 |
258.57 |
262.40 |
261.99 |
260.20 |
259.81 |
263.30 |
262.96 |
|
|
H |
31.50 |
31.40 |
31.90 |
31.85 |
31.80 |
31.78 |
31.80 |
31.74 |
31.70 |
31.67 |
| H2CO |
O |
−499.20 |
−505.66 |
−449.80 |
−455.91 |
−452.40 |
−458.45 |
−457.80 |
−463.93 |
−458.20 |
−464.28 |
|
|
C |
−42.10 |
−43.84 |
−29.30 |
−30.99 |
−27.90 |
−29.56 |
−26.30 |
−27.94 |
−23.30 |
−24.94 |
|
|
H |
20.10 |
20.11 |
21.10 |
21.07 |
20.80 |
20.77 |
21.40 |
21.36 |
21.20 |
21.21 |
| CH4 |
C |
193.00 |
192.62 |
186.30 |
185.84 |
190.30 |
189.93 |
188.70 |
188.21 |
192.70 |
192.25 |
|
|
H |
31.20 |
31.15 |
31.60 |
31.57 |
31.50 |
31.46 |
31.50 |
31.51 |
31.50 |
31.42 |
| C2H6 |
C |
40.30 |
38.84 |
44.60 |
43.21 |
47.50 |
46.12 |
46.70 |
45.31 |
50.30 |
49.00 |
|
|
H |
25.10 |
25.04 |
25.90 |
25.89 |
25.60 |
25.60 |
25.90 |
25.88 |
25.70 |
25.65 |
| AlF |
Al |
532.90 |
532.78 |
540.90 |
540.73 |
542.80 |
542.90 |
550.10 |
549.88 |
554.40 |
554.48 |
|
|
F |
138.40 |
136.16 |
152.70 |
150.60 |
150.50 |
148.34 |
171.90 |
169.89 |
175.60 |
173.63 |
| CH3F |
C |
103.10 |
102.18 |
100.60 |
99.69 |
105.20 |
104.27 |
106.30 |
105.44 |
111.90 |
111.05 |
|
|
F |
474.10 |
474.33 |
458.20 |
458.26 |
462.10 |
462.23 |
466.50 |
466.62 |
471.00 |
471.10 |
|
|
H |
26.60 |
26.57 |
27.20 |
27.21 |
27.10 |
27.07 |
27.40 |
27.34 |
27.30 |
27.29 |
| C3H4 |
C |
177.30 |
176.83 |
173.30 |
172.86 |
176.80 |
176.35 |
178.00 |
177.57 |
182.10 |
181.70 |
|
|
Cdb |
56.30 |
55.03 |
58.40 |
57.14 |
62.10 |
60.95 |
60.40 |
59.22 |
64.80 |
63.62 |
|
|
Hdb |
23.70 |
23.64 |
24.40 |
24.31 |
24.20 |
24.14 |
24.20 |
24.19 |
24.10 |
24.05 |
|
|
H |
30.20 |
30.18 |
30.70 |
30.70 |
30.60 |
30.55 |
30.70 |
30.70 |
30.60 |
30.60 |
| HCCF |
C(H) |
165.30 |
164.75 |
169.00 |
168.42 |
170.10 |
169.60 |
169.40 |
168.80 |
170.90 |
170.39 |
|
|
C(F) |
76.80 |
75.69 |
78.30 |
77.21 |
82.20 |
81.17 |
82.80 |
81.76 |
87.70 |
86.50 |
|
|
H |
30.60 |
30.57 |
31.10 |
31.10 |
31.00 |
30.94 |
30.90 |
30.90 |
30.80 |
30.74 |
|
|
F |
392.10 |
391.72 |
392.50 |
392.11 |
389.10 |
388.70 |
400.40 |
400.07 |
398.80 |
398.41 |
| FCN |
F |
343.50 |
342.86 |
343.00 |
342.39 |
338.70 |
338.09 |
351.10 |
350.53 |
348.60 |
348.01 |
|
|
C |
63.20 |
61.82 |
64.50 |
63.23 |
68.50 |
67.29 |
65.80 |
64.60 |
70.10 |
68.66 |
|
|
N |
89.60 |
88.04 |
96.70 |
95.20 |
99.40 |
97.89 |
92.40 |
90.78 |
94.70 |
93.20 |
| H2S |
S |
724.00 |
723.97 |
690.30 |
690.21 |
713.70 |
713.53 |
697.00 |
696.91 |
719.00 |
718.94 |
|
|
H |
30.40 |
30.33 |
31.10 |
31.03 |
30.80 |
30.79 |
30.90 |
30.84 |
30.60 |
30.61 |
| HCP |
H |
29.40 |
29.39 |
29.80 |
29.81 |
29.60 |
29.60 |
29.90 |
29.87 |
29.70 |
29.71 |
|
|
C |
4.80 |
3.28 |
10.20 |
8.66 |
13.10 |
11.67 |
8.80 |
7.29 |
11.90 |
10.48 |
|
|
P |
285.90 |
285.56 |
320.20 |
319.94 |
325.60 |
325.34 |
316.80 |
316.45 |
323.80 |
323.52 |
| HFCO |
O |
−143.90 |
−147.68 |
−131.00 |
−134.84 |
−127.70 |
−131.40 |
−137.00 |
−140.77 |
−133.80 |
−137.57 |
|
|
C |
15.10 |
13.56 |
17.40 |
15.95 |
20.90 |
19.49 |
19.60 |
18.13 |
23.60 |
22.25 |
|
|
F |
80.60 |
78.03 |
93.30 |
90.79 |
91.40 |
88.88 |
115.50 |
113.15 |
119.70 |
117.39 |
|
|
H |
22.90 |
22.84 |
23.40 |
23.39 |
23.30 |
23.23 |
23.60 |
23.58 |
23.60 |
23.52 |
| H2C2O |
C(O) |
186.00 |
185.49 |
182.50 |
181.99 |
185.40 |
184.88 |
183.80 |
183.29 |
186.70 |
186.24 |
|
|
C(H) |
−23.30 |
−25.06 |
−24.90 |
−26.70 |
−18.70 |
−20.46 |
−24.40 |
−26.15 |
−18.20 |
−19.96 |
|
|
O |
−26.30 |
−29.35 |
−26.50 |
−29.54 |
−22.40 |
−25.35 |
−30.10 |
−33.19 |
−26.60 |
−29.59 |
|
|
H |
28.90 |
28.88 |
29.60 |
29.52 |
29.40 |
29.33 |
29.40 |
29.39 |
29.30 |
29.23 |
| LiF |
Li |
85.30 |
85.19 |
86.50 |
86.33 |
86.60 |
86.46 |
87.50 |
87.41 |
88.00 |
87.84 |
|
|
F |
340.90 |
340.02 |
336.30 |
335.41 |
343.60 |
342.75 |
351.90 |
351.05 |
362.20 |
361.46 |
| LiH |
H |
25.80 |
25.79 |
26.50 |
26.53 |
26.30 |
26.34 |
26.60 |
26.58 |
26.40 |
26.44 |
|
|
Li |
86.40 |
86.30 |
88.40 |
88.33 |
88.20 |
88.12 |
88.30 |
88.21 |
88.30 |
88.26 |
| N2O |
Nmidt |
86.40 |
84.65 |
86.80 |
85.26 |
90.70 |
89.13 |
80.60 |
79.02 |
83.10 |
81.57 |
|
|
N |
−3.80 |
−5.63 |
−5.50 |
−7.23 |
0.80 |
−0.85 |
−12.30 |
−14.54 |
−7.80 |
−9.92 |
|
|
O |
178.50 |
177.11 |
173.80 |
172.38 |
175.60 |
174.24 |
172.90 |
171.44 |
174.20 |
172.79 |
| OCS |
O |
68.40 |
66.24 |
69.50 |
67.24 |
70.20 |
68.01 |
70.20 |
68.03 |
71.30 |
69.06 |
|
|
C |
17.80 |
16.27 |
17.30 |
15.79 |
22.40 |
20.99 |
13.80 |
12.18 |
18.10 |
16.69 |
|
|
S |
754.00 |
754.14 |
755.50 |
755.55 |
762.60 |
762.58 |
760.60 |
760.84 |
768.90 |
768.99 |
| OF2 |
O |
−672.30 |
−679.48 |
−641.50 |
−648.23 |
−629.50 |
−636.19 |
−588.80 |
−595.24 |
−562.10 |
−568.38 |
|
|
F |
−98.50 |
−102.35 |
−102.30 |
−106.30 |
−91.40 |
−95.35 |
−73.80 |
−77.52 |
−56.60 |
−60.18 |
| H4C2O |
O |
338.00 |
337.73 |
329.80 |
329.40 |
333.30 |
332.96 |
340.00 |
339.70 |
345.10 |
344.82 |
|
|
C |
136.00 |
135.28 |
133.20 |
132.46 |
137.50 |
136.81 |
138.30 |
137.63 |
143.50 |
142.83 |
|
|
H |
28.60 |
28.57 |
29.20 |
29.20 |
29.10 |
29.05 |
29.30 |
29.28 |
29.20 |
29.20 |
| PN |
N |
−429.30 |
−434.32 |
−421.20 |
−426.14 |
−415.00 |
−419.79 |
−443.30 |
−448.35 |
−441.60 |
−446.56 |
|
|
P |
−86.70 |
−88.28 |
−47.80 |
−49.40 |
−45.80 |
−47.05 |
−69.70 |
−71.30 |
−70.50 |
−71.87 |
| SO2 |
S |
−300.50 |
−301.70 |
−276.30 |
−277.60 |
−259.70 |
−260.95 |
−312.20 |
−313.51 |
−303.10 |
−304.33 |
|
|
O |
−322.70 |
−327.49 |
−315.60 |
−320.33 |
−311.70 |
−316.47 |
−327.70 |
−332.57 |
−326.40 |
−331.24 |
Table 9 Statistical basis set errors of all computed shielding constants (including O3) for the different methods employed in the paper, MW calculations at ε = 10−6 are taken as reference. For each combination of basis/functional the following errors are reported: medium error, medium absolute error, medium relative error, medium absolute relative error, standard deviation and maximum error. Average timings in minutes on 16 CPUs
|
|
|
HF |
LDA |
BLYP |
PBE |
B3LYP |
PBE0 |
| aug-cc-pCVTZ |
|
|
ME |
4.79 |
4.72 |
4.49 |
4.36 |
4.54 |
4.40 |
|
|
MAE |
4.85 |
4.72 |
4.49 |
4.36 |
4.54 |
4.40 |
|
|
MRE |
0.57 |
0.51 |
−0.72 |
−9.24 |
0.00 |
−1.03 |
|
|
MARE |
6.10 |
8.12 |
6.40 |
13.91 |
5.93 |
5.69 |
|
|
SD |
11.21 |
8.01 |
7.50 |
7.28 |
7.97 |
7.84 |
|
|
MaxE |
61.14 |
38.89 |
35.82 |
34.88 |
40.12 |
40.13 |
|
|
Time |
0.69 |
0.76 |
0.74 |
0.71 |
0.83 |
0.87 |
|
|
| aug-cc-pCVQZ |
|
|
ME |
1.79 |
1.57 |
1.55 |
1.51 |
1.58 |
1.56 |
|
|
MAE |
1.80 |
1.58 |
1.55 |
1.51 |
1.59 |
1.57 |
|
|
MRE |
0.11 |
0.14 |
−0.28 |
−2.86 |
−0.07 |
−0.43 |
|
|
MARE |
2.12 |
2.63 |
2.15 |
4.41 |
2.04 |
1.98 |
|
|
SD |
4.46 |
2.84 |
2.75 |
2.71 |
2.96 |
2.96 |
|
|
MaxE |
24.54 |
14.29 |
13.62 |
13.48 |
15.42 |
15.53 |
|
|
Time |
8.0 |
6.6 |
6.8 |
6.9 |
7.9 |
7.8 |
|
|
| aug-cc-pCV[TQ]Z |
|
α = 1.63 |
ME |
1.06 |
0.80 |
0.83 |
0.81 |
0.86 |
0.86 |
|
|
MAE |
1.11 |
0.87 |
0.88 |
0.87 |
0.92 |
0.92 |
|
|
MRE |
0.00 |
0.05 |
−0.17 |
−1.30 |
−0.09 |
−0.29 |
|
|
MARE |
1.18 |
1.31 |
1.14 |
2.10 |
1.11 |
1.10 |
|
|
SD |
2.83 |
1.61 |
1.62 |
1.62 |
1.77 |
1.79 |
|
|
MaxE |
15.73 |
8.29 |
8.22 |
8.26 |
9.41 |
9.54 |
|
|
| aug-cc-pCV[TQ]Z |
|
α = 1.05 |
ME |
0.18 |
−0.13 |
−0.04 |
−0.03 |
−0.01 |
0.03 |
|
|
MAE |
0.38 |
0.27 |
0.27 |
0.27 |
0.28 |
0.28 |
|
|
MRE |
−0.13 |
−0.06 |
−0.04 |
0.58 |
−0.10 |
−0.11 |
|
|
MARE |
0.26 |
0.42 |
0.31 |
0.86 |
0.23 |
0.21 |
|
|
SD |
0.97 |
0.52 |
0.51 |
0.52 |
0.54 |
0.54 |
|
|
MaxE |
5.19 |
2.40 |
1.96 |
2.14 |
2.13 |
2.29 |
|
|
| MW3 |
|
|
ME |
57.17 |
−15.99 |
−8.04 |
−10.13 |
−24.63 |
28.41 |
|
|
MAE |
101.93 |
25.02 |
22.51 |
24.48 |
32.52 |
59.18 |
|
|
MRE |
−1.87 |
−11.19 |
4.01 |
−6.74 |
−4.62 |
1.38 |
|
|
MARE |
24.68 |
33.50 |
18.98 |
27.53 |
21.31 |
20.75 |
|
|
SD |
463.45 |
57.43 |
43.87 |
48.69 |
91.44 |
245.76 |
|
|
MaxE |
2769.10 |
270.47 |
164.35 |
198.66 |
562.56 |
1697.14 |
|
|
Time |
92.8 |
6.0 |
6.0 |
6.0 |
87.2 |
86.7 |
|
|
| MW4 |
|
|
ME |
−0.08 |
−0.14 |
−0.41 |
−0.25 |
−0.02 |
0.14 |
|
|
MAE |
1.08 |
0.68 |
0.85 |
0.85 |
0.79 |
0.98 |
|
|
MRE |
0.27 |
0.03 |
0.21 |
−0.32 |
−0.21 |
−0.63 |
|
|
MARE |
0.83 |
0.80 |
0.80 |
1.23 |
1.03 |
1.22 |
|
|
SD |
2.67 |
1.14 |
1.64 |
1.65 |
1.39 |
1.98 |
|
|
MaxE |
16.77 |
3.87 |
10.08 |
9.36 |
5.76 |
9.76 |
|
|
Time |
215.8 |
14.5 |
14.6 |
15.7 |
221.5 |
248.2 |
|
|
| MW5 |
|
|
ME |
0.09 |
0.07 |
0.05 |
0.06 |
0.07 |
0.06 |
|
|
MAE |
0.17 |
0.15 |
0.14 |
0.14 |
0.16 |
0.16 |
|
|
MRE |
0.04 |
−0.08 |
−0.07 |
−0.53 |
−0.07 |
−0.08 |
|
|
MARE |
0.20 |
0.30 |
0.20 |
0.61 |
0.22 |
0.22 |
|
|
SD |
0.34 |
0.35 |
0.33 |
0.32 |
0.36 |
0.33 |
|
|
MaxE |
1.55 |
2.10 |
2.01 |
2.00 |
1.72 |
1.53 |
|
|
Time |
301.5 |
24.6 |
24.4 |
26.4 |
383.3 |
307.3 |
We can now compare MW6 results to the GTO values. In particular, the best aug-cc-pCVQZ results are accurate to within 1–2 ppm (MAE = 1.8/1.2 with/without O3), i.e. comparable to MW4. The extrapolated values (α = 1.63) show an improvement over the aug-cc-pCVQZ ones, and the error is reduced (MAE = 1.1/0.7), although not substantially. However, if we change the parametrization to α = 1.05, a much closer agreement is achieved (MAE = 0.38/0.25 with/without O3). Other measures for the error yield a similar picture. This result suggests that the extrapolation procedure, which is originally justified because the shielding is a second derivative of the energy, is a reasonable way to estimate CBS results. However, making use of the same exponent as the molecular energy, is improving over the aug-cc-pCVQZ values only slightly. If the exponent is set to 1.05 (larger corrections than α = 1.63) the improvement is substantial. Considering that α is the only adjustable parameter for 72 shielding values, this result is a confirmation of the validity of the two-point exponential parametrization.
We now turn our attention to DFT, where for clarity we present the raw data only for quadruple-ζ and MW6 for the chosen functionals in Table 8, while the statistical errors are given for all basis sets in Table 9. The sequence of MW calculations at increasing precision paints a similar picture to that seen for HF: MW3 yields results that are several ppm away from the MW6 values and also worse than triple-ζ quality numbers, MW4 is a huge leap forward, outperforming the quadruple-ζ results. MW5 yields results that are in most cases 0.1–0.2 ppm away from the MW6 values. This progression is again an indication that the error in the MW6 values can be considered well below 0.1 ppm from the CBS results, and MW6 values can in practice be taken as a reference.
The MW6 reference values enable us to apply to DFT the same extrapolation procedure used for HF. With α = 1.63, we observe a reduction of the errors (e.g. for B3LYP the MAE goes from 1.59 to 0.9). With α = 1.05 the reduction is more marked (for B3LYP MAE = 0.28/0.24 with/without O3). Slightly better results could be achieved if the parameter α was optimized for each functional separately, e.g. using α = 0.9 leads to a further substantial reduction in the standard deviation in the Hartree–Fock results, but we observe the opposite effect for all DFT functionals. The main point is, however, that neither for HF nor for DFT is α = 1.63 the optimal value, and our results indicate that a lower value, yielding a larger correction, performs much better for HF and DFT alike.
5.2.3 Computation times.
In Table 9, we also report the average timings for the GTO as well as the MW calculations. All timings include the ground-state SCF optimization (to obtain ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0)) followed by three response calculations (to obtain
(0)) followed by three response calculations (to obtain ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (B)μ for μ = x, y, z). The magnetizability and NMR shielding tensors of all nuclei in the molecule are then computed simultaneously according to eqn (26) and (27). The timings are given in minutes wall-time on a single compute node with 16 CPUs (2.6 GHz Intel E5-2670) using a shared memory parallelization strategy. For the GTO calculations, the timings are obtained from Dalton, on the same computer architecture and also using 16 processors using the message passing interface (MPI).
(B)μ for μ = x, y, z). The magnetizability and NMR shielding tensors of all nuclei in the molecule are then computed simultaneously according to eqn (26) and (27). The timings are given in minutes wall-time on a single compute node with 16 CPUs (2.6 GHz Intel E5-2670) using a shared memory parallelization strategy. For the GTO calculations, the timings are obtained from Dalton, on the same computer architecture and also using 16 processors using the message passing interface (MPI).
Whereas the MW code is far from optimized for production calculations, we can draw some interesting conclusions from the numbers. First of all, there is an order of magnitude difference in computation time between pure and hybrid density functionals: for HF, PBE0 and B3LYP, the exact-exchange is a clear bottleneck, especially in the magnetic response solver because the pure functionals do not contribute to the perturbed Fock operator (eqn (31)), but also in the ground-state calculation as the exact exchange scales quadratically with the number of orbitals. Although the current implementation fully supports orbital localization, which should have an effect on the exact exchange, no particular attempt has yet been made in exploiting localization to achieve linear scaling algorithms. The systems treated in the current work are anyway too small for this to have any appreciable effect.
Along the series of MW calculations, we observe that the computational costs roughly doubles at each ten-fold increase of the requested precision.
Concerning the comparison between MW and GTO, and limiting the comparison to pure functionals (hybrid functionals and HF are affected by the exchange bottleneck), we notice how TZ-quality results are quite cheap to achieve, being ten times faster than MW3 results. However MW4 results, which are comparable to the extrapolated [TQ]Z values, are only three times more expensive than QZ values: along the GTO series, the computational cost increases ten times at each step (aug-cc-pCV5Z confirmed the trend, for the 24 molecules where this basis set is available).
In conclusion, GTOs come from decades of developments, where a large effort has been poured into improving the underlying algorithms and fine-tuning the basis set compositions. This explains why a moderate basis set, such as TZ, is able to give reasonable results with good performance. But when the precision requirements are increased, a MW basis becomes eventually superior.
5.2.4 Comparison with coupled cluster and experiment.
With the proper CBS limits established for the different DFT functionals, we can assess their ability to reproduce the theoretical limit: full configuration interaction (FCI) in a CBS. In practice coupled cluster singles and doubles with perturbative triples corrections (CCSD(T)) including basis set extrapolation has been taken as a reference.22 Additionally, experimental data including zero-point vibrational corrections (ZPVCs) have been considered. Several investigations of this type have been conducted in the past,22,78–81 and our observations agree with the current consensus regarding the CBS limit. It is well known that the employed density functionals systematically underestimate the shielding constant: this has been attributed to a too small HOMO–LUMO gap.78 Some attempts have also been made to fix the problem by simple level shifting of the virtual orbital energies,78,82,83 although the theoretical justification is questionable.
We present in Table 10 the statistical errors with respect to coupled cluster (CC) and the empirical equilibrium (experimental values including ZPVC). In the comparison to CCSD(T), O3 is omitted, because it is an extreme outlier with errors on the order of 1000 ppm. In the comparison to experiments, around one fourth of the data set is instead omitted because accurate experimental data is lacking. The same data set as used by Teale et al.22 has been used, and details about the excluded systems can be found in their paper. All GTO calculations, as well as all experimental numbers, are taken from the work of Teale et al.22
Table 10 Statistical errors of shielding constants with respect to extrapolated CCSD(T) and empirical equilibrium (experiment minus zero-point vibrational corrections) results for the different methods employed in the paper. We report the basis set convergence of aug-cc-pCVXZ (X = D, T, Q) as well as MW6, which can be considered converged to the CBS limit. For the CCSD(T) comparison O3 is omitted, while only the molecules where good experimental values are available were included in the comparison with empirical equilibrium (see text for details). All GTO calculations, as well as all experimental numbers, are taken from ref. 22. For each combination of basis/functional the following errors are reported: medium error, medium absolute error, medium relative error, medium absolute relative error, standard deviation and maximum error
| |
Extrapolated CCSD(T) |
Empirical equilibrium |
|
D
|
T
|
Q
|
MW6 |
D
|
T
|
Q
|
MW6 |
| RHF |
ME |
−6.83 |
−13.68 |
−15.73 |
−16.87 |
−1.96 |
−9.13 |
−10.87 |
−11.85 |
|
|
MAE |
20.30 |
22.93 |
23.97 |
24.68 |
17.55 |
20.28 |
20.86 |
21.27 |
|
|
MRE |
−13.50 |
−26.74 |
−29.62 |
−31.01 |
−16.10 |
−24.30 |
−26.23 |
−27.28 |
|
|
MARE |
40.31 |
59.74 |
68.18 |
72.84 |
36.61 |
56.06 |
62.64 |
66.25 |
|
|
SD |
42.75 |
43.74 |
44.95 |
45.94 |
36.62 |
40.16 |
40.86 |
41.58 |
|
|
MaxE |
211.40 |
190.00 |
191.80 |
193.17 |
161.30 |
170.80 |
168.30 |
169.27 |
|
|
| LDA |
ME |
−16.76 |
−27.39 |
−30.04 |
−31.31 |
−13.56 |
−23.34 |
−25.62 |
−26.74 |
|
|
MAE |
19.21 |
28.72 |
31.36 |
32.62 |
14.39 |
23.45 |
25.70 |
26.82 |
|
|
MRE |
−33.50 |
−49.04 |
−52.92 |
−54.49 |
−19.88 |
−29.72 |
−32.25 |
−33.33 |
|
|
MARE |
51.45 |
90.37 |
102.03 |
107.61 |
35.90 |
71.58 |
80.88 |
85.31 |
|
|
SD |
36.09 |
46.61 |
49.82 |
51.53 |
34.37 |
44.44 |
47.21 |
48.75 |
|
|
MaxE |
180.50 |
212.70 |
225.20 |
232.38 |
178.40 |
210.60 |
223.10 |
230.28 |
|
|
| BLYP |
ME |
−14.34 |
−24.53 |
−27.01 |
−28.27 |
−11.83 |
−21.32 |
−23.48 |
−24.60 |
|
|
MAE |
16.53 |
26.02 |
28.48 |
29.72 |
12.96 |
21.60 |
23.73 |
24.83 |
|
|
MRE |
−18.25 |
−33.53 |
−36.84 |
−38.37 |
−10.35 |
−19.89 |
−22.07 |
−23.13 |
|
|
MARE |
33.18 |
72.29 |
83.02 |
88.54 |
23.94 |
59.09 |
67.66 |
72.02 |
|
|
SD |
29.36 |
39.23 |
42.27 |
43.93 |
27.50 |
37.41 |
40.19 |
41.74 |
|
|
MaxE |
149.10 |
182.30 |
194.40 |
201.13 |
147.00 |
180.20 |
192.30 |
199.03 |
|
|
| PBE |
ME |
−12.81 |
−21.87 |
−24.27 |
−26.71 |
−10.52 |
−18.98 |
−21.09 |
−22.32 |
|
|
MAE |
15.23 |
23.30 |
25.69 |
28.12 |
12.00 |
19.21 |
21.29 |
22.53 |
|
|
MRE |
−18.92 |
−33.04 |
−36.23 |
−38.58 |
−10.99 |
−19.83 |
−22.01 |
−25.57 |
|
|
MARE |
33.69 |
64.54 |
74.82 |
88.57 |
24.43 |
51.92 |
60.12 |
72.52 |
|
|
SD |
28.22 |
36.23 |
39.15 |
41.75 |
26.58 |
34.65 |
37.36 |
37.66 |
|
|
MaxE |
145.10 |
170.60 |
182.40 |
148.14 |
143.00 |
168.50 |
180.30 |
146.04 |
|
|
| B3LYP |
ME |
−13.40 |
−23.04 |
−25.46 |
−25.50 |
−9.99 |
−19.12 |
−21.22 |
−22.17 |
|
|
MAE |
15.02 |
24.49 |
26.89 |
26.90 |
10.98 |
19.39 |
21.45 |
22.36 |
|
|
MRE |
−18.74 |
−33.68 |
−37.07 |
−37.66 |
−12.88 |
−22.26 |
−24.48 |
−22.96 |
|
|
MARE |
30.84 |
72.33 |
83.10 |
80.14 |
24.51 |
59.58 |
68.17 |
64.33 |
|
|
SD |
27.99 |
37.23 |
40.12 |
40.78 |
23.71 |
33.67 |
36.18 |
38.86 |
|
|
MaxE |
101.10 |
130.40 |
141.70 |
189.09 |
106.80 |
128.80 |
139.60 |
186.99 |
|
|
| PBE0 |
ME |
−11.43 |
−19.85 |
−22.15 |
−23.37 |
−8.09 |
−16.17 |
−18.17 |
−19.23 |
|
|
MAE |
13.64 |
21.26 |
23.54 |
24.74 |
9.72 |
16.60 |
18.40 |
19.44 |
|
|
MRE |
−18.48 |
−32.24 |
−35.37 |
−36.84 |
−13.38 |
−22.05 |
−24.20 |
−25.21 |
|
|
MARE |
29.51 |
63.29 |
73.37 |
78.74 |
23.17 |
51.82 |
59.76 |
64.00 |
|
|
SD |
26.58 |
33.76 |
36.43 |
38.00 |
22.47 |
30.42 |
32.71 |
34.09 |
|
|
MaxE |
103.60 |
119.70 |
121.10 |
122.47 |
112.90 |
129.00 |
130.40 |
131.77 |
Focusing first on the CBS limit, represented here by the MW6 numbers, we observe an underestimation of 20–30 ppm, without significant variations throughout the set of functionals employed. The magnitude of the mean error (ME) and the mean absolute error (MAE) is about the same, indicating that the errors are systematic in sign. It is interesting to note that the cancellation between functional error and basis set error is rather systematic: a more or less uniform improvement of the results, compared to both CCSD(T) and experiment is obtained when a poorer basis set is employed. In particular, the aug-cc-pCVDZ basis set displays an improvement of around 10–15 ppm in the MAE, compared to the CBS limit, accompanied by a significant reduction in the standard deviation (SD). This trend has been already reported by Kupka and coworkers,79–81 and has also been recommended to NMR spectroscopists.84
Finally, taking experimental values without ZPVC as reference (not shown in the tables), the errors for generalized gradient approximation (GGA) and hybrid functionals with the double-ζ basis are further reduced to around 8 and 20 ppm for the MAE and SD, respectively. The combination of several errors eventually gives the right answer in the case of NMR shielding calculations with DFT. This demonstrates the challenges of optimizing functionals explicitly for a specific property, as for instance done for the Keal–Tozer functionals for magnetic properties.85
6 Conclusions and outlook
We have presented a new real-space implementation of a static linear response solver in a multiwavelet framework. We have applied the formalism to compute magnetizabilities and NMR shielding constants of small closed-shell molecules using HF and Kohn–Sham DFT. We have shown that the MW basis provides reliable numerical results for a wide range of molecular systems, including challenging cases such as MgO and O3. The accuracy of the MW basis depends only on a single input parameter: the overall relative precision ε. By tightening ε, the CBS values can be attained reliably and consistently. While high accuracy is attainable also with traditional GTO bases, they rely on a careful preoptimization of the parameters, and a wide variety of customized basis set families are available for different molecular properties, and it is the users responsibility to choose a basis set that is suited for the problem at hand.
We have shown that the MW basis provides magnetic response properties that are gauge invariant within the chosen relative precision, which means that the method does not rely on a GIAO parametrization using field-dependent phase factors for each AO (which complicates the implementation enormously) in order to provide high-accuracy results for small molecules. For larger systems, however, we expect a reduction of the overall accuracy, as the size of both the paramagnetic and diamagnetic contribution will grow faster than the total property, affecting the relative precision that can be achieved. In order to treat larger systems in the future, we plan to implement a local-origin method, such as the individual gauge for localized orbitals (IGLO) method of Kutzelnigg86 or the localized orbital/local origins (LORG) method of Hansen and Bouman.87 As in the London orbital approach, these methods also use different origins for different orbitals, but at the MO rather than AO level, placing the origin at the centroid of charge of each (localized) orbital. While these methods also lead to gauge-origin independent results, they rely on orbital localization, and in a GTO calculation also on the use of resolution-of-the-identity to simplify certain complicated integrals. The GIAO approach has therefore dominated the calculation of magnetic properties during the past two decades. However, some of these problems should not be present in the MW framework because the exact placement of the origin does not affect the quality of the results, as long as it keeps the size of the paramagnetic contribution as low as possible, and the MW basis satisfies the resolution-of-the-identity condition to within the selected precision. By employing local origin methods, the paramagnetic part can be decomposed into orbital contributions of much smaller magnitude (as the origin is chosen individually for each localized orbital), leading to good accuracy also for larger molecules.
We have employed our method to probe the CBS limit of HF and DFT for a large test set of small molecules, initially proposed by Lutnæs et al.21 for magnetizabilities and later Teale et al.22 for NMR shielding constants. We found that the aug-cc-pCVXZ basis sets performed very well for magnetizabilities, yielding typical errors of ∼0.1% for quadruple-ζ compared to the MW basis-set limit results. As expected, the NMR shielding constants were more challenging for GTOs, with an average error of 1–2 ppm (around 2–3%) for the largest aug-cc-pCVQZ basis. In order to improve on these numbers, a two-point exponential basis set extrapolation formula was employed. We found that the parametrization that is commonly used for total energies does not transfer directly to properties, and a significantly lower exponent (close to 1.0 rather than 1.63) should be used for the estimation of the basis-set limit for the shielding constants. Although the optimal value might differ somewhat between different functionals, a common exponent of 1.05 was able to reduce the errors by almost an order of magnitude for all functionals that were considered, compared to the quadruple-ζ value.
Finally, we performed a comparison between the CBS limit for HF and DFT and accurate CC and experimental values for the shielding constants. We found that the original study by Teale et al.22 using GTO basis sets were close enough to the CBS limit for their conclusions with respect to CC and experiment to hold. We found, however, that there is a significant systematic – yet fortuitous – cancellation of errors between the functionals and the basis set: with respect to raw experimental values (not zero-point vibrational energy corrected), surprisingly accurate shielding constants can be achieved with a moderate aug-cc-pCVDZ basis set.
The current implementation is limited to SCF levels of theory, and since correlated wave function methods rely on at least six-dimensional numerical representations, they are extremely expensive in a MW framework. However, developments in these directions have been presented by Bischoff and Valeev.88–90
The performance of our MW approach, compared to GTO calculations, gives a mixed picture. At moderate accuracy, GTOs deliver reasonable values with limited effort (aug-cc-pCVTZ), whereas our MW3 values are not as accurate and computationally more expensive. The picture changes dramatically if higher accuracy is demanded: increasing the accuracy with GTOs implies a 10-fold increase in the computational cost, whereas MW calculations are only twice as expensive at each step along the MWX (X = 3, 4, 5, 6) series. As a result, aug-cc-pCVQZ calculations are only 2–3 times faster but less accurate than MW4. Some preliminary tests show that MW5 is indeed less expensive than the aug-cc-pCV5Z basis. The main performance bottleneck in the current MW implementation is clearly the exact HF exchange, which yields a 10-fold increase in the timings compared to pure functionals.
Acknowledgements
This work has been supported by the Research Council of Norway through a Centre of Excellence Grant (Grant No. 179568/V30) and from the Norwegian Supercomputing Program (NOTUR) through a grant of computer time (Grant No. NN4654K). We would like to thank T. Helgaker (Oslo) and A. Teale (Nottingham) for helpful discussions.
References
-
C. J. Cramer, Essentials of Computational Chemistry, John Wiley & Sons, Chichester, 2013 Search PubMed.
-
F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons, Chichester, 2013 Search PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- R. G. Parr and W. Yang, Annu. Rev. Phys. Chem., 1995, 46, 701–728 CrossRef CAS PubMed.
- K. E. Riley, B. T. Op't Holt and K. M. J. Merz, J. Chem. Theory Comput., 2007, 3, 407–433 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1 CrossRef CAS.
- J. M. Tao, J. P. Perdew, J. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- S. F. Sousa, P. A. Fernandes and M. J. Ramos, J. Phys. Chem. A, 2007, 111, 10439–10452 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- C. Adamo, G. E. Scuseria and V. Barone, J. Chem. Phys., 1999, 111, 2889–2899 CrossRef CAS.
- D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- E. A. Carter, Science, 2008, 321, 800–803 CrossRef CAS PubMed.
- P. Huang and E. A. Carter, Annu. Rev. Phys. Chem., 2008, 59, 261–290 CrossRef CAS PubMed.
- P. Sałek, O. Vahtras, T. Helgaker and H. Ågren, J. Chem. Phys., 2002, 117, 9630–9645 CrossRef.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019 CrossRef CAS.
- O. B. Lutnæs, A. M. Teale, T. Helgaker, D. J. Tozer, K. Ruud and J. Gauss, J. Chem. Phys., 2009, 131, 144104 CrossRef PubMed.
- A. M. Teale, O. B. Lutnæs, T. Helgaker, D. J. Tozer and J. Gauss, J. Chem. Phys., 2013, 138, 024111 CrossRef PubMed.
- S. Goedecker, Rev. Mod. Phys., 1999, 71, 1085 CrossRef CAS.
- D. Moncrieff and S. Wilson, Int. J. Quantum Chem., 2005, 101, 363–371 CrossRef CAS.
- E. Artacho, T. L. Beck and E. Hernández, Phys. Status Solidi B, 2006, 243, 971–972 CrossRef CAS.
- L. Frediani and D. Sundholm, Phys. Chem. Chem. Phys., 2015, 17, 31357–31359 RSC.
- E. Briggs, D. Sullivan and J. Bernholc, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14362–14375 CrossRef CAS.
- E. Briggs, D. Sullivan and J. Bernholc, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5471–R5474 CrossRef CAS.
- X. Andrade, D. Strubbe, U. De Giovannini, A. H. Larsen, M. J. T. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig, M. J. Verstraete, L. Stella, F. Nogueira, A. Aspuru-Guzik, A. Castro, M. A. L. Marques and A. Rubio, Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- X. Andrade, J. Alberdi-Rodriguez, D. A. Strubbe, M. J. T. Oliveira, F. Nogueira, A. Castro, J. Muguerza, A. Arruabarrena, S. G. Louie, A. Aspuru-Guzik, A. Rubio and M. A. L. Marques, J. Phys.: Condens. Matter, 2012, 24, 233202 CrossRef PubMed.
- S. Mohr, L. E. Ratcliff, L. Genovese, D. Caliste, P. Boulanger, S. Goedecker and T. Deutsch, Phys. Chem. Chem. Phys., 2015, 17, 31360–31370 RSC.
- R. J. Harrison, G. I. Fann, T. Yanai, Z. Gan and G. Beylkin, J. Chem. Phys., 2004, 121, 11587 CrossRef CAS PubMed.
- T. Yanai, G. I. Fann, Z. Gan, R. J. Harrison and G. Beylkin, J. Chem. Phys., 2004, 121, 6680 CrossRef CAS PubMed.
- T. Yanai, G. I. Fann, Z. Gan, R. J. Harrison and G. Beylkin, J. Chem. Phys., 2004, 121, 2866 CrossRef CAS PubMed.
- T. Yanai, R. J. Harrison and N. C. Handy, Mol. Phys., 2005, 103, 413–424 CrossRef CAS.
- H. Sekino, Y. Maeda, T. Yanai and R. J. Harrison, J. Chem. Phys., 2008, 129, 034111 CrossRef PubMed.
- H. Sekino, Y. Yokoi and R. J. Harrison, J. Phys.: Conf. Ser., 2012, 352, 012014 CrossRef.
- T. Yanai, G. I. Fann, G. Beylkin and R. J. Harrison, Phys. Chem. Chem. Phys., 2015, 17, 31405–31416 RSC.
- J. S. Kottmann, S. Höfener and F. A. Bischoff, Phys. Chem. Chem. Phys., 2015, 17, 31453–31462 RSC.
- L. Frediani, E. Fossgaard, T. Flå and K. Ruud, Mol. Phys., 2013, 111, 1143–1160 CrossRef CAS.
- S. R. Jensen, J. Jusélius, A. Durdek, T. Flå, P. Wind and L. Frediani, Int. J. Mod. Sim. Sci. Comput., 2014, 5, 1441003 CrossRef.
- G. Beylkin and M. J. Mohlenkamp, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 10246–10251 CrossRef CAS PubMed.
- G. Beylkin, R. Coifman and V. Rokhlin, Comm. Pure Appl. Math., 1991, 44, 141–183 CrossRef.
- T. Helgaker, M. Jaszuński and K. Ruud, Chem. Rev., 1999, 99, 293–352 CrossRef CAS PubMed.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Chem. Rev., 2012, 112, 543 CrossRef CAS PubMed.
- B. Alpert, G. Beylkin, D. Gines and L. Vozovoi, J. Comput. Phys., 2002, 182, 149–190 CrossRef.
- S. F. Boys, Rev. Mod. Phys., 1960, 32, 296 CrossRef CAS.
- J. M. Foster and S. Boys, Rev. Mod. Phys., 1960, 32, 300 CrossRef CAS.
- M. H. Kalos, Phys. Rev., 1962, 128, 1791 CrossRef.
- R. J. Harrison, J. Comput. Chem., 2004, 25, 328–334 CrossRef CAS PubMed.
- G. Mahan, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 1780–1785 CrossRef CAS.
- J. I. Iwata, K. Yabana and G. F. Bertsch, J. Chem. Phys., 2001, 115, 8773 CrossRef CAS.
- X. Andrade, S. Botti, M. A. L. Marques and A. Rubio, J. Chem. Phys., 2007, 126, 184106 CrossRef PubMed.
- V. G. Malkin, O. L. Malkina and D. R. Salahub, Chem. Phys. Lett., 1993, 204, 80–86 CrossRef CAS.
- T. Helgaker, P. J. Wilson, R. D. Amos and N. C. Handy, J. Chem. Phys., 2000, 113, 2983–2989 CrossRef CAS.
- J. Autschbach, M. Seth and T. Ziegler, J. Chem. Phys., 2007, 126, 174103 CrossRef PubMed.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699 CrossRef CAS.
- A. Dalgarno and A. L. Stewart, Proc. R. Soc. A, 1958, 247, 245–259 CrossRef CAS.
- B. Kirtman, J. Chem. Phys., 1968, 49, 3895–3898 CrossRef CAS.
- M. Beer, J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2011, 134, 074102 CrossRef PubMed.
- C. Ochsenfeld, J. Kussmann and F. Koziol, Angew. Chem., Int. Ed. Engl., 2004, 43, 4485–4489 CrossRef CAS PubMed.
- J. Kussmann and C. Ochsenfeld, J. Chem. Phys., 2007, 127, 054103 CrossRef PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(3), 269–284 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F. Jensen, J. Chem. Theory Comput., 2008, 4, 719–727 CrossRef CAS PubMed.
- Multiresolution chemistry (mrchem) program package. See http://mrchemdoc.readthedocs.org/en/latest/, 2015.
- U. Ekström, L. Visscher, R. Bast, A. J. Thorvaldsen and K. Ruud, J. Chem. Theory Comput., 2010, 6, 1971–1980 CrossRef PubMed.
- F. London, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- R. Ditchfield, J. Chem. Phys., 1972, 56, 5688–5691 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- S. T. Epstein, J. Chem. Phys., 1973, 58, 1592 CrossRef CAS.
- E. Dalgaard, Chem. Phys. Lett., 1977, 47, 279 CrossRef CAS.
- K. Ruud, T. Helgaker, J. Olsen, P. Jørgensen and K. L. Bak, Chem. Phys. Lett., 1995, 235, 47 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper and J. Olsen, Chem. Phys. Lett., 1999, 302, 437–446 CrossRef CAS.
- G. Magyarfalvi and P. Pulay, J. Chem. Phys., 2003, 119, 1350–1357 CrossRef CAS.
- T. Kupka, B. Ruscic and R. E. Botto, J. Phys. Chem. A, 2002, 106, 10396–10407 CrossRef CAS.
- T. Kupka, Magn. Reson. Chem., 2009, 47, 210–221 CrossRef CAS PubMed.
- T. Kupka, M. Stachów, M. Nieradka, J. Kaminsky and T. Pluta, J. Chem. Theory Comput., 2010, 6, 1580–1589 CrossRef CAS PubMed.
- V. G. Malkin, O. L. Malkina, M. E. Casida and D. R. Salahub, J. Am. Chem. Soc., 1994, 116, 5898–5908 CrossRef CAS.
- A. M. Lee, N. C. Handy and S. M. Colwell, J. Chem. Phys., 1995, 103, 10095–10109 CrossRef CAS.
- R. Jain, B. Thomas and P. R. Rablen, J. Org. Chem., 2009, 74, 4017–4023 CrossRef CAS PubMed.
- T. W. Keal and D. J. Tozer, J. Chem. Phys., 2003, 119, 3015 CrossRef CAS.
- M. Schindler and W. Kutzelnigg, J. Chem. Phys., 1982, 76, 1919–1933 CrossRef CAS.
- A. E. Hansen and T. D. Bouman, J. Chem. Phys., 1985, 82, 5035–5047 CrossRef CAS.
- F. A. Bischoff and E. F. Valeev, J. Chem. Phys., 2011, 134, 104104 CrossRef PubMed.
- F. A. Bischoff, R. J. Harrison and E. F. Valeev, J. Chem. Phys., 2012, 137, 104103 CrossRef PubMed.
- F. A. Bischoff, J. Chem. Phys., 2014, 141, 184106 CrossRef PubMed.
Footnotes |
| † Calculations yielding “good” results are more likely to be published, whereas negative ones are often stopped along the process, either because the researchers themselves do not find it worth to write about negative outcomes or because referees will not let them through. |
| ‡ ĥ(MK) also contain triplet operators, but they do not contribute to these properties for closed-shell systems. |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article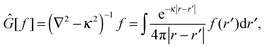
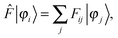
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) |φj〉,
|φj〉,![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) the Fock operator. The potential operator in Kohn–Sham DFT and HF theory can be written in a general form as
the Fock operator. The potential operator in Kohn–Sham DFT and HF theory can be written in a general form as![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) =
= ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) nuc + Ĵ − λ
nuc + Ĵ − λ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) +
+ ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) XC,
XC,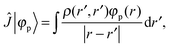
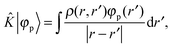
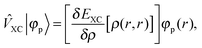
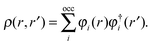
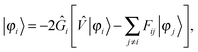
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − Fii)−1. The second term in the operator argument in eqn (9) corrects for the use of non-canonical (localized) orbitals, and vanishes if the Fock matrix is diagonalized.
− Fii)−1. The second term in the operator argument in eqn (9) corrects for the use of non-canonical (localized) orbitals, and vanishes if the Fock matrix is diagonalized.
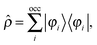
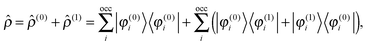
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0) is the ground-state density operator and
(0) is the ground-state density operator and ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (1) the first-order perturbed density. This change in electron density in turn changes the potential operators in eqn (5–7), and to first order we get
(1) the first-order perturbed density. This change in electron density in turn changes the potential operators in eqn (5–7), and to first order we get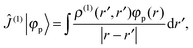
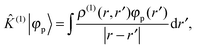
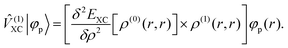
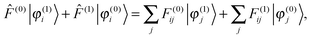
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1) = ĥ(1) +
(1) = ĥ(1) + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)). The perturbed Fock matrix elements are obtained by expanding eqn (3) and collecting all the first-order terms:
(1)). The perturbed Fock matrix elements are obtained by expanding eqn (3) and collecting all the first-order terms:![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (0)|φ(0)j〉 + 〈φ(0)i|
(0)|φ(0)j〉 + 〈φ(0)i|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1)|φ(0)j〉 + 〈φ(0)i|
(1)|φ(0)j〉 + 〈φ(0)i|![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (0)|φ(1)j〉.
(0)|φ(1)j〉.![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) 2 =
2 = ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) to first order. However, in the diagonal terms the orbital phase factors can be chosen arbitrarily, and the off-diagonal terms do not contribute to the density to first-order. Therefore one can in both cases impose the stronger orthogonality condition:
to first order. However, in the diagonal terms the orbital phase factors can be chosen arbitrarily, and the off-diagonal terms do not contribute to the density to first-order. Therefore one can in both cases impose the stronger orthogonality condition: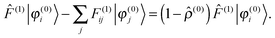
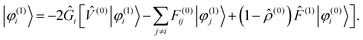
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − F(0)ii)−1. We remark that eqn (21) defines a set of coupled equations which corresponds to the static limit of the response equations of Sekino et al.36,37 and closely resembles the working equations of Yanai et al.35,38 for excitation energies in time-dependent HF/DFT. Kottmann et al.39 recently used the same equations to compute excitation energies in the configuration interaction singles (CIS) approximation.
− F(0)ii)−1. We remark that eqn (21) defines a set of coupled equations which corresponds to the static limit of the response equations of Sekino et al.36,37 and closely resembles the working equations of Yanai et al.35,38 for excitation energies in time-dependent HF/DFT. Kottmann et al.39 recently used the same equations to compute excitation energies in the configuration interaction singles (CIS) approximation.
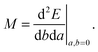
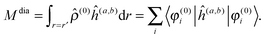
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (a), and computing the expectation value (tracing the density matrix) of the second operator ĥ(b)
(a), and computing the expectation value (tracing the density matrix) of the second operator ĥ(b)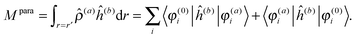
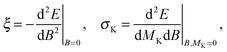
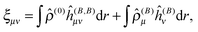
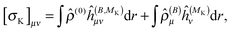
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (B)μ denotes the density perturbed by the μ component of the ĥ(B) operator. The interaction operators are obtained by differentiating the Hamiltonian with respect to B and/or MK and evaluating at zero perturbational strength. For closed-shell systems we get‡44,45
(B)μ denotes the density perturbed by the μ component of the ĥ(B) operator. The interaction operators are obtained by differentiating the Hamiltonian with respect to B and/or MK and evaluating at zero perturbational strength. For closed-shell systems we get‡44,45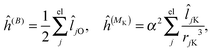
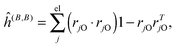
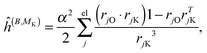
![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) jO = −irjO × ∇j is the angular momentum operator, rjO is the position of electron j relative to the gauge origin O, rK is the position of nucleus K, and α ≈ 1/137 is the fine-structure constant. The perturbed orbitals φ(B) are obtained by solving the Sternheimer equations (eqn (21)) with the following perturbed Fock operator (there is one for each component μ of the perturbing field)
jO = −irjO × ∇j is the angular momentum operator, rjO is the position of electron j relative to the gauge origin O, rK is the position of nucleus K, and α ≈ 1/137 is the fine-structure constant. The perturbed orbitals φ(B) are obtained by solving the Sternheimer equations (eqn (21)) with the following perturbed Fock operator (there is one for each component μ of the perturbing field)![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) (1) = ĥ(B) + Ĵ(1) − λ
(1) = ĥ(B) + Ĵ(1) − λ![[K with combining circumflex]](https://www.rsc.org/images/entities/i_char_004b_0302.gif) (1) +
(1) + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)XC.
(1)XC.![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (1)XC (if there is no explicit current dependence in the functional) can be omitted from this Fock operator. This means that for non-hybrid DFT (λ = 0), we do not get any two-electron contribution in the perturbed Fock operator, which leads to decoupled response equations (at least in the canonical case) that can be solved non-iteratively in a fixed basis of virtual orbitals.54–56 In our case, however, we only have the occupied orbitals, and the equations must still be solved iteratively to sample the (complete) virtual space by application of the BSH Green's function. Notice also that even if the perturbed density vanishes, the paramagnetic expectation value (e.g. with ĥ(MK)) does not
(1)XC (if there is no explicit current dependence in the functional) can be omitted from this Fock operator. This means that for non-hybrid DFT (λ = 0), we do not get any two-electron contribution in the perturbed Fock operator, which leads to decoupled response equations (at least in the canonical case) that can be solved non-iteratively in a fixed basis of virtual orbitals.54–56 In our case, however, we only have the occupied orbitals, and the equations must still be solved iteratively to sample the (complete) virtual space by application of the BSH Green's function. Notice also that even if the perturbed density vanishes, the paramagnetic expectation value (e.g. with ĥ(MK)) does not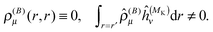
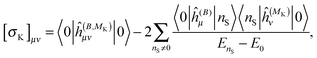
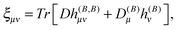
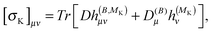
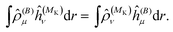

![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (0)) followed by three response calculations (to obtain
(0)) followed by three response calculations (to obtain ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (B)μ for μ = x, y, z). The magnetizability and NMR shielding tensors of all nuclei in the molecule are then computed simultaneously according to eqn (26) and (27). The timings are given in minutes wall-time on a single compute node with 16 CPUs (2.6 GHz Intel E5-2670) using a shared memory parallelization strategy. For the GTO calculations, the timings are obtained from Dalton, on the same computer architecture and also using 16 processors using the message passing interface (MPI).
(B)μ for μ = x, y, z). The magnetizability and NMR shielding tensors of all nuclei in the molecule are then computed simultaneously according to eqn (26) and (27). The timings are given in minutes wall-time on a single compute node with 16 CPUs (2.6 GHz Intel E5-2670) using a shared memory parallelization strategy. For the GTO calculations, the timings are obtained from Dalton, on the same computer architecture and also using 16 processors using the message passing interface (MPI).
