Polynuclear gold(I) complexes in photoredox catalysis: understanding their reactivity through characterization and kinetic analysis†
C. D.
McTiernan
,
M.
Morin
,
T.
McCallum
,
J. C.
Scaiano
* and
L.
Barriault
*
Department of Chemistry and Biomolecular Sciences and Centre for Catalysis Research and Innovation, University of Ottawa, 10 Marie Curie, Ottawa ON K1N 6N5, Canada. E-mail: scaiano@photo.chem.uottawa.ca; lbarriau@uottawa.ca
First published on 16th September 2015
Abstract
The light mediated reduction of unactivated carbon–halogen bonds using polynuclear gold(I) complexes provides a mild and temporally controlled route to the generation of C–H, and C–C bonds. Through complete photophysical and electrochemical charaterization of a series of gold(I) complexes we have been able to achieve a more intimate understanding of the complexities surrounding the excited state processes and mechanism which underly these transformations, allowing for, and facilitating further and future optimizations and applications.
Introduction
Although the lustrous character of gold has captivated people for centuries, only in the past few decades have chemists harnessed the exciting chemical properties of gold complexes.1–7 During this time the growing field of gold-catalyzed organic reactions has uncovered many complexes that serve as competent catalysts in a variety of reaction types, especially those requiring a Lewis acid.8–10 More recently, studies involving highly luminescent polynuclear gold complexes have found a wealth of applications for both their photophysical and photochemical properties.11–13 For example, their rich photochemistry has enabled their use in phosphorescent organic light-emitting diodes (OLEDs),14 cellular imaging,15,16 photocatalysis, and polymerization.17–21The transformation of solar energy into chemical energy, utilizing complexes that mimic the light harvesting abilities of biocomplexes found in nature,22 is an attractive use of radiative energy. Recently, there has been a wide interest in light mediated organic photoredox transformations.23–31 Currently the majority of photoredox transformations are accomplished through photoinduced electron transfers to or from transition metal complexes such as [Ru(bpy)32+, Ir(ppy)3], organic dyes [methylene blue, eosin Y]32–35 or inorganic semiconductors [TiO2, CdS].36,37 The main advantage of this process over more traditional oxidation and reduction reactions resides in the use of a robust photocatalyst which generates the oxidizing and/or reducing agent in situ by exciting the catalyst with light.
In addition to the enhanced temporal control inherent to photocatalyzed reactions, photoredox catalysis has offered chemists an array of new and mild ways to access highly reactive intermediates that were previously only attainable through the use of harsh conditions. For example in reductive dehalogenation reactions, photoredox catalysis has found mild and highly efficient strategies for the generation of C–H, C–C, C–N, and C–O bonds.25 However, there are limitations to the commonly employed photocatalysts, which relate back to their ground state redox properties and the energy of their excited state(s). That is, their substrate reactivity tends to be limited to activated C–X bonds, such as polyhalomethanes, bromomalonates, electron-deficient benzyl halides, and alkyl/aryl iodides which are more easily reduced.25
We recently demonstrated that a photocatalytic system based on the phosphorescent dinuclear gold(I) complex [Au2(dppm)2]2+ (1)38–41 (dppm = bis(diphenylphosphino) methane) and N,N-diisopropylethylamine (DIPEA) as sacrificial electron donor is capable of reducing unactivated bromoalkanes and bromoarenes (~ −1.9 to −2.5 V vs. SCE)39,41 and that the ensuing radicals participate in ring-forming cyclization reactions, resulting in the formation of new C–C bonds.18,19 Providing another alternative to some of the more commonly employed methods, which tend to involve harsh or chain propagating conditions.42–54
Although, similar light mediated transformations have been accomplished utilizing visible light absorbing Pt complexes55 and perylene diimides56 as photosensitizers, the reductive dehalogenation of unactivated C–Br bonds with photoexcited Au2(dppm)2Cl2 (1) remains an interesting find, with many questions as to the mechanism of these transformations remaining. Generally, photoredox catalysis can proceed through either an oxidative or reductive quenching pathway. In the reductive quenching pathway, the initial excited species is reduced through single electron transfer (SET) from a donor (D) molecule and the resulting reduced photocatalyst can then be oxidized in its ground state through subsequent reduction of an acceptor (A) molecule. Opposite to this is the oxidative quenching pathway in which the initial excited state species is oxidized through SET to an acceptor (A) molecule, and returned to its initial oxidation state through reduction by a donor (D) molecule. However, we were unsure of the specific details of the active pathway, in our systems. Was dehalogenation achieved through a reductive or oxidative quenching pathway? Or both? (Scheme 2) Also, many of the reduction potentials of the substrates fall outside the potential window attainable by the Au2(dppm)2Cl2 photocatalytic system. Could this be explained due to differences between both inner and outer sphere electron transfer processes?
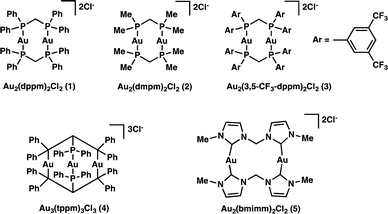
In an attempt to answer the above questions and gain further insight into the relevant excited state processes we set out to characterize the properties of a variety of polynuclear gold(I) complexes (Scheme 1), which we know are capable of bringing about the desired transformations. Through structural modification of the ligands and by changing the number of metal centers we are able to both satisfy our curiosity and explore the effect of electron donating and withdrawing ligands.
Results and discussion
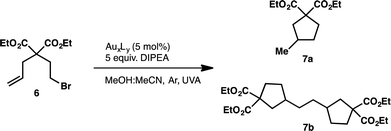
We began our investigation into the underlying mechanism of these transformations, by preparing a series of structurally divergent Au(I) complexes. Through exchange of the dppm (1) ligand with either bis(dimethylphos-phino)methane (dmpm) (2),57 or bis(bis(3,5-bis(trifluoromethyl)phenyl)phosphine)-methane (3,5-CF3-dppm) (3) we can examine the effect of electron donating and withdrawing ligands, respectively. To study the effect of adding a third metal center to the complex we have synthesized complex (4)58 using tris(diphenylphosphino)methane (tppm) as ligand. Lastly, due to the success of N-heterocyclic carbene ligands in gold(I) Lewis acid catalysis we have also prepared complex (5)59 using bis(N-methylimidazol-2-ylidene)methane (bmimm) as ligand. Asymmetric combinations of these ligands were not attempted at this time as preliminary studies showed difficulty controlling ligand exchange. The activity of each of the structurally modified catalysts was compared for their activity in converting substrate (6) to products (7a) from reductive cyclization and (7b, as a mixture of diastereomers) from the unexpected coupling of two cyclized intermediates. Table 1, shows the conversion of substrate 6 utilizing the different polynuclear gold(I) complexes under previously optimized conditions. Interestingly, all five of the complexes were able to promote the transformations, however some more efficiently than others. While complex 1 shows the highest reactivity, reaching completion in only 5 minutes of irradiation (Table 1, entry 1). Complex 2 and 4 with dmpm and tppm ligands, respectively, show modest reactivity with both, reaching completion in 2 hours (Table 1, entry 4 and 12). The trifluoromethylated dppm complex 3 shows the lowest reactivity taking 20 hours of irradiation to reach 82% conversion (Table 1, entry 9). Lastly, the bis-carbene complex 5 took 20 hours to reach complete conversion (Table 1, entry 17). To better understand these differences in reactivity, we set out to characterize the photophysical and electrochemical properties of all five complexes.| Entry | AuxLy complex | Time (h) | % conversion (7a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7b)b 7b)b |
|---|---|---|---|
a Reaction conditions: substrate (200 mM), DIPEA (5 eq.), AuxLy complex (5 mol%), MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeCN (1 MeCN (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–1 mL) under argon atmosphere. Irradiated with one UVA LED (365 nm).
b % conversion by 1H NMR. 1–1 mL) under argon atmosphere. Irradiated with one UVA LED (365 nm).
b % conversion by 1H NMR.
|
|||
| 1 | Au2(dppm)2Cl2 (1) | 0.1 | >95(40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60) 60) |
| 2 | Au2(dmpm)2Cl2 (2) | 0.1 | 21 |
| 3 | Au2(dmpm)2Cl2 (2) | 0.5 | 56 |
| 4 | Au2(dmpm)2Cl2 (2) | 2.0 | >95(73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27) 27) |
| 5 | Au2(3,5-CF3-dppm)2Cl2 (3) | 0.1 | <5 |
| 6 | Au2(3,5-CF3-dppm)2Cl2 (3) | 0.5 | 11 |
| 7 | Au2(3,5-CF3-dppm)2Cl2 (3) | 2.0 | 27 |
| 8 | Au2(3,5-CF3-dppm)2Cl2 (3) | 8.0 | 55 |
| 9 | Au2(3,5-CF3-dppm)2Cl2 (3) | 20.0 | 82(54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46) 46) |
| 10 | Au3(tppm)2Cl3 (4) | 0.1 | 12 |
| 11 | Au3(tppm)2Cl3 (4) | 0.5 | 41 |
| 12 | Au3(tppm)2Cl3 (4) | 2.0 | >95(63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37) 37) |
| 13 | Au2(bmimm)2Cl2 (5) | 0.1 | <5% |
| 14 | Au2(bmimm)2Cl2 (5) | 0.5 | 28% |
| 15 | Au2(bmimm)2Cl2 (5) | 2.0 | 35% |
| 16 | Au2(bmimm)2Cl2 (5) | 8.0 | 67% |
| 17 | Au2(bmimm)2Cl2 (5) | 20.0 | >95(80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) 20) |
Through a combination of both steady-state and time-resolved absorption and emission measurements as well as cyclic voltammetry, we were able to obtain the characterization data found in Table 2 (see ESI† for experimental details).
| Catalyst | λ ex | ε ex (M−1 cm−1)a | λ em | Φ em | 3 τ 0 | E*T (kJ mol−1)d | E pa (V vs. SCE)e | E pc (V vs. SCE)e |
|---|---|---|---|---|---|---|---|---|
| a Measured in MeCN at 298 K. b Photoluminescence quantum yield determined relative to Ru(bpy)3Cl2 as standard (ΦMeCN = 0.095).60 c Triplet lifetime measured in N2 degassed MeCN after 10 mJ laser pulse at λex. d Triplet-state energy determined from the low temperature (77 K) phosphorescence spectra. e Determined using cyclic voltammetry. Conditions: scan rate = 100 mV s−1; 0.5–2.0 mM Au(I) complex in Ar degassed MeCN containing 100 mM Bu4NClO4 supporting electrolyte; Pt wire working electrode; Pt wire counter electrode; Ag wire pseudo-reference electrode; Fc/Fc+ redox couple as internal reference (0.41 V vs. SCE); oxidation and reduction potential reported as peak anodic (Epa) and peak cathodic (Epc) potentials due to their irreversible nature. | ||||||||
| (1) Au2(dppm)2Cl2 | 355 nm | 73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 163 |
560 nm | 0.137 | 850 ns | 215 | 0.70 | −1.63 |
| (2) Au2(dmpm)2Cl2 | 308 nm | 3813 | 525 nm | 0.028 | 400 ns | 228 | 0.49 | −1.77 |
| (3) Au2(3,5-CF3-dppm)2Cl2 | 355 nm | 6539 | 590 nm | 0.006 | 10 μs | 203 | 1.41 | −1.65 |
| (4) Au3(tppm)2Cl3 | 355 nm | 3780 | 545 nm | 0.028 | 1.5 μs | 220 | 1.09 | −1.54 |
| (5) Au2(bmimm)2Cl2 | 308 nm | 491 | 510 nm | 0.017 | 20 ns | 235 | 0.34 | — |
Table 2 and the corresponding absorption spectra (see ESI†), show that the majority of the Au complexes absorb strongly in the UVA region and tail towards the visible with the exception of complexes 2 and 5, which only tail into the UVA region. Although the lack of absorption in the visible could limit the scope of these transformations, the availability of modern light sources such as UVA LEDs (see ESI,† section I for power spectrum) enables one to easily perform irradiations in the spectral region that is absorbed only by the photocatalyst, thus avoiding direct irradiation of substrates or reaction products that could lead to degradation or side-product formation. Further highlighting this idea is the recent work by the Hashmi group on the [Au2(dppm)2]2+ catalyzed photoredox α-C(sp3)–H alkynylation of tertiary aliphatic amines.11 Given that UVA radiation can readily pass through glass, no expensive, “special”, or quartz glassware is required to perform the reactions and in many cases the greater irradiance of specialized light sources can drastically reduce the required irradiation time. Interestingly, it should also be mentioned that photocatalytic systems requiring UVA excitation may in some cases be more potent excited state oxidizing and reducing agents than their visible light counterparts as the higher energy photons required for excitation would result in a higher excited state energy and more favourable redox processes.56 This chemistry likely occurs from the triplet manifold; thus, some of this energy will be lost to competing radiative and non-radiative decay pathways, including intersystem crossing.56
In Table 1 we observed that some of the catalysts were more efficient at bringing about the desired transformation. Although this could reflect the fact that not all the catalysts absorb the same fraction of incident light, if we compare the efficiency of complex 2 and 4, which have drastically different absorption spectra, we find that it takes both systems approximately 2 hours to reach quantitative conversion (Table 1, entry 4 and 12). Therefore, although preferential absorption of the incident light may be responsible for part of the differences observed in Table 1, it is likely that the thermodynamics and, in turn, the kinetics of the reaction, as well as other photophysical properties of the Au catalysts, such as triplet quantum yield and lifetime, are responsible for much of the observed differences.
In order to understand the efficiency of these reductions, it is necessary to examine the thermodynamic feasibility and kinetics of the plausible mechanistic steps outlined in the oxidative and reductive quenching mechanisms of Scheme 2. As illustrated in Scheme 2, the catalytic cycle begins with either an electron transfer to or from the excited state of the catalyst. By determining the Gibbs free energy associated with each the electron transfer process, it may be possible to determine which pathway is more favorable. However, in order to make these calculations one requires the ground state oxidation and reduction potentials of the catalyst as well as their corresponding triplet energy along with the reduction potential of the acceptor molecule (6) and the oxidation potential of the donor molecule (DIPEA). Through the use of cyclic voltammetry we have been able to estimate the oxidation and reduction potentials of the Au catalysts in their ground state. Since all the Au complexes exhibited irreversible oxidation and reduction waves (see ESI† for experimental details and corresponding CV curves) we have used the peak anodic (Epa) and peak cathodic (Epc) potentials as estimates of the oxidation and reduction potentials, respectively. While the electrochemical irreversibility of the Au catalysts could suggest that they are merely precatalysts, preliminary 1H and 31P NMR monitoring of the model reaction in deuterated solvent show the fate of the Au complex may be convoluted and warrant further studies for the characterization of reactive intermediates.
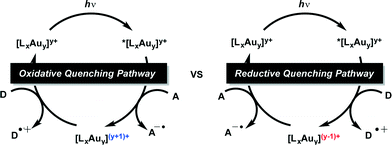 | ||
| Scheme 2 Oxidative and reductive quenching pathways for the reductive cyclizations and dimerizations. | ||
With the triplet energy (E*T) of the Au catalysts obtained from 77 K phosphorescence measurements we can employ eqn (1) and (2) to determine the excited state oxidation (E*ox) and reduction (E*red) potentials.
| E*ox = Epa − E*T | (1) |
| E*red = Epc + E*T | (2) |
For example, in the case of [Au2(dppm)2]2+ we find that E*ox = −1.53 V vs. SCE and E*red = 0.60 V vs. SCE. At −1.53 V vs. SCE the calculated E*ox is in good agreement with the literature value of −1.6 ± 0.1 V vs. SCE obtained through excited state quenching studies employing a series of pyridinium acceptors with known reduction potential.61 Since the reduction potential of substrate 6 is approximately −1.90 V vs. SCE and the oxidation potential of DIPEA is approximately 0.50 V vs. SCE62 we can use eqn (3) and (4) to determine the Gibbs free energy associated with either the oxidative or reductive quenching of the Au catalyst.
| ΔGox quenchingeT = E*ox(Au) − Ered(6) | (3) |
| ΔGred quenchingeT = Eox(DIPEA) − E*red(Au) | (4) |
Continuing with the E*ox and E*red potentials of the [Au2(dppm)2]2+ complex, we find that while the reductive quenching of the complex 1 by DIPEA is thermodynamically favored by −0.1 eV, the oxidative quenching by substrate 6 is actually thermodynamically uphill by 0.37 eV. Although this is a good indication that the reaction is proceeding through the reductive quenching mechanism when 1 is used as photocatalyst, it is important to remember that thermodynamics determine only if a reaction can take place and that there are examples in the photoredox literature in which reactions with significant free energy barriers proceed. Therefore, we must turn to kinetics, as from the kinetics we can determine if a reaction does take place.63 Although there are only small differences between the E*red potentials of the Au complexes, there are some significant differences in their E*ox potentials. The most important of these oxidation potentials are that of complexes 2 and 5, which are negative enough to make the initial electron transfer from the excited photocatalyst to substrate 6 energetically favorable.
In order to study the kinetics of the excited state processes, we have performed time-resolved transient spectroscopy on the Au complexes, using nanosecond laser flash photolysis (LFP), with the aim of determining the rate at which the different components of the system quench the triplet of the Au complexes. Fig. 1 shows the data used to determine the rate at which DIPEA reacts with the 3[Au2(dppm)2]2+ complex; the same technique was applied to all quenchers and Au complexes.
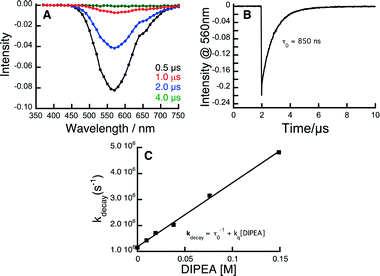 | ||
| Fig. 1 Kinetic analysis of the reaction between 3Au2(dppm)2Cl2 and DIPEA. A) Transient spectrum showing the 3Au2(dppm)2Cl2 emission signal at 560 nm obtained upon laser pulse excitation (355 nm, 10 mJ) of a Au2(dppm)2Cl2 sample which had been purged of oxygen. B) Corresponding decay trace of 3Au2(dppm)2Cl2 at 560 nm. C) Kinetic quenching plot showing the rate of 3Au2(dppm)2Cl2 quenching as a function of [DIPEA]. The slope of this plot corresponds to the bimolecular rate constant for this reaction (see ESI† for experimental details). | ||
Although we were not able to observe the growth of signals corresponding to either the reduced or oxidized forms of the Au complexes upon quenching by substrate 6 or DIPEA, the ability of the excited Au complexes to be quenched through electron transfer has been previously examined. Both methylviologen (MV2+) a good electron acceptor Ered1/2 (MV2+/MV+˙) = −0.46 V vs. SCE64 and N,N,N′,N′-tetramethyl-p-phenylenediamine (TMPD) a good electron donor Eox1/2 (TMPD/TMPD+˙) = 0.12 V vs. SCE65 quench 3[Au2(dppm)2]2+ at rates approaching diffusion control (kqMV2+ = 6.0 × 109 M−1 s−1 and kqTMPD = 6.6 × 109 M−1 s−1)38 and give rise to transient absorptions centered at 600 nm characteristic of their corresponding radical cations produced upon either reduction or oxidation.
Table 3 includes the bimolecular rate constant at which substrate 6, DIPEA, and butyl bromide quench the triplet of the various Au complexes. Although butyl bromide (Ered1/2 = −2.5 V vs. SCE) is not a component of the reaction mixture, we have included it here as reference. As one would expect, there is a strong relationship between the redox potentials of the quenchers and those of the Au complexes with the measured rate constants. For example, along the entire series of catalysts one finds that the rate constant for quenching by substrate 6 is greater than that of the more difficult to reduce butyl bromide. It is also observed that the rate of reductive quenching by DIPEA changes drastically throughout the series, with differences of up to 3 orders of magnitude between the different complexes. These differences can be readily explained through the reduction potentials of the Au complexes, as the slowest rates were measured for complexes 1 and 2 and the fastest rate for complex 3, the most difficult and easiest catalysts to reduce, respectively.
| Quencher | Au2(dppm)2Cl2(1) | Au2(dmpm)2Cl2(2) | Au2(3,5-CF3-dppm)2Cl2(3), kq (M−1 s−1)a | Au3(tppm)2Cl3(4) | Au2(bmimm)2Cl2(5) |
|---|---|---|---|---|---|
| a Determined from the slope of the corresponding kinetic quenching plot (kdecayvs. [Q]) see Fig. 1C and ESI. | |||||
| ButylBr | 2.9 × 106 | 1.1 × 109 | 4.8 × 105 | 4.5 × 106 | 1.2 × 109 |
| 6 | 3.1 × 107 | 1.7 × 109 | 5.1 × 106 | 2.8 × 107 | 1.3 × 109 |
| DIPEA | 2.7 × 107 | 2.1 × 107 | 1.1 × 109 | 1.6 × 109 | 1.6 × 108 |
Although complex 1 is the most efficient of the catalysts, it displays some of the slowest rate constants in Table 3. However, this observation fails to account for is the excited state lifetime of the catalyst or the concentration of quencher present in solution, without which it is difficult to compare these values. One way to employ the data in Table 3 is to use eqn (5) and (6) to calculate the percentage of triplets quenched by either substrate 6 or DIPEA under initial reaction conditions.

| (5) |

| (6) |
Included in both equations are terms corresponding to the concentration of oxygen and its bimolecular quenching constant. Since all the reactions have been purged with argon prior to irradiation, we can simply eliminate them from the equations. However, it is important to point out that due to the high solubility of O2 in acetonitrile (approx. 1.6 mM under air)66 and its propensity for quenching triplets (kqO2 3[Au2(dppm)2]2+ = 2.0 × 109 M−1 s−1),61 inefficient purging could lead to drastically reduced yields as many of the triplets would be intercepted by oxygen through non productive quenching events.
When we employ eqn (5) and (6) to calculate the percentage of 3[Au2(dppm)2]2+ quenched by substrate 6 and DIPEA under initial reaction conditions we find that while 18% of triplets are quenched by 6; the other 78% are intercepted by DIPEA. Even though the rate constants for both quenchers are similar, 78% was due to the fact that DIPEA was used in excess (5 times). When we combine this information with the fact that the reaction run with Au2(dppm)2Cl2 as photocatalyst reaches completion in 5 minutes of irradiation, it would seem likely that in this case the reductive quenching pathway is the major route to product formation. However, if one were to do similar calculations for the other catalysts, this may not always be the case. While it is most likely that complexes 3 and 4 bring about the desired transformation through the reductive quenching pathway, as in both cases >99% of triplets are quenched by DIPEA; for complex 2 we find that 93% of its triplets are intercepted by substrate 6 and only 6% by DIPEA, although this may be indicative of an oxidative quenching pathway, the productive pathway may still be reductive in nature with the explanation for the sluggish reaction being the poor efficiency of quenching.
Lastly, for complex 5 it is difficult to determine the major pathway as 55% of triplets would be quenched by 6, while another 34% by DIPEA. Thus If we were to assume that 100% of quenching events led to electron transfer (this is likely not the case) and that both the reductive and oxidative pathways were equally effective at bringing about the desired transformation, it would appear as though in addition to its poor UVA absorption, much of the inefficiency of complex 5 can be attributed to its short excited state lifetime and the fact that a significant fraction of triplets escape quenching. In the case of complex 3, much of its inefficiency may be attributed to its relatively long excited state lifetime, which makes competitive quenching by small impurities such as oxygen more likely. Therefore, while we can conclude that the processes represented by eqn (5) and (6) are kinetically competitive, it is becoming evident that these reductive transformations are quite complex with their being the possibility of both the oxidative and reductive quenching pathways leading to the formation of the desired product.
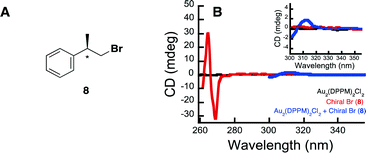
Further highlighting the complexity of the systems, is the ability of the Au complexes to reduce substrate 6, despite there being such a large barrier to electron transfer between the bromoalkanes redox potential and that of the excited state complex (1). There are two possible explanations for this behaviour. The first is that much of this energy barrier would be eliminated if one were to utilize the onset outer sphere potentials in place of the peak potentials. The second explanation involves a potential interaction between the Au complex and the starting bromoalkane, which somehow activates the substrate. Interestingly, it has been previously shown that [Au2(dppm)2]2+ undergoes substrate binding with LiCl and LiBr salts.61 In order to further explore this idea of substrate activation through catalyst interaction, we set out to examine the effect a chiral bromide substrate would have on the achiral Au2(dppm)2Cl2. The idea being that if there were some interactions between the two, perhaps the substrate would induce chirality within the Au complex. In order to test this hypothesis, we have synthesized chiral bromide (8) and probed the potential interaction between it and Au2(dppm)2Cl2, by measuring the circular dichroism spectrum of 8 and complex 1 alone and in the presence of each other (see Fig. 2 and ESI† for more experimental details). In Fig. 2B, it is clear that in the presence of both 8 and Au2(dppm)2Cl2 there is the appearance of a new CD signal centered at 312 nm, which can possibly be attributed to induction of chirality within the Au complex due to binding of substrate 8. On the basis of this result, one can propose that the reduction of the carbon-bromide bond may proceed through an inner sphere mechanism. While such an inner sphere mechanism would make the measured outer sphere potentials irrelevant, there is no evidence to eliminate the possibility of a mechanism involving both an inner sphere and outer sphere pathway.
It should also be mentioned that due to the basic conditions of the reactions; the radical cation of DIPEA, formed upon reductive quenching, will readily deprotonate to give a strongly reducing α-aminoalkyl radical (Eox1/2 = −1.12 V vs. SCE).67 Although it has been shown that these intermediates can actively participate in these types of transformations,33 they are not strong enough reductants to access the unactivated bromo alkane and bromoarene (~ −1.9 to −2.5 V vs. SCE)39,41 substrates of interest.
Conclusions
In conclusion, we have characterized the photophysical and electrochemical properties of a series of polynuclear gold(I) complexes (1–5). Through careful examination of the thermodynamic feasibility and rate constants of the key mechanistic steps involved in the light mediated activation of a model bromoallylmalonate, we have demonstrated that the mechanism(s) involved in these photoredox mediated transformations are quite complex with there being the possibility of multiple competing reaction processes possible. While the results have provided insight into many of the questions we posed, it also raises questions about the complexity of other systems, which involve the generation of long-lived, powerfully redox-versatile triplet excited states. Moving forward this data will not only help in reaction optimization but in rationalization of future applications. Further investigations into the process that gives rise to homocoupled products like (7b) are currently underway.Acknowledgements
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC), the University of Ottawa (for a University Research Chair to L. B.), the Canadian Foundation for Innovation and the Canada Research Chairs program (to J. C. S.). Acknowledgement is also made to the donor of the American Chemical Society Petroleum Research Fund for support of this research. C. D. M. and T. M. thank NSERC for post-graduate CGS-D scholarships. M. M. thanks the government of Ontario for an Ontario Graduate Scholarship (OGS).Notes and references
- A. Corma, A. Leyva-Pérez and M. J. Sabater, Chem. Rev., 2011, 111, 1657–1712 CrossRef CAS PubMed.
- D. J. Gorin and F. D. Toste, Nature, 2007, 446, 395–403 CrossRef CAS PubMed.
- A. S. K. Hashmi, Gold Bull., 2004, 37, 51–65 CrossRef CAS.
- A. S. K. Hashmi, Chem. Rev., 2007, 107, 3180–3211 CrossRef CAS PubMed.
- A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936 CrossRef PubMed.
- Z. Li, C. Brouwer and C. He, Chem. Rev., 2008, 108, 3239–3265 CrossRef CAS PubMed.
- N. D. Shapiro and F. D. Toste, Synlett, 2010, 2010, 675–691 CrossRef PubMed.
- A. Arcadi, Chem. Rev., 2008, 108, 3266–3325 CrossRef CAS PubMed.
- D. J. Gorin, B. D. Sherry and F. D. Toste, Chem. Rev., 2008, 108, 3351–3378 CrossRef CAS PubMed.
- M. Rudolph and A. S. K. Hashmi, Chem. Soc. Rev., 2012, 41, 2448–2462 RSC.
- V. Wing-Wah Yam and E. Chung-Chin Cheng, in Photochemistry and Photophysics of Coordination Compounds II, ed. V. Balzani and S. Campagna, Springer Berlin Heidelberg, 2007, pp. 269–309 Search PubMed.
- X. He and V. W.-W. Yam, Coord. Chem. Rev., 2011, 255, 2111–2123 CrossRef CAS.
- V. W.-W. Yam and E. C.-C. Cheng, Chem. Soc. Rev., 2008, 37, 1806–1813 RSC.
- V. Wing-Wah Yam, C.-L. Chan, S. Wing-Kin Choi, K. Man-Chung Wong, E. Chung-Chin Cheng, S.-C. Yu, P.-K. Ng, W.-K. Chan and K.-K. Cheung, Chem. Commun., 2000, 53–54 RSC.
- P. J. Barnard, M. V. Baker, S. J. Berners-Price and D. A. Day, J. Inorg. Biochem., 2004, 98, 1642–1647 CrossRef CAS PubMed.
- P. J. Barnard, L. E. Wedlock, M. V. Baker, S. J. Berners-Price, D. A. Joyce, B. W. Skelton and J. H. Steer, Angew. Chem., Int. Ed., 2006, 45, 5966–5970 CrossRef CAS PubMed.
- J. Xie, S. Shi, T. Zhang, N. Mehrkens, M. Rudolph and A. S. K. Hashmi, Angew. Chem., Int. Ed., 2015, 54, 6046–6050 CrossRef CAS PubMed.
- G. Revol, T. McCallum, M. Morin, F. Gagosz and L. Barriault, Angew. Chem., Int. Ed., 2013, 52, 13342–13345 CrossRef CAS PubMed.
- T. McCallum, E. Slavko, M. Morin and L. Barriault, Eur. J. Org. Chem., 2015, 2015, 81–85 CrossRef CAS.
- S. Kaldas, A. Canillo, T. McCallum and L. Barriault, Org. Lett., 2015, 17, 2864–2866 CrossRef CAS PubMed.
- F. Nzulu, S. Telitel, F. Stoffelbach, B. Graff, F. Marlet-Savary, J. Lalevée, L. Fensterbank, J.-P. Goddard and C. Ollivier, Polym. Chem., 2015, 6, 4605–4611 RSC.
- V. Balzani, A. Credi and M. Venturi, ChemSusChem, 2008, 1, 26–58 CrossRef CAS PubMed.
- M. Fagnoni, D. Dondi, D. Ravelli and A. Albini, Chem. Rev., 2007, 107, 2725–2756 CrossRef CAS PubMed.
- J. M. R. Narayanam and C. R. J. Stephenson, Chem. Soc. Rev., 2011, 40, 102–113 RSC.
- C. K. Prier, D. A. Rankic and D. W. C. MacMillan, Chem. Rev., 2013, 113, 5322–5363 CrossRef CAS PubMed.
- D. M. Schultz and T. P. Yoon, Science, 2014, 343 Search PubMed.
- L. Shi and W. Xia, Chem. Soc. Rev., 2012, 41, 7687–7697 RSC.
- F. Teplý, Collect. Czech. Chem. Commun., 2011, 76, 859–917 CrossRef.
- J. W. Tucker and C. R. J. Stephenson, J. Org. Chem., 2012, 77, 1617–1622 CrossRef CAS PubMed.
- J. Xuan and W.-J. Xiao, Angew. Chem., Int. Ed., 2012, 51, 6828–6838 CrossRef CAS PubMed.
- T. P. Yoon, M. A. Ischay and J. Du, Nat. Chem., 2010, 2, 527–532 CrossRef CAS PubMed.
- D. A. Nicewicz and T. M. Nguyen, ACS Catal., 2014, 4, 355–360 CrossRef CAS.
- H. Ismaili, S. P. Pitre and J. C. Scaiano, Catal. Sci. Technol., 2013, 3, 935–937 CAS.
- S. P. Pitre, C. D. McTiernan, H. Ismaili and J. C. Scaiano, ACS Catal., 2014, 4, 2530–2535 CrossRef CAS.
- D. Ravelli, M. Fagnoni and A. Albini, Chem. Soc. Rev., 2013, 42, 97–113 RSC.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- C. D. McTiernan, S. P. Pitre and J. C. Scaiano, ACS Catal., 2014, 4, 4034–4039 CrossRef CAS.
- C.-M. Che, H.-L. Kwong, V. W.-W. Yam and K.-C. Cho, J. Chem. Soc., Chem. Commun., 1989, 885–886 RSC.
- A. J. Fry and R. L. Krieger, J. Org. Chem., 1976, 41, 54–57 CrossRef CAS.
- H.-L. Kwong, V. Wing-Wah Yam, D. Dan Li and C.-M. Che, J. Chem. Soc., Dalton Trans., 1992, 3325–3329 Search PubMed.
- S. Rondinini, P. R. Mussini, P. Muttini and G. Sello, Electrochim. Acta, 2001, 46, 3245–3258 CrossRef CAS.
- P. A. Baguley and J. C. Walton, Angew. Chem., Int. Ed., 1998, 37, 3072–3082 CrossRef CAS.
- C. Chatgilialoglu, Acc. Chem. Res., 1992, 25, 188–194 CrossRef CAS.
- A. Ekomio, G. Lefèvre, L. Fensterbank, E. Lacôte, M. Malacria, C. Ollivier and A. Jutand, Angew. Chem., Int. Ed., 2012, 51, 6942–6946 CrossRef PubMed.
- B. C. Gilbert and A. F. Parsons, J. Chem. Soc., Perkin Trans. 2, 2002, 367–387 RSC.
- J. A. Murphy, T. A. Khan, S. Z. Zhou, D. W. Thomson and M. Mahesh, Angew. Chem., Int. Ed., 2005, 44, 1356–1360 CrossRef CAS PubMed.
- C. Ollivier and P. Renaud, Chem. Rev., 2001, 101, 3415–3434 CrossRef CAS PubMed.
- B. Quiclet-Sire and S. Z. Zard, Int. J. Pure Appl. Chem., 2011, 83, 519–551 CAS.
- A. Studer and S. Amrein, Synthesis, 2002, 835–849 CrossRef CAS.
- M. E. Weiss, L. M. Kreis, A. Lauber and E. M. Carreira, Angew. Chem., Int. Ed., 2011, 50, 11125–11128 CrossRef CAS PubMed.
- (a) S. Z. Zard, in Radical Reactions in Organic Synthesis, Oxford University Press, Oxford, 2003 Search PubMed; (b) P. Renaud and M. P. Sibi, in Radicals in Organic Synthesis, Wiley-VCH, Weinheim, 2001 Search PubMed.
- D. P. Curran, in Comprehensive Organic Synthesis, ed. B. M. Trost, I. Fleming and M. F. Semmelhack, Pergamon, Oxford, 1991, p. 715 Search PubMed.
- A. Gansuer, ed. Topics in Current Chemistry, Radicals in Synthesis I and II, Springer, Berlin, 2006 Search PubMed.
- Encyclopedia of Radicals in Chemistry, Biology and Materials, ed. A. S. C. Chatgilialoglu, Wiley, Chichester, 2012 Search PubMed.
- P.-K. Chow, G. Cheng, G. S. M. Tong, W.-P. To, W.-L. Kwong, K.-H. Low, C.-C. Kwok, C. Ma and C.-M. Che, Angew. Chem., Int. Ed., 2015, 54, 2084–2089 CrossRef CAS PubMed.
- I. Ghosh, T. Ghosh, J. I. Bardagi and B. König, Science, 2014, 346, 725–728 CrossRef CAS PubMed.
- W. Ludwig and W. Meyer, Helv. Chim. Acta, 1982, 65, 934–943 CrossRef CAS.
- A. Stützer, P. Bissinger and H. Schmidbaur, Chem. Ber., 1992, 125, 367–372 CrossRef.
- P. J. Barnard, M. V. Baker, S. J. Berners-Price, B. W. Skelton and A. H. White, Dalton Trans., 2004, 1038–1047 RSC.
- K. Suzuki, A. Kobayashi, S. Kaneko, K. Takehira, T. Yoshihara, H. Ishida, Y. Shiina, S. Oishi and S. Tobita, Phys. Chem. Chem. Phys., 2009, 11, 9850–9860 RSC.
- C.-M. Che, H.-L. Kwong, C.-K. Poon and V. W.-W. Yam, J. Chem. Soc., Dalton Trans., 1990, 3215–3219 RSC.
- M. Cherevatskaya, M. Neumann, S. Füldner, C. Harlander, S. Kümmel, S. Dankesreiter, A. Pfitzner, K. Zeitler and B. König, Angew. Chem., Int. Ed., 2012, 51, 4062–4066 CrossRef CAS PubMed.
- For more details regarding the excited state potentials of Au complexes 2–5 and their corresponding free energies see the ESI.† In some instances the catalysts may undergo counter-ion exchange during the time course of the reaction. Although this may result in small changes to both the photochemical and photophysical properties of the catalysts, it is apparent that such exchange does not impede the catalysis..
- L. Michaelis and E. S. Hill, J. Gen. Physiol., 1933, 16, 859–873 CrossRef CAS PubMed.
- G. Chaka and A. Bakac, Dalton Trans., 2009, 318–321 RSC.
- J. F. Coetzee and I. M. Kolthoff, J. Am. Chem. Soc., 1957, 79, 6110–6115 CrossRef CAS.
- M. Jonsson, D. D. M. Wayner and J. Lusztyk, J. Phys. Chem., 1996, 100, 17539–17543 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on reaction conditions, spectral data on products, absorption spectra, emission spectra, laser flash photolysis data, kinetic quenching plots, and NMR spectra. See DOI: 10.1039/c5cy01259g |
| This journal is © The Royal Society of Chemistry 2016 |