Spatial and temporal distributions of 134Cs and 137Cs derived from the TEPCO Fukushima Daiichi Nuclear Power Plant accident in the North Pacific Ocean by using optimal interpolation analysis†
Y.
Inomata
*a,
M.
Aoyama
b,
T.
Tsubono
c,
D.
Tsumune
c and
K.
Hirose
d
aAtmospheric Research Department, Asia Center for Air Pollution Research, 1182, Sowa, Nishiku, Niigata-shi, Niigata-ken 950-2144, Japan. E-mail: inomata@acap.asia; Fax: +81 25 263 0567; Tel: +81 25 263 0558
bInstitute of Environmental Radioactivity, Fukushima University, 1 Kanayagawa, Fukushima-shi, Fukushima-ken 960-1296, Japan
cEnvironmental Science Research Laboratory, Central Research Institute of Electric Power Industry, 1646 Abiko, Abiko-shi, Chiba-ken 270-1194, Japan
dDepartment of Material and Life Sciences, Faculty of Science and Technology, Sophia University, 7-1 Kioicho, Chiyodaku, Tokyo 102-8554, Japan
First published on 11th December 2015
Abstract
Optimal interpolation (OI) analysis was used to investigate the oceanic distributions of 134Cs and 137Cs released from the Tokyo Electric Power Company Fukushima Daiichi Nuclear Power Plant (FNPP1) accident. From the end of March to early April 2011, extremely high activities were observed in the coastal surface seawater near the FNPP1. The high activities spread to a region near 165°E in the western North Pacific Ocean, with a latitudinal center of 40°N. Atmospheric deposition also caused high activities in the region between 180° and 130°W in the North Pacific Ocean. The inventory of FNPP1-released 134Cs in the North Pacific Ocean was estimated to be 15.3 ± 2.6 PBq. About half of this activity (8.4 ± 2.6 PBq) was found in the coastal region near the FNPP1. After 6 April 2011, when major direct releases ceased, the FNPP1-released 134Cs in the coastal region decreased exponentially with an apparent half-time of about 4.2 ± 0.5 days and declined to about 2 ± 0.4 PBq by the middle of May 2011. Taking into account that the 134Cs/137Cs activity ratio was about 1 just after release and was extremely uniform during the first month after the accident, the amount of 137Cs released by the FNPP1 accident increased the North Pacific inventory of 137Cs due to bomb testing during the 1950s and early 1960s by 20%.
Environmental impactThe oceanic distributions of 134Cs and 137Cs released from the FNPP1 accident was investigated by using the optimal interpolation (OI) analysis. The total inventory of 134Cs in the North Pacific Ocean is estimated to be 15.3 ± 2.6 PBq. In this, about half of the total released amount is concentrated in the coastal region near the FNPP1. The total amount of 137Cs released by the FNPP1 accident increased the current North Pacific inventory of bomb-derived 137Cs injected in the 1950s and early 1960s by 20%. |
1. Introduction
As a result of an extraordinary earthquake and the subsequent accident at the Tokyo Electronic Power Company Fukushima Daiichi Nuclear Power Plant (hereafter referred to as FNPP1), located at a latitude of 37.42°N and a longitude of 141.03°E, large amounts of radionuclides were released into the atmosphere as well as in the ocean. 137Cs, with a half-life (T1/2) of 30.17 years, and 134Cs (T1/2 = 2.06 years) were the dominant long-lived radionuclides released as a result of the FNPP1 accident. Before the accident, 137Cs was already present in the North Pacific Ocean, derived from the atmospheric nuclear weapon tests conducted mainly in the late 1950s and the early 1960s and the Chernobyl accident that occurred in 1986.1 Most 137Cs in the marine environment exists in a dissolved form. The distribution of this dissolved 137Cs is dominated by physical oceanographic processes such as horizontal advection, diffusion, vertical mixing, and radioactive decay. 137Cs has therefore been regarded as a useful chemical tracer of water movements in the ocean since the 1950s.1–4 In the 2000s, the 137Cs activities in surface waters were a few Bq m−3, and the distribution was almost uniform,1,5,6 except for some relatively high 137Cs activities that exceeded 2 Bq m−3 in the western part of the North Pacific Ocean.7 On the other hand, the presence of 134Cs is recognized as a signature of FNPP1-released radionuclides, because there is no contribution remaining from global fallout and deposited 134Cs from the Chernobyl accident in 1986, which has decayed to the short half-life of 2.06 years. 134Cs is therefore an ideal tracer for investigating the distribution of radionuclides derived from the FNPP1.At the time of the FNPP1 accident, 134Cs and 137Cs were injected into the surface seawater by two major pathways, direct discharge from the FNPP1 and atmospheric deposition. The distributions of 137Cs and 134Cs after the accident have been reported by several researchers.7–16 However, these results are only snapshots in order to interpret the distribution and transport of the released 134Cs and 137Cs on a basin scale. Furthermore, it is recognized that the estimation of the total amount of released 134Cs and 137Cs is necessary to assess the radioecological impacts of their release on the environment. Although there have been many estimates of the amounts of 137Cs and 134Cs released, reported budgets still have high uncertainties.17–22
In this study, we used optimum interpolation (OI) analysis to investigate the spatial and temporal variations of the distributions of 134Cs and 137Cs. OI is an effective analytical scheme for depicting the horizontal distributions of irregularly distributed measurement data.23,24 Furthermore, the gridded analytical value by OI is useful for estimating abundance exactly. The optimal parameters of OI are determined by comparing with the gridded value obtained by another gridding method, the Akima spline method.24 Although the model simulations such as ocean general circulation models are effective analysis schemes to investigate the spatial and temporal distribution in the basin scale, the simulated results are largely different associated with using schemes such as advection diffusion processes. It is desirable to conduct statistical analysis, such as OI, by using only the measured activities. The results can also be used to investigate the validity of model simulations.2–4
The primary objectives of this study were to (i) investigate the spatial and temporal distributions of 134Cs and 137Cs derived from the FNPP1 in the surface seawater and (ii) estimate the total inventories of 134Cs and 137Cs in the North Pacific Ocean by using the numerous observed data. The data used in this study were derived from all of the available data reported by the Tokyo Electric Power Company (TEPCO), the Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT), and voluntary cargo ships.7–16 In this study, we focused on 134Cs as a tracer of radionuclides derived from the FNPP1. The results of analysis using 137Cs are presented in the ESI.†
2. Methods
2.1. Analysis by optimum interpolation
Because measurements of 134Cs and 137Cs activities in the oceanic surface waters have been performed by numerous research institutes, the locations and time of the data were spatially and temporally irregular. Data gridding procedures are useful to investigate the spatial and temporal distributions of chemical components as well as the physical ones because their methodologies were applied to assimilation processes and would be used for model inter-comparison. OI is a commonly used method to interpolate irregularly distributed data into regular grids.For one point (grid), the analytical data used for optimal interpolation (OI) were within a circle with an influence radius, R (km) (Fig. SI1†). We identify the 134Cs and 137Cs activities estimated by OI as OICs134 and OICs137, respectively. Hereafter in this section, the descriptions are changed to OICs. Because each observation is associated with some errors, we calculated OI-Csag as the sum of the first analyzed value OI-Csbg at point g plus a linear combination of the deviations of the observed values (Csj) from the first guess (OI-Csbj). The superscripts, a and b, refer to the analyses and background. The values of first guesses were equated to the average of the analyzed values in the region:
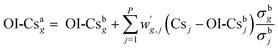 | (1) |
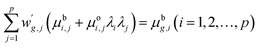 | (2) |
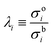 | (3) |
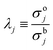 | (4) |
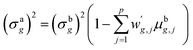 | (5) |
Just after the FNPP1 accident, extremely high activities of 134Cs and 137Cs were observed only in coastal waters near the FNPP1. The large gradient of the activities precluded an OI analysis of the entire North Pacific Ocean, because the differences between the measured and averaged values in the analysis region must be taken into consideration for the OI analysis. We therefore chose two analytical domains: one was the open ocean (D01; >141.5°E) and the other was the coastal area < 43 km from the FNPP1 (D02; ≤141.5°E). Data during the period from 21 March to 31 May 2011 were used in our analysis.
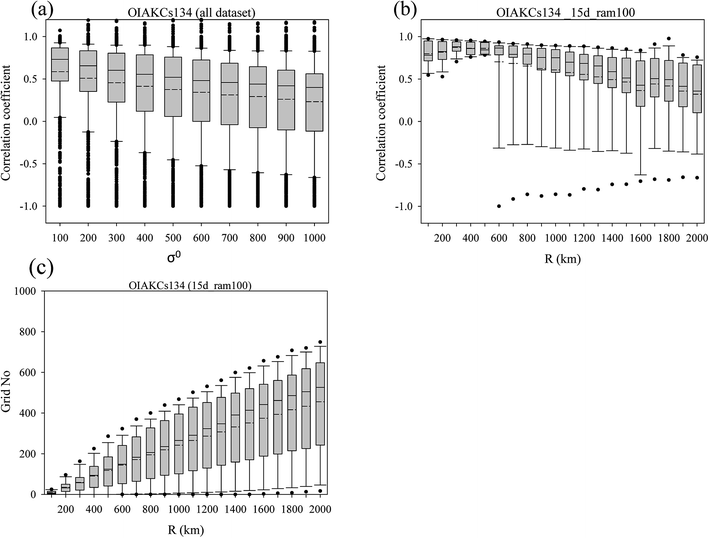
In domain D01, the 134Cs and 137Cs activities estimated by OI were produced on a grid with a horizontal resolution of 3° longitude × 2° latitude, because the area is approximately equal to the geodetic area of one grid exactly and the meridional transport prevails in the analytical area including the Kuroshio current, which corresponds to the wind-driven, subtropical and subarctic circulations of the North Pacific Ocean. In addition to this, this resolution was set based on the observation interval, because the seawater sample was obtained twice a day (<180°) or once (>180°) a day. Two optimization parameters, background error at the observation point and the influence radius (R: unit = km), were determined for OICs by comparisons to values obtained from another interpolation and gridding algorithm, i.e., the Akima spline method,25 described as AKCs. The data number, which is based on the analysis day, is also included as the parameter.
The data using the OI analysis were selected from a circle with an assumed radius equal to R. The values of σo and R were considered after taking into account the seawater transport time and spatial scale of the dataset. We conducted sensitivity analyses to select optimal values of the parameters. Furthermore, the OI analytical value was correlated with the observed 134Cs activities in seawater.
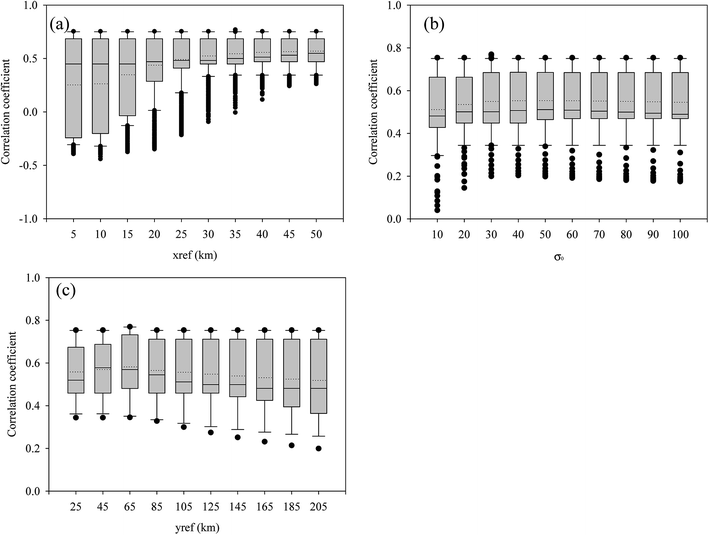
In D02, the horizontal resolution was set to 0.15° longitude × 0.1° latitude, in which the ratio between the longitude and latitude is considered as the geodetic length. The fine resolution in D02 compared with D01 is due to the closer distance among the sampling points. Considering that alongshore currents dominate the north-south transport in the coastal region off Fukushima,26 we selected data within an ellipse instead of a circle for the parameter, R. The two axes of the ellipse, xref (longitudinal axis; km) and yref (latitudinal axis; km), were considered as parameters as well as σo. In this case, the results using the Akima spline method,25 which uses only data from the next neighboring points to determine the coefficients of the interpolation polynomial, are largely different to the measurements. This would be caused by several reasons: (i) the distributions of the 134Cs and 137Cs activities in seawater were strongly controlled by north-south transport and (ii) the activities were rapidly decreased toward the offshore. Therefore, the optimal parameters were selected by only comparison with OICs against the measured activities.
2.2. Estimation of total inventories
The total OIC inventories of FNPP1-derived 134Cs and 137Cs were calculated as follows:| [Budget OICs] = ∑[OICs activities] × sea area for each grid in the North Pacific Ocean × gridded mixed-layer depth | (6) |
In domain D01, gridded mixed-layer depths (MLDs) in April and May of 2011 were estimated by using salinity and potential temperature distributions in the North Pacific Ocean provided by using the NCEP Global Ocean Data Assimilation System.27 Data of salinity and potential temperature are observed and changed to a grid value with 0.333° latitude × 1° longitude and 40 depth layers as the resolution. The MLD was equated to the shallower depth of the isothermal layer (TLD; defined by Δσo = 0.03 kg m−3) or isopycnal layer (PLD; defined by ΔT = 0.2 °C).28 To estimate the 134Cs and 137Cs budget in D01, fine MLD data (0.333° longitude × 1° latitude) were interpolated to coarse MLD values (3° longitude × 2° latitude) by using the Akima spline method. The distribution of MLDs in the North Pacific Ocean is shown in Fig. SI2.† The 134Cs activities in seawater were assumed to be homogeneous in the mixed layers, taking into account the finding that most of the 134Cs and 137Cs activities remained in the mixed layer from the vertical profiles of the 134Cs and 137Cs activities in seawater observed in the North Pacific Ocean (Fig. SI3†).9 In domain D02, the surface MLD was set to about 10 m based on the salinity profile, which was observed by the Japan Agency for Marine-Earth Science and Technology.21 Furthermore, we also used to calculate the inventories of 134Cs in the region of airborne monitoring within 30 km of the FNPP1, conducted on 18 April 2011, to determine the optimal parameters for D02.29 Therefore, the estimated total inventory is considered as a total sum in the water column.
2.3. Data sources
Almost all of the data used in the OI analysis were accessible in reports and research papers. These data were listed by Aoyama et al. (2015).9 Near the FNPP1, TEPCO has monitored 134Cs and 137Cs activities in seawater at several sites (e.g., discharge canal for reactor units 5–6 at the north of the FNPP1, discharge canal for reactor units 1–4 at the south of the FNPP1, 10 km south of the FNPP1, and 16 km south of the FNPP1) since 21 March 2011.30,31 MEXT has also started monitoring at eight points 30 km off a coastal site from 23 March 2011. In the North Pacific Ocean, sampling of seawater to measure 134Cs and 137Cs was conducted by using 17 cargo ships as voluntary observing ships and research vessels.7–16The first guess of the parameters, which is based on averaging values in the analytical area, is an important step in the calculation of the optimal parameters for the OI analysis. However, the 134Cs and 137Cs activities near the coastal region were too high (maximum activity was 6.8 × 107 Bq m−3 on 6 April 2011) compared with the activities in the offshore region to carry out the OI analysis for one domain. We therefore carried out the analysis with two analytical domains, the open ocean (D01, >141.5°E) and the coastal region within 43 km of the FNPP1 (D02, ≤141.5°E). There were 224 records of 134Cs in D01, 159 records of 137Cs in D01, 757 records of 134Cs in D02, and 799 records of 137Cs in D02. We arbitrarily removed data from the OI analysis if the data were less than the detection limit and there was no report on the detection limit.
Although we used almost all of the available data, the number of data for the OI analysis was very limited. We then compiled the data for the OI analysis. In D01, the OI dataset was made by using the observed data within spans of several days (available span: 3, 5, 7, 15, 21, 31, 45, and 61 days). In these datasets, the mid-day in each span is set as the reference day. In other words, the data within several days ((spans-1)/2 days) before and after the reference day were combined and regarded as one datum. As an example, the 3 days' data from 31 March to 2 April 2011 were combined and the reference day was assigned to 1 April 2011. We determined the optimal values of the parameters for the OI analysis based on data assigned to reference days, i.e. 1, 6, 11, 16, 21, and 26 days for each month. The overview of the data selecting method is shown in Fig. SI4.†
For D02 analysis, data observed during a 7 day span were combined as one datum (reference day ± 3 days), because the north-south flow in the along-shore region of the coastal current system dominated the flow and changed with a three-day periodicity.26 The activity concentrations of radionuclides in seawater were corrected radioactive decay to the reference day for each dataset.
3. Results
3.1. Determination of optimal values for the OIC parameters
Finally, we selected 35 km, 65 km, and 30 as the optimal values for xref, yref, and σo, respectively. It must be noted that the optimal values of these parameters are unique, because these optimal parameters are independent of the order of the statistical analyses.
The statistical results for selecting the optimal value of OICs137 for the parameters of D02 are shown in Fig. SI9.†
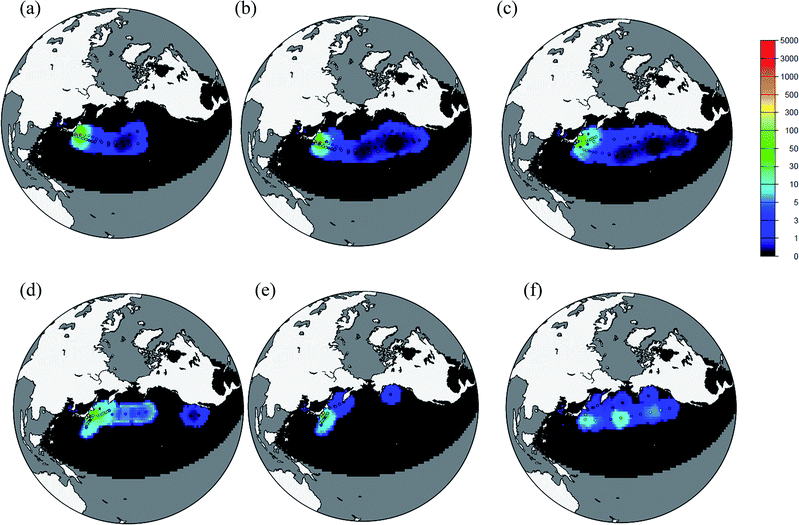
3.2. Spatial and temporal distribution of OICs134
4. Discussion
4.1. Temporal variation of total 134Cs inventory in the North Pacific Ocean
Fig. 5 shows the temporal changes of the total OICs134 inventory in the North Pacific Ocean, which means the sum of the OICs134 inventories in domains D01 and D02. It must be noted that this estimation is based on the region where the OI analysis was available. The total OICs134 inventory rapidly increased and reached a maximum value of 15.3 ± 2.6 PBq at the end of March. The total OICs134 inventory decreased until 6 April 2011, after which time it increased slightly. Following this slight increase, the total OICs134 inventory decreased exponentially to about 2 ± 0.4 PBq by the mid-May 2011. It should be noted that the OICs134 inventory at the end of April-early of May and after 18 May 2011 was small. At the end of April, the smaller inventory is caused by the very limited observation region, which did not cover the central and eastern parts of the North Pacific Ocean. After 18 May 2011, the result is due to an extremely limited number of observed data (Fig. SI12†). A distinct feature was that the OICs134 inventory in D02 accounted for 50% of the total inventory during the period of the direct discharge of radioactivity contaminated water from 26 March to 6 April 2011.18 The percentage of the total OICs134 inventory in D02 gradually decreased and reached 7% by the mid-May 2011. Instead of decreasing the OICs134 inventory in D02, that in D01 is slightly increased in mid-April. This trend suggests that the FNPP1-released radiocesium spreads out of the area encompassed by the OI analysis due to physical processes such as advection and diffusion. However, the increase of the OICs134 inventory after the end of April is not significant. This might be due to the physical processes throughout the transport or limited observed data.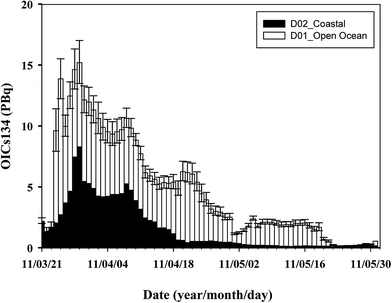 | ||
| Fig. 5 Daily OICs134 inventories during the period from 21 March 2011 to 31 May 2011 in sum of the two domains (D01 + D02). | ||
Furthermore, the estimated OICs134 inventory might be possibly underestimated because of limited data at the end of April and after 18 May 2011. Underestimation also occurs as a result of downward transport of 134Cs associated with vertical mixing processes because the monthly average value of the MLD (Fig. SI2†) was used in this study.
Although we estimate the total OICs134 inventory by using the optimal parameters, we have to consider the error for estimating the inventory. As mentioned above, this analysis was based on the observation data. The optimal parameters should be selected to reflect the distribution associated with the physical oceanographic processes. There are several errors for estimating the inventory such as measurement errors, OI analytical errors derived from calculating the grid value, variation of observed values in a space, representativeness of using data, mixed layer depth and its spatial distribution. With respect to variation of the observed values in a space and representativeness of using data, it depends on the location of the observations. In the D01, sampling of seawater in the open ocean was conducted twice a day (<180°) or once a day (>180°) by ships. Taking into account that the zonal speed of the FNPP1 derived radiocaesium was 7 km per day,9 the transport distance at the 15 d dataset was covered about 1° toward longitude. Although the dataset of a longer time span is increasing the data number, this does not reflect the actual distribution of radiocaesium in seawater. Furthermore, the data coverage toward meridional was coarse because the observation depended on the ships' route, toward zonal. With respect to the mixed layer depth, we have just defined the mixed layer depth as shown in Fig. SI3.† Selection of optimal R is also an important factor to estimate the inventory. Fig. SI13† shows that the OICs134 inventories increase with increasing R. Actually, smaller R did not cover the sea area for investigating the distribution and transport of radiocaesium. In contrast, larger R covers the wider region, but the spatial distribution of the radiocaesium in seawater at the analytical time did not reflect the real one. We also investigated the change of the OICs134 inventory against R for D01 and D02 (Fig. SI14†). This is normalized by the OICs134 inventory obtained at the optimal R (800 km) or yref (65 km). The characteristic for this sensitivity calculation is that the OICs134 inventory decreases with decreasing optimal R or yref, whereas it increases with increasing optimal R or yref. This is reasonable because the estimation of the OICs134 inventory is based on the calculated area. However, smaller R (yref) as well as larger R (yref) does not elucidate the distribution of 134Cs based on the transport scale. As shown in Fig. 1, higher r between OICs134 and AKCs134 finds the range from 500 to 1000 km in D01. The OICs134 inventory in these R values coincides with that from the optimal R within 10%. For D02, the OICs134 inventory within ±25 km also coincides with that from the optimal yref within 10%. Therefore, we think that the OICs134 inventories from 600 to 1000 km (as 800 ± 200 km) for R and 45 to 85 km for yref (as 65 ± 25 km) are used for the error estimation. The variation of the total OICs137 inventory is also shown in Fig. SI15.†
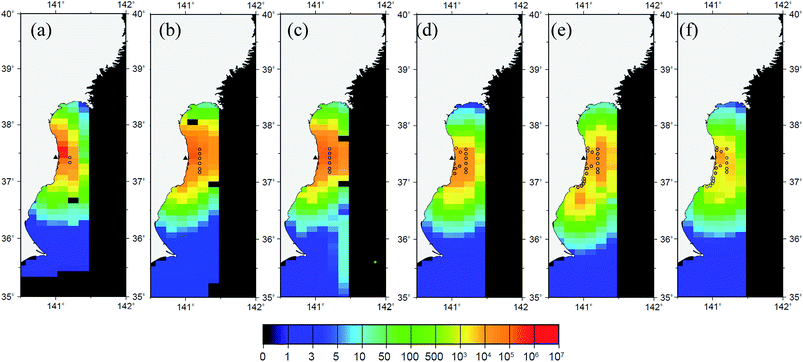
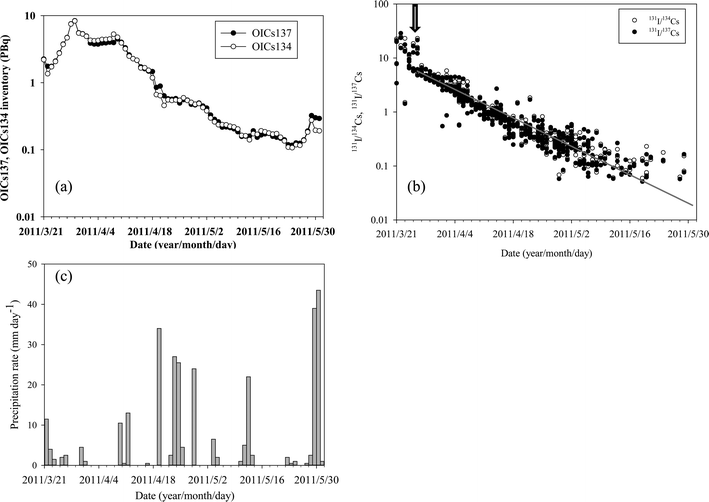
4.2. Factors controlling the amount of radioactivity in D02
As described in the previous section, the contribution of the OICs134 inventory in D02 to the total inventory in the North Pacific Ocean was large in the late March and early April 2011. We investigated the temporal variation of the OICs inventory in D02 in more detail. Fig. 6a shows the temporal variation of the OICs134 and OICs137 inventories in D02 on a logarithmic scale. It should be noted that the OICs134 and OICs137 (hereafter OICs) inventories are almost equal to each other. It is reasonable to suppose that the 134Cs/137Cs activity ratio in radionuclides released as a result of the FNPP1 accident was almost equal to unity.11 There were two high peaks of the OICs inventories at the end of March and early part of April. The OICs inventory rapidly increased until 29 March and attained a maximum value of 8.4 ± 2.6 PBq. After 29 March, the OICs inventory in D02 decreased to 4.2 PBq within a few days. The OICs inventory gradually increased again until 9 April, after which time it decreased exponentially, with small variations, until the end of May 2011. The half decrease time of the OICs inventory was about 4.2 ± 0.5 days. These variations reflect the influence of (i) atmospheric deposition, (ii) direct discharge, (iii) seawater current system, and (iv) other processes. We examine these factors in the following sections.To elucidate the contribution of atmospheric deposition and direct discharge of 134Cs and 137Cs to coastal waters, we have plotted the temporal variations of the 131I/134Cs and 131I/137Cs activity ratios in D02 in Fig. 6b, where we also show the corresponding radioactive decay curve based on the 131I/134Cs and 131I/137Cs activity ratios in the puddle water of the FNPP1 on 26 March 2011.18 The 131I/134Cs and 131I/137Cs activity ratios on March 26 in seawater near the FNPP1 were consistent with their ratios in the puddle water. Because most of the 131I, 134Cs, and 137Cs in seawater exists in dissolved forms, the activity ratios should decrease in accordance with the radioactive decay of 131I because the radioactive half-lives of 134Cs and 137Cs are much longer than that of 131I (T1/2 = 8 days). The fact that the 131I/134Cs and 131I/137Cs activity ratios from 26 March to 6 April 2011 can be plotted on the radioactive decay curve of the 131I/134Cs and 131I/137Cs suggests that the observed 134Cs and 137Cs in the coastal waters during this period were derived primarily from the direct release of the contaminated water from the FNPP1. In contrast, before 26 March 2011, the 131I/134Cs and 131I/137Cs activity ratios were higher, with much scatter, than the ratios estimated from the 131I decay curve. A possible explanation for these high activity ratios relative to the 131I decay curve and their large variability is that the 134Cs and 137Cs in the coastal water before 26 March 2011 were derived from atmospheric deposition. According to several studies, atmospheric deposition that occurred during March 2011 had a major effect on the activities of FNPP1-derived radionuclides in surface seawater in this region.34 In addition, the 131I released from the FNPP1 entered the atmosphere as a gas and as small particles with a diameter of less than 1 μm, whereas 134Cs and 137Cs were emitted to the atmosphere as particles larger than 1–2 μm in diameter.22 The fact that the rate of wet deposition depends on the particle size probably accounts for the large variability of the 131I/134Cs and 131I/137Cs activity ratios in the aerosols. In fact, the 131I/134Cs and 131I/137Cs activity ratios in surface air observed at Tsukuba showed large temporal changes.35 The temporal changes of the 131I/134Cs and 131I/137Cs activity ratios strongly suggest that the large total OIC inventories estimated from the end of March to early April 2011 resulted from the direct discharge of contaminated water rather than from atmospheric deposition.
Model simulations indicate that the coastal current system also affects the total 137Cs inventory in the coastal area.17,18 Although the major direct discharge of the contaminated water stopped on 6 April 2011, the total 137Cs inventory in D02 increased until 10 April. According to an analysis of the winds by the European Centre for Medium-Range Weather Forecasts (ECMWF),21 weak southeast or southwest flow in the coastal area off Fukushima prevailed during the period of the direct discharge of the contaminated water. The increase of the total OICs inventory on 8 April 2011 after the cease of the direct discharge could have been induced by southward transport and subsidence of the seawater. Although the OICs inventory in D02 mainly decreased with time, there were periods when the OICs inventory was almost constant (21–29 April 2011, 9–19 May 2011) or increased (27–31 May 2011). During these periods, trends of the 131I/134Cs and 131I/137Cs activity ratios, which followed the decay curve of 131I, suggested that the OICs inventory in D02 was controlled mainly by the direct discharges of the contaminated water and oceanographic transport processes and that there was only a minor contribution from atmospheric deposition of 134Cs and 137Cs in the surface seawater. There is no reason why the 134Cs and 137Cs activities did not decrease, because the major outflow of 134Cs and 137Cs from the D02 domain had ceased in early April. It is possible that a small amount of radiocesium leaked from the FNPP1 during these periods, as suggested.17,18 Another explanation is the radioactivity input via precipitation, which would cause an increase of radioactivity in coastal waters. As shown in Fig. 6c, heavy rainfall events (more than 20 mm) were recorded at the Hirono AMeDAS monitoring site (37.14°N, 141°E), which is located 31 km from the FNPP1, during the periods when the OICs inventory in D02 was almost constant or increasing. It has been reported that the activity of 134Cs in the stagnant water in the FNPP1 on 27 May 2011 was 2.5 GBq L−1.36 By the end of May, the OICs134 and OICs137 inventories had increased by about 0.4 PBq (Fig. 6a). An increasing or almost constant inventory can be explained by an inflow of contaminated water, such as stagnant water from the FNPP1, induced by heavy rainfall.
4.3. Comparison of the total inventory with other research studies and past release events
Table 1 shows the inventory, direct release amount in the ocean, and deposition amount in the ocean surface for 134Cs. The estimated total inventory of OICs134 was 15.3 ± 2.6 PBq. In these, a significant part of the OICs134 inventory (8.4 ± 2.6 PBq) existed in the coastal region near the FNPP1. The dominant input processes of 134Cs in the ocean are direct discharge and atmospheric deposition. It was reported that the direct discharge was in the range from 2.3 to 26.9 PBq.17–21,37–39 However, estimates of the total direct discharge of 134Cs from recent studies seem to converge on a value (3–6 PBq).17,18,21,37–39 Unreasonably high values are due to inclusion of the atmospheric deposition.20,37,39 The atmospheric deposition in the North Pacific Ocean was estimated to be 0.5–15 PBq.10,21,37 Considering that the estimated inventory in D02 was larger than that of the direct discharge (3.5 ± 0.7 PBq at the end of May 2011),17 the atmospheric deposition also contributes to the estimated inventory by OI analysis in this region.| Methods | Total amount in the North Pacific Ocean | Amount in coastal | Direct discharge | Atmospheric deposition | Periods | |
|---|---|---|---|---|---|---|
| (Direct release + deposition) | ||||||
| (PBq) | (PBq) | (PBq) | (PBq) | |||
| This study | Optimal interpolation | 15.3 ± 2.6 | 8.4 ± 2.6 | 21st Mar 2011–31st May 2011 | ||
| Aoyama et al. (2015) | Simple estimate based on observation | 15–18 | 3.6 ± 0.7 | 12–15 | 21st Mar 2011–31st May 2011 | |
| Model simulation | 16.1 ± 1.4 | 5.6 ± 0.5 | 3.6 ± 0.7 | 10.5 ± 0.9 | Mar 2011–Feb 2014 | |
| Kawamura et al. (2011) | Model simulation | 9 | 4 | 5 | 21st Mar 2011–30th Sep 2011 | |
| Estounel et al. (2012) | Model simulation | 9.8–10.4 | 4.1–4.5 | 5.1–5.5 | ||
| Tsumune et al. (2012) | Model simulation | 3.5 ± 0.7 | 26th Mar 2011–31st May 2011 | |||
| Baily du Bois et al. (2012) | Observation, point Kriging | 27 ± 15 | March 21–July 18 | |||
| UNSCEAR 2013* | 8–14 | 3–6 | 5–8 | Mar 2011–Jun 2011 | ||
| Tsumune et al. (2013) | Model simulation | 3.6 ± 0.7 | Mar 26 2001–29th Feb 2012 | |||
| Charette et al. (2013) | Ra based ocenographic model | 11–16 | Early April 2011 | |||
| Rypina et al. (2013) | Model simulation | 16.2 ± 1.6 | 0.5 ± 2.7 | 21st Mar 2011–30th June 2011 | ||
| Kobayashi et al. (2013) | Model simulation | 11.1 | 3.5 | 7.6 | 12th Mar–1st May 2011; entire North Pacific Ocean | |
| Miyazawa et al. (2013) | Model simulation | 5.5–5.9 | 5.5–9.7 | 21st Mar 2011–30th April 2011 | ||
The estimated 134Cs inventory in this study is almost the same as the results of the other research studies by other approaches; Aoyama et al.10 have estimated the total 137Cs inventory to be 15–18 PBq in the North Pacific Ocean due to the simple integration method based on the observation. Based on a modeling approach, the total 137Cs inventory in the North Pacific Ocean is 16.1 ± 1.4 PBq.10 The finding that the estimated OICs134 inventory in D02 was larger than that of the direct discharge (3.5 ± 0.7 PBq at the end of May 2011)17 suggests that the atmospheric deposition also significantly contributed to the 134Cs inventory in the coastal region near the FNPP1.
We also compared the inventory of 134Cs with the amount of 137Cs injected into the North Pacific Ocean historically by mechanisms such as global fallout, and the Chernobyl accident. The total inventory of 137Cs in the North Pacific Ocean in 1970 has been reported to be 290 ± 30 PBq.39 By the year 2003, the 137Cs inventory had decreased to 86 PBq based on a model simulation40 and to 81 PBq based on observations;7 by 2011 the 137Cs inventory was 69 PBq.7 Considering that (i) the 134Cs/137Cs activity ratios in radionuclides emitted due to the FNPP1 accident were very close to unity (0.99 ± 0.03) and were very uniform spatially and temporally during the first month,11 the total amount of 137Cs released from the FNPP1 was almost the same as that of the 134Cs, and (ii) no 134Cs derived from global fallout existed before the FNPP1 accident, these findings indicated that distributions or inventory of 137Cs was regarded the same as that of 134Cs derived from the FNPP1. Then, the OICs137 inventories can be approximated to increase by about 20% to the North Pacific 137Cs inventory before the FNPP1 accident.
5. Conclusion
We applied optimal interpolation analysis to investigate the spatial and temporal distributions of 134Cs and 137Cs in the North Pacific Ocean following the FNPP1 accident until the end of May 2011.Extremely high activities of 134Cs and 137Cs in seawater were observed in the coastal region near the FNPP1. The transport of 134Cs and 137Cs from the coastal region near the FNPP1 to the open ocean around 40°N caused a decrease of the activities in the coastal region. The fact that the activities of 134Cs and 137Cs in the Central North Pacific Ocean waters were higher than those expected based on ocean physics was the result of atmospheric deposition.
We used the OI results to estimate the total inventory of 134Cs and 137Cs in the North Pacific Ocean. In the North Pacific Ocean, the total OICs134 inventory reached 15.3 ± 2.6 PBq. In these, the total OICs134 inventory in the coastal area near the FNPP1 was estimated to be 8.4 ± 2.6 PBq, the suggestion being that half of the total amount of 134Cs released into the North Pacific Ocean via direct discharge and atmospheric deposition was present in the coastal region until early April 2011. Our analysis indicated that the total OICs134 inventory in the coastal area near the FNPP1 was controlled by a combination of direct release, atmospheric deposition, and transport by the coastal current system. A leak of stagnant water induced by heavy rainfall may also have caused an increase of the inventory. After the direct discharge of contaminated water was stopped, the total 134Cs inventory in the coastal region near the FNPP1 decreased exponentially with a half-time of 4.2 ± 0.5 days and equaled about 2 ± 0.4 PBq by the middle of May 2011. A comparison with the total 137Cs inventory in the North Pacific Ocean before the FNPP1 accident indicated that the total 137Cs inventory derived from the FNPP1 accident increased the pre-existing inventory of radioactive cesium in the North Pacific by about 20%.
Acknowledgements
This research was financially supported by Grant-in-Aid for Scientific Research on Innovative Areas, “Interdisciplinary study on environmental transfer of radionuclides from the Fukushima Daiichi NPP Accident” (Project No. 25110511) of the Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT).References
- M. Aoyama, in Radionuclides in the Environment, ed. D. A. Atwood, John Wiley & Sons, UK, 2010, pp. 339–345 Search PubMed.
- D. Tsumune, M. Aoyama and K. Hirose, J. Geophys. Res., 2003, 108(C8), 3262, DOI:10.1029/2002jc001434.
- D. Tsumune, M. Aoyama and K. Hirose, J. Environ. Radioact., 2003, 69, 61–84 CrossRef CAS PubMed.
- H. Nakano, T. Motoi, K. Hirose and M. Aoyama, J. Geophys. Res., 2009, 115, C06015, DOI:10.1029/2009jc005640.
- Y. Inomata, M. Aoyama and K. Hirose, J. Environ. Monit., 2009, 11, 116–125 RSC.
- T. Watabe, S. Oikawa, N. Isoyama, C. Suzuki, J. Misonoo and S. Morizono, Sci. Total Environ., 2013, 463–464, 913–921 CrossRef CAS PubMed.
- M. Aoyama, D. Tsumune and Y. Hamajima, J. Radioanal. Nucl. Chem., 2012, 296, 535–539 CrossRef.
- M. Aoyama, D. Tsumune, M. Uematsu, F. Kondo and Y. Hamajima, Geochem. J., 2012, 46, 321–325 CrossRef CAS.
- M. Aoyama, Y. Hamajima, M. Hult, M. Uematsu, E. Oka, D. Tsumune and Y. Kumamoto, J. Oceanogr., 2015 DOI:10.1007/s10872-015-0335-z.
- M. Aoyama, M. Kajino, T. Tanaka, T. T. Sekiyama, D. Tsumune, T. Tsubono, Y. Hamajima, Y. Inomata, T. Gamo, M. Uematsu, T. Kawano, A. Murata, Y. Kumamoto and M. Fukasawa, J. Oceanogr., 2015 DOI:10.1007/s10872-015-0332-2.
- K. O. Buesseler, M. Aoyama and M. Fukasawa, Environ. Sci. Technol., 2011, 45, 9931–9935 CrossRef PubMed.
- K. O. Buesseler, S. R. Jayne, N. S. Fisher, I. I. Rypina, H. Baumann, Z. Baumann, C. F. Breier, E. M. Douglass, J. George and A. M. Macdonald, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 5984–5988 CrossRef CAS PubMed.
- M. Inoue, H. Kofuji, S. Nagao, M. Yamamoto, Y. Hamajima, K. Yoshida, K. Fujimoto, T. Takada and Y. Iso, J. Environ. Radioact., 2012, 109, 45–51 CrossRef CAS PubMed.
- M. Inoue, H. Kofuji, Y. Hamajima, S. Nagao, K. Yoshida and M. Yamamoto, J. Environ. Radioact., 2012, 111, 116–119 CrossRef CAS PubMed.
- M. Honda, T. Aono, M. Aoyama, Y. Hamajima, H. Kawakami, M. Kitamura, Y. Masumoto, Y. Miyazawa, M. Takigawa and T. Saino, Geochem. J., 2012, 46, e1–e9 CrossRef.
- H. Kaeriyama, D. Ambe, Y. Shimizu, K. Fujimoto, T. Ono, S. Yonezaki, Y. Kato, H. Matsunaga, H. Minami, S. Nakatsuka and T. Watanabe, Biogeosciences, 2013, 10(6), 4287–4295 CrossRef.
- D. Tsumune, T. Tsubono, M. Aoyama and K. Hirose, J. Environ. Radioact., 2012, 111, 100–108 CrossRef CAS PubMed.
- D. Tsumune, T. Tsubono, M. Aoyama, M. Uematsu, K. Misumi, Y. Maeda, Y. Yoshida and Y. Hayami, Biogeosciences, 2013, 10, 5601–5617 Search PubMed.
- Y. Miyazawa, Y. Masumoto, M. Sergey, S. M. Varlamov and T. Miyama, Cont. Shelf Res., 2012, 50–51, 16–29 CrossRef.
- P. Bailly du Bois, P. Laguionie, P. Boust, D. Korsakissok, D. Didier and B. Fievet, J. Environ. Radioact., 2012, 114, 2–9 CrossRef CAS PubMed.
- C. Estournel, E. Bosc, M. Bocquet, C. Ulses, P. Marsaleix, V. Winiarek, I. Osvath, C. Nguyen, T. Duhaut, F. Lyard, H. Michaud and F. Auclair, J. Geophys. Res., 2012, 117, C11014, DOI:10.1029/2012jc007933.
- Y. Masumoto, Y. Miyazawa, D. Tsumune, T. Tsubono, T. Kobayashi, H. Kawamura, C. Estournel, P. Marsaleix, L. Lanerolle, A. Mehra and Z. D. Garraffo, Elements, 2012, 8, 207–212 CrossRef CAS.
- K. Bergman, Multivariate analysis of temperature and winds using optimum interpolation, Mon. Weather Rev., 1979, 107, 1423–1443 CrossRef.
- Y. Inomata, M. Aoyama, D. Tsumune, T. Motoi and H. Nakano, J. Environ. Monit., 2012, 14, 3146–3155 RSC.
- H. Akima, J. Assoc. Comput. Mach., 1970, 17, 589–602 CrossRef.
- Y. Nakamura, Fukushima Suisan Shikenjo Reseach Report, 1991, pp. 1–118, in Japanese Search PubMed.
- GODAS, http://www.cpc.ncep.noaa.gov/products/GODAS, accessed March 2015.
- S. Hosoda, T. Ohira, K. Sato and T. Suga, J. Oceanogr., 2010, 66, 773–787 CrossRef.
- Y. Inomata, M. Aoyama, K. Hirose, Y. Sanada, T. Torii, T. Tsubono, D. Tsumune and M. Yamada, J. Nucl. Sci. Technol., 2014, 51, 1059–1063 CrossRef CAS.
- TEPCO, http://www.tepco.co.jp/en/nu/fukushima-np/f1/smp/index-e.html, accessed March 2015.
- TEPCO, http://www.tepco.co.jp/en/nu/fukushima-np/interim/index-e.html, accessed March 2015.
- NOAA, http://www.star.nesdis.noaa.gov/corp/scsb/mspps/prod.html, accessed March 2015.
- N. Maximenco, P. Niiler, L. Centurioni, M.-H. Rio, O. Melnichenko, D. Chambers, V. Zlotnicki and B. Galperin, J. Atmos. Ocean. Tech., 2009, 26, 1910–1919 CrossRef.
- M. Chino, H. Nakayama, H. Nagai, H. Terada, G. Katada and H. Yamazawa, J. Nucl. Sci. Technol., 2011, 48, 1129–1134 CrossRef CAS.
- T. Doi, K. Masumoto, K. Toyoda, A. Tanaka, Y. Shibata and K. Hirose, J. Environ. Radioact., 2013, 122, 55–62 CrossRef CAS PubMed.
- K. Nishihara, I. Yamagishi, K. Yasuda, K. K. Tanaka, T. Kuno, S. Inada and Y. Gotoh, Trans. At. Energy Soc. Jpn., 2012, 11, 13–19 CrossRef CAS.
- H. Kawamura, T. Kobayashi, A. Furuno, T. In, Y. Ishikawa, T. Nakayama, S. Shima and T. Awaji, J. Nucl. Sci. Technol., 2011, 48, 1349–1356 CrossRef CAS.
- T. Kobayashi, H. Nagai, M. Chino and H. Kawamura, J. Nucl. Sci. Technol., 2013, 50, 255–264 CrossRef CAS.
- G. Smith, J. Radiol. Prot., 2014, 34, 725 CrossRef PubMed.
- M. Aoyama, K. Hirose and Y. Igarashi, J. Environ. Monit., 2006, 8, 431–438 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5em00324e |
| This journal is © The Royal Society of Chemistry 2016 |