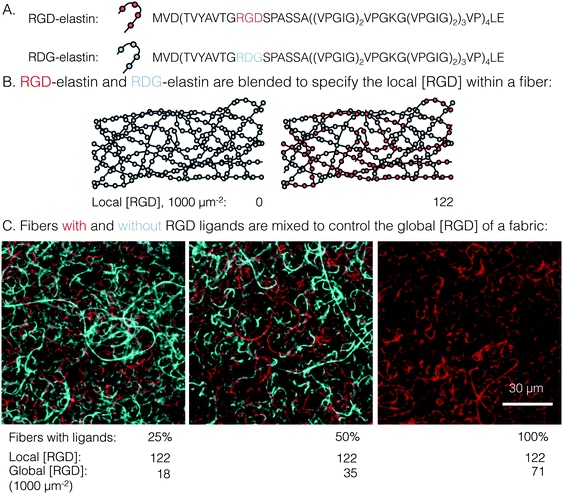
Use of protein-engineered fabrics to identify design rules for integrin ligand clustering in biomaterials†
Patrick L.
Benitez‡
a,
Shamik
Mascharak‡
a,
Amy C.
Proctor
b and
Sarah C.
Heilshorn
*c
aDepartment of Bioengineering, Stanford University, 476 Lomita Mall, Stanford, CA 94305, USA. E-mail: patrick.benitez@stanford.edu; shamikm@alumni.stanford.edu
bDepartment of Chemical Engineering, Stanford University, 476 Lomita Mall, Stanford, CA 94305. E-mail: aproctor@stanford.edu
cDepartment of Materials Science and Engineering, Stanford University, 476 Lomita Mall, Stanford, CA 94305. E-mail: heilshorn@stanford.edu
First published on 11th December 2015
Abstract
While ligand clustering is known to enhance integrin activation, this insight has been difficult to apply to the design of implantable biomaterials because the local and global ligand densities that enable clustering-enhanced integrin signaling were unpredictable. Here, two general design principles for biomaterial ligand clustering are elucidated. First, clustering ligands enhances integrin-dependent signals when the global ligand density, i.e., the ligand density across the cellular length scale, is near the ligand’s effective dissociation constant (KD,eff). Second, clustering ligands enhances integrin activation when the local ligand density, i.e., the ligand density across the length scale of individual focal adhesions, is less than an overcrowding threshold. To identify these principles, we fabricated a series of elastin-like, electrospun fabrics with independent control over the local (0 to 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ligands μm−2) and global (0 to 71
000 ligands μm−2) and global (0 to 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ligand μm−2) densities of an arginine–glycine–aspartate (RGD) ligand. Antibody blocking studies confirmed that human umbilical vein endothelial cell adhesion to these protein-engineered biomaterials was primarily due to αVβ3 integrin binding. Clustering ligands enhanced cell proliferation, focal adhesion number, and focal adhesion kinase expression near the ligand's KD,eff of 12
000 ligand μm−2) densities of an arginine–glycine–aspartate (RGD) ligand. Antibody blocking studies confirmed that human umbilical vein endothelial cell adhesion to these protein-engineered biomaterials was primarily due to αVβ3 integrin binding. Clustering ligands enhanced cell proliferation, focal adhesion number, and focal adhesion kinase expression near the ligand's KD,eff of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2. Near this global ligand density, cells on ligand-clustered fabrics behaved similarly to cells grown on fabrics with significantly larger global ligand densities but without clustering. However, this enhanced ligand-clustering effect was not observed above a threshold cut-off concentration. At a local ligand density of 122
000 RGD μm−2. Near this global ligand density, cells on ligand-clustered fabrics behaved similarly to cells grown on fabrics with significantly larger global ligand densities but without clustering. However, this enhanced ligand-clustering effect was not observed above a threshold cut-off concentration. At a local ligand density of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, cell division, focal adhesion number, and focal adhesion kinase expression were significantly reduced relative to fabrics with identical global ligand density and lesser local ligand densities. Thus, when clustering results in overcrowding of ligands, integrin receptors are no longer able to effectively engage with their target ligands. Together, these two insights into the cellular responses to ligand clustering at the cell–matrix interface may serve as design principles when developing future generations of implantable biomaterials.
000 RGD μm−2, cell division, focal adhesion number, and focal adhesion kinase expression were significantly reduced relative to fabrics with identical global ligand density and lesser local ligand densities. Thus, when clustering results in overcrowding of ligands, integrin receptors are no longer able to effectively engage with their target ligands. Together, these two insights into the cellular responses to ligand clustering at the cell–matrix interface may serve as design principles when developing future generations of implantable biomaterials.
Insight, innovation, integrationThe Technological Innovation of independently specifying ligand densities on the local scale of receptor clusters and the global scale of the entire cell was realized by combining a novel electrospinning process with a family of recombinant elastin-like proteins. The Integration of (1) engineered biomaterials and (2) quantitative analysis of integrin signaling provides Biological Insight into how ligand density and clustering interact to regulate cell behavior. At different regimes of local and global surface densities, microscale ligand clustering can either enhance or inhibit focal adhesion formation and turnover, thereby altering integrin signaling. |
Introduction
Integrins, a family of cell-displayed receptors, bind ligands in the extracellular matrix, enabling cell–matrix interactions such as cellular adhesion, signaling, and migration. Most commonly, peptide or protein ligands containing the arginine-glycine-aspartate (RGD) amino acid sequence are covalently tethered to implantable biomaterials in a uniform distribution.1,2 By changing the surface concentration of ligands over the cellular length scale, various “global” ligand densities may be achieved. Quantitative control of global ligand density is essential to promote potentially therapeutic cell–matrix interactions in many applications, including vascular grafts,3 bone grafts,4 wound dressings,5 and injectable drug depots.6 In addition to these studies on global ligand density, there is interest in controlling the surface concentration of ligands over the length scale of sub-cellular focal adhesion complexes, termed the “local” ligand density. Substrates with regions of local ligand density that are higher than the global ligand density are commonly referred to as having “clustered ligands”, since the ligands are grouped together into smaller, isolated areas.7–10 Clustering integrin ligands is thought to affect signal transduction by modulating formation of focal adhesions, the biochemically active complexes of many integrins and associated molecules at the cell-material interface. However, it is difficult to apply this concept to implantable materials because the local and global ligand densities that enable clustering-enhanced integrin signaling are unknown.While clustering-enhanced integrin activation has been observed in vitro, the global enhancement regime varies across RGD ligand-presenting materials. For example, osteoblasts11 and fibroblasts12,13 on ligand-presenting colloidal materials only adhered below a lower global density threshold of 190 RGD μm−2 if ligands were locally clustered (300 RGD μm−2). However, fibroblasts on ligand-presenting substrates prepared by electron beam lithography showed no sensitivity to clustering at a nearly equivalent global density of 200 RGD μm−2.14 Seemingly contradictory results were observed from preosteoblasts on RGD-presenting alginate hydrogels, where clustering at global densities up to 800 RGD μm−2 resulted in inhibition of integrin-dependent signaling.15 Furthermore, there has been disagreement on the lowest allowable local density for integrin activation. Arnold et al. found a local density ranging from 190 to 300 RGD μm−2 that promoted integrin activation and cell-ECM adhesion.11 However, Massia and Hubbell found that a much lesser local density of 50 RGD μm−2 was sufficient for fibroblast focal contact formation on non-adhesive glass substrates with grafted GRGDY peptide.16
We hypothesized that these incongruities could be resolved by showing that clustering-enhanced integrin activation requires global ligand density near the ligand's effective dissociation constant (KD,eff), a material-specific parameter that depends on ligand type, valency, and accessibility. Integrins are known to diffuse laterally in the plane of the cell membrane, accumulating in regions of sufficiently clustered ligands and becoming close enough to interact and form stable focal adhesion complexes.17 Integrins cannot dimerize to form a complex capable of enhancing ligand-dependent signaling if they are separated by too large a distance, nominally known as the “interaction radius”.17 Activation of integrins requires both integrin–ligand and integrin–integrin interactions, which can be competitive or synergistic depending on overall ligand presentation.17 At very low global ligand densities, most integrins should not be able to bind ligands due to poor availability. Thus, the integrins will remain randomly distributed across the cell membrane, limiting focal adhesion formation and associated cell survival signaling. At very high global ligand densities, most integrins can bind ligands while remaining randomly distributed across the membrane, due to excessive ligand availability. Ligand binding constrains lateral diffusion of integrins in the membrane, preventing integrin–integrin interactions and again limiting focal adhesion formation. However, at synergistic intermediate ligand densities, diffusion across the membrane results in integrins adopting the clustered ligand organization, becoming close enough to dimerize while binding available ligands, enhancing integrin activation, and promoting maturation of nascent adhesions into stable focal adhesion complexes. We reasoned that this synergistic intermediate regime would correlate with global ligand densities near the ligand's KD,eff, the system's half-maximal saturation point for ligand–integrin binding. We further hypothesized that very high levels of local ligand clustering might lead to ligand overcrowding and a biphasic effect on integrin activation due to steric interference between neighboring integrins.17,18
To test these hypotheses regarding clustered ligand distributions, a custom electrospinning process was developed to produce engineered protein fabrics with precisely controlled global and local ligand densities. Electrospun fabrics comprised of recombinant proteins have been proposed as a biomaterials platform to promote in situ adhesion and proliferation of endothelial cells in several vascular engineering applications.19–21 Several elastin-like proteins (ELPs), a family of recombinant proteins defined by tandem repeats of the elastin-like amino acid sequence valine–proline–glycine–X–glycine (VPGXG, where X is any amino acid except proline), have been designed to include a variety of cell-adhesive ligands, thereby enabling more precise presentation of cell-adhesive ligands than can be achieved using naturally occurring matrix proteins.22 Previously, we reported the electrospinning of aqueous solutions of ELPs containing the RGD integrin ligand into stable, cell-adhesive fabrics (bulk tensile modulus ∼60 kPa) comprised of individual ribbon-like fibers (width ∼1.5 μm, thickness ∼200 nm).23 Genetically engineering an otherwise identical, control ELP with swapped positioning of the glycine (G) and aspartate (D) amino acid residues (RDG) has been shown in numerous studies to yield a non-cell-adhesive material.22,24–26 In this work, the local ligand density was controlled by blending together these two ELP variants (RGD and RDG), yielding local ligand densities of 0 to 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 within a single, ribbon-like fiber. To specify global ligand density, fibers with ligands (i.e. blends of RGD and RDG variants) were mixed in a precise ratio with fibers completely devoid of ligands (i.e. RDG variant only) to yield composite ELP fabrics with global ligand densities spanning 0 to 71
000 RGD μm−2 within a single, ribbon-like fiber. To specify global ligand density, fibers with ligands (i.e. blends of RGD and RDG variants) were mixed in a precise ratio with fibers completely devoid of ligands (i.e. RDG variant only) to yield composite ELP fabrics with global ligand densities spanning 0 to 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 (Fig. 1 and Table S1, ESI†). A similar strategy was previously employed in a hydrogel system using alginate polymers with and without covalently attached RGD ligands.15 Our approach differed in two ways. First, the range of local and global densities achieved here spanned and exceeded those of previous studies, so as to explore the full array of ligand clustering-dependent responses. Second, the local mechanical and topographical properties of ELP fabrics significantly differ from those of planar hydrogel surfaces. Our combination of genetic protein engineering and advanced electrospinning enabled the fabrication of ELP fabrics with a broad range of independently tunable local and global ligand densities.
000 RGD μm−2 (Fig. 1 and Table S1, ESI†). A similar strategy was previously employed in a hydrogel system using alginate polymers with and without covalently attached RGD ligands.15 Our approach differed in two ways. First, the range of local and global densities achieved here spanned and exceeded those of previous studies, so as to explore the full array of ligand clustering-dependent responses. Second, the local mechanical and topographical properties of ELP fabrics significantly differ from those of planar hydrogel surfaces. Our combination of genetic protein engineering and advanced electrospinning enabled the fabrication of ELP fabrics with a broad range of independently tunable local and global ligand densities.
Materials and methods
Expression and purification of elastin-like proteins
As previously reported,22,24 ELP was expressed and purified using standard recombinant technology. Genes encoding the desired protein sequences were assembled within pJ401 plasmids using gene assembly (DNA 2.0) and traditional recombinant techniques. Escherichia coli strain BL21 Star (DE3) pLysS were transformed with plasmid and used to express ELP. Bacteria were cultured to optical density (wavelength 600 nm, OD600) of 0.6 in baffled flasks on a shaker (300 rpm, 37 °C, LB medium, 1.5 L). The culture was used to inoculate a fed-batch fermenter (Bioengineering, Inc.), grown to OD600 of 3 on batch medium (37 °C, pH 6.8, Terrific Broth plus 20 g L−1 glucose, 30 L), and grown to OD600 of 20 on feed (500 g L−1 glucose, 13 g L−1 ammonium chloride, 5.5 g L−1 magnesium sulfate, 9 mL min−1) before inducing expression with 1 mM β-isopropyl thiogalactoside. Expression (34 °C) was allowed to continue for 2 days. The wet cell pellet was resuspended in TEN Buffer (1 g mL−1, 1 mM PMSF), subjected to three freeze–thaw cycles, and digested with DNAse I. The suspension was adjusted to pH 3 with 5 N HCl, incubated at 4 °C for 1 h, and centrifuged at 4 °C (1 h, 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g). The supernatant was harvested, and NaCl was added to a final concentration of 0.2 M. This solution was agitated at 40 °C, shaking for 3 h, and centrifuged at 40 °C (1 h, 22
000 g). The supernatant was harvested, and NaCl was added to a final concentration of 0.2 M. This solution was agitated at 40 °C, shaking for 3 h, and centrifuged at 40 °C (1 h, 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g). After decanting, the pellet was resuspended in water (0.2 g mL−1), agitated overnight at 4 °C, and centrifuged at 4 °C (1 h, 8
000 g). After decanting, the pellet was resuspended in water (0.2 g mL−1), agitated overnight at 4 °C, and centrifuged at 4 °C (1 h, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g). Warm (40 °C, 0.2 M NaCl, 8000 g) and cold (4 °C, 8000 g) purification cycles were each repeated five times. The final supernatant was desalted by dialyzing into water (4 °C, 3000 MWCO) and lyophilized. Protein yield of ELP was approximately 200 mg L−1.
000 g). Warm (40 °C, 0.2 M NaCl, 8000 g) and cold (4 °C, 8000 g) purification cycles were each repeated five times. The final supernatant was desalted by dialyzing into water (4 °C, 3000 MWCO) and lyophilized. Protein yield of ELP was approximately 200 mg L−1.
Electrospinning and crosslinking of mixed-fiber fabrics
Recombinant ELP was dissolved overnight in deionized water (34% w/w ELP, 4 °C). To produce fabrics, solutions were electrospun at room temperature (electric field = 1 kV cm−1, gap from extrusion tip to collector = 15 cm, extrusion rate = 250 μL h−1, and deposition time = 70 min) onto aminated glass coverslips (diameter 12 mm). Aminated glass was prepared by reacting glass coverslips in silanization solution (10 μM 3-aminopropyltrimethoxysilane and 5% v/v acetic acid in 50 mL) for 30 min, sequentially rinsing with pure ethanol and water, and drying. For mixed-fiber fabrics, two ELP solutions were exchanged on the electrospinning unit in 12-min cycles: one containing a blend of RGD- and RDG-elastin (fibers with ligands, Table S1, ESI†) and one strictly of RDG-elastin (fibers without ligands). The time allotted to each solution varied according to the desired percentage of fibers with RGD ligands (Table S1, ESI†). To reduce pre-steady state artifacts, solutions were allowed to run 2 min before exposing to the electric field and beginning fiber deposition.Proof-of-principle studies for mixed-fiber fabrics were done by electrospinning one 12-min cycle of fibers with and without ligands. Fibers were spun from solutions with 0.5% of ELP replaced with ELP–fluorophore conjugate. Conjugation was achieved by reacting DyLight fluorophore/N-hydroxysuccinimide ester (Peirce) with ELP in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio (0.05 M sodium borate buffer, 4 volumes, pH 8.5, 4 °C, overnight). Unreacted dye was removed by dialysis to deionized water (4 °C, 3000 MWCO) followed by lyophilization to remove water.
1 molar ratio (0.05 M sodium borate buffer, 4 volumes, pH 8.5, 4 °C, overnight). Unreacted dye was removed by dialysis to deionized water (4 °C, 3000 MWCO) followed by lyophilization to remove water.
After electrospinning, fabrics on coverslips were cut from the rest of the deposited fabric in 12-mm diameter circles and crosslinked with glutaraldehyde as previously described.23 Fabrics were sterilized overnight by incubating in 70% ethanol and irradiating with ultraviolet light. Before culture, exposed glass was blocked (4% w/v bovine serum albumin (BSA), 37 °C, 2 h). For measurements of fiber width and thickness, hydrated fabrics were imaged with a Leica SPE confocal microscope using autofluorescence of crosslinked ELP fibers. Fiber width and thickness were measured using ImageJ; three independent fabrications were assessed to determine mean and standard error for fibers corresponding to each local ligand density.
Calculation of ligand density
To estimate local ligand density, swell ratio and fiber volume fraction were measured. Swell ratio (defined as wet mass:dry mass) was determined to be 12.0 ± 0.3 by dividing the mass of fully hydrated fabrics by that of desiccated fabrics. This value was converted to average volumetric density of protein in fabric using the densities of water (1 g mL−1) and ELP (1.35 g mL−1). The volume fraction of fibers in fabric (0.58 ± 0.04 v/v) was measured in ImageJ from confocal micrographs taken with a Leica SPE confocal microscope. The density of protein in a fiber was calculated by dividing the density of protein in fabric by volume fraction of fibers in fabric. Volumetric ligand density was then calculated by taking the following into account: the fraction of RGD-elastin within ELP fibers (Table S1, ESI†), ligands per RGD-elastin molecule (4), and the molecular weight of RGD-elastin (33.2 kDa). Surface ligand density was estimated from volumetric ligand density by assuming that cells could penetrate into the fabric no further than the extracellular length of a heterodimeric integrin (21 nm). Global ligand density was estimated by multiplying local ligand density by the fiber:fabric volume fraction and the fraction of fibers with ligands (Table S1, ESI†). This assumed that the fiber:fabric surface fraction is identical to the volume fraction at the cell-fabric interface. See ESI,† S1 for example calculations.Cell culture and quantification
Human umbilical vein endothelial cells (HUVEC, passages 2–5, Lonza, Walkersville) were used to study cellular responses to ligand clustering. Cell number was measured by quantifying DNA using CyQUANT (Life Technologies) according to manufacturer's protocol. For measurements of initial attachment at 16 h, HUVEC were seeded at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−2, and DNA was quantified after standard cell culture (37 °C, 5% CO2). Mean and standard error were calculated from six cultures (three cultures for each of two independent repeats).
000 cm−2, and DNA was quantified after standard cell culture (37 °C, 5% CO2). Mean and standard error were calculated from six cultures (three cultures for each of two independent repeats).
Integrin blockade
For analysis of ligand interactions with specific integrins, disassociated HUVEC were pre-treated (30 min) with and cultured (16 h) in the presence of integrin-blocking antibodies (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 dilution, Millipore). Cells were seeded at 20
50 dilution, Millipore). Cells were seeded at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−2. Antibodies against integrins αV (clone 272-17e6), αVβ3 (clone MAb 1969), αVβ5 (clone MAb 1961z), and β1 (clone p4c10) were used. After culture, cells on fabrics were fixed (4% paraformaldehyde) and labeled with wheat germ agglutinin, DyLight 550 conjugate for sialic acid, and DAPI for the nucleus. Projected area of 40 cells per condition was measured in ImageJ to calculate mean and standard error.
000 cm−2. Antibodies against integrins αV (clone 272-17e6), αVβ3 (clone MAb 1969), αVβ5 (clone MAb 1961z), and β1 (clone p4c10) were used. After culture, cells on fabrics were fixed (4% paraformaldehyde) and labeled with wheat germ agglutinin, DyLight 550 conjugate for sialic acid, and DAPI for the nucleus. Projected area of 40 cells per condition was measured in ImageJ to calculate mean and standard error.
Immunofluorescence
For determining cell spreading, elongation, division, and vinculin-based focal adhesion formation, standard immunofluorescence protocols were used. To control for differences in cell–cell interactions that may result from differences in cell proliferation rates on different surfaces, cells were sampled from the periphery of HUVEC monolayers. To create discrete monolayers, fabrics on coverslips were dried under laminar air flow for 4 h after blocking glass with BSA, and HUVEC were placed on dried fabrics in three discrete 4 μL drops of 3000 HUVEC μL−1 cell suspension, as previously described.27 After 30 min setting (37 °C, 5% CO2), monolayers were immersed in medium and then cultured for 2 days. Cells were fixed (4% w/v paraformaldehyde), permeabilized (0.2% v/v Triton X-100), and blocked (1.5% w/v BSA). Ki-67 (polyclonal, Cell Signaling Technologies) and vinculin (clone hVin-1, Abcam) were immunostained. Secondary antibodies (Sigma) and counterstains for actin (phalloidin, Sigma) and the nucleus (NucBlue, LifeTechnologies) were applied. Micrographs were taken on a Leica SPE confocal microscope. Cells were sampled from four 180 μm-by-180 μm view frames on the periphery of the monolayer. Cell axial ratio, projected area, and number of vinculin-puncta were measured in ImageJ. Images of segmented vinculin puncta were generated in MATLAB with Image Processing Toolbox (see S2, ESI†). To calculate mean and standard error, forty cells per condition were assessed for projected area; twenty cells per condition were assessed for focal adhesion number. For cell division, the fraction of Ki-67 positive nuclei was calculated for each condition from 300 cells over two independent repeats.Immunoblotting
HUVEC monolayers were seeded onto fabrics (120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 HUVEC) and cultured for two days. After culture, fabrics were gently detached from coverslips and placed into 90 μL of lysis buffer (M-PER, Peirce) supplemented with protease inhibitors (Halt Cocktail, Thermo Scientific), phosphatase inhibitors (Cocktails 2 and 3, Sigma), sodium dodecyl sulfate, and dithiothreitol. Fabrics were boiled and sonicated. Centrifugation was used to remove fabric from cell lysate before applying standard immunoblotting protocols and antibodies (Cell Signaling Technologies) to detect proteins of interest. Densitometry was performed using ImageJ. Intensities of FAK and pFAK-397 bands were normalized to intensity of glyceraldehyde 3-phosphate dehydrogenase bands. To calculate mean and standard error, three cultures per condition were analyzed.
000 HUVEC) and cultured for two days. After culture, fabrics were gently detached from coverslips and placed into 90 μL of lysis buffer (M-PER, Peirce) supplemented with protease inhibitors (Halt Cocktail, Thermo Scientific), phosphatase inhibitors (Cocktails 2 and 3, Sigma), sodium dodecyl sulfate, and dithiothreitol. Fabrics were boiled and sonicated. Centrifugation was used to remove fabric from cell lysate before applying standard immunoblotting protocols and antibodies (Cell Signaling Technologies) to detect proteins of interest. Densitometry was performed using ImageJ. Intensities of FAK and pFAK-397 bands were normalized to intensity of glyceraldehyde 3-phosphate dehydrogenase bands. To calculate mean and standard error, three cultures per condition were analyzed.
Statistical analysis
Given the biochemical nature of receptor–ligand binding,28 it was appropriate to fit cell responses to global ligand density to the rectangular hyperbola Y = a*L/(L + KD,eff), where L is the global ligand density, KD,eff is the bulk effective dissociation constant, and a is a scaling factor. A derivation of the hyperbolic fit equation is given below:First, we assumed that integrin–ligand interactions followed the equilibrium expression R + L ↔ RL, where ligands were homogeneously distributed and R denotes the concentration of unbound integrin receptors, L is the concentration of unbound ligand, and RL is the concentration of bound receptor–ligand complexes. So, the equilibrium dissociation constant KD = R*L/RL. Second, we assumed that the total number of receptors Rtot = R + RL. Thus, the fraction of receptor–bound ligands for changing ligand concentration was given by the expression 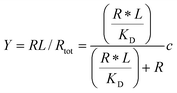 . Multiplying the top and bottom of the expression by KD/R gave
. Multiplying the top and bottom of the expression by KD/R gave 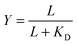 . Finally, we applied a scaling factor a, to give the final hyperbolic equation
. Finally, we applied a scaling factor a, to give the final hyperbolic equation 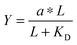 . We reasoned that all cell responses that are known to linearly depend on integrin engagement, such as cell spreading, would follow this same hyperbolic function. To highlight the fact that the hyperbolic fitting is performed on cell response data (as opposed to data that directly quantifies the number of bound receptor–ligand complexes), we have replaced KD with an effective parameter, KD,eff. While KD is the thermodynamic equilibrium dissociation constant for a specific receptor–ligand complex, KD,eff is an effective parameter of cell response for a specific cell–biomaterial interaction.
. We reasoned that all cell responses that are known to linearly depend on integrin engagement, such as cell spreading, would follow this same hyperbolic function. To highlight the fact that the hyperbolic fitting is performed on cell response data (as opposed to data that directly quantifies the number of bound receptor–ligand complexes), we have replaced KD with an effective parameter, KD,eff. While KD is the thermodynamic equilibrium dissociation constant for a specific receptor–ligand complex, KD,eff is an effective parameter of cell response for a specific cell–biomaterial interaction.
Significance and KD,eff of hyperbolic trends were calculated as follows. Data were first translated by a baseline amount in either input (global density) or output (cell response) variable. This was justified by noting that HUVEC exposed to no ligands have a non-zero projected area, rate of proliferation, etc. Next, the hyperbolic data were linearized by plotting the inverses of both axes and fit to the linear trend line (1/Y) = A + B*(1/L). The intercept A is the inverse of the scaling factor a and the slope B is the inverse of KD,eff. Regarding cell spreading, for example, a simpler direct linear regression would result in a quantitatively worse fit (R2 = 0.61 versus R2 = 0.83 for the linear transform). Direct linear regression is also a qualitatively poor fit, producing a systematic pattern in residuals. Differences between means were detected by Student's t-test. All error bars are standard error of the mean.
Results and discussion
Decoupling local and global ligand densities in electrospun fabrics
A novel electrospun fabric was employed to determine the biomaterial parameters that enable enhanced integrin signaling in response to local ligand clustering. To decouple local and global ligand densities, the classic electrospinning process was modified at two points. First, local ligand density on individual electrospun fibers was specified by precisely blending two ELP variants in the fiber precursor solution. Expression, purification, and characterization of the ELP variants in this study, RGD- and RDG-elastin, were previously reported.22,24 Both ELP variants (33.2 kDa) contained 60 repeats of an elastin-like pentapeptide. RGD-elastin contained four extended integrin ligands that were derived from residues 1517 through 1530 of human fibronectin and were evenly spaced within the ELP amino acid sequence. On the other hand, RDG-elastin contained scrambled, non-cell-adhesive ligands in which the aspartate and glycine residues in the minimally active tripeptide were reversed, but was otherwise identical. This change in amino acid sequence rendered the protein inactive to integrins.22,24–26 Varying the fraction of RGD-elastin from 0% to 50% of total ELP within the precursor solution (the remaining fraction of ELP was RDG-elastin) produced fibers with a theoretical average local ligand density from 0 to 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, a range that encompassed potentially interesting ligand densities explored in other studies of integrin engagement with biomaterials.11–14,16,29
000 RGD μm−2, a range that encompassed potentially interesting ligand densities explored in other studies of integrin engagement with biomaterials.11–14,16,29
Global and local ligand densities were varied independently to produce an array of clustered ligand distributions. Fabrics with varied global ligand densities but identical local ligand density were fabricated by mixing fibers with and without RGD ligands. To illustrate, fluorophore-labeled fibers with local ligand densities of 0 (i.e. pure RDG-elastin) and 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 (50% RGD-elastin and 50% RDG-elastin) were mixed (Fig. 1). Fabrics were produced with identical local ligand densities (122
000 RGD μm−2 (50% RGD-elastin and 50% RDG-elastin) were mixed (Fig. 1). Fabrics were produced with identical local ligand densities (122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 on fibers that contain ligands) and varied global ligand densities (18
000 RGD μm−2 on fibers that contain ligands) and varied global ligand densities (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 35
000, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 71
000, and 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2; corresponding to 25%, 50%, and 100% fibers containing ligands, respectively). Fabrics with other local and global ligand densities were prepared analogously (Table S1, ESI†). Alternating precursor solutions during electrospinning had no obvious effects on fiber morphology, and fibers were randomly distributed (Fig. 1, bottom). Fabrics were well-mixed with no discrete layers of particular fibers noted, owing to their slow vertical accumulation over 70 minutes of electrospinning. Consistent with previous characterization of crosslinked, electrospun ELP fabrics,23 fibers were ribbon-like with a width of 1.5 ± 0.2 μm and thickness of 200 ± 10 nm, as measured from confocal micrographs. No significant variations in fiber width were observed across all of the different local ligand densities tested (Fig. S1, ESI†).
000 RGD μm−2; corresponding to 25%, 50%, and 100% fibers containing ligands, respectively). Fabrics with other local and global ligand densities were prepared analogously (Table S1, ESI†). Alternating precursor solutions during electrospinning had no obvious effects on fiber morphology, and fibers were randomly distributed (Fig. 1, bottom). Fabrics were well-mixed with no discrete layers of particular fibers noted, owing to their slow vertical accumulation over 70 minutes of electrospinning. Consistent with previous characterization of crosslinked, electrospun ELP fabrics,23 fibers were ribbon-like with a width of 1.5 ± 0.2 μm and thickness of 200 ± 10 nm, as measured from confocal micrographs. No significant variations in fiber width were observed across all of the different local ligand densities tested (Fig. S1, ESI†).
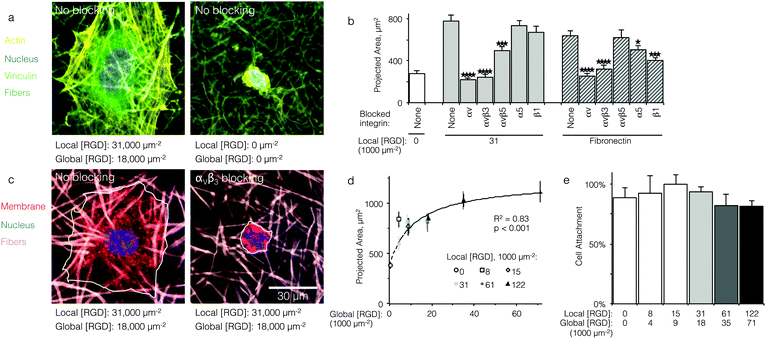
HUVEC spreading on RGD-containing ELP fabrics is mediated by the αVβ3 integrin
Qualitatively, HUVEC seeded on ELP fabrics without ligands remained compact and spherical (Fig. 2a). In contrast, HUVEC seeded on ELP fabrics containing RGD ligands adopted a well-spread morphology with numerous actin cytoskeletal stress fibers (Fig. 2a). Quantitatively, on fabrics containing a global ligand density of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, projected cell spread area was about three times larger than that of cells on fabrics without ligands (p < 10−4, n = 40 cells, Fig. 2b). Thus, HUVEC responded to the specific presence of RGD ligands within electrospun ELP fabrics. To identify the specific integrin receptors involved, HUVEC spreading was quantified on ELP fabrics and fibronectin-coated glass (positive control) in the presence and absence of function-blocking, anti-integrin antibodies. Blocking αv integrins broadly or the αvβ3 integrin specifically eliminated ligand-dependent spreading on ELP and fibronectin control surfaces (p < 10−4, n = 40 cells, Fig. 2c and d). Thus, spreading on RGD-presenting fabrics required the αVβ3 integrin. Blocking αVβ5 also reduced spreading on RGD-presenting ELP fabrics, although not to the same extent as blocking αVβ3 (p < 0.01, n = 40 cells). This result is consistent with the fact that the αVβ3 integrin requires no exogenous post-binding stimulation to mediate cell spreading, while the αVβ5 integrin requires activation of protein kinase C to mediate cell spreading and may therefore play an ancillary role to αVβ3.30,31 As expected, broadly targeting the β1 or α5 integrin sub-units on the control substrate fibronectin significantly reduced the projected cell area, consistent with the presence of the PHSRN synergy site in fibronectin, which is known to engage the α5β1 integrin in tandem with the RGD cell-binding domain.32 In contrast, blocking of the β1 or α5 integrin sub-units did not reduce projected cell area on RGD-presenting ELP fabrics, consistent with previous findings that RGD-based ligands alone are insufficient to engage β1 integrins.33,34
000 RGD μm−2, projected cell spread area was about three times larger than that of cells on fabrics without ligands (p < 10−4, n = 40 cells, Fig. 2b). Thus, HUVEC responded to the specific presence of RGD ligands within electrospun ELP fabrics. To identify the specific integrin receptors involved, HUVEC spreading was quantified on ELP fabrics and fibronectin-coated glass (positive control) in the presence and absence of function-blocking, anti-integrin antibodies. Blocking αv integrins broadly or the αvβ3 integrin specifically eliminated ligand-dependent spreading on ELP and fibronectin control surfaces (p < 10−4, n = 40 cells, Fig. 2c and d). Thus, spreading on RGD-presenting fabrics required the αVβ3 integrin. Blocking αVβ5 also reduced spreading on RGD-presenting ELP fabrics, although not to the same extent as blocking αVβ3 (p < 0.01, n = 40 cells). This result is consistent with the fact that the αVβ3 integrin requires no exogenous post-binding stimulation to mediate cell spreading, while the αVβ5 integrin requires activation of protein kinase C to mediate cell spreading and may therefore play an ancillary role to αVβ3.30,31 As expected, broadly targeting the β1 or α5 integrin sub-units on the control substrate fibronectin significantly reduced the projected cell area, consistent with the presence of the PHSRN synergy site in fibronectin, which is known to engage the α5β1 integrin in tandem with the RGD cell-binding domain.32 In contrast, blocking of the β1 or α5 integrin sub-units did not reduce projected cell area on RGD-presenting ELP fabrics, consistent with previous findings that RGD-based ligands alone are insufficient to engage β1 integrins.33,34
HUVEC spreading, but not attachment, is dependent on global RGD density
For comparison to more common studies, where ligands are homogeneously distributed (i.e., not clustered), we first evaluated endothelial cell responses to ELP fabrics with ligands present on every fiber. As with all studies of homogeneously distributed ligands, the total number of ligands per cell increased and average ligand spacing decreased concomitantly with global density. So, the effects of total ligand number and cell-scale ligand spacing could not be differentiated across these different “bulk” RGD densities. However, these data were useful for calculating the KD,eff value, since receptor–ligand binding curves are usually generated under the assumption of homogeneously distributed ligand. To infer the specific contribution of ligand clustering on integrin activation, we compared cell responses on ELP fabrics with identical global and varying local densities. For these conditions, each individual cell contacted the same average number of ligands, but those ligands were distributed across more or fewer clustered regions to vary the inter-ligand spacing.Consistent with previous studies, cell spreading on ELP fabrics with uniformly distributed ligands increased to a plateau value with respect to global ligand density (p < 0.001, Fig. 2d). This relationship indicates that integrin receptors were saturated with ligand within our experimental range, confirming our choice of global ligand densities as being appropriate for further study. We assume that integrin–ligand interactions in our system are described by the expression R + L ↔ RL, where R denotes the concentration of unbound integrin receptors, L is the concentration of unbound ligand, and RL is the concentration of bound receptor–ligand complexes. At equilibrium, the thermodynamic dissociation constant is given by KD = R*L/RL. Assuming that the total number of integrin receptors is kept constant, the hyperbolic function 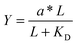 describes the fraction of integrins bound to ligand for varying global ligand density L (see Methods for derivation). We reasoned that all cell responses that are known to linearly depend on integrin engagement, such as cell spreading, would follow this same hyperbolic function. To highlight the fact that the hyperbolic fitting is performed on cell response data (as opposed to data that directly quantifies the number of bound receptor–ligand complexes), we replace KD with an effective parameter, KD,eff. While KD is the thermodynamic equilibrium dissociation constant for a specific receptor–ligand complex, KD,eff is an effective parameter of cell response for a specific cell-biomaterial interaction. Mathematical fitting of the data to this trend equation yielded a bulk, effective dissociation constant (KD,eff) of 12
describes the fraction of integrins bound to ligand for varying global ligand density L (see Methods for derivation). We reasoned that all cell responses that are known to linearly depend on integrin engagement, such as cell spreading, would follow this same hyperbolic function. To highlight the fact that the hyperbolic fitting is performed on cell response data (as opposed to data that directly quantifies the number of bound receptor–ligand complexes), we replace KD with an effective parameter, KD,eff. While KD is the thermodynamic equilibrium dissociation constant for a specific receptor–ligand complex, KD,eff is an effective parameter of cell response for a specific cell-biomaterial interaction. Mathematical fitting of the data to this trend equation yielded a bulk, effective dissociation constant (KD,eff) of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 1000 RGD μm−2. It is important to note that this is not the thermodynamic dissociation constant between a single integrin receptor and the engineered RGD ligand; in contrast, this is a bulk, cell-level dissociation constant that describes cell interactions with a given biomaterial. In practical terms, the KD,eff is the “half-max saturation point” of the system, or the ligand concentration for which 50% of the maximum cellular response is observed.
000 ± 1000 RGD μm−2. It is important to note that this is not the thermodynamic dissociation constant between a single integrin receptor and the engineered RGD ligand; in contrast, this is a bulk, cell-level dissociation constant that describes cell interactions with a given biomaterial. In practical terms, the KD,eff is the “half-max saturation point” of the system, or the ligand concentration for which 50% of the maximum cellular response is observed.
While the molecular KD commonly used to describe the affinity of a receptor to its ligand and the cell-level KD,eff are related, the distinction between them is critical when developing guidelines for biomaterials design. It has been widely reported that the biomaterial context in which a given engineered ligand is presented can have a large impact on the cell response.18,35–37 Thus, identical ligands (with identical receptor-level KD values) can result in a range of bulk, cell-level KD,eff values depending on confounding biomaterial properties (e.g., surface chemistry, topography, substrate stiffness). For this reason, we propose use of KD,eff as the relevant design parameter when developing ligand clustering strategies for engineered biomaterials. Further supporting this choice, ligand clustering was found to have little effect on cell spreading, and hence no effect on KD,eff (Fig. 2d). These data are consistent with the hypothesis that spreading primarily requires ligand–receptor binding without further downstream signaling.38 Thus, KD,eff is a quantitative measurement that is straight-forward to experimentally determine and that indicates the level of integrin–ligand binding for a given cell–biomaterial combination.
Interestingly, despite the significant decrease in cell spreading on fabrics without RGD ligands, initial cell attachment of HUVEC to ELP fabrics was consistent across all ligand densities tested. Based on DNA quantification after 16 h of culture, approximately 90% of cells originally seeded onto all fabrics were attached (Fig. 2e). This indicates that ELP fabrics enabled cell attachment regardless of ligand density, presumably due to the presence of microfibrous topography.39 In the absence of microfibrous topography, HUVEC attach poorly to ELP without cell-adhesive ligands, suggesting that fibers play an important role in cell attachment for this material system.40 This fortuitous result makes ELP electrospun fabrics an ideal platform for elucidating the ligand presentations that enable enhanced integrin signaling, as cell responses to changes in local ligand density are not confounded by changes in the number of attached cells.
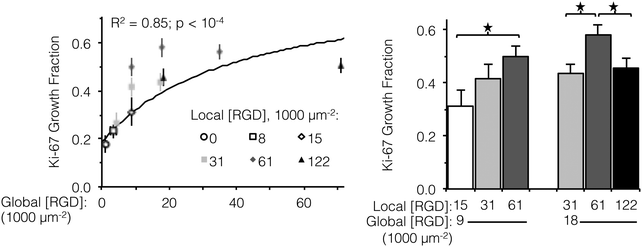
Ligand clustering enhances cell division at global ligand densities near KD,eff
Integrin engagement with the RGD ligand is known to stimulate endothelial cell proliferation.41 Similar to cell spreading, the fraction of HUVEC actively dividing (as determined by positive staining for nuclear Ki-67 at 16 h) followed a hyperbolic trend with global ligand density (Fig. 3, left, p < 10−4). Although cell division is well downstream from integrin–ligand binding, high global ligand density still resulted in behavior indicative of receptor saturation with a similar KD,eff of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000 RGD μm−2. Clustering of the ligands was observed to further increase HUVEC division on fabrics with a global ligand density near KD,eff. At global ligand densities of 9000 and 18
000 ± 2000 RGD μm−2. Clustering of the ligands was observed to further increase HUVEC division on fabrics with a global ligand density near KD,eff. At global ligand densities of 9000 and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, clustering ligands to achieve a local density of 61
000 RGD μm−2, clustering ligands to achieve a local density of 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 was found to significantly increase the percentage of cells undergoing division (Fig. 3, right). At sub-KD,eff global ligand densities, no significant responses to ligand clustering were observed. These observations were consistent with our hypothesis that enhanced integrin signaling via ligand clustering requires a global ligand density near KD,eff. At global densities below the KD,eff, integrins remained randomly distributed across the membrane regardless of local density due to low availability of ligands. At global densities above the KD,eff, integrins were again randomly distributed across the membrane, in this case due to high availability of ligands. Finally, at synergistic global densities near the KD,eff, integrins could undergo lateral diffusion in the membrane and cluster in regions of high local density, thereby enhancing integrin signaling. Further clustering ligands in this intermediate regime from a local density of 61
000 RGD μm−2 was found to significantly increase the percentage of cells undergoing division (Fig. 3, right). At sub-KD,eff global ligand densities, no significant responses to ligand clustering were observed. These observations were consistent with our hypothesis that enhanced integrin signaling via ligand clustering requires a global ligand density near KD,eff. At global densities below the KD,eff, integrins remained randomly distributed across the membrane regardless of local density due to low availability of ligands. At global densities above the KD,eff, integrins were again randomly distributed across the membrane, in this case due to high availability of ligands. Finally, at synergistic global densities near the KD,eff, integrins could undergo lateral diffusion in the membrane and cluster in regions of high local density, thereby enhancing integrin signaling. Further clustering ligands in this intermediate regime from a local density of 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 122
000 to 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 inhibited cell division on ELP fabrics that had a global ligand density of 18
000 RGD μm−2 inhibited cell division on ELP fabrics that had a global ligand density of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 (Fig. 3, right). Given that there was no inhibition of cell spreading at this high local density, we inferred that ligands were still active (i.e., available for integrin binding) but lost competence to induce signaling that would result in cell division. This hypothesis is consistent with previous simulations of integrin engagement on clustered ligands, where cell spreading correlated strongly with the total number of integrins bound.17 Thus, the lack of differences in cell spreading on overcrowded conditions implies that the number of integrin–ligand bonds was held constant and the RGD ligand was still available for integrin binding.
000 RGD μm−2 (Fig. 3, right). Given that there was no inhibition of cell spreading at this high local density, we inferred that ligands were still active (i.e., available for integrin binding) but lost competence to induce signaling that would result in cell division. This hypothesis is consistent with previous simulations of integrin engagement on clustered ligands, where cell spreading correlated strongly with the total number of integrins bound.17 Thus, the lack of differences in cell spreading on overcrowded conditions implies that the number of integrin–ligand bonds was held constant and the RGD ligand was still available for integrin binding.
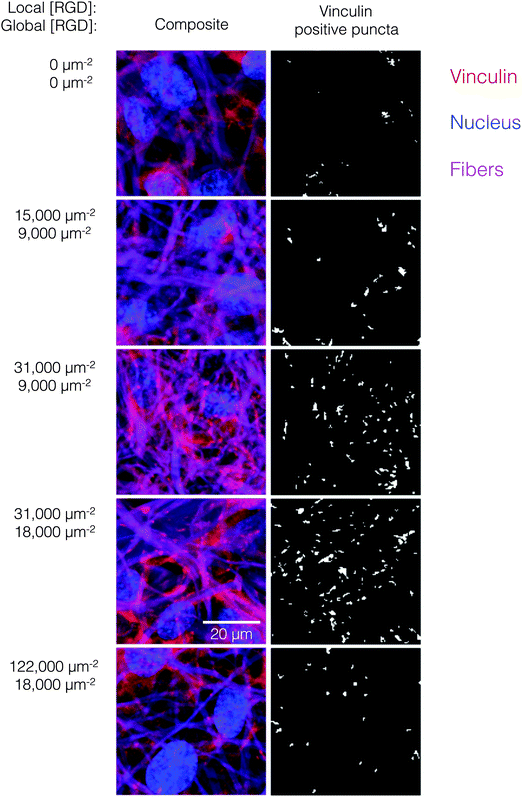
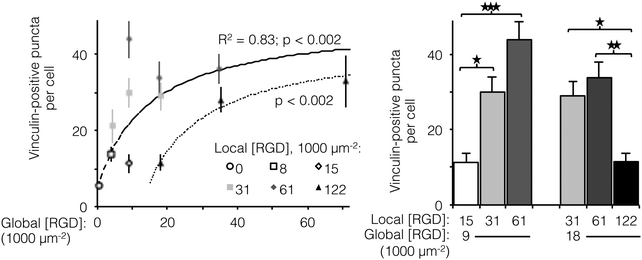
Ligand clustering enhances focal adhesion formation at global ligand densities near KD,eff
The number of focal adhesions between a cell and its substrate has been correlated to integrin-dependent signaling and cell-substrate adhesion force.42,43 To visualize focal adhesion distributions for HUVEC cultured on ELP fabrics with different global and local ligand densities, we immunostained for vinculin (an essential component of focal adhesions) and the cell nucleus (Fig. 4, left). Crosslinked ELP fibers were fluorescent in every channel without any added fluorophores; therefore MATLAB analysis was employed to identify vinculin puncta (Fig. 4, right, see ESI,† for detailed method). On fabrics without RGD ligands, very few vinculin structures were observed. As the global ligand density approached KD,eff, numerous vinculin puncta were formed, and ligand clustering was found to further increase focal adhesion formation. For fabrics with a global density of 9000 RGD μm−2, clustering the ligands to increase the local density from 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 31
000 to 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 61
000 to 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 resulted in further enhancements in focal adhesion formation (Fig. 5, right).
000 RGD μm−2 resulted in further enhancements in focal adhesion formation (Fig. 5, right).
Interestingly, for fabrics with a slightly higher global density of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, intermediate amounts of ligand clustering initially promoted focal adhesion formation, while further clustering to a local density of 122
000 RGD μm−2, intermediate amounts of ligand clustering initially promoted focal adhesion formation, while further clustering to a local density of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 resulted in a marked reduction in the number of focal adhesions (Fig. 4 and 5). This is the same local ligand density that suppressed cell division (Fig. 3), further supporting the notion that once ligands are clustered above a threshold value, their overcrowding results in inefficient integrin signaling. Similar to cell spreading and cell division, the number of vinculin-positive puncta increased along a hyperbolic trend-line with respect to global ligand density for fabrics with uniform ligand distributions (dashed curve: p < 0.002, KD,eff = 14
000 RGD μm−2 resulted in a marked reduction in the number of focal adhesions (Fig. 4 and 5). This is the same local ligand density that suppressed cell division (Fig. 3), further supporting the notion that once ligands are clustered above a threshold value, their overcrowding results in inefficient integrin signaling. Similar to cell spreading and cell division, the number of vinculin-positive puncta increased along a hyperbolic trend-line with respect to global ligand density for fabrics with uniform ligand distributions (dashed curve: p < 0.002, KD,eff = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000 RGD μm−2). These data indicate that integrin saturation occurs at high global ligand densities. At a fixed local ligand density of 122
000 ± 2000 RGD μm−2). These data indicate that integrin saturation occurs at high global ligand densities. At a fixed local ligand density of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, the relationship between focal adhesion number and global ligand density was positive and reached a plateau (dotted hyperbolic curve, p < 0.002), similar to the general trend-line for ELP fabrics without ligand clustering. For these fabrics with overcrowded ligands, the KD,eff was determined to be 27
000 RGD μm−2, the relationship between focal adhesion number and global ligand density was positive and reached a plateau (dotted hyperbolic curve, p < 0.002), similar to the general trend-line for ELP fabrics without ligand clustering. For these fabrics with overcrowded ligands, the KD,eff was determined to be 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 2000 RGD μm−2. This value is significantly higher than the KD,eff for ELP fabrics with homogeneous ligand distributions, indicating that overcrowded ligands result in decreased integrin signaling. This change is consistent with a mechanistic hypothesis that binding of cytoplasmic, integrin accessory proteins within the focal adhesion complex is disrupted when ligands are overcrowded, thus inhibiting focal adhesion maturation.17,18 This hypothesis is also consistent with our cell spreading data suggesting that integrin–ligand interactions were unaffected by local ligand overcrowding.17 It is therefore unlikely that overcrowding effects were caused by loss of RGD availability, but rather due to steric inhibition of intracellular integrin accessory proteins.
000 ± 2000 RGD μm−2. This value is significantly higher than the KD,eff for ELP fabrics with homogeneous ligand distributions, indicating that overcrowded ligands result in decreased integrin signaling. This change is consistent with a mechanistic hypothesis that binding of cytoplasmic, integrin accessory proteins within the focal adhesion complex is disrupted when ligands are overcrowded, thus inhibiting focal adhesion maturation.17,18 This hypothesis is also consistent with our cell spreading data suggesting that integrin–ligand interactions were unaffected by local ligand overcrowding.17 It is therefore unlikely that overcrowding effects were caused by loss of RGD availability, but rather due to steric inhibition of intracellular integrin accessory proteins.
Ligand overcrowding suppresses integrin signaling via decreased expression of FAK
To investigate sensitivity to ligand clustering on the molecular level, we measured total expression and relative phosphorylation of focal adhesion kinase (FAK), a component of focal adhesions from incipient complexes to turnover and release.44 Of particular consequence to cell proliferation, FAK promotes expression of cyclin D1, a driver of cell division.45 FAK itself is regulated in a double negative feedback loop with p53, an effector of cell-cycle arrest: p53 represses FAK transcription,46 and FAK targets p53 for proteasomal degradation.47 Although the direct mechanism of how focal adhesions and αVβ3 integrin binding affect FAK expression is unclear, it is known that blocking the function of αVβ3 integrins increases p53 expression.48 Given the feedback between FAK and p53, we expected that fabric-displayed αVβ3 ligands would increase FAK expression.Unlike cell proliferation, a minimal threshold of global ligand density was necessary for αVβ3 ligands to drive increased FAK expression, as no significant differences in FAK expression were observed at global ligand densities less than 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2. However, trends in FAK expression at global ligand densities at or greater than 18
000 RGD μm−2. However, trends in FAK expression at global ligand densities at or greater than 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 were consistent with the other integrin-dependent phenotypes explored in this study (Fig. 6a, left). For a fixed local ligand density of 61
000 RGD μm−2 were consistent with the other integrin-dependent phenotypes explored in this study (Fig. 6a, left). For a fixed local ligand density of 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, FAK expression increased with global ligand density according to a hyperbolic curve (gray curve, p < 0.002, KD,eff = 14
000 RGD μm−2, FAK expression increased with global ligand density according to a hyperbolic curve (gray curve, p < 0.002, KD,eff = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ± 1000 RGD μm−2), indicating integrin saturation also impacts integrin-dependent FAK expression. Near this KD,eff, clustering ligands from a local density of 31
000 ± 1000 RGD μm−2), indicating integrin saturation also impacts integrin-dependent FAK expression. Near this KD,eff, clustering ligands from a local density of 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 61
000 to 61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 up-regulated FAK expression (p < 0.1, Fig. 6a, right). Local overcrowding was also evident in FAK expression levels. At a local ligand density of 122
000 RGD μm−2 up-regulated FAK expression (p < 0.1, Fig. 6a, right). Local overcrowding was also evident in FAK expression levels. At a local ligand density of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2, FAK expression was significantly depressed compared to fabrics with identical global ligand density (p < 0.05). Strikingly, this reduction in expression occurred across global ligand densities that would otherwise have caused integrin saturation and high FAK expression, confirming the significant impact of ligand overcrowding on integrin signaling.
000 RGD μm−2, FAK expression was significantly depressed compared to fabrics with identical global ligand density (p < 0.05). Strikingly, this reduction in expression occurred across global ligand densities that would otherwise have caused integrin saturation and high FAK expression, confirming the significant impact of ligand overcrowding on integrin signaling.
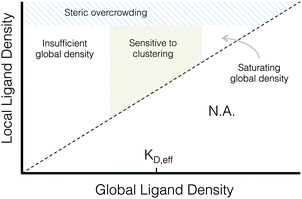 | ||
| Fig. 7 Proposed phase diagram of integrin signaling in various global and local ligand density regimes. | ||
Significant changes in total expression of FAK do not necessarily imply changes in relative FAK phosphorylation, which is commonly expressed as the ratio of FAK phosphorylated at tyrosine 397 to total FAK expression (pFAK-397/FAK).49–52 In contrast to FAK expression, the relationship between αVβ3 ligands and relative FAK phosphorylation is less well understood, although it has been linked to adhesion cycling, focal adhesion turnover, and cell motility.44,53 Although relative pFAK-397 did not systematically vary with respect to global ligand density (Fig. 6b, left), a negative association between relative pFAK-397 and focal adhesion number was observed. Local/global ligand density pairings that produced pFAK-397/FAK significantly above baseline (dashed line) also yielded low focal adhesion number. For example, at a global ligand density of 9000 RGD μm−2, which is near the previously determined KD,eff, clustering ligands from a local density of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 31
000 to 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 decreased specific FAK phosphorylation (Fig. 6, right, p < 0.05) and increased focal adhesion complex formation (Fig. 5, right). These data are consistent with an understanding that pFAK-397/FAK is related to focal adhesion turnover. This further suggests that, when ligand clustering enhances integrin signaling, focal adhesions are not only more common but also less prone to turnover. Similarly, clustering ligands to an overcrowded local density of 122
000 RGD μm−2 decreased specific FAK phosphorylation (Fig. 6, right, p < 0.05) and increased focal adhesion complex formation (Fig. 5, right). These data are consistent with an understanding that pFAK-397/FAK is related to focal adhesion turnover. This further suggests that, when ligand clustering enhances integrin signaling, focal adhesions are not only more common but also less prone to turnover. Similarly, clustering ligands to an overcrowded local density of 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RGD μm−2 increased specific FAK phosphorylation (Fig. 6, right, p < 0.05) and decreased focal adhesion complex formation (Fig. 5, right), suggesting that focal adhesions formed on fabrics with overcrowded ligands were both fewer and more susceptible to turnover. As was the case with focal adhesion number and FAK expression, the impact of local overcrowding on relative pFAK-397 was mitigated by increasing global ligand density (Fig. 6, left, p < 0.05). This observation suggests that materials with a high density of uniformly distributed ligands may be masking biochemical effects of ligand overcrowding by saturating the cell-material interface with ligands.
000 RGD μm−2 increased specific FAK phosphorylation (Fig. 6, right, p < 0.05) and decreased focal adhesion complex formation (Fig. 5, right), suggesting that focal adhesions formed on fabrics with overcrowded ligands were both fewer and more susceptible to turnover. As was the case with focal adhesion number and FAK expression, the impact of local overcrowding on relative pFAK-397 was mitigated by increasing global ligand density (Fig. 6, left, p < 0.05). This observation suggests that materials with a high density of uniformly distributed ligands may be masking biochemical effects of ligand overcrowding by saturating the cell-material interface with ligands.
A proposed phase diagram of ligand distributions
This work demonstrates that microscale ligand clustering influences integrin-dependent signals in a manner that significantly depends on both global and local ligand densities. By surveying a wide range of local and global ligand densities, we were able to collect a rich data set that bridges the previous observations of cell responses to ligand clustering. Based on this study, we identified two general design rules for ligand clustering that presents a unified interpretation of existing data. These design rules can be depicted using a phase diagram of integrin signaling that displays the various regimes of global/local ligand densities, Fig. 7. First, at global ligand densities near the material-specific KD,eff, ligand clustering significantly enhanced integrin activation, consistent with our understanding of the local biochemistry of focal adhesions. It is possible that at saturating global ligand densities, integrins bind to immediately accessible ligands and do not laterally diffuse across the cell membrane to form large integrin clusters capable of maturing into stable focal adhesions with limited turnover. Instead, a stochastic integrin distribution may be observed with limited integrin–integrin interactions that are more commonly associated with low ligand density, leading to fewer and smaller initial integrin clusters that do not reach the threshold size needed to overcome disruptive thermal fluctuations and mature into stable focal adhesions. Second, we found that integrin ligands could be clustered to overcrowded local densities, an effect associated with a reduction in focal adhesion formation that is distinct from receptor-saturating global density. This effect occurs despite no obvious inhibition of integrin–ligand binding interactions at high local densities, as evidenced by cell spreading.Conclusions
A complex interaction between global and local ligand densities modulates integrin-dependent signals by altering the synergy between integrin–ligand and integrin–integrin interactions, and understanding these effects will improve how integrin ligands are used in implantable biomaterials. While many strategies for engineering heterogeneous ligand distributions exist, translation into preclinical models is still in its infancy. Our quantitative analysis of the effects and necessary context of ligand clustering can (i) be generalized to a wide range of materials with different ligand tetherings and affinities using the material-specific parameter KD,eff, (ii) elucidate future studies of ligand clustering and heterogeneity in biomaterials, and (iii) provide a starting point for designing fibrous, recombinant, elastin-like protein scaffolds for biomedical applications.Acknowledgements
The authors acknowledge support NIH F31-HL114315-01 (P. L. B.), Stanford Bio-X Undergraduate Summer Research Program (S. M.), NSF DMR 1508006, NIH R21 EB018407, NIH U19 AI116484, (S. C. H.). We thank Vicky Robles and Wilson Torres for assistance with protein expression. We thank Ngan Huang, Kunal Mehta, Wei Chan, and Jim Swartz for helpful discussions.References
- D. I. Leavesley, G. D. Ferguson, E. A. Wayner and D. A. Cheresh, J. Cell Biol., 1992, 117, 1101–1107 CrossRef CAS PubMed.
- X. Zhou, F. R. Murphy, N. Gehdu, J. Zhang, J. P. Iredale and R. C. Benyon, J. Biol. Chem., 2004, 279, 23996–24006 CrossRef CAS PubMed.
- S. M. Sagnella, F. Kligman, E. H. Anderson, J. E. King, G. Murugesan, R. E. Marchant and K. Kottke-Marchant, Biomaterials, 2004, 25, 1249–1259 CrossRef CAS PubMed.
- K. Eid, E. Chen, L. Griffith and J. Glowacki, J. Biomed. Mater. Res., 2001, 57, 224–231 CrossRef CAS PubMed.
- E. Fong, S. Tzlil and D. A. Tirrell, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19302–19307 CrossRef CAS PubMed.
- C. L. Waite and C. M. Roth, Biotechnol. Bioeng., 2011, 108, 2999–3008 CrossRef CAS PubMed.
- B. L. Ekerdt, R. A. Segalman and D. V. Schaffer, Biotechnol. J., 2013, 8, 1411–1423 CrossRef CAS PubMed.
- G. Maheshwari, G. Brown, D. A. Lauffenburger, A. Wells and L. G. Griffith, J. Cell Sci., 2000, 113, 1677–1686 CAS.
- D. J. Irvine, K. Hue, A. M. Mayes and L. G. Griffith, Biophys. J., 2002, 82, 120–132 CrossRef CAS PubMed.
- C. J. Brinkerhoff and J. J. Linderman, Tissue Eng., 2005, 11, 865–876 CrossRef CAS PubMed.
- M. Arnold, E. A. Cavalcanti-Adam, R. J. B. Glass, W. Eck, M. Kantlehner and J. P. Spatz, ChemPhysChem, 2004, 5, 383–388 CrossRef CAS PubMed.
- E. A. Cavalcanti-Adam, T. Volberg, A. Micoulet, H. Kessler, B. Geiger and J. P. Spatz, Biophys. J., 2007, 92, 2964–2974 CrossRef CAS PubMed.
- C. Selhuber-Unkel, T. Erdmann, M. Lopez-Garcia and H. Kessler, Biophys. J., 2010, 98, 543–551 CrossRef CAS PubMed.
- M. Schvartzman, M. Palma, J. Sable, J. Abramson, X. Hu, M. P. Sheetz and S. J. Wind, Nano Lett., 2011, 11, 1306–1312 CrossRef CAS PubMed.
- K. Y. Lee, E. Alsberg, S. Hsiong, W. Comisar, J. Linderman, R. Ziff and D. J. Mooney, Nano Lett., 2004, 4, 1501–1506 CrossRef CAS PubMed.
- S. P. Massia and J. A. Hubbell, J. Cell Biol., 1991, 114, 1089–1100 CrossRef CAS PubMed.
- W. A. Comisar, D. J. Mooney and J. J. Linderman, J. Theor. Biol., 2011, 274, 120–130 CrossRef CAS PubMed.
- L. Saux, A. Magenau, T. Böcking, K. Gaus and J. J. Gooding, PLoS One, 2011, 6, e21869 Search PubMed.
- Z. G. Chen, P. W. Wang, B. Wei, X. M. Mo and F. Z. Cui, Acta Biomater., 2010, 6, 372–382 CrossRef CAS PubMed.
- E. D. Boland, J. A. Matthews, K. J. Pawlowski, D. G. Simpson, G. E. Wnek and G. L. Bowlin, Front. Biosci., 2004, 9, 1422–1432 CrossRef CAS.
- S. G. Wise, M. J. Byrom, A. Waterhouse, P. G. Bannon, M. K. C. Ng and A. S. Weiss, Acta Biomater., 2011, 1, 295–303 CrossRef PubMed.
- K. S. Straley and S. C. Heilshorn, Front. Neuroeng., 2009, 2, 00009, DOI:10.3389/neuro.16.009.2009.
- P. L. Benitez, J. A. Sweet, H. Fink, K. P. Chennazhi, S. V. Nair, A. Enejder and S. C. Heilshorn, Adv. Healthcare Mater., 2013, 2, 114–118, DOI:10.1002/adhm.201200115.
- K. S. Straley and S. C. Heilshorn, Soft Matter, 2009, 5, 114–124 RSC.
- K. J. Lampe, A. L. Antaris and S. C. Heilshorn, Acta Biomater., 2013, 9, 5590–5599 CrossRef CAS PubMed.
- H. Wang, L. Cai, A. Paul, A. Enejder and S. C. Heilshorn, Biomacromolecules, 2014, 15, 3421–3428 CrossRef CAS PubMed.
- X. Trepat, M. R. Wasserman, T. E. Angelini, E. Millet, D. A. Weitz, J. P. Butler and J. J. Fredberg, Nat. Phys., 2009, 5, 426–430 CrossRef CAS.
- A. Christopoulos, Trends Pharmacol. Sci., 1998, 19, 351–357 CrossRef CAS PubMed.
- D. Sengupta, P. M. Gilbert, K. J. Johnson, H. M. Blau and S. C. Heilshorn, Adv. Healthcare Mater., 2012, 1, 785–789, DOI:10.1002/adhm.201200195.
- J. M. Lewis, D. A. Cheresh and M. A. Schwartz, J. Cell Biol., 1996, 5, 1323–1332 CrossRef.
- R. L. van Leeuwen, I. G. Yoshinaga, T. Akasaka, S. K. Dekker, B. J. Vermeer and H. R. Byers, Exp. Dermatol., 1996, 6, 308–315 CrossRef.
- S. Aota, M. Nomizu and K. M. Yamada, J. Biol. Chem., 1994, 7, 24756–24761 Search PubMed.
- E. Fong and D. A. Tirrell, Adv. Mater., 2010, 22, 5271–5275 CrossRef CAS PubMed.
- W. J. Kao, D. Lee, J. C. Schense and J. A. Hubbell, J. Biomed. Mater. Res., 2001, 55, 79–88 CrossRef CAS PubMed.
- B. T. Houseman and M. Mrksich, Biomaterials, 2001, 9, 943–955 CrossRef.
- E. Battista, F. Causa, V. Lettera, V. Panzetta, D. Guarnieri, S. Fusco, F. Gentile and P. A. Netti, Biomaterials, 2015, 45, 72–80 CrossRef CAS PubMed.
- D. A. Puleo and R. Bizios, Biological Interactions on Materials Surfaces: Understanding and Controlling Protein, Cell, and Tissue Responses, Springer Science and Business Media, Berlin, 2009 Search PubMed.
- C. A. Reinhart-King, M. Dembo and D. A. Hammer, Biophys. J., 2005, 89, 676–689 CrossRef CAS PubMed.
- I. S. Lee, O. H. Kwon, W. Meng, I. Kang and Y. Ito, Macromol. Res., 2004, 12, 374–378 CrossRef CAS.
- J. C. Liu and D. A. Tirrell, Biomacromolecules, 2008, 9, 2984–2988 CrossRef CAS PubMed.
- M. A. Schwartz and R. K. Assoian, J. Cell Sci., 2001, 14, 2553–2560 Search PubMed.
- N. Q. Balaban, U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky and L. Addadi, Nat. Cell Biol., 2001, 3, 466–472 CrossRef CAS PubMed.
- K. Burridge and M. Chrzanowska-Wodnicka, Annu. Rev. Cell Dev. Biol., 1996, 12, 463–519 CrossRef CAS PubMed.
- S. K. Mitra, D. A. Hanson and D. D. Schlaepfer, Nat. Rev. Mol. Cell Biol., 2005, 6, 56–68 CrossRef CAS PubMed.
- J. Zhao, Z. C. Bian, K. Yee, B. P. Chen, S. Chien and J. Guan, Mol. Cell, 2003, 11, 1503–1515 CrossRef CAS PubMed.
- D. Ilic, E. A. Almeida, D. D. Schlaepfer, P. Dazin, S. Aizawa and C. H. Damsky, J. Cell Biol., 1998, 143, 547–560 CrossRef CAS PubMed.
- S. Lim, X. L. Chen, Y. Lim, D. A. Hanson, T. Vo, K. Howerton, N. Larocque, S. J. Fisher, D. D. Schlaepfer and D. Ilic, Mol. Cell, 2008, 29, 9–22 CrossRef CAS PubMed.
- B. P. Eliceiri and D. A. Cheresh, J. Clin. Invest., 1999, 103, 1227–1230, DOI:10.1172/JCI6869.
- M. L. Megison, K. A. Gillory, J. E. Stewart, H. C. Nabers, E. Mrozcek-Musulman and E. A. Beierle, Mol. Cancer Res., 2014, 12, 514–526 CrossRef CAS PubMed.
- M. V. deOliveira, T. M. Marin, C. F. Clemente, A. P. Dalla Costa, C. C. Judice and K. G. Franchini, FEBS Lett., 2009, 18, 2975–2981 CrossRef PubMed.
- V. J. Thannickal, D. Y. Lee, E. S. White, Z. Cui, J. M. Larios, R. Chacon, J. C. Horowitz, R. M. Day and P. E. Thomas, J. Biol. Chem., 2003, 14, 12384–12389 CrossRef PubMed.
- X. Zhang, S. W. Moore, T. Iskratsch and M. P. Sheetz, J. Cell Sci., 2014, 7, 1394–1405 CrossRef PubMed.
- D. J. Webb, K. Donais, L. A. Whitmore, S. M. Thomas, C. E. Turner, J. T. Parsons and A. F. Horwitz, Nat. Cell Biol., 2004, 6, 154–161 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ib00258c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |