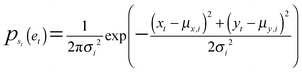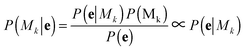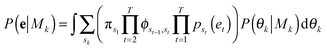Time series modeling of live-cell shape dynamics for image-based phenotypic profiling†
Simon
Gordonov
 ab,
Mun Kyung
Hwang
b,
Alan
Wells
c,
Frank B.
Gertler
bd,
Douglas A.
Lauffenburger‡
*abd and
Mark
Bathe§
*a
ab,
Mun Kyung
Hwang
b,
Alan
Wells
c,
Frank B.
Gertler
bd,
Douglas A.
Lauffenburger‡
*abd and
Mark
Bathe§
*a
aDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA
bThe David H. Koch Institute for Integrative Cancer Research, Cambridge, MA, USA
cDepartment of Pathology, University of Pittsburgh, and Pittsburgh VA Health System, Pittsburgh, PA, USA
dDepartment of Biology, Massachusetts Institute of Technology, Cambridge, MA, USA
First published on 26th November 2015
Abstract
Live-cell imaging can be used to capture spatio-temporal aspects of cellular responses that are not accessible to fixed-cell imaging. As the use of live-cell imaging continues to increase, new computational procedures are needed to characterize and classify the temporal dynamics of individual cells. For this purpose, here we present the general experimental–computational framework SAPHIRE (Stochastic Annotation of Phenotypic Individual-cell Responses) to characterize phenotypic cellular responses from time series imaging datasets. Hidden Markov modeling is used to infer and annotate morphological state and state-switching properties from image-derived cell shape measurements. Time series modeling is performed on each cell individually, making the approach broadly useful for analyzing asynchronous cell populations. Two-color fluorescent cells simultaneously expressing actin and nuclear reporters enabled us to profile temporal changes in cell shape following pharmacological inhibition of cytoskeleton-regulatory signaling pathways. Results are compared with existing approaches conventionally applied to fixed-cell imaging datasets, and indicate that time series modeling captures heterogeneous dynamic cellular responses that can improve drug classification and offer additional important insight into mechanisms of drug action. The software is available at http://saphire-hcs.org.
Insight, innovation, integrationShape is a quantifiable property reflecting the phenotype of a cell that can change over time in response to extracellular cues and pharmacological perturbations. Characterizing the temporal changes of individual cells is essential to understanding cellular response in asynchronous, heterogeneous populations. This work presents an integrated experimental–computational framework to profile live-cell shape from high-content fluorescence imaging data. Probabilistic time series modeling is applied to classify single-cell shape dynamics as discrete morphological states explored in time. The framework reveals important similarities and identifies key differences in shape dynamics following inhibition of molecular regulators of cytoskeletal organization in breast cancer cells. Accounting for temporal dynamics of individual cells within heterogeneous populations helps to distinguish and interpret cellular response to diverse drug perturbations. |
Introduction
High-content imaging (HCI) is widely used to perform quantitative in vitro cell phenotyping in a broad range of applications from RNAi and drug screening to prediction of stem cell differentiation fates.1–4 In contrast to population-level assays that measure concentrations and activities of molecular species pooled over heterogeneous cellular populations, HCI has the advantage of profiling cells in situ in a manner that captures both overall cellular morphology as well as sub-cellular features such as protein localization and their relative levels.5,6 Shape is the most common property used to characterize cellular phenotype in part due to the ease of image-based quantification enabled by cytoskeletal staining and the importance of morphology in a wide variety of cellular processes. In practice, fixed-cell imaging is typically performed because it avoids large-scale handling of live cultures during imaging or generation of fluorescent reporter cell lines, and enables quantification of large numbers of cells at a single time point, increasing statistical power for comparing cellular phenotypes across experimental conditions.7,8 Multivariate statistical modeling of fixed-cell image features has been effective in phenotype-based drug classification, providing important insight into signaling pathways involved in cellular morphogenesis.9,10 Single-cell analysis using imaging has been particularly instrumental in identifying and deciphering cellular phenotypes in disease states.11 User-defined shape categories coupled with supervised learning such as support vector machines, as well as unsupervised methods such as principal component analysis (PCA), have been used to generate quantitative profiles for comparing experimental perturbations and inferring spatial signaling mechanisms of shape regulation.12–15However, fixed-cell assays, while relatively simple to perform through fluorescent staining and imaging, suffer from several important limitations. Principal among these is the loss of information regarding cellular dynamics in response to long-term or transient drug treatments. In addition, imaging artifacts may occur due to cell fixation and permeabilization, which may distort spatially resolved protein distributions.16 For these reasons, live-cell imaging is increasingly being used to characterize cellular phenotypes, particularly in the subcellular analysis of cell shape dynamics and polarization. For example, computational tools for cell boundary tracking,17–19 morphodynamics profiling,20–23 measurement of fluorescent reporters,24,25 and quantitative morphology and subcellular protein distribution analyses26 in live cells have become an integral component of high-resolution analyses of cell shape and its regulation, particularly in the context of cell migration. In cell migration studies, live-cell shape and signaling analyses have been complemented by direct quantification of motility properties such as cell speed and persistence of motion to establish links between molecular mechanisms and migratory phenotypes.27–32
In these applications, the relative strengths of high-resolution, live-cell imaging versus fixed-cell HCI assays are apparent: the former captures rich, dynamic properties of single-cell behavior while the latter enables large-scale screening of hundreds to thousands of cells. In an effort to bridge this gap, several mathematical approaches have been developed to infer dynamic properties of cell populations from fixed-cell measurements in HCI studies. For example, ergodic rate analysis based on differential equation modeling has been used to infer transition rates through cell cycle stages from images of molecular reporters that define various mitotic phases in individual fixed cells.33 Additionally, Bayesian network modeling of shape parameters coupled with RNAi knockdown of cytoskeleton-regulatory proteins has been used to infer shape state transitions of migratory cells and reveal underlying regulatory signaling modules.34,35 However, these approaches assume quasi-steady-state of the cell population, assign cells into pre-defined phenotypic categories, and, in the case of Bayesian networks, face difficulties in modeling repetitive processes such as motility cycle stages in migrating cells. Moreover, they are not directly applicable to the analysis of live cells over time to monitor individual cellular responses to drug perturbations.
To address these limitations, here we present a live-cell HCI framework that captures the dynamics of a large number of cells on the scale of a phenotypic screen. The approach combines high-content live imaging, image processing, multivariate data analysis, and probabilistic modeling to characterize cell shape dynamics in a drug-screening context. Inspired by existing methods for modeling cell cycle stages from time series images,36,37 our framework employs hidden Markov modeling to describe shape dynamics as temporal sequences of morphological states that are observed as noisy, multivariate image data. Describing temporal trajectories of multivariate shape measurements as a finite set of states that is limited in number by Bayesian model selection that penalizes model complexity, results in an efficient description of time-dependent shape categories explored by a cell. This approach provides a means of modeling the shape dynamics of hundreds of individual cells, capturing temporal evolution in cell morphology directly from live images without assumptions of steady-state cell populations or predefined shape categories assumed by fixed-cell analyses. We show here in a proof-of-principle study that drug-response profiles derived from these models can be used for phenotypic drug comparisons and can reveal spatially distinct and pathway-specific roles that drug-targeted species play in modulating shape dynamics. Our computational framework is available as open source for the computational cell biology community to apply using MATLAB at http://saphire-hcs.org.
Results
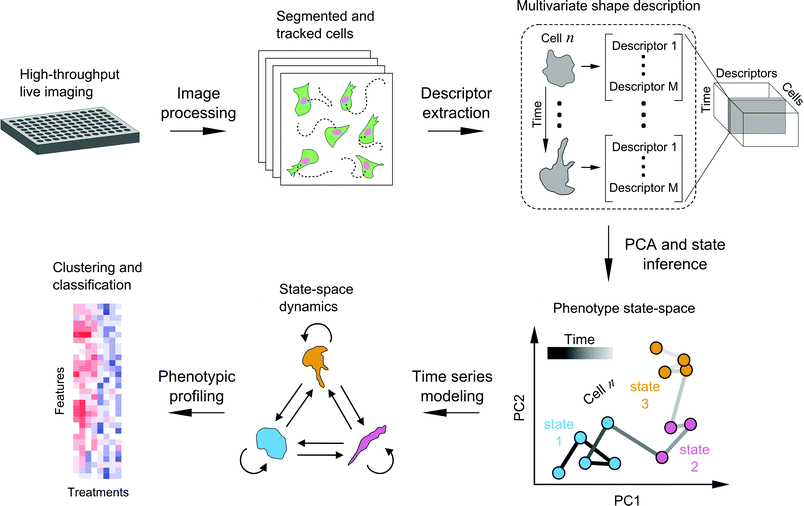
We developed a framework to characterize single-cell shape dynamics for large collections of cells from live-imaging assays (Fig. 1). Fluorescent cells treated with a variety of drug perturbations are imaged in a multi-well format followed by image processing and analysis to track and outline individual cells over time. Image-derived features, or descriptors, of cell shape are extracted to generate a data cube for the entire imaging screen, with the three dimensions corresponding to shape features, individual cells, and time points. PCA is used for dimensionality reduction along the shape feature axes to generate temporal “shape-space” trajectories of individual cells in principal component (PC) space. HMM is then used to annotate each cell shape trajectory using a small set of shape states that are determined using Bayesian model selection, revealing important time-dependent features of cell morphology while substantially reducing live-cell data size and complexity. Features extracted from temporal model annotations of hundreds of cells are then used for clustering and classifying perturbations. In the following sections we detail the steps of the framework and present a proof-of-principle study in profiling the heterogeneity in cell shape dynamics from a small-scale drug screen.Live imaging enables temporally-resolved readout of cell phenotypes
We first generated a triple negative breast cancer cell line, MDA-MB-231, with stable expression of two fluorescent reporters, LifeAct-eGFP and histone H2B-mCherry, for concurrent imaging of actin and nuclear dynamics, respectively. This enabled the unambiguous identification, isolation, and tracking of individual cells using the segmented nuclei, while the actin reporter enabled quantitative characterization of cytoskeletal morphology. MDA-MB-231 cells were chosen for their mesenchymal-like properties and lack of epithelial-type intercellular junctions, making this cell line particularly amenable to studying phenotypic behavior on the single-cell level. The two-color fluorescent reporter cells were seeded in 96-well plate format and treated with different drugs that target distinct components of the actomyosin cytoskeleton-regulatory pathways including ROCK (Rho-associated protein kinase), myosin II, EGFR (epidermal growth factor receptor), calpain, MLCK (myosin light chain kinase), and MEK (mitogen-activated protein kinase kinase), to probe their effects on cell shape dynamics in two independent imaging experiments (Materials and methods).In one experiment, we included two controls in order to set a baseline for cell behavior under no drug treatment: one of growth media only and the other with 0.1% v/v DMSO in growth media to assess effects of DMSO alone since it was used to dissolve drug stock. We also included two different doses for the ROCK and MLCK inhibitors to assess drug concentration effects on cell shape dynamics characterized in our framework. In an additional experiment, we expanded the panel of drug treatments and used a different microscope, culture media, and cell passage number to assess these factors on reproducibility of experiments and subsequent analyses. Epifluorescence 2-D microscopy using a 10×/0.3NA air objective offered a suitable tradeoff between field-of-view and resolution, enabling us to maximize the number of cells captured with sufficient detail to characterize individual cell morphologies over approximately eighteen hours for each treatment condition.
Visual inspection of the compiled time series movies revealed asynchronous populations of dividing, apoptotic, and migratory cell phenotypes (Videos S1–S3, ESI†). For cells not undergoing division or death, we observed a broad range of shape changes, with some cells changing shape rapidly with pronounced cell body protrusions and retractions, while others exhibited less noticeable morphodynamic activity. Although the cells generally exhibited autonomous behavior that was largely independent of one another, we observed frequent contact and spatial overlapping of some cells in addition to entry and exit of cells into and out of the imaging fields of view. Collectively, the large quantity of imaging data and phenotypic cell behaviors rendered fully manual data parsing and analysis intractable, thereby motivating the need for an automated computational analysis pipeline for processing the time-series images.
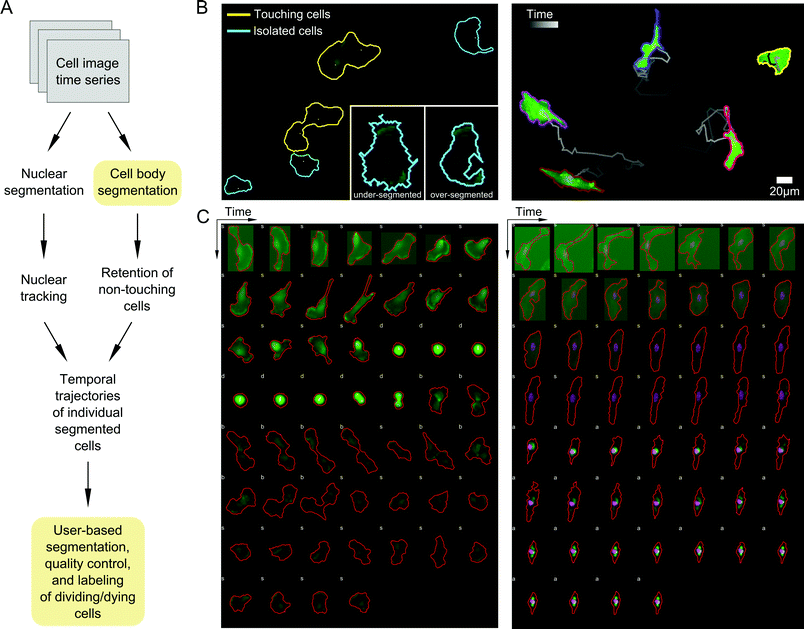
Automated processing with quality control ensures accurate parsing of image data
A priority in formulating our probabilistic modeling approach was to ensure that any data input into the model accurately captures cell shape properties. We therefore developed an image processing pipeline to segment and track cells with as many automated, user-free steps as possible to increase throughput and minimize user subjectivity (Materials and methods; Fig. 2A). Automated image parsing, cell segmentation, and tracking were first performed for all acquired image time series (see examples in Videos S1–S3, ESI†). A major challenge, however, involved the treatment of variations in image illumination between fields and within fields over time, as well as variability in fluorescent reporter levels between cells, leading to occasional image processing errors such as over- or under-segmentation of cells (Fig. 2B). We therefore developed a GUI-based quality control (QC) module that enabled manual validation and modification of segmented regions and cell tracks. Here, user input is desirable because cell boundaries can be defined unambiguously by the human eye while automated segmentation is notoriously sensitive to image properties. This module was used to discern and correct artifacts introduced during image acquisition and automated processing steps. The QC module also enabled us to identify and label dividing and dying cells, which were removed from subsequent analyses (Fig. 2C).Drug treatments diversify morphologies of MDA-MB-231 cells
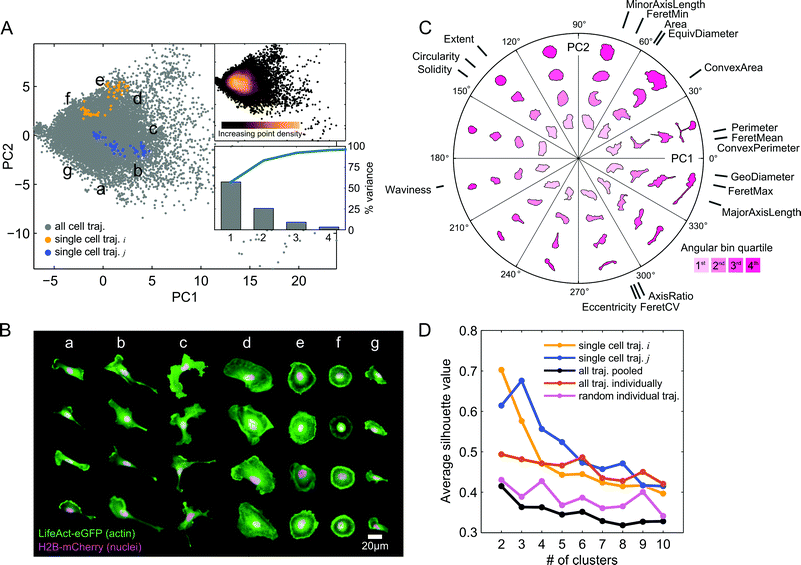
The automated image processing and QC pipeline resulted in a collection of accurately segmented and tracked cell trajectories. We next extracted a set of eighteen morphological features from segmentation masks of each cell and time point (Table S1, ESI†). Following z-score normalization of each feature across cells, we applied PCA to the data in order to capture and visualize the variability in shape between all cell images from the imaging experiment with the expanded panel of drug treatments (Fig. 3A). Here, we call the basis of the projected data onto the first two PCs the “shape-space.” The first two PCs captured over 80% of the shape variability in the observations. In order to assess how PCA distributes and orients morphological properties of cells in shape-space, we selected random time snapshots from four different cells in seven regions of PC space and visualized the overlaid actin and nuclei images (Fig. 3B). This visualization revealed that morphologies of MDA-MB-231 cells across all seven drug treatments vary from large and spread (Fig. 3B, panel d), to round cells with pronounced cortical actin at the cell periphery (Fig. 3B, panels e and f), as well as polarized cells with varying degrees of elongation (Fig. 3B, panels a, b and g), and branched morphologies (Fig. 3B, panel c).To visualize how morphologies vary in different directions and radial distances away from the data mean in shape-space, we created a polar representation of the two PCs. The polar shape-space was subdivided into twelve equal angular bins, with each bin subdivided further into quartiles. Fig. 3C shows the representative cell shapes in each radial quartile of the angular bins as well as the contributions of the original eighteen shape features to the values of the two PCs. The highest variance in shape, along the first PC, predominantly captures cell elongation and branching, while the second PC captures cell spreading area and roundness. Features such as major axis length, geodesic diameter, and maximum Feret length capture similar length properties of cells and therefore have similar PC coefficients and directions in shape-space. These features are anti-correlated with solidity, circularity, and extent, which point in the opposite direction for both PCs, showing that branched and elongated morphologies have smaller solidities and circularities, as expected. As captured mainly by the second PC, cells with longer minor axes and larger areas have generally lower eccentricities and smaller ratios of major to minor axis lengths.
Furthermore, we found that cells are densely packed around the data mean at the origin in shape-space, with the point density dissipating radially (Fig. 3A). This suggests that although MDA-MB-231 morphologies are visually distinct, shape properties of the population as a whole vary on a continuum, with no clearly distinguishable groups. Interestingly, however, when we plotted cell shape trajectories one at a time we found increased grouping and clustering of points. We applied k-means clustering to individual cells and to the cell population as a whole for k = 2 to k = 10 clusters, and computed average silhouette values in order to quantify the degree to which points form well separated, or cohesive, groups (Fig. 3D). As may visually be discerned in Fig. 3A, example cell trajectory i forms 2 groups while cell trajectory j forms 3 groups, which is confirmed by the maximum silhouette value that occurs for k = 2 and k = 3 clusters, respectively. On average, points from individual cell trajectories had higher cluster cohesion than did random samples with the same number of points as the trajectories or the entire cell population as a whole.
Probabilistic modeling of morphological states reveals heterogeneity in cell shape dynamics
Having observed that individual cell trajectories form more cohesive clusters than the population as a whole, we next sought to develop a principled and reproducible means of modeling morphological dynamics on a single-cell basis. We reasoned that the higher cluster cohesiveness within individual trajectories signifies the presence of underlying “states” that the cell explores in shape-space over time. Although Gaussian mixture modeling (GMM) is a highly useful approach for unsupervised, model-based data clustering that would eliminate subjective, user-defined delineation of states,37 it typically ignores the temporal nature of data. Including temporal information during model inference is reasonable a priori because GMM inherently assumes that observations are independent,38 which is not necessarily satisfied for sequential time series measurements from the same cell, whose shape may be highly correlated in time. We therefore applied an HMM framework in which temporal dependencies are directly incorporated during model inference, using a modified approach developed for annotating modes of single-particle motion in live cells.39 Within this HMM framework, the “hidden” underlying states correspond to cell shape states that produce observable emissions that are associated with the measureable cell shapes computed in PC shape-space (Materials and methods). Additionally, Bayesian model selection enables us to penalize models with greater numbers of underlying shape states to fit the set of time series points satisfying Occam's razor or the Principle of Parsimony.40,41To compare our approach with GMMs that ignore dependencies in time series data, we simulated shape-space trajectories from underlying hidden Gaussian states to explore differences with HMM-based annotation using SAPHIRE. Specifically, we sought to compare state identification capability of the two methods, with SAPHIRE using Bayesian model selection and GMM using the Bayesian information criterion to penalize model complexity. Our two-state model simulations revealed that SAPHIRE is more likely to choose the model with the correct number of states and has better accuracy in inferring locations of state means compared with GMM due to SAPHIRE's incorporation of temporal dependencies in the data during the state inference steps (Fig. S1, ESI†).
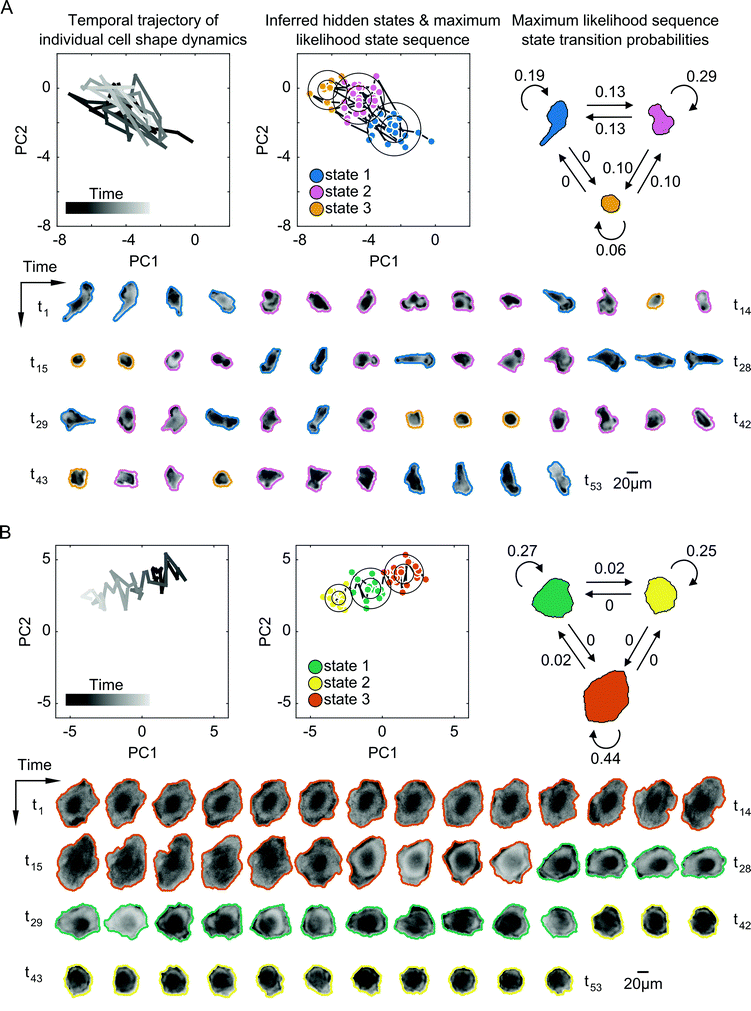
Next, we applied SAPHIRE to experimental observations of cells in the two-dimensional PC shape-space to infer a time series model for each cell individually. The inferred model specifies the most probable number of hidden shape states, which is unknown a priori, as well as the state parameters. Each state is a symmetric, bivariate Gaussian distribution in shape-space with two variables corresponding to the two PCs. The inferred parameters for each Gaussian distribution are the standard deviation and the mean, which capture temporal shape variation and average morphology of the cell within the state, respectively. The model also specifies a state transition probability matrix that describes the probability of transitions between shape states. Each cell is annotated in time with the most probable, or maximum likelihood, shape state sequence, enabling us to determine the most likely state that the cell exists in at each point in time. We first compared shape state inference of our approach with that of commonly-used GMM under different model constraints. Allowing for elliptically-shaped Gaussian states in the GMM led to undesirable grouping of cell shapes with visually-dissimilar morphologies into the same state (Fig. S2, ESI†), and, similar to the results of the numerical simulations (Fig. S1, ESI†), SAPHIRE was better able to capture distinct morphological phases of cells that gradually move between distinct regions of shape-space (Fig. S3, ESI†). In certain cases of cells moving between two visually distinguishable underlying states, the state annotations of cell trajectories were similar for SAPHIRE and GMM (Fig. S4, ESI†). Moreover, from all modeled cell trajectories we found that a larger fraction of cells exists in two to three underlying states, while fewer cells explore either a single state or four or more states (Fig. S5, ESI†).
Despite some similarities in the numbers of states explored by cells, the inferred parameters of transition dynamics and state annotations varied considerably between cells. These variations not only existed for cells across different drugs, but also across cells within a given treatment and for cells with the same number of shape states. Fig. 4 shows the inferred shape states for two example cells treated with the same drug having the same number of inferred states, but with notable heterogeneity in state parameters and transition dynamics. Some cells exhibited rapid back-and-forth switching between states corresponding to periodicity in actin protrusions and retractions, resulting in shapes that are elongated, rounded, or those in between (Fig. 4A). Other cells exhibited individual instances of state transitions, progressively changing shape in a given direction in shape-space, such as going from larger and more spread to smaller and rounder morphologies (Fig. 4B). The maximum likelihood state annotations capture different phases in the morphodynamic history of a cell, with state transition parameters derived from the state sequence providing useful insights into its dynamic behavior. For instance, the model for the cell in Fig. 4A reveals that the cell is more likely to stay in state 1 (p = 0.19) or state 2 (p = 0.29) than transition to other states, and that direct transitions between elongated (state 1) and a rounded (state 3) morphology without going through an intermediate shape (state 2) is not likely (p = 0).
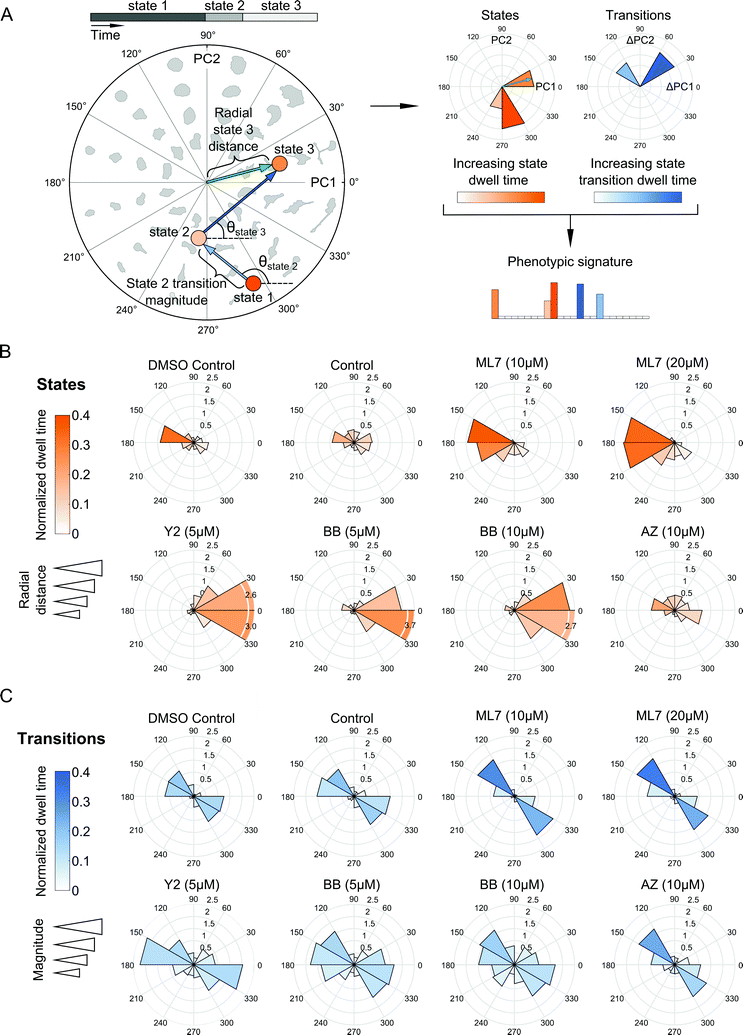
Shape state annotations serve as phenotypic readouts of drug action
Our probabilistic modeling framework produced annotated sequences of shape dynamics for all individual cell trajectories from the inhibitor screen, with each trajectory comprised of morphological states evolving in PC shape-space over time. We next explored how shape dynamics compare between cells treated with the distinct compounds. We first generated phenotypic signatures from the annotated state sequences for each cell. These signatures capture where in PC shape-space states are located, how long a cell spends in its inferred states, and how frequently and in what directions in PC space a cell makes shape transitions (Fig. 5A).We next assessed how the distribution of cellular shape states in polar PC space was affected by the experimental treatment conditions (Fig. 5B). Cells in the DMSO and growth media controls were positioned closely and were fairly evenly distributed around the mean of the shape-space data without exhibiting biased morphologies in any particular direction compared with the morphologies induced by drugs. The ROCK and myosin II inhibitors pushed cells predominantly towards highly elongated and branched morphologies with longer dwell times in these states. On the other hand, MLCK inhibition had the opposite effect, biasing cells toward smaller and rounder morphologies along the negative first PC axis. In the experiment with the expanded panel of drugs, both MEK inhibitors tested led to a broader variety of states, predominantly either rounder, or more elongated, shapes, although no strong biases of shape state location or state dwell time were observed upon MEK inhibition (Fig. S6A, ESI†). Similarly, EGFR inhibition led to a broader and relatively more uniform distribution of morphological states around shape-space, albeit with a noticeable shift towards less elongated morphologies, whereas calpain inhibition biased cells into more elongated morphologies. Further, doubling the dose of the myosin II inhibitor shifted cells slightly towards more branched morphologies while diminishing elongated states, whereas an increase in dose of the MLCK inhibitor appeared to accentuate the bias towards smaller and more rounded shapes (Fig. 5B). For either drug, however, the overall distributions of cellular shape states and state dwell times were similar across both doses tested, as well as between the two imaging experiments.
Live-cell analysis also enables the determination of whether drugs differentially affect the trajectories that cells take through shape-space when they transition between distinct morphological states. To our surprise, state transition directions were similar across the drugs tested, with cells moving between two relatively narrow angular ranges, 120 to 180 degrees or 300 to 360 degrees in shape-space (Fig. 5C and Fig. S6B, ESI†) that correspond to decreased elongation with increased roundness versus increased elongation and decreased roundness, respectively (Fig. 3C). This finding suggests that most of the dynamics in shape that MDA-MB-231 cells undergo are along this morphological axis of increasing or decreasing elongation, regardless of drug treatment, which may be indicative of cytoskeletal protrusion and retraction cycles, while transitions toward larger, spread morphologies, for example, are quite rare for this cell type. Despite the similarity in the directions of state transitions taken by cells across drugs, ROCK and myosin II inhibition led to larger magnitudes and slightly broader distributions in state transitions, suggesting that these drugs induce more pronounced variations along the roundness-elongation axis of cell shape, likely by reducing transcellular actomyosin tension.
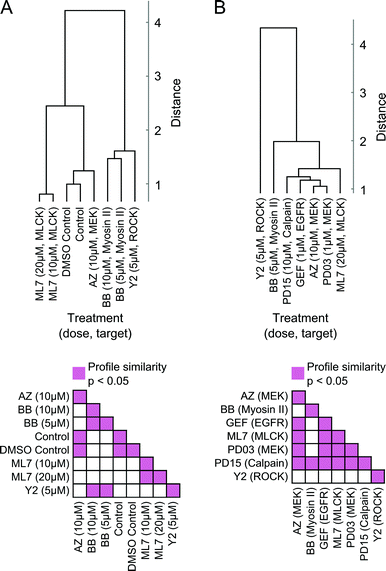
Moreover, readouts of shape state locations and state transitions can be used to group treatments based on similarities in induced phenotype dynamics. We derived a dynamic shape state “profile” for each treatment from the shape state and state transition histograms (Fig. 5B, C and Fig. S6A, B, ESI†) and hierarchically clustered the treatments using profile similarities for each imaging experiment separately (Fig. 6A and B). As anticipated based on the preceding results, the two MEK inhibitors clustered closest together, as did the DMSO and growth media controls. These results serve as internal controls to validate the HMM annotation and phenotypic drug comparison procedure proposed here. The MEK inhibitors were also found to have dynamic shape state profiles more similar to those of the EGFR and calpain inhibitors than to the MLCK, ROCK, and myosin II inhibitors. Myosin II inhibition with Blebbistatin produced phenotypes most similar to those with ROCK inhibition. Perhaps surprisingly, MLCK inhibition, which is known to alter myosin II activity, induced shape dynamics more similar to those under MEK and EGFR inhibition than under myosin II and ROCK inhibition. Overall, the computational analyses from these imaging experiments demonstrate that temporal dynamics of individual cells can be combined into quantitative profiles that serve as useful readouts for phenotypic drug comparison and for inferring shape-regulatory roles of targeted signaling molecules.
State-space temporal modeling of cell morphology improves drug classification over existing image-based profiling methods
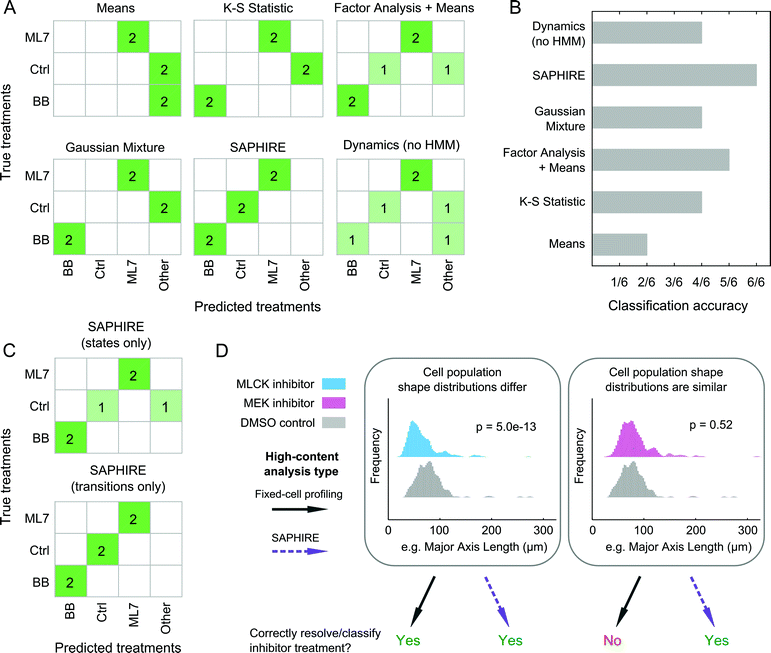
SAPHIRE generates phenotypic profiles of experimental treatments from single-cell models of HMM-annotated morphological state trajectories in shape-space. This approach differs from existing fixed-cell HCI profiling methods, which, instead of modeling cellular properties of a given cell over time, characterize cellular properties for different cells in a population at a given time point. Therefore, we sought to assess the benefit that live-cell temporal modeling on a per-cell basis has in comparison with fixed-cell approaches10,42–44 in classifying treatment conditions in our screen (Fig. 7). We chose four profiling methods that have previously been compared amongst one another and have shown high drug classification accuracies in a large-scale drug screen study (see ref. 15 and Materials and methods). To make a fair comparison with live-cell analyses, we used live-cell population data from our inhibitor screen at five different time points post-treatment for the fixed-cell analysis methods in order to mimic a fixed-cell time course experiment. We additionally profiled the dynamics of individual cells but without the HMM that is used in SAPHIRE to assess the value of the HMM state-space shape representation for classifying treatments.For the three treatments tested that were amenable to the classification analysis approach as in ref. 15, of the four fixed-cell methods the “Factor Analysis + Means” profiles performed best, correctly classifying 5 of 6 treatments (Fig. 7A and B). This approach has also previously been shown to have good classification performance in a large-scale screen of dozens of drugs from different mechanistic classes.15,44 Profiles generated using Gaussian mixtures43 and the K–S statistic10 correctly classified 4 of 6 treatments, whereas the simplest “Means”42 approach only classified 2 of 6 treatments correctly. Treatment profiles generated using SAPHIRE resulted in correct classification of all 6 treatments, demonstrating improvement over the fixed-cell profiling methods tested. Moreover, the HMM annotation of morphological states using SAPHIRE appears to be critical for improving correct treatment classification, as profiles derived from single-cell temporal dynamics without the HMM misclassified 2 of the 6 treatments.
To further understand which properties of the state-space treatment profiles generated using SAPHIRE improve treatment classification, we separately considered the use of features that capture state transitions versus features that only consider properties of the states themselves (Fig. 7C). Treatment classification confusion matrices using these state features separately revealed that state transitions correctly classify all six treatments, whereas exclusion of temporal transition information leads to misclassification of a treatment, yielding a classification performance similar to the fixed-cell “Factor Analysis + Means” profiling approach.
Collectively, these results demonstrate that all of the methods implemented, with the exception of the “Means” approach, correctly classify the MLCK and myosin II inhibitors, but fail to differentiate between cells treated with MEK inhibitor versus control, or those treated with ROCK versus myosin II inhibitors. Thus, as shown in Fig. 7D, when the shape distributions of two treatments differ, both state-space modeling of individual cells over time and existing fixed-cell profiling methods that measure features of different cells at multiple time points, can correctly classify and resolve treatment effects on cell shape. When shape distributions of two treatments are similar, however, state-space modeling of single-cell temporal transitions within the population distributions can improve discriminability and classification of treatments compared with existing methods that only capture shape properties of distinct cells within a population. Therefore, annotation of cell morphologies with a state-space representation using HMM, and in particular capturing state transition dynamics on a per-cell basis, can improve the accuracy of classifying treatment conditions in an HCI experiment.
Discussion
Here, we presented a computational framework that applies probabilistic time series modeling to characterize shape dynamics of individual cells under the action of drug perturbations assayed using live-cell imaging. Modeling temporal dynamics of cell shape using HMM condenses complex multivariate imaging data into simpler sequences of morphological states that evolve over time. Advantages of our approach over existing methods that are designed for fixed-cell imaging applications were explored. Quantitative features extracted from HMM state sequences using our approach serve as temporal signatures for comparing morphodynamic behaviors between cells, which are not available from fixed-cell analysis procedures. Temporal signatures from multiple identically treated cells are combined to serve as phenotypic profiles for clustering and classifying experimental perturbations.It has been proposed that cell populations can assume either discrete or continuous morphological landscapes, principally determined by cell type, extracellular environment, types of perturbations, and the particular phenotype captured.45 For example, in cases when particular morphologies are reached under effect of genetic perturbations, cells may exhibit more stable steady-state morphologies leading to discrete shape states.13 Our results suggest, however, that shorter-term responses to pharmacological perturbation of highly asynchronous cell populations fall on a more continuous, finely graded morphological spectrum of shapes that conceals more cohesive and well separated shape state clusters within temporal trajectories of individual cells (Fig. 3). Consequently, two different approaches to cell profiling, one using commonly-applied fixed-cell analyses of populations of distinct cells and the other using temporal modeling of individual live cells presented here, may collectively serve as a powerful combined approach to reveal idiosyncrasies in phenotypic effects of different molecular perturbations (Fig. 8).
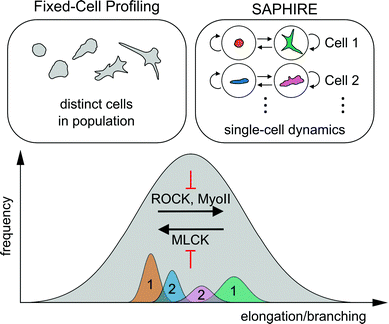 | ||
| Fig. 8 Schematic of the conceptual difference between fixed-cell analyses versus SAPHIRE, and their combined insights into molecular mechanisms of cell shape regulation. The distribution of morphologies of drug-treated MDA-MB-231 breast cancer cells falls on a continuum, illustrated in gray. The extent of cell elongation and branching is the dominantly varying morphological property of the breast cancer cell line analyzed in our drug screen (Fig. 3). Fixed-cell profiling captures the morphological landscape of distinct cells in the population at a given time point. In contrast, SAPHIRE captures the morphological evolution of individual cells over time. SAPHIRE uses an HMM framework to detect the presence of morphological states (e.g. orange and green states for one cell, blue and pink states for another) used to model the temporal dynamics of each cell independently within the population. Application of both of these approaches to live-cell shape profiling reveals that MLCK inhibition decreases, while ROCK and myosin II inhibition increases, cellular elongation and branching. | ||
In particular, within the context of image-based phenotypic profiling, our results illustrate that state-space temporal modeling of cell shape using HMM can improve the resolution of cellular classification in response to distinct drug treatments. This result, shown in Fig. 7D, highlights an important practical outcome of this work in the context of HCI. Existing phenotypic profiling methods correctly classified some treatments and misclassified others in the actomyosin cytoskeleton-focused drug screen. Our analyses demonstrate that modeling morphological transitions over time on an individual cell basis using HMM can provide useful live-cell phenotypic information for discriminating between treatment effects. Some of these effects are not captured by simply modeling cell shape distribution properties of different cells in a population, even if the same population is profiled over time. This suggests that the framework presented offers additional information beyond fixed-cell profiling in image-based classification using morphological data. An interesting application of temporal modeling would be to complement fixed-cell assays that utilize immunofluorescence staining in order to augment phenotypic profiling and better resolve underlying molecular differences driving distinct cellular drug responses assayed using live imaging.
In addition to investigating the utility of temporal shape modeling in HCI applications, we characterized differential cell shape dynamics induced by small-molecule inhibitors in order to infer relationships between actomyosin signaling mechanisms and shape phenotypes. Similarities in shape dynamics between DMSO and non-DMSO controls, between the two MEK inhibitors, and under different doses of the same drugs, validates the morphological states and state transitions as fundamentally reflecting target-specific effects. Similar dynamic responses in cell shape induced by EGFR, MEK, and calpain inhibition suggest that these species function along a common signaling axis of cell shape regulation in MDA-MB-231 breast cancer cells (Fig. 6B). This result is in concordance with previous molecular mechanistic studies performed in fibroblasts, which showed that m-calpain activity is directly regulated by Erk by altering its spatial localization and association with PI(4,5)P2 at the plasma membrane.46 This process can be mediated by EGFR signaling through PLC-γ, which depletes PI(4,5)P2 at the leading edge resulting in localization and activation of m-calpain at the trailing end that plays an important role in migratory cell polarization. The increased elongation phenotype induced by calpain inhibition revealed from our analysis (Fig. S6A, ESI†) reflects the role of m-calpain in adhesion remodeling, the inhibition of which leads to trailing end retraction defects.47,48
Moreover, our observation that ROCK and myosin II inhibitors biased cells toward branched and elongated morphologies is consistent with reported effects of increased actomyosin tension promoting cell polarization and limiting the formation of new protrusions.49–52 The increased elongation and branching dynamics we observed reflect the impairment in actomyosin contractility and loss of cell polarity upon ROCK and myosin II inhibition, leading to multiple competing protrusions extending outwards around the cell periphery. Given that MLCK and ROCK are both known to induce myosin II phosphorylation and activation, we may have expected their inhibition to promote similar shape dynamics. Instead, the surprisingly dissimilar and near-opposite morphologies that their inhibition produced (Fig. 5B) suggests that MLCK and ROCK differentially affect cytoskeletal dynamics; this notion is supported by previous studies which showed that MLCK and ROCK have spatially distinct roles in regulating myosin II activity, and whose activities have opposite effects on the number of lamellipodial protrusions, cell elongation, and polarization.50,53 The MDA-MB-231 cell shapes induced by MLCK inhibition in our work are reflective of single-front motile cell morphologies for which formation of additional lamellipodial protrusions is limited (Video S3, ESI†), as has been suggested to also occur in keratocytes at different stages of development.53 The differential effects of ROCK and MLCK inhibition on shape dynamics that we identified through our analyses (Fig. 8) may have consequential effects on overall cell polarization and migratory behavior in cancer that warrants further investigation in future work.
More generally, the plasticity and variability in shape revealed in our analyses reflects the highly dynamic cytoskeletal changes characteristic of protrusion and retraction events, such as those of migratory cells undergoing directional changes or motility cycles. In light of this, further exploration of interest would be to characterize and understand what cellular functions the morphological states captured by HMM annotation may represent. Qualitative visual inspection suggests that cells in rounder states have higher amounts of cortical actin, whereas those in more elongated states are polarized and may therefore be migratory (Fig. 2B and Videos S1–S3, ESI†). Future studies will focus on characterizing morphological state properties in more depth by quantifying cytoskeletal organization in addition to whole-cell shape, incorporating signaling status from live or fixed-cell fluorescent reporters in post-capture analysis,24,54 and combining model-annotated state-space dynamics with motility measurements to establish temporal relationships between morphology and migratory behavior.27,55,56
Notwithstanding, the current work demonstrates that phenotypic information derived from imaging-based models of temporal shape dynamics reflects underlying signaling pathway activities that regulate cell shape, which enables hypothesis generation for more in-depth, mechanistic follow-up studies. In vitro profiling of phenotype dynamics is also relevant in the context of early-phase drug discovery. In that context, time series modeling of live-cell phenotypes can complement existing fixed-cell imaging methods as well as genetic and biochemical approaches for understanding cellular drug responses, particularly with the advent of genome editing approaches such as CRISPR/Cas9.57–61 The collective implementation and application of these approaches will become an increasingly important component of integrative drug profiling and holistic understanding of cell function.
Materials and methods
Software and image data availability
The files necessary to run SAPHIRE are available as a software package that can be downloaded in its latest version at http://saphire-hcs.org. A demo with sample cell image data, instructions, and scripts is provided for using the trajectory editing GUI tool, time series modeling, phenotypic profile computation for groups of cells, and visualization of SAPHIRE outputs.Generation of fluorescent reporter cells
Cells were generated with fluorescent reporters for both actin to provide for cell shape and histones to label nuclei. A pBABE-HistoneH2B-mCherry retroviral plasmid was a gift from Dr Iain Cheeseman (MIT Whitehead Institute). LifeAct-eGFP was inserted between the XhoI-EcoRI sites in pMSCV-puro vector using standard molecular biology techniques. Replication-incompetent virus was purified from HEK-293T cells using standard protocols. Supernatants containing LifeAct-eGFP or H2B-mCherry packaged virus were harvested at 48–72 h after transfection, and passed through 0.45 μm filter prior to use for transduction of target cells (Pall Corp., Cortland, NY). MDA-MB-231 cells were transduced with LifeAct-eGFP and H2B-mCherry filtered viral supernatants containing 8 μg mL−1 polybrene (Millipore). Selection and propagation of transduced MDA-MB-231 cells was performed by culture in 1 μg mL−1 Puromycin (Sigma) in complete DMEM media. To make the stable fluorescent cell population more uniform in the expression of the two reporters, cells were sorted for double-positive intensities in the 80–90 percentile of the population using a MoFlo3 flow cytometer (Beckman Coulter, Inc.).Cell culture, live-cell imaging, and drug perturbations
The triple negative breast cancer cell line MDA-MB-231 (ATCC) stably expressing LifeAct-eGFP and histone H2B-mCherry was used in all experiments. Cells were cultured in high-glucose Dulbecco's Modified Eagle Medium (DMEM) (Life Technologies) supplemented with 10% HyClone fetal bovine serum (Thermo Scientific), 1% penicillin/streptomycin (Gibco), and 1% GlutaMAX (Life Technologies) at 37 °C and 5% CO2. For drug perturbation imaging experiments, Nunclon Delta 96-well optical bottom plates (Thermo Scientific) were coated with 5 μg cm−2 pH-neutralized, acid-extracted, nonpepsin digested collagen I (BD Biosciences) for 1 hour at 37 °C and 5% CO2. All wells were then washed twice with PBS and once with culture media prior to cell seeding. Following plate coating with collagen, cells were seeded at a density of 1000 cells per cm2 in culture medium and incubated at 37 °C and 5% CO2 for 24 hours. Following the 24 hour incubation, the culture media was replaced with drug-containing imaging culture media and the plates were immediately transferred to the microscope for live imaging. The time delay between drug addition and start of image acquisition was approximately 30 minutes to 1 hour.Two imaging experiments were performed: for the experiment with the expanded panel of drugs cells were imaged on an IncuCyte ZOOM system incubated at 37 °C and 5% CO2 under a standard scanning protocol (Essen Bioscience) in drug-containing DMEM growth media (see above). Cells were imaged over approximately 18 hours at 20 minute intervals, with three wells per drug condition and four fields of view per well, producing an image data set of 84 fields (4452 time series image frames), from which 293 individual cell trajectories, with an average of 53 time frames, were obtained for further analyses. For the other experiment, which contained the experimental controls, cells were imaged in Leibovitz's L-15 media (Life Technologies) supplemented with the same additives as the DMEM culture media above, on a Nikon Eclipse Ti microscope equipped with an Andor Zyla sCMOS camera. Cells were imaged over approximately 18 hours at 8 minute intervals, with three wells per drug condition and four fields of view per well, producing an image data set of 96 fields (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 128 time series image frames), from which 435 individual cell trajectories, with an average of 100 time frames, were obtained for further analyses. All inhibitor stocks were dissolved in dimethyl sulfoxide (DMSO) (Sigma), other than Y-27632, which was dissolved in high-purity water. All final concentrations of inhibitors in culture media used for imaging were at 0.1% v/v DMSO or lower. In both experiments cells were imaged using a 0.30 NA Nikon Plan Fluor 10× air objective. The inhibitors used in this work and their vendor sources were as follows: AZD6244 (MEK inhibitor; Selleck Chem.), ML-7 (MLCK inhibitor; Enzo Life Sciences), Blebbistatin(+/−) (non-muscle myosin II inhibitor; Enzo Life Sciences); Gefitinib (EGFR inhibitor; LC Labs), PD0325901 (MEK inhibitor; LC Labs), Y-27632 (ROCK inhibitor; Enzo Life Sciences), PD150606 (Calpain inhibitor; EMD Millipore).
128 time series image frames), from which 435 individual cell trajectories, with an average of 100 time frames, were obtained for further analyses. All inhibitor stocks were dissolved in dimethyl sulfoxide (DMSO) (Sigma), other than Y-27632, which was dissolved in high-purity water. All final concentrations of inhibitors in culture media used for imaging were at 0.1% v/v DMSO or lower. In both experiments cells were imaged using a 0.30 NA Nikon Plan Fluor 10× air objective. The inhibitors used in this work and their vendor sources were as follows: AZD6244 (MEK inhibitor; Selleck Chem.), ML-7 (MLCK inhibitor; Enzo Life Sciences), Blebbistatin(+/−) (non-muscle myosin II inhibitor; Enzo Life Sciences); Gefitinib (EGFR inhibitor; LC Labs), PD0325901 (MEK inhibitor; LC Labs), Y-27632 (ROCK inhibitor; Enzo Life Sciences), PD150606 (Calpain inhibitor; EMD Millipore).
Image processing
Time series stacks were exported as monochrome images from the red and green channel for LifeAct-eGFP (actin) and histone H2B-mCherry (nuclei) reporters, respectively. All images were batch processed using a custom pipeline written in MATLAB (Mathworks, Inc.). First, time series images were drift-corrected with the StackReg plugin in ImageJ using the nuclear reporter channel relative to the first time frame and cropped to maintain identical field of view regions in the nuclei and actin reporter image stacks for each field individually. Nuclei in each image were then segmented using point-source detection.62 User-assisted cell body segmentation from the actin reporter channel was performed for the first frame of each time series stack. Otsu intensity and Canny edge detection thresholds were set by the user for the first frame of a time series for each field of view, with the cell masks generated by combining the binary Otsu foreground and Canny edge pixels. The thresholds were modified through time for each field of view automatically for the second frame onward using a parameter gradient search that minimized the sum of the difference in area, perimeter, and solidity of foreground objects between a previous and subsequent frame. For each connected foreground object, nuclei centers were used to form holes in the binary object mask that enabled detection of touching cells by computing the Euler number for the object. Segmented cell body regions without spatial overlap with segmented nuclei were removed. Segmented nuclei were tracked over time using the IDL tracking method implementation.63 To avoid bias of cell–cell interaction effects on morphology, touching cells were automatically identified as two or more segmented nuclei within a segmented cell body region in a given frame, and subsequently flagged for removal. A graphical user interface was developed to correct cell body segmentation inaccuracies and to label dividing or dying cells (Fig. 2). Continuous cell trajectories with no division, death, or intercellular spatial interactions were retained for both imaging experiments and subsequent analyses.Cell shape quantification and shape-space definition
Eighteen whole-cell shape features were computed from the binary masks of each cell at every time point in both imaging experiments (Table S1, ESI†). Here, we call a temporal snapshot of a cell a “cell object”. For each imaging experiment separately, the raw shape features from all cell objects were combined into an n × m matrix A, where n is the total number of cell objects and m is the number of shape features. The matrix was z-score normalized across cell objects for each feature (along columns). For the imaging experiment where the expanded panel of drugs was tested, we performed dimensionality reduction using PCA onto a two-dimensional basis from the covariance matrix of A, making the PCs linear combinations of the shape features with points in PC space corresponding to cell objects. The PCA coefficients derived from cells imaged in the expanded drug panel experiment were then used to project the shape features from the other experiment (with drug doses and controls) onto the same two-dimensional PC basis. Reducing data dimensionality using PCA dampens the effects of features in the model that contribute little to shape variability across cells and removes correlations between features used for subsequent modeling steps. With this projection, the shape trajectory of a cell is converted from a T × m matrix, where T is the number of time points, to a T × 2 matrix, where the two columns correspond to the two linearly independent PCs. The T × 2 matrices for each cell represent bivariate temporal trajectories in the two-dimensional PC space that we define as the “shape-space”. The bivariate temporal trajectories are then used for subsequent shape state identification and time series modeling. GMM using expectation maximization and Bayesian information criterion (BIC) for model selection were used for GMM analyses of simulated and experimental data and implemented using the mclust package in R.Probabilistic time series modeling
A bivariate temporal trajectory for an individual cell whose shape dynamics we wish to model is comprised of T time points each with an (xt, yt) coordinate at each time point t ∈ {1,…,T} in two-dimensional PC shape-space. We model the coordinates as emissions et = (xt, yt) from K number of “hidden” shape states, {si}Ki=1, K = {1, 2, 3,…}. We represent each shape state as a symmetric, bivariate Gaussian distribution with mean μi = (μx,i, μy,i) and standard deviation along both PC coordinates, σi = σx,i = σy,i. The covariance matrix of x and y is diagonal, and we write the probability of the point et in shape-space coming from shape state si as:We next consider the set of points et for the entire cell trajectory (et∀t ∈ {1,…,T}), resulting in a T × 2 matrix, e. Because the number of hidden shape states, and the parameters μi and σi for each state si that lead to the emissions e are unknown, we test models Mk with different numbers of hidden states, k ∈ K, and select the model that best fits the cell trajectory shape-space data, e. Bayesian model selection is used to evaluate how well each model fits the data in order to select the best model, inherently penalizing increased model complexity (i.e., increasing number of states),
with the proportionality holding since we consider the prior probabilities of all models Mk to be equal. Importantly, points in e are not independent as they represent a temporal evolution in shape of the same cell. A hidden Markov model in the framework is used to incorporate the temporal dependencies in e and infer parameters that describe the dynamic properties (state transitions). Therefore, for each model, Mk, its full set of parameters θk that must be inferred from the data are
| θk = [{μx,i,μy,i,σi}Ki=1, {πi}Ki=1, {ϕij}Ki,j=1] |
The summation over states in brackets, [·], is the probability, P(e|Mk, θk), of the observed temporal sequence of coordinates in shape-space of the cell trajectory, e, conditioned on a particular model with k hidden shape states, Mk, and its parameters, θk. Summation over the hidden state sequences is performed using the forward algorithm. Metropolis Markov Chain Monte Carlo (MCMC) with importance sampling is used to sample parameter space in order to integrate the marginalized likelihood, with the prior probability of the parameters given the model, P(θk|Mk), taken as constant.39 The resulting MCMC integration yields the total marginalized likelihood of each model, P(e|Mk), and its maximum likelihood (ML) parameters,
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) k. The model with the highest marginalized likelihood is chosen to describe the shape dynamics of the cell, with the most likely hidden shape state sequence calculated by the Viterbi algorithm using the ML parameters.
k. The model with the highest marginalized likelihood is chosen to describe the shape dynamics of the cell, with the most likely hidden shape state sequence calculated by the Viterbi algorithm using the ML parameters.
SAPHIRE model-derived phenotypic profiles for drug comparisons
Annotated shape state sequences of individual trajectories from identically treated cells were combined to generate a phenotypic profile for that treatment condition. A phenotypic profile is a 48-element numerical vector composed of four types of histograms that capture shape dynamics: state radial distances and state dwell times, collectively called “state location features”, as well as state transition magnitudes and state transition dwell times, collectively called “state transition features”. These features are derived as follows (see illustration in Fig. 5A).For each inferred Gaussian state si in shape-space from a temporally annotated sequence, we convert the coordinates of the state mean value in the Cartesian PCA axes (μx,si, μy,si) to polar coordinates (μr,si, μθ,si). As a result, rsi becomes the location vector of the state in shape-space and |rsi| is the radial distance of the state from the origin, where |·| denotes vector magnitude. θ is the angle rsi makes in the counterclockwise direction with the positive PC1 axis for state si. For each state si the state radial distance is described by |rsi|, or equivalently 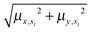 . The normalized state dwell time for si is calculated as
. The normalized state dwell time for si is calculated as 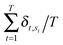 , where δt,si = 1 if the state is si in the model-annotated state sequence at time t, and 0 otherwise, with T equal to the number of elements in the sequence (i.e. number of time frames in the cell trajectory). For a given cell trajectory, we derive an angular histogram with twelve bins on the range of 0 to 360 degrees, with the first bin 0 to 30 degrees, second bin 30 to 60 degrees, and so on until the twelfth bin that ranges from 330 to 360 degrees. For all states si ∈ S in the cell sequence, the state radial distance value of each bin is computed as 〈|rsi|〉 where 〈·〉 denotes the mean, for all states si with μθ,si falling within the angular range of the bin, to generate a histogram of state radial distances. A state radial distance profile for a treatment condition is then computed as the average within each bin in the twelve-bin state radial distance histograms for all cells in that treatment condition. The state dwell time profile of the treatment condition is similarly computed except averaging normalized state dwell time values for states of each cell instead of the state radial distances for twelve angular bins.
, where δt,si = 1 if the state is si in the model-annotated state sequence at time t, and 0 otherwise, with T equal to the number of elements in the sequence (i.e. number of time frames in the cell trajectory). For a given cell trajectory, we derive an angular histogram with twelve bins on the range of 0 to 360 degrees, with the first bin 0 to 30 degrees, second bin 30 to 60 degrees, and so on until the twelfth bin that ranges from 330 to 360 degrees. For all states si ∈ S in the cell sequence, the state radial distance value of each bin is computed as 〈|rsi|〉 where 〈·〉 denotes the mean, for all states si with μθ,si falling within the angular range of the bin, to generate a histogram of state radial distances. A state radial distance profile for a treatment condition is then computed as the average within each bin in the twelve-bin state radial distance histograms for all cells in that treatment condition. The state dwell time profile of the treatment condition is similarly computed except averaging normalized state dwell time values for states of each cell instead of the state radial distances for twelve angular bins.
We additionally derive state transition profiles for each treatment condition. Consider for a given cell a state transition from si to sj. The state transition direction θsji for sj from state si is the angle that the vector rsj − rsi makes in the counterclockwise direction with the positive PC1 axis in shape-space. The state transition magnitude for sj from state si is computed as |rsj − rsi| scaled by the normalized state transition dwell time. The normalized state transition dwell time for sj from state si is calculated as the number of time points a cell spends in state sj after transitioning to it from state si, divided by the sequence length, T. The state transition dwell time value of each of the twelve angular bins is the mean of the normalized state transition dwell times of all states whose means (μr,si, μθ,si) are in the bin. For transition directions θsji for all i ≠ j and a given cell, the state transition magnitude value of each of the twelve angular bins is computed as 〈|rsj − rsi|〉 for all θsji falling within the angular range of each bin, to produce a histogram of state transition magnitudes. A state transition magnitude profile for a treatment condition is then calculated as the average within each bin in the twelve-bin state transition histograms for all cells in that treatment condition. A state transition dwell time profile is similarly computed except averaging normalized state transition dwell times across cells for the twelve angular bins instead of the transition magnitudes.
To quantify similarities in effects of treatment conditions on cell shape dynamics, clustering using average linkage of Euclidean distances between phenotypic profiles was performed for treatment pairs to generate cluster dendrograms. Internal nodes were re-sorted into optimal leaf order without dividing the clusters or changing overall tree connectivity so that treatments with similar profiles are next to each other by maximizing the sum of similarities (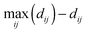 , where i is a leaf adjacent to leaf j) between adjacent tree leaves.
, where i is a leaf adjacent to leaf j) between adjacent tree leaves.
Permutation testing was used to assess significance of Euclidean distances (similarities) between all pairs of treatments as follows. Dynamic phenotype profiles (48-element vectors) based on state locations and state transitions and corresponding dwell times (see above) of individual cells within any two treatment conditions being compared were randomly reassigned into the two treatments while preserving the number of cells and their signatures. Signature values were averaged between the randomly-assigned cells for a given treatment to generate a treatment profile. A permutation test p-value for similarity between two treatment profiles was quantified by comparing the actual Euclidean distance between the treatment profiles relative to the null distribution of distances between profiles that were obtained by repeating the cell assignment randomizations and distance calculations 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times for each pair of treatments.
000 times for each pair of treatments.
Drug classification and comparison with existing methods
To compare between various image-based profiling methods for classifying treatment conditions, we followed an analysis procedure similar to the one described previously.15 Four existing state-of-the-art methods for generating treatment profiles from fixed-cell measurements were implemented for comparison with the temporal modeling framework presented in this work: “Means”,42 “K–S Statistic”,10 “Factor Analysis + Means”,44 and “Gaussian Mixture”,43 all of which were previously compared in an HCI drug classification performance study.15 For each method, all cellular image snapshots were extracted from the time series movies for all treatment conditions at 1, 4, 8, 12, and 16 hours following treatment addition, as if a researcher would make fixed-cell imaging measurements at these time points in an HCI experiment.Briefly, the “Means” approach averages each of the 18 cell shape features for each treatment condition for the five time points to generate a phenotypic profile for a treatment. For the “K–S Statistic”, the cumulative distribution function (cdf) is compared between the treatment and DMSO control cells for each shape feature separately. A signed Kolmogorov–Smirnov (K–S) statistic is then computed for each treatment, which is equal to the maximum distance between the two cdfs and set to positive if the treatment cdf is above the control cdf and negative otherwise. A “K–S Statistic” profile for a treatment is a vector of concatenated signed K–S statistics for each shape feature. For the “Factor Analysis + Means” method we first performed factor analysis on cells from all treatments at the five time points, selecting the number of factors using the Kaiser criterion, and then computed the average value of the scores of each factor for the cells in each treatment condition to generate a profile for that treatment. Finally, for the “Gaussian Mixture” method, a GMM with no covariance matrix constraints was fit to cell observations from all treatments at each time point separately using all shape features as variables, testing models with 2 to 30 mixtures, and selecting the best-fitting model using BIC. For each treatment, the posterior probability of each cell under that treatment belonging to each of the mixtures was computed and averaged across cells for each mixture to generate a profile at a given time point. The averaged posterior probabilities of all mixtures and time points were combined to generate a phenotypic profile for each treatment.
Treatment classification accuracy was assessed for each of the profiling methods described above, as well as using the profiles derived from the single-cell temporal modeling using SAPHIRE. To assess the value of the HMM in treatment classification, treatment profiles extracted from shape-space analyses of cellular dynamics without the HMM annotations were generated identically as for SAPHIRE but by treating each time point in a cell trajectory as a separate “state” (i.e. no modeling of PCA coordinates from underlying hidden Gaussian states). Treatment condition classification accuracy was assessed by computing pair-wise Euclidean distances between phenotypic profiles of treatments using each of the profiling approaches separately. A treatment was designated as being correctly classified if its phenotypic profile was closest, in terms of distance, to that of the same treatment at a different dose, compared to the profiles from other treatments.15
Abbreviations
| BIC | Bayesian information criterion |
| EGFR | Epidermal growth factor receptor |
| GMM | Gaussian mixture modeling |
| HCI | High-content imaging |
| HMM | Hidden Markov modeling |
| PC | Principal component |
| PCA | Principal component analysis |
| MEK | Mitogen-activated protein kinase kinase |
| MLCK | Myosin light chain kinase |
| ROCK | Rho-associated protein kinase |
| SAPHIRE | Stochastic annotation of phenotypic individual-cell responses |
Acknowledgements
We would like to acknowledge Shannon Hughes for guidance on experimental elements of this work, and Nilah Monnier, Syuan-Ming Guo, Zachary Barry, and Russell McConnell for helpful discussions. We are grateful to the assistance of staff from the Imaging and Flow Cytometry cores of the Swanson Biotechnology Center at the MIT Koch Institute for Cancer Research. This work was supported by NIGMS grant GM69668 (A.W., D.A.L.), NSF PoLS PHY 1305537 (M.B.), and the Ludwig Postdoctoral Fellowship (M.K.H.).References
- F. Fuchs, G. Pau, D. Kranz, O. Sklyar, C. Budjan, S. Steinbrink, T. Horn, A. Pedal, W. Huber and M. Boutros, Mol. Syst. Biol., 2010, 6, 370 CrossRef PubMed.
- L.-H. Loo, L. F. Wu and S. J. Altschuler, Nat. Methods, 2007, 4, 445–453 CAS.
- M. D. Treiser, E. H. Yang, S. Gordonov, D. M. Cohen, I. P. Androulakis, J. Kohn, C. S. Chen and P. V Moghe, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 610–615 CrossRef CAS PubMed.
- S. Vega, A. Dhaliwal, V. Arvind, P. J. Patel, N. R. M. Beijer, J. De Boer, N. S. Murthy, J. Kohn and P. V Moghe, Integr. Biol., 2015, 7, 435–446 RSC.
- E. Glory and R. F. Murphy, Dev. Cell, 2007, 12, 7–16 CrossRef CAS PubMed.
- A. Mazumder, L. Q. Pesudo, S. McRee, M. Bathe and L. D. Samson, Nucleic Acids Res., 2013, 41, 9310–9324 CrossRef CAS PubMed.
- M. J. Wawer, K. Li, S. M. Gustafsdottir, V. Ljosa, N. E. Bodycombe, M. a Marton, K. L. Sokolnicki, M.-A. Bray, M. M. Kemp, E. Winchester, B. Taylor, G. B. Grant, C. S.-Y. Hon, J. R. Duvall, J. A. Wilson, J. a Bittker, V. Dančík, R. Narayan, A. Subramanian, W. Winckler, T. R. Golub, A. E. Carpenter, A. F. Shamji, S. L. Schreiber and P. a Clemons, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10911–10916 CrossRef CAS PubMed.
- A. Y. J. Ng, J. C. Rajapakse, R. O. Y. E. Welsch, P. T. Matsudaira, V. Horodincu and J. G. Evans, J. Biomol. Screening, 2010, 15, 858–868 CrossRef CAS PubMed.
- C. Bakal, J. Aach, G. Church and N. Perrimon, Science, 2007, 316, 1753–1756 CrossRef CAS PubMed.
- Z. E. Perlman, M. D. Slack, Y. Feng, T. J. Mitchison, L. F. Wu and S. J. Altschuler, Science, 2004, 306, 1194–1198 CrossRef CAS PubMed.
- J. Candia, R. Maunu, M. Driscoll, A. Biancotto, P. Dagur, J. P. McCoy, H. N. Sen, L. Wei, A. Maritan, K. Cao, R. B. Nussenblatt, J. R. Banavar and W. Losert, PLoS Comput. Biol., 2013, 9, e1003215 CAS.
- T. R. Jones, A. E. Carpenter, M. R. Lamprecht, J. Moffat, S. J. Silver, J. K. Grenier, A. B. Castoreno, U. S. Eggert, D. E. Root, P. Golland and D. M. Sabatini, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 1826–1831 CrossRef CAS PubMed.
- Z. Yin, A. Sadok, H. Sailem, A. McCarthy, X. Xia, F. Li, M. A. Garcia, L. Evans, A. R. Barr, N. Perrimon, C. J. Marshall, S. T. C. Wong and C. Bakal, Nat. Cell Biol., 2013, 15, 1–13 CrossRef PubMed.
- C.-J. Ku, Y. Wang, O. D. Weiner, S. J. Altschuler and L. F. Wu, Cell, 2012, 149, 1073–1083 CrossRef CAS PubMed.
- V. Ljosa, P. D. Caie, R. Ter Horst, K. L. Sokolnicki, E. L. Jenkins, S. Daya, M. E. Roberts, T. R. Jones, S. Singh, A. Genovesio, P. a Clemons, N. O. Carragher and A. E. Carpenter, J. Biomol. Screening, 2013, 18, 1321–1329 CrossRef CAS PubMed.
- U. Schnell, F. Dijk, K. A. Sjollema and B. N. G. Giepmans, Nat. Methods, 2012, 9, 152–158 CrossRef CAS PubMed.
- L. Bosgraaf and P. J. M. Van Haastert, Cell Adh. Migr., 2010, 4, 46–55 CrossRef PubMed.
- D. Tsygankov, C. G. Bilancia, E. a. Vitriol, K. M. Hahn, M. Peifer and T. C. Elston, J. Cell Biol., 2014, 204, 443–460 CrossRef CAS PubMed.
- D. J. Barry, C. H. Durkin, J. V. Abella and M. Way, J. Cell Biol., 2015, 209, 163–180 CAS.
- M. Machacek and G. Danuser, Biophys. J., 2006, 90, 1439–1452 CrossRef CAS PubMed.
- Y. Tsukada, K. Aoki, T. Nakamura, Y. Sakumura, M. Matsuda and S. Ishii, PLoS Comput. Biol., 2008, 4, e1000223 Search PubMed.
- M. K. Driscoll, C. Mccann, R. Kopace, T. Homan, J. T. Fourkas, C. Parent and W. Losert, PLoS Comput. Biol., 2012, 8, e1002392 CAS.
- M. Veronika, R. Welsch, A. Ng, P. Matsudaira and J. C. Rajapakse, BMC Bioinf., 2011, 12, S19 CrossRef CAS PubMed.
- C. M. Welch, H. Elliott, G. Danuser and K. M. Hahn, Nat. Rev. Mol. Cell Biol., 2011, 12, 749–756 CrossRef CAS PubMed.
- M. K. Driscoll, W. Losert, K. Jacobson and M. Kapustina, Cytoskeleton, 2015, 281, 1–27 Search PubMed.
- D. Tsygankov, P.-H. Chu, H. Chen, T. C. Elston and K. M. Hahn, in Methods in Cell Biology, ed. J. Waters and T. Wittman, Elsevier, Amsterdam, 1st edn, 2014, vol. 123, pp. 409–427 Search PubMed.
- K. Keren, Z. Pincus, G. M. Allen, E. L. Barnhart, G. Marriott, A. Mogilner and J. A. Theriot, Nature, 2008, 453, 475–480 CrossRef CAS PubMed.
- J. E. Bear and J. M. Haugh, Curr. Opin. Cell Biol., 2014, 30C, 74–82 CrossRef PubMed.
- X. Liu, E. S. Welf and J. M. Haugh, J. R. Soc., Interface, 2015, 12, 20141412 CrossRef PubMed.
- M. C. Weiger, S. Ahmed, E. S. Welf and J. M. Haugh, Biophys. J., 2010, 98, 67–75 CrossRef CAS PubMed.
- M. C. Weiger, C.-C. Wang, M. Krajcovic, A. T. Melvin, J. J. Rhoden and J. M. Haugh, J. Cell Sci., 2009, 122, 313–323 CrossRef CAS PubMed.
- S. J. Henry, C. Crocker and D. A. Hammer, Integr. Biol., 2014, 6, 348–356 RSC.
- R. Kafri, J. Levy, M. B. Ginzberg, S. Oh, G. Lahav and M. W. Kirschner, Nature, 2013, 494, 480–483 CrossRef CAS PubMed.
- H. Sailem, V. Bousgouni, S. Cooper and C. Bakal, Open Biol., 2014, 4, 130132 CrossRef PubMed.
- J. E. Sero, H. Z. Sailem, R. C. Ardy, H. Almuttaqi, T. Zhang and C. Bakal, Mol. Syst. Biol., 2015, 11, 790 CrossRef PubMed.
- M. Held, M. H. a Schmitz, B. Fischer, T. Walter, B. Neumann, M. H. Olma, M. Peter, J. Ellenberg and D. W. Gerlich, Nat. Methods, 2010, 7, 747–754 CrossRef CAS PubMed.
- Q. Zhong, A. G. Busetto, J. P. Fededa, J. M. Buhmann and D. W. Gerlich, Nat. Methods, 2012, 9, 711–713 CrossRef CAS PubMed.
- C. Fraley and A. E. Raftery, J. Am. Stat. Assoc., 2002, 97, 611–631 CrossRef.
- N. Monnier, Z. Barry, H. Y. Park, K. Su, Z. Katz, B. P. English, A. Dey, K. Pan, I. M. Cheeseman, R. H. Singer and M. Bathe, Nat. Methods, 2015, 12, 1–7 CrossRef PubMed.
- D. Posada and T. Buckley, Syst. Biol., 2004, 53, 793–808 CrossRef PubMed.
- A. E. Raftery, Sociol. Methodol., 1995, 25, 111–163 CrossRef.
- M. Tanaka, R. Bateman, D. Rauh, E. Vaisberg, S. Ramachandani, C. Zhang, K. C. Hansen, A. L. Burlingame, J. K. Trautman, K. M. Shokat and C. L. Adams, PLoS Biol., 2005, 3, e128 Search PubMed.
- M. D. Slack, E. D. Martinez, L. F. Wu and S. J. Altschuler, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 19306–19311 CrossRef CAS PubMed.
- D. W. Young, A. Bender, J. Hoyt, E. McWhinnie, G.-W. Chirn, C. Y. Tao, J. a Tallarico, M. Labow, J. L. Jenkins, T. J. Mitchison and Y. Feng, Nat. Chem. Biol., 2008, 4, 59–68 CrossRef CAS PubMed.
- Z. Yin, H. Sailem, J. Sero, R. Ardy, S. T. C. Wong and C. Bakal, BioEssays, 2014, 36, 1195–1203 CrossRef PubMed.
- L. Leloup, H. Shao, Y. H. Bae, B. Deasy, D. Stolz, P. Roy and A. Wells, J. Biol. Chem., 2010, 285, 33549–33566 CrossRef CAS PubMed.
- A. Glading, D. a Lauffenburger and A. Wells, Trends Cell Biol., 2002, 12, 46–54 CrossRef CAS PubMed.
- S. J. Franco and A. Huttenlocher, J. Cell Sci., 2005, 118, 3829–3838 CrossRef CAS PubMed.
- H. Elliott, R. S. Fischer, K. a. Myers, R. a. Desai, L. Gao, C. S. Chen, R. S. Adelstein, C. M. Waterman and G. Danuser, Nat. Cell Biol., 2015, 17, 137–147 CrossRef CAS PubMed.
- G. Totsukawa, Y. Wu, Y. Sasaki, D. J. Hartshorne, Y. Yamakita, S. Yamashiro and F. Matsumura, J. Cell Biol., 2004, 164, 427–439 CrossRef CAS PubMed.
- M. Vicente-Manzanares, J. Zareno, L. Whitmore, C. K. Choi and A. F. Horwitz, J. Cell Biol., 2007, 176, 573–580 CrossRef CAS PubMed.
- M. Vicente-Manzanares, M. a Koach, L. Whitmore, M. L. Lamers and A. F. Horwitz, J. Cell Biol., 2008, 183, 543–554 CrossRef CAS PubMed.
- S. S. Lou, a. Diz-Munoz, O. D. Weiner, D. a. Fletcher and J. a. Theriot, J. Cell Biol., 2015, 209, 275–288 CrossRef CAS PubMed.
- N. Komatsu, K. Aoki, M. Yamada, H. Yukinaga, Y. Fujita, Y. Kamioka and M. Matsuda, Mol. Biol. Cell, 2011, 22, 4647–4656 CrossRef CAS PubMed.
- J. G. Lock, M. J. Mamaghani, H. Shafqat-Abbasi, X. Gong, J. Tyrcha and S. Strömblad, PLoS One, 2014, 9, e90593 Search PubMed.
- a. Schoenauer Sebag, S. Plancade, C. Raulet-Tomkiewicz, R. Barouki, J.-P. Vert and T. Walter, Bioinformatics, 2015, 31, i320–i328 CrossRef PubMed.
- M. J. Garnett, E. J. Edelman, S. J. Heidorn, C. D. Greenman, A. Dastur, K. W. Lau, P. Greninger, I. R. Thompson, X. Luo, J. Soares, Q. Liu, F. Iorio, D. Surdez, L. Chen, R. J. Milano, G. R. Bignell, A. T. Tam, H. Davies, J. a. Stevenson, S. Barthorpe, S. R. Lutz, F. Kogera, K. Lawrence, A. McLaren-Douglas, X. Mitropoulos, T. Mironenko, H. Thi, L. Richardson, W. Zhou, F. Jewitt, T. Zhang, P. O'Brien, J. L. Boisvert, S. Price, W. Hur, W. Yang, X. Deng, A. Butler, H. G. Choi, J. W. Chang, J. Baselga, I. Stamenkovic, J. a. Engelman, S. V. Sharma, O. Delattre, J. Saez-Rodriguez, N. S. Gray, J. Settleman, P. A. Futreal, D. a. Haber, M. R. Stratton, S. Ramaswamy, U. McDermott and C. H. Benes, Nature, 2012, 483, 570–575 CrossRef CAS PubMed.
- M. P. Menden, F. Iorio, M. Garnett, U. McDermott, C. H. Benes, P. J. Ballester and J. Saez-Rodriguez, PLoS One, 2013, 8, e61318 CAS.
- M. Niepel, M. Hafner, E. a Pace, M. Chung, D. H. Chai, L. Zhou, B. Schoeberl and P. K. Sorger, Sci. Signaling, 2013, 6, ra84 CrossRef PubMed.
- L. Cong, F. A. Ran, D. Cox, S. Lin, R. Barretto, N. Habib, P. D. Hsu, X. Wu, W. Jiang, L. A. Marraffini and F. Zhang, Science, 2013, 339, 819–823 CrossRef CAS PubMed.
- P. Mali, L. Yang, K. M. Esvelt, J. Aach, M. Guell, J. E. DiCarlo, J. E. Norville and G. M. Church, Science, 2013, 339, 823–826 CrossRef CAS PubMed.
- F. Aguet, C. N. Antonescu, M. Mettlen, S. L. Schmid and G. Danuser, Dev. Cell, 2013, 26, 279–291 CrossRef CAS PubMed.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Fig. S1–S6, Table S1, Videos S1–S3. See DOI: 10.1039/c5ib00283d |
| ‡ 77 Massachusetts Avenue, Building 16, Room 343, Cambridge, MA 02139 USA. E-mail: E-mail: lauffen@mit.edu; Fax: +1-617-258-0204; Tel: +1-617-252-1629 |
| § 77 Massachusetts Avenue, Building 16, Room 255, Cambridge, MA 02139 USA. E-mail: E-mail: mbathe@mit.edu; Fax: +1-617-324-7554; Tel: +1-617-324-5685 |
| This journal is © The Royal Society of Chemistry 2016 |