A surface acoustic wave biosensor for interrogation of single tumour cells in microcavities†
Sukru U.
Senveli
*ac,
Zheng
Ao
bc,
Siddarth
Rawal
bc,
Ram H.
Datar
bc,
Richard J.
Cote
bc and
Onur
Tigli
*abc
aElectrical and Computer Engineering Department, University of Miami, Coral Gables, FL 33146, USA. E-mail: senveli@umiami.edu; tigli@miami.edu
bDepartment of Pathology, University of Miami Miller School of Medicine, Miami, FL 33136, USA
cDr. John T. Macdonald Foundation Biomedical Nanotechnology Institute at University of Miami, Miami, FL 33136 USA
First published on 9th November 2015
Abstract
In this study, biological cells are sensed and characterized with surface acoustic wave (SAW) devices utilising microcavities. After tumour cells in media are transported to and trapped in microcavities, the proposed platform uses SAW interaction between the substrate and the cells to extract their mechanical stiffness based on the ultrasound velocity. Finite element method (FEM) analysis and experimental results show that output phase information is an indicator of the stiffness modulus of the trapped cells. Small populations of various types of cells such as MCF7, MDA-MB-231, SKBR3, and JJ012 were characterized and characteristic moduli were estimated for each cell population. Results show that high frequency stiffness modulus is a possible biomarker for aggressiveness of the tumour and that microcavity coupled SAW devices are a good candidate for non-invasive interrogation of single cells.
Introduction
Circulating tumour cell (CTC) research has become increasingly more important in recent years. CTCs have been shown to be linked to recurrence of cancer and relevant to metastasis.1,2 Consequently, a great deal of effort has been made towards capturing and enrichment of these cells in the recent literature. These approaches range from immunomagnetic separation3 to density gradient centrifugation4 and microfluidic separation.5 After capture, interrogation of these cells is the next challenge.Traditionally, biological cell analysis has been carried out in large cell populations due to lack of tools and means to reach smaller dimensions. This caused researchers to interpret results mainly in terms of averages, and events occurring at cell level were not observable. Furthermore, cell populations are inherently heterogeneous as demonstrated for eukaryotic cells as well as for other biological entities such as homogeneously grown bacteria.6,7 Consequently, it has become increasingly attractive to characterise the properties of single cells in the recent years. Advances in this front are expected to provide better insight into the behaviour of cells, diagnosis of their health and viability, and even treatment of certain diseases. This augmented understanding is being drawn from mainly electrical, optical, and mechanical sensors.8,9 A frontrunner among these technologies is the biomechanics approach to study the mechanics of cells and their connections to diseases.10 Recent pathophysiological studies of various diseases suggest that their etiologies might stem from changes in mechanical properties of cells. Significant examples with strong correlations include malaria and cancer.11
Studies on cancer show that one basis for cancer is the changes in cell mechanics, tissue structure, or both.12 Mechanobiology research shows that epithelial and fibroblast cells change in deformability with cancerous growth.13 Most studies yield 100% or more increase in deformation of cancerous cells for the same mechanical input and even more deformation for metastasized cells. In terms of mechanical parameters, this corresponds to a drop in elasticity or stiffness modulus of the cell, implying that a correlation exists between cancer and mechanical properties. There are various ways of extracting the mechanical properties on cells, and the most widespread technique today is atomic force microscopy (AFM).
An AFM is a table-top device where a very fine tipped stylus on a cantilever comes in contact with a sample for measurement. The deflection of this microcantilever is read out by a laser to obtain the thickness variations and deformability of a sample under test. Studies run by different research groups yielded elasticities in the order of 1 kPa for various types of cancer cells such as MCF7 and mouse mammary cells.14–16 The healthy counterparts of these cells used for control studies yielded much higher elasticities, usually double that of cancer cells. These results along with similar results in the literature show that there are mechanical differences between tumour cells and healthy counterparts as well as between different populations of cells.17 Therefore, the capability of observing the biophysical properties of cells is a definitive asset for better understanding of cancer.
Acoustics and ultrasound technology are tools available for direct investigation of tumours in a non-invasive manner. Ultrasound has been used to study the differences between cancerous and healthy tissues as far back as 1976 and 1986 where different attenuation levels were demonstrated and reported.18,19 More recently, acoustic microscopy methods have been targeting biological specimens at the single cell level. Studies of MCF7 human breast cancer cells with high frequency acoustic microscopy were shown to be capable of distinguishing between apoptotic and non-apoptotic cells.20 The differences between cells and between tissues mainly arise from attenuation and sound velocity that affect the ultrasound waves. Promising candidates for miniaturisation of a similar platform are surface acoustic wave (SAW) devices.
Previous studies in the literature analysed the interaction of SAW with large amounts of liquids placed on the delay line with emphases on manipulation purposes.21,22 For instance, SAW devices have been utilised successfully for effective CTC sorting23 and sorting with fluorescence activation.24 Further cell sorting based on adhesion differences25 was demonstrated as well as cell enrichment directly on blood samples.26 Some other studies used the coupling of other types of waves, such as SH-waves, to viscous liquids to obtain viscosity.27 On the other hand, there were computational studies concerned with applying microcavities for reducing insertion loss and increasing mass loading sensitivity, but not as a direct method of sensing.28 There are also some innovative examples of recent systems for cell measurements where elongation of cells in a flow29 or in constriction30 is analysed using microfluidics. This kind of study also provides insight into the mechanical properties of cells within the context of a microsystem. However, this system works at a low frequency of observation compared to the proposed system in addition to stressing and physically straining the cells to a considerable extent. One of the advantages of using very high frequencies is that the changes in viscous behaviour of cells are not a big concern as will be explained in the following sections. Furthermore, the straining is negligible as compared to low frequency studies.
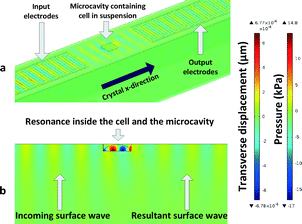
The platform presented in this study follows from the high frequency acoustic interaction idea and utilises direct coupling of Rayleigh type SAWs with cells placed inside microcavities. The microcavity helps trap a predetermined volume of sample inside and facilitates the interaction of the surface waves with the sample via a resonance condition. Through interaction with the samples, the resultant SAW reaching output incurs a phase delay. In our previous studies, the authors analysed the integration of SAW devices with microcavities to enable the interrogation of minute amounts of liquids.31 Now, a model based on that of viscoelastic fluids is used to model stiffness in biological cells and characterize them. The platform is suited to target cells in the range of 10–20 μm, comparable to the wavelength and microcavity dimensions.
The next section explains the use of the physics models for cells. Simulation results from finite element method (FEM) studies are given to form a basis for what to expect from the system. After a brief discussion of fabrication methods, experimental results are presented along with the conclusion and suggestions for future studies.
Results
Modelling single cells in a medium
The mechanical properties of cells have been studied in many different contexts in the literature. One important conclusion from these discussions is that cell behaviour is very heavily dependent on their environment and state as well as the measurement technique. This first set of variables includes parameters such as liquid or dry surroundings of the cell and the chemistry of the cell (for instance, if the cells have been fixed or not). The second set of parameters involves specifics of the setup such as frequency of measurement, applied force, and amount of strain in the cell.Most low frequency studies report cells as elastic with certain recovery characteristics.32 When external stimuli at frequencies lower than the mechanical relaxation time are applied, they deform and then recover accordingly. However, if the frequency of the stimulus is larger than the relaxation time, they act more like solids as they do not have time to react. However, the time constants and elastic moduli obtained from these studies are in the order of ~1 second and ~0.1–10 kPa, respectively. These properties cannot be applied to higher frequency studies since the very soft elastic media defined by these parameters cannot support high frequency acoustic wave propagation. This means that no waves would be transferred to the cell due to its low characteristic acoustic impedance. However, studies suggest that biological tissues as well as single cells can sustain ultrasound frequencies larger than 100 MHz.20,33,34 This is in line with the expectation that different components and properties of the cell can be dominant for different frequencies of the spectrum.
Another factor that defines the behaviour of cells is the nature of the experiments. AFM measurements are taken via sharp probes and therefore represent the response of a very small area of the cell rather than the whole cell. Micropipette aspiration deals with large deformations which are comparable to the cell dimensions in magnitude. The proposed system has displacements in the order of picometres to generate ultrasound waves and considering the size of the cells studied (~10–20 μm), the deformations are many orders of magnitude smaller (~1–10 pm) for applied electrical power levels around 0 dBm. This permits the use of a linear model for elasticity and keeps the platform non-invasive as the cells are not put under large amounts of stress.
In order to achieve appropriate non-invasive high frequency interaction and for the cells to remain viable, they need to remain suspended in a medium for the duration of experiments. The medium needs to contain a minute amount of glycerine as explained in the experiments section. This brings about the question of how viscoelasticity should be accounted for since glycerine has certain viscoelastic properties. However, in the presented case, viscosities associated with aqueous solutions containing small amounts of glycerine remain well within the Newtonian region for common Rayleigh wave SAW device frequency ranges of 100–500 MHz35 as explained in the ESI.†
In the light of these data, the only studies comparable to the proposed one are the acoustic microscopy studies considering the frequency range and experimental conditions. Consequently, the parameters for cells were obtained from acoustic microscopy studies. If a viscoelastic model is considered as before, the velocity of ultrasound in the liquid can be written in terms of density and bulk and shear moduli as
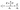 | (1) |
| E = 3K(1 − 2ν) | (2) |
Putting all these together, the cells at high frequencies are modelled as Maxwell materials in suspension with the exception that no shear waves are supported in the bulk of the cell. The elasticity modulus is related to cell density and ultrasound velocity. The apparent or effective viscosity coefficient of the cell can be obtained using the frequency dependent attenuation constant (details are given in the ESI†). Common figures for density, ultrasound velocity, viscosity, and the related stiffness modulus are therefore ~1000 kg m−3, ~1500–1700 m s−1, ~5–10 mPa s, and ~2–3 GPa, respectively. As given by the operation frequency orders of magnitude lower than the Newtonian upper limit, cells act more similar to liquids than inelastic materials with lossy characteristics.
FEM analysis of the platform
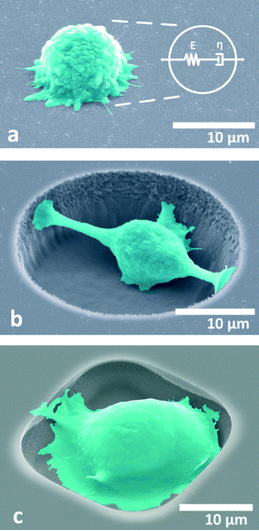
Three dimensional models were set up in Comsol Multiphysics using the coupling of piezoelectric and acoustic domains. As a first approximation it was assumed that the cells occupy most of the space inside microcavities so that the interaction in the microcavity is mostly with cells. Scanning electron microscopy (SEM) investigation shows that cells tend to conform to the shape of sample microcavities as shown in Fig. 1(b and c).Since the shearing effects can be neglected as explained in the previous section and given in (1) and (2), the bulk modulus (or equivalently, elasticity or stiffness modulus) will be given by:
E ≈ ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v2u v2u | (3) |
The simulation models prepared in three dimensions consist of approximately 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tetrahedral elements with approximately 1
000 tetrahedral elements with approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 degrees of freedom. Due to the low electromechanical coupling coefficient of quartz (cited as 0.11% in most sources), 64 electrode pairs were used for both input and output IDTs. The wavelength of the device is 16 μm, and the thickness of the model was set to 80 μm with geometrically increasing element size with distance from the surface to capture the most detail in the surface wave. The highest element detail is at the surface and around the microcavity. Perfectly matched layers were used to terminate the outer edges and corners of the simulation model to avoid standing wave formation and keep the simulation manageable. Periodic voltages were applied to alternating input IDT electrodes as boundary conditions whereas the bottom of the model was mechanically fixed with another boundary condition. Further details on a similar setup were discussed in our previous studies where a more detailed account can be found.38 The difference in the proposed system in this study is that the viscosities of cells differ over a narrow window compared to the large viscosity windows which were investigated in previous studies. Therefore, the sensitivity of the system to viscosity is low. The finite element model used is shown in Fig. 2.
000 degrees of freedom. Due to the low electromechanical coupling coefficient of quartz (cited as 0.11% in most sources), 64 electrode pairs were used for both input and output IDTs. The wavelength of the device is 16 μm, and the thickness of the model was set to 80 μm with geometrically increasing element size with distance from the surface to capture the most detail in the surface wave. The highest element detail is at the surface and around the microcavity. Perfectly matched layers were used to terminate the outer edges and corners of the simulation model to avoid standing wave formation and keep the simulation manageable. Periodic voltages were applied to alternating input IDT electrodes as boundary conditions whereas the bottom of the model was mechanically fixed with another boundary condition. Further details on a similar setup were discussed in our previous studies where a more detailed account can be found.38 The difference in the proposed system in this study is that the viscosities of cells differ over a narrow window compared to the large viscosity windows which were investigated in previous studies. Therefore, the sensitivity of the system to viscosity is low. The finite element model used is shown in Fig. 2.
It was shown in previous studies of finite element method analysis and measurements of the authors that phase angle provides an appropriate way of reading out material properties in the form of delays introduced to the wave being transmitted to the output.31 The viscosity, in contrast to previous observations with high viscosity liquids, is not a good indicator. This is because the observed viscosity from cell to cell is expected to vary by only a small amount of less than about 5 mPa s according to acoustic microscopy studies20 and the platform is not capable of responding to such small viscosity changes as was found in FEM studies.
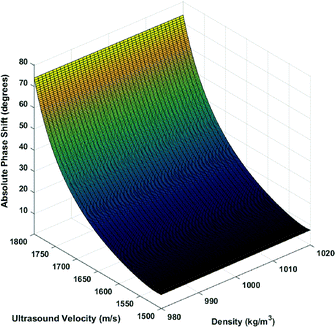
The main property of importance is the ultrasound velocity. The ultrasound velocity changes the angle of incidence of the ultrasound wave emitted into the microcavity, directly affecting the phase of the output. The density also has a small effect as the changes in the acoustic impedance alter the amount of acoustic energy transferred to the liquid domain. However, it is observed in the simulations that the variation due to density is much smaller and can be neglected compared to the effect of ultrasound velocity. Fig. 3 shows the variation in the output phase angle as a function of both density and ultrasound velocity. Therefore, for the models used in this study, the stiffness is mostly a function of ultrasound velocity.
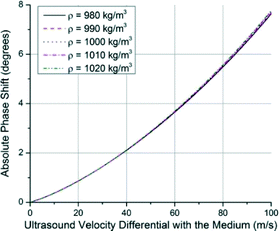
If it is assumed for simulations that the cell density is the same as the medium it is in, ultrasound velocity is left as the determining factor for the modulus of elasticity. In Fig. 4, the change in the phase shift as a function of ultrasound velocity is shown relative to the medium. Ultimately, the phase shift that occurs as a result of placing the cell in the medium is compared to the case where only the medium is occupying the microcavity. The modulus of the cell can be calculated by working back from the phase shift to the velocity differential and plugging it into eqn (3) to find a figure for bulk modulus. The sensitivity increases as the difference between the ultrasound velocity differential grows. A figure for system sensitivity can be calculated from this figure by curve fitting as roughly 0.05° m−1 s−1 or ~0.35° MPa−1 for the region of interest.
Microfabrication
In order to prove the concept for analysing cellular level interrogation, the choice of substrate has been ST-cut quartz (SiO2) excited in the x-direction for Rayleigh wave generation. This specific cut of quartz has an easy and reliable microcavity fabrication process despite a low coupling constant. Furthermore, it has almost perfect temperature stability around room temperature to rule out such environmental contributions. The surface is also hydrophobic and enables dispensation of the droplets using microprobes. A lift-off process was used to fabricate the IDTs whereas the microcavities were etched into the substrate using reactive ion etching (RIE). Details on the fabrication processes are given in the ESI.† The SEM image of a finished device is given in Fig. 5(a).The dispensation of the cells inside microcavities poses a formidable challenge in terms of manipulation. The evaporation of small droplets, strong capillary forces that arise in the physical dimensions of the cells and microcavities (around 20 μm), and the fragility of the cells are the main issues. The first problem was tackled using 5% glycerine in the medium to decrease the vapour pressure considerably to prevent evaporation. It should also be noted that a balanced salt solution (1× HBSS) was used instead of respective cell growth media. The reason for this is to delay the occurrence of lethal pH levels upon excess carbon dioxide production by the cell in such a small volume.39
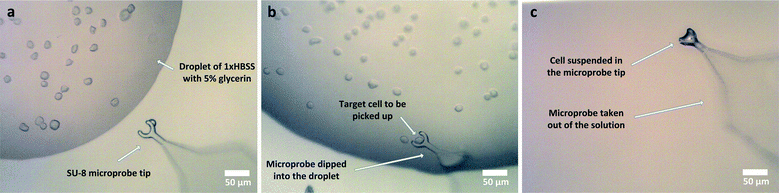
The fragility of the cells makes it difficult to use metal probes for manipulation of droplets in a similar way to previous studies by the authors.31 For this reason, microprobes made out of SU-8, an epoxy based negative photoresist, were used for dispensing the cells into microcavities. SU-8 provides the robust but soft mechanical structure needed. The microfabrication flow for the microprobes is given in the ESI† whereas an SEM image and the microprobe used in the test setup are shown in Fig. 5(b) and (c), respectively. The microprobe tips were designed to simply trap and hold liquid samples using surface tension on the curved tip in the shape of a hook when the tip is brought out of the solution. The tension on the hook shaped tip is larger than the outer perimeter of a droplet so the liquid payload sticks to the tip. However, when the microprobe tip with a small protruding liquid droplet makes contact with the substrate, the droplet expands in diameter, loses contact with the microprobe tip and is released onto the substrate. The result is a uniform and repeatable dispensing process as shown over several microcavities and different angles of incidence in Fig. 6.
The microprobe tip dimensions and shape were determined empirically through experiments as the capillary forces are very hard to determine for the scales used. It was seen that the probes work best when the tip is in a circular shape with an inner diameter of 24 μm with an SU-8 thickness of 6 μm. In order to increase the liquid contact angle on the microprobes for cell studies, i.e. to increase the holding efficiency of the probes, they were dipped in a 100 mM ethanolamine solution for 20 minutes at 50 °C. This process results in an increased number of surface OH groups on the SU-8 and makes it easier for water molecules to attach.40 After ethanolamine treatment, microprobes were attached to 3D printed connector pieces made of ABS plastic which are in turn attached to micropositioners. The operation of the microprobes with cells is shown in Fig. 7 and explained in the next section.
Experiments
SAW delay lines with a wavelength of 16 μm at passband peak frequencies of 196.7 MHz on ST cut quartz were used for direct interrogation of cells. The aperture sizes for the devices correspond to 2λ. All structures have a constant finger overlap and a metallization ratio of unity. Mainly, rectangular shapes of microcavities are used with dimensions of 16 × 16 μm and 16 × 32 μm which correspond to λ × λ and λ × 2λ, respectively. The microcavity depth has been designated as 4 μm or 0.25λ. The given volume is instrumental in that most of the sample volume contained in the microcavity is occupied by the cell in the direction of wave propagation. The results for λ × 2λ microcavity geometries that are larger than the cells were normalized according to their respective sensitivities.Sample testing was carried out one device at a time after cells were dispensed into the microcavities using the microprobes. The operation of microprobes shown in Fig. 7 is based on the surface tension of the samples. The surface tension which was increased due to the presence of glycerine helped the probe tip to hold onto a certain amount of medium. This medium fully covered the cell of interest. When brought to the microcavity site, the microprobe was lowered and brought into contact with the structure to transfer the contents. In the whole process, the cell was never brought out of the liquid surroundings and allowed to dry out. It takes under 30 minutes to dispense a typical batch of cells into microcavities and then measure them with the platform. After measurements were taken, running DI water was applied to the substrate for 15 minutes to clean the residues from the previous measurements. It was visually confirmed using the optical microscope that the microcavities were clean before applying a new sample.
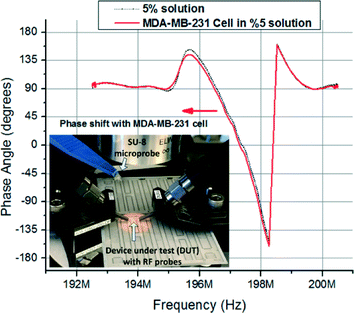
Frequency domain data from devices were collected using an Agilent E5061-B vector network analyser (VNA) and RF probes in the frequency domain. Sample data collected from the VNA are given in Fig. 8. The probes used were ground-signal-ground type RF probes with 100 μm pitch to minimize electromagnetic crosstalk. The input power applied to the devices was −10 dBm. The intermediate frequency bandwidth (IFBW) was set to 300 Hz to ensure stable measurements. Choosing a low IFBW also causes the measurements to take considerably longer but maintains consistent results. Furthermore, measurements were averaged eight times during collection to reduce noise. Analysis of the data was carried out using Matlab, and the phase shift data were measured along the passband of the device. The results were obtained by comparing the cases where the medium alone fills the microcavity and where the cell is in the microcavity. Using this process, the differential properties of the cell in comparison to the medium it displaces are measured and uncertainties due to the glycerine based medium are minimized. Microscope images of cells placed in microcavities are shown in Fig. 9.
 | ||
| Fig. 8 Sample raw data collected from MDA-MB-231 cells whereas the inset shows the setup during measurements. | ||
 | ||
| Fig. 9 (a and b) Dispensed cells. Shown are the cases where the microcavity is empty and when it is filled with only the medium. | ||
A human chondrosarcoma cell line, JJ012, along with breast cancer cell lines MDA-MB-231, SKBR3, and MCF7 were used in the biological cell studies. The breast cancer cell lines were all obtained from ATCC whereas the JJ012 cells were obtained from Dr. Jonathan Trent at Sylvester Comprehensive Cancer Center at University of Miami. All breast cancer cells are epithelial cells derived from the metastatic site originating from pleural effusion. JJ012 cells are of mesenchymal origin (obtained from cartilage tissue) and are known for being hard to treat with radiation methods. All types of cells were cultured separately in RPMI medium. They were incubated at 37 °C under dark conditions and 5% CO2 atmosphere until they reached confluence. They were removed from culture flasks using trypsin, formed into pellets, and resuspended in the measurement medium prepared beforehand. The measurement medium consists of 1× HBSS to maintain isotonicity to extend cell life and to maintain a healthy pH level along with 5% v/v glycerine. The augmentation with glycerine is necessary in order to avoid evaporation during measurements as well as to increase the surface tension for microprobe use as mentioned before. After mixing, the media were vortexed for 1 min and treated in an ultrasonic bath for 30 min to attain homogeneity before addition of the cells.
The residual content from RPMI left in the measurement medium at the resuspension step adversely affected the surface tension of small sized droplets (<50 μm). This makes it very difficult to use the microprobes. In order to address this issue, the cells were processed using a centrifuge machine to form pellets and resuspended in the measurement medium three times, while carefully aspirating the remaining RPMI to the maximum extent.
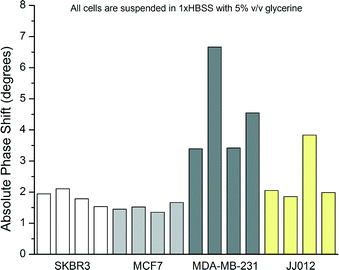
The sizes of the cells were measured using the optical microscope before and after dispensation to ensure that similar size cells were used in order to keep the results consistent. The diameters of the cells were found to be 16.0 ± 0.7 μm, 14.7 ± 2.0 μm, 14.3 ± 1.1 μm, and 15.8 ± 2.1 μm for SKBR3, MCF7, MDA-MB-231, and JJ012 cells, respectively, over the populations used for stiffness measurements. At least five different cells were measured from each population. Single results from some sample cells are shown in Fig. 10. Similar dimensions of the cells given above also further justify the correlation between ultrasound velocity and phase shift by ruling out solely size-based detection. Overall populations yield phase shifts of 1.84° ± 0.24°, 1.62° ± 0.57°, 4.26° ± 1.43°, and 2.43° ± 0.94° for SKBR3, MCF7, MDA-MB-231, and JJ012 cell lines, respectively.
One advantage of the system is that the SAW device is not operating in the mass loading mode, meaning that the contribution of density is very small. Since it is negligible in the shifting phase, density becomes important only for estimation of elasticity but cannot be accurately determined by the proposed system. For this reason, wet weighing tests were run on MDA-MB-231 and MCF7 cell lines. After the cells were submerged in HBSS/5% glycerine solution for 15 minutes, pellets were formed. The masses of individual cells were determined by counting in the small effect of the glycerine intake in the form of volume expansion and the number of cells. Cell sizes and counts were obtained using a Nexcelom Cellometer T4. Densities of 0.987 ± 0.016 and 0.990 ± 0.013 g cm−3 were obtained for MDA-MB-231 and MCF7, respectively, from 4 different samples. It is thought that with a certain finite glycerine intake, cells settle at a certain level below the density of the HBSS/5% glycerine medium. On the other hand, the density of the measurement medium was measured as 1.013 g cm−3 which agrees with the expected value41 of 1.014 g cm−3. The cells are expected to have a density of 0.990 g cm−3 which was obtained from the averages and plugged in for calculating the estimated stiffness moduli.
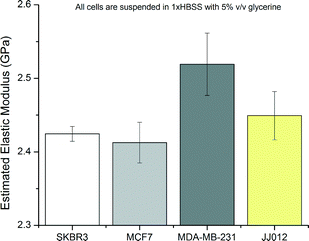
The elastic moduli of the cells were extracted from the phase shift measurements according to the trends of Fig. 4 by curve fitting and by using eqn (3). The compilation of results with estimated elastic moduli extracted from phase angle measurements for all cell lines is given in Fig. 11.
Certain cell lines as tested were seen to form discernible populations. Statistical analysis of the results with ANOVA showed that the null hypothesis can be rejected. Subsequent testing was carried out using Student's t-tests among the groups of data. Results from MDA-MB-231 cells were statistically different from all other cell lines with greater than 99.9% confidence. Results from SKBR3 and MCF7 lines are not statistically different as well as SKBR3 and JJ012 lines. However, MCF7 and JJ012 lines are distinguishable with 95% confidence.
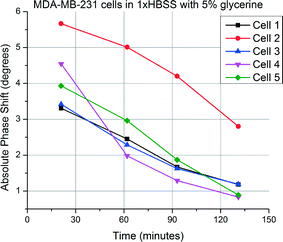
Glycerine is known to be readily metabolized by cells and change the cytoplasmic contents. This, in turn, is expected to lower the apparent bulk moduli of the cells after a certain amount of time. Measurements taken from MDA-MB-231 cells over a period of over two hours show decreasing phase shifts as anticipated. Different phase shifts are obtained as starting points; however, the glycerine intake is observed in all of them in roughly the same manner. Measurement results are given in Fig. 12.
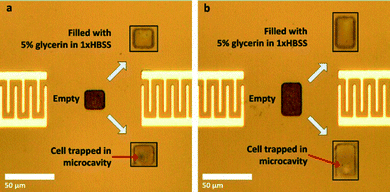
Keeping the practical applications in mind, cell viability tests have to be carried out to ascertain the non-invasive nature of the platform. For this test, MDA-MB-231 cells in regular HBSS/5% glycerine were augmented with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) 0.4% Trypan blue solution and placed in the microcavities as shown in Fig. 13. Acoustic waves were applied for 3–10 minutes with an electrical input power level of −10 dBm to the input IDT. With the estimated acoustic pressure of around 10–20 kPa (derived from acoustics simulations not shown here), it was seen that there is no observable cell damage despite the rather strong resonance formed in the microcavity.
v) 0.4% Trypan blue solution and placed in the microcavities as shown in Fig. 13. Acoustic waves were applied for 3–10 minutes with an electrical input power level of −10 dBm to the input IDT. With the estimated acoustic pressure of around 10–20 kPa (derived from acoustics simulations not shown here), it was seen that there is no observable cell damage despite the rather strong resonance formed in the microcavity.
 | ||
| Fig. 13 Microscope images of MDA-MB-231 cells after ultrasound application. One viable and one dead cell in a separate large droplet are included on the left for comparison purposes. | ||
Conclusions
Analysis of certain different cell lines revealed pronounced differences. However, it was not possible to safely distinguish between SKBR3 and MCF7 as the elastic moduli of these cell lines were not distinguishable at 2.425 ± 0.011 GPa and 2.413 ± 0.028 GPa, respectively, according to Student's t-tests. On the other hand, MDA-MB-231 shows a pronounced difference from all other cell lines with an estimated stiffness of 2.516 ± 0.054 GPa. MCF7 and SKBR3 are similar, normally non-metastatic cells of the same origin whereas MDA-MB-231 cell line is known to be metastatic and thus different from the former lines.42,43 On the other hand, JJ012 cells are also placed between the other lines in terms of stiffness at 2.449 ± 0.038 GPa; however, the results from this cell line are not statistically distinguishable from those of the SKBR3 cell line. This lack of distinguishability despite their different origins and the contrast of the results from MDA-MB-231 cells compared to the rest point to the notion that high frequency stiffness modulus of the cells is a possible biomarker for aggressiveness or metastatic potential as opposed to cell origin.In comparison to popular mechanical characterization methods, the obtained elasticity values are about six orders of magnitude larger than the results obtained from AFM studies; however, this was expected due to the high frequency nature of the measurements. On the other hand, stiffness differentials between the cells are in the order of MPas, meaning that distinguishing between certain cell populations is possible. Comparison to other studies is hard as there are few studies that analyse the given cell lines at similar frequencies. However, acoustic microscopy studies done by Strohm et al. report the MCF7 cell stiffness as 2.47 ± 0.03 GPa which is close to our findings of 2.413 ± 0.028 GPa. Considering different media and methods, such discrepancies should be expected among different studies.
Ultimately, the novel SAW device with embedded microcavity outlined in this study is a low cost microsystem capable of analysing biological cell samples at high frequencies similar to acoustic microscopy techniques but in a miniaturised fashion. Furthermore, it can analyse sample volumes smaller than 10 pL which is orders of magnitude smaller than that of any other study reported to the best of the authors' knowledge, and it is capable of analysing single cells with sizes similar to those of the microcavities. SAW devices have been used to analyse for proteins and other biomarkers in the past but this is the first time that single cells are analysed within this context. Possible ways to improve on reliability and functionality are addition of simultaneous density measurement capability for complete single cell characterization and increasing sensitivity further with specialized designs. Integration of this study with acoustic manipulation techniques44 is also possible further down the road in order to obtain higher throughput.
Acknowledgements
Support from the National Science Foundation (NSF) under grant No. ECCS-1349245 is gratefully acknowledged by the authors. The authors would like to thank Rajapaksha Gajasinghe for constructive feedback as well as Neal Ricks and Kevin Luongo for their devotion to keep the cleanroom functioning properly. The authors would also like to express their gratitude to Dr. Jonathan Trent for the JJ012 cells he provided.Notes and references
- E. S. Lianidou and A. Markou, Clin. Chem., 2011, 57, 1242–1255 CAS.
- S. K. Arya, B. Lim and A. R. A. Rahman, Lab Chip, 2013, 13, 1995–2027 RSC.
- K. Hoshino, Y.-Y. Huang, N. Lane, M. Huebschman, J. W. Uhr, E. P. Frenkel and X. Zhang, Lab Chip, 2011, 11, 3449–3457 RSC.
- J. M. Park, J. Y. Lee, J. G. Lee, H. Jeong, J. M. Oh, Y. J. Kim, D. Park, M. S. Kim, H. J. Lee, J. H. Oh, S. S. Lee, W. Y. Lee and N. Huh, Anal. Chem., 2012, 84, 7400–7407 CrossRef CAS PubMed.
- S. Y. Zheng, H. K. Lin, B. Lu, A. Williams, R. Datar, R. J. Cote and Y. C. Tai, Biomed. Microdevices, 2011, 13, 203–213 CrossRef PubMed.
- J. L. Spudich and D. E. Koshland, Nature, 1976, 262, 467–471 CrossRef CAS PubMed.
- J. V. Sweedler and E. A. Arriaga, Anal. Bioanal. Chem., 2007, 387, 1–2 CrossRef CAS.
- R. B. Brown and J. Audet, J. R. Soc., Interface, 2008, 5, S131–S138 CrossRef CAS PubMed.
- J. L. Arlett, E. B. Myers and M. L. Roukes, Nat. Nanotechnol., 2011, 6, 203–215 CrossRef CAS PubMed.
- M. Makale, Birth Defects Res., Part C, 2007, 81, 329–343 CrossRef CAS PubMed.
- S. Suresh, Acta Mater., 2007, 55, 3989–4014 CrossRef CAS.
- D. E. Ingber, Ann. Med., 2003, 35, 564–577 CrossRef PubMed.
- G. Y. H. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118 CrossRef CAS PubMed.
- S. E. Cross, Y. S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS PubMed.
- Q. S. Li, G. Y. H. Lee, C. N. Ong and C. T. Lim, Biochem. Biophys. Res. Commun., 2008, 374, 609–613 CrossRef CAS PubMed.
- M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, R. Y. H. Lim and C. A. Schoenenberger, Nat. Nanotechnol., 2012, 7, 757–765 CrossRef CAS PubMed.
- S. E. Cross, Y. S. Jin, J. Tondre, R. Wong, J. Rao and J. K. Gimzewski, Nanotechnology, 2008, 19 Search PubMed.
- C. Calderon, D. Vilkomerson, R. Mezrich, K. Etzold, B. Kingsley and M. Haskin, J. Clin. Ultrasound, 1976, 4, 249–254 CrossRef CAS PubMed.
- F. d'Astous and F. Foster, Ultrasound Med. Biol., 1986, 12, 795–808 CrossRef.
- E. M. Strohm, G. J. Czarnota and M. C. Kolios, IEEE Trans. Sonics Ultrason., 2010, 57, 2293–2304 CrossRef PubMed.
- Z. Wang and J. Zhe, Lab Chip, 2011, 11, 1280–1285 RSC.
- X. Ding, P. Li, S. C. S. Lin, Z. S. Stratton, N. Nama, F. Guo, D. Slotcavage, X. Mao, J. Shi and F. Costanzo, Lab Chip, 2013, 13, 3626–3649 RSC.
- P. Li, Z. Mao, Z. Peng, L. Zhou, Y. Chen, P.-H. Huang, C. I. Truica, J. J. Drabick, W. S. El-Deiry and M. Dao, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4970–4975 CrossRef CAS PubMed.
- L. Schmid, D. A. Weitz and T. Franke, Lab Chip, 2014, 14, 3710–3718 RSC.
- N. Sivanantha, C. Ma, D. J. Collins, M. Sesen, J. Brenker, R. L. Coppel, A. Neild and T. Alan, Appl. Phys. Lett., 2014, 105, 103704 CrossRef.
- Y. Bourquin, A. Syed, J. Reboud, L. C. Ranford-Cartwright, M. P. Barrett and J. M. Cooper, Angew. Chem., 2014, 126, 5693–5696 CrossRef.
- T. Nomura, A. Saitoh and Y. Horikoshi, Sens. Actuators, B, 2001, 76, 69–73 CrossRef CAS.
- S. Cular, S. K. R. S. Sankaranarayanan and V. R. Bhethanabotla, Appl. Phys. Lett., 2008, 92, 244104 CrossRef.
- S. C. Hur, N. K. Henderson-MacLennan, E. R. B. McCabe and D. Di Carlo, Lab Chip, 2011, 11, 912–920 RSC.
- Y. Luo, D. Chen, Y. Zhao, C. Wei, X. Zhao, W. Yue, R. Long, J. Wang and J. Chen, Sens. Actuators, B, 2014, 202, 1183–1189 CrossRef CAS.
- S. U. Senveli and O. Tigli, Sens. Actuators, B, 2014, 196, 272–281 CrossRef CAS.
- C. T. Lim, E. H. Zhou and S. T. Quek, J. Biomech., 2006, 39, 195–216 CrossRef CAS PubMed.
- Y. Hagiwara, Y. Saijo, A. Ando, E. Chimoto, H. Suda, Y. Onoda and E. Itoi, Ultrasonics, 2009, 49, 386–388 CrossRef CAS PubMed.
- E. C. Weiss, P. Anastasiadis, G. Pilarczyk, R. M. Lemor and P. V. Zinin, IEEE Trans. Sonics Ultrason., 2007, 54, 2257–2271 CrossRef.
- M. Hoummady and F. Bastien, Rev. Sci. Instrum., 1991, 62, 1999–2003 CrossRef CAS.
- T. Kundu, Ultrasonic Nondestructive Evaluation: Engineering and Biological Material Characterization, CRC Press, Boca Raton, FL, 2004 Search PubMed.
- F. G. Schmidt, F. Ziemann and E. Sackmann, Eur. Biophys. J., 1996, 24, 348–353 CrossRef CAS PubMed.
- S. U. Senveli and O. Tigli, J. Appl. Phys., 2013, 114 Search PubMed.
- D. R. Gray, S. Chen, W. Howarth, D. Inlow and B. L. Maiorella, Cytotechnology, 1996, 22, 65–78 CrossRef CAS PubMed.
- M. Nordström, R. Marie, M. Calleja and A. Boisen, J. Micromech. Microeng., 2004, 14, 1614 CrossRef.
- N. S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288 CrossRef CAS.
- D. L. Holliday and V. Speirs, Breast Cancer Res., 2011, 13, 215 CrossRef PubMed.
- S. Goodison, C. Viars, M. Grazzini and V. Urquidi, BMC Genomics, 2003, 4, 39 CrossRef PubMed.
- M. Sesen, T. Alan and A. Neild, Lab Chip, 2015, 15, 3030–3038 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: SUS and OT conceived and designed the devices and the study, performed the experiments, and co-wrote the manuscript. SUS fabricated the devices. ZA, SR, RD, and RJC provided the cell cultures. See DOI: 10.1039/c5lc01212k |
| This journal is © The Royal Society of Chemistry 2016 |