Coherence and organisation in lanthanoid complexes: from single ion magnets to spin qubits

Abstract

Molecular magnetism is reaching a degree of development that will allow for the rational design of sophisticated systems. Among these, here we will focus on those that display single-molecule magnetic behaviour, i.e. classical memories, and on magnetic molecules that can be used as molecular spin qubits, the irreducible components of any quantum technology. Compared with candidates developed from physics, a major advantage of molecular spin qubits stems from the power of chemistry for the tailored and inexpensive synthesis of new systems for their experimental study; in particular, the so-called lanthanoid-based single-ion magnets, which have for a long time been one of the hottest topics in molecular magnetism. They have the potential to be chemically designed, tuning both their single-molecule properties and their crystalline environment. This allows the study of the different quantum processes that cause the loss of quantum information, collectively known as decoherence. The study of quantum decoherence processes in the solid state is necessary to answer some fundamental questions and lay the foundations for next-generation quantum technologies. This perspective article reviews the state of the art research in this field and its currently open problems.

---

Alejandro Gaita-Ariño

A. Gaita Ariño obtained his PhD in 2003 working with Prof. Coronado and Dr Clemente Juan at the University of Valencia (UV). After collaborations with Dr Suaud in Toulouse and Prof. Loss in Basel, he moved on to a three-year postdoctoral stay with Prof. Stamp in Vancouver. Since 2010 he has enjoyed a postdoctoral position at the UV, and since August 2015 he has been funded by an ERC Consolidator Grant. He is currently interested in the theoretical modelling of rare-earth single-ion magnets, the rational design of coherent molecular spin qubits and the modelling of the coupling of lattice phonons with molecular excitations.

1. Introduction

All electronics “run on quantum mechanics”, from semiconductors and lasers to giant-magnetoresistance-based hard drives and memory devices. A number of spectacular technologies even depend very explicitly of quantum effects, from medical MRI to quantum dots.¹ Nevertheless, there is ample room for research, development and innovation in next-generation quantum technologies such as quantum computation, quantum key distribution and quantum metrology, which all revolve around the coherent manipulation of the wave function and the concept of the quantum two-state system or qubit.

Very different physical, chemical or even biological systems can embody a qubit, but not all are equally well suited. For decades, a large number of physicists – including some of world fame such as Haroche and Cirac – have performed experiments on trapped ions and resonant cavities, performing quantum manipulations that often were beyond what was possible using other quantum hardware proposals such as quantum dots or SQUIDs.^2,3 However, in recent times we have seen spectacular results using Nitrogen-Vacancy (NV) defects in a diamond matrix^4,5 or phosphorus impurities in a silicon matrix.⁶ This has shown the potential of systems that physicists consider as condensed matter, which in practice means that they can be studied with the tools of chemistry and materials science.

On a fundamental level that applies to any quantum hardware, the key to quantum technologies is basic quantum effects: quantum superposition and quantum correlations (e.g. the so-called “cat states”, Fig. 1).⁷ In real systems, and especially in the solid state, these quantum states are very fragile: any interaction with the environment that cannot be controlled during the experiment has the potential to destroy any existing quantum superposition and/or quantum correlations. This phenomenon, called decoherence, is a major obstacle for quantum applications.^8,9 As a result, it will not be possible to exploit the advantages of solid systems (such as stable circuits or scalability) that would make them disruptive technologies until we have a realistic model for decoherence.⁹

Fig. 1 Decoherence killed the cat state: uncontrolled interactions destroy any quantum superposition.

Understanding and eventually controlling the processes that give rise to quantum decoherence will lay the foundations of any conceivable advance in present or future quantum technologies, but the fundamental questions we are dealing with are also formidable. Do we really understand why quantum effects are not persistent in time? Is quantum mechanics valid in the macroscopic world?¹⁰ Of course, these questions are general but to give practical answers one needs to study a particular system.

In our case we will focus on molecular spin qubits, as this molecular approach is uniquely suited both for chemical design and the processing of spins in solid matter. A major advantage of molecular spin qubits over other candidates stems from the power of chemistry for a tailored and inexpensive synthesis of systems for their experimental study. Molecular magnetism has produced an array of tools to study, design and fine-tune magnetic molecules.¹¹ In particular, single-molecule magnets (SMMs) vastly outnumber the variations that can be performed on a particular type of crystalline defect in diamond. Indeed, performing two Scopus searches restricted to papers in chemical journals either containing the keywords “Single Molecule Magnet” or citing Ishikawa's seminal SIM article results for both cases in 150–200 hits per year for the last three years, indicating that the gigantic family of SMMs, the workhorse of molecular magnetism, is still growing by a new member every couple of days.

Theoretical and experimental work on molecular spins for quantum applications has been going on for several years now.¹² Experimentally, magnetic molecules have already been used to perform experiments on coherent oscillations,¹³ and even ultrafast entangling gates have been performed using nuclear spins,¹⁴ pointing in a direction not completely unlike the advances achieved in nitrogen-vacancy centers in diamond.¹⁵ Chemical strategies are being developed to engineer the coupling in multinuclear molecular spin qubits.^16,17 The coherent manipulation of a single qubit with electric fields has been both suggested theoretically¹⁸ and achieved experimentally.¹⁹ Single Molecule Magnets are being coupled to quantum circuits.²⁰ Single Ion Magnets (SIMs) have been especially prolific in this sense, as experiments involving single-molecule spintronics continue to open new frontiers.^21,22 In particular, lanthanide-based SIMs have the potential to be optically manipulated and thus extend the success achieved by qubits of solid-state physics to the molecular world.²³ This of course benefits from the extensive work on the optical properties of lanthanoid ions, which present singularly well-defined optical transitions, compared with transition metal ions. Moreover, since extremely coherent nuclear-specific transitions at high concentration have been described in these systems,²⁴ it should be possible to use lanthanoid nuclear spins as a quantum resource, as was recently suggested in the case of quantum error correction.²⁵ Of course, in general only a few low-energy levels from the ground J manifold are available to EPR energy; typically this is just the ground electronic spin doublet. On the other hand, a recent explosion in highly-coherent transition metal qubits has resulted from measuring simple complexes with no nuclear spins,^26,27 a strategy that should also be used on lanthanoid complexes.

2. Design-oriented theoretical modelling: from the naïve to the sophisticated

A reasonable first milestone for this field would be to reach the point where theory is able to consistently produce a correct crystal-field (CF) Hamiltonian starting from the molecular structure. For this to be helpful in actual design of a new system, ideally this theory should be implemented in a computationally inexpensive manner. Over the past few years, we have been very committed to this goal, providing some advances towards this direction. Putting this in a historical context, this quest started with the design of the first generation of single-molecule magnets, which are the conceptual ancestors of current mononuclear spin qubits, with single ion magnets being the intermediate link.

The recipes for the fabrication of such nanomagnets, based on transition metal clusters, were mainly based on the obtention of a high spin ground state, which meant coupling as many magnetic ions as possible in the same cluster plus a large and negative zero-field-splitting, achieved by the magnetically exchange-coupled anisotropic spins of these ions.²⁸ This viewpoint changed in 2003, when a mononuclear lanthanide complex exhibited slow relaxation of the magnetization and magnetic hysteresis.²⁹ The discovery of such a behaviour in the series (NBu₄)[Ln(Pc)₂] (Pc₂⁻ = phthalocyaninato anion, Ln = Tb³⁺ Dy³⁺) opened the door to the possibility of developing new derivatives based on mononuclear rare earth coordination compounds. This resulted in a rapid expansion of the field, especially after some of us reported that the erbium derivative of the family of polyoxometalates (POMs) [Ln(W₅O₁₈)₂]⁹⁻ exhibited the targeted behaviour.³⁰ The comparison between these two families, with the same coordination number and slightly distorted D_4d coordination symmetry, but different type of ligands and different behaviour for the same magnetic ion, paved the way for geometrical reasoning and magnetostructural correlations.³¹ Since then, the impact of this class of molecular nanomagnets has been dramatically increased and now hundreds of SIMs have been reported.³² These SIMs have shown very different coordination environments and different types of coordinated ligands.³³ Some relevant examples include the organometallic double-decker Er³⁺ compound^34,35 and the acetylacetonate lanthanoid complexes,^36,37 studied by Jiang et al. and Chen et al. respectively, as well as the Na[Dy(DOTA)(H₂O)]·4H₂O complex, where H₄DOTA = 1,4,7,10-tetraazacyclododecane-N,N′,N′′,N′′′-tetraacetic acid, reported by Sessoli et al.³⁸ Beyond the routine magnetic characterisation, the molecular magnetic easy axis of Na[Dy(DOTA)(H₂O)]·4H₂O was determined by single crystal X-ray diffraction. The combination of these experimental results with ab initio theoretical calculations evidenced the significant impact that the capping coordinated molecule of water has over the calculated anisotropy axis.^39,40 The manipulation of the hydrogen atoms of the water molecule around the C₄ axis envisaged the large effects that minor modifications may have over magnetic anisotropy. This means that one must be very careful when assuming that the easy axis of magnetisation is oriented along the same direction as the molecular (pseudo-)symmetry axis using simple magneto-structural correlations.³²

Practically simultaneously with the first qualitative efforts,⁴¹ we developed the SIMPRE (Single Ion Magnet PREdiction) program, which is a computational package that calculates the full set of crystal field parameters and the spectroscopic and magnetic properties of mononuclear lanthanide complexes using their chemical structures.^42,43 As a starting point, we implemented the classical point-charge electrostatic model (PCEM) due to its simplicity and versatility. This permitted a preliminary attempt to rationalise the conditions that a molecule needs to meet to act as a mononuclear magnet.⁴⁴ Even a minimalistic approach having well-known inherent limitations could provide some insights that are interesting to take into account for the rational design of lanthanide SIMs, as it shows how the energy level splitting of the ground J multiplet depends mainly on the lanthanide ion, the charge distribution symmetry and the distortion of the coordination environment. Taking into account these considerations, it was described that lanthanide-based SIMs require a high M_J ground state, to create an energy barrier leading to slow spin relaxation and low mixing in the ground doublet wave functions, to minimize fast spin relaxation through quantum tunneling processes. Depending on the metal, the most favourable situation can be reached by increasing the electron density either near the uniaxial axis (in the case of Tb, Dy, and Ho) or near the basal plane (in the particular case of Er but also for Tm and Yb).

In order to improve the description of f-block mononuclear coordination complexes and overcome the main drawbacks of the PCEM, we developed two new effective electrostatic models that take into account the character of the ligand. These are the Radial Effective Charge (REC) and the Lone-Pair Effective Charge (LPEC) models, in which the crystal field potential is created by electrons participating in the chemical bonds.⁴⁵ Both are approximations that rely on experimental data to associate to each type of ligand with a reduced set of effective parameters (two or three) that permit the prediction of the properties of new derivatives. Thus, a series of analogous compounds are of fundamental interest for the goal of building a general reusable library of ligands for the rational design of lanthanide-based molecular nanomagnets. Recently, we systematically applied the REC model to four families of homoleptic compounds where a lanthanide is coordinated by halides using high-quality spectroscopic data.⁴⁶ The collective study of these series allowed us to estimate two simple relations to have an initial guess of the REC parameters, by relating them to chemical concepts such as Pauling electronegativity and the coordination number. This also permits one to obtain in a quick manner an initial set of CFPs that can be used for further phenomenological fits. On the other hand, we have investigated two isostructural families of polyoxometalates ([Ln(W₅O₁₈)₂]⁹⁻ and [Ln(β₂-SiW₁₁O₃₉)₂]¹³⁻) using a collective fit of magnetic susceptibility data. The ligand parameterization obtained from such a fit was used as a spyglass to predict the SMM behavior in the NdW₁₀ analogue.⁴⁷ The system was synthesized and magnetically characterized, becoming the second neodymium-based SIM in the literature. Analogously, the collective treatment of the magnetic data of heteropolyoxopalladate complexes of general formula [LnPd₁₂(AsPh)₈O₃₂]⁵⁻ with exact cubic symmetry⁴⁸ allowed us to explore the consequences of breaking the degeneracy by reducing the symmetry around the Ho³⁺ ion or by applying a magnetic field, over the quantum coherence of the molecular spin qubit.⁴⁹ Other recent successes derived from the REC approach in systems coordinated by oxygen atoms were the structurally-guided prediction of the first example of a metal–organic framework with nodes that have SMM behavior using lanthanide SIMs, namely SIM-MOF,⁵⁰ and the interpretation of the magnetic properties of two layered dysprosium hydroxides.⁵¹

Finally, we have explored the possibilities of these effective charge models to deal with the understanding of uranium SIMs, which are the next frontier in molecular magnetism, offering a starting point for their rational design.⁵² Further efforts with these systems, using the full Hamiltonian in the CONDON package to complement the drawbacks of SIMPRE, have permitted the rationalization of the first U(IV) SIM.⁵³ Other challenging examples include the molecular magnetic anisotropy description of an erbium-based organometallic SIM using the LPEC model⁵⁴ and of a heteroleptic dysprosium-based β-diketonate SIM in terms of the REC model.⁵⁵ In this latter example, the single-crystal data was reproduced and, for the first time, the influence of the thermal evolution of the molecular structure in the electronic structure and magnetic anisotropy was quantified.

3. Inexpensive estimates of decoherence

We need to move on from magnetic molecules to molecular spin qubits, and this means thinking in terms of quantum decoherence instead of simply in terms of magnetic relaxation. Let us recall the current theoretical consensus on decoherence in SMMs. Three main environmental decoherence mechanisms have been described (see Fig. 2):^56,57 the electronic spins couple (1) to phonons (described as an oscillator bath), (2) to nuclear spins (described as a spin bath) (3) to other electronic spins, causing magnon waves. Magnon waves have been shown to be quenchable at ultra-low temperatures and high tunneling splittings, which can in principle – but not yet in practice – be achieved by chemical design. The effect of nuclear spins can also be minimized by a combination of chemical design and isotopic purification, a demanding but well-defined path. As in the case of magnons, the effect of the nuclear spin bath is also minimized at high tunneling splittings. In contrast, the mechanism of phonon-caused decoherence is the least understood, as the system-dependent spin–phonon coupling has not been properly studied. To make matters worse, the current understanding of the field is that below a certain threshold in the vicinity of 1 K, phonon-caused decoherence is almost completely insensitive to temperature, and that to decrease it we need lower, rather than higher, tunneling splitting. This means that the critical parameters to be studied are the chemical design of the tunneling splitting and the spin–phonon coupling. Advances in the understanding of the coupling between the state of the spin qubit and the lattice phonons would also have potential consequences in the recently invigorated field of spin caloritronics.^58,59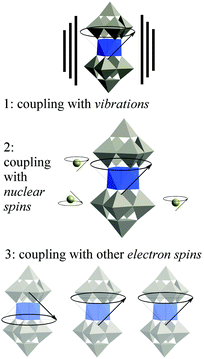

Fig. 2 The three main sources of decoherence in a molecular spin qubit, resulting from the coupling of the qubit with different parts of the environment.

Recently, the software package SIMPRE 1.2 has been developed,⁶⁰ which, compared with previous versions takes into account two further phenomena. Firstly, SIMPRE 1.2 now considers the hyperfine and quadrupolar interactions within the rare-earth ion, resulting in a more complete and realistic set of energy levels and wave functions. Secondly, and in order to widen the predictive capabilities of SIMPRE regarding potential molecular spin qubits, it now includes a routine that calculates a best-case scenario estimate for the decoherence time by considering only the dipolar coupling between the electron spin and the surrounding nuclear spin bath. A critical improvement that is still lacking is to include the excited J manifolds in the Hamiltonian: this would allow the inexpensive theoretical estimate to extend into the optical properties, with potential implications for quantum coherent manipulation of the ground-state spin.

4. Optimal working points and optimal systems

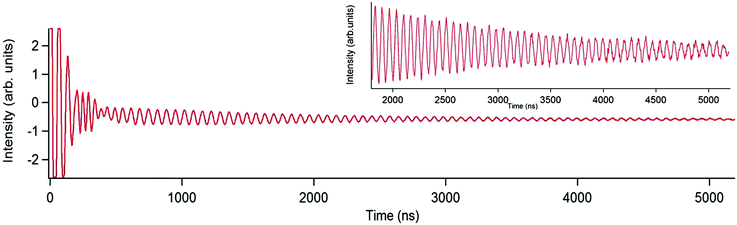
Optimal working points (OWPs) are special conditions that allow for extraordinary coherence times. They can be achieved by a careful design of the magnetic molecule under study, by the tuning of the experimental setup, or a combination of both. Of course this rational design can only take place after a proper understanding. At the present time, we are mostly in a trial-and-error situation where serendipity plays a vital role. Here we will discuss two such cases of OWPs that have been encountered by studying lanthanoids encapsulated by polyoxometalates.

The polyoxometalate gadolinium complex [GdW₃₀P₅O₁₁₀]¹²⁻ (GdW₃₀) was found to present SMM behavior at low temperature.⁶¹ This is rather unexpected at first sight, since Gd³⁺ is well-known as a spherical ion with almost no anisotropy. After recognizing its behavior as SMM, this system was also studied by pulsed EPR, in particular by means of generalized Rabi oscillation experiments. It was possible to increase the number of coherent rotations tenfold through matching the Rabi frequency with the frequency of the proton (Fig. 3).⁶² Achieving high coherence with polyoxometalate chemistry, their excellent potential was demonstrated not only for the storage of quantum information but even for the realization of quantum algorithms, particularly in the case of Gd³⁺ complexes which display a number of transitions available to EPR energies. Nevertheless, this promising experimental observation has not yet been properly rationalized and thus it has not been possible to exploit this effect in other systems.

Fig. 3 After a fast decay at short times, a large number of coherent oscillations are observed in GdW₃₀ at the Hartmann-Hahn condition, i.e. at a microwave power such that the Rabi frequency is very close to the Larmor frequency of the proton. The inset shows how the pattern of 15 oscillations per microsecond can be clearly recognized for over 5 microseconds.

Another polyoxometalate single ion magnet (SIM)⁶³ [Ho(W₅O₁₈)₂]⁹⁻ has recently been the subject of a pulsed EPR study finding a quenching of decoherence at particular fields and frequencies.²⁴ In this case, the key phenomenon is a clock transition, i.e. a transition frequency that is insensitive in the first order to small changes in the magnetic field. This effect, that arises because when the energy of the microwave pulse coincides with the tunneling splitting, protects the spin qubit from the magnetic noise. The key here is that the coherence is preserved even at high concentration: the clock transitions avoid most of the decoherence created by the magnon bath. This is critical, since it lifts the requirement of extreme dilution, and thus opens an avenue for scalability. By relating the energy level scheme with the coordination sphere, it is in principle possible to engineer magnetic molecules which present multiple clock transitions, facilitating their coherent quantum manipulation.

Yet another polyoxometalate has been the subject of a theoretical proposal concerning OWPs. By studying [HoPd₁₂(AsPh)₈O₃₂]⁵⁻, it has been theoretically shown that it is possible to obtain clock transitions by applying a moderate magnetic field and/or through the moderate distortion of a perfect cubic environment. Even in the absence of tunneling splitting, if the expectation values of the magnetic moment in the two qubit states are very similar, the decoherence time is expected to be very long.⁴⁹ This occurs because the nuclear spins in the environment cannot distinguish between the two states of the qubit, and thus are effectively uncoupled from it, so the spin bath dynamics becomes independent from the qubit dynamics and does not contribute to decoherence. This offers an alternate to the previous kind of OWP, in practice extending its use to Kramers’ systems which cannot display a quantum tunneling splitting.

All of the aforementioned OWPs deal with magnetic noise, which is important at low temperatures. At high temperatures, the dominant source of decoherence tends to be phonons, and while the case of the NV centers in diamond seem to favour absolute rigidity, the optimization of molecular structures to minimize vibrational decoherence is still an open problem. Thus, it would be desirable to establish rational chemical criteria for the design of lanthanoid complexes with desired spin–phonon coupling. Should one aim for an absolutely rigid lattice, for a rigid coordination sphere with flexible side groups, or perhaps for rigid complexes, such as POMs, with loose counterions? An experimental effort is already underway and has resulted in a complex where the qubit energy is mostly insensitive to the most common molecular distortion.⁶⁴

In this sense, it is worthwhile to explore the possibilities of new structural developments such as Metal–Organic-Frameworks (MOFs) which combine rigidity with flexibility in different parts of the same crystal, especially since lanthanide-containing MOFs are being studied.^50,65 The theoretical method by Efros and Shklovskii,⁶⁶ allows one to intuitively expect that MOFs are optimal structures to minimize decoherence caused by spin–phonon coupling. In particular, this would happen because of the energy separation between the binding energy in the MOF structure (covalent) compared with the solvent and counterions in the cavity. Thus, low-energy phonons taking place in the cavities (dominated by weaker intermolecular interactions) could gap higher-energy vibrations happening in the MOF structure. This effect, analogous to the one described in the study of universality of low-temperature thermal and mechanical behavior in disordered solids,⁶⁷ would result in an extremely reduced density of states for the relevant phonons i.e. those that couple more strongly to the spin state, and in turn this would minimize phonon-based decoherence.

5. Open problems, mid-term perspectives

5.1 Understanding the quantum dynamics

A proper understanding of OWPs would result in a useful guide to optimize chemical and physical conditions for future molecular spin qubits, ideally operating at reasonable temperatures. However, this requires the theoretical description of the system to go beyond a static picture, and in particular deal with the problem of vibrations. This problem has been solved, up to a point, for particular systems and parameter regions, such as the weakly anisotropic V₁₅ at sub-K temperatures,⁶⁸ or certain Gd³⁺ in water at high magnetic fields and room temperature.⁶⁹ Combined molecular dynamics–quantum chemical calculations have simulated T1 and T2 for Ni²⁺ in water at room temperature.⁷⁰ Indeed, the interest in the influence of transient zero field splitting effects on the relaxation of aqueous solutions of transition metals has led for some time to parametrical analyses of these effects.⁷¹ On the other hand, general solutions (as a function of parameter sets) have been found for exactly solvable qubit models, such as a bath of harmonic oscillators with a certain initial correlation.⁷² The interest of these studies goes beyond the analysis of EPR data and into the active manipulation of quantum information: very recently, it has even been possible to mechanically drive the state of a NV centre spin qubit in a coherent way.⁵⁹

An open problem that we are trying to address focusing on the case of lanthanoid complexes is the systematic, inexpensive determination of the coupling between a spin qubit and the local and non-local vibrational modes, allowing the rational chemical design of magnetic molecules that behave as coherent spin qubits. In this sense, a recent effort to understand the coupling of the spin qubit states with phonons has characterized the coupling of each of the normal vibrational modes of different copper complexes with the qubit energy.⁷³ This approach is based on a combination of theoretical methods. First, the normal vibrational modes are determined e.g. by DFT, and this intermediate result is used to generate non-equilibrium geometries as input to calculate spin energy levels by a CAS method. These qubit energies as a function of geometric distortion are subsequently integrated quantum-mechanically to obtain expectation values. This allows for the quantification of the coupling between the qubit energy and the different vibrational modes. To actually estimate decoherence times, further efforts will be needed to calculate the coupling of the relevant molecular vibrations with the lattice phonons.

In the case of [Cu(mnt)₂]²⁻, a rigid and extraordinarily coherent molecular complex,²⁶ this method was capable of rationalizing the thermal stability of its Landé factor g, which in turn is thought to be related with a weak coupling of the qubit energy with the molecular vibrations and high coherence at relatively high temperatures (Fig. 4). The complex [CuCl₄]²⁻, which displays a large and well characterized thermal dependence of g, is currently being used as a model system to validate the method.⁷⁴ This strategy will eventually be applied to lanthanoid complexes and benefit from the inexpensive estimate of the energy level structure provided by the SIMPRE software package and the REC model.

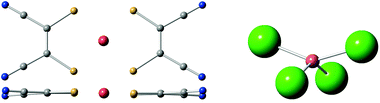Fig. 4 Left: top and side views of [Cu(mnt)₂]²⁻, a markedly rigid molecular structure with high quantum coherence. Right: side view of [CuCl₄]²⁻, an ionic structure.

Once the main terms of the Hamiltonian have been evaluated as explained above, an open problem is the (inexpensive) calculation of the dynamical properties of the systems under study. Several approaches are available for the so-called central spin problem, which studies the quantum evolution focusing on the Hamiltonian of a single effective spin in the center of an environment which introduces different interaction terms. Ordered from the least to the most ambitious method, they are:

(a) Obtaining dimensionless decoherence rates (starting from a path integral approach and within the spin-boson model) as a function of all relevant variables.^56,57 This would allow to effectively quantify decoherence for each system under study, or in general as a function of the chemical structure and composition. Furthermore, as the different contributions to decoherence are calculated separately, it would allow to distinguish and quantify the weight in total decoherence of the different processes, an invaluable aid for molecular-crystalline design.

(b) Applying time-dependent perturbation theory,⁷⁵ distinguishing between time-independent major terms such as the crystal field and minor perturbations such as the coupling with a fluctuating bath of nuclear spins. This would allow the detailed prediction of the time evolution of the quantum state of the systems, both for spontaneous decoherence processes and for induced coherent transitions. Artificially activating and deactivating terms in the Hamiltonian, it can serve the function of approach (a), but with a much richer result in terms of information, and also at a much higher computational cost.

(c) Solving a master equation to calculate the evolution of the wavefunction,⁷⁶i.e. integrating to different final times with the complete Hamiltonian, without treating any of the processes as perturbations. This is essentially the same as approach (b), but without making assumptions about the energy ratios of different processes. This means a higher computational cost but also has the benefit of being able to explore the full parameter space, because for certain cases the “time-varying perturbation” will be a major term.

5.2 Achieving complex organisation

A further open problem is related with extending the study not in time, but in space. The organisation of devices with a resolution below the nanometer scale and total size above the micrometer scale is characteristic of molecular biology. Since the first use of ferritin as a template for magnetic nanoparticles,⁷⁷ major steps towards this goal have been achieved as a part of what has been called synthetic biology.⁷⁸ DNA has been used as a programmable building block,⁷⁹ while short, self-assembling peptides have been shown to form a variety of stable nanostructures which have already been used for the rational design of functional devices.⁸⁰ It is likely that the bio-nanotechnological strategy will eventually be applied in the quest for scalability in quantum computing. This could happen by the use of either the original proposal by Lloyd,⁸¹ or one of its variations,⁸² which require the ability to organize different kinds of quantum building blocks.

Note that the nascent field of quantum biology, devoted to the study of coherent quantum effects in processes as diverse as photosynthesis in plants,⁸³ geolocation in birds⁸⁴ and possibly smell in insects,⁸⁵ shows that this complex organization of quantum coherent processes already takes place in nature. The challenge is then to achieve this artificially. In this sense, spin-carrying metalloproteins, which are already being studied by manipulating their quantum states via pulsed EPR,⁸⁶ are promising systems for this synthetic quantum biology. Nevertheless, other systems, such as triple-stranded metallo-hellicates have been suggested to implement Lloyd's proposal.⁸⁷ Here we will focus on magnetic lanthanoid complexes because of the interest they generate both as SIMs and as spin qubits, that is, because of their favourable magnetic and quantum properties.⁸⁸

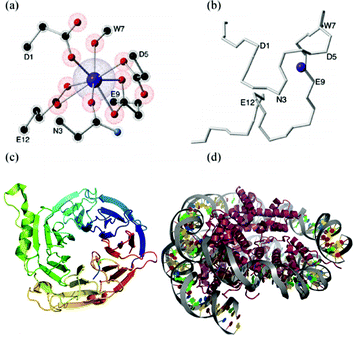
A key experimental advance in this context are Lanthanide Binding Tags (LBTs).⁸⁹ These are oligopeptides based on calcium-binding motifs of EF-hand proteins (Fig. 5b) that have been designed to interact very specifically with lanthanoids.⁹⁰ These new building blocks constitute a major step towards an interdisciplinary field, since a LBT can be seen as a standard coordination complex (Fig. 5(a)) but also as a small part of a protein (Fig. 5(b)).

Fig. 5 (a) Coordination environment created by a 17 amino acid-long Lanthanide Binding Tag (LBT). Only the coordinating lateral residues are shown, α-carbons are labeled. (b) Polypeptidic chain of the LBT without lateral residues, the α-carbons of amino acids involved in the coordination sphere are labeled. (c) All-protein strategy: chimeras based on proteins combining β sheets with loops could be designed to harbour LBTs while preserving their overall structure. (d) DNA-histone strategy: nucleosomes could be used to organise spin qubits if the protein moiety is modified to contain at least one LBT motif.

We recently proposed the use of Ln³⁺–LBT complexes as a path for an extremely specific and spatially-resolved organisation of lanthanoid ions as spin qubits.⁹¹ Our proposal is based on the fact that LBTs are easily incorporated at the DNA level into any recombinant protein, (Fig. 5(c)) a potential route to highly complex organisation, e.g. via histones, a key structural protein for chromatin.⁹² If histones are thus decorated with LBT-qubits, they would have the potential to be further organized via nucleosome-positioning sequences,⁹³ which are DNA sequences which specifically prompt the binding of histones to constitute chromatin.

While peptides are typically challenging to crystallize, several LBT structures have already been characterized by X-ray crystallography, including examples with two or up to four crystallographically independent LBT sites. Combining this fact with the possibility to coordinate different ions, the scheme was evaluated theoretically for 63 different Ln³⁺–LBT combinations, both in terms of their behavior as SIMs and by estimating the decoherence caused by the nuclear spin bath and the interqubit interaction strength by dipolar coupling. We concluded that while Dy³⁺ LBT complexes are expected to behave as SIMs, Yb³⁺ derivatives are the ones that show more promise as spin qubits. The interqubit interaction strength, while weak, is estimated to be sufficient. Indeed, recently pulsed EPR experiments have been performed on lanthanide–LBT complexes, demonstrating high quantum coherence (Rabi oscillations) and the possibility to quantify the lanthanide–lanthanide interaction via a PELDOR pulse sequence.⁹⁴

6. Concluding remarks

Lanthanoid complexes offer a great potential as molecular spin qubits, among other reasons because of their unique optical properties. However, there is still a long way ahead before a non-trivial organization of coherent qubits can be achieved. The practical application of the present theoretical understanding of the sources and mechanisms of quantum decoherence can be of crucial help along this road. The underlying quantum phenomena are understood in principle, but only in terms of parameters that cannot be easily predicted. Thus, in practice, experiments in quantum coherence in magnetic molecules are still years ahead of their corresponding theoretical description. Nevertheless, there are reasons to think that we can achieve some theoretical understanding of decoherence in terms of parameters that can be obtained in a computationally inexpensive way. These kinds of design-oriented theoretical tools are currently being developed for this purpose by building upon previous work that has proven useful to rationalize the magnetic behavior of SIMs. In terms of complex organisation, the situation is reversed: the theory about complex arrays of qubits that allow non-spatial addressing is years ahead of the experimental efforts. In this case, a potential solution consists of the use of biological structures for the organization of molecular spin qubits.

Acknowledgements

The present work has been funded by the EU (ERC Advanced Grant SPINMOL and ERC Consolidator Grant DECRESIM), the Spanish MINECO (grant MAT2014-56143-R, CTQ2014-52758-P and Unidad de Excelencia María de Maeztu MDM-2015-0538 granted to ICMol), and the Generalitat Valenciana (Prometeo and ISIC Programmes of Excellence). A. G.-A. acknowledges funding by the MINECO (Ramón y Cajal contract). J. J. B. acknowledge the Blaise Pascal International Chair for financial support. J. J. B. also thanks the Spanish MECD for an FPU predoctoral grant. L. E. M. acknowledges the Generalitat Valenciana for a VALi+D predoctoral grant. S. C.-S. acknowledges the Generalitat Valenciana for a VALi+D postdoctoral grant.

References

1. I. Georgescu and F. Nori, Phys. World, 2012, 25, 16–17.
2. J. M. Raimond, M. Brune and S. Haroche, Rev. Mod. Phys., 2001, 73, 565–582.
3. J. I. Cirac and P. Zoller, Phys. Rev. Lett., 1995, 74, 4091–4094.
4. H. Bernien, B. Hensen, W. Pfaff, G. Koolstra, M. S. Blok, L. Robledo, T. H. Taminiau, M. Markham, D. J. Twitchen, L. Childress and R. Hanson, Nature, 2013, 497, 86–90.
5. F. Dolde, I. Jakobi, B. Naydenov, N. Zhao, S. Pezzagna, C. Trautmann, J. Meijer, P. Neumann, F. Jelezko and J. Wrachtrup, Nat. Phys., 2013, 9, 139–143.
6. J. T. Muhonen, A. Laucht, S. Simmons, J. P. Dehollain, R. Kalra, F. E. Hudson, S. Freer, K. M. Itoh, D. N. Jamieson, J. C. McCallum, A. S. Dzurak and A. Morello, J. Phys.: Condens. Matter, 2015, 27, 154205.
7. C. Monroe, D. M. Meekhof, B. E. King and D. J. Wineland, Science, 1996, 272, 1131–1136.
8. W. P. Schleich, Nature, 2000, 403, 256–257.
9. A. M. Zagoskin, Quantum engineering: Theory and design of quantum coherent structures, Cambridge University Press, Cambridge, 2011.
10. P. C. E. Stamp, Studies in History and Philosophy of Science Part B - Studies in History and Philosophy of Modern Physics, 2006, 37, 467–497.
11. J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41, 7464–7478.
12. F. Troani and A. Affronte, Chem. Soc. Rev., 2012, 40, 3119–3129.
13. C. J. Wedge, G. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204.
14. V. Filidou, S. Simmons, S. D. Karlen, F. Giustino, H. L. Anderson and J. J. L. Morton, Nat. Phys., 2012, 8, 596–600.
15. L. C. Bassett, F. J. Heremans, D. J. Christle, C. G. Yale, G. Burkard, B. B. Buckley and D. D. Awschalom, Science, 2014, 345, 1333–1337.
16. G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. L. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173–178.
17. A. Fernandez, J. Ferrando-Soria, E. Moreno Pineda, F. Tuna, I. J. Vitorica-Yrelabal, C. Knappke, J. Ujma, C. A. Muryn, G. A. Timco, P. E. Barran, A. Aradavan and R. E. P. Winpenny, Nat. Commun., 2016, 7, 10240.
18. F. Troiani, D. Stepanenko and D. Loss, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 161409.
19. R. E. George, J. P. Edwards and A. Ardavan, Phys. Rev. Lett., 2013, 110, 027601.
20. M. Jenkins, T. Hümmer, M. J. Martínez-Pérez, J. García-Ripoll, D. Zueco and F. Luis, New J. Phys., 2013, 15, 095007.
21. S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138.
22. M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458–4464.
23. F. Bussières, C. Clausen, A. Tiranov, B. Korzh, V. B. Verma, S. W. Nam, F. Marsili, A. Ferrier, P. Goldner, H. Herrmann, C. Silberhorn, W. Sohler, M. Afzelius and N. Gisin, Nat. Photonics, 2014, 8, 775–778.
24. M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016 DOI:10.1038/nature16984.
25. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, L. Escalera-Moreno, A. Gaita-Ariño and G. Mínguez Espallargas, Europhys. Lett., 2015, 110, 33001.
26. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. Slageren, Nat. Commun., 2014, 5, 5304.
27. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492.
28. R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816.
29. N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
30. M. AlDamen, J. M. Clemente Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875.
31. M. AlDamen, S. Cardona-Serra, J. M. Clemente Juan, E. Coronado, A. Gaita-Ariño, C. Martí-Gastaldo, F. Luis and O. Montero, Inorg. Chem., 2009, 48, 3467–3479.
32. H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33.
33. P. Zhang, Y. N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763.
34. S. D. Jiang, B. W. Wang, H. L. Sun, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733.
35. S. D. Jiang, L.-N. N. Liu, S.-S. S. Zhou, B.-W. W. Wang, Z.-M. M. Wang and S. Gao, Inorg. Chem., 2012, 51, 3079–3087.
36. S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 122, 7610–7613.
37. G.-J. Chen, C.-Y. Gao, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, D.-Z. Liao and P. Cheng, Dalton Trans., 2011, 40, 5579–5583.
38. P.-E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751–3753.
39. G. Cucinotta, M. Perfetti, J. Luzón, M. Etienne, P.-E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610.
40. M.-E. Boulon, G. Cucinotta, J. Luzón, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., 2013, 125, 368–372.
41. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
42. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967.
43. J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2014, 35, 1930–1934.
44. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51, 12565–12574.
45. J. J. Baldoví, J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Dalton Trans., 2012, 41, 13705–13710.
46. J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Dalton Trans., 2015, 44, 12535–12538.
47. J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Ariño and C. Giménez-Saiz, Inorg. Chem., 2014, 53, 9976–9980.
48. M. Barsukova, N. V. Izarova, R. N. Biboum, B. Keita, L. Nadjo, V. Ramachandran, N. S. Dalal, N. S. Antonova, J. J. Carbó, J. M. Poblet and U. Kortz, Chem. – Eur. J., 2010, 16, 9076–9085.
49. J. J. Baldoví, L. E. Rosaleny, V. Ramachandran, J. Christian, N. S. Dalal, J. M. Clemente Juan, P. Yang, U. Kortz, A. Gaita-Ariño and E. Coronado, Inorg. Chem. Front., 2015, 2, 893–897.
50. J. J. Baldoví, E. Coronado, A. Gaita-Ariño, C. Gamer, M. Giménez-Marqués and G. Mínguez Espallargas, Chem. – Eur. J., 2014, 20, 10695–10702.
51. B. Monteiro, J. T. Coutinho, C. C. L. Pereira, L. C. J. Pereira, J. Marçalo, M. Almeida, J. J. Baldoví, E. Coronado and A. Gaita-Ariño, Inorg. Chem., 2015, 54, 1949–1957.
52. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Sci., 2013, 4, 938–946.
53. M. A. Antunes, J. T. Coutinho, I. C. Santos, J. Marçalo, M. Almeida, J. J. Baldoví, L. C. J. Pereira, A. Gaita-Ariño and E. Coronado, Chem. – Eur. J., 2015, 21, 17817–17826.
54. J. J. Baldoví, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Inorg. Chem., 2014, 53, 11323–11327.
55. K. Qian, J. J. Baldoví, S. D. Jiang, A. Gaita-Ariño, Y. Q. Zhang, J. Overgaard, B. W. Wang, E. Coronado and S. Gao, Chem. Sci., 2015, 6, 4587–4593.
56. S. Takahashi, I. S. Tupitsyn, J. Van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79.
57. P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19, 1718–1730.
58. G. E. W. Bauer, E. Saitoh and B. J. Van Wees, Nat. Mater., 2012, 11, 391–399.
59. A. Barfuss, J. Teissier, E. Neu, A. Nunnenkamp and P. Maletinsky, Nat. Phys., 2015, 11, 820–824.
60. S. Cardona-Serra, L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño, J. M. Clemente-Juan and E. Coronado, J. Comput. Chem., 2016 DOI:10.1002/jcc.24313.
61. M. J. Martinez-Perez, S. Cardona-Serra, C. Schlegel, F. Moro, P. J. Alonso, H. Prima-Garcia, J. M. Clemente Juan, M. Evangelisti, A. Gaita-Ariño, J. Sesé, J. Van Slageren, E. Coronado and F. Luis, Phys. Rev. Lett., 2012, 108, 247213.
62. J. J. Baldoví, S. Cardona-Serra, J. M. Clemente Juan, E. Coronado, A. Gaita-Ariño and H. Prima-Garcia, Chem. Commun., 2013, 49, 8922–8924.
63. M. AlDamen, J. M. Clemente Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875.
64. J. M. Zadrozny, S. M. Greer, S. Hill and D. E. Freedman, Chem. Sci., 2016, 7, 416–423.
65. X. Zhang, V. Vieru, X. Feng, J. L. Liu, Z. Zhang, B. Na, W. Shi, B. W. Wang, A. K. Powell, L. F. Chibotaru, S. Gao, P. Cheng and J. R. Long, Angew. Chem., Int. Ed., 2015, 54, 9861–9865.
66. A. L. Efros and B. I. Shklovskii, J. Phys. C: Solid State Phys., 1975, 8, L49–L51.
67. M. Schechter and P. Stamp, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 174202.
68. V. V. Dobrovitski, M. I. Katsnelson and B. N. Harmon, Phys. Rev. Lett., 2000, 84, 3458–3461.
69. S. Rast, P. H. Fries, E. Belorizky, A. Borel, L. Helm and A. E. Merbach, J. Chem. Phys., 2001, 115, 7554.
70. J. Rantaharju, J. Mareš and J. Vaara, J. Chem. Phys., 2014, 141, 014109.
71. S. Rast, P. H. Fries and E. Belorizky, J. Chem. Phys., 2000, 113, 8724–8735.
72. V. G. Morozov, S. Mathey and G. Röpke, Phys. Rev. A, 2012, 85, 022101–022110.
73. L. Escalera-Moreno, N. Suaud and A. Gaita-Ariño, arXiv:1512.05690v1, 2015.
74. L. Escalera-Moreno, N. Suaud and A. Gaita-Ariño, work in preparation.
75. J. H. Shim, S. Bertaina, S. Gambarelli, T. Mitra and A. Müller, Phys. Rev. Lett., 2012, 050401.
76. E. Barnes, Ł. Cywiński and S. D. Sarma, Phys. Rev. Lett., 2012, 140403.
77. S. Mann, D. D. Archibald, J. M. Didymus, T. Douglas, B. R. Heywood, F. C. Meldrum and N. J. Reeves, Science, 1993, 261, 1286–1292.
78. Y. Ding, F. Wu and C. Tan, Life, 2014, 4, 1092–1116.
79. T. Tørring, N. V. Voigt, J. Nangreave, H. Yan and K. V. Gothelf, Chem. Soc. Rev., 2011, 40, 5636–5646.
80. A. Lakshmanan, S. Zhang and C. A. E. Hauser, Trends Biotechnol., 2012, 30, 155–165.
81. S. Lloyd, Science, 1993, 261, 1569–1571.
82. S. C. Benjamin, Phys. Rev. A: At., Mol., Opt. Phys., 2000, 61, 203011–203014.
83. G. S. Engel, T. R. Calhoun, E. L. Read, T. K. Ahn, T. Mančal, Y. C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782–786.
84. N. Lambert, Y. N. Chen, Y. C. Cheng, C. M. Li, G. Y. Chen and F. Nori, Nat. Phys., 2013, 9, 10–18.
85. E. R. Bittner, A. Madalan, A. Czader and G. Roman, J. Chem. Phys., 2012, 137, 22A551.
86. S. Lyubenova, H. Schwalbe and T. F. Prisner, Acc. Chem. Res., 2010, 181–189.
87. Y. Morita, Y. Yakiyama, S. Nakazawa, T. Murata, T. Ise, D. Hashizume, D. Shiomi, K. Sato, M. Kitagawa, K. Nakasuji and T. Takui, J. Am. Chem. Soc., 2010, 132, 6944–6946.
88. R. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, Wiley, 2015.
89. M. Elbanowski and B. Makowska, J. Photochem. Photobiol., A, 1996, 99, 85–92.
90. K. Tóth, V. Böhm, C. Sellmann, M. Danner, J. Hanne, M. Berg, I. Barz, A. Gansen and J. Langowski, Cytometry, Part A, 2013, 83, 839–846.
91. L. E. Rosaleny and A. Gaita-Ariño, Inorg. Chem. Front., 2016, 3, 61–66.
92. M. M. Müller and T. W. Muir, Chem. Rev., 2015, 115, 2296–2349.
93. J. I. Nishikawa and T. Ohyama, Nucleic Acids Res., 2013, 41, 1544–1554.
94. D. Barthelmes, M. Gränz, K. Barthelmes, K. N. Allen, B. Imperiali, T. Prisner and H. Schwalbe, J. Biomol. NMR, 2015, 63, 275–282.

---