Magnetic relaxations in four-coordinate Dy(III) complexes: effects of anionic surroundings and short Dy–O bonds

Abstract

Two four-coordinate Dy(III) complexes, [LiTHF₄][Dy(NPh₂)₄] (1) and DyLi(Ph₃CO)₃(NPh₂)THF (2), with similar distorted tetrahedral geometries and a pure anionic coordination environment were synthesized under anaerobic conditions. Magnetic studies reveal that only 2 having a short Dy–O bond (2.07 Å) shows slow magnetic relaxation behaviour under zero dc field. Quantitative analyses of energy-levels and eigenstates using the program PHI reveal that the ground state doublets for both the complexes are mixed with low-lying states, though complex 2 shows much higher purity of ground state doublets. This study presumably indicates that the spherically coordinated anions with evenly distributed charges are adverse to the enhancement of the axial magnetic anisotropy of the Dy(III) ions, while the strong Dy–O bond may break such a high symmetry and hence promote the axial magnetic anisotropy of the Dy(III) ions.

---

Introduction

In recent years the magnetic properties of mononuclear lanthanide complexes have been intensively investigated for single-molecule information storage materials, the so-called single-ion magnets (SIMs), because the large magnetic anisotropic energy barrier for spin-reversal (ΔE) originating from the strong spin–orbit coupling effect of unpaired 4f electrons may significantly enhance the magnetic blocking temperature.^1–4 Since the spin–orbit coupling effect of the lanthanide ions is considered to be directly related to the crystal-field terms,⁵ the coordination environments, including the coordination number (CN), coordination symmetry and coordination ligands, are highly important in the design of high-performance lanthanide SIMs.

Because the ionic radii of lanthanide ions are large, the CN of lanthanide complexes is often high, ranging from 7 to 12.⁴ From a literature review we can see that many low-coordinate (CN < 6) lanthanide complexes were synthesized by organometallic chemists,⁶ but their low temperature magnetic dynamics were seldom studied. Indeed, the geometric control of low-coordinate lanthanide complexes is relatively easier since the topological variants are much reduced as the coordination number decreases. Hence, the magnetic investigation of such complexes may be beneficial to understand the magneto-structural correlation of lanthanide SIMs and has already drawn some attention in recent studies.^7–12 Surprisingly, most of the reported low-coordinate lanthanide SIMs that exhibit slow magnetic relaxation without the assistance of an external magnetic field are based on Er(III) ions.^7,9 Low-coordinate, especially for CN = 3 or 4, Dy(III) complexes were rarely reported as SIMs.¹²

Recently we reported the magnetic properties of a series of Dy(III) complexes with crown ethers.¹³ We found that when the Dy(III) ions are coordinated by some counter-anions such as NO₃⁻ and OH⁻, the magnetic performance will be better. We then reasoned that if more anions were coordinated to the Dy(III) ion, the magnetic anisotropy may be further enhanced. Low-coordinate lanthanide complexes thus provide us a good testing bed.

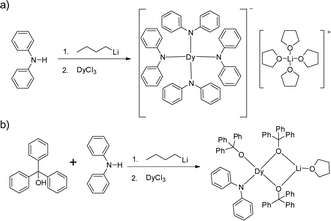
Herein we show two four-coordinate Dy(III) complexes, [LiTHF₄][Dy(NPh₂)₄] (1) and DyLi(Ph₃CO)₃(NPh₂)THF (2), with a pure anionic coordination environment and similar distorted tetrahedral geometries. However, magnetic studies reveal that only complex 2 exhibits slow magnetic relaxation under zero dc field presumably due to the very short Dy–O (2.068(3) Å) bond when compared with other Dy–O/N bonds in both 1 and 2.

Results and discussion

Syntheses and crystal structures

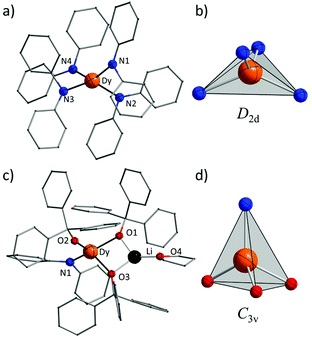
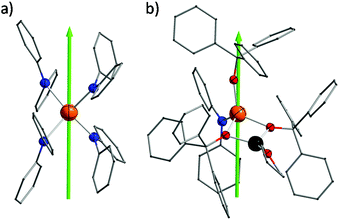
Complexes 1 and 2 were prepared in similar reactions of deprotonated amine/alcohol ligands and anhydrous DyCl₃ in THF overnight (Scheme 1). The solvent was then removed under vacuum and the residue was extracted with hot toluene for 1 and THF for 2, respectively. Single crystals suitable for X-ray analysis were obtained by cooling the toluene extracts to −35 °C overnight for 1, and layering pentane above the THF extracts for 2 (for details, see the Experimental section).

Scheme 1 Syntheses and structures of complexes 1 (a) and 2 (b).

Complex 1 crystallizes in the orthorhombic space group Pbcn and comprises a [Dy(Ph₂N)₄]⁻ anion balanced by a counterion [Li(C₄H₈O)₄]⁺ (Fig. 1a). The Dy(III) ion in the [Dy(Ph₂N)₄]⁻ anion is bound to four NPh₂⁻ groups, generating a distorted DyN₄ tetrahedron. The Dy–N bonds are in distances ranging from 2.28 Å to 2.30 Å (Table 1), whereas the N–Dy–N angles are in a much wide range (from 93.84° to 134.09°, Table S1†). This reveals a significant deviation from the ideal tetrahedral angle of 109.28°. These results are similar to its Y(III) analogue as reported previously.¹⁴ The Li⁺ ion in the [Li(C₄H₈O)₄]⁺ cation is four-coordinated in a tetrahedral geometry with four oxygen atoms from four THF molecules. The Li–O distances lie in the range of 1.93 Å–1.94 Å. The O–Li–O angles range from 101.53° to 112.86°. For the crystal packing of complex 1, the shortest intermolecular Dy⋯Dy separation is about 11.33 Å (Fig. S1†).

Fig. 1 (a) Structure of [Dy(Ph₂N)₄]⁻ anion in 1. The [Li(C₄H₈O)₄]⁺ cation and H atoms are omitted for clarity. (b) The coordination polyhedron of 1. (c) Molecular structure of 2. H atoms have been omitted for clarity. (d) The coordination polyhedron for 2.

Table 1 Selected bond lengths (Å) for 1 and 2

1		2
Dy–N(1)	2.2948(15)	Dy–N(1)	2.273(4)
Dy–N(2)	2.2825(16)	Dy–O(1)	2.195(3)
Dy–N(3)	2.2947(15)	Dy–O(2)	2.068(3)
Dy–N(4)	2.2825(16)	Dy–O(3)	2.152(3)

---

Complex 2 crystallizes in the monoclinic space group P2₁/n. Different from 1, the Dy(III) ion is coordinated to three Ph₃CO⁻ and one NPh₂⁻ groups in a distorted DyO₃N tetrahedron (Fig. 1c). Remarkably, the terminal triphenylmethanol provides a very strong Dy–O bond (2.068(3) Å) (Table 1), which is one of the shortest coordination bonds among all the reported Ln-SIMs.¹³ The Dy–O bond lengths for the two other triphenylmethanol ligands that bridge the Li⁺ ion and the Dy(III) ion are 2.15 Å and 2.20 Å, respectively (Table 1). The length of the Dy–N bond is 2.273(4) Å, which is a bit shorter than those in 1. The angles in the DyO₃N tetrahedron range from 78.04° to 127.30° (Table S2†). The Li⁺ ion lies in a planar triangle geometry additionally coordinated to a THF molecule. In the crystal packing of 2, the shortest intermolecular Dy⋯Dy separation is 11.90 Å (Fig. S2†).

To gain a further insight into the coordination geometry of these two complexes, the continuous shape measures (CSM) were used to determine the degree of the deviation from the ideal polyhedron (a larger value means a larger distortion).¹⁵ There are four kinds of ideal polyhedra for four-coordinate complexes: namely tetrahedron, seesaw, vacant trigonal-bipyramid and square. For 1, the lowest value of 4.73 was found for the tetrahedron geometry; for 2, two similar CSM values were obtained (3.36 for tetrahedron and 3.35 for vacant trigonal bipyramid) (Table 2), indicating two possibilities. Nevertheless, the coordination geometry for 1 (Fig. 1b) shows an oblate tetrahedron with a D_2d local symmetry for the central Dy(III) ion and the umbrella-opening distortion from the ideal tetrahedron for 2 gives a C_3v local symmetry (Fig. 1d).¹⁵

Table 2 Continuous shape measures calculations for complexes 1 and 2

Structure^a [ML4]	SP-4	T-4	SS-4	vTBPY-4
a SP-4, D4h, square; T-4, Td, tetrahedron; SS-4, C2v, seesaw; vTBPY-4, C3v, vacant trigonal bipyramid.
1	15.427	4.731	5.366	8.001
2	27.053	3.364	6.536	3.347

---

Magnetic properties

Dc magnetic studies. Direct current (dc) magnetic susceptibility measurements have been carried out in the temperature range of 2–300 K under a 0.1 T applied field. The room temperature χT products for both the compounds are slightly lower than the calculated values for free lanthanide ions, being 14.07 cm³ K mol⁻¹ for 1 and 14.04 cm³ K mol⁻¹ for 2 (calc. 14.17 cm³ K mol⁻¹ for ⁶H_15/2, g = 4/3) (Fig. 2). Upon cooling, the χT product decreases gradually and then rapidly down to 8.13 cm³ K mol⁻¹ and 11.38 cm³ K mol⁻¹ at 2 K for 1 and 2, respectively, which indicates the progressive depopulation of the excited m_J sublevels split by the crystal field. The field dependence of magnetizations was measured at low temperatures (inset in Fig. 2), which shows a rapid increase at a low field and reaches the maximum values of 5.58μ_B and 5.27μ_B for 1 and 2, respectively. Such unsaturated features of magnetizations suggest the presence of a significant magnetic anisotropy.

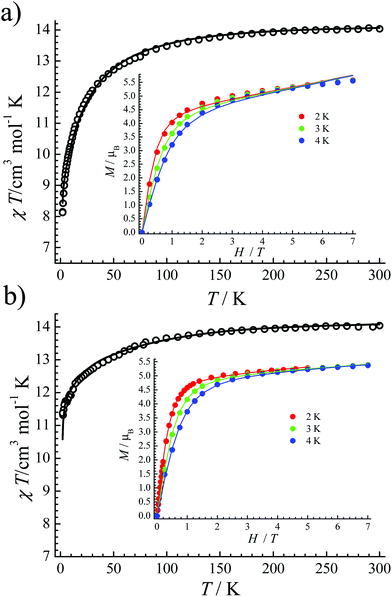Fig. 2 The χT versus T plot of 1 (a) and 2 (b). Inset: The field-dependent magnetization plots at indicated temperatures. The solid lines are best fits.

With the dc magnetic susceptibilities, quantitative information of energy-levels and eigenstates can be obtained by using the program PHI.¹⁶ For complex 1, its Dy(III) ion locates in the D_2d local symmetry, and for 2, the local symmetry is C_3v (see above), so their effective crystal-field (CF) Hamiltonians are proposed as:

Ĥ_CF = B²₀C²₀ + B⁴₀C⁴₀ + B⁴₄C⁴₄ + B⁶₀C⁶₀ + B⁶₄C⁶₄

and

Ĥ_CF = B²₀C²₀ + B⁴₀C⁴₀ + B⁴₃C⁴₃ + B⁶₀C⁶₀ + B⁶₃C⁶₃ + B⁶₆C⁶₆

for 1 and 2, respectively.¹⁷

The crystal-field parameters of the CF Hamiltonians were obtained by fitting their χT versus T plot and M–H at the same time (solid lines in Fig. 2), which were then used to simulate their energy-levels and eigenstates (Tables S5 and S6†). Both complexes 1 and 2 have impure ground state doublets. For 1, its ground state doublets are mixed with ±15/2 (69.8%), ±7/2 (30.1%) and ±1/2 (0.1%) m_J states, which are about 24.26 cm⁻¹ separated from the excited Kramers doublets. For 2, ±15/2 (92.0%), ±9/2 (7.8%) and ±3/2 (0.2%) m_J states comprise its main components of ground state doublets. The barrier for the first excited state is about 59.9 cm⁻¹. From these fitting results we can conclude: (1) the ground states for both 1 and 2 are all mixed; (2) the first excited states are not high in both 1 and 2. Obviously, the mixed m_J states are the key, because the mixture of different m_J states will cause strong quantum tunneling of magnetization (QTM).¹⁸ Relatively, complex 2 shows much higher purity of ground state doublets and ΔE compared to 1.

Ac magnetic studies. To investigate the magnetization dynamics, alternating current (ac) susceptibility measurements were carried out at low temperatures for complexes 1 and 2. In the absence of a dc field, no peaks were observed for both in-phase (χ′) and out-of-phase (χ′′) signals for 1, which may be caused by the strong QTM effect. But for 2, small tails of χ′′ signals without reaching the maximum could be observed above 2 K (Fig. S5†). This behaviour is indicative of slow magnetization relaxation, suggesting a higher ΔE for complex 2 than 1, which is in agreement with the simulation based on their dc magnetic susceptibilities.

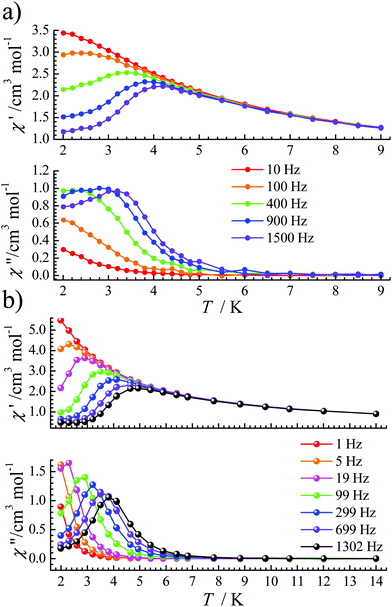
Under an optimized dc field, the QTM is effectively reduced so that obvious signals were observed in both χ′(T) and χ′′(T) plots for complexes 1 and 2 (Fig. 3). For 1, under a 1600 Oe dc field, ac signals appear below 3.5 K (Fig. 3a) at high frequencies. Its frequency-dependent ac susceptibility data were recorded from 2.0 K to 3.5 K to evaluate the relaxation times (Fig. S3†), which were fitted by the generalized Debye function using the CC-FIT program.¹⁹ The α parameters range from 0.17 to 0.35 between 2.0 and 3.5 K (Table S3†). For 2, the optimized dc field is 700 Oe. The peaks of χ′′ signals became sharp and move to a slightly higher temperature than that of 1. For a frequency of 1302 Hz, a maximum signal appears at about 4.0 K (Fig. 3b). Frequency-dependent ac susceptibility data were measured from 2.0 K to 4.9 K (Fig. S6†). The distribution coefficient value (α) is 0.18–0.26 (Table S4†).

Fig. 3 Temperature-dependence of the χ′ and χ′′ susceptibility signals under the optimized dc field (1600 Oe for 1 and 700 Oe for 2) at the indicated frequencies for 1 (a) and 2 (b). The solid lines are guides for the eye.

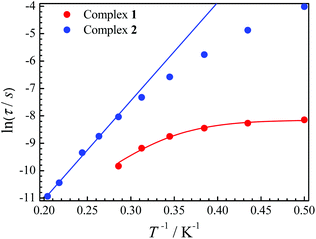
The relaxation time τ is one of the main parameters to evaluate the success of SMMs. Only when the relaxation time is long enough to observe the magnetic hysteresis, it can be called a magnet.^1a In our cases, the relaxation time for 2 is more than 100 times longer than that for 1 at the same temperature (Fig. 4). For complex 1, a large curvature appears at a low temperature, which is probably caused by QTM. If an Orbach process and the QTM are assumed to be dominant relaxation processes, fitting those data with the equation τ⁻¹ = τ_QTM⁻¹ + τ₀⁻¹ exp(−ΔE/T) gives ΔE = 24.8 K with τ_QTM = 2.89 × 10⁻⁴ s and τ₀ = 6.41 × 10⁻⁸ s for 1. The ln(τ) values increase linearly with 1/T at a higher temperature, and then a slight curvature appears for 2. Fitting of the high temperature regime with the Arrhenius law τ = τ₀ exp(ΔE/T) gives ΔE = 35.9 K and τ₀ = 1.22 × 10⁻⁸ s. The curvature at a low temperature is usually caused by other relaxation processes, such as direct and Raman.²⁰ The latter process may be dominant at low temperatures for 2 as we can well simulate the data below 3 K using τ⁻¹ = cTⁿ with c = 0.59 K⁻ⁿ s⁻¹ and n = 6.53 (Fig. S8†).

Fig. 4 Plots of ln(τ) versus 1/T for 1 and 2. The solid lines are best fits.

Moreover, the correlation between the ground state magnetic anisotropy and the coordination environment for Dy(III) complexes was performed using the program Magellan (Fig. 5).²¹ This program clearly shows that the principal magnetic axis of 1 is not aligned in any of the Dy–N bonds, whereas the principal magnetic axis for 2 lies exactly along the shortest Dy–O bond direction. The result for 1 may suggest competition of the anionic donors in such a cubic symmetry environment, which is fairly even and there is no obvious winner in each direction. However, for 2 there exists a Dy–O bond with a obvious shorter distance that may affect the charge distribution of the central metal ion more profoundly than in other directions, which in other words, may enhance the axial magnetic anisotropy of Dy(III) ions. So complex 2 has a higher energy barrier for magnetization reversal and hence displays magnetic relaxation under zero dc field even in such a cubic environment.

Fig. 5 Principal magnetic axis (green arrow) for 1 (a) and 2 (b).

Discussions

As far as we know, only a limited number of low-coordinate mononuclear lanthanide complexes have been magnetically studied in the literature, and some Er(III) analogues exhibit SIM behaviour.^7,9,12 For instance, the three-coordinated Er{N(SiMe₃)₂}₃ displays magnetic relaxation behaviours under zero dc field with an ΔE of 122 K,⁷ while its Dy(III) analogue did not show any SIM behaviour above 2 K; the four-coordinated [Li(THF)₄[Er{N(SiMe₃)₂}₃Cl]·2THF shows an ΔE of 66.4 K,⁹ but its Dy(III) counterpart was reported to have a ΔE of only 17 K under the assistance of a 600 Oe dc field.¹² The reason behind these phenomena is that both the equatorial and the spherical coordination environments often generate small or mixed ground m_J state doublets,^7,12 while the latter situation is rather similar to 1 and 2.

However, a short coordination bond may weaken such disadvantages as we can find high performance Dy(III) single-molecule magnets to usually associate it.^22–27 For example, the lanthanide alkoxides often contain short coordination bonds, so that some of their Dy(III) complexes are reported as high performance SIMs.²² In particular the polymetallic complex Dy@[Y₄K₂O(OtBu)₁₂], which shows an ΔE of 842 K, contains a very short Dy–O bond of 2.07 Å.^22b Other high performance Dy(III) SIMs, such as [Zn₂DyL′₂(MeOH)]NO₃·3MeOH·H₂O with a ΔE of 439 K,²³ [Dy(BIPM^TMS)₂][K(18C6)(THF)₂] with a ΔE of 813 K,²⁴ Dy(Cy₃PO)₂(H₂O)₅]Br₃·2(Cy₃PO)·2H₂O·2EtOH with the blocking temperature 20 K,²⁵ Dy(bbpen)Br with a ΔE of 1025 K (ref. 26) and [L′′₂Dy(H₂O)₅][I]₃·L′′₂·(H₂O) with a ΔE of 735 K,²⁷ the axial coordination bonds are also found to be much shorter than the equatorial bonds. Hence, we suspect that the short Dy–O bond in 2 is vital to fight against the adverse spherical symmetry, which results in a slightly higher ΔE compared to 1. Nevertheless, short Dy–O bonds cannot ensure a high ΔE for Dy-SIMs. Though the Dy–O bond in 2 is shorter than any reported Dy-SIMs, its magnetic property is not better than others. Thus, the combination of highly axial local symmetry is also very important to strengthen the magnetic anisotropy of the Dy(III) ions.

Conclusions

In conclusion, the magnetic properties of two four-coordinate Dy(III) complexes with a distorted cubic T_d symmetry have been investigated. All the coordinated atoms are negatively charged, providing an overall spherical anionic coordination environment, which we believe is disadvantageous to enhance the axial magnetic anisotropy for Dy(III) ions. Only complex 2 with a shorter Dy–O bond can differentiate its direction from the others and hence displays magnetic relaxation under zero dc field. For higher performance Dy-SIMs the combination of the local axial symmetry of the Dy(III) ions is obviously necessary.

Experimental section

Materials and methods

All the reactions were carried out under a dry and oxygen-free argon atmosphere by using Schlenk techniques or in a glovebox. All the solvents used were dried and degassed by standard techniques. Anhydrous LnCl₃ salts were prepared according to the literature procedure.²⁸ The ligands were purchased from TCI and used without further treatment. n-Butyllithium (2.5 mol L⁻¹ in n-hexane) was purchased from Chemetal.

Synthesis of [Li(C₄H₈O)₄][Dy(Ph₂N)₄] (1)

Diphenylamine (0.85 g, 5 mmol) was dissolved in 5 ml THF, and 2.0 ml of n-butyllithium (2.5 mol L⁻¹) in n-hexane solution was added through a syringe at 0 °C, which produced a yellow solution. The solution was stirred for further 2 h at 0 °C. Then anhydrous DyCl₃ (0.27 g, 1 mmol) was added, forming a cloudy solution immediately. The reaction mixture was heated to reflux overnight. After evaporation of the solvent followed by extraction of the residue with hot toluene, the crystals of [Li(C₄H₈O)₄][Dy(Ph₂N)₄] were obtained by cooling the extracts. The products were filtered and washed with n-pentane (2 × 5 ml), then dried under vacuum. Yield 0.85 g (75.2% based on metal Dy).

Synthesis of DyLi(Ph₃CO)₃(NPh₂)THF (2)

Diphenylamine (0.085 g, 0.5 mmol) and triphenylmethanol (0.39 g, 1.5 mmol) were dissolved in 5 ml THF, and then 0.8 ml of n-butyllithium (2.5 mol L⁻¹) in n-hexane solution was added using a syringe at 0 °C, producing a yellow cloudy solution, which was stirred for further 2 h at 0 °C. Then anhydrous DyCl₃ (0.14 g, 0.5 mmol) was added. The reaction mixture was heated to reflux overnight. After evaporation of the solvent followed by extraction of the residue with THF, the crystals of DyLi(Ph₃CO)₃(NPh₂)THF were obtained by layering n-pentane above the extracts. The products were filtered and washed with n-pentane (2 × 5 ml), and then dried under vacuum. Yield 0.48 g (80.8% based on metal Dy).

X-ray crystallography data

Single crystals suitable for X-ray analysis were coated with deoxygenated Paratone-N oil. All the data were collected on a Bruker Apex II DUO area-detector diffractometer with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). Cell refinement and data reduction were accomplished with the SAINT processing program. The structures were solved by direct methods and refined on F² using SHELXTL (Table 3). CCDC 1469847 (1) and 1469848 (2) contain the supplementary crystallographic data for this paper.

Table 3 Crystallographic data for complexes 1 and 2

	1	2
Empirical formula	C64H72DyLiN4O4	C73H63DyLiNO4
Formula weight (g mol^−1)	1130.70	1187.68
Crystal system	Orthogonal	Monoclinic
Space group	Pbcn	P21/n
T (K)	150	150
a (Å)	17.2073(11)	17.1728(13)
b (Å)	15.8244(10)	18.0592(13)
c (Å)	20.0712(13)	19.3313(14)
β (°)	90	95.0640(10)
V (Å^3)	5465.3(6)	5971.8(8)
Z	4	4
T (K)	150(2)	150(2)
ρ calcd (g cm^−3)	1.374	1.321
F (000)	2340	2436
Reflns collected	31 463	67 577
Unique reflns	6288	13 802
R int	0.02	0.0326
GOF	1.043	1.184
R 1 [I > 2σ(I)]	0.0223	0.0552
wR2 [all data]	0.0545	0.1105
Largest diff. peak/hole (e Å^−3)	0.899/−0.473	2.018/−1.888

---

Magnetic properties

Magnetic susceptibility measurements have been carried out with a Quantum Design MPMS-XL7 SQUID magnetometer upon cooling from 300 to 2 K in variable applied fields. Ac susceptibility measurements have been performed at frequencies between 1 and 1500 Hz with an ac field of 3.5 Oe and with a variable dc applied field. Powder samples were embedded in eicosane to avoid any field induced crystal reorientation. A diamagnetic correction has been calculated from Pascal constants and embedding eicosane has been applied to the observed magnetic susceptibility.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

This work was supported by the “973 projects” (2012CB619401 and 2012CB619402), the NSFC (21473129, 21503155 and IRT13034), the “National Young 1000-Plan” program, the Fundamental Research Funds for the Central Universities and the Wuhan National High Magnetic Field Center (2015KF06).

Notes and references

1. (a) D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, 2006; (b) C. Benelli and D. Gatteschi, Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, John Wiley & Sons, 2015; (c) S. Gao, Molecular Nanomagnets and Related Phenomena, Springer, 2015.
2. (a) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341; (b) D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148; (c) H. L. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1–33; (d) P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923–3929; (e) M. Ren and L.-M. Zheng, Acta Chim. Sin., 2015, 73, 1091–1113; (f) K. Liu, X. Zhang, X. Meng, W. Shi, P. Cheng and A. K. Powell, Chem. Soc. Rev., 2016, 45, 2423–2439.
3. (a) M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506; (b) S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138.
4. (a) N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695; (b) J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733; (c) M. A. AlDamen, J. M. Clemente-Juan, E. Coronado, C. Martí-Gastaldo and A. Gaita-Ariño, J. Am. Chem. Soc., 2008, 130, 8874–8875; (d) S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 122, 7610–7613; (e) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730–4733; (f) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239; (g) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542; (h) J. W. Sharples, Y. Z. Zheng, F. Tuna, E. J. L. McInnes and D. Collison, Chem. Commun., 2011, 47, 7650–7652; (i) F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976–6980; (j) L. Zou, L. Zhao, P. Chen, Y.-N. Guo, Y. Guo, Y.-H. Li and J. Tang, Dalton Trans., 2012, 41, 2966–2971; (k) J. J. Le Roy, M. Jeletic, S. I. Gorelsky, I. Korobkov, L. Ungur, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 3502–3510; (l) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952–17957; (m) S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711; (n) S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711; (o) Y. N. Guo, L. Ungur, G. E. Granroth, A. K. Powell, C. Wu, S. E. Nagler, J. Tang, L. F. Chibotaru and D. Cui, Sci. Rep., 2014, 4, 5471; (p) W. Cao, C. Gao, Y.-Q. Zhang, D. Qi, T. Liu, K. Wang, C. Duan, S. Gao and J. Jiang, Chem. Sci., 2015, 6, 5947–5954; (q) W. Cao, C. Gao, Y.-Q. Zhang, D. Qi, T. Liu, K. Wang, C. Duan, S. Gao and J. Jiang, Chem. Sci., 2015, 6, 5947–5954.
5. (a) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085; (b) S.-D. Jiang and S.-X. Qin, Inorg. Chem. Front., 2015, 2, 613–619.
6. (a) M. Lappert, A. Protchenko, P. Power and A. Seeber, Metal amide chemistry, John Wiley & Sons, 2008; (b) C.-H. Huang, Rare earth coordination chemistry: fundamentals and applications, John Wiley & Sons, 2011.
7. P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, J. Am. Chem. Soc., 2014, 136, 4484–4487.
8. S. K. Singh, T. Gupta, M. Shanmugam and G. Rajaraman, Chem. Commun., 2014, 50, 15513–15516.
9. A. J. Brown, D. Pinkowicz, M. R. Saber and K. R. Dunbar, Angew. Chem., Int. Ed., 2015, 127, 5962–5966.
10. N. F. Chilton, C. A. Goodwin, D. P. Mills and R. E. Winpenny, Chem. Commun., 2015, 51, 101–103.
11. N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099.
12. P. Zhang, J. Jung, L. Zhang, J. Tang and B. Le Guennic, Inorg. Chem., 2016, 55, 1905–1911.
13. Y.-S. Ding, T. Han, Y.-Q. Hu, M. Xu, S. Yang and Y.-Z. Zheng, Inorg. Chem. Front., 2016, 3, 798–807.
14. Y. Yao, X. Lu, Q. Shen and K. Yu, J. Chem. Crystallogr., 2004, 34, 275–279.
15. J. Cirera, P. Alemany and S. Alvarez, Chem. – Eur. J., 2004, 10, 190–207.
16. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175.
17. C. Görller-Walrand, K. Binnemans, K. A. Gschneidner and L. Eyring, Handbook on the Physics and Chemistry of Rare Earths, 1996, vol. 23.
18. Z.-X. Jiang, J.-L. Liu, Y.-C. Chen, J. Liu, J.-H. Jia and M.-L. Tong, Chem. Commun., 2016, 52, 6261–6264.
19. Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton. Trans., 2011, 40, 9953–9963.
20. K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. Schau-Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe and O. Waldmann, Chem. Sci., 2014, 5, 1650–1660.
21. N. F. Chilton, D. Collison, E. J. McInnes, R. E. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551.
22. (a) R. J. Blagg, C. A. Muryn, E. J. L. McInnes, F. Tuna and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 6530–6533; (b) R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678.
23. J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310–3316 . L′ = 2,2′,2′′-(((nitrilotris(ethane-2,1-diyl))tris(azanediyl)).
24. M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. McInnes and R. E. Winpenny, Chem. Sci., 2016, 7, 155–165.
25. Y. C. Chen, J. L. Liu, L. Ungur, J. Liu, Q. W. Li, L. F. Wang, Z. P. Ni, L. F. Chibotaru, X. M. Chen and M. L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837.
26. J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441–5450 . bbpen = N,N′-Bis(2-hydroxybenzyl)-N,N′-bis(2-methylpyridyl) ethylenediamine.
27. S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016 10.1039/C6SC00279J . L′′ = (^tBuPO(NHⁱPr)₂.
28. J. B. Reed, B. Hopkins, L. Audrieth, P. Selwood, R. Ward and J. Dejong, Inorg. Synth., 1939, 1, 28–33.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 1469847 and 1469848. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6qi00117c

‡ These authors contributed equally to this work.

---