DFT investigation of the ring contraction reaction of (η4-1,2-disilacyclohexadiene)iron tricarbonyls: a crucial intramolecular Si–Si bond activation†
Changzhi
Lin
a,
Qian
Liu
*b,
Yang
Zhang
c,
Jie
Liu
c and
Chenggang
Zheng
a
aState Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development, Petroleum Exploration and Production Research Institute, Sinopec, Beijing 100083, China
bDepartment of Chemical and Materials Engineering, University of Alberta, Edmonton, AB T6G 2V4, Canada. E-mail: liuqian331@sdu.edu.cn
cDepartment of Chemistry, Nankai University, Tianjin 300071, People's Republic of China
First published on 8th February 2016
Abstract
The mechanism of the ring contraction reaction of (η4-1,2-disilacyclohexadiene)iron tricarbonyls was studied at the M06/LACVP* level. The Si–Si bond of (η4-1,2-disilacyclohexadiene)iron tricarbonyls 1 was initially broken to form an η4-intermediate 3 by an intramolecular activation reaction with iron via the transition state 2TS. The Si–C bond of intermediate 3 was then activated by an intramolecular cheletropic reaction with iron, which generated a high energy state 5 through the transition state 4TS. Because of the dissociation of the silacarbenoid from 5, the π electrons of one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond coordinated to iron produced an intermediate 6 and [:SiMe2]. In particular, the silacarbenoids rapidly formed aggregations by oligomerizations. Finally, intermediate 6 achieved the six membered ring product 8 with the intramolecular nucleophilic reaction to accomplish the ring contraction reaction using the transition state 7TS. The rate-determining step was the intramolecular activation reaction of the Si–Si bond using iron.
C bond coordinated to iron produced an intermediate 6 and [:SiMe2]. In particular, the silacarbenoids rapidly formed aggregations by oligomerizations. Finally, intermediate 6 achieved the six membered ring product 8 with the intramolecular nucleophilic reaction to accomplish the ring contraction reaction using the transition state 7TS. The rate-determining step was the intramolecular activation reaction of the Si–Si bond using iron.
Introduction
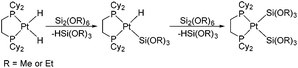
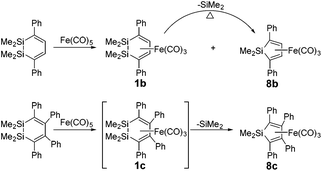
The activation of silicon–silicon bonds is regarded as a crucial step in various transition-metal-inspired silylations,1,2 such as bis(silylation) reactions3 and the dehydrocoupling of hydrosilanes.4 Since the first Si–Si bond activation reactions were reported by using transition metal complexes,5 many experimental studies have been performed on the activation of Si–Si bonds with platinum complexes and the formation of disilyl complexes over the past decades.6–18 Braun et al. have recently synthesized the bis(silyl) complexes [Pt{Si(OR)3}2(dcpe)] (R = Me or Et) by the Si–Si bond activation of Si2(OR)6 at [Pt(H)2(dcpe)] at room temperature (see Scheme 1).2aHowever, platinum as a noble metal is very rare and expensive. Iron, on the other hand, has many potential advantages such as low cost, low toxicity, and high natural abundance.19,20 Furthermore, Sakurai et al. have discovered Si–Si bond activation by iron in the ring contraction reaction of η4-1,2-disilacyclohexadiene.21 Two 1,2-disilacyclohexadienes 1b22 and 1c23 were prepared and their ring contraction reactions were studied in experiments. The products of 1b and 8b could be obtained via 1,1,2,2-tetramethyl-3,6-diphenyl-1,2-disilacyclohexadiene with Fe(CO)5 in xylene at 160 °C for 19 h (see Scheme 2) and 72% of 1b was converted to 8b at 160 °C after 37.5 h. A similar reaction also occurred for 1,1,2,2-tetramethyl-3,4,5,6-tetraphenyl-1,2-disilacyclohexadiene and Fe(CO)5, but 1c could not be separated and obtained during the reaction process.
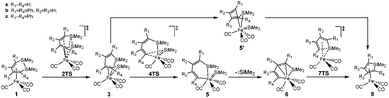
From the limited experimental results, Sakurai et al. proposed a reaction mechanism, in which 1 was induced by intramolecular Si–Si bond activation with iron (see Scheme 3).21 Then, the product 8 was generated from 3via an intermediate 5′ with an irregular six membered ring structure. However, it was not possible to corroborate the proposed mechanism because the crucial intermediates 3 and 5 were not isolated successfully and the amount of dissociated silylene was not monitored.
 | ||
| Scheme 3 The proposed mechanism of the ring contraction reaction of (η4-1,2-disilacyclohexadiene)iron tricarbonyls. | ||
In recent years, theoretical calculation as an effective method was widely used to study the structures and reactions of transition metal–silicon complexes.24–30 To explore this mechanism, density functional theory (DFT) was used to perform full optimizations of all structures in this process including the reactants, intermediates and products. The computational results showed that an intermediate 5 with a regular six membered ring was obtained from 3via the cheletropic removal of the silacarbenoid. Then complex 6 was formed by the π-electrons of one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond coordinated to iron. The product 8 was generated by an intramolecular nucleophilic reaction of 6. These calculated results clarified the connection between the structures and reaction for supporting the potential in situ source of SiMe2, the Si–Si activation and the cheletropic reaction.
C bond coordinated to iron. The product 8 was generated by an intramolecular nucleophilic reaction of 6. These calculated results clarified the connection between the structures and reaction for supporting the potential in situ source of SiMe2, the Si–Si activation and the cheletropic reaction.
Computational details
All geometries of the complexes were optimized based on the M06 method and the LACVP* basis set. The iron atom was calculated by the effective core potential valence basis set LANL2DZ31 and the main group elements (C, O, H and Si) were calculated using the 6-31G* basis set. Zhao and Truhlar reported that the M06 method had high accuracy for the calculation of the thermochemistry and kinetics of transition metals and main-group elements.32,33 Frequency analyses were performed under the same conditions to identify all stationary points as minima (zero imaginary frequency) or transition states (TS, only one imaginary frequency) and to provide free energies at 298.15 K and 1 atm. Intrinsic reaction coordinate (IRC)34 analysis was carried out to confirm that all stationary states are smoothly connected to each other. The bonding modes of certain geometries were performed on the basis of a natural bond orbital (NBO).35 The calculated total electronic energies, thermal corrections to enthalpies and Gibbs free energies are provided in the ESI.† All calculations were performed with the Gaussian 09 packages.36Results and discussion
A simple structure, η4-C4H4(SiMe2)2Fe(CO)3, was initially employed as a model system to study the mechanism of the intramolecular ring contraction reaction. Based on the calculated results from the simplified model, the two model reactants η4-C4H2Ph2(SiMe2)2Fe(CO)3 and η4-C4Ph4(SiMe3)2Fe(CO)3 were also investigated using the same theoretical method.The intramolecular activation of the Si–Si bond via iron in complex η4-C4H4(SiMe2)2Fe(CO)3
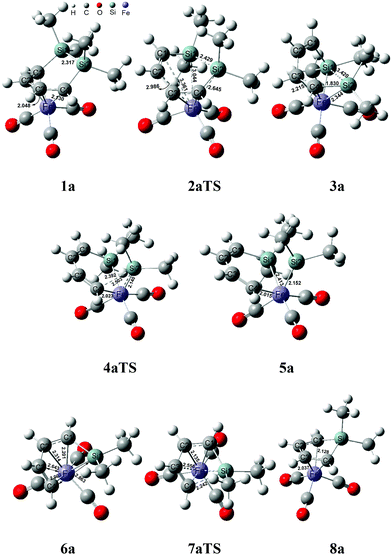
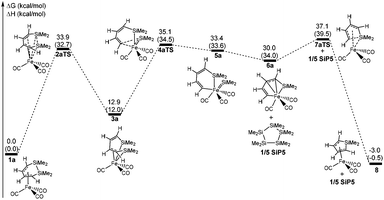
Fig. 1 shows that the reactant 1a initially forms an intermediate 3a through the transition state 2aTS to accomplish the ring cleavage reaction. In particular, the free energy barrier of 33.9 kcal mol−1 was very high for this process. From the geometry of 1a, the four C(ring)–Fe bond corresponded to two bond lengths, 2.130 and 2.048 Å, respectively (see Fig. 2), which indicated that an η4-coordinated structure was constructed between the six membered ring and the iron. The coordinated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond donating electrons made the iron achieve an 18 electron structure in 1a, which significantly improved the thermodynamic stability.
C bond donating electrons made the iron achieve an 18 electron structure in 1a, which significantly improved the thermodynamic stability.
 | ||
| Fig. 1 Free energy profiles of the ring contraction reaction of 1a. The values shown are relative to the free energies of 1a (kcal mol−1, ΔH in the parenthesis). | ||
From 1a to 2aTS, the bond lengths of C1–Fe and C2–Fe increased to 3.361 Å and 2.986 Å, respectively; whereas, Si–Fe bond lengths reduced to 3.044 Å and 2.645 Å, respectively. Although two silicon atoms concertedly coordinated to iron during the C1 and C2 atom dissociation, they did not fully compensate for the donated electrons of the coordinated C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 bond. Thus, the transition state 2aTS caused a high free energy due to a seriously unsaturated electronic structure of iron. The IRC calculation, in this case, showed that an intermediate 3a was generated after the transition state 2aTS.
C2 bond. Thus, the transition state 2aTS caused a high free energy due to a seriously unsaturated electronic structure of iron. The IRC calculation, in this case, showed that an intermediate 3a was generated after the transition state 2aTS.
Compared with the geometries of 1a and 3a, the coordinated interaction between the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 bond and the iron was replaced by two formed Si–Fe σ bonds by transferring to the sp3-hybridized orbital of the Si and d-orbital of iron. The Si–Fe bonding interaction caused the Si–Si bond length to be increased to 3.420 Å from 2.317 Å. Furthermore, the C1C2C3C4 dihedral angle of 80.1° presented the delocalized conjugation interaction of C
C2 bond and the iron was replaced by two formed Si–Fe σ bonds by transferring to the sp3-hybridized orbital of the Si and d-orbital of iron. The Si–Fe bonding interaction caused the Si–Si bond length to be increased to 3.420 Å from 2.317 Å. Furthermore, the C1C2C3C4 dihedral angle of 80.1° presented the delocalized conjugation interaction of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C being broken. These two factors largely reduced the thermodynamic stability of 3a, and it was endergonic by 12.9 kcal mol−1 for 1a → 3a.
C being broken. These two factors largely reduced the thermodynamic stability of 3a, and it was endergonic by 12.9 kcal mol−1 for 1a → 3a.
The Si–C bond activation achieved by an intramolecular cheletropic reaction with iron
The η4-intermediate 3a then transferred to an η3-coordinated intermediate 5a through the transition state 4aTS, which corresponded to a free energy barrier of 22.2 kcal mol−1. Comparing 4aTS with 3a, the bond length of C4–Si2 was extended from 1.830 Å to 2.503 Å. Due to the breaking of the C4–Si2 bond, the π-coordinated interaction between the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bond and the iron concertedly transferred towards a σ-bond of C4–Fe in 4aTS. As a result, the C1C2C3C4 dihedral angle reduced to 4.5° and the shape was a coplanar six membered ring which indicated that the delocalized conjugation interaction resumed between the C1
C4 bond and the iron concertedly transferred towards a σ-bond of C4–Fe in 4aTS. As a result, the C1C2C3C4 dihedral angle reduced to 4.5° and the shape was a coplanar six membered ring which indicated that the delocalized conjugation interaction resumed between the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and C3
C2 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bonds. Moreover, the separated Si2 atom donated two p electrons to the d orbital of iron in order to form its 18-electronic stable structure.
C4 bonds. Moreover, the separated Si2 atom donated two p electrons to the d orbital of iron in order to form its 18-electronic stable structure.
Next, an intermediate 5a was achieved using the cheletropic interaction of the Si1 and C4 atoms with iron. Due to the σ electron of the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bond coordinating to iron, the SiMe2 group was concertedly dissociated from C4 and migrated to iron. Then the Si2
C4 bond coordinating to iron, the SiMe2 group was concertedly dissociated from C4 and migrated to iron. Then the Si2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Fe bond of 5a was shaped from the sp2-hybrid electrons of Si2 atom and d orbital of iron. Here the Si2–C4 bond activation was also achieved by the intramolecular cheletropic interaction. The intermediate 5a was a high energy state, which had an extra high free energy of 33.4 kcal mol−1 relative to 1a. This indicated that 5a was a thermodynamically unstable intermediate and only had a short lifetime during the reaction. Therefore, it was impossible to be observed in experiments.21
Fe bond of 5a was shaped from the sp2-hybrid electrons of Si2 atom and d orbital of iron. Here the Si2–C4 bond activation was also achieved by the intramolecular cheletropic interaction. The intermediate 5a was a high energy state, which had an extra high free energy of 33.4 kcal mol−1 relative to 1a. This indicated that 5a was a thermodynamically unstable intermediate and only had a short lifetime during the reaction. Therefore, it was impossible to be observed in experiments.21
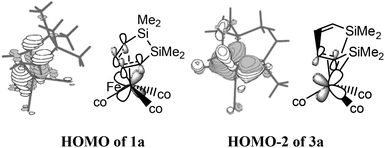
NBO analyses were subsequently performed for the structures of 1a, 3a, and 5a to investigate the unexpected difference of the thermodynamic stability. For these geometries, all of the iron atoms had an 18-electronic structure. As shown in Fig. 3, the HOMO of 1a indicated that the d electrons of iron were shifted to the π* orbital of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, which effectively enhanced the thermodynamic stability. Even though the conjugation of the two C
C, which effectively enhanced the thermodynamic stability. Even though the conjugation of the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds was broken in 3a, the HOMO−2 orbital still showed a bonding interaction between the d electrons of iron and the π* orbital of the C3
C bonds was broken in 3a, the HOMO−2 orbital still showed a bonding interaction between the d electrons of iron and the π* orbital of the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bond. But the intermediate 5a did not possess such an effective interaction and its thermodynamic stability was reduced to a large extent.
C4 bond. But the intermediate 5a did not possess such an effective interaction and its thermodynamic stability was reduced to a large extent.
The dissociation and the oligomerizations of [:SiMe2]
Due to poor thermodynamic stability, the dimethylsilylene group was facile to dissociate from 5a and formed intermediate 6a. After the release of one silacarbenoid, the iron of 5a became a more unsaturated electronic structure. From 6a, the bond lengths of C1–Fe and C2–Fe were 2.201 Å and 2.134 Å, respectively. This presented that the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 bond donated π electrons to iron again, which satisfied the 18 electronic structure of iron. At the same time, an irregular six-membered ring was formed in the geometry of 6a, which effectively shrank the distance between the C4 and Si1 atoms. In particular, the separated free [:SiMe2] group of this step had never been isolated or even monitored in experiments.23 This implied that the free silacarbenoid should not be the final product due to its high reactivity toward the oligomerization.37,38
C2 bond donated π electrons to iron again, which satisfied the 18 electronic structure of iron. At the same time, an irregular six-membered ring was formed in the geometry of 6a, which effectively shrank the distance between the C4 and Si1 atoms. In particular, the separated free [:SiMe2] group of this step had never been isolated or even monitored in experiments.23 This implied that the free silacarbenoid should not be the final product due to its high reactivity toward the oligomerization.37,38
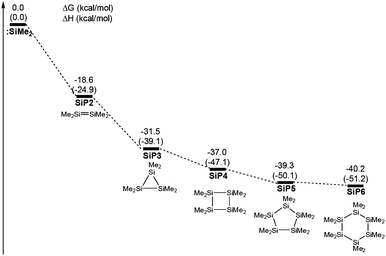
According to previous reports, some stable aggregations of [:SiMe2] groups were possibly generated by the oligomerizations of silacarbenoids.39–42Fig. 4 shows that four potential geometries are designed for the oligomerizations of the [:SiMe2] groups, which are then performed with full optimizations. Compared with various aggregated complexes, the free energy significantly decreased to −40.2 kcal mol−1 from a free :SiMe2 to the six membered ring SiP6, which showed that the thermodynamic stability was improved against the aggregated number of the silacarbenoid increased. However, the free energy of SiP5 was only 0.9 kcal mol−1 higher than that of SiP6, which meant that many oligomerization products would exist in the reaction system via multiple equilibria after SiP5. Then, SiP5 was selected as a model product of oligomerization and used to calculate the energy of the ring contraction reaction. The ΔH was 0.4 kcal mol−1 for 5a → 6a + 1/5 SiP5, but it was exergonic by 3.4 kcal mol−1 due to the entropic advantage of the bimolecular reaction, which was thermodynamically feasible.
 | ||
| Fig. 4 Free energy profiles of potential aggregations of the silacarbenoid oligomerizations. The values shown are relative to the free energies of :SiMe2 (kcal mol−1, ΔH in the parenthesis). | ||
The intramolecular nucleophilic reaction of 6a
The intermediate 6a finally achieved the product 8avia the transition state 7aTS to accomplish the nucleophilic reaction. The free energy barrier was 7.1 kcal mol−1 for 6a → 8a, which was a kinetically facile process. From 7aTS, the distance of Si1–C4 was shrunk to 2.242 Å, which indicated that the σ electron of C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 attacked the silicon atom. Besides, C3 was also close to the iron atom and the distance of C3–Fe was shrunk to 2.556 Å from 2.643 Å of 6a. These indicated that the C3
C4 attacked the silicon atom. Besides, C3 was also close to the iron atom and the distance of C3–Fe was shrunk to 2.556 Å from 2.643 Å of 6a. These indicated that the C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 bond was transforming to the π-coordination with iron from the σ-coordination during the nucleophilic reaction. Then a five membered ring of Si1C1C2C3C4 was again formed in product 6a, which also finally achieved the ring contraction reaction of 1a. It was tempestuously exergonic by 33.0 kcal mol−1 for this step.
C4 bond was transforming to the π-coordination with iron from the σ-coordination during the nucleophilic reaction. Then a five membered ring of Si1C1C2C3C4 was again formed in product 6a, which also finally achieved the ring contraction reaction of 1a. It was tempestuously exergonic by 33.0 kcal mol−1 for this step.
For the ring contraction reaction of 1a, the total free energy barrier was 37.1 kcal mol−1, and the rate-determining step was the intramolecular activation of the Si–Si bond with a free energy barrier of 33.9 kcal mol−1. Actually, the reversal of the last step was an intramolecular Si–C activation catalyzed by iron. But the free energy barrier and the ΔG were 40.1 kcal mol−1 and 33.0 kcal mol−1 for 8a → 6a, and which was not kinetically and thermodynamically feasible.
Link to experiments
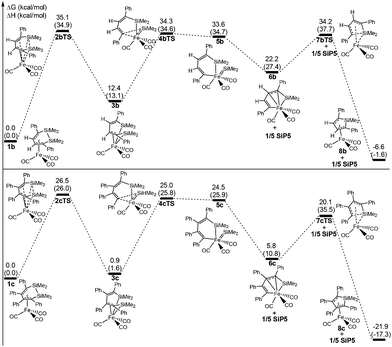
To investigate the actual reaction, two experimental reactants η4-C4H2Ph2(SiMe2)2Fe(CO)3 (1b) and η4-C4Ph4(SiMe3)2Fe(CO)3 (1c) were studied for their ring contraction reactions using the same theoretical method. Fig. 5 shows that the total free energy barriers of 1b and 1c are 35.4 and 26.5 kcal mol−1, respectively, which are also the rate-determining steps. There was a difference with 1a, in which 2bTS and 2cTS corresponded to the highest free energy instead of 7bTS and 7cTS.The total free barrier of 1b was 9.1 kcal mol−1 higher than that of 1a, so the reaction rate of the former was far slower than the latter according to the Eyring equation. Thus, 1b occurred under more strict experimental conditions, which needed a high temperature of 160 °C with 37.5 h. As a result of the slow reaction rate, 1b was possibly obtained from the reaction system in experiments. But 1c was difficult to synthesize under the same conditions, due to a rapid reaction rate of the ring contraction reaction. This was in good agreement with the experimental results.23
Fig. 6 shows that the arrangement of four phenyls is shaped like the propeller conformation in the structure of 1c, where four C–Fe bond lengths are 2.197 Å, 2.095 Å, 2.074 Å and 2.123 Å, respectively. Compared with 1a, the increase of all the C–Fe bond lengths was caused by the steric hindrance of four phenyls in 1c, which was unfavorable to the coordinated interaction between the six membered ring and iron. And the thermodynamic stability of 1c was significantly reduced. From 1c to 3c, the steric hindrance among the phenyls was largely lowered because of the distortion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C
C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, which increased the thermodynamic stability of 3c. Therefore, it was actually an equilibrium with a rapid reaction rate for 1c ⇌ 3c. The steric hindrance decreasing among the phenyls also improved the stabilities of 6c, 7cTS and 8c, which caused the highest free energy barrier transferred to 26.5 kcal mol−1 of 2cTS from 20.1 kcal mol−1 of 7cTS. However, the free energy barrier was increased to 14.3 kcal mol−1 for 6c → 7cTS → 8c compared with 6a → 7aTS → 8a. Here the Si–C bond activation of 8c was also kinetically unfeasible due to a higher ΔG≠ of 42.0 kcal mol−1. In addition, the thermodynamic stability of 8b and 8c was significantly improved compared with 8a, especially the ΔG of −21.9 kcal mol−1 for 1c → 8c + 1/5 SiP5. This indicated that the increase of the phenyl substituent was kinetically and thermodynamically favorable to perform the ring contraction reaction of 1 → 8 + 1/5 SiP5.
C bond, which increased the thermodynamic stability of 3c. Therefore, it was actually an equilibrium with a rapid reaction rate for 1c ⇌ 3c. The steric hindrance decreasing among the phenyls also improved the stabilities of 6c, 7cTS and 8c, which caused the highest free energy barrier transferred to 26.5 kcal mol−1 of 2cTS from 20.1 kcal mol−1 of 7cTS. However, the free energy barrier was increased to 14.3 kcal mol−1 for 6c → 7cTS → 8c compared with 6a → 7aTS → 8a. Here the Si–C bond activation of 8c was also kinetically unfeasible due to a higher ΔG≠ of 42.0 kcal mol−1. In addition, the thermodynamic stability of 8b and 8c was significantly improved compared with 8a, especially the ΔG of −21.9 kcal mol−1 for 1c → 8c + 1/5 SiP5. This indicated that the increase of the phenyl substituent was kinetically and thermodynamically favorable to perform the ring contraction reaction of 1 → 8 + 1/5 SiP5.
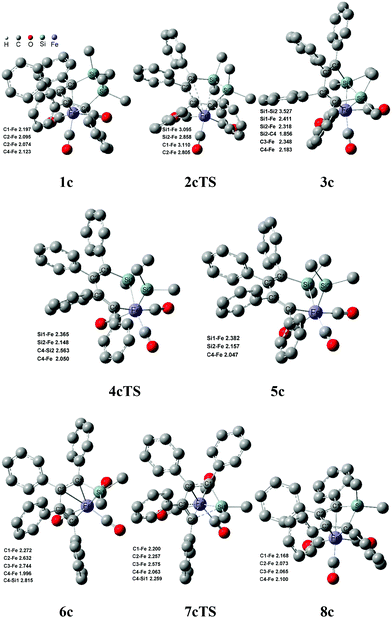 | ||
| Fig. 6 Structures and bond lengths (Å) for the ring contraction reaction of 1c. Hydrogen atoms were omitted. | ||
Conclusions
The mechanism of the ring contraction reaction of (η4-1,2-disilacyclohexadiene)iron tricarbonyls was investigated based on M06/LACVP*, which involved a process of 1 → 2TS → 3 → 4TS → 5 → 6 + 1/5 SiP5 → 7TS + 1/5 SiP5 → 8 + 1/5 SiP5. The Si–Si bond of 1 was initially broken via an intramolecular activation reaction with iron and an intermediate 3 was generated by the transition state 2TS. The Si–C bond activation of intermediate 3 was then achieved by an intramolecular cheletropic reaction with iron. A high energy state 5 was also formed via the transition state 4TS here. Next, the π electrons of one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond coordinated to iron in order to satisfy with the 18 electronic structure of iron after the dissociation of the silacarbenoid, which produced an intermediate 6 and [:SiMe2]. In particular, the [:SiMe2] groups preferred to form aggregations by oligomerizations instead of free silacarbenoids, due to the higher thermodynamic stability.
C bond coordinated to iron in order to satisfy with the 18 electronic structure of iron after the dissociation of the silacarbenoid, which produced an intermediate 6 and [:SiMe2]. In particular, the [:SiMe2] groups preferred to form aggregations by oligomerizations instead of free silacarbenoids, due to the higher thermodynamic stability.
Finally, intermediate 6 produced the six membered ring product 8 with an intramolecular nucleophilic reaction via the transition state 7TS, which also achieved the ring contraction reaction of 1. The rate-determining step was the intramolecular activation reaction of the Si–Si bond using iron. The increase of the phenyl substituents of the ring group could effectively reduce the total free energy barrier and significantly enhance the thermodynamic stability of product 8. The ring contraction reaction of 1c was thermodynamically and kinetically most favorable in the three reactants.
Acknowledgements
We thank the National Natural Science Foundation of China (no. D0308/41573068 and no. B0111/21571188) and the Key project of Ministry of Science and Technology of Sinopec (no. G5800-15-ZS-KJB025) for research funding.Notes and references
- J. Y. Corey, Chem. Rev., 2011, 111, 863–1071 CrossRef CAS PubMed.
- (a) C. Mitzenheim and T. Braun, Angew. Chem., Int. Ed., 2013, 52, 8625–8628 CrossRef CAS PubMed; (b) J. Voigt and T. Braun, Dalton Trans., 2011, 40, 12699–12704 RSC; (c) J. Voigt, M. A. Chilleck and T. Braun, Dalton Trans., 2013, 42, 4052–4058 RSC.
- H. K. Sharma and K. H. Pannell, Chem. Rev., 1995, 95, 1351–1374 CrossRef CAS.
- J. Y. Corey, Adv. Organomet. Chem., 2004, 51, 1–52 CrossRef CAS.
- M. Kumada, K. Mimura, M. Ishikawa and K. Shiina, Tetrahedron Lett., 1965, 6, 83–88 CrossRef.
- (a) K. H. Pannell, J. Cervantes, C. Hernandez, J. Cassias and S. Vincenti, Organometallics, 1986, 5, 1056–1057 CrossRef CAS; (b) K. H. Pannell, J. M. Rozell and C. Hernandez, J. Am. Chem. Soc., 1989, 111, 4482–4485 CrossRef CAS; (c) H. K. Sharma, K. H. Pannell, R. N. Kapoor and F. Cervantes-Lee, J. Am. Chem. Soc., 1997, 119, 9315–9316 CrossRef; (d) H. K. Sharma and K. H. Pannell, Chem. Rev., 1995, 95, 1351–1374 CrossRef CAS.
- (a) K. Ueno, H. Tobita, M. Shimoi and H. Ogino, J. Am. Chem. Soc., 1988, 110, 4092–4093 CrossRef CAS; (b) H. Tobita, K. Ueno, M. Shimoi and H. Ogino, J. Am. Chem. Soc., 1990, 112, 3415–3420 CrossRef CAS.
- U. Schubert, Angew. Chem., Int. Ed. Engl., 1994, 33, 419–421 CrossRef.
- M. Suginome, H. Oike and Y. Ito, J. Am. Chem. Soc., 1995, 117, 1665–1666 CrossRef CAS.
- G. P. Mitchell and T. D. Tilley, Organometallics, 1996, 15, 3477–3479 CrossRef CAS.
- S. Nlate, E. Herdtweck and R. A. Fisher, Angew. Chem., Int., Ed. Engl., 1996, 35, 1861–1863 CrossRef CAS.
- M. Suginome, Y. Kato, N. Takeda and H. Oike, Organometallics, 1998, 17, 495–497 CrossRef CAS.
- H. Tobita, T. Sato, M. Okazaki and H. Ogino, J. Organomet. Chem., 2000, 611, 314–322 CrossRef CAS.
- A. Naka, M. Ishikawa, S. H. Cha, K. K. Lee and Y. W. Kwak, J. Organomet. Chem., 2002, 645, 47–53 CrossRef CAS.
- K. Ueno, S. Asami, N. Watanabe and H. Ogino, Organometallics, 2002, 21, 4897–4908 CrossRef.
- U. Schubert, J. Pfeiffer, F. Stöhr, D. Sturmayr and S. Thompson, J. Organomet. Chem., 1997, 548, 57–63 CrossRef.
- Y. Zhang, F. Cervantes-Lee and K. H. Pannell, Organometallics, 2003, 22, 2517–2524 CrossRef CAS.
- M. Zirngast, C. Marschner and J. Baumgartner, Organometallics, 2006, 25, 1326–1328 CrossRef.
- B. A. F. L. Bailly and S. P. Thomas, RSC Adv., 2011, 1, 1435–1445 RSC.
- V. W. Goldschmidt, Geochemistry, Oxford Press, London, 1958, 647 Search PubMed.
- Y. Nakadaira, T. Kobayashi and H. Sakurai, J. Organomet. Chem., 1979, 165, 399–405 CrossRef CAS.
- Y. Nakadaira, S. Kanouchi and H. Sakurai, J. Am. Chem. Soc., 1974, 96, 5623–5624 CrossRef CAS.
- Y. Nakadaira and H. Sakurai, J. Organomet. Chem., 1973, 47, 61–65 CrossRef CAS.
- X. Lu, Y. Zhang, P. Yun, M. Zhang and T. Li, Org. Biomol. Chem., 2013, 11, 5264–5277 CAS.
- (a) X. Lu, Y. Zhang, M. Zhang and T. Li, J. Organomet. Chem., 2014, 749, 69–74 CrossRef CAS; (b) X. Lu, Y. Zhang, N. Turner, M. Zhang and T. Li, Org. Biomol. Chem., 2014, 12, 4361–4371 RSC.
- K. K. Pandey and P. P. Power, Organometallics, 2011, 30, 3353–3361 CrossRef CAS.
- V. A. Du, G. N. Stipicic, M. Bendova and U. Schubert, Monatsh. Chem., 2010, 141, 671–675 CrossRef CAS.
- Y. Y. Zhao, X. L. Cheng, X. X. Bi and S. W. Bi, J. Mol. Struct. (THEOCHEM), 2008, 869, 59–66 CrossRef CAS.
- U. Böhme, J. Organomet. Chem., 2006, 691, 4400–4410 CrossRef.
- M. Vögler, I. Pavel, M. Hofmann, D. Moigno, M. Nieger, W. Kiefer and W. Malisch, Inorg. Chem., 2003, 42, 3274–3284 CrossRef PubMed.
- (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. J. Frisch et al. , Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- E. G. Sheila and L. K. Cindy, Macromolecules, 2002, 35, 2871–2872 CrossRef.
- J. S. Edgar, J. Am. Chem. Soc., 1967, 89, 6793–6794 CrossRef.
- S. Tsutsui, K. Sakamoto and M. Kira, J. Am. Chem. Soc., 1998, 120, 9955–9956 CrossRef CAS.
- M. Kira, J. Organomet. Chem., 2004, 689, 4475–4488 CrossRef CAS.
- S. Tsutsui, E. Kwon, H. Tanaka, S. Matsumoto and K. Sakamoto, Organometallics, 2005, 24, 4629–4638 CrossRef CAS.
- J. Oláh and T. Veszprémi, J. Organomet. Chem., 2003, 686, 112–117 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Total electronic energies, thermal corrections to Gibbs free energies and Cartesian coordinates, and so on. See DOI: 10.1039/c5qo00402k |
| This journal is © the Partner Organisations 2016 |