Effects of C1–3-doping on electronic and structural properties of Stone–Wales defective boron nitride nanotubes as well as their NO gas sensitivity
Hossein Roohi* and
Layla Maleki
Department of Chemistry, Faculty of Science, University of Guilan, Rasht, Iran. E-mail: hrouhi@gmail.com; hroohi@guilan.ac.ir; Fax: +98 1333 323262
First published on 14th December 2015
Abstract
Doping nanotubes is a useful way to tune their electronic, optical and magnetic properties, and enhance their chemical reactivity for nanoelectronic device applications. In this work we investigate the electronic and structural properties of C-doped Stone–Wales (SW) defective (6,0) single-walled boron nitride nanotubes (BNNTs) at B3LYP/6-31+G(d) and M06-2X/6-31+G(d) levels of theory as well as their chemical sensitivity towards NO gas at ONIOM(M06-2X/6-31++G(d,p):M06-2X/STO-6G) levels. The different positions and concentrations of C dopant atoms are explored. Interaction energies and global reactivity descriptors are used to predict the overall reactivity of the studied C-doped SW-BNNTs. The results show that the doping of C at the neighboring B and N sites located in the 7-7 ring fusion (CNB and CNBB) leads to lower defect formation energies. In addition, we find that C impurities can substitute into the boron site due to the low formation energy. Owing to formation of the mid-gap states induced by substituting 3C atoms for three B atoms, a transformation from electrical insulator (band gap of 4.27 eV) to an electrical conductor (band gap of 1.65 eV) is predicted. Therefore, from these results it can be predicted that the 3CB-doped SW-BNNTs can be used to improve solar cell efficiency. The results obtained at M06-2X/6-31++G(d,p) level reveal that the NO adsorptions on the surface of C-doped SW-BNNTs are energetically favorable and are stronger than pristine and undoped SW-BNNTs. It is expected that the present results will provide a useful guide to develop novel C-doped BNNTs based sensors for the detection of toxic NO molecules.
1. Introduction
Boron nitride nanotubes (BNNTs) have the same atomic structure as the corresponding carbon nanotubes (CNTs). CNTs with small band gaps (Eg) in the range 0.2–2.0 eV might be metallic or semiconductors. BNNTs have profound chemical and thermal stabilities, and with much wider band gaps of about 5.5 eV, are electrically insulating.1–5 Due to the thermal issues of CNTs based devices, it was speculated that BNNTs could be better candidates for nanoelectronic engineering. The large band gap makes BNNTs promising materials for a number of potential applications such as polymeric composites,6 sensors,7 catalysts,8 molecule based logic gates, nanoelectronics and optoelectronic9 devices. Thus, it is important to find a way to tune BNNT electronic properties in order to widen the application field. Although some methods have been predicted to be useful for BNNT band gap engineering using theoretical calculations,5 in practice, such methods are very difficult to realize due to the extreme conditions involved, such as very high electric field or pressure.If the electronic properties of BN nanotubes, e.g., their band gaps can be controlled through a simple mechanism, their application would be greatly extended, particularly in the sensor and nanoelectronic fields. Various methods including physical methods (such as applying an electric field10 and strain11,12) and chemical methods13–15 have been used to tune the electronic properties of BNNTs. The physical methods change the band gap directly while the chemical methods tune it by introducing localized energy levels inside the gap.16 Tuning the electronic properties of NTs can be achieved by doping the nanotube as predicted in theoretical calculations17–22 and as found in experimental studies.23–29
A very important topological defect in BNNTs is Stone–Wales (SW), which is comprised of two pairs of five-membered and seven-membered rings (5-7-7-5) formed by rotating one bond of the traditional six-membered ring by 90°.30 Atomistic simulations12,31 and experiments32,33 have shown that the topological defect (5-7-7-5) in BNNTs generate two unfavorable homoelemental B–B and N–N bonds that increase the total energy of the system. However, formation of these bonds can be prohibited if there is a C–C defect in BNNT. Kim et al.34 studied the physical properties of SW-BNNTs with the substitutional C pair defect. Jalili et al. investigated the effect of SW defects on the structural and electronic properties of zigzag C3N nanotubes.35 The effect of carbon doping on SW defective sites in armchair BNNTs have been studied by Anafcheh et al.36
Nitric oxide (NO) is a toxic free radical gas that is a known bioproduct in almost all types of organisms, ranging from bacteria to plants, fungi, and animal cells.37 Selective reduction of NO in oxidizing atmospheres has recently received much attention because it has potential as a practical measure to remove NOx emitted from diesel and lean burn engines.38 A very different area, where NO sensing is also required, is in the medical industry, specifically in breath analysis for diagnosis of respiratory ailments.39 Although it is infamous for its harmful impact on the environment, its removal and sensing is still a challenge. Therefore, reliable and low-cost NO sensors with high selectivity and sensitivity are required for human health and environmental safety. Recently great advances have been made in demonstrating the capability of using nanotubes to detect NO gas. Defected SWCNTs, if embedded in physiological systems, can serve as a sensor for biological NO.40 Yates et al.41 studied the physical adsorption of NO on purified single-walled CNTs at low temperatures by means of transmission infrared spectroscopy. The adsorption of NO molecules on CNTs42 and BNNTs43 has been theoretically investigated. Rafati et al.43 found that an NO molecule can be physisorbed on the surface of CNTs endothermically. Adsorption of CO and NO on the boron site (CB) and at a nitrogen site (CN) in the 1C-doped BNNTs using the local density approach (LDA) has been studied by Baierle et al.44 They showed that a chemical bond between the tube and the adsorbed molecule is observed when a carbon substitution impurity is inserted into the tube wall. The chemisorptions of NO and NNO molecules on SiCNTs, CNTs and BNNTs were investigated by Kang et al.45 They found that NO and NNO molecules can be chemisorbed on SiCNTs with an appreciable binding energy and that this is not the case for either CNTs or BNNTs. Recently, Chen et al.46 investigated the adsorption and reduction of NO molecule on Si-doped graphene. They found that NO was easily converted into N2O through a dimer mechanism.
To the best of our knowledge, there are no theoretical studies on the adsorption of NO molecules on C-doped SW-BNNTs. Recently, we investigated the adsorption sensitivity of pristine and SW defective BNNTs towards NO gas by means of DFT.47 Our results showed that the NO adsorption on the outer and inner surface sites of pristine and SW-BNNTs were energetically favorable and unfavorable, respectively. Besides, NO adsorption on the pristine BNNTs is stronger than that of SW ones. We previously studied the effect of CH3CO on the molecular and electronic properties of BNNTs.48 We have also investigated the response of (6,0) BNNTs and (6,0) SW-BNNTs to axial tension and compression11,49 and green chemical functionalization of CNTs with ionic liquids,50 as well as chemical functionalization of BNNTs via the 1,3-dipolar cycloaddition reaction of azomethine ylide.51 In this paper, the effects of C1–3-doping on the electronic and structural properties of SW-BNNTs are investigated. Moreover, the second part of the work is devoted to a first-principle investigation of C-doped SW-BNNTs as a sensor and adsorbent of NO molecules. The C-doped SW-BNNTs CB, CN, C2B, C2N, CNB, C3N, C3B, C2N1B and C1N2B are considered. The CB and CN symbols denote doping of C atoms at the B and N sites, respectively. C atom substitution for two N atoms and one B atom is abbreviated by C2N1B. The structural parameters, defect formation energy, highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap, dipole moment, global reactivity descriptors including chemical potential, chemical hardness, softness, electrophilicity index and density of states (DOS) are calculated.
These results will be useful to understand adsorption capability of BNNTs, and also to develop BNNT-based sensors. Calculated data for the electronic DOS and the electronic charge densities indicate that the doping of C atoms not only improves the electronic transport property of BNNTs but also induces magnetism in the odd carbon doped SW-BNNTs. In addition, doping SW-BNNTs with C is expected to be a simple strategy for improving the properties of BNNTs, and C doped SW-BNNTs is expected to be a potential resource for detecting the presence of NO and, in turn, to develop BNNT-based sensors in the environment.
2. Computational details
All geometry optimization calculations were performed using the B3LYP hybrid functional52,53 and 6-31+G(d) basis set as implemented in the computational program packages.54,55 Furthermore, single-point energies have been obtained at the M06-2X/6-31+G(d) level.We have investigated the effects of SW defect and C-doping in different sites of SW defect regions on the electronic and structural properties of (6,0) zigzag single-walled BNNTs. For this purpose a single-walled BNNT with 36 B and 36 N atoms with average length of about 11.39 Å was used to model the (6,0) BNNTs. Both ends of the BNNT segment were capped with H atoms to saturate dangling bonds. The formation energies of the C-doped SW defective BNNTs were estimated using eqn (1) given below:
| Eform = Ed + (a + b)EB or N − mEC − EP | (1) |
Global reactivity descriptors measure the overall reactivity of a molecule. They do not contain any information about regioselectivity. Some of the descriptors are chemical potential, chemical hardness, global softness etc. Chemical potential plays an especially important role in semiconductor physics57 and their reactivity in chemistry. The DFT-based reactivity descriptors are good prediction tools for studying reactivity especially in probing the regiochemistry of different types of chemical reactions.58–60
The relation of chemical potential (μ) and the electronegativity (χ)61,62 can be written as follows:
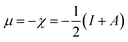 | (2) |
The global chemical hardness (η) is defined as63
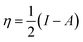 | (3) |
In the finite different approximation, the ionization energy and electron affinity can be replaced by the EHOMO and ELUMO, respectively, using Koopmans’ theorem.64
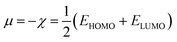 | (4) |
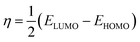 | (5) |
The electrophilicity index (ω),65 which measures the capacity of an electrophile to accept the maximal number of electrons in a neighboring reservoir of electron sea, is defined according to the following equation
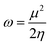 | (6) |
The chemical softness (S) is defined as following equation
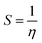 | (7) |
An ONIOM methodology66 is used to study the adsorption of NO gas on the C-doped SW-BNNTs. ONIOM approach has clear advantages for modeling interactions involving nanostructures.67–69 In this approach, the full system is divided into a reactive part, which is treated at an appropriately high level of theory, while the remainder of the system is included at a less expensive lower level of theory. This ensures an appropriately high level of accuracy for the reactive part of the system, while reducing the computational cost by only calculating this smaller part with the expensive method. Atoms in a lower level bound to an atom in a higher level are replaced by hydrogen atoms during the higher-level part of the ONIOM calculation. In the ONIOM methodology used in this work, a small part of the nanotube including the NO molecule and the atoms of SW region was treated using the M06-2X functional together with the 6-31++G(d,p) basis set, while the rest of the system (low theoretical level) was treated using the same method and the STO-6G basis set. In addition, single point calculations were performed on the optimized structures at the M06-2X/6-31++G(d,p) level of theory to obtain the most reliable energies. To confirm the results of the ONIOM model, we also carried out the full optimization at the M06-2X/6-31++G(d,p) level of theory and in turn calculated the adsorption energy for 2C-doped SW-BNNT complexes.
3. Results and discussion
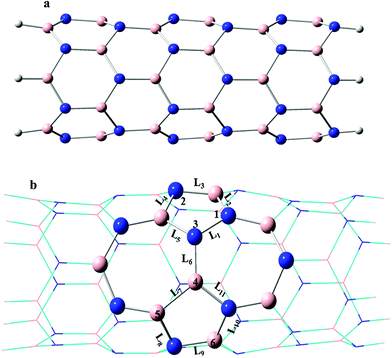
The nine kinds of C-doped SW-BNNTs are investigated. The calculated models are shown in Fig. 1. The studied BNNTs are pristine B36N36H12 (D), SW-BNNT B36N36H12 (E) and C-doped SW-B36N35CH12 (FN), SW-B35N36CH12 (GB), SW-B35N35C2H12 (H13), SW-B36N34C2H12 (I34), SW-B34N36C2H12 (J45), SW-B36N33C3H12 (K123), SW-B35N34C3H12 (L134), SW-B34N35C3H12 (M345) and SW-B33N36C3H12 (N456). We have used symbols GB, FN, H13, I34, J45, K123, L134, M345 and N456 for C-doped SW-BNNTs CB, CN, C2N, CNB, C2B, C3N, C2N1B, C1N2B and C3B, respectively.3.1. 1C-doped (6,0) SW defective BNNTs
In the one C-doped SW-BNNTs, one N or B atom of the vertical B–N bond in the SW defect region was substituted by one carbon atom (denoted as FN and GB, respectively). The bond length values of L1 to L11 bonds are listed in Table 1. Due to the presence of the unfavorable electronic interactions N–N and B–B, the stability of SW-BNNTs decreases with respect to pristine BNNT. The homonuclear N–N (1.469 Å) and B–B (1.711 Å) bonds are longer than the corresponding bonds in C-doped SW-BNNTs (1.419 Å in FN and 1.533 Å in GB). The L6 bond length is 1.438 Å, 1.540 Å and 1.427 Å in the SW-BNNT (E), FN and GB models, respectively, indicating that a vertical B–C bond is longer than vertical B–N and C–N bonds. Therefore, substitution of C atom increases and decreases the L6 bond in FN and GB models, respectively. Since the atomic radius of C atoms is larger than N and smaller than B atoms, substitution of N by C in the vertical B–N bond increases the L6 bond. The two other bond lengths between N3 atoms and the neighboring atoms (L1 and L5) in SW-BNNTs is 1.469 and 1.495 Å, and change to 1.419 and 1.595 Å in FN nanotubes, respectively. L7 (1.711 Å) and L11 (1.468 Å) bonds around the B4 atom decrease to 1.553 and 1.431 Å upon substitution of B by C atoms in the GB nanostructure, respectively. This reduction can be attributed to the lower atomic radius of C with respect to the B. In general, the change in bond lengths upon C doping into the N atom in FN nanostructures is greater than B atoms in the GB one.| BNNTs | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 1.469 | 1.449 | 1.421 | 1.451 | 1.495 | 1.438 | 1.711 | 1.458 | 1.442 | 1.464 | 1.468 |
| FN | 1.419 | 1.474 | 1.426 | 1.463 | 1.595 | 1.540 | 1.714 | 1.464 | 1.441 | 1.468 | 1.469 |
| GB | 1.467 | 1.446 | 1.419 | 1.444 | 1.512 | 1.427 | 1.553 | 1.468 | 1.422 | 1.466 | 1.431 |
| H13 | 1.380 | 1.565 | 1.436 | 1.469 | 1.625 | 1.568 | 1.721 | 1.458 | 1.444 | 1.473 | 1.470 |
| I34 | 1.587 | 1.457 | 1.430 | 1.461 | 1.446 | 1.370 | 1.446 | 1.461 | 1.430 | 1.457 | 1.587 |
| J45 | 1.488 | 1.444 | 1.418 | 1.441 | 1.516 | 1.449 | 1.382 | 1.443 | 1.413 | 1.451 | 1.428 |
| K123 | 1.393 | 1.569 | 1.519 | 1.555 | 1.629 | 1.575 | 1.722 | 1.459 | 1.443 | 1.474 | 1.467 |
| L134 | 1.430 | 1.548 | 1.439 | 1.463 | 1.611 | 1.405 | 1.591 | 1.453 | 1.431 | 1.470 | 1.441 |
| M345 | 1.460 | 1.463 | 1.430 | 1.457 | 1.561 | 1.409 | 1.439 | 1.428 | 1.423 | 1.447 | 1.437 |
| N456 | 1.482 | 1.443 | 1.419 | 1.441 | 1.512 | 1.442 | 1.375 | 1.440 | 1.396 | 1.441 | 1.419 |
Table 2, presents the sum of three bond angles around the six structures given in Fig. 1. The sum of the three bond angles is 342.6° around the third situation in E model and 345.8° and 336.0° in FN and GB models, respectively. Moreover, it is 351.8° and 353.3° around the fourth site in E and GB models, respectively. These changes show that the C doped atoms increase the sum of three mentioned bond angles. The presence of a lone pair in the N atom decreases the bond angle between the bonding pair of electrons and the sum of three bond angles. There is a simple interpretation; the carbon atom in F model is a radical that has unpaired valence electrons or an open electron shell, therefore radical carbon decreases bond angles less than the lone pair of nitrogen.
| BNNTs | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| E | 355.2 | 339.7 | 342.6 | 351.8 | 356.3 | 357.1 |
| FN | 355.1 | 338.5 | 345.8 | 347.0 | 356.6 | 356.9 |
| GB | 357.3 | 339.3 | 336.0 | 353.3 | 358.8 | 356.5 |
| H13 | 353.6 | 336.0 | 347.2 | 347.6 | 356.5 | 357.0 |
| I34 | 354.5 | 337.9 | 350.2 | 350.3 | 358.1 | 356.5 |
| J45 | 357.3 | 338.5 | 321.8 | 359.3 | 360.0 | 354.5 |
| K123 | 353.6 | 330.7 | 350.0 | 349.2 | 356.7 | 356.9 |
| L134 | 352.4 | 337.0 | 350.7 | 350.7 | 358.3 | 356.4 |
| M345 | 354.8 | 336.0 | 342.2 | 356.0 | 359.1 | 355.1 |
| N456 | 357.4 | 338.0 | 323.1 | 359.6 | 360.0 | 339.5 |
Li et al. reported that the defect formation energies of SW-BNNTs depend on the tube radii.70 They calculated defect formation energies in a series of zigzag (n,0) (n = 7, 8, 10, 12) SW-BNNTs. They have shown that defect formation energy increases with increasing tube diameters. The calculated defect formation energies of BNNTs are given in Table 3. The formation energy of SW-BNNT (E) is greater than the pristine BNNT (D) by 3.95 eV, indicating that the formation of SW defects destabilizes the BNNT. Our calculated defect formation energy (3.95 eV using B3LYP and 4.21 eV using M06-2X) is in good agreement with that reported by Li et al.70 for (7,0) SW-BNNTs (4.5 eV). The presence of pentagon and heptagon rings having B–B and N–N bonds violates the [4n + 2] aromatic rule and causes the undoped SW-BNNTs to be less stable electronically compared with the perfect hexagonal structures with six π electrons. The calculated formation energies of FN and GB models are 4.06 eV and 3.41 eV, respectively, indicating a greater probability for the C atom to replace the B atom rather than the N atom. The formation energy of GB is approximately 0.5 eV and 0.6 eV lower than undoped SW-BNNTs and FN, respectively. Therefore, the GB model appeared to be more energetically stable than E and FN models, in good agreement with the calculated structural parameters. However, the higher positive values of formation energies in the C substitution also show the low probability of finding B and N defects in the SW-BNNTs. These computational results are consistent with the observations which were obtained for formation energy of native defects in BN nanotubes.71
| BNNTs | B3LYP | M06-2X | ||||||
|---|---|---|---|---|---|---|---|---|
| Eform/eV | EHOMO/eV | ELUMO/eV | Eg/eV | Eform/eV | EHOMO/eV | ELUMO/eV | Eg/eV | |
| D | 0.00 | −6.83 | −2.32 | 4.50 | 0.00 | −8.30 | −1.41 | 6.89 |
| E | 3.95 | −6.52 | −2.25 | 4.27 | 4.21 | −7.94 | −1.34 | 6.60 |
| FN | 4.06 | −5.71 | −2.18 | 3.53 | 4.33 | −6.92 | −0.91 | 6.02 |
| GB | 3.41 | −4.46 | −2.26 | 2.20 | 3.86 | −5.67 | −1.44 | 4.23 |
| H13 | 4.33 | −6.75 | −3.16 | 3.58 | 4.56 | −8.18 | −2.28 | 5.90 |
| I34 | 0.71 | −6.12 | −2.26 | 3.86 | 1.01 | −7.38 | −1.36 | 6.02 |
| J45 | 2.27 | −5.12 | −2.27 | 2.86 | 2.75 | −6.36 | −1.37 | 4.99 |
| K123 | 6.92 | −6.39 | −3.21 | 3.18 | 7.28 | −7.74 | −2.29 | 5.45 |
| L134 | 1.87 | −5.56 | −2.26 | 3.31 | 2.29 | −6.71 | −1.36 | 5.34 |
| M345 | 0.75 | −4.35 | −2.27 | 2.08 | 1.32 | −5.37 | −1.40 | 3.97 |
| N456 | 2.83 | −3.98 | −2.33 | 1.65 | 3.58 | −5.17 | −1.43 | 3.74 |
The defect formation energies calculated using the highly parameterized empirical M06-2X functional, that implicitly accounts for “medium-range” electron correlation, are greater than B3LYP. In spite of the greater formation energies calculated using the M06-2X functional; the order of the stability of BNNTs comes out the same using either method.
The electronic energies of NTs are studied for further investigation of the effects of one carbon-doping in (6,0) SW-BNNTs. The energies of the HOMO, the LUMO and the energy gap between LUMO and HOMO are tabulated in Table 3. The role of the doping C atom can be explained by comparing HOMO energies. As can be seen in Table 3, the HOMO energy of undoped E NT is −6.52 eV and increases to −5.71 and −4.46 eV in C-doped FN and GB NTs, respectively. This makes the GB NT a better electron donor than the undoped BNNT and FN NT. In addition, C-doping slightly increases the LUMO energy in FN and decreases it in GB as compared with that of E NT. The greater increase in HOMO energy level makes the donor level near the conducting band, and in turn decreases the band gap.
The band gaps of CNTs are small (from 0.2 to 2.0 eV), so CNTs are either metallic or semiconductive, while band gaps of pure BNNTs are much bigger (of 5.0–6.0 eV width), so they are wide-gap semiconductors or insulators. The number of electrons excited thermally is proportional to e(−Egap/2RT). Increasing the temperature or decreasing the band gap energy leads to higher conductivity for an intrinsic semiconductor. According to our calculations, the band gap energy of the D and E NTs are 4.3 and 4.5 eV, respectively. The calculated band gap energy of the FN and GB is 3.5 and 2.2 eV, respectively, indicating the band gap is decreased on going from pristine and SW-BNNTs to one carbon doped SW-BNNT. Substituting C for B atoms decreases the band gap more than that when substituting F for the N atom. This makes GB a wide-gap semiconductor. There is a simple interpretation for the lower band gap of GB (C substitution for B atom); the C atom (donor impurity atom) without the donor electron (fourth valence electron) is positively charged. At very low temperatures, the donor electron is bound to the C atom. However, intuitively it should be clear that the energy required to elevate the donor electron into the CB is considerably less than that for the electrons involved in the covalent bonding.
Calculated results show that one C-doped BNNTs have an energy band gap between CNTs and BNNTs, and present characteristics of a semiconductor. In this way, BNNTs can also be transformed from insulators to semiconductors through intentional C doping. These results are in complete agreement with the early experimental and theoretical results.29,72 The band gaps of all models obtained using M06-2X are qualitatively similar to those calculated by using the B3LYP approach.
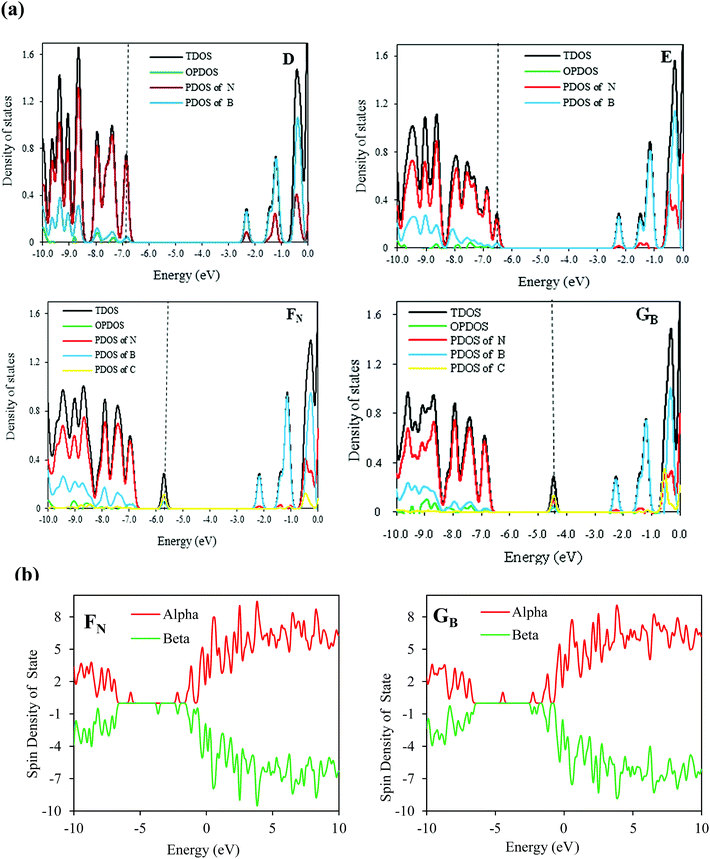
To gain deeper insight into the electronic structure of the C-doped SW-BNNTs, we further calculated their DOS. The DOS for D, E, FN, and GB nanostructures are shown in Fig. 2. The energy difference between HOMO and LUMO orbitals makes the D model an insulator with a wide band gap. The HOMO–LUMO gap of the E model compared with the D model is slightly narrowed because of the SW defect.73 The DOS curves are changed by the B or N substitutions for C in vertical B–N bond of SW-BNNT. The C atom has one electron different to B and N atoms. Therefore, when a B or N atom is substituted by a C atom, an electron (or hole) is introduced into the relevant structure. This extra valence electron (or hole) provides defect levels within the HOMO–LUMO gap of (6,0) SW-BNNT.74–76 Accordingly, the band gap of the FN model on top of the valence band (VB) consists of an acceptor level, and the GB model at the bottom of the conduction band (CB) consists of a donor level. As can be seen in Fig. 4, DOS curves of C-doped NTs are different from the undoped NTs (D and E). It is clear that the C impurity has a significant contribution to the DOS appearing in the band gap. For the GB model, there is a peak in the middle of the band gap, and the DOS at Fermi level is non-zero indicating that electrons will be able to transfer from the donor level to the conducting band. The C doping in FN NTs provides an empty level to the band gap. For the FN model, there is a peak near the VB and the DOS is also non-zero at the Fermi level. Electrons in the FN model can be more easily excited from the filled band to the acceptor level than to the conducting band, so that excitation from the filled band to the acceptor level yields an electron hole. This formed hole leads to the conductivity of P-type semiconductors.13,72,77
As we know, the B or N atoms in BNNTs are connected to three neighbor atoms by three single bonds, therefore all electrons in a BN hexagonal structure should be paired and the structure should not present spin polarization. Therefore, ground states of the pure (6,0) SW-BNNT is nonmagnetic while the isolated NO has clear magnetism for the unpaired electron. However, the presence of a carbon atom in the FN and GB structures and three C atoms in K123, L134, M345 and N456, causes the appearance of an unpaired electron and therefore a net spin polarization. The pz orbital is isolated with one electron occupation leading to a spin moment. Therefore, C doping results in spin polarization and induces spontaneous magnetization. It is possible to deduce that a C-doped SW-BNNT with odd numbers of carbon atoms will always present unpaired spins while, for even numbers, it would display paired spins. To explore whether C doping can induce the spin polarization, the spin DOS of the most stable FN and GB C-doped SW-BNNTs are calculated and are shown in Fig. 2b. From this figure, it can be seen that new local states appear and spin-up and spin-down DOS are different in the band gap region, indicating that C-doping results in spin polarization and induces spontaneous magnetization. Carbon atoms have one less or more electron than N or B, respectively. Therefore, when a B (or N) atom is substituted by a C atom, an electron (or hole) is introduced, accompanied by the formation of defect levels within the HOMO–LUMO gap.
As the computational results revealed, the band gap energy of C-doped SW-BNNTs was smaller than undoped BNNTs. Therefore the conductivity of SW-BNNTs may easily be modified by introducing C doping into their structures and can be converted to semiconductors. This defect affects the global descriptors and electric dipole moments. The calculated amounts of μ, η, S, ω and dipole moment (Q) are tabulated in Table 4. It can be observed that hard molecules have a large Eg and soft molecules have a small one. It should be mentioned that the soft molecules with a small gap will be more polarizable than the hard ones. Chemical potential of the electrons has much the same significance as the chemical potential in the classical thermodynamics of macroscopic systems. In the Hohenberg–Kohn DFT of the ground state, chemical potential is defined as the partial derivative of the systems energy with respect to the number of electrons at constant external potential v: 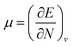 . The physical meaning of chemical potential in DFT is to measure the escaping tendency of an electron cloud. It is constant in three dimensional space for the ground state of an atom, molecule or solid and equals the slope of E versus N curve at constant external potential.41 As can be seen, μ for all NTs is negative. The absolute values of chemical potential, |μ|, of E and GB models are smaller than their own corresponding models (D and FN), respectively. For D to GB models, the lowest absolute value of chemical potential belongs to the GB model (3.36 eV). Thus, D and, E and FN NTs have a much steeper slope than GB. The lowest |μ| means that there is a little accepting tendency of an electron for GB. The hardness index, η, is positive for all NTs, indicating that the charge transfer is an energetically favorable process. D and E NTs have a larger hardness than the FN and GB doped NTs, indicating that in the gas phase the D and E NTs should be more stable than the FN and GB. There is a correlation between chemical potential and hardness index. Among the mentioned NTs, the lowest η and |μ|, corresponds to doped GB NTs. Therefore, GB with the lowest η is less stable. In contrast to η, as expected, the softness index S increases on going from D (0.44 eV−1) to GB (0.91 eV−1). The softness index is proportional to the polarizability of the system. The hardness can be thought of as a resistance to charge transfer, while the softness measures the ease of transfer. The thermodynamic aspects of ω helps to explain, qualitatively favorable product formation, because ω is positive for all NTs, charge transfer is an energetically favorable process. The greater electrophilicity index of GB doped NT shows that the energy lowering of NT (stabilization energy) due to maximal electron flow between the donor and acceptor is bigger than others. Since GB doped NT possesses a bigger electrophilicity index, it has better capability to accept electrons than the others. The rate of the reaction can be associated with the global electrophilicity value. If the substrate is an electron acceptor then a higher ω value will favor the reaction, and for the electron donor substrate naturally the lower ω value will favor the reaction leading to the lower activation energy. The maximum value of dipole moment, Q, is related to the FN model (7.20 Debye).
. The physical meaning of chemical potential in DFT is to measure the escaping tendency of an electron cloud. It is constant in three dimensional space for the ground state of an atom, molecule or solid and equals the slope of E versus N curve at constant external potential.41 As can be seen, μ for all NTs is negative. The absolute values of chemical potential, |μ|, of E and GB models are smaller than their own corresponding models (D and FN), respectively. For D to GB models, the lowest absolute value of chemical potential belongs to the GB model (3.36 eV). Thus, D and, E and FN NTs have a much steeper slope than GB. The lowest |μ| means that there is a little accepting tendency of an electron for GB. The hardness index, η, is positive for all NTs, indicating that the charge transfer is an energetically favorable process. D and E NTs have a larger hardness than the FN and GB doped NTs, indicating that in the gas phase the D and E NTs should be more stable than the FN and GB. There is a correlation between chemical potential and hardness index. Among the mentioned NTs, the lowest η and |μ|, corresponds to doped GB NTs. Therefore, GB with the lowest η is less stable. In contrast to η, as expected, the softness index S increases on going from D (0.44 eV−1) to GB (0.91 eV−1). The softness index is proportional to the polarizability of the system. The hardness can be thought of as a resistance to charge transfer, while the softness measures the ease of transfer. The thermodynamic aspects of ω helps to explain, qualitatively favorable product formation, because ω is positive for all NTs, charge transfer is an energetically favorable process. The greater electrophilicity index of GB doped NT shows that the energy lowering of NT (stabilization energy) due to maximal electron flow between the donor and acceptor is bigger than others. Since GB doped NT possesses a bigger electrophilicity index, it has better capability to accept electrons than the others. The rate of the reaction can be associated with the global electrophilicity value. If the substrate is an electron acceptor then a higher ω value will favor the reaction, and for the electron donor substrate naturally the lower ω value will favor the reaction leading to the lower activation energy. The maximum value of dipole moment, Q, is related to the FN model (7.20 Debye).
| SW-BNNTs | μ/eV | η/eV | S/eV | ω/eV | Q/Debye |
|---|---|---|---|---|---|
| D | −4.58 | 2.25 | 0.44 | 4.65 | 6.54 |
| E | −4.39 | 2.13 | 0.47 | 4.51 | 6.21 |
| FN | −3.94 | 1.76 | 0.57 | 4.41 | 7.20 |
| GB | −3.36 | 1.10 | 0.91 | 5.13 | 6.43 |
| H13 | −4.95 | 1.79 | 0.56 | 6.85 | 7.17 |
| I34 | −4.19 | 1.93 | 0.52 | 4.55 | 6.13 |
| J45 | −3.70 | 1.43 | 0.70 | 4.78 | 6.23 |
| K123 | −4.80 | 1.59 | 0.63 | 7.23 | 7.44 |
| L134 | −3.91 | 1.65 | 0.60 | 4.62 | 6.23 |
| M345 | −3.31 | 1.04 | 0.96 | 5.28 | 6.00 |
| N456 | −3.15 | 0.82 | 1.22 | 6.05 | 5.52 |
3.2. Two carbon-doping in (6,0) SW defective BNNTs
As mentioned above, the presence of homoelemental N–N and B–B bonds destabilises the SW-BNNT. Two substitutional carbon atoms in C–C doping of SW-BNNTs prohibit the formation of N–N and B–B bonds. The vertical N–B bond as well as the N–N and B–B bonds were chosen in SW-BNNTs for substitution of the C–C pair atoms. The C–C doped nanostructures H13, I34 and J45 are shown in Fig. 1. The calculated C–C bond lengths are 1.380, 1.370 and 1.382 Å in the H13, I34 and J45 models, respectively, indicating that the vertical C–C bond is shorter than two slanted ones. The C–C bond length in all H13, I34 and J45 structures is shorter than C–N, B–N and B–C bond lengths; all the B–C bond lengths are longer than the C–N and B–N bond lengths. Wan et al.72 have reported similar results on (3,2) BNNTs. After C–C bonds, the heteroatom C–N bond in I34 (1.446 Å) and J45 (1.428 Å) and heteroatom B–N bond in H13 (1.470 Å) are the smallest bonds. The B–B (1.721 Å) and N–N (1.488 Å) bonds in H13 and J45 are longer than those of undoped SW-BNNT (1.711 Å and 1.469 Å). The longest bond in the defective region of H13 and J45 models is L7 (B–B) and L5 (B–N), respectively. The change in bond lengths upon substitution of C atoms are due to the order of covalent radius of anions is B > C > N. The sum of three bond angles around the 1 to 6 sites of the H13, I34 and J45 models given in Fig. 1 are listed in Table 2. After C atom doping, the difference between the maximum and the minimum bond angles increases. This difference for undoped SW-BNNT, H13, I34 and J45 models is 17.5, 21.0, 20.2 and 38.2°, respectively. The sum of three bond angles around the C atom in the central 7-7 ring fusion (vertical L6 bond) of H13, I34 and J45 NTs is 347.2, 350.2 and 359.3°, respectively. Therefore, when BNNTs have an impurity in the SW defect region, the local geometry will change around the impurity.The stability of 2C-doped structures is evaluated through calculating the defect formation energy given in Table 3. As can be seen, the defect formation energy for H13, I34 and J45 NTs is 4.33, 0.71 and 2.27 eV, respectively, indicating that its value for NT including the vertical C–C bond is the smallest. Defect formation energy of I34 is approximately 3.2 eV, 3.6 eV and 1.36 eV lower than undoped SW-BNNT, H13, and J45, respectively, are in good agreement with the results given in ref. 34. Consequently, substitution of vertical B–N bonds in the defect region by C–C bonds leads to a nanostructure that is more stable than other 2C-doped SW-BNNTs. The smallest defect formation energy is observed for I34 NT which has the smallest C–C bond. It should be mentioned that unfavorable B–B and N–N bonds are removed upon substitution of C–C bonds in I34 NT. Therefore, the I34 model is the most favorable among all of the 2C-doped models. The high defect formation energy in H13 and J45 NTs is due to the presence of one unstable B–B and N–N bond.
We have also used the high parameterized functional M06-2X for calculation of defect formation energy. The results in Table 3 show that defect formation energies calculated using M06-2X functional are greater than the B3LYP functional.
The electronic properties of 2C-doped (6,0) SW-BNNT are calculated. Moreover the HOMO–LUMO gaps for H13, I34 and J45 models are calculated and the results are shown in Table 3. According to the results, the band gap of the 2C-doped SW-BNNTs changes from 2.9 eV to 3.6 eV at B3LYP/6-31+G(d) level. These values are smaller than that of the pristine BNNT (4.50 eV) and SW-BNNT (4.27 eV). The results show that the energy gap depends on the 2C-doped positions.49 In comparison with the band gap of H13 (3.58 eV) and J45 (2.86 eV) models, the energy gap in the most stable NT I34 is greater (3.86 eV). For pristine BNNTs, SW-BNNTs and 2C-doped SW-BNNTs, the order of energy gap is pristine > SW-BNNT > I34 > H13 > J45. The presence of carbon atoms in 2C-doped SW-BNNTs leads to a decrease of band gap. The decrease in the band gap is 0.69, 0.41 and 1.41 eV for H13, I34 and J45 models, respectively. The band gaps values calculated using the M06-2X functional are noticeably overestimated as compared to those obtained using the B3LYP one.
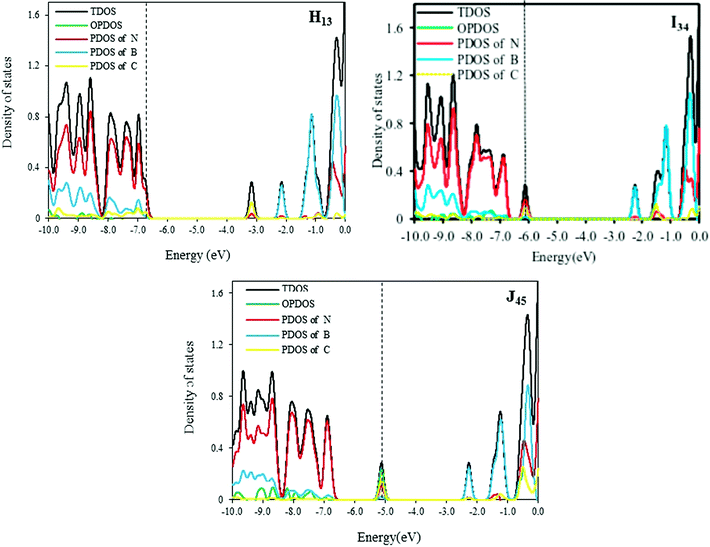
The total and partial DOS of H13, I34 and J45 models are shown in Fig. 3. According to these curves, the band gaps of 2C-doped SW-BNNTs depend on situations where carbon atoms are replaced. In H13 NT, two N atoms are substituted with two C atoms so that each carbon atom is connected to one C atom and two B atoms. In contrast to E NT, the DOS curve of H13 has one impurity state which is close to the unoccupied molecular orbital as shown in Fig. 3. The Fermi level in I34 moves towards a more positive energy compared with the Fermi level of E. The DOS curves of J45 show a bulge near the valence bond in HOMO–LUMO gap that is created by the carbon impurity.
The calculated values of μ, η, S, ω, and Q for H13, I34 and J45 models are reported in Table 4. As can be seen, the μ for J45 model is (−3.70 eV) greater than those of H13 and I34 models. In addition, the hardest structure corresponds to the I model, so this model with a large η is less polarizable than the I34 and J45 models. The values of S, ω and Q for I34 model are smaller than those of the H13 and J45 ones. The electrophilicity index ω determines to what extent partial electron transfer contributes to the lowering of the total binding energy by maximal flow of electrons. As a result, the tendency of I34 doped NT to react with a nucleophile is smaller than others. In other words, the low value of ω for I34 compared with H13 and J45 makes it little more likely for I34 to react with a nucleophile than others.
3.3. Three carbon-doping in (6,0) SW defective BNNTs
Different B and N atoms of the pentagon pair of SW-BNNTs are doped with three carbon atoms. The defective nanostructures are modeled by using K123, L134, M345 and N, as shown in Fig. 1. The K123 and N456 models have an unfavorable homoelemental N–N and B–B bond, respectively. In addition, four C–B bonds and one C–C bond in the structure of K123 and four C–N bonds and one C–C bond in the structure of N456 are observed. In L134, one B and two N atoms in the SW defect region are substituted by three C atoms so that two neighboring C–C bonds are formed between them. In M345, one N and two B atoms in the SW defect region are replaced by three C atoms so that two C–C bonds are formed between them. However, 3C-doped L134 and M345 have no unfavorable homoelemental B–B and N–N bonds.The bond length values for these models are also shown in Table 1. The only C–C bond in K123 (1.393 Å) and N456 (1.375 Å) is shorter than the other bonds. Besides, L7 (B–B) bond length in the K123 model and L5 (N3–B) bond length in the N456 model are longer than the other bonds. There is two C–C bonds in L134 (L1 = 1.430 Å and L6 = 1.405 Å) and M345 (L6 = 1.409 Å and L7 = 1.439 Å) models so that their bond lengths are shorter than other bonds in the SW defect region. The C–C bond at the 7-7 ring fusion (L6) is shorter than the C–C bond at the 5-7 ring fusion (L7 in M345 and L1 in L134). Besides, L1 in L134 is shorter than L7 in M345.
According to the results given in Table 2, the sum of three bond angles around the C atom in K123, L234, M345, and N456 models change compared to those of similar positions in the E model. These changes are more sensible when either the N–N bond or the B–B bond is replaced by one C–C bond. For example, the sum of three bond angles around the 4, 5 and 6 positions in the N456 model are 359.6°, 360°, and 339.5°, respectively, whereas the sum of three bond angles around these points in the E model are 351.8°, 356.3°, and 357.1°, respectively. For L134 and M345 models, the sum of the bond angles around the C atom at the 5-7 ring fusion (i.e., 3 and 4 in L134 and 4 and 5 in M345) are greater than those of the 7-7 ring fusion.
Based on the results given in Table 3, the maximum value of defect formation energy belongs to the K123 model in which the three nitrogen atoms in 1, 2, and 3 sites are replaced by three C atoms. After K123, defect formation energy for the N456 model, in which B atoms are substituted with C atoms, is greater than others. The minimum value of defect formation energy corresponds to the M345 model in which one N atom and two B atoms are replaced by three C atoms in the third, fourth, and fifth sites. Hence, the M345 model is the most stable structure. The stability of 3C-doped SW-BNNTs is arranged as K123 < N456 < L134 < M345. From these results, it can be proposed that the pairs of neighboring C–C defects lead to lower formation energies than configurations where these defects are spatially separated, due to the charge compensation between them. As can be seen in Table 3, defect formation energies obtained by the M06-2X functional are greater than those from B3LYP.
The effects of three carbon doping of SW-BNNT on the electronic properties of (6,0) SW-BNNTs are also investigated. The results are shown in Table 3. The electrical conductivity of a semiconductor can be greatly increased by doping with impurities. The value of band gap energy of 3C-doped SW-BNNTs is arranged as L134 > K123 > M345 > N456. The maximum value of band gap energy belongs to the L134 model in which two N and one B atoms are replaced with three C atoms, and the minimum value belongs to the N456 model where three B atoms are substituted with three C atoms. From the difference in band gaps, it can be concluded that the C substituting B are narrow-gap semiconductors, while C substituting N are wide-gap semiconductors. In other words, the decrease in B atoms of the SW defect region is accompanied with a decrease in band gap energy. These results lead us to suggest that SW-BNNTs can be transformed from electrical insulators or wide band gap semiconductors to narrow-band gap semiconductors or a conductor. Also, such nanostructures exhibit tunable semiconductivity. In addition, minimizing band gap energy in nanostructures so as to harvest more sunlight is one of the critical factors enabling high-efficiency solar cells. Therefore, from these results it can be predicted that CB-doped SW-BNNTs with lower band gap energy can be used to improve solar cell efficiency.
The effect of 3C-doping on electronic properties of SW-BNNTs can be explained by comparing HOMO and LUMO energies. The results show that the value of HOMO energy depends on the location of C impurities. As can be seen in Table 3, HOMO energy of N456 NT (−3.98 eV) (three B atoms are replaced by three C atoms) is greater than others and for K123 (−6.39 eV) (three N atoms are replaced by three C atoms) it is smaller than others. The HOMO energy values of L134 and M345 lie between N456 and K123. Therefore, doped BNNTs including two neighboring C atoms and one separated C atom have the greatest and lowest HOMO energy. The LUMO energy of 3C-doped NTs is ordered as L134 ∼ M345 > N456 > K123. The greater increase in HOMO energy level of N456 makes the donor level move near the conducting band and in turn decreases the band gap. The results show that the presence of three neighboring C atoms causes the energy of LUMO in M345 and N456 to be greater than others.
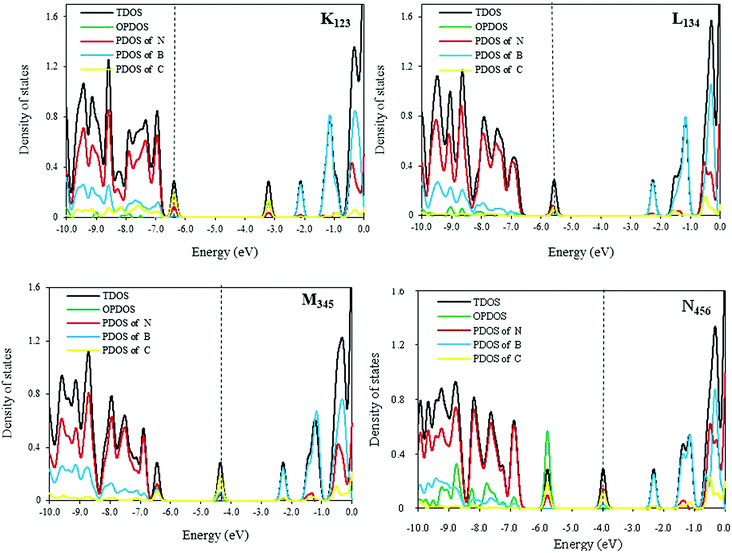
DOS curves of 3C-doped BNNTs are shown in Fig. 4. As illustrated in this figure, the DOS curves are sensitive to the position of dopant atoms. As expected, DOS curves in the K123 model (as a P-type semiconductor) and L134 models have one bulge near the conducting and VB, respectively. In addition, position and electron density of the Fermi level are different in these two models. Compared with the K123, the Fermi level in the L134 model is closer to the middle of the band gap. The electron density in the Fermi level is greater for K123 than L134. The formation of new peaks and the presence of the Fermi level in the middle of the band gap of M345 and N456 SW-BNNTs is predicted to be the main doping effect on the greater conductivity of these NTs. The mid-gap states positioned inside the band gap of 3C-doping NTs make them attractive for band gap engineering in, for example, photocatalytic applications.
The global quantities μ, η, S, ω, and Q for 3C-doped BNNTs are given in Table 4. The greatest value μ is (−3.15 eV) which belongs to the N456 doped NT in which three B atoms are replaced by three C atoms. Therefore, escaping tendency of an electron cloud in N456 is greater than other 3C-doped BNNTs. The μ value of M345 with the lowest defect formation energy is greater than those of L134 and K123 and smaller than N456. Therefore, after N456 the tendency of electrons to escape from 3C-doped NT is greater in M345 than others. From values of η and S, it can be estimated that the resistance to charge transfer in N456 and M345 is smaller than other 3C-doped NTs. Among the 3C-doped NTs, the greatest ω values correspond to the K123 (7.23 eV) and N456 (6.05 eV) including the two neighboring C atoms and one separated C atom. Since K123 and N456 doped NT possesses a bigger electrophilicity index, they have better capability to accept electrons than the others. The results show that the dipole moment of N456 is smaller than others.
3.4. General comparison or general review
Comparison of structural parameters in C-doped NTs shows that all the C–C bond lengths are shorter than the C–N, B–N and B–C bond lengths. The B–C bond lengths at the different situations of the SW-BNNTs are longer than the C–N and B–N bond lengths. These results are in good agreement with previous work.35,50According to the obtained results, defect formation energies obtained using two B3LYP and M06-2X functionals are arranged as: I34 < M345 < L134 < J45 < N456 < GB < E < FN < H13 < K123. As can be seen, defect formation energy for doped SW-BNNTs in which two B and one N atom at the central 7-7 ring fusion (vertical bond) are substituted with C (I34, M345 and L134) is smaller than others. Therefore, formation of these type of doped NTs are energetically most favorable. In contrast, doped NTs formed by substitution of N atom by C atom (FN, H13 and K123) have the greatest formation energy. Among the C-doped NTs, the lowest defect formation energy belongs to the I34 (0.71 eV) and M345 (0.75 eV) and the greatest value corresponds to K123 (6.92 eV) which is formed by substitution of three carbon atoms with three nitrogen atoms in the pentagon ring of the SW defect region.
The band gap energies of FN to N456 models depend on the number of B or N atoms which are substituted by C atoms as well as the positions. Generally, a decrease in band gap is more evident when the boron atoms are replaced by carbon atoms (GB, N456 and M345). Accordingly, band gap energies of studied NTs are ordered as: N456 < M345 < GB < J45 < K123 < L134 < FN < H13 < I34 < E < D. As a result, N456 NT that is formed by substitution of three B atoms with three C atoms has the smallest band gap energy and in turn more conductivity.
Comparison of global descriptors shows that the N456 BNNTs with a narrow band gap have the greatest value of μ, S and ω and the smallest value of η, indicating that the reactivity and conductivity properties of this NT is greater than others. Based on the Pearson’s maximum hardness principle,78 which states that the minimum energy structure has the maximum chemical hardness and energy gap, the I34 C-doped SW-BNNT is the most stable structure among the C-doped nanostructures. There is a correlation between S and the band gap energy of studied BNNTs. As can be seen in Table 3 and 4, an increase in S index is accompanied with a decrease in band gap. According to the DOS curves of D to N456 models, the energy of Fermi levels increases (decreases) when B (N) atoms are substituted with the carbon atoms in the (6,0) SW-BNNT.
3.5. Adsorption of a single NO molecule on C-doped SW-BNNT
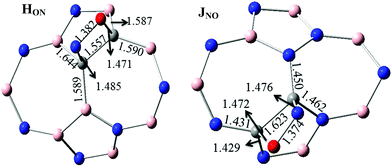
The various possibilities of NO adsorption on the outer surface of C-, 2C- and 3C-doped SW-BNNTs were explored to achieve the intuitive understanding of the adsorption process. The NO monomer can be attached to BNNTs through the N-atom (Nad), O-atom (Oad), and N–O (NadOad) bond.For 1C-doped SW-BNNTs, four chemisorbed FON, FNO, GON and GNO complexes were found on the potential energy surface and the selected structural parameters are given in Fig. 5. The ON (N-down) and NO (O-down) symbols represent the different direction of NO toward the tube axis. As can be observed, the NO molecule is located on top of the NT and interacts with the C atom of NT via both O and N atoms (in FNO), O atom (in GON) and N atom (in GNO and FNO).
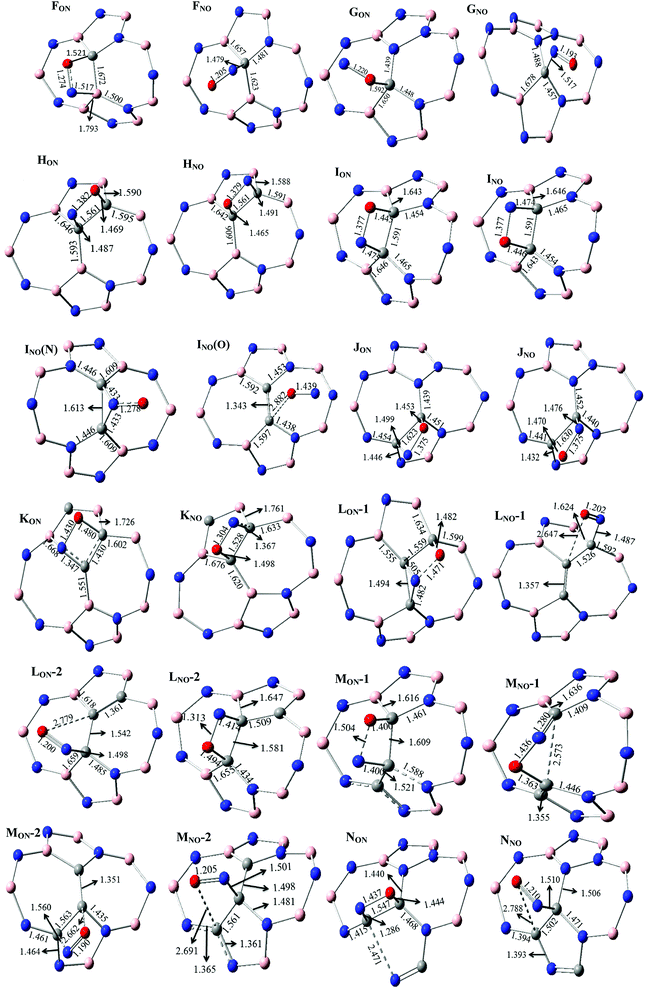 | ||
| Fig. 5 Selected structural parameters of C-doped SW-BNNT complexes calculated at ONIOM(M06-2X/6-31++(d,p):M06-2X/STO-6G) level. Distances are given in Å. | ||
The HOMO (EH), LUMO (EL), and band gap energies (Eg) of free H–N nanotubes calculated at the M06-2X/6-31++(d,p) level are given in Table 5. Also, the electronic adsorption energies (AEs), HOMO, LUMO and band gap energies obtained at M06-2X/6-31++(d,p) level for complexed BNNTs are given in Table 6.
| EHOMO/eV | ELUMO/eV | Eg/eV | |
|---|---|---|---|
| FN | −6.99 | −1.15 | 5.84 |
| GB | −5.69 | −1.27 | 4.42 |
| H13 | −8.16 | −2.33 | 5.83 |
| I34 | −7.46 | −1.23 | 6.23 |
| J45 | −6.41 | −1.25 | 5.16 |
| K123 | −7.78 | −1.10 | 6.67 |
| L134 | −6.79 | −1.23 | 5.56 |
| M345 | −5.41 | −1.28 | 4.13 |
| N456 | −5.33 | −1.31 | 4.02 |
| Eads/kcal mol−1 | EHOMO/eV | ELUMO/eV | Eg/eV | qN/a.u | qO/a.u | CTNBO | |
|---|---|---|---|---|---|---|---|
| FON | −9.63 | −8.03 | −2.55 | 5.48 | 0.067 | −0.214 | −0.147 |
| FNO | −31.29 | −7.91 | −1.65 | 6.26 | 0.166 | −0.312 | −0.146 |
| GON | 6.96 | −6.75 | −1.31 | 5.44 | −0.261 | −0.039 | −0.300 |
| GNO | −33.62 | −7.70 | −1.32 | 6.37 | 0.139 | −0.261 | −0.123 |
| HON | 4.55 (5.11) | −6.99 (−6.90) | −1.64 (−1.71) | 5.36 (5.18) | −0.039 | −0.357 | −0.396 |
| HNO | 5.11 | −7.04 | −1.8 | 5.23 | −0.039 | −0.354 | −0.393 |
| ION | −0.46 | −7.78 | −1.36 | 6.42 | −0.043 | −0.370 | −0.413 |
| INO | −0.47 | −7.79 | −1.37 | 6.42 | −0.044 | −0.370 | −0.414 |
| INO(O) | 62.10 | −7.46 | −3.43 | 4.05 | 0.283 | −0.276 | 0.007 |
| INO(N) | 2.05 | −7.75 | −1.31 | 6.44 | −0.021 | −0.325 | −0.346 |
| JON | −10.35 | −8.01 | −1.29 | 6.72 | −0.045 | −0.382 | −0.427 |
| JNO | −11.53 (−11.5) | −7.88 (−7.83) | −1.32 (−1.46) | 6.56 (6.37) | −0.043 | −0.386 | −0.429 |
| KON | −29.59 | −7.13 | −2.48 | 4.65 | −0.226 | −0.332 | −0.558 |
| KNO | −5.01 | −7.26 | −2.5 | 4.76 | −0.244 | −0.158 | −0.086 |
| LNO-1 | −29.36 | −7.75 | −1.34 | 6.41 | −0.302 | 0.153 | −0.149 |
| LNO-2 | 17.98 | −6.94 | −2.66 | 4.28 | 0.172 | −0.284 | −0.112 |
| LON-1 | 24.63 | −7.81 | −1.33 | 6.49 | −0.128 | −0.373 | −0.501 |
| LON-2 | −24.29 | −7.99 | −1.9 | 6.09 | 0.170 | −0.291 | −0.121 |
| MNO-1 | −29.39 | −6.69 | −1.37 | 5.32 | −0.149 | −0.410 | −0.559 |
| MNO-2 | 1.16 | −5.9 | −1.68 | 4.23 | 0.134 | −0.320 | −0.186 |
| MON-1 | 11.78 | −5.59 | −2.01 | 3.57 | −0.477 | −0.422 | −0.899 |
| MON-2 | −25.15 | −7.59 | −1.42 | 6.17 | 0.145 | −0.258 | −0.113 |
| NON | −31.72 | −7.98 | −1.29 | 6.69 | −0.093 | −0.438 | −0.531 |
| NNO | −5.61 | −5.34 | −1.35 | 3.99 | 0.088 | −0.331 | −0.243 |
The calculated AEs of FON, FNO, GON and GNO, are −9.963, −31.29, 6.96 and −33.62 kcal mol−1, respectively. The results indicate that the adsorption process of NO on 1C-doped SW-BNNTs (FON, FNO and GNO) is energetically favorable. Comparison of AEs shows that the FNO and GNO complexes, in which the N atom of NO is bonded to C, are the most stable. Therefore, an energetically favored site for adsorption of NO gas in 1C-doped SW-BNNTs is above the C substitution for B site. After FNO and GNO complexes, the FON complex is energetically favorable to be formed. The AE is positive for GON complex in which the O atom of NO is connected to a C one, indicating that this site is not energetically suitable for adsorption.
For 2C-doped SW-BNNTs, eight chemisorbed HON, HNO, ION, INO, INO(N), INO(O), JON and JNO NO–SW-BNNT complexes were optimized at ONIOM(M06-2X/6-31++(d,p):M06-2X/STO-6G) level and selected structural parameters are given in Fig. 5. As can be seen, the NO molecule in most complexes is located on top of the NT and interacts with the C–C bond of NT via both O and N atoms, resulting in the formation of a four-membered ring. In complexes LNO-1, LNO-2, MNO-2, INO(N) and INO(O), NO molecules are connected with the C atoms through the N and or O atoms.
The AEs calculated for HON, HNO, ION, INO, INO(N), INO(O), JON, JNO, KON, KNO, LNO-1, LNO-2, LON-1, LON-2, MNO-1, MNO-2, MON-1, MON-2, NON, NNO complexes are 4.55, 5.11, −0.46, −0.47, 2.05, 62.10, −0.35, −10.35, −11.53, −29.59, −5.01, −29.36, 17.98, 24.53, −24.29, −29.39, 1.16, 11.78, −25.15, −31.72 and −5.61 kcal mol−1, respectively. The results indicate that the adsorption process of NO on 2C-doped SW-BNNTs ION, INO, JON and JNO is energetically favorable. Comparison of AEs shows that the JON and JNO complexes, in which two B atoms in SW-BNNTs are replaced by two C atoms, are the most stable. Thus, the best adsorption site for NO in 2C-doped SW-BNNTs is found to be above the slanted C–C bond located between pentagon and heptagon rings. After JON and JNO complexes, ION and INO complexes (in which vertical C–C bonds between two pentagon rings are involved in the interaction) are energetically favorable. From calculated AEs, the stability order of NadOad complexes is J > I > H.
To confirm the results obtained using the ONIOM model, adsorption energies of 2C-doped SW-BNNT complexes were calculated after full optimization of the complexes. The AEs resulting from this approach for H and J complexes are 5.1 and −11.5 kcal mol−1, respectively, and are close to the AEs found using the ONIOM model.
Adsorption of NO molecules on (8,0) CNTs and BNNTs as well as SiCNTs have been investigated by Gao et al.45 They show that in contrast to CNTs and BNNTs, the SiCNTs exhibit highly exothermic binding to NO (−14.3 kcal mol−1). The AE calculated47 for the most stable NO-undoped SW-BNNT complex is ≈−3.5 kcal mol−1 that is smaller than those found in this work for 2C-doped SW-BNNTs (−11.53 kcal mol−1 for JON and −10.35 for JNO kcal mol−1). Therefore, although adsorption of NO molecules on some sites of 2C-doped SW-BNNTs is energetically unfavorable, our findings imply that 2C-doped SW-BNNTs can be practically useful for the removal of NO molecules and as a sensor for the detection of NO molecules.
When an NO molecule is adsorbed on the NT, structural parameters of adsorbent and adsorbate species change. These structural deformations in NT are attributed to the change from sp2 to sp3 hybridization of the C atoms. The selected structural parameters are given in Fig. 5. The results obtained for 1C-doped SW-BNNTs show that the NO molecule prefers to lie on top of C atoms. The N–O bond (1.147 Å in free molecule) is elongated upon adsorption so that its bond length in most stable for FNO and GNO, 1.205 Å and 1.193 Å, respectively. The results show that the N–C bond in FNO is shorter than the O–C bond in FON, in good agreement with the greater AE obtained for FNO. A similar situation is observed for the G model. There is a direct correlation between NT–NO distance and AEs. Also it is interesting to note that the NO–NT distance is significantly reduced when compared with the molecule on the undoped SW-BNNT47 in which the NO molecule is perpendicular to the tube surface.
For 2C-doped SW-BNNTs, the results show that the NO molecule prefers to lie on top of the C–C bonds and parallel to the surface of NT. Accordingly, the NO molecule in most stable complexes adopts the parallel pattern on C–C sites. The N–O bond (1.147 Å in free molecule) is elongated upon adsorption so that its bond length in most stable JON and JNO complexes (1.375 Å) is smaller than others. In addition, C–C bonds involved in interactions are weakened after adsorption of NO molecules. As can be seen, in contrast to NO–NT distance, elongation of the C–C bond in most stable complexes is greater than other ones. The results show that the N–C bond in all 2C-doped complexes is longer than the O–C bond. As observed for NO–SiCNT complexes,45 there is no direct correlation between NT–NO distance and AEs. The results show that the bond lengths of N–C and O–C in most stable J complexes are greater than other ones. Also, it is interesting to note that the NO–NT distance is significantly reduced when compared with the molecule on the undoped SW-BNNT47 in which the NO molecule is perpendicular to the tube surface. Due to NO adsorption, the C atoms are slightly detached from the BNNT surface and, in turn, the corresponding C–N or C–B bonds of NT are slightly elongated. The results of full optimization given in Fig. 6 are in good agreement with those obtained using the ONIOM approach.
 | ||
| Fig. 6 Selected structural parameters of 2C-doped SW-BNNT complexes obtained using full optimization at the M06-2X/6-31++G(d,p) level. Distances are given in Å. | ||
Upon adsorption of NO on the nanotube surface, some charge is transferred from the HOMO of C-doped NT to the 2π* orbital of NO, resulting in changes in the electronic properties of NT. To determine the amount of charge transferred between NO and NT, the charge transfer values were calculated through the NBO79 charge difference between the adsorbed molecule on the NT surface and an isolated NO molecule. The CT values calculated at M06-2X/6-31++G(d,p) level of theory are given in Table 5. The negative value of CT (with exception of that found in INO–O) indicates that the charge is transferred from NT to NO. The charge transferred from NT to NO in most stable complexes of JON and JNO is 0.427 and 0.429 a.u, respectively. It is clear that CT values for the most stable configurations are at maximum, and are in good agreement with the greatest AEs found for these complexes. The less stable complexes have small CT and AE values.
The HOMO, LUMO and band gap energies (Egap) of H–N complexes are also given in Table 6. Comparison of the Egap given in Table 5 (calculated at M06-2X/6-31+G(d) level) and those listed in Table 6 (calculated at M06-2X/6-31++G(d,p) level), shows that the Egap decreases as the basis set is improved. The results reveal that there is no definite trend in the change of the band gap as a function of AE of adsorbed molecule. It is clear that Egap for most stable complexes is greater than for others. Similar results have been observed for adsorption of NO molecules on SiCNT.45 To confirm the Egap values calculated using ONIOM method, Egap in HNO and JON were calculated using fully optimized geometry obtained at M06-2X/6-31++G(d,p) level of theory. As can be seen in Table 6, Egap values for HON and GNO are 5.19 and 6.37 eV that are very close to those found using ONIOM geometry (5.36 and 6.56 eV).
In order to investigate the impact of number of doping sites on the adsorption properties of C-doped SW-BNNTs, 3C-doped nanotubes were also examined. For 3C-doped SW-BNNTs, twelve chemisorbed species were found in four groups K, L, M and N. The optimized structures are given in Fig. 5. The AEs, HOMO, LUMO and band gap energies CT values are given in Table 5. The calculated AEs range from −5.0 to −29.6 kcal mol−1 for K, 24.6 to −29.4 kcal mol−1 for L, 11.78 to −29.4 kcal mol−1 for M, and −5.8 to −31.7 kcal mol−1 for N configurations. Comparison of AEs shows that the KON in K group, LNO-1 in L group, MNO-1 in M group and NON in N group are the most stable complexes. Among the NO-3C-doped SW-BNNTs, NON chemisorbed complex with AE of −31.7 kcal mol−1 is the most stable. As mentioned previously, three B atoms in N nanotube are replaced by three C atoms. Comparison of AE in 2C-doped and 3C-doped NTs reveals that the best adsorption site for the NO gas molecule in 3C-doped and 2C-doped SW-BNNTs is above the slanted C–C bond located between the pentagon and heptagon rings. In both most stable complexes NON and JON, only B atoms are replaced by C atoms, indicating that the doping structures are similar in both adsorbed complexes.
The ONIOM(M06-2X/6-31++(d,p):M06-2X/STO-6G) optimized structures of 3C-doped SW-BNNTs are also listed in Fig. 5. The N–O bond length in different complexes is greater than that of isolated one (1.147 Å). Increase in N–O bond length upon adsorption for most stable complex of each series is greater than others. In addition, the C–C bond length of doped NT involved in interaction shows a significant increase upon adsorption of NO molecule. In 3C-doped NTs, There is no a correlation between AEs and C–C as well as NO–NT distances. Also it is interesting to compare the distance between the NO and NT in most stable configurations of 2C- and 3C-doped NTs. As can be seen in Table 5, N–C and O–C distances in 3C-doped NT is smaller than that of 2C-doped ones, although AEs of complexes have no significant difference.
The NBO results show that both N and O atoms have negative charges. The CT value calculated from the sum of negative charges of N and O atoms are given in Table 5. As shown in this table, the charge transferred from NT to NO molecule in complexes having negative AE is considerable. In some less stable complexes, for example in MNO-1, owing to stretching of the C–C bond (bond length is 2.573 Å) and position of N and O atoms on top of the C–C bond, charge transferred from NT to N and O atoms is greater than those found in most stable complexes. Thus, NBO population analysis confirms that there is greater elongation of the C–C bond in MNO-1.
The band gap energies for 3C-doped SW-BNNT–NO complexes are given in Table 5. Similar to 2C-doped NTs, there is no definite trend in change of band gap. However, Egap for most stable complex NON is greatest.
4. Conclusions
By means of DFT methods, the effects of C-doping on the structural and electronic properties of SW-BNNTs as well as adsorption sensitivity of C-doped SW-BNNTs toward NO gas are explored. The results indicate that C substitution for B is favored over C substitution for N. The maximum value defect formation energy corresponds to the replacement of three C atoms with three N atoms present in the pentagon rings of SW defect. It is predicted that an increase in conductivity of CB complexes is greater than CN ones. The substituting C for B atom can modify the electronic structures of the SW-defective BNNTs by introducing C states into their band gaps and can thus make these nanotubes more reactive. The Fermi levels move to a high energy region when boron atoms are substituted with the carbon atoms in (6,0) SW-BNNT. The results show that the adsorption of NO on some configurations of 2C- and 3C-doped SW-BNNTs is energetically favorable.References
- D. Golberg, Y. Bando, Y. Huang, T. Terao, M. Mitome, C. Tang and C. Zhi, Boron Nitride Nanotubes and Nanosheets, ACS Nano, 2010, 4, 2979–2993 CrossRef CAS PubMed.
- X. Blase, A. Rubio, S. G. Louie and M. L. Cohen, Stability and Band Gap Constancy of Boron Nitride Nanotubes, Europhys. Lett., 1994, 28, 335 CrossRef CAS.
- N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Boron Nitride Nanotubes, Science, 1995, 269, 966–967 CrossRef CAS PubMed.
- G. G. Fuentes, E. Borowiak-Palen, T. Pichler, X. Liu, A. Gra, G. Behr, J. Kalenczuk, M. Knupfer and J. Fink, Electronic structure of multiwall boron nitride nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035429 CrossRef.
- G. Y. Guo and J. C. Lin, Systematic ab initio study of the optical properties of BN nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 165402 CrossRef.
- L. F. He, J. Shirahata, H. Suematsu, T. Nakayama, T. Suzuki, W. Jiang and K. Niihara, Synthesis of BN nanosheet/nanotube-Fe nanocomposites by pulsed wire discharge and high-temperature annealing, Mater. Lett., 2014, 117, 120–123 CrossRef CAS.
- Y. Q. Zhang, Y. J. Liu, Y. Liu and J. X. Zhao, Boosting sensitivity of boron nitride nanotube (BNNT) to nitrogen dioxide by Fe encapsulation, J. Mol. Graphics Modell., 2014, 51, 1–6 CrossRef CAS PubMed.
- M. D. Esrafili and N. Roghaye, A DFT study on the possibility of using boron nitride nanotubes as a dehydrogenation catalyst for methanol, Appl. Surf. Sci., 2014, 314, 90–96 CrossRef CAS.
- R. Chegel and B. Somayeh, Electro-optical properties of zigzag and armchair boron nitride nanotubes under a transverse electric field: Tight binding calculations, J. Phys. Chem. Solids, 2012, 73.2, 154–161 CrossRef.
- A. Freitas, S. Azevedo and J. R. Kaschny, Effects of a transverse electric field on the electronic properties of single- and multi-wall BN nanotubes, Solid State Commun., 2013, 15, 40–45 CrossRef.
- H. Roohi and S. Bagheri, Effect of axial strain on structural and electronic properties of zig-zag type of boron nitride nanotube (BNNT): a quantum chemical study, Struct. Chem., 2013, 24, 409–420 CrossRef CAS.
- Z. G. Wang, Z. Li and D. M. Cheng, Effects of uniaxial strain on the band structure of boron nitride nanotubes: A first principle study, Eur. Phys. J.: Appl. Phys., 2009, 46.02, 20601 CrossRef.
- Y. F. Zhukovskii, S. Piskunov, J. Begens, J. Kazerovskis and O. Lisovski, Geometries and stabilities of transition metals doped perfect and Stone–Wales defective armchair (5,5) boron nitride nanotubes, Phys. Status Solidi B, 2013, 250, 793–800 CrossRef CAS.
- S. Tontapha, N. Morakot, V. Ruangpornvisuti and B. Wanno, Boron Nitride Nanotubes Chemically Functionalized with Glycol Chitosan for Gene Transfection in Eukaryotic Cell Lines, Struct. Chem., 2012, 23, 1819–1830 CrossRef CAS.
- T. H. Ferreira, L. M. Hollanda, M. Lancellotti and E. M. B. de Sousa, Boron Nitride Nanotubes, J. Biomed. Mater. Res., Part A, 2015, 103, 2176–2185 CrossRef CAS PubMed.
- C. Zhi, Y. Bando, C. Tang and D. Golberg, Mater. Sci. Eng., R, 2010, 70, 92–111 CrossRef.
- L. Silva, S. Guerini, V. Lemos and J. Filho, Electronic and Structural Properties of Oxygen Doped BN Nanotubes, IEEE Trans. Nanotechnol., 2006, 5, 517–522 CrossRef.
- H. Liu and C. H. Turner, Adsorption properties of nitrogen dioxide on hybrid carbon and boron-nitride nanotubes, Phys. Chem. Chem. Phys., 2014, 16, 22853–22860 RSC.
- J. X. Zhao and Y. H. Ding, Theoretical Study of Ni Adsorption on Single-Walled Boron Nitride Nanotubes with IntrinsicDefects, J. Phys. Chem. C, 2008, 112, 5778–5783 CAS.
- Y. Xie and J. M. Zhang, First-principles study on substituted doping of BN nanotubes by transition metals V, Cr and Mn, Comput. Theor. Chem., 2011, 976, 215–220 CrossRef CAS.
- Y. F. Zhukovskii, S. Piskunov, J. Kazerovskis, D. Makaev and P. Dyachkov, Comparative Theoretical Analysis of BN Nanotubes Doped by Al, P, Ga, As, In, and Sb, J. Phys. Chem. C, 2013, 117, 14235–14240 CAS.
- H. F. Bettinger, T. Dumitrica, G. E. Scuseria and B. I. Yakobson, Mechanically induced defects and strength of BN nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 041406 CrossRef.
- C. Tang, Y. Bando, Y. Huang, S. L. Yue, C. Z. Gu and F. F. Xu, Fluorination and Electrical Conductivity of BN Nanotubes, J. Am. Chem. Soc., 2005, 127, 6552–6553 CrossRef CAS PubMed.
- O. Stephan, P. M. Ajayan, C. Colliex, P. Redlich, J. M. Lambert, P. Bernier and P. Lefin, Doping Graphitic and Carbon Nanotube Structures with Boron and Nitrogen, Science, 1994, 266, 1683–1685 CAS.
- D. Golberg, Y. Bando, P. Dorozhkin and Z. C. Dong, Synthesis, Analysis, and Electrical Property Measurements of Compound Nanotubes in the B–C–N Ceramic System, MRS Bull., 2004, 29, 38–42 CrossRef CAS.
- L. Ci, L. Song, C. Jin, D. Jariwala, D. Wu, Y. Li, A. Srivastava, Z. F. Wang, K. Storr and L. M. Balicas, Atomic Layers of Hybridized Boron Nitride and Graphene Domains, Nat. Mater., 2010, 9, 430–435 CrossRef CAS PubMed.
- O. L. Krivanek, M. F. Chisholm, V. Nicolosi, T. J. Pennycook, G. J. Corbin, N. Dellby, M. F. Murfitt, C. S. Own, Z. S. Szilagyi, M. P. Oxley, S. T. Pantelides and S. J. Pennycook, Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy, Nature, 2010, 464, 571 CrossRef CAS PubMed.
- X. Wei, M. Wang, Y. Bando and D. Golberg, Post-Synthesis Carbon Doping of Individual Multiwalled Boron Nitride Nanotubes via Electron-Beam Irradiation, J. Am. Chem. Soc., 2010, 132, 13592 CrossRef CAS PubMed.
- X. Wei, M. Wang, Y. Bando and D. Golberg, Electron-Beam-Induced Substitutional Carbon Doping of Boron Nitride Nanosheets, Nanoribbons, and Nanotubes, ACS Nano, 2011, 5, 2916 CrossRef CAS PubMed.
- A. J. Stone and D. J. Wales, Theoretical Studies of Icosahedral C60 and Some Related Species, Chem. Phys. Lett., 1986, 128, 5 CrossRef.
- T. Dumitrica and B. I. Yakobson, Rate theory of yield in boron nitride nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035418 CrossRef.
- J. Choi, S. Pyo, D. H. Baek, J. I. Lee and J. Kim, Thickness, alignment and defect tunable growth of carbon nanotube arrays using designed mechanical loads, Carbon, 2014, 66, 126 CrossRef CAS.
- Y. Miyamoto, A. Rubio, S. Berber, M. Yoon and D. Toanek, Spectroscopic characterization of Stone–Wales defects in nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 121413 CrossRef.
- G. Kim, J. Park and S. Hung, First principle study of substitutional carbon pair and Stone–Wales defect complexes in boron nitride nanotubes, Chem. Phys. Lett., 2012, 522, 79–82 CrossRef CAS , and references cited therein.
- S. Jalili, F. Molani, M. Akhavan and J. Schofield, Role of defects on structural and electronic properties of zigzag C3N nanotubes: A first-principle study, Phys. E, 2014, 56, 48–54 CrossRef CAS.
- M. Anafcheh and R. Ghafouri, Carbon Doping of Defect Sites in Stone–Wales Defective Boron-nitride Nanotubes: A Density Functional Theory Study, J. Cluster Sci., 2013, 24.3, 865–879 CrossRef.
- T. Roszer, The biology of subcellular nitric oxide, Springer Science & Business Media, 2012 Search PubMed.
- T. Fujitani, I. Nakamura, Y. Kobayashi, A. Takahashi, M. Haneda and H. Hamada, Adsorption and reactions of NO on clean and CO-precovered Ir (111), J. Phys. Chem. B, 2005, 109, 17603–17607 CrossRef CAS PubMed.
- C. Chang, G. Maduraiveeran, J. Xu, G. Hunter and P. Dutta, Design, fabrication, and testing of MEMS-based miniaturized potentiometric nitric oxide sensors, Sens. Actuators, B, 2014, 204, 183–189 CrossRef CAS.
- C. S. Yeung, Y. K. Chen and Y. A. Wang, Sensors, Defected and Substitutionally Doped Nanotubes: Applications in Biosystems, Sensors, Nanoelectronics, and Catalysis, 2011 Search PubMed.
- O. Byl, P. Kondratyuk and J. Yates, Adsorption and Dimerization of NO Inside Single-Walled Carbon Nanotubes an Infrared Spectroscopic Study, J. Phys. Chem. B, 2003, 107, 4277–4279 CrossRef CAS.
- T. Kyotani and A. Tomita, Analysis of the reaction of carbon with NO/N2O using ab initio molecular orbital theory, electronic properties of adsorption nitrogen monoxide on inside and outside of the armchair single wall carbon nanotubes: a density functional theory calculations, J. Phys. Chem. B, 1999, 103, 3434–3441 CrossRef CAS.
- A. A. Rafati, S. M. Hashemianzadeh and Z. B. Nojini, Adsorption of CO and NO molecules on carbon doped boron nitride nanotubes, J. Phys. Chem. C, 2008, 112, 3597–3604 CAS.
- R. J. Baierle, T. M. Schmidt and A. Fazzio, Adsorption of CO and NO molecules on carbon doped boron nitride nanotubes, Solid State Commun., 2007, 142, 49–53 CrossRef CAS.
- G. Gao and H. S. Kang, First principles study of NO and NNO chemisorption on silicon carbide nanotubes and other nanotubes, J. Chem. Theory Comput., 2008, 4, 1690–1697 CrossRef CAS PubMed.
- Y. Chen, Y. J. Liu, H. X. Wang, J. X. Zhao, Q. Cai, X. Z. Wang and Y. Ding, Silicon-doped graphene: an effective and metal-free catalyst for NO reduction into N2O?, ACS Appl. Mater. Interfaces, 2013, 5, 5994–6000 CAS.
- H. Roohi and M. Jahantab, Adsorption sensitivity of the perfect and Stone–Wales defective BNNTs towards NO gas: A DFT study, J. Mol. Graphics Modell. Search PubMed , submitted.
- H. Roohi, A. R. Nowroozi, A. Ebrahimi and B. Makiabadi, Effect of CH3CO functional group on the molecular and electronic properties of BN43zz nanotube: A computational chemistry study, J. Mol. Struct.: THEOCHEM, 2010, 952, 36–45 CrossRef CAS.
- H. Roohi, M. Jahantab and M. Yakta, Effect of the Stone–Wales (SW) defect on the response of BNNT to axial tension and compression: a quantum chemical study, Struct. Chem., 2015, 26(1), 11–22 CrossRef CAS.
- H. Roohi and S. Khyrkhah, Green chemical functionalization of single-wall carbon nanotube with methylimidazolium dicyanamide ionic liquid: A first principle computational exploration, J. Mol. Liq., 2015, 211, 498–505 CrossRef CAS.
- H. Roohi, M. Jahantab, S. Rahmdel Delcheh and B. Pakdel Khoshakhlagh, Chemical functionalization of boron nitride nanotube via the 1,3-dipolar cycloaddition reaction of azomethine ylide: A quantum chemical study, Strut. Chem., 2015, 26(3), 749–759 CrossRef CAS.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 5648–5672 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Rob, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Gaussian, Inc., Wallingford, CT, 2003 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General Atomic and Molecular Electronic Structure System, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580 CrossRef CAS PubMed.
- D. A. Neamen, Semiconductor Physics and Devices Basic Principles, McGraw-Hill, 4th edn, 2011, p. 784 Search PubMed.
- R. G. Parr and W. Yang, Density functional theory of atoms and molecules, Oxford University Press, New York, 1989 Search PubMed.
- P. Geerlings, F. De Proft and W. Langenaeker, Conceptual density functional theory, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- R. K. Roy and S. Saha, Studies of regioselectivity of large molecular systems using DFT based reactivity descriptors, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2010, 106, 106–118 RSC.
- E. P. Gyftopoulos and G. N. Hatsopoulos, Quantum-thermodynamic definition of electronegativity, Proc. Natl. Acad. Sci. U. S. A., 1968, 60, 786 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, Electronegativity: the density functional viewpoint, J. Chem. Phys., 1978, 68, 380 CrossRef.
- R. G. Parr and R. G. Pearson, Absolute hardness: companion parameter to absolute electronegativity, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- T. Koopmans, U ber die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms, Physica, 1934, 1, 104–113 CrossRef.
- R. G. Parr, L. Szentpaly and S. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, Combining quantum mechanics methods with molecular mechanics methods in ONIOM, J. Chem. Theory Comput., 2006, 2, 815–826 CrossRef CAS PubMed.
- T. Vreven, L. M. Thompson, S. M. Larkin, I. Kirker and M. J. Bearpark, Deconstructing the ONIOM Hessian: Investigating Method Combinations for Transition Structures, J. Chem. Theory Comput., 2012, 8, 4907–4914 CrossRef CAS PubMed.
- L. V. Liu, W. Q. Tian and Y. A. Wang, Ozonization at the Vacancy Defect Site of the Single-Walled Carbon Nanotube, J. Phys. Chem. B, 2006, 110, 13037–13044 CrossRef CAS PubMed.
- H. Choi, Y. C. Park, Y.-H. Kim and Y. S. Lee, Ambient Carbon Dioxide Capture by Boron-Rich Boron Nitride Nanotube, J. Am. Chem. Soc., 2011, 133, 2084–2087 CrossRef CAS PubMed.
- Y. Li, Z. Zhou, D. Colberg, Y. Bando, P. v. R. Schleyer and Z. Chen, Stone–Wales defects in single-walled boron nitride nanotubes: Formation energies, electronic structures and reactivity, J. Chem. Phys. C, 2008, 112, 1365 CrossRef CAS.
- P. Piquini, R. J. Baierle, T. M. Schmidt and A. Fazzio, Formation energy of native defects in BN nanotubes: an ab initio study, Nanotechnology, 2005, 16, 827 CrossRef CAS.
- T. Zhao, J. Shi, M. Huo and R. Wan, Electronic properties of C-doped boron nitride nanotubes studied by first-principles calculations, Phys. E, 2014, 64, 123–128 CrossRef CAS.
- Y. K. Chen, L. V. Liu and Y. A. Wang, Density Functional Study of Interaction of Atomic Pt with Pristine and Stone–Wales-Defective Single-Walled Boron Nitride Nanotubes, J. Phys. Chem. C, 2010, 114, 12382–12388 CAS.
- C. Kittel and H. Kroemer, Thermal Physics, W. H. Freeman, 1980, p. 363 Search PubMed.
- R. A. Swalin, Thermodynamics of Solids, Wiley, Day, 1972, vol. 8, p. 244 Search PubMed.
- Y. Xi, X. Zhao, A. Wang, X. Wang, H. Bu and M. Zhao, Tuning the electronic and magnetic properties of triangular boron nitride quantum dots via carbon doping, Phys. E, 2013, 49, 52–60 CrossRef CAS.
- J. X. Zhao and B. Q. Dai, DFT studies of electro-conductivity of carbon-doped boron nitride nanotube, Mater. Chem. Phys., 2004, 88, 244–249 CrossRef CAS.
- R. G. Pearson, Hard and soft acids and bases, Dowden, Hutchison & Ross, Stroudsburg, PA, 2001 Search PubMed.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO version 3.1 Search PubMed.
| This journal is © The Royal Society of Chemistry 2016 |