In situ growth of SnS absorbing layer by reactive sputtering for thin film solar cells

Abstract

The semiconductor SnS is a promising candidate for low cost earth-abundant photovoltaic absorbing layers and presents some interesting challenges in single phase material preparation. An in situ growth process via reactive sputtering was employed in this work to fabricate SnS thin films. The effect of growth temperature on the properties of prepared films was investigated to obtain phase-pure SnS. It is revealed that the films grown at 400 °C presented a single orthorhombic SnS phase with a direct optical band gap of 1.14 eV, a high optical absorption coefficient above 9.0 × 10⁴ cm⁻¹, and a p-type conductivity with a high carrier concentration around 10¹⁷ cm⁻³. The associated device with a structure of ITO/i-ZnO/CdS/SnS/Mo/glass achieves a power conversion efficiency of 0.26%. Based on the TEM characterization, the limiting factors for SnS device performance are revealed and discussed.

---

1. Introduction

Tin monosulfide (SnS) has increasingly being studied as a promising light absorbing material for low cost solar cells due to its more abundant and cheaper constituent elements and lower toxic nature, compared with commercially available Cu(In,Ga)Se₂ and CdTe.¹ SnS is an intrinsic p-type semiconductor with a high absorption coefficient of 10⁴ to 10⁵ cm⁻¹ in the visible region, a near-optimal direct band gap of 1.3 eV and indirect band gap of 1.1 eV, and a high free carrier concentration of 10¹⁶ cm⁻³.^2,3 These excellent qualities make SnS a very attractive candidate for the fabrication of solar cells on a large scale. So far, the reported highest efficiency of SnS-based thin-film solar cells has achieved 4.63%,⁴ which is substantially less than the theoretical maximum efficiency around 30% for SnS single-junction devices with a band gap of 1.3 eV according to the detailed balance theory predicted by Shockley–Queisser.⁵

It is generally believed that the poor performance of current SnS solar cells is mainly related to the low quality of SnS films, detrimental impurity phases like Sn₂S₃ or SnS₂,⁶ and non-optimal device architecture.^7,8 Various methods have been investigated for the preparation of high quality SnS films, e.g. chemical vapor deposition (CVD),^1,9 atomic layer deposition (ALD),³ thermal evaporation,^10–13 sputtering,^2,14,15 chemical bath deposition (CBD),¹⁶ spray pyrolysis,^7,17,18 and electrochemical deposition (ED).^19,20 So far most successful methods of fabricating high quality SnS films are related to simultaneous deposition of two elements and crystallization,^11,18 such as ALD which produced pure, stoichiometric and homogeneous SnS films from the reaction of bis(N,N′-diisopropylacetamidinato)tin(II) [Sn(MeC(N-iPr)₂)₂] and H₂S at 200 °C and achieved the highest efficiency of 4.63% for SnS-based thin film solar cells.⁴ However, ALD is a rather slow and expensive method for films fabrication and therefore a direct one-step, high-rate and low-cost deposition process is desperate for large scale production.¹¹ An attractive way that can meet such requirements is reactive sputtering. Sputtering is suitable for the continuous deposition of compound films in large-area, and especially common for oxides and nitrides.^21,22 Reactive sputtering can directly provide a homogeneous and crystalline film with tunable composition by adjusting the parameters of sputtering process, such as power, pressure, substrate temperature and H₂S/Ar ratio.²³ In addition, reactive sputtering has been successfully developed for the deposition of CuInS₂ and Cu₂ZnSnS₄ films,²⁴ with associated devices achieved energy conversion efficiencies of 11.4% and 7.9%, respectively.^25,26

In this work, we present a comprehensive exploration of reactive sputtering technique for the in situ growth of SnS thin films. The effects of growth temperature on the structural (including crystal structure, phase, composition, and morphology), optical and electrical properties of the grown films have been investigated. At last, based on SnS films grown by reactive sputtering, the solar cells have been fabricated for the first time and the preliminary performance has been presented.

2. Experimental

The in situ growth of tin sulfide thin films on Mo-coated soda-lime glass substrates was performed by RF reactive sputtering from metal Sn target in Ar/H₂S working gas. Simultaneously, soda-lime glasses were also used as substrates for the sake of sulfur content measurement, optical and electrical characterization. The Sn target is 60 mm in diameter and 5 mm in thickness with a purity of 99.99%. The distance between target and substrate was 120 mm and the substrate holder rotated at a frequency of 4 revolutions per minute. The base pressure of the sputtering system was approximately 10⁻⁴ Pa. The flow of Ar (purity: 99.999%) and H₂S (purity: 99.9%) were 30 sccm and 10 sccm respectively with a total pressure of 0.5 Pa. The sputtering power and time is 80 W and 30 min, respectively. During the deposition, the substrate was heated to the designed growth temperatures, i.e. room temperature (RT), 200 °C, 300 °C and 400 °C, respectively.

The surface and cross-sectional morphology of the films were analyzed by scanning electron microscopy (SEM, FEI Quanta-200) combined with an energy dispersive X-ray spectroscopy (EDS, EDAX-GENSIS60S). The film thickness was measured via a combination of cross-sectional SEM and profile meter (Veeco Dektak 150). The crystal structure of the films was analyzed by X-ray diffraction (XRD, Rigaku3014). Raman scattering measurements (LabRAM HR800) were performed at an excitation wavelength of 480 nm. The optical transmittance was recorded by a UV-Vis-near IR spectrophotometer (Hitachi U-4100) in the wavelength range of 300 to 2000 nm. The carrier concentration, carrier mobility and resistivity of the films were measured by the Hall effect measurement (HMS-3000/0.55 T) using the van der Pauw method at 300 K. A FEI Tecnai G2 equipped with energy dispersive spectroscopy (EDS) detector was used for the transmission electron microscopy (TEM) analysis.

Solar cell based on SnS thin films were fabricated by depositing a CdS buffer layer via chemical bath deposition according to the procedure described elsewhere,²⁷ and an i-ZnO/ITO window layer via magnetron sputtering. The solar cell performance was characterized by current–voltage (I–V) measurements using an AM 1.5 solar simulator (NEWPORT, 100 mW cm⁻²) and a digital source meter (Keithley 2400).

3. Results and discussion

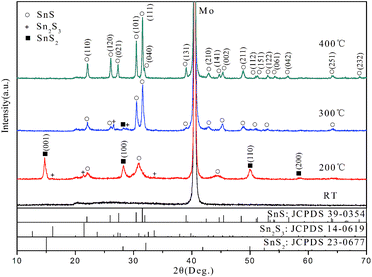
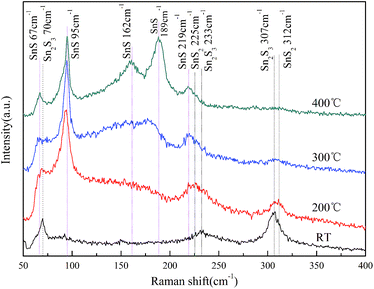
Fig. 1 shows the XRD patterns of the films grown at different temperatures ranging from RT to 400 °C. It is demonstrated that the growth temperature plays a crucial role in determining the phase and purity of films. For the films grown at RT, no obvious diffraction peaks can be observed except for that corresponding to Mo from Mo-coated substrate, which indicate indefinite phase of the film within sensitivity limit of the instrument. As the growth temperature increased to 200 °C, mixed phases including SnS₂, Sn₂S₃ and SnS were presented according to the diffraction patterns. The peaks at 2θ = 14.8, 28.3, 49.9 and 58.5° match the standard pattern of hexagonal SnS₂ (JCPDS no. 23-0677). Also trace orthorhombic Sn₂S₃ phase (JCPDS no. 14-0619) was detected. The broad peak at 2θ = 30.9° should result from the overlap and cross bonding between (101) and (111) peaks of SnS due to the low crystallinity. When the growth temperature increased to 300 °C, the intensity of SnS₂ and Sn₂S₃ peaks decrease greatly and the peaks of SnS become the dominant ones. Only few weak peaks at 2θ = 26.6, 28.9 and 28.3° corresponding to the residual Sn₂S₃ and SnS₂ were observed. Further increasing the growth temperature to 400 °C, the film is highly crystallized and consists of phase-pure SnS within the detection limit of XRD. The XRD feature matches well with orthorhombic structure of SnS (JCPDS no. 39-0354, a = 4.329 Å, b = 11.192 Å, c = 3.984 Å) and shows preferred orientation along (111) plane, which is in agreement with the reported results for SnS thin films grown by other techniques.^3,11,28 In general, the crystallinity and SnS phase of deposited films are improved with elevating the growth temperature.

Fig. 1 XRD patterns of the films grown at different temperatures.

Raman scattering measurement has performed to further confirm the phases of films grown at different temperatures and the results are shown in Fig. 2. The films grown at RT show only three band peaks at 70, 233 and 307 cm⁻¹ which match well with the reported spectra of Sn₂S₃.⁹ This indicates that Sn₂S₃ was the main product while SnS was not formed in the RT growth process. The spectrum of the films grown at 200 °C confirms the presence of SnS from the band peaks at 95 and 219 cm⁻¹.^9,29 Meanwhile, SnS₂ and Sn₂S₃ were detected in the films due to their characteristic Raman peaks at 312 and 307 cm⁻¹, respectively.⁹ When it comes to the films grown at 300 °C, the peaks of Sn₂S₃ and SnS₂ reduce in intensity significantly but still remain. The major component turns over to be SnS phase, which agrees well with the aforementioned XRD analysis. The films grown at 400 °C shows the band peaks at 67, 95, 162, 189 and 219 cm⁻¹, which well correspond to the reference spectrum of SnS.^3,9 The characteristic peaks from the other secondary phases such as Sn₂S₃ and SnS₂ cannot be observed, which indicate that a phase-pure SnS film was successfully in situ grown by reactive sputtering at 400 °C.

Fig. 2 Raman spectra of the films grown at different temperatures.

In order to provide further evidence of the phase identities, the ratio of tin to sulfur (Sn : S) for the films grown at different temperatures was determined by EDS analysis, as shown at Table 1. The results are in good agreement with the structural assignment. The films grown at RT and 200 °C had a Sn : S ratio close to 1 : 1.5, corresponding most closely to Sn₂S₃ or the mixture of SnS₂ and SnS. As the grown temperature increases, the Sn : S ratio increased clearly. Finally, a single phase of SnS was obtained at 400 °C with a slightly sulfur-rich composition of SnS_1.02.

Table 1 Properties of films grown at different temperatures, growth temperature T_grow, carrier concentration n, mobility μ, resistivity ρ

Tgrow (°C)	RT	200	300	400
Phase composition	Sn2S3	SnS2 + SnS + Sn2S3 (traces)	SnS + SnS2 (traces) + Sn2S3 (traces)	SnS
Elemental composition	SnS1.51	SnS1.52	SnS1.16	SnS1.02
Thickness (μm)	1.00	1.40	1.25	0.87
Eg (eV)	1.92	1.42	1.40	1.14
n (cm^−3)	−3.81 × 10^11	−1.82 × 10^17	6.04 × 10^17	2.11 × 10^17
μ (cm^2 V^−1 s^−1)	31.32	1.29	0.51	2.69
ρ (Ω cm)	6.28 × 10^5	28.59	20.61	12.83
Type	n	n	p	p

---

The SEM images in Fig. 3 show the surface and cross-sectional morphology of the films grown at different temperatures. The film grown at RT shows fairly smooth surface and consists of small grains without any void from surface (Fig. 3(a)) and cross-sectional (Fig. 3(e)) SEM images. The crystalline faces or edges cannot be seen clearly, which implies low crystallinity of the film. As the growth temperature increases, rougher surface and larger grains are observed from Fig. 3(b and c). As it can be seen from the cross-sectional view (Fig. 3(f and g)), lengthy and flaky grains extending the full thickness of the films are observed and the lateral grain size increases obviously, which should be beneficial to the solar cell performance according to the previous experience in CIGS and CZTS thin film solar cells.^30,31 When the growth temperature rises to 400 °C, clear and sharp crystal facets appeared on SnS grains (see Fig. 3(d and h)). The above results show that the crystallinity of the films was improved and clearer growth orientation perpendicular to the substrates was observed with increasing growth temperature. It is worth noting that growth temperature has a considerable effect on film thickness which has been analyzed and shown in Table 1. This should be mainly caused by different sulfur content, density and compactness of various tin sulfides, e.g. SnS, Sn₂S₃ and SnS₂ which present in the films grown at different temperatures. Besides, SnS has a high volatility and may be evaporated at high temperature and low pressure, which might be another reason for the thinner film grown at 400 °C.

Fig. 3 Surface and cross-sectional SEM images of films grown at RT (a and e), 200 °C (b and f), 300 °C (c and g) and 400 °C (d and h).

In order to further confirm the valence states and purity of the film grown at 400 °C, XPS measurements were performed after Ar sputtering for 3 min and the results presented in the Fig. 4. The XPS peaks were calibrated by XPS line of C1s at 284.5 eV. O1s, N1s and C1s were not detected which indicate high purity of reactively sputtered SnS films. The peaks at 485.88 and 494.38 eV correspond to the binding energy of Sn3d_5/2 and Sn3d_3/2, respectively and the peak splitting of 8.50 eV is consistent with that for Sn in the oxidation state of +2. The S2p peak at 161.46 eV corresponds to that for S in the oxidation state of −2. All the binding energies and peak splitting of the SnS film are in good agreement with the values reported earlier for Sn²⁺, and S²⁻ in SnS.^3,32 Besides, from the XPS results we find that no other valences, such as Sn(VI) could not be detected.

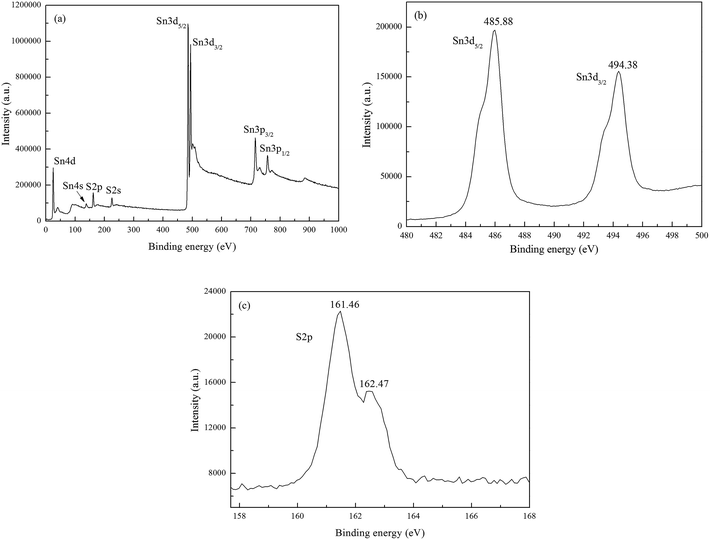Fig. 4 XPS spectra of the films grown at 400 °C, (a) wide scan pattern, (b) Sn3d emission peaks, (c) S2p emission peaks.

The absorption coefficient (α) was determined from the transmittance spectra which were recorded by a UV-Vis-near IR spectrophotometer, as shown in Fig. 5(a). It can be observed clearly that SnS film grown at 400 °C has the highest α above 9.0 × 10⁴ cm⁻¹ in the wavelength of 400 nm to 800 nm, which indicates that only 260 nm is enough for the thickness of SnS film to absorb 90% of the incident photons. According to Tauc et al.,^3,33 the optical band gap (E_g) is determined by the calculation

(αhν)ⁿ = A(hν − E_g) (1)

where h is Planck's constant, ν is the photon frequency, A is a constant, and n characterizes the transition process. n = 2 and 1/2 represent direct and indirect transitions, respectively. The band gap of the films is determined by plotting the (αhν)ⁿ versus hν, and extrapolating the linear portion of the curve to αhν = 0. Both of direct and indirect transition for SnS films are reported by previous published work,^2,3 and the reported band gap of SnS films has a wide range from 0.9 eV to 1.8 eV.¹ In this work, both n = 1/2 and 2 were used to plot the (αhν)ⁿ versus hν, and we found that no straight line region was observed in a reasonable interval of photon energy near the absorption edge when n = 1/2 was put. While n = 2 gave a well linear fit as shown in Fig. 5(b), indicating more likely direct transition for the prepared films. The obtained values of E_g for the four samples are estimated and also listed in Table 1. It is found that E_g decreases from 1.92 eV to 1.14 eV with increasing growth temperature from RT to 400 °C, which can be ascribed to the difference of phase composition and crystallinity. The tendency of the transformation can be supported by XRD and Raman analysis as SnS has lower band gap than Sn₂S₃ and SnS₂. The band gap of the film grown at RT is close to the earlier reported values of Sn₂S₃.^34,35 This reconfirm the result of Raman analysis that Sn₂S₃ is the dominant product by reactive sputtering at RT. The film grown at 400 °C shows a smaller band gap of 1.14 eV compared with the published values of SnS.^3,12 The dependence of the band gap of SnS on the degree of the crystallinity has been previously reported by Arun³⁶ and Hartman,² who found that the E_g decreases with the increasing grain size of SnS thin films.

Fig. 5 Optical properties of the films grown at different temperatures, (a) α versus hν, (b) a plot of (αhν)² versus hν corresponding direct band gap transition.

The electrical properties of the films grown at different temperatures were measured by the Hall effect measurement using the van der Pauw method at 300 K and the obtained results are summarized in Table 1. It is observed that the conductivity type of the films changed from n-type to p-type as the growth temperature increases. This phenomenon is related to different stoichiometry and phase of the films grown at different temperatures, as Sn₂S₃ and SnS₂ have been reported as n-type materials^37,38 and SnS is a natural p-type semiconductor.^3,39 The film grown at RT shows a relative low carrier concentration, which leads to a high resistivity. As the growth temperature increase, the obtained films present high carrier concentration and lower resistivity. The obtained SnS film has a carrier concentration up to 2.11 × 10¹⁷ cm⁻³, which is comparable with that of CIGS device⁴⁰ and similar to those reported by Yanuar et al.⁴¹ and Wangperawong et al.,⁴² but higher than those found by Sinsermsuksakul et al. (10¹⁵ to 10¹⁶ cm⁻³), who reported that low carrier concentrations may be due to native point defects such as Sn²⁺ vacancies caused by slight deviations from stoichiometry. The mobility is slightly lower than those reported by others.^3,41,43 This can be explained by lots of voids between vertical grains causing the decrease of hole mobility along the layer direction.

The SnS film gown at 400 °C was used to fabricate thin film solar cells with the device configuration of ITO/i-ZnO/CdS/SnS/Mo/glass and the active area of cell was 0.15 cm². As shown in Fig. 6, the J–V characteristic of the cell revealed the efficiency of 0.26% with an open-circuit voltage (V_oc) of 162 mV, a short-circuit current density (J_sc) of 6.19 mA cm⁻², and a fill factor (FF) of 0.26 was obtained. These performance parameters are much less than those of the record SnS devices.⁴ It is generally believed that low efficiencies can be due to various reasons, such as bulk material impurities and defects, interface trap states, and notably unfavorable heterojunction band alignment, etc.^44–47 To gain insight into the possible reasons for the low efficiency, TEM was used for investigating the cross-section of the SnS solar cell as shown in Fig. 7(a). The presence of long strips of voids is clearly observable in the SnS films. The elemental profiles were determined by EDS scan along the lateral (L1) and vertical (L2) red arrows as shown in Fig. 7(b) and (c), respectively. It is clear that sulfur is homogeneously distributed in the entire area of the film except in the void region. But the intensity of Sn in the surface is relative lower than that in the bulk of SnS film. Besides, Cd was also detected in the surface of SnS film and decreased with the internal extension. This phenomenon is frequently observed in CIGS solar cells and is resulted from the interfacial reaction with an ion exchange between Cd and Cu in the CBD-CdS process.^48–50 Furthermore, the presence of pores and voids may accelerate Cd diffusion in the CIGS film.⁴⁹ Indeed, EDS analysis show that higher concentration of Cd was observed in the void region of SnS absorber layer (see Fig. 7(b)). The band mis-alignment of p-SnS/n-CdS heterojunction leads to large interface recombination due to the “cliff” in the conduction-band offset (E_c,SnS > E_c,CdS).^51,52 Theories and experiments suggest that a small positive conduction band offset (CBO) in the range of 0 eV to +0.34 eV is the optimal band alignment for high efficiency solar cells.^53–55 That means a material with higher conduction band energy than CdS is preferable for SnS-based thin film solar cells, such as Zn(O,S),⁴⁶ In₂S₃,⁵⁶ (Zn,Cd)S,⁵⁷ and (Zn,Mg)O.⁵⁸ Actually, the record high efficiency of 4.63% based on SnS solar cells was achieved by employing Zn(O,S) as the buffer layer.⁴ Besides, the low conductivity (12.83 Ω cm) of SnS film might be a potential contributor to the poor V_oc.⁵⁴ Also ion-induced defects are common present in the surface of absorber layers grown by sputtering and act as recombination centers.²⁵ A rational surface passivation process could reduce the density of defect states. Gordon et al. reported that recombination near the p-SnS/n-Zn(O,S) junction is reduced by inserting a few monolayers of ALD-SnO₂ between these layers.⁴ Further optimization including increasing the length of minority carrier diffusion, reducing the intrinsic conductivity, improving band-alignment, and passivating the surface defects, etc. is under investigation to boost the efficiency of the reactive sputtering processed SnS thin film solar cells.

Fig. 6 I–V characteristics of device based on SnS film grown at 400 °C.

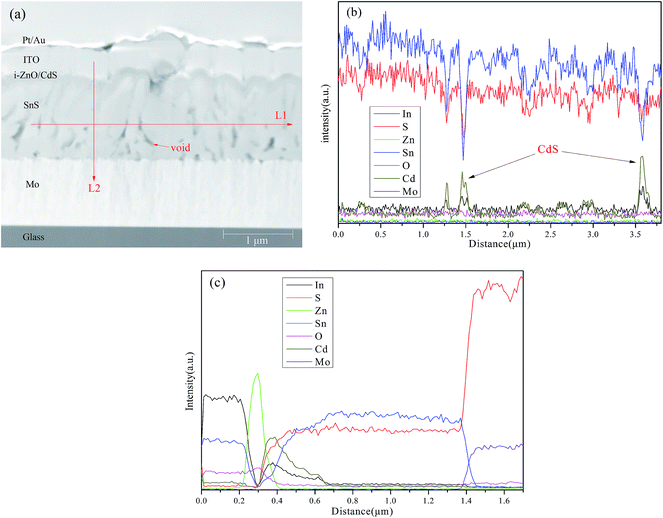Fig. 7 TEM image (a) of device based on SnS film grown at 400 °C, the elemental profiles determined by EDS scan along the lateral (L1) (b) and vertical (L2) (c) red arrow in (a).

4. Conclusions

Tin sulfide thin films were in situ grown by RF reactive sputtering of Sn target in Ar/H₂S mixed atmosphere at growth temperatures from RT to 400 °C. Phase-pure SnS has been obtained when the growth temperature reach 400 °C, while Sn₂S₃ and SnS₂ are easier to generate at low growth temperature. As the growth temperature increases, the films show increasingly oriented structure with better crystallinity, the direct band gap decreased from 1.92 to 1.14 eV, and the conduction type changed from n to p-type as well as the resistivity decreased from 6.28 × 10⁵ to 12.83 Ω cm. The suitable optical and electrical properties suggest that the SnS thin film is qualified as a promising absorber material for thin film solar cells. The best solar cell based on the grown SnS films produces a V_oc, J_sc and η of 162 mV, 6.19 mA cm⁻², and 0.26%, respectively. The deficiencies of SnS and non-optimal device structure may lead to the increase of charge carrier recombination, and therefore limit the cell performance.

Acknowledgements

This work was supported by the Fundamental Research Funds for the Central Universities of Central South University (Grant No. 2014zzts031) and the Funds for College Students Innovation Training Project (Grant No. 201410533040).

Notes and references

1. L. A. Burton, D. Colombara, R. D. Abellon, F. C. Grozema, L. M. Peter, T. J. Savenije, G. Dennler and A. Walsh, Chem. Mater., 2013, 25, 4908–4916.
2. K. Hartman, J. L. Johnson, M. I. Bertoni, D. Recht, M. J. Aziz, M. A. Scarpulla and T. Buonassisi, Thin Solid Films, 2011, 519, 7421–7424.
3. P. Sinsermsuksakul, J. Heo, W. Noh, A. S. Hock and R. G. Gordon, Adv. Energy Mater., 2011, 1, 1116–1125.
4. P. Sinsermsuksakul, L. Sun, S. W. Lee, H. H. Park, S. B. Kim, C. Yang and R. G. Gordon, Adv. Energy Mater., 2014, 4, 1400496.
5. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
6. K. T. Ramakrishna Reddy, P. Purandar Reddy, R. W. Miles and P. K. Datta, Opt. Mater., 2001, 17, 295–298.
7. M. Patel and A. Ray, ACS Appl. Mater. Interfaces, 2014, 6, 10099–10106.
8. L. A. Burton and A. Walsh, Appl. Phys. Lett., 2013, 102, 132111.
9. L. S. Price, I. P. Parkin, A. M. E. Hardy, R. J. H. Clark, T. G. Hibbert and K. C. Molloy, Chem. Mater., 1999, 11, 1792–1799.
10. B. Ghosh, M. Das, P. Banerjee and S. Das, Sol. Energy Mater. Sol. Cells, 2008, 92, 1099–1104.
11. V. Steinmann, R. Jaramillo, K. Hartman, R. Chakraborty, R. E. Brandt, J. R. Poindexter, Y. S. Lee, L. Sun, A. Polizzotti, H. H. Park, R. G. Gordon and T. Buonassisi, Adv. Mater., 2014, 26, 7488–7492.
12. H. Noguchi, A. Setiyadi, H. Tanamura, T. Nagatomo and O. Omoto, Sol. Energy Mater. Sol. Cells, 1994, 35, 325–331.
13. N. Revathi, S. Bereznev, M. Loorits, J. Raudoja, J. Lehner, J. Gurevits, R. Traksmaa, V. Mikli, E. Mellikov and O. Volobujeva, J. Vac. Sci. Technol., A, 2014, 32, 061506.
14. M. G. Sousa, A. F. da Cunha and P. A. Fernandes, J. Alloys Compd., 2014, 592, 80–85.
15. G. P. Wei, Z. L. Zhang, W. M. Zhao, X. H. Gao, W. Q. Chen, H. Tanamura, M. Yamaguchi, H. Noguchi, T. Nagatomo and O. Omoto, Photovoltaic Energy Conversion, IEEE Photovoltaic Specialists Conference, 1994.
16. A. R. Garcia-Angelmo, M. T. S. Nair and P. K. Nair, Solid State Sci., 2014, 30, 26–35.
17. M. Calixto-Rodriguez, H. Martinez, A. Sanchez-Juarez, J. Campos-Alvarez, A. Tiburcio-Silver and M. E. Calixto, Thin Solid Films, 2009, 517, 2497–2499.
18. K. T. Ramakrishna Reddy, N. Koteswara Reddy and R. W. Miles, Sol. Energy Mater. Sol. Cells, 2006, 90, 3041–3046.
19. Z. Zainal, M. Z. Hussein and A. Ghazali, Sol. Energy Mater. Sol. Cells, 1996, 40, 347–357.
20. M. Kul, Vacuum, 2014, 107, 213–218.
21. P. Frach, D. Gloss, K. Goedicke, M. Fahland and W. M. Gnehr, Thin Solid Films, 2003, 445, 251–258.
22. H. C. Barshilia, N. Selvakumar, B. Deepthi and K. S. Rajam, Surf. Coat. Technol., 2006, 201, 2193–2201.
23. T. Ericson, T. Kubart, J. J. Scragg and C. Platzer-Björkman, Thin Solid Films, 2012, 520, 7093–7099.
24. F. Y. Liu, Y. Li, K. Zhang, B. Wang, C. Yan, Y. Q. Lai, Z. A. Zhang, J. Li and Y. X. Liu, Sol. Energy Mater. Sol. Cells, 2010, 94, 2431–2434.
25. T. Unold, I. Sieber and K. Ellmer, Appl. Phys. Lett., 2006, 88, 213502.
26. J. J. Scragg, T. Kubart, J. T. Wätjen, T. Ericson, M. K. Linnarsson and C. Platzer-Björkman, Chem. Mater., 2013, 25, 3162–3171.
27. F. Liu, Y. Lai, J. Liu, B. Wang, S. Kuang, Z. Zhang, J. Li and Y. Liu, J. Alloys Compd., 2010, 493, 305–308.
28. P. D. Antunez, D. A. Torelli, F. Yang, F. A. Rabuffetti, N. S. Lewis and R. L. Brutchey, Chem. Mater., 2014, 26, 5444–5446.
29. H. Chandrasekhar, R. Humphreys, U. Zwick and M. Cardona, Phys. Rev. B: Solid State, 1977, 15, 2177–2183.
30. M. Gloeckler, J. R. Sites and W. K. Metzger, J. Appl. Phys., 2005, 98, 113704.
31. T. K. Todorov, K. B. Reuter and D. B. Mitzi, Adv. Mater., 2010, 22, E156–E159.
32. C. Gao, H. Shen, L. Sun, H. Huang, L. Lu and H. Cai, Mater. Lett., 2010, 64, 2177–2179.
33. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637.
34. M. Khadraoui, N. Benramdane, C. Mathieu, A. Bouzidi, R. Miloua, Z. Kebbab, K. Sahraoui and R. Desfeux, Solid State Commun., 2010, 150, 297–300.
35. E. Güneri, F. Göde, B. Boyarbay and C. Gümüş, Mater. Res. Bull., 2012, 47, 3738–3742.
36. P. Jain and P. Arun, Thin Solid Films, 2013, 548, 241–246.
37. A. Sanchez-Juarez and A. Ortíz, Semicond. Sci. Technol., 2002, 17, 931.
38. L. Amalraj, C. Sanjeeviraja and M. Jayachandran, J. Cryst. Growth, 2002, 234, 683–689.
39. B. D. Malone, A. Gali and E. Kaxiras, Phys. Chem. Chem. Phys., 2014, 16, 26176–26183.
40. L. Zhang, Q. He, W.-L. Jiang, F.-F. Liu, C.-J. Li and Y. Sun, Sol. Energy Mater. Sol. Cells, 2009, 93, 114–118.
41. F. Yanuar, G. El-Haj Moussa, F. Guastavino and C. Llinares, Mediterranean Conference for Environment and Solar, 2000.
42. A. Wangperawong, S. M. Herron, R. R. Runser, C. Hägglund, J. T. Tanskanen, H.-B.-R. Lee, B. M. Clemens and S. F. Bent, Appl. Phys. Lett., 2013, 103, 052105.
43. C.-C. Huang, Y.-J. Lin, C.-Y. Chuang, C.-J. Liu and Y.-W. Yang, J. Alloys Compd., 2013, 553, 208–211.
44. W. Jaegermann, A. Klein and T. Mayer, Adv. Mater., 2009, 21, 4196–4206.
45. M. Sugiyama, K. T. R. Reddy, N. Revathi, Y. Shimamoto and Y. Murata, Thin Solid Films, 2011, 519, 7429–7431.
46. L. Sun, R. Haight, P. Sinsermsuksakul, S. Bok Kim, H. H. Park and R. G. Gordon, Appl. Phys. Lett., 2013, 103, 181904.
47. A. Schneikart, H. J. Schimper, A. Klein and W. Jaegermann, J. Phys. D: Appl. Phys., 2013, 46, 305109.
48. T. Nakada and A. Kunioka, Appl. Phys. Lett., 1999, 74, 2444–2446.
49. C. Lei, M. Duch, I. M. Robertson and A. Rockett, J. Appl. Phys., 2010, 108, 114908.
50. T. Nakada, Thin Solid Films, 2000, 361–362, 346–352.
51. H. H. Park, R. Heasley, L. Sun, V. Steinmann, R. Jaramillo, K. Hartman, R. Chakraborty, P. Sinsermsuksakul, D. Chua, T. Buonassisi and R. G. Gordon, Prog. Photovoltaics, 2014, 23, 901–908.
52. A. Wangperawong, P. C. Hsu, Y. Yee, S. M. Herron, B. M. Clemens, Y. Cui and S. F. Bent, Appl. Phys. Lett., 2014, 105, 173904.
53. T. Minemoto, T. Matsui, H. Takakura, Y. Hamakawa, T. Negami, Y. Hashimoto, T. Uenoyama and M. Kitagawa, Sol. Energy Mater. Sol. Cells, 2001, 67, 83–88.
54. P. Sinsermsuksakul, K. Hartman, S. Bok Kim, J. Heo, L. Sun, H. Hejin Park, R. Chakraborty, T. Buonassisi and R. G. Gordon, Appl. Phys. Lett., 2013, 102, 053901.
55. M. Gloeckler and J. R. Sites, Thin Solid Films, 2005, 480–481, 241–245.
56. M. Patel and A. Ray, J. Electron. Mater., 2015, 44, 558–567.
57. M. Gunasekaran and M. Ichimura, Sol. Energy Mater. Sol. Cells, 2007, 91, 774–778.
58. T. Ikuno, R. Suzuki, K. Kitazumi, N. Takahashi, N. Kato and K. Higuchi, Appl. Phys. Lett., 2013, 102, 19390.

---