Fluorine substitution effects of halide anion receptors based on the combination of a distinct hydrogen bond and anion–π noncovalent interactions: a theoretical investigation†
Yan-Zhi Liua,
Kun Yuan*ab,
Zhao Yuan c,
Yuan-Cheng Zhu*a and
Ling-Ling Lva
c,
Yuan-Cheng Zhu*a and
Ling-Ling Lva
aCollege of Chemical Engineering and Technology, Tianshui Normal University, Tianshui, 741001, China. E-mail: tsnuyk@yeah.net; yczhu@tsnc.edu.cn
bInstitute for Chemical Physics & Department of Chemistry, State Key Laboratory of Electrical Insulation and Power Equipment, Xi'an Jiaotong University, Xi'an 710049, China
cDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, 32306, USA
First published on 25th January 2016
Abstract
Noncovalent interactions between halide anions and a series of N-(4-vinyl-2-benzoic acid benzyl ester)-phenyl-urea containing receptors (1–8) based on hydrogen bond and (or) anion–π interactions were investigated via theoretical calculations based on dispersion corrected density functional B3LYP-D3. Particularly, the fluorine substitution effects were deeply explored. The results showed that the substituent number and position of fluorine groups on the phenyl ring of the benzoic acid esters group has a significant effect on the configuration and cooperative properties of the hydrogen bond and anion–π interactions. Consequently, a more feasible and rational geometric criterion for either a strong or weak halide-anion–π contact was proposed via three inequalities independent of any empirical parameters, which is different from the criterion proposed very recently by Albrecht and Rissanen based on their experience with solid state anion–π interactions (Chem. Sci., 2015, 6, 354–359). Additionally, electronic properties and behavior of the systems were discussed according to the calculations on the frontier molecular orbital, total electrostatic potential and visualized weak interactions regions. It is expected that the theoretical explorations from a molecular level in this work may be useful for future experimental study and helpful for understanding the structure–activity relationship between aromatic rings and anion–π interactions in the case of combination of distinct noncovalent interactions.
1. Introduction
Due to the ubiquity and importance of anions in biochemical processes, medical catalysts, sensors and environmental detection, chemists have driven intensive research activities into the development of synthetic anion receptors.1–8 Despite the great importance and significant progress of anion recognition and sensing,9–20 the molecular design and synthesis of anion receptors still remains a challenging field of chemistry. Presently, the conventionally adopted supramolecular synthons of anion receptors include electrostatic, hydrogen bonding (HB),17,19,20 halogen bonding (XB),21–24 Lewis acid–base,25 and anion–π26,27 interactions. Among these noncovalent interactions in anion recognition and reception, HB is the foremost, the most popular and classical. In contrast, anion–π interactions have been overlooked for a long time primarily due to their counterintuitive nature, in which anions are expected to exhibit repulsive interactions with aromatic π-systems owing to their electron donating character.Since the pioneering work describing gas-phase clustering reactions between anions and hexafluorobenzene,28 much more attention has been attracted to the anion–π noncovalent interactions including theoretical and experimental methodologies.26,27,29–34 Typically, anion–π interactions are termed as favorable noncovalent contacts between an electron deficient (π-acidic) aromatic system and an anion.26,30 Elegant studies have revealed that the anion–π interaction is, in general, dominated by electrostatic and anion-induced polarization contributions.35,36
Recently, the strategy of cooperative multiple different noncovalent interactions for anion recognition has shown some promising benefits for the design of anion receptors.37–39 Taylor' group successfully synthesized a series of urea-based anion receptors composed of both –(CO)NH– and –C6H4–X (X = F, I) groups, suggesting the possibility to employ hydrogen- and halogen-bond interactions cooperatively in molecular recognition, and to modulate the anion selectivity with combinations of the above two distinct noncovalent interactions.40 Most recently, a hydroxyl functionalized tetraoxacalix[2]arene[2]triazine host molecule was synthesized,41 and its infinite self-assemblies were also produced under the directing of cooperative anion–π, lone-pair electron–π interactions and intermolecular hydrogen bond. In our previous work,42 a novel electron-deficient-aromatic structural unit- and urea-based anion receptor (N-p-nitrophenyl-N-(4-vinyl-2-five fluoro-benzoic acid benzyl ester)-phenyl-urea, FUR) was designed to probe its potential for halide-anion recognition through cooperation of hydrogen bond and anion–π weak interactions via theoretical calculation. It is found that the N–H⋯F− hydrogen bond is much stronger than N–H⋯X (X = Cl−, Br− and I−), but the F−–π interaction might be slightly weaker than X–π (X = Cl−, Br− and I−) interactions. More importantly, F− anion would be prior recognized and highly affined by the anion receptor FUR either in vacuum or in solution phase when it is coexistence with other halide-anions or their mixture, indicating that the designed FUR could be an ideal receptor for highly sensitive and selective recognition of F− anion through the cooperation of N–H⋯F− hydrogen bond and anion–π weak interactions.
In the course of our ongoing research on the halide anion recognition capabilities of the N-p-nitrophenyl-N-(4-vinyl-2-five-fluoro-benzoic acid benzyl ester)-phenyl-urea and its derivatives, it was found that the fluorine substitution effects should be re-clarified and deeply investigated since the substituent number and position of fluorines on the phenyl ring of the benzoic acid ester have significant effect on the configuration and cooperative property of the hydrogen bond and anion–π interactions, while anion binding energies are not obviously effected. Herein, the eight anion receptors 1–8 used in this investigation of the fluorine substitution effects are shown in Scheme 1. We hope that this theoretical study is useful for judging an anion–π interaction, understanding the impact of fluorine substitution, and further design and synthesis of the fluorine-containing N-p-nitrophenyl-N-(benzoic acid benzyl ester)-phenyl-urea derivatives.
2. Computational methods
In the current work, the density functional theory of Grimme's DFT-D3 (ref. 43) was mainly employed for the study of anion-receptor@X− systems (X = F, Cl, Br and I). DFT-D3 method provides an empirical dispersion correction for DFT.43,44 The ability of this new density functional to predict and explain the supramolecular chemistry at van der Waals distances is very encouraging since density functional theory can be used conveniently for supramolecular systems.45,46 All the geometric configurations were optimized at the B3LYP-D3/6-31+G(D,P) levels, while for I atom, the basis set of MIDIX47 was used, which is considered as a well-balanced and economical double-ζ basis set that gives reasonably good geometries and partial atomic charges. No symmetry constraints were applied during optimizations. Harmonic frequency analyses were performed at the same level to confirm that these structures were local minima or transition state on the potential energy surfaces. The intermolecular interaction energies (ΔECPint) with basis set superposition errors (BSSE) corrected were calculated by the counterpoise method.48 Energy decomposition analyses were carried out with the LMO-EDA method49 implemented in GAMESS-US 2014.50 Additionally, a visual study of intermolecular noncovalent interaction between host and guest was performed via calculating the reduced density gradient (RDG),51 coming from the electron density (ρ(r)) and its first derivative (RDG(r) = 1/(2(3π2)1/3)|∇ρ(r)|/ρ(r)4/3), and the second largest eigenvalue of Hessian matrix of electron density (λ2) functions by using Multiwfn program.52,53 All the other calculations were performed with the Gaussian 09 program.543. Results and discussion
Geometric configurations
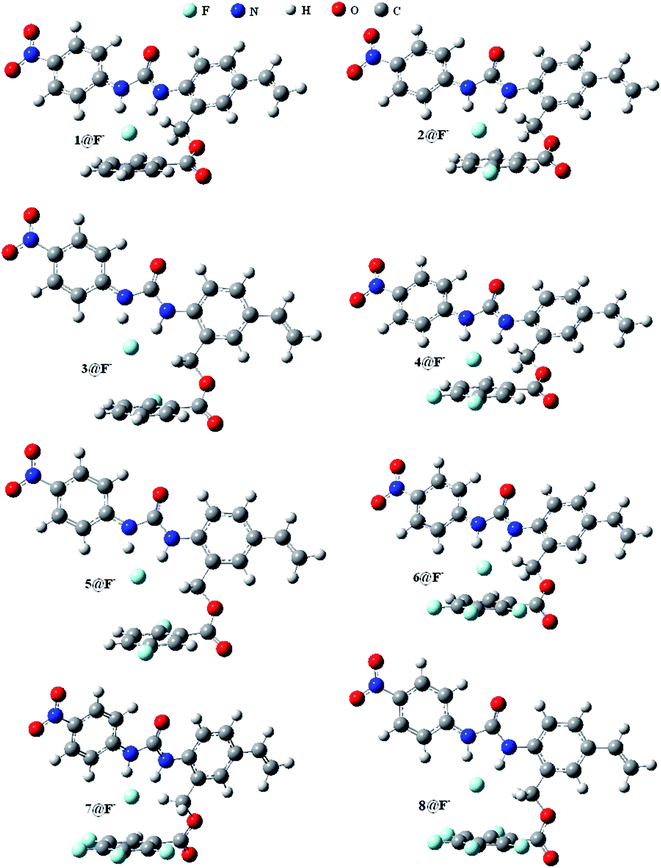
Fig. 1 shows the optimized geometric configurations of the 1–8@F− systems at B3LYP-D3/6-31+G(D,P). The configurations of 1–8@halide-anion systems involving Cl−, Br− and I− are given by their Cartesian coordinates in Table S1–S24 in the ESI.† Independent on the four halides, there are two kinds of receptor@halide-anion configurations. In the first one, the halide anions bind with receptors only by using N–H⋯X−⋯H–N (X = F, Cl, Br and I) double-dentate hydrogen bond, including 1@X−, 2@X−, 4@X− and 6@X−; in the other one, the complexes are formed via both double-dentate hydrogen bond and anion–π interaction, i.e. 3@X−, 5@X−, 7@X− and 8@X−. For a simple and clear expression, the key geometric parameters (defined as Fig. 2 showing) of the 1–8@F− complexes were listed in Table 1. It can be seen that the substituent number and position of the fluorine substitutions on the benzoic acid benzyl ester group of the anion receptors affect very little on the structures of the double-dentate hydrogen bonds, but it should be pointed out that the elongations of one donor (N1–H1) of the double-dentate hydrogen bond in 3@X− or 5@X− are a little larger than that of another (N2–H2), and the corresponding parameter of d1 are shorter than another (d2), indicating that the two branches of double-dentate hydrogen bond are not symmetrical. In order to further confirm these geometric characteristics of the N–H⋯X−⋯H–N double-dentate hydrogen bonds, another density functional method M06-2X,55 which can also provide accurate description for the noncovalent interactions, was used at the same basis set for the optimizations of the free 8 and 8@X− (X = F, Cl, Br and I) complexes. The results (see Table S25†) show the same features as the previous one obtained by B3LYP-D3 method.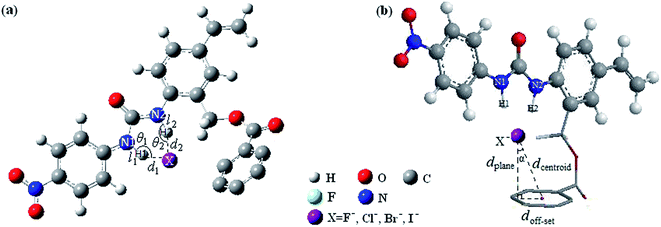 | ||
| Fig. 2 Definitions of the related geometric parameters the N–H⋯X− double-dentate hydrogen bond (a) and anion–π (b) in receptor@halide-anion systems.42 | ||
| l1/Å | l2/Å | d1/Å | d2/Å | θ1/° | θ2/° | dpenetration/Åa | |
|---|---|---|---|---|---|---|---|
| a dpenetration, mutual penetration distance between F− and H atom, is defined as sum of the van der Waals radii of H atom and halide-anion substrate the average of d1 and d2, namely dpenetration = ∑vdW-radii − 1/2(d1 + d2). | |||||||
| 1@F− | 1.058 | 1.046 | 1.576 | 1.636 | 158.08 | 158.06 | 1.301 |
| 2@F− | 1.056 | 1.045 | 1.583 | 1.640 | 156.18 | 157.98 | 1.296 |
| 3@F− | 1.065 | 1.048 | 1.535 | 1.625 | 158.55 | 156.92 | 1.327 |
| 4@F− | 1.054 | 1.044 | 1.593 | 1.644 | 157.87 | 158.36 | 1.289 |
| 5@F− | 1.063 | 1.048 | 1.543 | 1.629 | 158.50 | 157.07 | 1.321 |
| 6@F− | 1.054 | 1.043 | 1.596 | 1.650 | 158.03 | 158.50 | 1.284 |
| 7@F− | 1.057 | 1.047 | 1.580 | 1.623 | 157.70 | 158.52 | 1.306 |
| 8@F− | 1.056 | 1.047 | 1.583 | 1.627 | 157.74 | 158.58 | 1.302 |
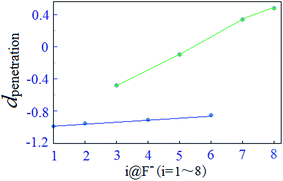
Moreover, the average mutual penetration distances, dpenetration, between F− and H atom in 3@X− and 5@X− systems are larger than those in the other complexes, indicating that fluorine substitution on the fifth position of the benzoic structure unit may enhance the double dentate hydrogen bond. This is probably owing to the field effect which might occur as the fluorine substitutions on the fifth position of the benzoic are relatively close to the anion. We also noted that the average mutual penetration distances of double-dentate hydrogen bonds in 1@X− and 8@X− are almost identical, indicating that either fluorine-free or five-fluorine substituents on the benzoic acid benzyl ester give the same strengths of the N–H⋯X−⋯H–N double-dentate hydrogen bond. For the double-dentate hydrogen bond in 2@X− and 6@X−, the dpenetration are smaller than those in the other systems. In contrast, fluorine substituents in receptor 2 and 6 are relatively far away from the anion and hydrogen bond donors, thereby, the corresponding field effect has little contribution on the stabilization for the double-dentate hydrogen bond.
Compared to the effect on the structures and strength of the double-dentate hydrogen bonds in 1–8@F− systems, the fluorine substitution has significant impact on the anion–π interactions. The substituent number and position of the fluorine substitution determine the efficiency and even existence of the anion–π interaction in current systems. As can be seen from the configurations of 1@F−, 2@F−, 4@F−, 6@F− presented in Fig. 1, all of the F− are far away from the center of benzoic acid group and nearly lie on the same plane of benzoic acid group. Table 2 lists some key geometric parameters (defined as Fig. 2(b) showing) related to anion–π structure in 1–8@F− systems at B3LYP-D3/6-31+G(D,P) level. The configuration parameters of α in these four configurations are high as 76.33, 77.57, 79.00 and 72.36°, respectively. Therefore, from the view of geometric consideration, the anion–π interactions are not possible if 1, 2, 4, and 6 were used as halide receptors. However, in the configurations of 3@F−, 5@F−, 7@F−, 8@F− configurations, F− anions are all located on above of the benzoic group with smaller α values in the range of 12–36°, revealing the rational geometric possibilities of the formations of the anion–π interactions. It has been evidenced that, in many of the X-ray structures exhibiting anion–π contact, the anion is not located exactly over the center of the ring.29 Instead, it is displaced with respect to the center of the ring. Since most aromatic rings are asymmetrically substituted, the more favorable location of anion is probably not above the center of the ring. Obviously, if α is too large, the anion–π interaction would not form. In fact, it should be mentioned that it is difficult to clearly define and establish a criterion which allows to classify the given anion-aromatic geometric parameters as an anion–π interaction.
| Receptor@F− | dcentroid/Å | dplane/Å | doff-set/Å | α/° | adpenetration/Å |
|---|---|---|---|---|---|
| a Here, the dpenetration, mutual penetration distance between halide-anion and aromatic π system, is defined as sum of the van der Waals radii of C atom and halide-anion substrate dcentroid, namely dpenetration = ∑vdW-radii − dcentroid. | |||||
| 1@F− | 4.400 | 1.040 | 4.275 | 76.33 | −0.988 |
| 2@F− | 4.358 | 0.938 | 4.256 | 77.57 | −0.948 |
| 3@F− | 3.584 | 2.913 | 2.088 | 35.63 | −0.471 |
| 4@F− | 4.317 | 0.824 | 4.238 | 79.00 | −0.907 |
| 5@F− | 3.499 | 2.877 | 1.991 | 34.69 | −0.089 |
| 6@F− | 4.251 | 1.288 | 4.051 | 72.36 | −0.841 |
| 7@F− | 3.158 | 2.879 | 1.298 | 24.26 | 0.352 |
| 8@F− | 2.989 | 2.917 | 0.652 | 12.60 | 0.493 |
The geometric structure of the anion–π noncovalent interaction can be characterized by the parameters of dcentroid, dplane and doff-set, which are defined as shown in Fig. 2(b). Table 2 lists the related geometric parameters of the receptor@F− (receptor = 1–8) at B3LYP-D3/6-31+G(D,P). According to Frontera's recommendation,29 when the anion is located at any place over the ring since the π-system covers the entire ring at distances ≤∑vdW-radii + r, where r = 0.7/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α (0.7 is an empirical constant), an anion–π contact could be considered. However, as has been pointed out,42 this is not a very easy understandable criterion since the definition of the distance between the anion and the involving aromatic ring is ambiguous and empirical. Moreover, it is also a relatively loose criterion, that might overestimate the maximum allowable anion–π contact distance. In our previous work,42 we suggested using mutual penetration distance dpenetration > 0 (defined as the footnote of Table 2) as criterion to judge an anion–π contact. However, this is a very restrictive criterion, and it may be used only for strong anion–π interaction. For a relatively weak anion–π interaction, dpenetration is not recommended. For example, the dpenetration in 5@F− and 3@F− are both negative values (listed in Table 2), but the weak anion–π contacts cannot be excluded. Therefore, it is very necessary to establish much more reasonable and reliable geometric criterion, which is suitable for either strong or weak anion–π contact.
α (0.7 is an empirical constant), an anion–π contact could be considered. However, as has been pointed out,42 this is not a very easy understandable criterion since the definition of the distance between the anion and the involving aromatic ring is ambiguous and empirical. Moreover, it is also a relatively loose criterion, that might overestimate the maximum allowable anion–π contact distance. In our previous work,42 we suggested using mutual penetration distance dpenetration > 0 (defined as the footnote of Table 2) as criterion to judge an anion–π contact. However, this is a very restrictive criterion, and it may be used only for strong anion–π interaction. For a relatively weak anion–π interaction, dpenetration is not recommended. For example, the dpenetration in 5@F− and 3@F− are both negative values (listed in Table 2), but the weak anion–π contacts cannot be excluded. Therefore, it is very necessary to establish much more reasonable and reliable geometric criterion, which is suitable for either strong or weak anion–π contact.
Significantly, based on the experience with solid state anion–π interactions, Albrecht and Rissanen et al.56 recently proposed an evaluation criteria by using of the hapticity concept and recommended a definition for anion–π contact as following three points:
(1) The anion has to be located above the π-system. Therefore, any centroid-ring atom–anion angle should not be higher than 90° (+10% of tolerance).
(2) The distance between the anion and the plane of the π-system has to be shorter than ∑vdW + 0.4 Å.
(3) The hapticity of the anion–π interactions is given by the number of contacts to ring atoms which are <∑vdW + 0.4 Å.
However, the criterion proposed by Albrecht and Rissanen et al.56 is also restrictive and maybe reasonable for anion–π interaction involving pentafluorophenyl group as aromatic ring for anion in solid state. For a more common cases on this issue, we propose our opinion and idea in the following discussion.
As has been experimentally evidenced and mentioned above, the anion in the anion–π contact especially for asymmetrically substituted aromatic ring, is not exactly located over the center of the aromatic ring, but displaced with respect to the center of the ring. Therefore, we need two geometric parameters at least to determine an anion–π contact. One is the distance between the anion and the plane of the aromatic ring (dplane), and the other one is α (as defined in Fig. 2). If dplane is very large, the interaction between anion and aromatic ring may not exist. On the other hand, if dplane is small, but the value of α is quite large, the anion–π interaction is also nonexistent. So, how to determine the critical values of dplane and α in an anion–π contact is the key step of establishing the geometric criterion.
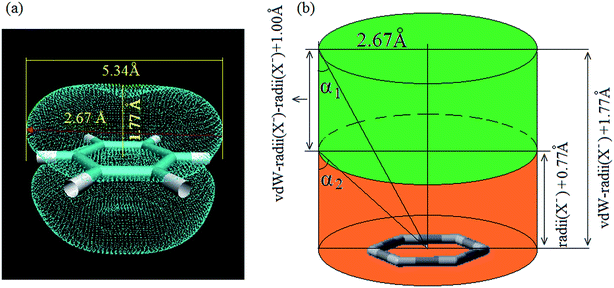
For a noncovalent interaction, the distance of the involved atom pair is smaller than the sum of the van der Waals radii but larger than that of the covalent radii. Base on this principle, it can be approximately considered that the distance between anion and the plane of aromatic ring, dplane, should be smaller than the sum of van der Waals radii of anion and the length from the aromatic center to the van der Waals surface of the aromatic ring along the direction perpendicular to the aromatic plane in an anion–π interaction, and larger than the sum of covalent radii of C (0.77 Å) atom and radii of X− anion, which is only a necessary condition. Simultaneously, α should not be larger than a certain value (the maximum allowable value, which can be defined as critical value of α). This means doff-set should not be larger than its critical value, and the critical value of doff-set should be the maximum distance from the aromatic center to van der Waals surface of the aromatic ring along the direction parallel to the ring. In fact, this distance is a constant which can be determined via calculating van der Waals surface of the aromatic ring involving anion–π interaction. Fig. 3(a) shows the benzene ring's van der Waals surface, which is defined as the π electron density iso-surface with the value of 0.001 a.u. This definition reflects specific electron structure features of a molecule, such as lone pairs, π electrons etc. The total probability (Ω, as described in eqn (1)) of π electron within the region, where electron density is larger than 0.001 a.u., is up to 97%.
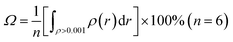 | (1) |
The maximum distance from the center of the aromatic ring to van der Waals surface of the benzene ring is 2.67(5.34/2) Å, suggesting that the critical value of doff-set is 2.67 Å. Furthermore, the length from the center of benzene ring to the van der Waals surface of benzene ring along the direction perpendicular to the benzene plane is 1.77(3.54/2) Å. Based on this result and the intrinsic parameters of anion, such as ionic radii, van der Walls radii, geometry definition of anion–π contact can be plotted as shown in Fig. 3(b), in which green pillar region presents the location of anion in an anion–π interaction. This means that if an anion is not in this region, an anion–π contact could basically be exclude. Thereby, we can give the geometric criterion of an anion–π contact as following three inequalities (eqn (2)–(4)):
| dplane < vdW-radii (X−) + 1.77 Å | (2) |
| doff-set < 2.67 Å | (3) |
| α < α2 | (4) |
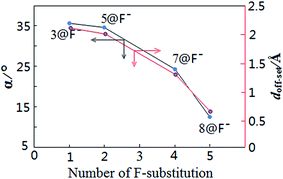
For the present halide-anion systems, we can easily list out the related intrinsic and critical parameters (see Table 3) as defined in Fig. 3(b). Compared with the calculated results listed in Table 2 together with the above criterion (eqn (2)–(4)), the existence of anion–π interaction in each configuration could be approximately evaluated. As seen from Table 2, dplane in the eight complexes are all shorter than 3.48 Å, but the doff-set and α in 1@F−, 2@F−, 4@F− and 6@F−, are larger than 51.81° and 2.67 Å, respectively. Apparently, this does not meet the condition of the geometric criterion proposed above, indicating that anion–π interaction does not exist between F− and the aromatic group. The doff-set and α in 3@F−, 5@F−, 7@F− and 8@F−, are all well agreed with the geometric criterion as eqn (2)–(4) given, suggesting the existence of anion–π contacts between F− and aromatic rings in these complexes. Simultaneously, it is noted that the doff-set and α in 7@F− and 8@F− are much smaller than those in 3@F− and 5@F−, respectively (Fig. 4), indicating that the anion–π interactions in 7@F− and 8@F− are much stronger than those in 3@F− and 5@F−, and much more fluorine substitutions benefit the strength of the anion–π interaction. Additionally, though dpenetration is not recommended for extrapolating the existence or non-existence of anion–π interactions, it may be useful to qualitatively estimate the strength of them. As shown in Fig. 5, for no anion–π contact in 1@F−, 2@F−, 4@F− and 6@F−, the dpenetration are much negative values since there is no anion–π interaction in them, while the dpenetration in strong anion–π interactions (7@F− and 8@F−) are distinctly larger than those in weak anion–π contact (3@F− and 5@F−).
Table 3 shows that the critical value of dplane increases from 3.48 to 4.30 Å, and that of α decreases from 51.81 to 41.96°, with the increasing of the ionic radii of halide anion. The anion–π contacts in the receptor@X− (receptor = 1–8, X = Cl, Br, and I) complexes are not discussed here in detail, but the interactions between X− (X = Cl, Br, and I) and the related aromatic ring can be classified according to the criterion (eqn (2)–(4)) together with the critical values listed in Table 3. The corresponding configuration features (see Table S1–S24†) are similar to those of receptor@F− (receptor = 1–8) systems. It is worth to note that the model shown in Fig. 3 is based on single-atom–anion system, but this kind of treatment and method is effective and portable for explorations on multi-atom complex-anion–π interaction systems as well.
Energy and its decomposition
Binding energy and related data are valid references for evaluating the stability of receptor@X− complexes. Table 4 lists the intermolecular interaction energy (ΔECPint, kcal mol−1) in the optimized geometries of the receptor@X− (receptor = 1–8; X = F, Cl, Br, and I) at B3LYP-D3/6-31+G(D,P) theoretical level, which is the energy difference between the complex and the sum of the individual energies of monomers with the correction of BSSE. It can be seen that the relative orders of the eight receptors binding to F−, Cl−, Br−, and I− are completely same. For the receptor@F−, the ΔECPint are in the range of 84–92 kcal mol−1, which are quite larger than those in receptor@Cl−, receptor@Br− and receptor@I− by about 28, 32 and 37 kcal mol−1, respectively. The relative stability of the four kinds complexes increases in the order receptor@I− < receptor@Br− < receptor@Cl− ≪ receptor@F−, revealing that these receptors exhibit selective binding to F−. However, for a given halide anion, the ΔECPint between any one of the receptors (1–8) and anion are not significantly large, indicating all of the four halide anions not showing the feature of selective binding towards to the eight receptors. The energy (ΔECPint) differences of the eight receptors binding to the same halide anion are not large enough, suggesting that the fluorine substituents do not have obvious substitution effect on the binding energy. This is probably, on one hand, because the energy loss caused by the deform energy of the receptor counteracts the stabilization of the anion–π interaction. On the other hand, the anion–π interaction is much weaker than the double-dentate N–H⋯X− hydrogen bond which plays a leading role in the recognition of anions.| Species | ΔECPint | |||
|---|---|---|---|---|
| X = F | X = Cl | X = Br | X = I | |
| 1@X− | −87.91 | −60.26 | −55.48 | −50.17 |
| 2@X− | −90.32 | −62.47 | −57.66 | −51.95 |
| 3@X− | −84.30 | −57.74 | −53.16 | −48.99 |
| 4@X− | −92.57 | −64.33 | −59.44 | −53.13 |
| 5@X− | −86.55 | −59.93 | −55.31 | −50.87 |
| 6@X− | −93.32 | −65.36 | −60.45 | −56.08 |
| 7@X− | −89.95 | −63.30 | −58.63 | −53.77 |
| 8@X− | −92.14 | −65.29 | −60.42 | −55.25 |
Although anion–π interaction does not significantly effect on the total binding energy and the structures of double-dentate N–H⋯X− (X = F, Cl, Br and I) hydrogen bonds, F-substitution on the aromatic ring is very important to the configuration and the formation of effective anion–π interaction between receptor and halide. Different F-substitution position and substituent number lead to the selectivity of the receptors in the anion–π interaction. In the present systems, anion–π contact may not take place without F-substitution on the aromatic ring. Although the strength of the anion–π interaction is weak as F-substituent occupies the fifth position of the benzene ring, the F-group on this position is crucial to meet the geometric criterion of anion–π contact. Independently on other substitution positions, anion–π would form if the fifth position on the benzene ring is substituted by F group. In addition, it is noted that when the number of F-substituents is not smaller than 4, anion–π contact will exist no matter if there is F-substituent on the fifth position. Nevertheless, when the number of F-substituents is smaller than 4, F-substitution on the fifth position is prerequisite for the existence of anion–π contact. Unexpectedly, independently on halide anion, the total binding energies of receptor 4 and 6 to the four anions are relatively larger than those of others, which probably is attributed to electron effect of F groups on the strength of double-dentate N–H⋯X− hydrogen bond in part.
For further understanding the nature of the interactions between the receptors and halide anions, energy decomposition analysis based on LMO-EDA was performed, and the results are listed in Table 5. The binding energy ΔEb is defined as the sum of deformation energy ΔEd of the receptors and intermolecular interaction energy ΔECPint, and can be further decomposed into electrostatic (EES), exchange (EEX), polarization (EPOL), repulsion (EREP) and dispersion (EDISP) components as shown in eqn (5) based on LMO-EDA method:
| ΔEb = ΔEES + ΔEEX + ΔEPOL + ΔEDISP + ΔEREP | (5) |
| Species | ΔEES | ΔEEX | ΔEPOL | ΔEDISP | ΔEREP | ΔEb |
|---|---|---|---|---|---|---|
| 1@F− | −100.69 | −44.11 | −57.55 | −11.84 | 128.99 | −85.20 |
| 2@F− | −103.43 | −44.10 | −57.23 | −11.12 | 128.60 | −87.58 |
| 3@F− | −97.77 | −44.58 | −59.49 | −11.49 | 131.99 | −81.35 |
| 4@F− | −106.13 | −44.83 | −57.02 | −12.38 | 130.56 | −89.81 |
| 5@F− | −100.19 | −44.68 | −58.85 | −11.71 | 131.90 | −83.54 |
| 6@F− | −106.24 | −44.04 | −56.16 | −12.36 | 128.25 | −90.55 |
| 7@F− | −104.88 | −45.61 | −57.86 | −12.07 | 133.72 | −86.70 |
| 8@F− | −106.95 | −45.28 | −56.99 | −12.21 | 132.66 | −88.78 |
Among them, the contributors EES, EEX, EDISP and EPOL are attractive while the EREP is repulsive. It is quite obvious that the total interaction energy ΔEb has a trend which closely resembles that of the electrostatic energy ΔEES. This leads to the inference that, in the current interactions, the term EES is the dominating contributor rather than EPOL or EEX in stabilizing the complex. The EDISP contribution is the smallest among the four attractive components.
Frontier molecular orbital (FMO) and visualized weak interactions regions
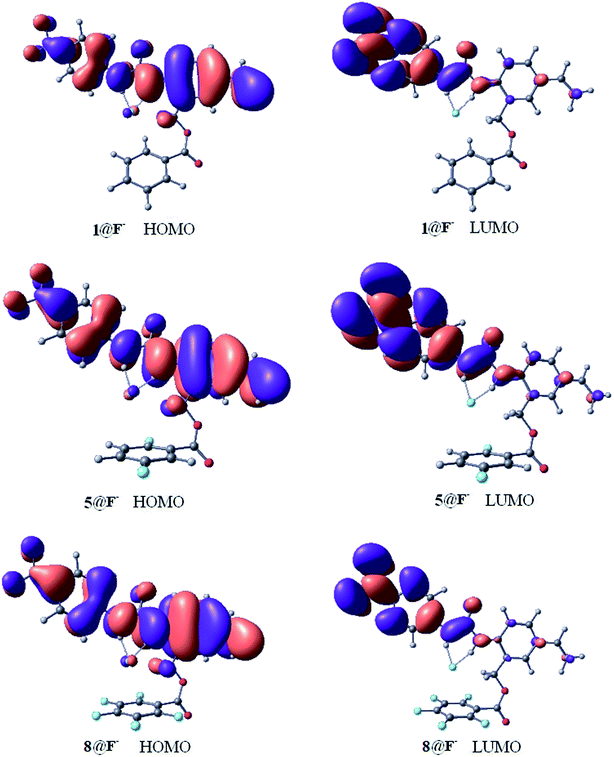
Fig. 6 shows the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the 1@F−, 5@F−, and 8@F− complexes, and the frontier orbital of 2@F−, 3@F−, 4@F−, 6@F−, and 7@F− complexes are presented in Fig. S1 of the ESI.† It is known that molecular orbitals are not able to be observed physically, however, the properties of the frontier orbitals are often closely related to the electron behaviors. Generally speaking, if the frontier orbitals are extended across the two fragments of the complex, charge transfer is suggested. As shown in Fig. 6 and S1,† free from the influence of F-substitutions on the aromatic rings, all the HOMOs of different configurations have similar shapes and distributions, and all the LUMOs are similar as well. Moreover, the HOMOs of the complexes are localized both on the receptor molecules and halide anion, indicating the charge transfers between receptors and halide anions due to the strong hydrogen bond interaction.42 For more completeness, the energy level and gaps of the frontier molecular orbital of receptor@F− (receptor = 1–8) are listed in Table 6. Although F-substitutions on the phenyl ring have significant effect on the gaps, the FMO gaps of the two complexes (7@F− and 8@F−) with the strongest anion–π interaction among the eight complexes, are the largest, indicating that 7@F− and 8@F− are the two most kinetically stable complexes among the receptor@F− systems.| Species | EHOMO/eV | ΔELUMO/eV | EGap/kJ mol−1 |
|---|---|---|---|
| 1@F− | −3.26 | −0.31 | 284.64 |
| 2@F− | −3.33 | −0.36 | 286.46 |
| 3@F− | −3.20 | −0.26 | 283.80 |
| 4@F− | −3.38 | −0.39 | 288.65 |
| 5@F− | −3.26 | −0.30 | 285.98 |
| 6@F− | −3.42 | −0.41 | 289.82 |
| 7@F− | −3.35 | −0.32 | 291.90 |
| 8@F− | −3.39 | −0.35 | 293.13 |
The electrostatic potential (ESP) distributed on molecular van der Waals surface (iso-surface of electron density = 0.001 a.u.) is very meaningful for the understanding the characteristic of noncovalent interactions. Fig. 7 shows the contour maps (upper) of ESP together with van der Waals interfaces (bold blue) and 3D maps of ESP surfaces (lower) of 1@F− and 8@F−. In additional, the contour maps of ESP together with van der Waals interfaces (bold blue) and 3D maps of ESP surfaces of free receptor 1 and 5@F− complex are presented in Fig. S2 in the ESI.† ESP distributions of free 1 and 1@F− are nearly identical to each other, and their van der Waals surfaces are also similar. ESP near anion F− in 5@F− is slightly different compared to those in 1 and 1@F−, but that in 8@F− is obviously deformed owing to the induced-polarization, manifesting some nature of the anion–π interaction.26,34 As has been seen from 3D maps of ESP surface, more fluorine groups on the aromatic ring benefit enhancing the anion–π interaction.
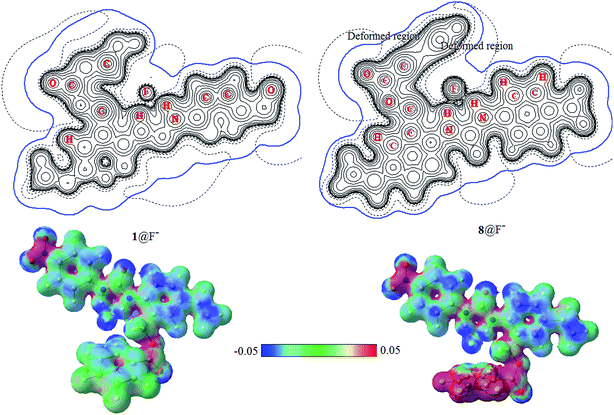 | ||
| Fig. 7 Contour maps (upper) of electrostatic potential and van der Waals interface (bold blue) and 3D maps (lower) of ESP surface of 1@F− and 8@F−. | ||
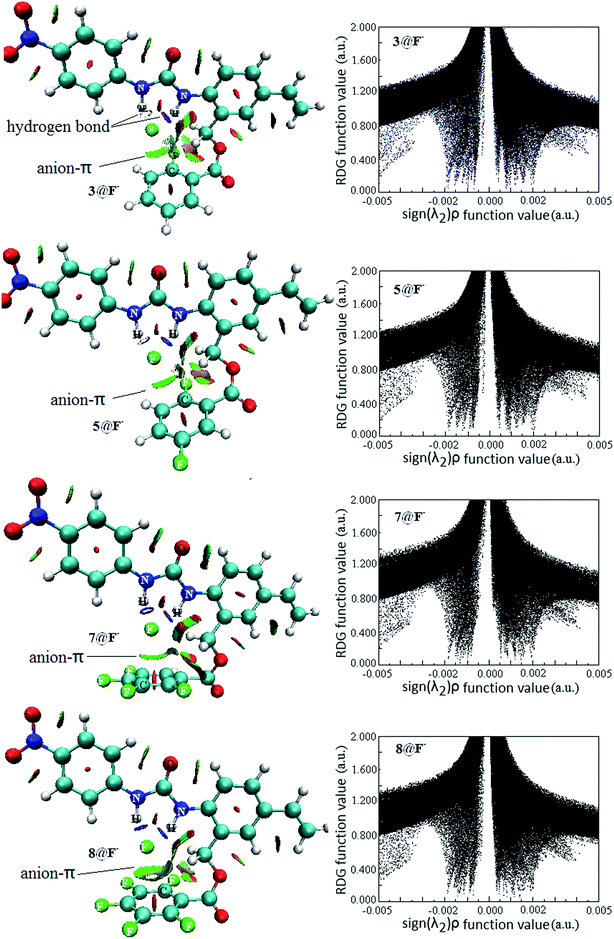
Intermolecular weak interactions can be detected and visualized in real space based on the electron density ρ and its derivatives,51 viz. the reduced density gradient (RDG), coming from the electron density (ρ(r)) and its first derivative (RDG(r) = 1/(2(3π2)1/3)|∇ρ(r)|/ρ(r)4/3), and the second largest eigenvalue (λ2) of Hessian matrix of electron density functions. Fig. 8 shows the visualized weak interaction regions (left) and the scatter graph (right) of reduced density gradient versus the electron density multiplied by the sign of the second Hessian eigenvalue of 3@F−, 5@F−, 7@F− and 8@F−. Those of 1@F−, 2@F−, 4@F− and 6@F− are also plotted in Fig. S2 in the ESI.†
It is clearly shown that the heavy blue disc-shapes between N–H and F− exist in all receptor@F− complexes, suggesting a very strong hydrogen bond interaction. However, they are very different in the anion–π interaction regions. In 3@F−, 5@F−, 7@F− and 8@F−, the dish-shapes regions marked in green accompanied with light-brown between F− and aromatic ring mirror the anion–π noncovalent interaction. However, the corresponding weak interaction regions in 1@F−, 2@F−, 4@F− and 6@F− do not exist anymore (Fig. S3†). Additionally, the anion–π interaction regions in 8@F− and 7@F− are obviously larger than those in 3@F− and 5@F−, implying that the anion–π interactions in former two are relatively stronger, which is well consistent with the geometric feature and criterion discussion. Generally, the RDG spike appearing at higher electron density (more negative function value of sign(λ2)ρ) region corresponds to a stronger hydrogen bond, and the RDG spike appearing at lower electron density near to zero (near zero of function value of sign(λ2)ρ) region corresponds to other weak intermolecular interactions. There is no substantial difference between scatter graphs of 3@F−, 5@F−, 7@F− and 8@F− in the whole range of sign(λ2)ρ function, so does for those of 1@F−, 2@F−, 4@F− and 6@F−. Whereas, by a close comparison, the RDG spikes in the former four complexes appearing at lower electron density are more closer to zero than those in the later four complexes, which probably derived from the contributions of the anion–π interaction in 3@F−, 5@F−, 7@F− and 8@F− complexes.
4. Conclusions
The design and structure–activity relationship of anion receptors represents important advances in the field of supramolecular chemistry. In this paper, the interactions between halide anions and a series N-(4-vinyl-2-benzoic acid benzyl ester)-phenyl-urea containing receptors (1–8) based on hydrogen bond and (or) anion–π contact were investigated via theoretical calculations based on DFT B3LYP-D3/6-31+G(D,P)/MIDIX levels. Especially, the fluorine substitution effects were re-clarified and deeply explored owing to the number and position of fluorine groups on the phenyl ring of the benzoic acid ester, which is significantly effect on the configuration and cooperative property of the hydrogen bond and anion–π interactions, w anion binding energies are not effected obviously. Based on Frontera's research29 on the geometry of the anion–π interaction, we proposed a new geometric criterion of halide-anion–π contact independently of any empirical parameters, as following three inequalities (eqn (2)–(4)):Although the above criterion was established based on single-atom-anion involving system, this kind of treatment and method is effective and portable for explorations on multi-atom complex-anion–π interaction systems as well. Moreover, it is expected that the theoretical exploration from a molecular level in this work should be useful for understanding of aromatic system-based anion–π interactions and benefit the future experimental study.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (21362029 and 21263022), the Youth Science Research Funds of Tianshui Normal University (TSA1507) and the Key Laboratory for New Molecule Materials Design and Function of Gansu Universities. We are indebted to Dr Tian Lu of Beijing Kein Research Center for Nature Science for discussions and Dr Zhi-Feng Li of Tianshui Normal University for help on EDA calculation of the present study.References
- C. Caltagirone and P. A. Gale, Chem. Soc. Rev., 2009, 38, 520–563 RSC.
- Y. Hua and A. H. Flood, Chem. Soc. Rev., 2010, 39, 1262–1271 RSC.
- P. A. Gale, R. Perez-Tomas and R. Quesada, Acc. Chem. Res., 2013, 46, 2801–2813 CrossRef CAS PubMed.
- M. A. Yawer, V. Havel and V. Sindelar, Angew. Chem., Int. Ed., 2015, 54, 276–279 CrossRef CAS PubMed.
- S. H. Jungbauer, S. M. Walter, S. Schindler, L. Rout, F. Kniep and S. M. Huber, Chem. Commun., 2014, 50, 6281–6284 RSC.
- W. He, Y. C. Ge and C. H. Tan, Org. Lett., 2014, 16, 3244–3247 CrossRef CAS PubMed.
- C. J. E. Haynes and P. A. Gale, Chem. Commun., 2011, 47, 8203–8209 RSC.
- J. Mareda and S. Matile, Chem.–Eur. J., 2009, 15, 28–37 CrossRef CAS PubMed.
- R. Kakuchi, S. Nagata, Y. Tago, R. Sakai, I. Otsuka, T. Satoh and T. Kakuchi, Macromolecules, 2009, 42, 1476–1481 CrossRef CAS.
- R. Sakai, S. Okade, E. B. Barasa, R. Kakuchi, M. Ziabka, S. Umeda, K. Tsuda, T. Satoh and T. Kakuchi, Macromolecules, 2010, 43, 7406–7411 CrossRef CAS.
- S. Kubik, Chem. Soc. Rev., 2010, 39, 3648–3663 RSC.
- H. T. Ngo, X. Liu and K. A. Jolliffe, Chem. Soc. Rev., 2012, 41, 4928–4965 RSC.
- A. J. Lowe, B. M. Long and F. M. Pfeffer, J. Org. Chem., 2012, 77, 8507–8517 CrossRef CAS PubMed.
- H. J. Mo, Y. Shen and B. H. Ye, Inorg. Chem., 2012, 51, 7174–7184 CrossRef CAS PubMed.
- A. Rostami and M. S. Taylor, Macromol. Rapid Commun., 2012, 33, 21–34 CrossRef CAS PubMed.
- P. A. Gale, N. Busschaert, C. J. E. Haynes, L. E. Karagiannidis and I. L. Kirby, Chem. Soc. Rev., 2014, 43, 205–241 RSC.
- J. Pang, F. Jiang, D. Yuan, J. Zheng, M. Wu, G. Liu, K. Su and M. Hong, Chem. Sci., 2014, 5, 4163–4166 RSC.
- A. Brugnara, F. Topic, K. Rissanen, A. de la Lande, B. Colasson and O. Reinaud, Chem. Sci., 2014, 5, 3897–3904 RSC.
- P. A. Gale and C. Caltagirone, Chem. Soc. Rev., 2015, 44, 4212–4227 RSC.
- Z. Yuan and F. Liang, Curr. Org. Chem., 2014, 18, 2016–2036 CrossRef CAS.
- B. R. Mullaney, B. E. Partridge and P. D. Beer, Chem.–Eur. J., 2015, 21, 1660–1665 CrossRef CAS PubMed.
- R. Tepper, B. Schulze, M. Jäger, C. Friebe, D. H. Scharf, H. Görls and U. S. Schubert, J. Org. Chem., 2015, 80, 3139–3150 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- S. W. Robinson, C. L. Mustoe, N. G. White, A. Brown, A. L. Thompson, P. Kennepohl and P. D. Beer, J. Am. Chem. Soc., 2015, 137, 499–507 CrossRef CAS PubMed.
- C. R. Wade, A. E. J. Broomsgrove, S. Aldridge and F. P. Gabbai, Chem. Rev., 2010, 110, 3958–3984 CrossRef CAS PubMed.
- B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68–83 RSC.
- M. M. Watt, L. N. Zakharov, M. M. Haley and D. W. Johnson, Angew. Chem., Int. Ed., 2013, 52, 10275–10280 CrossRef CAS PubMed.
- K. Hiraoka, S. Mizuse and S. Yamabe, J. Phys. Chem., 1987, 91, 5294–5297 CrossRef CAS.
- C. Estarellas, A. Bauza, A. Frontera, D. Quinonero and P. M. Deya, Phys. Chem. Chem. Phys., 2011, 13, 5696–5702 RSC.
- S. E. Wheeler and J. W. G. Bloom, Chem. Commun., 2014, 50, 11118–11121 RSC.
- D. X. Wang and M. X. Wang, J. Am. Chem. Soc., 2013, 135, 892–897 CrossRef CAS PubMed.
- T. Lu and S. E. Wheeler, Org. Lett., 2014, 16, 3268–3271 CrossRef CAS PubMed.
- Y. Zhao, C. Beuchat, Y. Domoto, J. Gajewy, A. Wilson, J. Mareda, N. Sakai and S. Matile, J. Am. Chem. Soc., 2014, 136, 2101–2111 CrossRef CAS PubMed.
- M. Giese, M. Albrecht and K. Rissanen, Chem. Rev., 2015, 115, 8867–8895 CAS.
- D. Quinonero, C. Garau, C. Rotger, A. Frontera, P. Ballester, A. Costa and P. M. Deya, Angew. Chem., Int. Ed., 2002, 41, 3389–3392 CrossRef CAS.
- C. Garau, A. Frontera, D. Quinonero, P. Ballester, A. Costa and P. M. Deya, ChemPhysChem, 2003, 4, 1344–1348 CrossRef CAS PubMed.
- B. Notash, N. Safari and H. R. Khavasi, Inorg. Chem., 2010, 49, 11415–11420 CrossRef CAS PubMed.
- B. Notash, N. Safari and H. R. Khavasi, CrystEngComm, 2012, 14, 6788–6796 RSC.
- S. Saha and G. N. Sastry, J. Phys. Chem. B, 2015, 119, 11121–11135 CrossRef CAS PubMed.
- M. G. Chudzinski, C. A. McClary and M. S. Taylor, J. Am. Chem. Soc., 2011, 133, 10559–10567 CrossRef CAS PubMed.
- W. Liu, Q. Q. Wang, Y. Wang, Z. T. Huang and D. X. Wang, RSC Adv., 2014, 4, 9339–9342 RSC.
- Y. Z. Liu, K. Yuan, L. L. Lv, Y. C. Zhu and Z. Yuan, J. Phys. Chem. A, 2015, 119, 5842–5852 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119 CrossRef PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- Y. Zhao and D. G. Truhlar, J. Am. Chem. Soc., 2007, 129, 8440–8442 CrossRef CAS PubMed.
- T. M. Simeon, M. A. Ratner and G. C. Schatz, J. Phys. Chem. A, 2013, 117, 7918–7927 CrossRef CAS PubMed.
- R. E. Easton, D. J. Giesen, A. Welch, C. J. Cramer and D. G. Truhlar, Theor. Chim. Acta, 1996, 93, 281–301 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102–014105 CrossRef PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- M. Giese, M. Albrecht, A. Valkonenb and K. Rissanen, Chem. Sci., 2015, 6, 354–359 RSC.
- http://www.webelements.com/fluorine/contents.html.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra26068j |
| This journal is © The Royal Society of Chemistry 2016 |