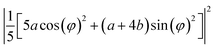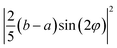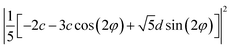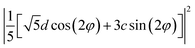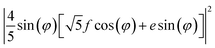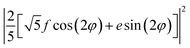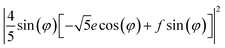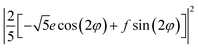Optical phonons in the kesterite Cu₂ZnGeS₄ semiconductor: polarized Raman spectroscopy and first-principle calculations

Abstract

A comprehensive vibrational analysis of the kesterite Cu₂ZnGeS₄ semiconductor (space group I4̄) is reported, which includes experimental in-plane rotation polarized Raman scattering measurements from the (1 0 1)-single crystal facet as well as first principle lattice dynamic calculations. 17 out of the 27 expected vibrational modes of the kesterite structure are unambiguously identified. Raman scattering measurements performed under resonant excitation conditions show a pronounced enhancement of the longitudinal optical components of the polar modes. The appearance of several additional lines in the Raman spectra have been interpreted as being due to the presence of inclusions of Cu₂ZnGeS₄ polymorph with the P4̄2c lattice symmetry, which differs from the kesterite by cation sublattice arrangement.

---

1 Introduction

Fine tuning of the anion ratio in active layers is known to be an effective way to achieve photovoltaic cell efficiency up to 12.6% for Cu₂ZnSn(S_x,Se_1−x)₄ thin film solar cells.¹ An alternative approach for absorber band gap engineering is the cation ratio adjustment. The highest efficiency of 10.1% was achieved by partial substitution of Sn cations with Ge atoms.^2,3 Further development of photovoltaic technologies with improved device efficiency requires a deeper knowledge of the fundamental properties of these active layers. In the case of tin-based Cu₂ZnSnS₄ or Cu₂ZnSnSe₄ quaternary compounds the fundamental studies are already at a relatively high level.^4–8 This contrasts with the Ge-based compounds Cu₂ZnGe(S,Se)₄, that have been only explored a little so far.⁹

It has been known since the early 1970's that the Cu₂ZnGeS₄ (CZGS) semiconductor crystallizes in either the orthorhombic or tetragonal lattice.^10–12 The majority of early publications on CZGS were focused on the analysis of the basic structure and electrical properties. Recently, some optical properties of the orthorhombic^13,14 and tetragonal^{10,12,15–19} CZGS modifications have been reported. Over the past several years there has also been theoretical interest in tetragonal CZGS semiconductor as a representative member of I₂–II–IV–VI₄ (I = Cu, Ag; II = Zn, Cd, Mn, Fe; IV = Si, Ge, Sn; VI = S, Se) quaternary family and its structural,²⁰ electronic^20,21 and optical²² properties were calculated. As far as vibrational properties of the tetragonal CZGS are concerned, they are limited to experimental non-polarized Raman measurements on polycrystalline thin films^17,19 and IR experiments on powder samples.²³ In contrast to the orthorhombic CZGS,²⁴ no theoretical lattice dynamics calculation data for tetragonal (either kesterite or stannite) CZGS are reported.

In this work we present the results of first principle calculations of optical phonons for CZGS semiconductor of kesterite structural modification (space group I4̄). Theoretical predictions of mode frequencies and symmetries are compared with the results of a detail in-plane rotation polarized Raman scattering experiments, that have been performed from the (1 0 1) facets of CZGS single crystal. Experimental identification of the symmetry of dominating Raman modes is achieved via the analysis of scattering selection rules for various polarisation configurations in comparison with those predicted by the group theory. Relative values of relevant Raman tensor elements have been determined for these modes. Further, a comparison of Raman scattering data under non-resonant and resonant excitation conditions is performed, which allows to unambiguously identify several longitudinal optical (LO) modes, that dominate the resonant Raman scattering spectra. Finally, the presence of several additional modes, that were not accounted for within the ideal kesterite structure, are argued to be due to presence of tetragonal CZGS polymorph with the P4̄2c structure, which differs from the kesterite by cation sublattice order.

2 Experimental

Cu₂ZnGeS₄ single crystals were grown by chemical vapor transport. The pure elements of Cu, Zn, Ge and S in the stoichiometric mixture with 5 mg cm⁻³ of iodine were placed in an evacuated quartz tube. The growth process was performed during two weeks in the vertical two zone furnace with evaporation and growth temperatures of about 800 °C and 750 °C, respectively. The subsequent homogenization of the samples was performed at 600 °C during a month.

The chemical composition of single crystals was determined by using X-ray fluorescence. The measurements were performed in 5 points of the selected sample and the average values were close to stoichiometry Cu : Zn : Ge : S = 24.6 : 12.1 : 13.3 : 50.0 (all values in at%) with deviation from point to point of about 0.1 at%.

The crystal orientation of Cu₂ZnGeS₄ single crystals was determined by the rotating XRD method,²⁵ which revealed that the crystal basal plane is (1 0 1) and the long edge of the crystal platelet coincides with the [010] direction. The position of observed peaks in the XRD pattern agrees well with the one registered in the database as ISCD#152752 for Cu₂ZnGeS₄ compound with tetragonal lattice (see ESI†).

Raman spectra were measured in backscattering configuration by a LabRam HR800-UV Horiba Jobin Yvon spectrometer with a CCD detector and excited by solid state laser 785 nm and Ar⁺ laser 514.5 nm, for non-resonant and resonant conditions, respectively. A more detailed description of the experimental set up can be found in ref. 26 and 27.

3 Results and discussions

3.1 Lattice dynamics calculations

The first principle calculations of the electronic ground state of the kesterite structural modification of Cu₂ZnGeS₄ were performed within the generalized gradient approximation using the Perdew–Burke–Ernzerhof local functional²⁸ as implemented in the CASTEP code.²⁹ Norm-conserving pseudopotentials were used. The cutoff energy for the plane wave basis was set to 850 eV. A self-consistent field (SCF) tolerance better than 10⁻⁷ eV per atom and the phonon SCF threshold of 10⁻¹² eV per atom were imposed. Prior to performing calculations the structure was relaxed while keeping lattice parameters fixed and equal to the experimentally determined ones, so that forces on atoms in the equilibrium position did not exceed ∼1 meV A⁻¹ and the residual stress was below 0.01 GPa. An integration over the Brillouin zone was performed over a 3 × 3 × 3 Monkhorst–Pack grid³⁰ in reciprocal space of the primitive unit cell. The material clearly showed semiconducting behaviour with the direct band gap situated at the center of the Brillouin zone. Lattice dynamics of Cu₂ZnGeS₄ was further calculated within the density functional perturbation theory (linear response scheme),³¹ which allows to obtain not only transverse optical (TO), but also longitudinal (LO) mode frequencies. As it was recently shown for several quaternary semiconductors, Cu₂CdGeS₄ and Cu₂CdSiS₄, e.g. ref. 32, the results of similar calculations agree very well with experimental data on mode frequencies.

Here we would like to mention several important points. The results of earlier reported total energy first-principle calculations predicted the kesterite structural modification of Cu₂ZnGeS₄ to be the ground state of the material, closely followed by other phases of wurtz-kesterite, stannite, and wurtz-stannite,³³ whose energies are higher by 3.7, 11.9, and 12.6 meV per atom, respectively. Experimentally both tetragonal kesterite and orthorhombic wurtz-stannite phases have been reported.^24,34,35

Our non-spin-polarized total energy calculations showed, however, that the orthorhombic wurtz-stannite structural modifications of Cu₂ZnGeS₄ has slightly lower energy in comparison with the kesterite (by only 1.8 meV per atom). Despite of this fact it was possible to perform precise lattice optimization with the parameters mentioned above. We noticed, however, that due to a weaker convergence of the self-consistent field calculations for kesterite, more dense integrations grid over the Brillouin zone was required to perform the phonon calculations. Moreover, the system revealed some kind of “dynamic instability” and showed one or two modes with slightly negative mode frequencies at the Brillouin zone center. However, this fact did not affect optical mode frequencies above 80 cm⁻¹, which will be discussed further on.

3.2 Modes symmetry assignment

At the center of the Brillouin zone the group theory yields the following irreducible representation of the vibrational modes for CZGS kesterite type structure (I4̄-space group):

Γ = 3A ⊕ 7B ⊕ 7E, (1)

where 3A ⊕ 6B ⊕ 6E modes are Raman active and 6B ⊕ 6E modes are simultaneously IR-active and exhibit LO-TO splitting, while the remaining B ⊕ E modes are acoustic. Here E modes are doubly degenerated.

In polarization dependent Raman scattering measurements the intensity of a vibrational mode, I, depends on the polarizations of the incident (v_i) and scattered light (v_s) via the Raman tensor for the crystal plane on which measurements are performed³⁶

I ∝ |v_i[scr R, script letter R]_XYZv_s|², (2)

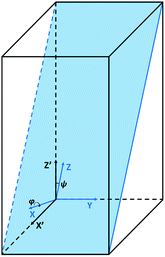
where [scr R, script letter R]_XYZ is the corresponding Raman tensor of the vibrational mode. In this work we chose the following laboratory system (X Y Z) associated with (1 0 1) facet, where X, Y and Z lie along the [401], [010] and [1̄01] crystallographic directions, respectively. This (1 0 1) crystal plane, drawn in Fig. 1, could be obtained from transformation of (1 0 0) plane after clockwise rotation of around the Y direction by an angle ψ = arcsin[a_l/(a_l² + c_l²)] ≈ 27°, where a_l and c_l are CZGS lattice parameters.¹¹ The Raman tensors for (1 0 1) plane were calculated using Euler's rotation matrix and the Raman tensors for kesterite³⁶ in the (X′ Y′ Z′) principle tetragonal coordinate system (X′ = [100], Y′ = [010] and Z′ = [001]). Finally, formulae of angular dependence of Raman modes intensities for (1 0 1) plane obtained within eqn (2) are presented in Table 1. Note, that in our experiment the direction of propagation of the polarized scattered laser radiation is parallel to X, while in-plane angle φ = 0(90)° corresponds to the case of the laser polarization parallel to Y(Z), respectively. In addition, Raman scattering intensities for particular polarization geometries (using Porto notations)³⁷ are specified in Table 1, which allow us to assign the observed peaks to different symmetry modes.

Fig. 1 Tetragonal crystal lattice with marked (1 0 1) basal plane. (X′ Y′ Z′) principle coordinate system, (X Y Z) laboratory coordinate system after clockwise rotation around the Y axis by an angle ψ. Here the Y′ axis coincides with the Y axis.

Table 1 Angular dependence of Raman mode intensities for kesterite type structures in case of (1 0 1) crystal plane (upper part of the table) and intensity values for the selected geometries (lower part of the table)

Mode	‖	⊥
A
B(Z)
E(X)
E(Y)

---

Mode	〈X̄|YY|X〉	〈X̄|ZZ|X〉	〈X̄|YZ|X〉
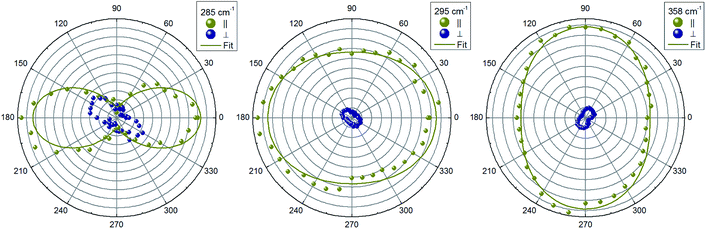
A	a^2	((a + 4b)/5)^2	0
B(Z)	c^2	c^2/25	d^2/5
0.5 × E(X) + 0.5 × E(Y)	0	(8/25) (f^2 + e^2)	(10/25) (f^2+e^2)

---

It should be noted that eqn (2) is, in general, valid for isotropic system. The analyzed tetragonal CZGS lattice is in fact uniaxial and thus is expected to exhibit some anisotropy effects. Following ref. 38 and 39, the anisotropy is related to the existence of the ordinary and extraordinary refractive indices, that could affect polarization properties of the incident and scattered radiation and, therefore Raman modes intensities for a certain experimental polarization geometry. In our case, however, we did not register any noticeable experimental data deviations from equations in Table 1 for both non-polar and polar modes. Thus, the phase shift angle between ordinary and extraordinary rays turns out not to exceed several degrees. Such a small value of phase angle shift could be related to either a small effective probing depth due to confocal arrangement of optical system or to a small difference of refractive indices for ordinary and extraordinary rays at the 785 nm laser wavelength.

The Raman spectra measured in 〈X̄|YY|X〉, 〈X̄|ZZ|X〉 and 〈X̄|YZ|X〉 polarization configurations with 785 nm excitation wavelength are plotted in Fig. 2(a). The intensity of 285, 295, and 358 cm⁻¹ peaks strongly decreases in the crossed-polarized spectrum 〈X̄|YZ|X〉 in comparison with 〈X̄|YY|X〉. Following the scattering selection rules of Table 1, the three peaks in question could unambiguously be attributed to the A-symmetry modes. It should be noted that the relative position of two closely lying lower frequency A modes (285 and 295 cm⁻¹), which are somewhat separated from the higher frequency dominant A mode at 358 cm⁻¹, resembles well the observed position of A modes in spectra of kesterite Cu₂ZnSnS₄,⁴⁰ Cu₂ZnSnSe₄, and Cu₂ZnGeSe₄ (ref. 27) compounds.

Fig. 2 (a) – Polarized Raman spectra of Cu₂ZnGeS₄ measured in different scattering configurations. Letters A, B, and E denote the peaks symmetry. The mode at 332 cm⁻¹ will be further discussed in the text. (b–d) – Unpolarized Raman spectra of Cu₂ZnGeS₄ measured under non-resonant (b) and resonant conditions at 300 K (c) and 80 K (d) from the (1 0 1) plane. Position of the most intense peaks is indicated.

The E symmetry peaks are assigned with those having vanishing intensity in the 〈X̄|YY|X〉 scattering configuration and, at the same time, comparable intensity in the 〈X̄|ZZ|X〉 and 〈X̄|YZ|X〉 configurations, in accordance with their selection rules (Table 1). The assignment of peaks to the B symmetry is more complicated as their intensity depends on the actual values of c and d Raman tensor elements. Although one can expect a reduction of the intensity for 〈X̄|ZZ|X〉 in comparison to 〈X̄|YY|X〉 case, we found that 〈X̄|YZ|X〉 cross geometry is a better marker for the B modes determination as they possess the highest intensity in this scattering geometry. This behavior has been attributed to a much large value of the d Raman tensor element in relation to that of c, so that d ≫ c. In fact, this has also been found from the analysis of spectra measured at different in-plane angles for both parallel and cross configurations, as will be shown below. Notably, a relatively strong peak at 332 cm⁻¹ behaves as an A symmetry mode, and its possible origin will be discussed later on. All observed peaks with their experimentally determined symmetries are summarized in Table 2.

Table 2 Experimental zone center phonon frequencies of kesterite Cu₂ZnGeS₄. The peak symmetry assignment is based on the polarization Raman mode behavior. Peaks in italic were obtained from RR spectra and their symmetry is proposed based on DFT calculation results. The ratio of Raman tensor elements was obtained from the angular dependence of line intensity

A	a/b		B (TO/LO)	c/d		E (TO/LO)	e/f
	‖	⊥^a		‖	⊥		‖	⊥
a The ratio of Raman tensor elements could not be calculated in this geometry as Raman scattering intensity is directly proportional to these tensor elements (see Table 1).
285	4.88 ± 0.71	—	—	—	—	72	—	—
295	1.19 ± 0.03	—	—	—	—	112	0.88 ± 0.03	0.84 ± 0.05
358	0.81 ± 0.01	—	—	—	—	152/158	0.84 ± 0.03/0.85 ± 0.04	0.94 ± 0.04/0.72 ± 0.05
			261	<0.1	0.14 ± 0.14	272	0.85 ± 0.05	1.03 ± 0.07
			337/353	—	—	309/317	—	—
			383/409	<0.1/<0.1	<0.1/—	378/400	0.83 ± 0.06/0.76 ± 0.05	0.92 ± 0.06/1.36 ± 0.06

---

In Table 3 the DFT-calculated mode frequencies of kesterite type Cu₂ZnGeS₄ are listed.⁴¹ As far as the A-symmetry modes are concerned, there is an excellent agreement between the experimental and the calculated position of the highest energy mode (358 and 359 cm⁻¹, respectively). The two other A modes are predicted to be higher in energy when compared with those observed experimentally. This discrepancy has been argued to be related to possible resonant interaction of these modes with closely situated two-phonon excitations of the same symmetry.⁴¹

Table 3 DFT-calculated optical mode frequencies of kesterite Cu₂ZnGeS₄ (space group I4̄)⁴¹

A	B(TO/LO)	E(TO/LO)
305	50/50	63/71
309	64/65	83/93
359	172/177	177/180
	275/288	293/294
	355/359	318/320
	377/395	374/375

---

For several other modes (e.g. 112, 261 cm⁻¹), which possess B- and E-symmetry type of behavior, there are no calculated counterparts in Table 3. Possible origin of these modes will be discussed further on.

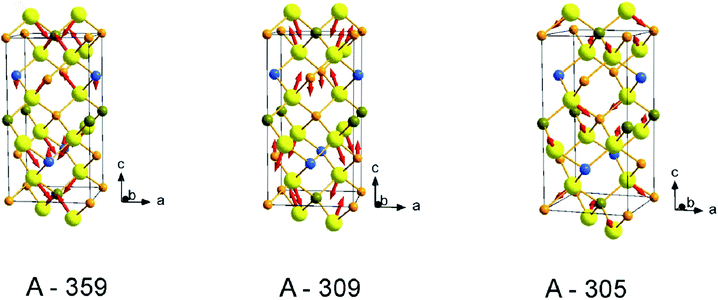
Next, we will analyze the angular dependence of the Raman modes intensities. Raman spectra were measured at different rotation angles φ in cross and parallel geometries and were decomposed into Lorentzian peaks. Typical patterns for different mode symmetries are presented in polar coordinate system (Fig. 3 and 4). Elliptical shape patterns are observed for two dominant A modes. A two-petal shape is established for the lowest frequency A mode in parallel scattering geometry (Fig. 3). For the B symmetry modes, four-petals shapes are seen in cross and parallel geometries. On the other hand, for E symmetry a two-petal pattern is found in parallel and a four-petal one is observed for cross scattering geometry, respectively.

Fig. 3 Angular dependence of intensity of Raman peaks with A symmetry. Solid lines are fitting to corresponding equations from Table 1 for parallel configuration.

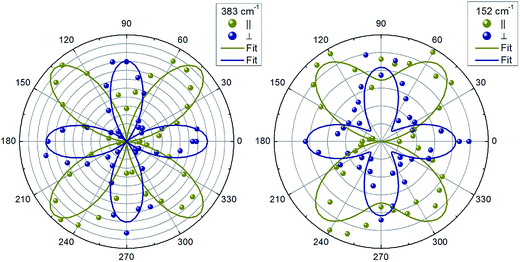Fig. 4 Examples of the angular dependencies of intensity of Raman peaks with B (peak at 383 cm⁻¹) and E (peak at 152 cm⁻¹) symmetries. Solid lines are fitting to corresponding equations from Table 1 for parallel and cross configurations.

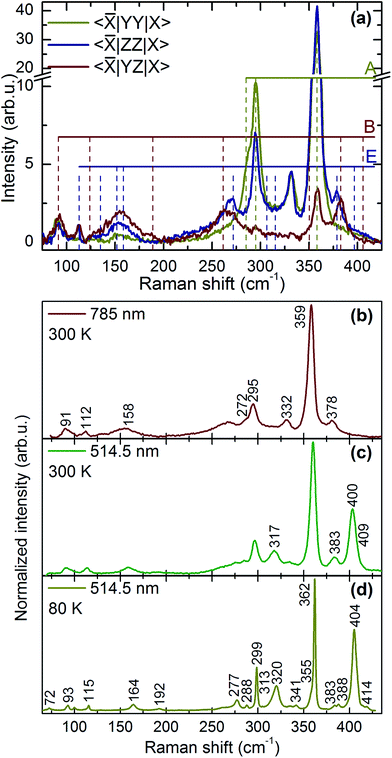
In order to estimate the ratio of the Raman tensor elements, a fitting procedure of the intensity of the modes as function of the in-plane angle φ according to the expressions listed in Table 1 was performed and fitting results are summarized in Table 2. For the most intense A symmetry modes at 295 cm⁻¹ and 358 cm⁻¹ a/b ≈ 1 are obtained, whereas a/b ≈ 4.9 is estimated for the less intense mode at 285 cm⁻¹. It is instructive in this respect to analyze the vibrational pattern of these modes in an attempt to find out the reason for the observed Raman scattering tensor element variations. Calculated vibrational pattern for the three A-symmetry modes are shown in Fig. 5. It is obvious that the highest energy mode corresponds to the “breathing” of sulfur atoms around Ge, i.e. stretching of Ge–S bonds. The mode at 309 cm⁻¹ is due to symmetric bending of Ge–S bonds. The lowest frequency A symmetry mode at 305 cm⁻¹, however, is predominantly related to the rotational motion along the c-axis of Ge–S tetrahedra, and also involves some Ge–S bond bending. The difference of vibrational pattern for various A-symmetry modes is probably responsible for the observed variation of corresponding tensor elements values.

Fig. 5 Calculated atomic displacement for the three fully symmetric A modes of kesterite Cu₂ZnGeS₄. Mode frequencies are listed under each picture. Here the yellow spheres are S, orange – Cu, blue – Zn and dark yellow – Ge.

Note, that for other kesterite type quaternary compounds a/b ≈ 1 has been also reported.^27,40 In case of B and E symmetry modes we found a strong anisotropy of c and d elements (c/d < 0.1) and, at the same time, a small anisotropy for e and f elements (e/f ≈ 0.9), in good agreement with what was previously found in Cu₂ZnSnS₄,⁴⁰ Cu₂ZnSnSe₄ and Cu₂ZnGeSe₄ (ref. 27) kesterites.

3.3 Resonant Raman scattering

A comparison of the resonant Raman (RR) scattering spectrum with the non-resonant one of the CZGS single crystal is presented in Fig. 2(b–d). An enhancement of the intensity of some modes in the RR spectra is clearly seen, especially in the high frequency range above the dominant A mode. As it follows from calculations, it is indeed the range where polar modes possess the largest TO-LO splitting. It is known that, for the polar modes, the Fröhlich electron–phonon interaction determines an increase of the relative intensity of the LO components in the RR spectra with respect to that of TO modes.⁴² This has been observed for many crystals, in particular for polar A^IIB^VI compounds,^43,44 as well as for orthorhombic quaternary chalcogenides.^24,26,41 In the case of Cu₂ZnGeS₄, this effect is most pronounced for the modes at 317, 383, 400, 409 cm⁻¹ (room temperature data).

The low temperature Raman spectra measured in resonant conditions showed the shift of all modes to higher wavenumbers and a decrease of the background intensity in the 260–340 cm⁻¹ spectral range, including the peak at 332 cm⁻¹ (Fig. 2(d)). The latter is attributed to a temperature decrease of the intensity of multiphonon excitations with participation of B and E symmetry modes from the 130–170 cm⁻¹ spectral region.⁴¹ As a result, in the low temperature spectra one clearly observes individual peaks at 313, 320, 341 and 355 cm⁻¹. Some of these peaks could reasonably be assigned to the fundamental lattice eigen modes based on their agreement with the results of theoretical calculations (318/320(E), 353/359(B)).

However, there are still lines at 91 and 189 cm⁻¹ (in addition to those mentioned above at 112 and 332 cm⁻¹), which could not be assigned to the vibrations of kesterite. Taking into account the fact that several polymorphs of Cu₂ZnGeS₄ could be realized in the structure, one might reasonably assume the presence of other related phases in the crystal along with the kesterite, for example the one with space group P4̄2c. Indeed, according to ref. 45 in the case of the Cu₂ZnSnS₄ compound this polymorph exhibits the closest formation energy to that of the kesterite type modification. Moreover, this polymorph has the same chemical composition, but differs from the true (ideal) kesterite by the Zn/Cu ordering within the z = 1/4 plane of the unit cell.⁴⁶ Such simple Cu/Zn exchange of atoms within the z = 1/4 unit cell plane removes the unit cell centering and, as a result, doubles the primitive cell volume and, correspondingly, the number of fundamental vibrational modes.

The DFT-calculated mode frequencies for the crystalline polymorph with space group P4̄2c are listed in Table 4. Following the above assumption, it is rather natural to explain the origin of peaks at 91 and 189 cm⁻¹ as corresponding to E symmetry modes of the proposed structure. Wherein, two of the A₁ symmetry modes, which are expected to be the most intense in the spectra, are probably overlapping with the already strong A symmetry peaks of kesterite type polymorph; but the one calculated at 335 cm⁻¹ is the one which is apparently observed in the experimental spectra of Fig. 2(a) at 332 cm⁻¹. As far as other modes, especially in the range 260–340 cm⁻¹, their overlap could not be excluded with vibrational bands of dominant kesterite type phase.

Table 4 Calculated transverse optical mode frequencies of Cu₂ZnGeS₄ with P4̄2c lattice symmetry. A₂ modes are silent

A1	A2	B1	B2	E
308	101	103	81	72
335	153	150	114	78
359	314	287	207	87
	352	306	281	91
	367	406	331	115
			384	190
				200
				292
				298
				317
				326
				380
				385

---

4 Conclusions

Polarized Raman scattering investigations performed on kesterite Cu₂ZnGeS₄ single crystals have allowed to experimentally determine the symmetry of 17 from the 27 modes expected in this crystalline structure according to group theory analysis. By examination of the polarization dependence of the Raman active modes, the ratios of the main Raman tensor elements have been established. For the two dominant non-polar A-symmetry modes at 295 and 358 cm⁻¹ the a/b ratio is found to be close to one, while for the lowest frequency A mode at 285 cm⁻¹ this ratio is around 5. This has been attributed to the different underlying vibrational patterns of the S-atoms contributing to those modes. As for the case of polar modes: B modes exhibit a noticeable difference in c and d elements, whereas E modes show no significant difference of e and f elements. Under resonant conditions a pronounced enhancement of polar E- and B-mode intensities was observed in the high frequency range. Several additional modes in the spectra, which could not be accounted for within the ideal kesterite structure have been related to the presence of inclusions of other Cu₂ZnGeS₄ polymorphs, as the one within the space group P4̄2c.

Acknowledgements

The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union's Seventh Framework Programme FP7/2007–2013/under REA Grant agreement no. 269167 (PVICOKEST) and the Spanish MINECO (Ministerio de Economía y Competitividad de España) under the SUNBEAM project (Ref. ENE2013-49136-C4-1 R). Authors from the Institute of Applied Physics appreciate the financial supports from STCU 5985 and from the Institutional Project CSSDT 15.817.02.04A. The research was also partially supported by European Regional Development Funds (ERDF, FEDER Programa Competitivitat de Catalunya 2007–2013) and the State of Texas though TcSUH. Authors from IREC and the University of Barcelona belong to the M-2E (Electronic Materials for Energy) Consolidated Research Group and the XaRMAE Network of Excellence on Materials for Energy of the “Generalitat de Catalunya”.

References

1. W. Wang, M. T. Winkler, O. Gunawan, T. Gokmen, T. K. Todorov, Y. Zhu and D. B. Mitzi, Adv. Energy Mater., 2014, 4, 1301465.
2. C. J. Hages, S. Levcenco, C. K. Miskin, J. H. Alsmeier, D. Abou-Ras, R. G. Wilks, M. Bär, T. Unold and R. Agrawal, Progress in Photovoltaics: Research and Applications, 2015, 23, 376.
3. S. Giraldo, M. Neuschitzer, T. Thersleff, S. López-Marino, Y. Sánchez, H. Xie, M. Colina, M. Placidi, P. Pistor, V. Izquierdo-Roca, K. Leifer, A. Pérez-Rodríguez and E. Saucedo, Adv. Energy Mater., 2015, 5, 1501070.
4. S. Siebentritt and S. Schorr, Progress in Photovoltaics: Research and Applications, 2012, 20, 512.
5. S. Chen, A. Walsh, X. G. Gong and S. H. Wei, Adv. Mater., 2013, 25, 1522.
6. D. Han, Y. Y. Sun, J. Bang, Y. Y. Zhang, H. B. Sun, X. B. Li and S. B. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155206.
7. S. Chen, J. H. Yang, X. G. Gong, A. Walsh and S. H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245204.
8. K. Ito, Copper Zinc Tin Sulfide-Based Thin Film Solar Cells, John Willey & Sons Ltd., West Sussex, 2015.
9. S. Adachi, Earth-abundant materials for solar cells Cu₂–II–VI–VI₄ semiconductors, John Willey & Sons Ltd., West Sussex, 2015; O. Y. Khyzhun, V. L. Bekenev, V. A. Ocheretova, A. O. Fedorchuk and O. V. Parasyuk, Phys. B, 2015, 461, 75; S. G. Choi, J.-S. Park, A. L. Donohue, S. T. Christensen, B. To, C. Beall, S.-H. Wei and I. L. Repins, Phys. Rev. Appl., 2015, 4, 054006; A. P. Litvinchuk, Phys. Status Solidi B, 2016, 253 DOI:10.1002/pssb.201552415.
10. K. Doverspike, K. Dwight and A. Wold, Chem. Mater., 1990, 2, 194.
11. O. V. Parasyuk, L. V. Piskach, Y. E. Romanyuk, I. D. Olekseyuk, V. I. Zaremba and V. I. Pekhnyo, J. Alloys Compd., 2005, 397, 85.
12. Y. Li, W. Ling, Q. Han and W. Shi, RSC Adv., 2014, 4, 55016.
13. S. Levcenco, D. Dumcenco, Y. S. Huang, K. K. Tiong and C. H. Du, Opt. Mater., 2011, 34, 183.
14. S. Levcenko, M. Guc, C. Merschjann, G. Gurieva, S. Schorr, M. Lux-Steiner and E. Arushanov, Phys. Status Solidi C, 2013, 10, 1079.
15. M. León, S. Levcenko, R. Serna, G. Gurieva, A. Nateprov, J. M. Merino, E. J. Friedrich, U. Fillat, S. Schorr and E. Arushanov, J. Appl. Phys., 2010, 108, 093502.
16. W. G. Zeier, C. P. Heinrich, T. Day, C. Panithipongwut, G. Kieslich, G. Brunklaus, G. J. Snyder and W. Tremel, J. Mater. Chem. A, 2014, 2, 1790.
17. D. B. Khadka and J. H. Kim, J. Phys. Chem. C, 2015, 119, 1706.
18. R. Caballero, J. M. Cano-Torres, E. Garcia-Llamas, X. Fontané, A. Pérez-Rodríguez, D. Greiner, C. A. Kaufmann, J. M. Merino, I. Victorov, G. Baraldi, M. Valakh, I. Bodnar, V. Izquierdo-Roca and M. León, Sol. Energy Mater. Sol. Cells, 2015, 139, 1.
19. J. Chen, W. Li, C. Yan, S. Huang and X. Hao, J. Alloys Compd., 2015, 621, 154.
20. S. Chen, X. G. Gong, A. Walsh and S. H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165211.
21. Y. Zhang, X. Sun, P. Zhang, X. Yuan, F. Huang and W. Zhang, J. Appl. Phys., 2012, 111, 063709.
22. S. Korbel, D. Kammerlander, R. Sarmiento-Perez, C. Attaccalite, M. A. L. Marques and S. Botti, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 075134.
23. M. Himmrich and H. Haeuseler, Spectrochim. Acta, Part A, 1991, 47, 933.
24. M. Guc, A. P. Litvinchuk, S. Levcenko, V. Izquierdo-Roca, X. Fontané, M. Ya. Valakh, E. Arushanov and A. Pérez-Rodríguez, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205205.
25. Z. Guo, L. Jin, F. Li and Y. Bai, J. Phys. D: Appl. Phys., 2009, 42, 012001.
26. M. Guc, S. Levcenko, V. Izquierdo-Roca, X. Fontane, M. Ya. Valakh, E. Arushanov and A. Pérez-Rodríguez, J. Appl. Phys., 2013, 114, 173507.
27. M. Guc, S. Levcenko, V. Izquierdo-Roca, X. Fontane, E. Arushanov and A. Pérez-Rodríguez, J. Appl. Phys., 2013, 114, 193514.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
29. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Z. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
31. K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114.
32. A. P. Litvinchuk, V. M. Dzhagan, V. O. Yukhymchuk, M. Ya. Valakh, I. S. Babichuk, O. V. Parasyuk, L. V. Piskach, O. D. Gordan and D. R. T. Zahn, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 165201.
33. S. Chen, A. Walsh, Y. Luo, J. H. Yang, X. G. Gong and S. H. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195203.
34. D. M. Schleich and A. Wold, Mater. Res. Bull., 1977, 12, 111.
35. A. F. Moodie and H. J. Whiteld, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 236.
36. R. Loudon, J. Phys., 1965, 26, 677.
37. S. P. S. Porto and R. S. Krishnan, J. Chem. Phys., 1967, 47, 1009.
38. P. Alonso-Gutiérrez, M. L. Sanjuán and M. C. Morón, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 085205.
39. P. Alonso-Gutiérrez and M. L. Sanjuán, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045212.
40. M. Guc, S. Levcenko, I. V. Bodnar, V. Izquierdo-Roca, X. Fontane, L. V. Volkova, E. Arushanov and A. Pérez-Rodríguez, Sci. Rep., 2016, 5, 19414.
41. M. Ya. Valakh, A. P. Litvinchuk, V. M. Dzhagan, V. O. Yukhymchuk, A. M. Yaremko, Yu. A. Romanyuk, M. Guc, I. V. Bodnar, A. Perez-Rodriguez and D. R. T. Zahn, J. Phys.: Condens. Matter, 2016, 28, 065401.
42. P. Y. Yu and M. Cardona, Fundamentals of Semiconductors, Springer, Berlin, 3rd edn, 2002.
43. M. Ya. Valakh and A. P. Litvinchuk, Fiz. Tverd. Tela, 1985, 27, 1958.
44. M. Ya. Valakh, A. P. Litvinchuk, G. S. Pekar and G. N. Polisskii, Phys. Status Solidi B, 1981, 104, 743.
45. J. Paier, R. Asahi, A. Nagoya and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115126.
46. S. Schorr, Sol. Energy Mater. Sol. Cells, 2011, 95, 1482.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra26844c

---