Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Geometry-based control of instability patterns in cellular soft matter†
Shahram
Janbaz
*a,
Harrie
Weinans
ab and
Amir A.
Zadpoor
a
aDepartment of Biomechanical Engineering, Faculty of Mechanical, Maritime, and Materials Engineering, Delft University of Technology (TU Delft), Mekelweg 2, 2628 CD, Delft, The Netherlands. E-mail: s.janbaz@tudelft.nl; Tel: +31-15-2783133
bDepartment of Orthopedics and Department of Rheumatology, UMC Utrecht, Heidelberglaan100, 3584CX Utrecht, The Netherlands
First published on 9th February 2016
Abstract
Recent research has shown the potential of rationally designed geometrical features for controlling the functionality of advanced materials. Of particular recent interest has been the use of geometry for controlling the buckling behaviour of soft materials under compression. However, the effects of geometry may be mixed with those of the mechanical properties. In this paper, we present a specific class of 2D cellular soft matter for which the geometry, independent from the mechanical properties of the bulk material, activates the instability pathways of the material, thereby controlling the instability threshold and the instability mode (instability pattern). The geometrical parameters include those characterizing the shape of the voids and the porosity of the cellular solid. A critical strain that solely depends on the geometry controls the transition to instability. Depending on the above-mentioned geometrical parameters, the onset of instability is followed by either symmetric compaction or side buckling. We provide instability maps that relate the geometrical parameters to the critical strain and the instability mode of the presented cellular soft material. These open up the possibility of using geometry for programming the functionalities of materials.
The relationship between geometry and functional properties of (soft) materials has recently received increasing attention. For example, magnificent mechanical and physical properties of natural materials such as iridescent and lightweight structures may be achieved via a certain arrangement of the microstructures forming a cellular solid.1–3 Using similar principles, some creatures disguise themselves by switching their structural color in response to environmental factors.1,4 A major theme within this line of research is the rational geometrical design of materials so as enable them to exhibit desired and occasionally unprecedented properties and functionalities.
An important example, which defines the context for the current study, is the case of soft cellular solids that exhibit sudden transformation in their original structural patterns under compression, when a certain loading threshold is reached.5,6 The geometry of pores and mechanical properties of the materials can regulate buckling instability in this kind of periodic structures so as to make them show specific behaviors in response to diverse stimuli.7–10 For example, soft cellular solid composed of an array of repetitive unit cells may display reversible and repeatable pattern switching.6,7,11–13 This type of behavior could be used for a variety of applications where artificial responsive materials change their configuration in response to diverse stimuli such as loads, moisture, etc.9,14,15 Equipped with cellular configuration, activated structures can exhibit shape shifting that could be of tremendous value in soft robotics and smart bodies.16,17 Moreover, cellular configuration of materials in combination with optimization techniques opens an avenue towards design of optimal materials.18–21 Notably, Bertoldi and co-workers have extensively explored 2D periodic cellular materials.5,7,8,12,13,22–25
In this paper, we use both experimental and computational approaches to study how n-fold symmetric voids, a square array of soft hyperelastic porous unit cells, control the critical strain of 2D soft periodic structures under compression, where n (the number of folds) is an even number. The pore shapes considered here conform to a modified version of an analytical angular function that was originally used to formulate the shape evolutions caused by deposition of graphene monolayers on Cu foils.26 That original function was modified and re-written as a polar vector (V) to generate n-fold symmetric shapes:
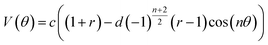 | (1) |
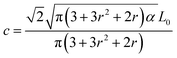 | (2) |
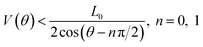 to maintain the integrity of the unit cells.
to maintain the integrity of the unit cells.
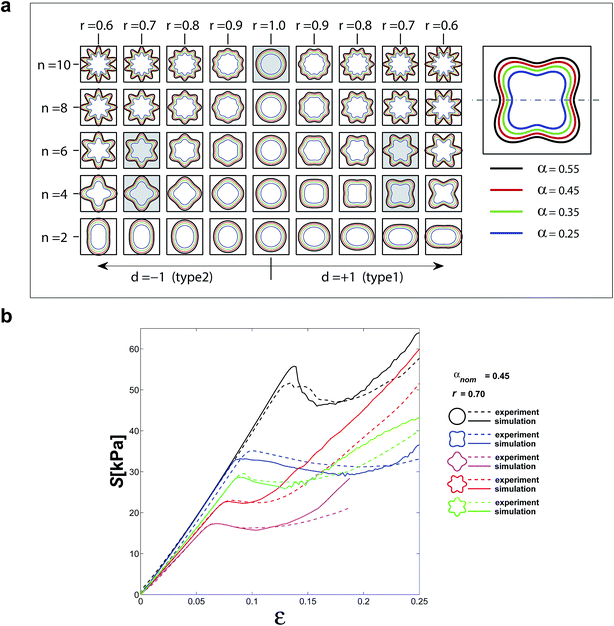
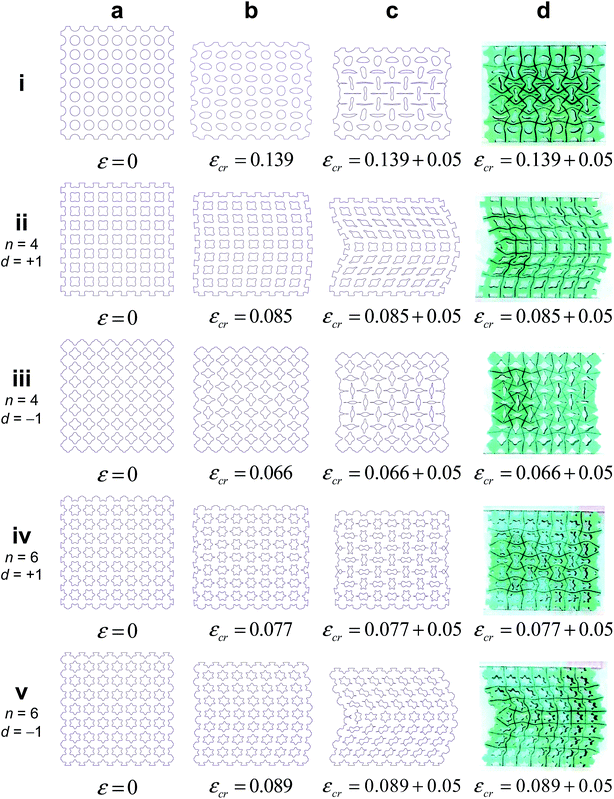
All geometries depicted in Fig. 1a were included in our computational study. The geometries were chosen so as to preserve the integrity of the structure while ensuring that the size of voids allows for pattern transition. Five sample structures were chosen for an experimental study to validate our computational findings. In both computational and experimental studies, the specimens comprised arrays of 7 by 7 repeating unit cells with two additional half unit cells on both sides of the specimens (Fig. 2d). This arrangement of unit cells is the minimum size that finite structures need for symmetric pattern transition. The actual dimensions of the pores in the experimental specimens were measured and used for creating the computational models whose results were compared with the experimental observations. That involved offsetting the boundaries of the pores inwards by 250 μm (the approximate deviation of the dimensions of the actual specimens from the designed dimensions).
Specimens were compressed uniaxially in the vertical direction with a deformation rate of 2–10 mm min−1. A digital camera was used to follow the deformation and instability patterns as loading progressed. The height and cross-section area of the structure were respectively used for calculating the nominal strain and nominal stress values.
The incompressible Neo-Hookean material model with a material parameter C10 = 105 kPa was used to describe the mechanical behaviour of the bulk material. An implicit nonlinear finite element solver (abaqus/standard) was used to solve the governing equations of deformation. An explicit nonlinear solver (abaqus/explicit) was used when the contact between the internal sides of the closing pores was taken into account. A mesh convergence study was conducted to select the appropriate mesh density. Based on the convergence study, a maximum seed size equal to 3.5% of the length of the unit cell edges was selected, resulting in 800–1350 elements per unit cell. Triangular quadratic plane strain hybrid elements (CPE6H) were used for the implicit solutions, while the modified type of the same element (CPE6M) was used for explicit analysis. To detect the instability patterns, eigenvalue buckling analysis (subspace technique) was performed. The post-bulking simulations included an initial geometric imperfection equal to 0.01 of the magnitude of the deformation in the first buckling mode of the structure. The finite element simulations were quasi-static. Clamped boundary conditions were used on both sides of the specimens.
There was generally good agreement between the experimentally determined stress–strain curves and the corresponding computational curves except for the very final stages of deformation where the experimental and computational curves started to deviate from each other (Fig. 1b). The predicted instability patterns very well matched the experimentally observed instability patterns for all the structures for which both experimental and computational data were available (Fig. 2).
The stress–strain curves generally showed an initial linear behaviour followed by a stress plateau region where the stress did not substantially increase (Fig. 1b). The stress finally started to increase due to the closing pores and the resulting contact between the internal walls of the pores (Fig. 1b). For every cellular structure, the transition from the linear region to the stress plateau occurred after a specific level of strain that is called the critical strain in the current study (Fig. 1b). We defined the critical strain as the strain for which the maximum stress at the end of the linear region was recorded (Fig. 1b), unless there was no clear stress peak in which case the maximum radius of curvature in the stress–strain curve was used as a criterion for detecting the critical strain. A parametric study showed that the computational results are not over-sensitive to the magnitude of the imperfections and do not drastically change when the imperfection size is perturbed around the chosen values. Once the loading progressed beyond the critical strain, a rapid transformation in the pattern of the cellular structures occurred, which was considered as the hallmark of buckling (Fig. 2). Depending on the geometry of the pores, e.g. the number of folds and the porosity of the cellular structures, two different types of instability patterns were observed, namely side buckling (Fig. 2ii and v) and symmetric compaction (Fig. 2i, iii and iv).
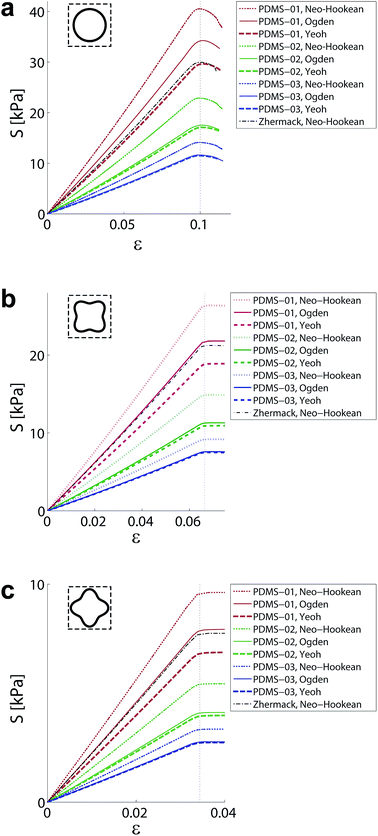
To study the material effect on the critical strain of soft cellular structures, in addition to the material used in our experiments, the mechanical properties of three different types of polydimethylsiloxane (PDMS) elastomers were taken from.27 The difference between the mixing ratio of the base polymer and the curing agent causes a great difference in the mechanical properties of PDMS elastomers. Three different material models Neo-Hookean, Yeoh, and Ogden (order 3) were chosen to evaluate the effect of constitutive equation on the response of the considered structures. The material model constants of PDMS elastomers were obtained by fitting the uniaxial stress–strain curves up to the point where the stress started to increase as a result of bond stretching.‡ This led to closer material properties for all the three models, especially in compression. Three extreme geometries (circular as well as four-fold types 1 and 2, all having porosities of 0.45 and fold sharpness of r = 0.7) were used to study the effects of material properties on the buckling behaviour. All considered cases showed pattern transition at relatively large strains. Numerical results clearly showed that the critical strain remains the same regardless of the material properties (Fig. 3). This independency from material properties held also for the type of instability, i.e. side buckling vs. symmetric compaction. The sole effect of the material properties was shifting the load at which pattern transition occurred (Fig. 3). Microstructures experience both tensile and compressive stresses when the structures are compressed uniaxially.
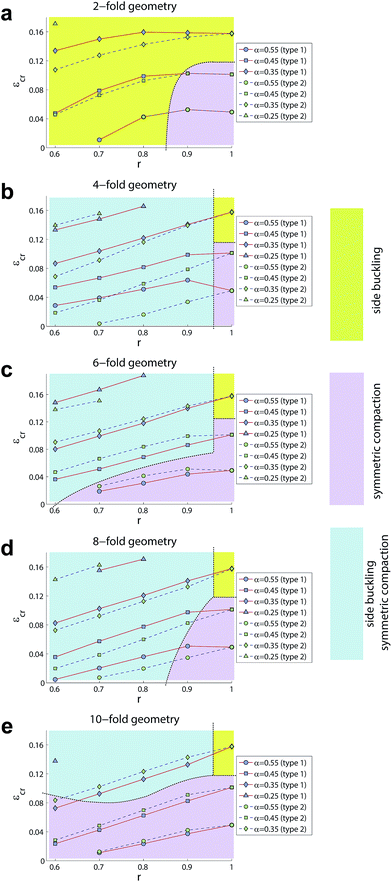
Geometry of pores influences both the pattern instability and critical strain. For the circular pores, the instability pattern was symmetric compaction for larger (i.e. >0.35) porosities and side buckling for smaller (i.e. <0.35) porosities (Fig. 4). For 2-fold structures, the instability pattern was similar to that of the structures with circular pores when r ≈ 1 (Fig. 4). For r ≪ 1, side buckling was the instability pattern of the 2-fold structures (Fig. 4). For n-fold structures (n > 2), three distinct regions could be observed in the maps of the instability patterns (Fig. 4). In the first region (painted yellow in Fig. 4), the instability pattern was side buckling. In the second region (painted magenta in Fig. 4), the instability pattern was symmetric compaction. In the third region (painted blue in Fig. 4), the instability pattern was dependent on the convexity/concavity of the curve that defines the pore shape at the location where the curve meets the horizontal symmetry line (see Fig. 1a). When the curve defining the pore shape was convex/concave at its intersection with the horizontal symmetry line, the instability pattern was always side buckling/symmetric compaction (Fig. 4). The concavity/convexity were defined with respect to the observer standing at the centre of the unit cell.
In side buckling, the middle row of the specimens experienced relatively small deformation (Fig. 2) that means specific areas that are protected from excessive deformation could exist even when the other areas experienced excessive deformation. This type of areas may need to be included in the positions within the structure that require protection from excessive deformation. Even before reaching the critical strain, pre-cursors to the instability patterns could be identified both for side buckling and symmetric compaction (Fig. 2b). In the case of side buckling, the pre-cursors were manifested in terms of curvy boundaries, while the boundaries between the unit cells exhibited increasing levels of waviness in the case of symmetric compaction (Fig. 2d–i, iii and iv). In symmetric compaction, the contact between the inner walls of closing pores, which occurs for very large strains, induced some levels of geometric frustration that elicited side buckling in addition to symmetric compaction. As r approaches 1, the pore shapes approach a circle (Fig. 1a). A sudden shift in the type of the instability pattern was therefore detected for some structures somewhere between r = 0.9 and r = 1.0 (Fig. 4).
Except for structures with 2-fold pores, the critical strains of all other types of structures more or less linearly increased as r increased from 0.6 to 1.0 (Fig. 4). The same linear behaviour was observed for all porosities and both orientations of the pores (i.e. d = ±1) (Fig. 4). One could therefore conclude that the critical strain values are smaller when pores with sharper folds are used in the cellular structure. In general, the difference between the critical strains of structures with different orientation of pores (i.e. d = ±1) tended to decrease, as the number of folds, n, increased. This can be attributed to the more symmetry lines in pore shapes with larger number of folds that minimizes the effect of orientation (i.e. rotation) of pores on the stress distribution of the cellular structures.
In summary, we presented a specific class of cellular soft matter whose instability patterns and instability thresholds (i.e. critical strains) are exclusively controlled by the geometry of the pores. The possibility of decoupling instability patterns and instability thresholds from the properties of the bulk material opens new avenues for utilizing geometry as a tool for programing and controlling the state of the so-called ‘programmable materials’. Despite the rich mechanical behaviour that the presented cellular structures exhibit, in most cases, their critical strains linearly change with the sharpness of the folds and are simple functions of the other geometrical parameters. These relatively simple relationships together with the instability maps (Fig. 4) provide us with some design rules that could be potentially used in development of programmable materials that exploit geometry as a way of controlling the buckling behaviour.
References
- J. Huang, X. Wang and Z. L. Wang, Nano Lett., 2006, 6, 2325–2331 CrossRef CAS PubMed.
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2015, 14, 23–36 CrossRef CAS PubMed.
- K. Muamer, B. Tiemo, S. Robert and W. Martin, Rep. Prog. Phys., 2013, 76, 126501 CrossRef PubMed.
- H. Wang and K.-Q. Zhang, Sensors, 2013, 13, 4192–4213 CrossRef CAS PubMed.
- T. Mullin, S. Deschanel, K. Bertoldi and M. C. Boyce, Phys. Rev. Lett., 2007, 99, 084301 CrossRef CAS PubMed.
- T. Mullin, S. Willshaw and F. Box, Soft Matter, 2013, 9, 4951–4955 RSC.
- J. T. Overvelde, S. Shan and K. Bertoldi, Adv. Mater., 2012, 24, 2337–2342 CrossRef CAS PubMed.
- S. H. Kang, S. Shan, W. L. Noorduin, M. Khan, J. Aizenberg and K. Bertoldi, Adv. Mater., 2013, 25, 3380–3385 CrossRef CAS PubMed.
- C. R. Tipton, E. Han and T. Mullin, Soft Matter, 2012, 8, 6880–6883 RSC.
- J. Shen, Y. M. Xie, S. Zhou, X. Huang and D. Ruan, J. Mech. Behav. Biomed. Mater., 2014, 34, 283–293 CrossRef CAS PubMed.
- S. Babaee, J. Shim, J. C. Weaver, E. R. Chen, N. Patel and K. Bertoldi, Adv. Mater., 2013, 25, 5044–5049 CrossRef CAS PubMed.
- J. Shim, S. Shan, A. Košmrlj, S. H. Kang, E. R. Chen, J. C. Weaver and K. Bertoldi, Soft Matter, 2013, 9, 8198–8202 RSC.
- K. Bertoldi, M. C. Boyce, S. Deschanel, S. M. Prange and T. Mullin, J. Mech. Phys. Solids, 2008, 56, 2642–2668 CrossRef.
- G. Wu, Y. Xia and S. Yang, Soft Matter, 2014, 10, 1392–1399 RSC.
- X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 67–72 CrossRef CAS PubMed.
- L. Yao, R. Niiyama, J. Ou, S. Follmer, C. Della Silva and H. Ishii, PneUI: pneumatically actuated soft composite materials for shape changing interfaces, United Kingdom, 2013 Search PubMed.
- Y. Cho, J.-H. Shin, A. Costa, T. A. Kim, V. Kunin, J. Li, S. Y. Lee, S. Yang, H. N. Han, I.-S. Choi and D. J. Srolovitz, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17390–17395 CrossRef CAS PubMed.
- P. G. Coelho and H. C. Rodrigues, Structural and Multidisciplinary Optimization, 2015, 1–14 Search PubMed.
- M. P. Bendsoe and O. Sigmund, Arch. Appl. Mech., 1999, 69, 635–654 CrossRef.
- J. C. Álvarez Elipe and A. Díaz Lantada, Smart Mater. Struct., 2012, 21, 105004 CrossRef.
- H. A. Eschenauer and N. Olhoff, Appl. Mech. Rev., 2001, 54, 331–390 CrossRef.
- J. T. B. Overvelde and K. Bertoldi, J. Mech. Phys. Solids, 2014, 64, 351–366 CrossRef.
- K. Bertoldi, P. M. Reis, S. Willshaw and T. Mullin, Adv. Mater., 2010, 22, 361–366 CrossRef CAS PubMed.
- P. Wang, J. Shim and K. Bertoldi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014304 CrossRef.
- S. H. Kang, S. Shan, A. Košmrlj, W. L. Noorduin, S. Shian, J. C. Weaver, D. R. Clarke and K. Bertoldi, Phys. Rev. Lett., 2014, 112, 098701 CrossRef PubMed.
- L. Fan, J. Zou, Z. Li, X. Li, K. Wang, J. Wei, M. Zhong, D. Wu, Z. Xu and H. Zhu, Nanotechnology, 2012, 23, 115605 CrossRef PubMed.
- T. K. Kim, J. K. Kim and O. C. Jeong, Microelectron. Eng., 2011, 88, 1982–1985 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra00295a |
| ‡ Material constants and related uniaxial stress–strain curves are provided in the ESI file.† |
| This journal is © The Royal Society of Chemistry 2016 |