Insight into the antioxidant properties of non-phenolic terpenoids contained in essential oils extracted from the buds of Cleistocalyx operculatus: a DFT study†
Thi Chinh Ngoa,
Duy Quang Dao*a,
Nguyen Minh Thongb and
Pham Cam Nam*cd
aInstitute of Research and Development, Duy Tan University, K7/25 Quang Trung, Danang, Vietnam. E-mail: daoduyquang@gmail.com
bThe University of Danang, Campus in Kon Tum, 704 Phan Dinh Phung, Kon Tum, Vietnam
cDepartment of Chemistry, University of Science and Technology – The University of Danang, 54 Nguyen Luong Bang, Lien Chieu, Danang, Vietnam. E-mail: camnamp@yahoo.com
dVN-UK, Institute for Research & Executive Education – The University of Da Nang, Vietnam
First published on 8th March 2016
Abstract
The antioxidant properties of 21 non-phenolic terpenoids contained in essential oil extracted from the buds of Cleistocalyx operculatus have been investigated using density functional theory (DFT)-based computational methods. The C–H bond dissociation enthalpy (BDE), proton dissociation enthalpy (PDE), proton affinity (PA), electron transfer enthalpy (ETE) and ionization energy (IE) were calculated in the gas phase and in two different solvents (water and ethanol) at the ROB3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p) level of theory for the former and with the PM6 method for the latter. Quantum chemical descriptors like chemical potential (μ), chemical hardness (η), and global electrophilicity (ω) were calculated in order to evaluate the reactivity and stability of all studied compounds. The interaction of the HOO˙ radical with α-terpinene, an example molecule, was also studied in detail by establishing a potential energy surface (PES). As a result, a kinetic concurrence between the H-abstraction reaction at the weakest C–H bond and addition reactions at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds was clarified. On the basis of this mechanism, the antioxidant capacity may happen via the termination-enhancing process. Among the studied compounds, α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene represent potential antioxidants.
C double bonds was clarified. On the basis of this mechanism, the antioxidant capacity may happen via the termination-enhancing process. Among the studied compounds, α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene represent potential antioxidants.
1. Introduction
Biological oxidation, which is caused by reactive oxygen species such as HO˙, O2˙−, and ROO˙ present in living organisms, is one of the main reasons of much oxidative damage and various diseases including allergies, cancer, viral infections, inflammation and so on.1 Antioxidants have therefore become very important to reduce the effect of oxidants on the human biological system as well as on the environment. Natural antioxidants have particularly received great attention for medicinal applications. They are mainly extracted from leaves, seeds and other parts of plants, in which various chemical compounds acting as antioxidants have been found.2 For example, a number of spices and herbs used in food due to their flavor contain a high concentration of phenolic compounds that have significant antioxidant effects.3–6 Tea and grape seed extracts include catechins, epicatechins, phenolic acids, proanthocyanidins and resveratrol, all of which contribute to their antioxidant activity.2,7–11Among natural products, Cleistocalyx operculatus in (Roxb) Merr and Perry (Myrtaceae), common beverages in Vietnam as well as in some other tropical countries, is of great interest thanks to its various biological activities. Several studies have shown that the essential oil extracted from the buds of Cleistocalyx operculatus represents antimicrobial, antioxidant,12,13 and anti-inflammatory activities,14,15 and cholinesterase inhibitory activity.16 Analysis of this essential oil by GC/MS has been reported.12,17 Five classes including monoterpenes, oxygenated monoterpenes, sesquiterpenes, oxygenated desquiterpenes, diterpenes and some other compounds were identified.12 The molecular structure of these compounds reveals a wide range of biological activities involving the antioxidant property. Their antioxidant capacity was expressed as the number of equivalents of ascorbic acid and was also experimentally measured on the basis of the scavenging activities of the stable 1,1-diphenyl-2-picrylhydrazyl (DPPH) free radical.12
Regarding the mechanism of action, the protective role of the potential antioxidants can be described by three main mechanisms: hydrogen atom transfer (HAT), single electron transfer followed by proton transfer (SET-PT), and sequential proton loss electron transfer (SPLET). The HAT mechanism is characterized by the bond dissociation enthalpy (BDE) of the considered X–H bond. SET-PT relates to the ionization energy (IE) and proton dissociation enthalpy (PDE). SPLET is determined by the proton affinity (PA) and electron transfer enthalpy (ETE).
The antioxidant capacity of hydrocarbon families available in essential oils has been a subject of different experimental and theoretical works in the literature. Generally, common essential oils contain two main structural component families:18–20 terpenoids (monoterpenes, sesquiterpenes or diterpenes) and phenylpropanoids. Such compounds are comprised of normally either phenolic rings (such as carvacrol, thymol, eugenol…) or cyclohexadiene cores (such as γ-terpinene, α-terpinene, α-pinene, α-phellandrene…) in their structure. It is presumed that an essential oil with a high content of phenolic and unsaturated terpenes could offer good antioxidant properties.18,21 However, this rough prediction is not always exact. The overall antioxidant capacity of essential oil is a complex consequence of interference between oxidizable materials and potential antioxidant components. Non-phenolic terpenoids, especially unsaturated ones, can be oxidized in a similar manner with unsaturated lipids to be protected. Their auto-oxidation mechanism is initiated by either a H atom abstraction reaction with peroxyl radicals (ROO˙) or addition of ROO˙ to an unsaturated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond (e.g. epoxidation reaction).18,22,23 This auto-oxidation mechanism is characterized by a very fast termination process as reported in detail in the case of α-pinene,24 α-phellandrene25 as well as γ-terpinene.26 In fact, this type of component will cause an overall increase in the rate of oxidative chain termination and reduce the overall rate of oxidation, thus will behave as an antioxidant.18 On the basis of this behavior, they were called termination-enhancing antioxidants.
C bond (e.g. epoxidation reaction).18,22,23 This auto-oxidation mechanism is characterized by a very fast termination process as reported in detail in the case of α-pinene,24 α-phellandrene25 as well as γ-terpinene.26 In fact, this type of component will cause an overall increase in the rate of oxidative chain termination and reduce the overall rate of oxidation, thus will behave as an antioxidant.18 On the basis of this behavior, they were called termination-enhancing antioxidants.
In this study, our purpose is firstly to evaluate the antioxidant capacity of 21 different non-phenolic compounds containing three hydrocarbon classes (monoterpenes, sesquiterpenes and diterpenes) of the essential oils of Cleistocalyx operculatus12 in determining their ability of H-donation and/or electron transfer to the free radicals. Three main antioxidant mechanisms will be evaluated based on the thermodynamic parameters as mentioned above (i.e. BDE, IE, PDE, PA and ETE). We will then classify the antioxidant capacity strength of these studied compounds. As the polarity of the solvent has effects on the ability of the donating hydrogen, the effects of solvent will also be considerably studied. Based on the vertical ionization energy and electron affinity calculated by the PM6 method, several quantum chemical descriptors like chemical potential (μ), chemical hardness (η) and global electrophilicity (ω) will also be calculated in order to give more insight into the reactivity and stability of all the studied compounds. Finally, potential energy surface (PES) of several initiative reactions in the auto-oxidation mechanism of α-terpinene, a representative antioxidant, with hydroperoxyl radicals (HOO˙) will be evaluated for insight into their mechanism of action.
2. Computational methods
The geometry optimization and the vibrational frequency calculation of each compound and the related radicals, cationic radicals and anions were primarily performed at the B3LYP/6-311G(d,p) level of theory.27 Their single point electronic energies were then calculated at the ROB3LYP/6-311++G(2df,2p) level of theory. The transition states, intermediates and products of the reaction between the HOO˙ radical and the studied molecules were optimized and calculated at the same level of theory. All transition states were characterized by the existence of only one single imaginary frequency. To ensure that each transition state connects to the expected reactant and product, the intrinsic reaction coordinate (IRC) calculation was also carried out at the same computational level of theory. The solvent was treated implicitly using integral equation formalism of polarizable continuum model (IEF-PCM) at the same level of theory as in the gas phase.28,29Generally, three common mechanisms of antioxidant action are proposed and widely accepted as follows:30–33
Hydrogen atom transfer (HAT)
| R–H → R˙ + H˙ (BDE(R–H)) |
Single electron transfer followed by proton transfer (SET-PT)
| R–H → RH+˙ + e− (IE) |
| RH+˙ → R˙ + H+ (PDE) |
Sequential proton loss electron transfer (SPLET)
| R–H → R− + H+ (PA) |
| R− → R˙ + e− (ETE) |
The reaction enthalpies of an antioxidant in the gas phase at 298.15 K and 1 atm are calculated as follows:30,31,33
| BDE = H(R˙) + H(H˙) − H(R–H) | (1) |
| IE = H(RH˙+) + H(e−) − H(R–H) | (2) |
| PDE = H(R˙) + H(H+) − H(RH˙+) | (3) |
| PA = H(R−) + H(H+) − H(R–H) | (4) |
| ETE = H(R˙) + H(e−) − H(R−) | (5) |
| H = E0 + ZPE + Htrans + Hrot + Hvib + RT |
Htrans, Hrot, and Hvib are the translational, rotational, and vibrational contributions to the enthalpy, respectively. E0 is the total energy at 0 K and ZPE is the zero-point vibrational energy. The enthalpy value for the hydrogen atom in the solvent was calculated at the same level of theory, while this value in the gas phase was taken at its exact energy of −0.5 Hartree at 0 K and thermal correction at the given temperature was added by the value of 2.5RT. The calculated enthalpies of the proton (H+) and electron (e−) were taken from the literature.33–37 Vibrational frequencies obtained at the B3LYP/6-311G(d,p) level of theory were scaled by a factor of 0.9669.38,39 In this work, all computational calculations were performed using the Gaussian 09 software package.40 The finite differences method proposed by Pearson and Parr allows approximation of the chemical potential (μ),41,42 chemical hardness (η),43 and global electrophilicity (ω)44 on the basis of electron affinity (EA) and vertical ionization energy (IE) of chemical species as follows:
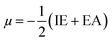 | (6) |
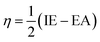 | (7) |
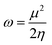 | (8) |
3. Results and discussion
3.1. Bond dissociation enthalpies (BDEs)
In order to qualitatively find out the weakest bond positions, the semi-empirical PM6 method was firstly used to primarily calculate the BDE of all possible C–H bonds breaking in the studied compounds. The vibrational frequency obtained at PM6 was scaled by a factor of 1.078.39 The corresponding BDEs are presented in Table S1 (ESI).† The results show that several C–H bonds with similarly low BDE values are found in various cases of the studied compounds. For example, the lowest BDEs of camphene, which are 74.8 and 73.9 kcal mol−1, are found at the C5 and C6 positions, respectively. Axinissene has also four C–H bonds located at the C4, C3, C9 and C13 atoms where the PM6 calculated BDEs(C–H) are very low, i.e. 62.1, 63.0, 62.6 and 62.6 kcal mol−1, respectively. It is generally observed that all the weak C–H bonds are found nearby one or several conjugated π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) bonds (as seen in Fig. 1). This phenomenon will be explained clearly in the next section when the BDEs were calculated at a higher ROB3LYP/6-311++G (2df,2p) level of theory.
C) bonds (as seen in Fig. 1). This phenomenon will be explained clearly in the next section when the BDEs were calculated at a higher ROB3LYP/6-311++G (2df,2p) level of theory.
Table 1 shows the calculated BDEs of three cyclohexadiene-like component classes, i.e. monoterpenes, sesquiterpenes and diterpenes, in the gas phase and two different solvents, namely water and ethanol, at the ROB3LYP/6-311++G(2df,2p) level of theory. The carbon atom position of the easiest breaking bond is highlighted by a bold number (as described in Fig. 1).
| Classes | Compounds | Bondsa | BDEs (kcal mol−1) | PDEs (kcal mol−1) | ||
|---|---|---|---|---|---|---|
| Gas phase | Water | Ethanol | Gas phase | |||
| a See Fig. 1 for definition of atom numbering. | ||||||
| Monoterpenes | α-Pinene | C4–H | 83.9 | 85.2 | 84.6 | 216.3 |
| β-Pinene | C3–H | 82.7 | 84.2 | 83.6 | 213.3 | |
| Camphene | C6–H | 97.1 | 98.6 | 98 | 219.0 | |
| Myrcene | C5–H | 81.4 | 84.2 | 83.6 | 215.6 | |
| α-Terpinene | C6–H | 74.8 | 76.2 | 75.6 | 221.1 | |
| γ-Terpinene | C6–H | 74.4 | 75.7 | 75.1 | 206.5 | |
| Limonene | C3–H | 83.0 | 84.8 | 84.2 | 210.7 | |
| Sesquiterpenes | α-Copanene | C5–H | 83.1 | 84.5 | 83.8 | 219.8 |
| Sesquithujene | C9–H | 82.1 | 83.4 | 82.8 | 224.8 | |
| β-Cedrene | C9–H | 82.8 | 84.4 | 83.7 | 207.2 | |
| 6-epi-Beta-cubebene | C7–H | 85.1 | 86.8 | 86.1 | 225.4 | |
| Aromadendr-9-ene | C3–H | 81.0 | 82.7 | 82.0 | 209.6 | |
| γ-Muurolene | C9–H | 82.5 | 84.1 | 83.4 | 215.2 | |
| γ-Amorphene | C9–H | 81.0 | 82.8 | 82.2 | 222.6 | |
| Cyclobazzanene | C5–H | 82.0 | 83.3 | 82.7 | 215.1 | |
| α-Cadinene | C9–H | 79.5 | 81.0 | 80.4 | 215.3 | |
| Diterpenes | Axinissene | C9–H | 82.3 | 83.9 | 83.3 | 225.1 |
| Rimuene | C11–H | 80.4 | 82.0 | 81.3 | 214.8 | |
| Cembrene | C5–H | 73.9 | 74.8 | 74.2 | 221.3 | |
| Kaur-16-ene | C3–H | 84.5 | 86.0 | 85.4 | 209.8 | |
| Abieta-7,13-diene | C5–H | 75.5 | 78.1 | 77.7 | 227.8 | |
As can be seen in Table 1, the BDEs(C–H) generally vary from 73.9 to 97.1 kcal mol−1. The BDEs(C–H) of α-pinene, β-pinene, γ-terpinene and limonene are 83.9, 82.7, 74.4 and 83.0 kcal mol−1, respectively. In comparison with the available results obtained in previous studies,46,47 our data are in good agreement. For example, Almeida et al.46 calculated the BDEs(C–H) of α-pinene, β-pinene and limonene at the B3LYP/6-311++G(2d,2p) level as being 336 kJ mol−1 (or 80.3 kcal mol−1), 331 kJ mol−1 (or 79.1 kcal mol−1) and 323 kJ mol−1 (or 77.2 kcal mol−1), respectively. The BDEs(C–H) of β-pinene, γ-terpinene and limonene, which are 79.5, 70.7 and 79.4 kcal mol−1, respectively, were computed at the B3LYP/6-311++G(d,p) level by Sharopov and coworkers.47
Thus, on the basis of the obtained BDEs the hydrogen-donating ability of the studied compounds of each hydrocarbon class in the gas phase follows the sequence:
(i) Monoterpenes: α-terpinene > γ-terpinene > myrcene > β-pinene > limonene > α-pinene > camphene.
(ii) Sesquiterpenes: α-cadinene > aromadendr-9-ene > γ-amorphene > cyclobazzanene ≈ sesquithujene > γ-muurolene > β-cedrene > α-copanene > 6-epi-beta-cubebene.
(iii) Diterpenes: cembrene > abieta-7,13-diene > rimuene > axinissene > kaur-16-ene.
Regarding the literature, our results are in good agreement with the data obtained by Youdim et al.48 In their work, they investigated the antioxidant activities of thyme oil and its components. It is shown that the order of antioxidant activity of the tested components is γ-terpinene > myrcene > limonene > α-pinene.
Particularly, the easiest C–H scavenging corresponds to four compounds (α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene) with the BDE values of 74.8, 74.4, 73.9 and 75.5 kcal mol−1, respectively.
In studying the molecular structural characteristics of all potential antioxidants, it is found that the easiest C–H breaking bond is usually found at the C atoms located nearby C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. This observation can be explained by the electron-withdrawing inductive effect (¬I) of the π bond. This effect induces an electron-releasing phenomenon from the carbon atoms, and respectively results in the increased polarization of the C–H bonds. This favors C–H bond breaking, and thus leads to lower BDEs of these bonds compared to other ones. Particularly, the number of C
C double bonds. This observation can be explained by the electron-withdrawing inductive effect (¬I) of the π bond. This effect induces an electron-releasing phenomenon from the carbon atoms, and respectively results in the increased polarization of the C–H bonds. This favors C–H bond breaking, and thus leads to lower BDEs of these bonds compared to other ones. Particularly, the number of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds present in the molecular system also influences the BDEs. In fact, the lowest BDEs(C–H) of the four compounds (α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene) are related to the presence of two conjugated π bonds nearby those C positions (as can be seen in Fig. 1).
C double bonds present in the molecular system also influences the BDEs. In fact, the lowest BDEs(C–H) of the four compounds (α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene) are related to the presence of two conjugated π bonds nearby those C positions (as can be seen in Fig. 1).
The polarity of solvents affects the hydrogen-donating ability that results in the change of the BDE values. In this study, the BDE calculations were carried out in the gas phase and two different solvents (i.e. water and ethanol). Ethanol is chosen because the experimental studied essential oil is normally extracted with 70% ethanol.12 In the meantime, water is also considered as a studied solvent since the buds of Cleistocalyx operculatus are usually used as beverages in boiled water. The results obtained for all compounds show no remarkable difference in the BDEs(C–H) in the gas phase compared to the two used solvents. Indeed, the BDEs(C–H) of α-terpinene in the gas phase, water and ethanol are approximately 74.8, 76.2 and 75.6 kcal mol−1, respectively. In the case of γ-terpinene, the BDEs(C–H) in these three phases nearly equal 74.4, 75.7 and 75.1 kcal mol−1, respectively. Similarly, the BDEs(C–H) of abieta-7,13-diene are about 75.5, 78.1 and 77.7 kcal mol−1, respectively. These values obtained in the gas phase, water and ethanol of cembrene are 73.9, 74.8 and 74.2 kcal mol−1, respectively. In addition, the smallest BDEs(C–H) are obtained for the same compounds in all used solvents. This leads to the conclusion that the BDEs(C–H) follow the same tendencies. Solvents have a slight effect on the BDEs(C–H). On the basis of these calculated values, it is preliminary said that among the studied compounds, α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene represent potential antioxidants.
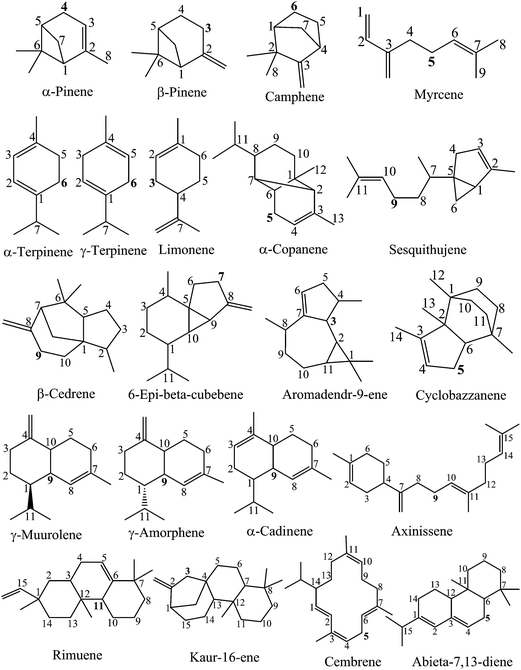
As discussed in the previous section, the strong H atom donating ability of the terpenoids containing a cyclohexadiene skeleton does not allow us to certainly conclude the antioxidant performance of these compounds based on the HAT mechanism. The carbon-centered radicals formed by H atom abstraction could provide, in the presence of oxygen, reactive peroxyl radicals which propagate the auto-oxidation chain of the terpenoids. For this reason, a structural study of the radical species formed after the H atom breaking reaction is necessary to evaluate their reactivity and ability continuing the oxidative chain. Fig. 2 displays the structural conformation, highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of four carbon-centered radicals which are formed from H atom breaking at the C position with the lowest BDE(C–H) of the four compounds α-terpinene, γ-terpinene, abieta-7,13-diene and cembrene.
The previous obtained results showed that the easiest C–H breaking bond is usually found at the C atoms located nearby C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds. The formed free radicals adjacent to a π bond are spread out over two or more carbons, resulting in a π-conjugation chain (as shown in the structural conformations in Fig. 2 (left)). In addition, the HOMO and LUMO profiles also demonstrate an overlap of molecular p orbitals over multiple adjacent carbons of the π-conjugation chain. The electron density of each π bond of the electron-deficient free radical is therefore delocalized over a larger volume, thus lowering the energy of molecule. This leads to relatively stable radicals by the resonance effect.
C double bonds. The formed free radicals adjacent to a π bond are spread out over two or more carbons, resulting in a π-conjugation chain (as shown in the structural conformations in Fig. 2 (left)). In addition, the HOMO and LUMO profiles also demonstrate an overlap of molecular p orbitals over multiple adjacent carbons of the π-conjugation chain. The electron density of each π bond of the electron-deficient free radical is therefore delocalized over a larger volume, thus lowering the energy of molecule. This leads to relatively stable radicals by the resonance effect.
Regarding the effect of the number of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds of cembrene, one observed that the radical formed with the dissociation of the C5–H bond is the most stable one, in which the π-conjugation spreads out over seven adjacent C atoms. Moreover, the C5–H BDE of cembrene is found to be the lowest (73.9 kcal mol−1) value compared to the other C–H ones. It is a good approximation to think that low BDE reflects the formation of a stable free radical.
C double bonds of cembrene, one observed that the radical formed with the dissociation of the C5–H bond is the most stable one, in which the π-conjugation spreads out over seven adjacent C atoms. Moreover, the C5–H BDE of cembrene is found to be the lowest (73.9 kcal mol−1) value compared to the other C–H ones. It is a good approximation to think that low BDE reflects the formation of a stable free radical.
On the other hand, the H atom abstraction reaction by the peroxyl radical (ROO˙) is also competing with the addition reaction to the unsaturated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond of the cyclohexadiene ring of the terpenoids,18,24 which tends to form an epoxide compound after eliminating the RO˙ radical. Insight into kinetic competition between H atom abstraction by the peroxyl radical and peroxyl radical addition to the C
C bond of the cyclohexadiene ring of the terpenoids,18,24 which tends to form an epoxide compound after eliminating the RO˙ radical. Insight into kinetic competition between H atom abstraction by the peroxyl radical and peroxyl radical addition to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond allows the auto-oxidation mechanism of these terpenoids to be brought out, as well as their potential antioxidant performance. Evaluation of the energy profiles of these initiative reactions will be presented in the final section of the paper.
C bond allows the auto-oxidation mechanism of these terpenoids to be brought out, as well as their potential antioxidant performance. Evaluation of the energy profiles of these initiative reactions will be presented in the final section of the paper.
3.2. Ionization energy and proton dissociation enthalpy
The calculated IE is defined as the energy difference between the parent molecule and its cationic radical (eqn (2)). It represents the electron transfer capacity of the antioxidants to donate an electron to the free radicals. The lower IE value is assigned to the easier electron transfer and the higher antioxidant activity.
The PM6 method has been considered as an appropriate method to calculate the IE values.30,31 The computed IEs of the studied compounds and its deviations (ΔIEs) compared to that of phenol are reported in Table 2. The calculated IEs of some compounds including α-pinene (8.35 eV), camphene (9.04 eV) and limonene (8.49 eV) are also compared with the experimental ones49,50 (8.07 eV, 8.86 eV and 8.30 eV, respectively). It should be found that PM6 overestimated the IE values with the deviations of 0.28 eV, 0.18 eV and 0.19 eV, respectively.
| Compounds | IE | EA | μ | η | ω |
|---|---|---|---|---|---|
| a Data in parentheses are deviation of the IEs (ΔIEs) compared to the IE of phenol: ΔIE = IEcalc − IEphenol (IEphenol = 8.49 eV).49 *IEexpt (α-pinene): 8.07 (eV);49,50 IEexpt (camphene): 8.86 (eV);49 IEexpt (limonene): 8.3 (eV).49 | |||||
| α-Pinene* | 8.35 (−0.14) | −0.84 | −3.76 | 4.60 | 1.54 |
| β-Pinene | 8.86 (0.37) | −0.80 | −4.03 | 4.83 | 1.68 |
| Camphene* | 9.04 (0.55) | −0.81 | −4.11 | 4.92 | 1.72 |
| Myrcene | 8.62 (0.13) | −0.45 | −4.09 | 4.53 | 1.84 |
| α-Terpinene | 7.74 (−0.75) | −0.17 | −3.78 | 3.96 | 1.81 |
| γ-Terpinene | 8.36 (−0.13) | −0.88 | −3.74 | 4.62 | 1.51 |
| Limonene* | 8.49 (0.00) | −0.83 | −3.83 | 4.66 | 1.58 |
| α-Copanene | 8.24 (0.25) | −0.79 | −3.72 | 4.52 | 1.53 |
| Sesquithujene | 8.41 (−0.08) | −0.73 | −3.84 | 4.57 | 1.61 |
| β-Cedrene | 8.79 (0.30) | −0.82 | −3.98 | 4.80 | 1.65 |
| 6-epi-Beta-cubebene | 8.67 (0.18) | −0.70 | −3.99 | 4.69 | 1.70 |
| Aromadendr-9-ene | 8.28 (−0.21) | −0.79 | −3.74 | 4.53 | 1.55 |
| γ-Muurolene | 8.43 (−0.06) | −0.76 | −3.83 | 4.60 | 1.60 |
| γ-Amorphene | 8.31 (−0.18) | −0.88 | −3.72 | 4.59 | 1.50 |
| Cyclobazzanene | 8.24 (−0.25) | −0.90 | −3.67 | 4.57 | 1.47 |
| α-Cadinene | 8.29 (−0.20) | −0.85 | −3.72 | 4.57 | 1.52 |
| Axinissene | 8.49 (0.00) | −0.63 | −3.93 | 4.56 | 1.69 |
| Rimuene | 8.15 (−0.34) | −0.78 | −3.68 | 4.47 | 1.52 |
| Cembrene | 7.94 (−0.55) | −0.09 | −3.93 | 4.02 | 1.92 |
| Kaur-16-ene | 9.39 (0.90) | −0.89 | −4.25 | 5.14 | 1.76 |
| Abieta-7,13-diene | 7.58 (−0.91) | 0.04 | −3.81 | 3.77 | 1.92 |
As can be seen, the obtained IEs of all the compounds are very close to the value of phenol, and the deviation between them is relatively small (data presented in parentheses in Table 2). The smallest IE is 7.58 eV corresponding to abieta-7,13-diene with a deviation of −0.91 eV compared to phenol. According to the standardized methods proposed by Prior et al.51 for the phenolic-type antioxidant capacity evaluation, the SET-PT antioxidant mechanism is predominant when the ΔIE of the potential antioxidant is larger than −1.95 eV (or −45 kcal mol−1). It means that the electron transfer capacity of the studied compounds is not favored in the gas phase.
In addition, based on the calculated IEs and additional electron affinity (EA), the global reactivity descriptors including chemical potential (μ), chemical hardness (η) and global electrophilicity (ω) which are required to analyze the tendency of selectivity and chemical reactivity of each compound, are also computed and given in Table 2.52,53
In principle, chemical hardness is defined as the resistance of cloud polarization or deformation of chemical species.54 The compound with the lowest value of hardness is predicted to have the highest reactivity. Among the studied compounds, abieta-7,13-diene, α-terpinene and cembrene are displayed as the most reactive compounds due to their relative low hardness values of 3.77, 3.96 and 4.02, respectively. In addition, the second chemical parameter called global electrophilicity, which represents the capacity of a system to acquire an electron, is also an appropriate parameter for evaluating the chemical reactivity of a compound.44,53 It is observed that the most reactive compounds in terms of electrophilicity are found for cembrene and abieta-7,13-diene, which show the values of 1.92 eV while the less reactive one corresponds to cyclobazzanene (ω = 1.47 eV). Regarding the four potential antioxidants according to the HAT mechanism (α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene), α-terpinene, cembrene and abieta-7,13-diene are demonstrated as the most reactive compounds in terms of the chemical descriptors compared to the other ones.
As a result, the deprotonation process can be found at several positions of the cationic radical species. However, the obtained results show that the easiest deprotonation generally is assigned to the carbon position of the easiest C–H bond to break with the lowest BDE. Among the studied compounds, the lowest PDE is 206.8 kcal mol−1 corresponding to γ-terpinene. The deprotonation ability of the cationic radicals of each hydrocarbon class in the gas phase follows the order:
(i) Monoterpenes: γ-terpinene > limonene > β-pinene > myrcene > α-pinene > camphene > α-terpinene.
(ii) Sesquiterpenes: β-cedrene > aromadendr-9-ene > α-cadinene ≈ γ-muurolene ≈ cyclobazzanene > α-copanene > γ-amorphene > sesquithujene > 6-epi-beta-cubebene.
(iii) Diterpenes: kaur-16-ene > rimuene > cembrene > axinissene > abieta-7,13-diene.
3.3. Proton affinity and electron transfer enthalpy
The proton loss process is an important step of the SPLET mechanism which is characterized by proton affinity (PA) values. The lower PA is described for a higher antioxidant capacity via this mechanism. The obtained PAs are reported in Table 3.
| Classes | Compounds | C–H bond positions | PAs (kcal mol−1) | ETEs (kcal mol−1) | ||||
|---|---|---|---|---|---|---|---|---|
| Gas phase | Water | Ethanol | Gas phase | Water | Ethanol | |||
| a See Fig. 1 for definition of atom numbering. | ||||||||
| Monoterpenes | α-Pinene | C8–H | 385.2 | 75.6 | 93.0 | 15.0 | 31.8 | 50.7 |
| β-Pinene | C3–H | 382.3 | 73.2 | 90.6 | 15.0 | 31.9 | 50.7 | |
| Camphene | C7–H | 405.7 | 94.8 | 112.5 | 12.1 | 30.6 | 49.2 | |
| Myrcene | C9–H | 382.2 | 74.7 | 92.1 | 20.8 | 35.4 | 54.3 | |
| α-Terpinene | C6–H | 375.0 | 68.1 | 85.5 | 12.9 | 28.9 | 47.8 | |
| γ-Terpinene | C6–H | 374.4 | 66.7 | 84.7 | 14.6 | 29.8 | 48.1 | |
| Limonene | C4–H | 381.5 | 75.4 | 92.8 | 17.0 | 30.8 | 49.7 | |
| Sesquiterpenes | α-Copanene | C13–H | 384.6 | 76.3 | 93.7 | 15.8 | 31.6 | 50.4 |
| Sesquithujene | C9–H | 384.7 | 80.2 | 97.4 | 12.0 | 24.1 | 43.1 | |
| β-Cedrene | C9–H | 382.0 | 74.8 | 92.2 | 15.4 | 30.4 | 49.2 | |
| 6-epi-Beta-cubebene | C1–H | 372.4 | 62.9 | 80.3 | 33.2 | 50.5 | 69.3 | |
| Aromadendr-9-ene | C8–H | 386.6 | 82.6 | 100.0 | 11.7 | 23.4 | 42.3 | |
| γ-Muurolene | C6–H | 381.6 | 78.1 | 95.4 | 17.4 | 28.7 | 47.6 | |
| γ-Amorphene | C6–H | 376.1 | 79.8 | 97.1 | 18.7 | 27.8 | 46.7 | |
| Cyclobazzanene | C14–H | 385.9 | 79.3 | 96.7 | 15.4 | 29.6 | 48.4 | |
| α-Cadinene | C9–H | 383.2 | 82.0 | 99.2 | 10.8 | 19.9 | 38.9 | |
| Diterpenes | Axinissene | C4–H | 378.6 | 73.7 | 91.1 | 19.1 | 31.6 | 50.5 |
| Rimuene | C11–H | 380.0 | 81.6 | 98.8 | 14.9 | 21.2 | 40.3 | |
| Cembrene | C5–H | 358.9 | 58.9 | 76.2 | 29.5 | 36.7 | 55.8 | |
| Kaur-16-ene | C3–H | 380.5 | 74.4 | 91.9 | 18.6 | 32.4 | 51.2 | |
| Abieta-7,13-diene | C5–H | 371.0 | 71.5 | 88.7 | 20.5 | 27.4 | 46.7 | |
The lowest PAs are found for four compounds including α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene with the values of 375.0, 374.4, 358.9 and 371.0 kcal mol−1, respectively. In addition, the results show that the solvents (both water and ethanol) affect significantly the PA and lead to a dramatic decrease in its value. In fact, the PA of α-terpinene in the gas phase is 375.0 kcal mol−1 while its values in water and ethanol are 68.1 and 85.5 kcal mol−1, respectively. Similarly, PA(cembrene) decreases from 358.9 kcal mol−1 in the gas phase to 58.9 and 71.1 kcal mol−1 in water and ethanol, respectively. And the PA(abieta-7,13-diene) values are 371.0, 71.5 and 83.7 kcal mol−1 in the gas phase, water and ethanol, respectively. The polar solvents seem to support the deprotonation process. Thus, the PA values obtained in water and ethanol are far lower than the ones obtained in the gas phase, due to the high solvation enthalpy of the proton. This observation is in good agreement with several previous studies.30,55–59 In conclusion, the presence of the polar solvents (water and ethanol) significantly involves a dramatic decrease in the PAs. SPLET is thermodynamically preferred pathway in polar solvents.
Regarding the solvent effects, the obtained results show that the solvents (both water and ethanol) lead to a significant increase in the ETEs of all studied compounds compared with the values obtained in the gas phase. It means that the polar solvents are unfavorable for the following electron transfer process.
3.4. Interaction of HOO˙ radicals with antioxidant molecules
As is already known in the literature, the preventive role of a RH antioxidant is demonstrated by the H atom transfer reaction as below:| HOO˙ + RH → HOOH + R˙ |
The H atom transfer from the antioxidant molecule to the HOO˙ radical, a typical oxidative radical available in the human body, interrupts the chain reaction that is responsible for the antioxidant capacity.
In this study, our interest is set on the investigation of the interaction of the HOO˙ radical with one of the antioxidant molecules which showed the lowest BDE value. For this purpose, α-terpinene, which contains two conjugated double bonds, was chosen as a representative compound of non-phenolic terpenoids to examine the mechanism of its reaction with HOO˙. All optimized structures of the species related to the mentioned reaction computed at the B3LYP/6-311G(d,p) level are given in the ESI.†
Obviously, two kinds of reactions called addition and abstraction are observed in the potential energy surface (PES). Therefore, we will discuss in turn the H-abstraction channel at the easiest C6–H bond breaking and the addition channel at C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and C3
C2 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 double bonds.
C4 double bonds.
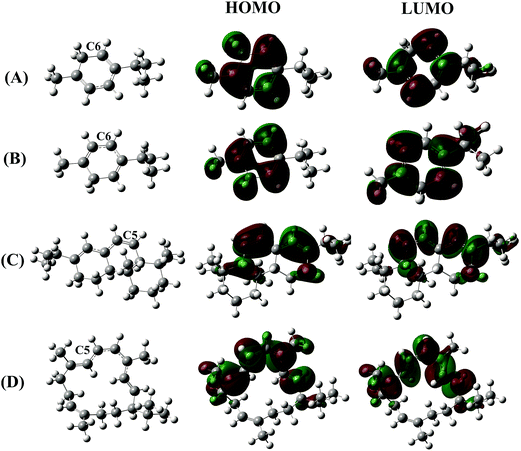
Following this channel, two intermediates (Int6-1 and Int6-2) and one transition state (TS6) were found before yielding the final products involving P6 + HOOH (as shown in Fig. 3).
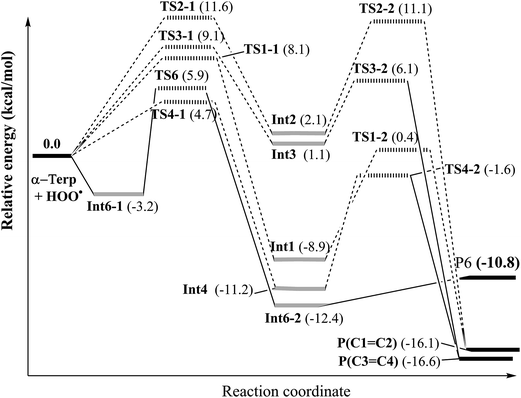 | ||
| Fig. 3 Potential energy surface (PES) of the reaction between the HOO˙ radical and α-terpinene calculated at ROB3LYP/6-311++G(2df,2p)//B3LYP/6-311G(d,p). | ||
The H-abstraction reaction starts with the formation of Int6-1, in which the HOO˙ radical forms a hydrogen bond with the H–C6 bond of α-terpinene. Int6-1 lies below the reactants by −3.2 kcal mol−1. The HOO⋯HC6 distance in Int6-1 is 2.683 Å (as shown in Fig. 4). Then, the H atom abstraction occurs to produce the second intermediate (Int6-2) via a transition state (TS6) lying at 5.9 kcal mol−1 above the reactants. In the structure of TS6, the H atom comes closer to the O atom of the HOO˙ radical and locates nearly midway between the C6 and O atoms (the H⋯OOH and C6⋯H distances are 1.311 Å and 1.265 Å, respectively) (Fig. 4). The ∠C6–H–O angle is relatively bent, being 176.7°.
After passing TS6, the second intermediate (Int6-2) is formed lying at −12.4 kcal mol−1 below the reactants. The C6–H and H–O distances of Int6-2 are 2.237 and 0.974 Å, respectively. The final products of the reaction between HOO˙ and α-terpinene are the α-terpinene-C6˙ radical (P6) and isolated HOOH. The formed α-terpinene-C6˙ radical is stabilized by π-conjugation spreading out over five carbon atoms (as can be seen in Fig. 4D).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C2 and C3
C2 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C4). The potential energy surface (PES) of the addition reaction when the HOO˙ radical makes the attack on the double bond positions of α-terpinene is displayed in Fig. 3. It is observed that the tendency is quite similar for the attack of the HOO˙ radical to the C1
C4). The potential energy surface (PES) of the addition reaction when the HOO˙ radical makes the attack on the double bond positions of α-terpinene is displayed in Fig. 3. It is observed that the tendency is quite similar for the attack of the HOO˙ radical to the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and C3
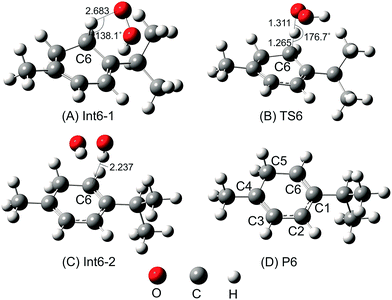
C2 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 double bonds. Along the addition channels, the O atom of HOO˙ and the C1, C2, C3 and C4 atoms of α-terpinene approach each other. The first transition states, namely TS1-1, TS2-1, TS3-1 and TS4-1, are formed and the C1–O, C2–O, C3–O and C4–O distances reach 2.112, 1.909, 1.889 and 2.088 Å, respectively. The energy barriers of the first step are 8.1, 11.6, 9.1 and 4.7 kcal mol−1 in sequence. When the forming C1–O, C2–O, C3–O and C4–O bonds are shortened to 1.469, 1.472, 1.474 and 1.466 Å, respectively (as described in Fig. 5), the local minima with formation of Int1, Int2, Int3 and Int4 appear on the potential energy surface.
C4 double bonds. Along the addition channels, the O atom of HOO˙ and the C1, C2, C3 and C4 atoms of α-terpinene approach each other. The first transition states, namely TS1-1, TS2-1, TS3-1 and TS4-1, are formed and the C1–O, C2–O, C3–O and C4–O distances reach 2.112, 1.909, 1.889 and 2.088 Å, respectively. The energy barriers of the first step are 8.1, 11.6, 9.1 and 4.7 kcal mol−1 in sequence. When the forming C1–O, C2–O, C3–O and C4–O bonds are shortened to 1.469, 1.472, 1.474 and 1.466 Å, respectively (as described in Fig. 5), the local minima with formation of Int1, Int2, Int3 and Int4 appear on the potential energy surface.
The relative energies of the intermediates corresponding to the addition at the C1, C2, C3 and C4 positions are −8.9, 2.1, 1.1 and −11.2 kcal mol−1, respectively (Fig. 3). The lowest relative energies are found when the HOO˙ radical attacks the C1 and C4 positions of the cyclohexadiene ring. This finding could be explained by the fact that the C1 and C4 atoms are bonded with substituent methyl and isopropyl groups, respectively, which are both electron-donating groups whose effects increase the electron density of the cyclohexadiene ring notably at the C2, C3 and C5, C6 positions. The Mulliken charges calculated at the same level of theory for the neutral α-terpinene at these positions are −0.265, −0.447, −0.965 and −0.668, respectively. The computed Mulliken charges of the C1 and C4 carbons equal 0.880 and 0.766, respectively. These values allow us to explain the more preferable attack of a nucleophile radical like HOO˙ whose O atom carries a negative charge of −0.143. On the other hand, the C4 position represents the most attractive site although its Mulliken charge is less positive than that of C1. This may result from the less important steric hindrance of the methyl group located at the C4 position as compared to that of the isopropyl group at the C1 atom.
After forming intermediates, the addition channels pass through the second transition states (TS1-2, TS2-2, TS3-2 and TS4-2), immediately followed by unimolecular ring-closure to form a peroxide bridge between the two C atoms of each double bond. The final epoxy products (P(C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2) and P(C3
C2) and P(C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4)) are yielded by eliminating the HO˙ free radical, and their relative energies are predicted as about −16.1 and −16.6 kcal mol−1, lying underneath the reactants. In comparison with the energy of the radical product of H-abstraction (P6) (−10.8 kcal mol−1), the epoxy products are significantly more stable. Moreover, the energy barrier required for the addition reactions at C1, C2, and C3 and the H atom transfer process at C6 is 8.1, 11.6, 9.1 and 9.1 kcal mol−1, respectively, which is significantly higher than the one at C4, being 4.7 kcal mol−1. These results highlight that the addition reaction at C4 is the most favorable from the thermodynamics point of view. This may induce a conclusion that the studied cyclohexadiene terpenoids are potential antioxidants in enhancing the oxidation chain termination. However, further detailed kinetic study including the reaction rate and quenching ratios calculation should be performed to ensure that the addition reaction to the double bond is sufficiently rapid compared to the H-abstraction one.
C4)) are yielded by eliminating the HO˙ free radical, and their relative energies are predicted as about −16.1 and −16.6 kcal mol−1, lying underneath the reactants. In comparison with the energy of the radical product of H-abstraction (P6) (−10.8 kcal mol−1), the epoxy products are significantly more stable. Moreover, the energy barrier required for the addition reactions at C1, C2, and C3 and the H atom transfer process at C6 is 8.1, 11.6, 9.1 and 9.1 kcal mol−1, respectively, which is significantly higher than the one at C4, being 4.7 kcal mol−1. These results highlight that the addition reaction at C4 is the most favorable from the thermodynamics point of view. This may induce a conclusion that the studied cyclohexadiene terpenoids are potential antioxidants in enhancing the oxidation chain termination. However, further detailed kinetic study including the reaction rate and quenching ratios calculation should be performed to ensure that the addition reaction to the double bond is sufficiently rapid compared to the H-abstraction one.
4. Conclusions
In this study, the antioxidant activities of 21 non-phenolic compounds extracted from the essential oil of Cleistocalyx operculatus in the gas phase and two different solvents (water and ethanol) have been studied via their thermochemical properties including the BDE, IE, PDE, PA and ETE. The obtained results show that the HAT is dominant in the gas phase whereas SPLET is the thermodynamically preferred pathway in a polar solvent. Indeed, solvents have a slight effect on the BDEs, while the PAs decrease drastically from the gas phase to polar solvents. Among the studied compounds, α-terpinene, γ-terpinene, cembrene and abieta-7,13-diene represent potential antioxidants. Quantum chemical descriptors including chemical potential (μ), chemical hardness (η) and global electrophilicity (ω) were calculated, which show that the most reactive compounds correspond to α-terpinene, cembrene and abieta-7,13-diene. For insight into the HOO˙ radical scavenging mechanism of these studied cyclohexadiene terpenoids, α-terpinene has been selected as a typical compound to establish the potential energy surface. A kinetic competition between the hydrogen-abstraction from the C6–H bond and the addition of the HOO˙ radical to the C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2 and C3
C2 and C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4 double bonds have also been clarified. The relative energy of epoxy products resulting from the addition reactions (i.e. P(C1
C4 double bonds have also been clarified. The relative energy of epoxy products resulting from the addition reactions (i.e. P(C1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C2) and P(C3
C2) and P(C3![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C4): −16.1 and −16.6 kcal mol−1, respectively) is much lower than the H-abstraction at C6 (i.e. P6: −10.8 kcal mol−1). In respect to the energy required for each addition reaction (i.e. 8.1, 11.9, 9.1 and 4.7 kcal mol−1, corresponding to the addition at C1, C2, C3 and C4, respectively), it is found that the addition reaction at the C4 atom is the most favorable.
C4): −16.1 and −16.6 kcal mol−1, respectively) is much lower than the H-abstraction at C6 (i.e. P6: −10.8 kcal mol−1). In respect to the energy required for each addition reaction (i.e. 8.1, 11.9, 9.1 and 4.7 kcal mol−1, corresponding to the addition at C1, C2, C3 and C4, respectively), it is found that the addition reaction at the C4 atom is the most favorable.
Acknowledgements
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2013.21.References
- Z. Dhaouadi, M. Nsangou, N. Garrab, E. H. Anouar, K. Marakchi and S. Lahmar, J. Mol. Struct.: THEOCHEM, 2009, 904, 35–42 CrossRef CAS
.
- M. S. Brewer, Compr. Rev. Food Sci. Food Saf., 2011, 10, 221–247 CrossRef CAS
.
- M. Suhaj, J. Food Compos. Anal., 2006, 19, 531–537 CrossRef CAS
.
- A. Wojdyło, J. Oszmiański and R. Czemerys, Food Chem., 2007, 105, 940–949 CrossRef
.
- M. C. Rojas and M. S. Brewer, J. Food Sci., 2007, 72, S282–S288 CrossRef CAS PubMed
.
- M. Nackz, R. Zadernowski and F. Shahidi, in Antioxidant Measurement and Applications, American Chemical Society, 2007, vol. 956, ch. 13, pp. 184–194 Search PubMed
.
- P.-D. Duh, G.-C. Yen, W.-J. Yen, B.-S. Wang and L.-W. Chang, J. Agric. Food Chem., 2004, 52, 8169–8176 CrossRef CAS PubMed
.
- I. F. Abdullin, E. N. Turova and G. K. Budnikov, J. Anal. Chem., 2001, 56, 557–559 CrossRef CAS
.
- A. Radovanović, B. Radovanović and B. Jovančićević, Food Chem., 2009, 117, 326–331 CrossRef
.
- G. Cao, E. Sofic and R. L. Prior, J. Agric. Food Chem., 1996, 44, 3426–3431 CrossRef CAS
.
- H. Wang, G. Cao and R. L. Prior, J. Agric. Food Chem., 1996, 44, 701–705 CrossRef CAS
.
- N. T. Dung, J. M. Kim and S. C. Kang, Food Chem. Toxicol., 2008, 46, 3632–3639 CrossRef CAS PubMed
.
- B.-S. Min, C. V. Thu, N. T. Dat, N. H. Dang, H.-S. Jang and T. M. Hung, Chem. Pharm. Bull., 2008, 56, 1725–1728 CrossRef CAS PubMed
.
- N. T. Dung, V. K. Bajpai, J. I. Yoon and S. C. Kang, Food Chem. Toxicol., 2009, 47, 449–453 CrossRef CAS PubMed
.
- Y. Sone, J.-K. Moon, T. T. Mai, N. N. Thu, E. Asano, K. Yamaguchi, Y. Otsuka and T. Shibamoto, J. Sci. Food Agric., 2011, 91, 2259–2264 CAS
.
- B. Min, T. Cuong, J.-S. Lee, B.-S. Shin, M. Woo and T. Hung, Arch. Pharm. Sci. Res., 2010, 33, 1665–1670 CrossRef CAS PubMed
.
- N. X. Dung, H. V. Luu, T. T. Khoi and P. A. Leclercq, J. Essent. Oil Res., 1994, 6, 661–662 CrossRef CAS
.
- R. Amorati, M. C. Foti and L. Valgimigli, J. Agric. Food Chem., 2013, 61, 10835–10847 CrossRef CAS PubMed
.
- M. C. Foti and R. Amorati, J. Pharm. Pharmacol., 2009, 61, 1435–1448 CrossRef CAS PubMed
.
- F. Bakkali, S. Averbeck, D. Averbeck and M. Idaomar, Food Chem. Toxicol., 2008, 46, 446–475 CrossRef CAS PubMed
.
- T. Kulisic, A. Radonic and M. Milos, Inhibition of lard oxidation by fractions of different essential oils%B, 2005, vol. 2005 Search PubMed
.
- K.-G. Lee and T. Shibamoto, J. Agric. Food Chem., 2002, 50, 4947–4952 CrossRef CAS PubMed
.
- M. T. Baratta, H. J. D. Dorman, S. G. Deans, A. C. Figueiredo, J. G. Barroso and G. Ruberto, Flavour Fragrance J., 1998, 13, 235–244 CrossRef CAS
.
- U. Neuenschwander, F. Guignard and I. Hermans, ChemSusChem, 2010, 3, 75–84 CrossRef CAS PubMed
.
- L. Valgimigli and D. A. Pratt, in Encyclopedia of Radicals in Chemistry, Biology and Materials, John Wiley & Sons Ltd, 2012, DOI:10.1002/9781119953678.rad055
.
- M. C. Foti and K. U. Ingold, J. Agric. Food Chem., 2003, 51, 2758–2765 CrossRef CAS PubMed
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef
.
- J. Tomasi, B. Mennucci and E. Cancès, J. Mol. Struct.: THEOCHEM, 1999, 464, 211–226 CrossRef CAS
.
- N. M. Thong, D. T. Quang, N. H. T. Bui, D. Q. Dao and P. C. Nam, Chem. Phys. Lett., 2015, 625, 30–35 CrossRef
.
- N. M. Thong, T. Duong, L. T. Pham and P. C. Nam, Chem. Phys. Lett., 2014, 613, 139–145 CrossRef CAS
.
- J. S. Wright, E. R. Johnson and G. A. DiLabio, J. Am. Chem. Soc., 2001, 123, 1173–1183 CrossRef CAS PubMed
.
- J. Rimarčík, V. Lukeš, E. Klein and M. Ilčin, J. Mol. Struct.: THEOCHEM, 2010, 952, 25–30 CrossRef
.
- J. E. Bartmess, J. Phys. Chem., 1994, 98, 6420–6424 CrossRef CAS
.
- P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, 6th edn, 1998 Search PubMed
.
- A. Urbaniak, M. Szeląg and M. Molski, Comput. Theor. Chem., 2013, 1012, 33–40 CrossRef CAS
.
- W. A. Donald, M. Demireva, R. D. Leib, M. J. Aiken and E. R. Williams, J. Am. Chem. Soc., 2010, 132, 4633–4640 CrossRef CAS PubMed
.
- K. K. Irikura, R. D. Johnson and R. N. Kacker, J. Phys. Chem. A, 2005, 109, 8430–8437 CrossRef CAS PubMed
.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
- I. B. Obot, D. D. Macdonald and Z. M. Gasem, Corros. Sci., 2015, 99, 1–30 CrossRef CAS
.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS
.
- R. P. Iczkowski and J. L. Margrave, J. Am. Chem. Soc., 1961, 83, 3547–3551 CrossRef CAS
.
- R. G. Parr, L. V. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS
.
- P.-C. Nam, M. T. Nguyen and A. K. Chandra, J. Phys. Chem. A, 2005, 109, 10342–10347 CrossRef CAS PubMed
.
- N. E. C. D. Almeida, I. D. Aguiar and D. R. Cardoso, J. Braz. Chem. Soc., 2015, 26, 2362–2368 Search PubMed
.
- F. S. Sharopov, M. Wink and W. N. Setzer, Nat. Prod. Commun., 2015, 10, 153–156 Search PubMed
.
- K. A. Youdim, S. G. Deans and H. J. Finlayson, J. Essent. Oil Res., 2002, 14, 210–215 CrossRef CAS
.
- http://webbook.nist.gov/chemistry/, 2015.
- M. I. Al-Joboury and D. W. Turner, J. Chem. Soc., 1964, 4434–4441, 10.1039/jr9640004434
.
- R. L. Prior, X. Wu and K. Schaich, J. Agric. Food Chem., 2005, 53, 4290–4302 CrossRef CAS PubMed
.
- N. Flores-Holguín, A. Aguilar-Elguézabal, L. M. Rodríguez-Valdez and D. Glossman-Mitnik, J. Mol. Struct.: THEOCHEM, 2008, 854, 81–88 CrossRef
.
- E. Osorio, E. G. Pérez, C. Areche, L. M. Ruiz, B. K. Cassels, E. Flórez and W. Tiznado, J. Mol. Model., 2013, 19, 2165–2172 CrossRef CAS PubMed
.
- I. B. Obot, S. Kaya, C. Kaya and B. Tüzün, Res. Chem. Intermed., 2015, 1–21, DOI:10.1007/s11164-015-2339-0
.
- G. Wang, Y. Xue, L. An, Y. Zheng, Y. Dou, L. Zhang and Y. Liu, Food Chem., 2015, 171, 89–97 CrossRef CAS PubMed
.
- A. Urbaniak, M. Szeląg and M. Molski, Comput. Theor. Chem., 2013, 1012, 33–40 CrossRef CAS
.
- Y. Xue, Y. Zheng, L. Zhang, W. Wu, D. Yu and Y. Liu, J. Mol. Model., 2013, 19, 3851–3862 CrossRef CAS PubMed
.
- J. Lengyel, J. Rimarcik, A. Vaganek and E. Klein, Phys. Chem. Chem. Phys., 2013, 15, 10895–10903 RSC
.
- A. Vagánek, J. Rimarčík, V. Lukeš and E. Klein, Comput. Theor. Chem., 2012, 991, 192–200 CrossRef
.
- M. Li, W. Liu, C. Peng, Q. Ren, W. Lu and W. Deng, Int. J. Quantum Chem., 2013, 113, 966–974 CrossRef CAS
.
- A. Pérez-González and A. Galano, Int. J. Quantum Chem., 2012, 112, 3441–3448 CrossRef
.
- A. Pérez-González and A. Galano, J. Phys. Chem. B, 2011, 115, 1306–1314 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra02683d |
| This journal is © The Royal Society of Chemistry 2016 |