Mechanism and free energy profile of base-catalyzed Knoevenagel condensation reaction†
Ellen V. Dalessandro,
Hugo P. Collin,
Marcelo S. Valle and
Josefredo R. Pliego Jr.*
Departamento de Ciências Naturais, Universidade Federal de São João del-Rei, 36301-160, São João del-Rei, MG, Brazil. E-mail: pliego@ufsj.edu.br
First published on 10th June 2016
Abstract
The Knoevenagel condensation reaction is a classical method for carbon–carbon bond formation. This reaction can be catalyzed by homogeneous or heterogeneous bases, and in the past ten years many different solid bases catalysts have been investigated. In this report, we have done a reliable theoretical analysis of the reaction mechanism and free energy profile of acetylacetone reaction with benzaldehyde catalyzed by methoxide ion in methanol solution. The analysis was extended for solventless conditions and solid base catalysis. We have found that the enolate addition to the benzaldehyde is a rapid step, contrary to general assumptions on the mechanism. The rate-determining step is the leaving of the hydroxide ion from the anionic intermediate, with a predicted overall free energy barrier of 28.8 kcal mol−1. This finding explains the experimental observation that more polar medium favor the reaction, once the transition state is product-like and involves the formation of the highly solvated hydroxide ion. The present results provides useful insights on this reaction system.
Introduction
Reactions leading to carbon–carbon bond formation play a very important role in synthetic organic chemistry. Among the many possible processes, the Knoevenagel reaction is a classical example. The reaction needs a catalyst to proceed and the most usual homogeneous catalyst is an amine.1–3 A recent report has indicated that a combination of N-methyl-piperidine and a phenol compound is an effective catalyst.4 In the past two decades, many solid superbase heterogeneous catalysts have been developed,5 and some examples of heterogeneous catalysts of Knoevenagel reaction are modified Mg–Al hydrotalcite,6 modified zeolites,7,8 alkali modified metal oxide,9 amine immobilized on silica gel10 and 1,4-diazabicyclo[2.2.2]octane immobilized on polystyrene,11 amino-based metal–organic frameworks,12,13 bifunctional acid–base ionic liquid,14 proton sponges in mesoporous sílica,15 and several other catalysts.13,16–20 Recently, List and co-workers have reported the first example of a catalytic asymmetric version of the Knoevenagel reaction.21The reaction mechanism can follow at least two main pathways: (a) iminium ion formation, in the case of primary and secondary amines, and (b) formation of enolate via deprotonation by a tertiary amine, homogeneous base or solid base. In the present work, we have investigated the enolate mechanism and our results should provide important insights on the base catalyzed process in both homogeneous and heterogeneous conditions. A general view of the mechanism is presented in Scheme 1. The species (B−) can be a homogeneous or heterogeneous base. In the second case, we consider that the proton exchange step takes place through a rapid equilibrium at the surface, and the remaining of the reaction occurs in solution.
In experimental studies, Zhang et al. have proposed a mechanism and kinetic model with enolate addition to benzaldehyde as the rate determining step in conditions of no solvent and temperature of 393 K for ethyl acetoacetate conversion.7 In the same way, Ziolek and co-workers have investigated alkali metal-modified oxide supports for catalyzing the same reaction in high temperature and no solvent. They have investigated several catalysts and measured the reaction kinetics.9 Yet another mechanism, not investigated in this work, is the possibility of a rate determining reaction step to take place on the solid catalyst surface. Thus, Saravanamurugan et al. has investigated the zeolite heterogeneous catalyzed Knoevenagel reaction and have proposed a mechanism taking place on the catalyst surface.8
Some theoretical studies of the Knoevenagel reaction have been published.14,22,23 Although these studies provide insights on the mechanism, a reliable picture of the process needs an accurate theoretical approach. Nevertheless, in some cases the authors have used the B3LYP functional for calculating energy, which is not reliable for this system,24 or have not investigated all the mechanisms. It is also important the inclusion of the solvent effect, correction for adequate standard state, and computation of the Gibbs free energy. As it was emphasized by Plata and Singleton,25 multistep ionic reactions in polar solvents requires careful use of theoretical methods. Thus, it is important an adequate choice of the electronic structure theory approach and reliable treatment of the solvent effect. In this report, we have used high level of theory for electronic energies and a sound approach for including solvent effects, mixing SMD solvation model with empirical corrections. The aim of this work is to present a reliable mechanism and free energy profile for a model Knoevenagel reaction. The system is the Knoevenagel condensation of acetylacetone with benzaldehyde, catalyzed by methoxide ion in methanol solution, presented in Scheme 2.
Theoretical methods
The reaction system presented in Scheme 2 was investigated by theoretical calculations. We have included the solvent effect on the geometry optimizations and frequencies, leading to more reliable description of this highly polar reaction. The optimizations were done with the X3LYP functional26 and the 6-31G(d) basis set for carbon and hydrogen, and 6-31+G(d) basis set for oxygen. We have named this basis set as 6-31(+)G(d). The solvent effect in the optimizations was included through the CPCM method27–32 for methanol solvent, and using 240 tesserae for atom to obtain more reliable potential of mean force surface.33 Following this CPCM/X3LYP/6-31(+)G(d) optimizations, we have done the corresponding harmonic frequency calculations. In order to obtain accurate electronic energies, we have done single point energy calculations with the X3LYP and M08-HX34 functionals using the TZVPP basis set,35 augmented with sp diffuse functions on the oxygen atom. Additional calculations at higher level of theory, the LPNO-CEPA/1 method36–38 in conjunction with the ma-TZVPP basis set,39 were also performed.A comment should be done on our choice of the electronic structure methods. The X3LYP (and the closely related B3LYP) functional predicts reliable geometries and harmonic frequencies. However, it may not be accurate for reaction energies. On the other hand, the M08-HX functional is much more reliable for reaction energies as documented by Zhao and Truhlar.40 Thus, M08-HX calculations should provide more confident energies. We have also used a wave function based method, the LPNO-CEPA/1, recently developed for reliable calculations of medium size systems.41 The performance of this method is between the CCSD and CCSD(T) approaches, and it will be considered our best electronic energy values.
The CPCM optimizations include the electrostatic contribution to the solvation free energy, the most important effect. However, for more reliable solvation contribution, we have done single point energy calculations using the SMD method42 and the X3LYP/6-31(+)G(d) electronic density. Thus, the reaction and activation free energy in solution were computed through the eqn (1) and (2) below:
| ΔGsol = ΔEel + ΔGvrt + ΔΔGsolv | (1) |
| ΔG‡sol = ΔE‡el + ΔG‡vrt + ΔΔG‡solv | (2) |
The first term in the right side is the electronic energy (LPNO-CEPA/1), the second term is the vibrational, rotational and translational free energy contribution (CPCM/X3LYP harmonic frequency calculation, corrected to 1 mol L−1 standard state) and the last term is the solvation free energy contribution (SMD). All the X3LYP and M08-HX calculations were carried out with the GAMESS program,43,44 and the LPNO-CEPA/1 method was done with the ORCA program system.45
Although the SMD model performs well for neutral solutes in methanol solution,46 this model has a systematic deviation in the solvation free energy of ions.47 Thus, we have done empirical corrections in the relative free energy in order to obtain more reliable free energy reaction profile. The first correction was done in the calculation of pKa of some species, leading to the respective anions. The calculation is based in the proton exchange reaction with the phenoxide ion:
| HA + PhO−→A−+ PhOH ΔGdep(HA–PhOH) |
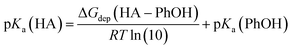 | (3) |
In the next step, it is done an empirical correction in the pKa, through the equation:47
| pKa(HA, corrected) = 0.6025pKa(HA) + 5.691 |
Based on this corrected pKa's, we have obtained the free energy for deprotonation reaction in methanol solution:
| HA → A− + H+ ΔGdep (HA) |
The calculated values are presented in Table 1. These values, the relative free energy of neutral species, and the free energy of activation for transition states closer to the reference point were used to obtain the corrected free energy profile. The next equations show how each calculation was done, taking acetylacetone, benzaldehyde and methoxide ion as the reference point (zero free energy).
| Values relative to benzaldehyde + acetylacetone + methoxide | ||||||
|---|---|---|---|---|---|---|
| X3LYPb | M08-HXb | LPNO-CEPA/1c | ΔGmold | ΔΔGsolve | ΔGsolf | |
| a Units of kcal mol−1. Standard state of 1 mol L−1, 25 °C, for free energy values.b Using the TZVPP + diff. basis set.c Using the ma-TZVPP basis set.d We have defined ΔGmol = ΔEel + ΔGvrt, and ΔEel at LPNO-CEPA/1 level.e Solvent effect.f Solution phase free energy. | ||||||
| Enol isomer | −5.58 | −2.64 | −0.78 | 2.48 | 1.70 | |
| MS1 | −0.72 | −13.14 | −11.93 | 3.37 | 1.81 | 5.18 |
| P1 + H2O | 4.90 | 0.57 | 0.75 | 2.66 | −6.50 | −3.84 |
| Enolate + benzaldehyde | −38.32 | −37.78 | −35.36 | −33.22 | 16.94 | −16.28 |
| TS2N | 26.79 | 31.39 | 44.43 | −0.95 | 43.48 | |
| Calculation of pKa and deprotonation free energy in methanol solution | ||||||
|---|---|---|---|---|---|---|
| ΔGmol | ΔΔGsolv | ΔGsol | pKa | pKa (corr.) | ΔGdep | |
| CH3OH | 33.66 | −17.51 | 16.15 | 26.17 | 21.46 | 29.27 |
| H2O | 41.82 | −25.45 | 16.37 | 26.33 | 21.55 | 29.40 |
| Acetylacetone | 0.43 | −0.57 | −0.14 | 14.23 | 14.26 | 19.46 |
| MS1(OH) | 3.68 | 12.65 | 16.33 | 26.30 | 21.54 | 29.38 |
| MS1(CH) | −3.61 | 3.93 | 0.32 | 14.56 | 14.47 | 19.73 |
| Final relative free energy values in relation to benzaldehyde + acetylacetone + methoxide, with empirical corrections | |
|---|---|
| ΔG | |
| TS2N | 43.5 |
| MS1 | 5.2 |
| Enolate | −9.8 |
| TS2 | 5.8 |
| MS1a | 5.3 |
| MS1b | −4.4 |
| TS4 | 19.0 |
| P1 + OH− | −3.7 |
| P1 + H2O | −3.8 |
Enolate:
| μ*(enolate) = μ*(acetylacetone) + ΔGdep(acetylacetone) − ΔGdep(MeOH) | (4) |
MS1a:
| μ*(MS1a) = μ*(MS1) + ΔGdep(MS1a) − ΔGdep(MeOH) | (5) |
TS2:
| μ*(TS2) = μ*(MS1a) + ΔG‡sol(MS1a → TS2, SMD) | (6) |
MS1b:
| μ*(MS1b) = μ*(MS1) + ΔGdep(MS1b) − ΔGdep(MeOH) | (7) |
P1 + OH−
| μ*(P1) + μ*(OH−) = μ*(P1) + μ*(H2O) + ΔGdesp(H2O) − ΔGdep(MeOH) | (8) |
TS4:
| μ*(TS4) = μ*(P1) + μ*(OH−) + ΔG‡sol(P1 + OH− → TS4, SMD) | (9) |
These equations leads to more reliable stability of the ions, and better barriers of the transition states, because we have used transition states with higher similarity with the reference point of the reaction. In addition, we have found the SMD model has a reasonable performance for ion–molecule reactions in methanol solution.48
Experiments
We have done some experiments to provide more support to the view of this reaction obtained from theoretical calculations.Reaction using 10 mol% of NaOH
To a solution of acetylacetone (0.51 mL, 0.50 g, 5.0 mmol) and benzaldehyde (0.51 mL, 0.53 g, 5.0 mmol) in methanol (10.0 mL) was added NaOH (0.02 g, 0.5 mmol) at room temperature. The reaction mixture was stirred for 1 h and then warmed to reflux temperature during 24 h. The reaction was monitored by TLC (Thin Layer Chromatography) and no reaction was observed.Reaction using 100 mol% of NaOH
To a solution of acetylacetone (0.51 mL, 0.50 g, 5.0 mmol) and benzaldehyde (0.51 mL, 0.53 g, 5.0 mmol) in methanol (10.0 mL) was added 0.5 mmol of NaOH at room temperature. After 24 h of reaction under reflux, the reaction mixture was diluted with ethyl acetate (EtOAc) (10.0 mL) and saturated aqueous NaCl (5.0 mL). The layers were separated, and the aqueous layer was extracted with EtOAc (2 × 10.0 mL). The organic extracts were combined, dried over Na2SO4, and evaporated to dryness under vacuum. The residue obtained was purified by chromatography on silica gel (EtOAc/heptane 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 then EtOH) to furnish two major fractions containing each one a mixture of compounds that could not be isolated. Polar fraction (Rf 0.4–0.1; EtOAc/heptane 3
7 then EtOH) to furnish two major fractions containing each one a mixture of compounds that could not be isolated. Polar fraction (Rf 0.4–0.1; EtOAc/heptane 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7) 1H NMR (500 MHz, CDCl3): δ 7.2 (s, l), 4.10 (dd, 14.3, 7.2 Hz), 3.3 (s), 2.61 (s), 2.15 (d, 1.5 Hz), 2.06 (s), 2.02 (s), 1.99 (s, l), 1.24 (m, 7.0, 2.3 Hz) ppm; 13C NMR (125 MHz, CDCl3): 197.3, 182.9, 129.4, 127.3, 126.4, 68.9, 60.5, 29.8, 21.1, 14.2. Apolar fraction (Rf 0.8–0.4; EtOAc/heptane 3
7) 1H NMR (500 MHz, CDCl3): δ 7.2 (s, l), 4.10 (dd, 14.3, 7.2 Hz), 3.3 (s), 2.61 (s), 2.15 (d, 1.5 Hz), 2.06 (s), 2.02 (s), 1.99 (s, l), 1.24 (m, 7.0, 2.3 Hz) ppm; 13C NMR (125 MHz, CDCl3): 197.3, 182.9, 129.4, 127.3, 126.4, 68.9, 60.5, 29.8, 21.1, 14.2. Apolar fraction (Rf 0.8–0.4; EtOAc/heptane 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7); 1H NMR (500 MHz, CDCl3): δ 7.39 (dd, 7.0, 1.4 Hz), 7.36 (d, 1.8 Hz), 7.35 (d, 1.7 Hz), 7.34 (d, 1.5 Hz) 7.32 (s), 7.30 (s), 7.28 (d, 2.1 Hz), 7.27 (s), 7.24 (s), 7.22 (s), 7.19 (t, 4.2 Hz), 7.17 (s), 6.91 (m), 6.09 (d, 2.1 Hz), 4.03 (m, 7.2 Hz), 2.94 (dd, 4.0, 2.1 Hz), 2.6 (m), 1.96 (s), 1.17 (t, 14.2, 7.2 Hz). Spectra in the ESI.†
7); 1H NMR (500 MHz, CDCl3): δ 7.39 (dd, 7.0, 1.4 Hz), 7.36 (d, 1.8 Hz), 7.35 (d, 1.7 Hz), 7.34 (d, 1.5 Hz) 7.32 (s), 7.30 (s), 7.28 (d, 2.1 Hz), 7.27 (s), 7.24 (s), 7.22 (s), 7.19 (t, 4.2 Hz), 7.17 (s), 6.91 (m), 6.09 (d, 2.1 Hz), 4.03 (m, 7.2 Hz), 2.94 (dd, 4.0, 2.1 Hz), 2.6 (m), 1.96 (s), 1.17 (t, 14.2, 7.2 Hz). Spectra in the ESI.†
Results and discussion
Mechanism and transition states
We have investigated the mechanistic possibilities presented in Scheme 1, and included the direct reaction of acetylacetone to benzaldehyde. This transition state, named TS2N, is presented in Fig. 1. We can notice that this step needs an almost complete transfer of proton from acetylacetone in the enol form to benzaldehyde before to reach the transition state. The carbon–carbon distance is very high, 2.51 Å. Although the reaction free energy profile will be discussed in the next section, we can anticipate that its free energy barrier is very high, 43.5 kcal mol−1 (Table 1). Thus, this pathway is not viable and no reaction will take place by this mechanism. | ||
| Fig. 1 Transition states and a key minimum for the acetylacetone (enolate) reaction with benzaldehyde in methanol solvent. | ||
In the anionic mechanism (Scheme 1), the nucleophilic attack of the enolate ion to the benzaldehyde corresponds to TS2. The carbon–carbon distance in this structure is 1.79 Å and the corresponding free energy barrier is only 15.6 kcal mol−1. Therefore, this process is very favorable and leads to a rapid kinetics. The formed product, MS1a, has a structure close to TS2, with a slightly shorter carbon–carbon distance of 1.77 Å. In the same way, it is slightly less stable, staying 15.1 kcal mol−1 above of the enolate plus benzaldehyde reactants. The other transition state is TS4, and corresponds to leaving of the hydroxide ion from MS1b (Fig. 2) in step 4. The carbon–oxygen distance is high, 2.32 Å, suggesting a transition state very similar to the products.
Other point which deserves attention is the comparison between the X3LYP functional and the reliable LPNO-CEPA/1 method. For example, the energy of the MS1 structure in relation to the reactants is −11.9 kcal mol−1 at LPNO-CEPA/1 level, whereas the X3LYP method predicts −0.7 kcal mol−1, an error of 11 kcal mol−1. On the other hand, the M08-HX functional performs much better, with an energy of −13.1 kcal mol−1 and a deviation of only 1.2 kcal mol−1. In the case of critical TS4 structure, the X3LYP functional deviates 5 kcal mol−1 from the LPNO-CEPA/1 method. Considering the similarity between X3LYP and B3LYP functionals, both of them should not be used for predicting reaction energies for this class of reactions, although these methods are reliable for calculating geometries.
Theoretical calculation of the pKa of some species in methanol
We have done a reliable calculation of the pKa of key species in methanol. The results are presented in Table 1. Methanol and water have calculated pKa of 21.5 and 21.6, respectively, in good agreement with the experimental value of 18.6 for methanol.49 For comparison, the uncorrected calculated pKa of methanol is 26.2. For acetylacetone, we have predicted a pKa of 14.3. For the intermediate MS1 structure, the pKa's values are 21.5 for deprotonation of the OH group and 14.5 for deprotonation of the CH group.Free energy profile
A general view of the reaction is presented in Fig. 2. The reaction steps of the ionic mechanism are numbered in line with Scheme 1. In the uncatalyzed mechanism, there is an isomerization from keto to enol form before the reaction. The barrier for this nucleophilic attack is very high, 43.5 kcal mol−1, and the formed product intermediate, MS1, is 5.2 kcal mol−1 above of the reactants. Thus, for this system, the keto-alcohol intermediate should not be observed as a reaction product. Once the barrier by this pathway is very unfavorable, we have not investigated the uncatalyzed elimination step.The base catalyzed mechanism begin by deprotonation of the acetylacetone, a process favorable by 9.8 kcal mol−1. This easy deprotonation is due the predicted pKa of acetylacetone in methanol, 14.3. For methanol, the predicted pKa is 21.5. Based on this free energy, all of the methoxide base will react. We should emphasize that the methoxide base is present in catalytic quantity.
The second step is the nucleophilic attack of the enolate to the benzaldehyde. The small barrier of 15.6 kcal mol−1 indicates that this step is very rapid and it is not rate determining. Then, the mechanistic view of this reaction needs be revised. The MS1a intermediate is very similar to TS2 and is slightly more stable. In the next step, there is isomerization to MS1b, involving proton exchange with the solvent. Because these reactions are usually rapid, we consider this step as a rapid equilibrium. The MS1b structure is only 5.4 kcal mol−1 above of the enolate plus benzaldehyde reactants, and is more stable than MS1a due to high charge dispersion. We should observe that at microscopic level, the MS1a should take a proton of the solvent to generate MS1. In the next step, it lose a proton to the medium to become MS1b. However, considering these steps are rapid and MS1 is less stable than MS1b, we have not taken in account these additional equilibria.
The critical step is the elimination of the hydroxide ion via TS4. The structure is 19 kcal mol−1 above of the neutral reactants and 28.8 kcal mol−1 above of the enolate plus benzaldehyde. Therefore, this is the rate-determining step and the overall barrier for this process is 28.8 kcal mol−1, resulting in a very slow kinetics at room temperature. The hydroxide ion eliminated can exchange proton with methanol, leading to the final product and reforming the methoxide catalyst. The product is 3.8 kcal mol−1 below of the neutral reactants, indicating that this process is thermodynamically favorable. Therefore, the catalytic process is thermodynamically viable. On the other side, the final product plus methoxide is 6 kcal mol−1 above of the enolate ion plus benzaldehyde. It means that the use of stoichiometric quantity of methoxide ion makes the reaction thermodynamically inviable. Consequently, increasing the quantity of catalyst, decrease the maximum yield. Thus, using 10 mol% of the catalyst means that the maximum yield will be 90%. This fact is due the high basicity of the methoxide ion. Hence, using less basic catalyst, with pKa close to the acetylacetone reactant, is thermodynamically advantageous.
The free energy profile in Fig. 2 allow us to write a kinetic law for the catalyzed mechanism. The reaction rate expression is:
 | (10) |
| kobs = k4K2K3Cbase = 4.8 × 10−10 s−1 | (11) |
Even considering the ebullition point of methanol, 64.7 °C, and taking the same free energy, we can estimate:
| kobs = 1.6 × 10−7 s−1 | (12) |
Experimental observations
The experiments in methanol solvent using 10 mol% of NaOH catalyst point out that no reaction product was observed. This is in agreement with our predicted kinetics, because based on eqn (10), we should observe less than 1% of product. In the case of reaction using 100 mol% of NaOH, the NMR analysis of aqueous and organic fractions showed that benzaldehyde was fully consumed, since only a trace chemical shift at 9.94 ppm was detected. The presence of only one chemical shift at 199.7 ppm proves that no product was obtained, since it has two chemical shifts on that region. At 143.5 and 68.9 ppm we can note the presence of chemical shifts from the benzyl alcohol. In addition, there are chemical shifts from the carboxylic acid at 175.3 and 135.9. Other chemical shifts from the protonated and unprotonated acetylacetone can be seen at 182.9, 60.5, 40.7 and 33.7 ppm. Thus, using 100 mol% of NaOH base in methanol under reflux, no Knoevenagel condensation product was obtained. Rather, we have observed the Cannizzaro reaction. This is in line of our prediction that the Knoevenagel product is thermodynamically unfavorable when using 100 mol% of NaOH.Comparison with experimental data for similar system
Rodriguez et al. have reported the kinetics of the reaction of ethyl acetoacetate (and ethyl cyanoacetate) with benzaldehyde catalyzed by 1,8-bisdimethylamino naphthalene (DMAN, a proton sponge) in different solvents.50 They have observed an important solvent effect: the reaction rate increases with the polarity. Thus, the reaction of ethyl acetoacetate in DMSO was observed, while in acetonitrile not. The DMSO and acetonitrile have similar solvation of cations. However, for small anions like the fluoride ion, the solvation in DMSO is 8 kcal mol−1 more negative.51 This is in line with our model, where the formation of a small and highly solvated OH− ion in TS4 should be sensible to the solvent. Other important observation is the much higher reactivity of ethyl cyanoacetate in DMSO. Thus, while they have observed 18% conversion of ethyl acetoacetate during 120 min in DMSO and 80 °C, the ethyl cyanoacetate has presented 50% conversion in a time of 50 min in room temperature and DMSO solvent. We can make a rough estimate of the catalyzed free energy barrier for ethyl acetoacetate reaction, considering that the reaction is first order in the reactants and in the catalyst, finding a value of 26 kcal mol−1. This is in reasonable agreement with our value, even considering the differences in the reactants and solvents.Comparison with literature data for OH− addition to activated alkene
The reaction kinetics of hydroxide ion addition to activated alkenes has been reviewed.52 In the case of benzylideneacetylacetone (P1 in this paper, see Fig. 2), Bernasconi et al. have reported an overall second order rate constant (k−4 in this work, in their report) of 0.05 L mol−1 s−1 for reverse of step 4, leading to ΔG‡ = 19.2 kcal mol−1 in aqueous solution.53 Our calculation is in methanol. However, the reaction rate in both solvents must be close, considering these solvents has similar solvation of ions. Classical measurements of the rate constant of anion-molecule reactions in water and methanol support this view.54 Thus, considering our free energy profile (Fig. 2), the reverse of step 4 has a free energy barrier of 22.7 kcal mol−1, in good agreement with the experimental results. Other important observation from Bernasconi et al. results is that the reverse reaction is thermodynamically favorable, once they have observed the formation of benzaldehyde and acetylacetone products. This finding provides more support on the quality of our predicted free energy profile.
in their report) of 0.05 L mol−1 s−1 for reverse of step 4, leading to ΔG‡ = 19.2 kcal mol−1 in aqueous solution.53 Our calculation is in methanol. However, the reaction rate in both solvents must be close, considering these solvents has similar solvation of ions. Classical measurements of the rate constant of anion-molecule reactions in water and methanol support this view.54 Thus, considering our free energy profile (Fig. 2), the reverse of step 4 has a free energy barrier of 22.7 kcal mol−1, in good agreement with the experimental results. Other important observation from Bernasconi et al. results is that the reverse reaction is thermodynamically favorable, once they have observed the formation of benzaldehyde and acetylacetone products. This finding provides more support on the quality of our predicted free energy profile.
Although the good agreement of our results with the Bernasconi et al. kinetics data, as well as the higher thermodynamic stability of the enolate plus benzaldehyde in relation to P1, they have suggested the reverse of step 4 is not rate determining. Rather, they have proposed that decomposition of MS1b to the acetylacetone and benzaldehyde reactants is slower. It is important to emphasize that the kinetics analysis has some assumptions, which can lead to mistake. Our analysis point out that the reverse of step 4 is the rate-determining one and the decomposition of MS1b is very rapid, with ΔG‡ = 10.2 kcal mol−1. Therefore, we think their analysis should be revisited on the light of our results.
Base catalyzed heterogeneous catalysis
The free energy profile calculated in this work can be adapted for the reaction involving the solid base. In this case, the first step in Scheme 1 involves a proton exchange with base sites on the solid surface. Thus, the equilibrium equation can be written as:
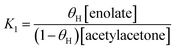 | (13) |
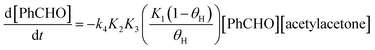 | (14) |
The term in parenthesis is related to the strength of the base and it should be smaller than 1. Stronger base leads to higher value of this term. From a kinetics viewpoint, this term add a “free energy barrier” to the overall barrier of 28.8 kcal mol−1, considering the reaction of the enolate to benzaldehyde. We should consider that in experimental conditions, there is not methanol solvent. Nevertheless, the Table 1 point out the solvent effect from enolate plus benzaldehyde to TS4 has ΔΔGsolv = 0. Considering that we have done a correction for this step, the solvent effect should be some kcal mol−1 negative, in line with the idea that more polar media favor the reaction. Thus, we should observe an increase of the reaction rate with more polar solvent, although the effect amount few kcal mol−1.
In order to apply the model proposed in this work, lets analyze some experimental data of Ziolek and co-workers.9 Those authors have measured the Knoevenagel reaction of benzaldehyde with ethyl acetoacetate, using potassium-doped silica as catalyst. They have observed the formation of 75% of the condensation product in a time of 300 min at 413 K without solvent. Thus, considering a concentration of 5 mol L−1 for each reactant, we can estimate an observed free energy barrier of 33 kcal mol−1. This result is in line with our free energy barrier, even considering that our reaction is simulated in methanol solvent. Therefore, we believe that the present analysis provides the real free energy profile for this important and classical reaction system for both homogeneous and heterogeneous base catalysis.
Conclusion
The mechanism and free energy profile of the Knoevenagel condensation reaction between benzaldehyde and acetylacetone catalyzed by methoxide ion in methanol solution have been investigated by theoretical methods. It was found that the nucleophilic addition of the enolate to benzaldehyde is rapid and leads to the unstable intermediate MS1a, similar to the transition state. This species can rearrange to MS1b carbanion and the rate-determining step is the hydroxide ion elimination from this intermediate, with an overall free energy barrier of 28.8 kcal mol−1. The analysis was extended to solid base catalysis and solventless conditions, suggesting the important role of base strength to generate enolate on this low polarity conditions. Based on these findings, any improvement of the catalytic efficiency should pay attention on the hydroxide ion elimination step.Acknowledgements
The authors thank the agencies CNPq, FAPEMIG, and CAPES for support. This work is a collaboration research project of members of the Rede Mineira de Química (RQ-MG) supported by FAPEMIG (Project: CEX-RED-00010-14).References
- A. Erkkilä, I. Majander and P. M. Pihko, Chem. Rev., 2007, 107, 5416 CrossRef PubMed.
- Y. Wang, Z.-C. Shang, T.-X. Wu, J.-C. Fan and X. Chen, J. Mol. Catal. A: Chem., 2006, 253, 212 CrossRef CAS.
- B. List, Angew. Chem., Int. Ed., 2010, 49, 1730 CrossRef CAS PubMed.
- S. K. Panja, N. Dwivedi and S. Saha, RSC Adv., 2015, 5, 65526 RSC.
- L. Chen, J. Zhao, S.-F. Yin and C.-T. Au, RSC Adv., 2013, 3, 3799 RSC.
- M. Lakshmi Kantam, B. M. Choudary, C. Venkat Reddy, K. Koteswara Rao and F. Figueras, Chem. Commun., 1998, 1033 RSC.
- X. Zhang, E. S. Man Lai, R. Martin-Aranda and K. L. Yeung, Appl. Catal., A, 2004, 261, 109 CrossRef CAS.
- S. Saravanamurugan, M. Palanichamy, M. Hartmann and V. Murugesan, Appl. Catal., A, 2006, 298, 8 CrossRef CAS.
- V. Calvino-Casilda, R. M. Martín-Aranda, A. J. López-Peinado, I. Sobczak and M. Ziolek, Catal. Today, 2009, 142, 278 CrossRef CAS.
- K. Isobe, T. Hoshi, T. Suzuki and H. Hagiwara, Mol. Diversity, 2005, 9, 317 CrossRef CAS PubMed.
- D.-Z. Xu, S. Shi and Y. Wang, RSC Adv., 2013, 3, 23075 RSC.
- J. Gascon, U. Aktay, M. D. Hernandez-Alonso, G. P. M. van Klink and F. Kapteijn, J. Catal., 2009, 261, 75 CrossRef CAS.
- A. Burgoyne and R. Meijboom, Catal. Lett., 2013, 143, 563 CrossRef CAS.
- M. Boronat, M. J. Climent, A. Corma, S. Iborra, R. Montón and M. J. Sabater, Chem.–Eur. J., 2010, 16, 1221 CrossRef CAS PubMed.
- E. Gianotti, U. Diaz, S. Coluccia and A. Corma, Phys. Chem. Chem. Phys., 2011, 13, 11702 RSC.
- K. Sugino, N. Oya, N. Yoshie and M. Ogura, J. Am. Chem. Soc., 2011, 133, 20030 CrossRef CAS PubMed.
- G. Li, J. Xiao and W. Zhang, Green Chem., 2012, 14, 2234 RSC.
- X. Dong, Y. Hui, S. Xie, P. Zhang, G. Zhou and Z. Xie, RSC Adv., 2013, 3, 3222 RSC.
- G. B. B. Varadwaj, S. Rana and K. M. Parida, Dalton Trans., 2013, 42, 5122 RSC.
- L. Zhang, H. Wang, Z. Qin, J. Wang and W. Fan, RSC Adv., 2015, 5, 22838 RSC.
- A. Lee, A. Michrowska, S. Sulzer-Mosse and B. List, Angew. Chem., Int. Ed., 2011, 50, 1707 CrossRef CAS PubMed.
- G. Frapper, C. Bachmann, Y. Gu, R. Coval De Sousa and F. Jerome, Phys. Chem. Chem. Phys., 2011, 13, 628 RSC.
- E. Bermúdez, O. N. Ventura and P. Saenz Méndez, J. Phys. Chem. A, 2010, 114, 13086 CrossRef PubMed.
- R. Singh, T. Tsuneda and K. Hirao, Theor. Chem. Acc., 2011, 130, 153 CrossRef CAS.
- R. E. Plata and D. A. Singleton, J. Am. Chem. Soc., 2015, 137, 3811 CrossRef CAS PubMed.
- X. Xu, Q. Zhang, R. P. Muller and W. A. Goddard III, J. Chem. Phys., 2005, 122, 014105 CrossRef PubMed.
- H. Li and J. H. Jensen, J. Comput. Chem., 2004, 25, 1449 CrossRef CAS PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem., 1998, 102, 1195 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed.
- E. Cances, C. Le Bris, B. Mennucci and J. Tomasi, Math. Models Methods Appl. Sci., 1999, 9, 35 CrossRef.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027 CrossRef CAS.
- C. M. Silva, I. C. Dias and J. R. Pliego, Org. Biomol. Chem., 2015, 13, 6217 CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- T. Schwabe, J. Comput. Chem., 2012, 33, 2067 CrossRef CAS PubMed.
- F. Neese, A. Hansen, F. Wennmohs and S. Grimme, Acc. Chem. Res., 2009, 42, 641 CrossRef CAS PubMed.
- F. Wennmohs and F. Neese, Chem. Phys., 2008, 343, 217 CrossRef CAS.
- J. J. Zheng, X. F. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 669 CrossRef CAS.
- F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, p. 1167 Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73 CrossRef CAS.
- C. C. Zanith and J. R. Pliego Jr, J. Comput.-Aided Mol. Des., 2015, 29, 217 CrossRef CAS PubMed.
- E. L. M. Miguel, P. L. Silva and J. R. Pliego, J. Phys. Chem. B, 2014, 118, 5730 CrossRef CAS PubMed.
- E. L. M. Miguel, C. I. L. Santos, C. M. Silva and J. R. Pliego Jr, J. Braz. Chem. Soc., 2016 DOI:10.5935/0103-5053.20160095.
- C. Reichardt, Solvents and Solvent Effects, in Organic Chemistry, Wiley-VHC, Weinheim, Germany, 2011 Search PubMed.
- I. Rodriguez, G. Sastre, A. Corma and S. Iborra, J. Catal., 1999, 183, 14 CrossRef CAS.
- N. F. Carvalho and J. R. Pliego, Phys. Chem. Chem. Phys., 2015, 17, 26745 RSC.
- C. F. Bernasconi, Tetrahedron, 1989, 45, 4017 CrossRef CAS.
- C. F. Bernasconi, M. W. Stronach and A. Kanavarioti, J. Org. Chem., 1994, 59, 3806 CrossRef CAS.
- A. J. Parker, Chem. Rev., 1969, 69, 1 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The coordinates of the optimized structures and the NMR spectra are available. See DOI: 10.1039/c6ra10393f |
| This journal is © The Royal Society of Chemistry 2016 |



