Experimental determination and model correlation for the solubilities of trialkyl phosphates in supercritical carbon dioxide
K. C. Pitchaiaha,
N. Sivaraman*a,
Neha Lambab and
Giridhar Madras b
b
aChemistry Group, Indira Gandhi Centre for Atomic Research, Kalpakkam-603102, India. E-mail: sivaram@igcar.gov.in; Fax: +91-044-27480065; Tel: +91-044-27480500-24166
bDepartment of Chemical Engineering, Indian Institute of Science, Bangalore-560012, India
First published on 19th May 2016
Abstract
The solubilities of a series of trialkyl phosphates in supercritical carbon dioxide have been investigated. The solubility measurement was carried out using a dynamic flow method. The measurements were performed at 313, 323 and 333 K and in the pressure range of 10 to 25 MPa. The trialkyl phosphates were found to be highly soluble in supercritical carbon dioxide and the solubilities were in the range of 0.01 to 0.1 mol fraction. The solubility of trialkyl phosphates increases with an increase in pressure at constant temperature. A reverse behavior was observed, wherein the solubilities decreased with increase in temperature in the investigated pressure region. At constant temperature and pressure, the solubilities of the trialkyl phosphates decrease with the alkyl chain length. The solubility data was found to be consistent with the Mendez–Teja model. The solubilities were correlated by the Chrastil model and an association model based on the van Laar activity coefficient model with absolute deviations of less than 10%. A key result is that the model parameters based on the association model varied linearly with the carbon number.
1. Introduction
Supercritical Fluid Extraction (SFE) of metal ions from diverse matrices is considered as an environmentally friendly alternative to conventional solvent extraction. SFE is an attractive technique for nuclear applications because it can minimize the amount of liquid waste generation. Supercritical fluids have many interesting properties such as liquid-like densities, high diffusivity, low viscosity and low surface tension.1,2 CO2 is a widely used supercritical fluid and is considered as a green solvent. It has moderate critical constants and it is also inexpensive, non-flammable, non-toxic and easily recyclable. Supercritical carbon dioxide (SCCO2) has several applications in material synthesis and processing3 and it is also used as a solvent for the extraction of non-polar and moderately polar compounds.2 Extraction of metal ions using neat CO2 is not possible because of its weak solute–solvent interactions and charge neutralization.4,5 However, metal ion extraction can be achieved by complexing them with suitable ligands and the resultant metal complex could become quite soluble in SCCO2.4,6 The extraction behavior mainly depends on the (a) solubility of ligand/complexing agent and (b) solubility and stability of the resultant metal-complex in SCCO2.7 The primary criterion for the use of a ligand in SFE is that it should have appreciable solubility in SCCO2. Therefore, the solubility of ligand as well as that of metal complex plays a crucial role in designing and optimization of a SFE process.The organophosphorus compounds contain the phosphoryl group that is used in the extraction and purification of various metal ions in chemical and hydrometallurgical industries. Extraction of actinides from acidic waste solutions is an important task in nuclear waste management that can reduce the radiological burden of the waste. Neutral organophosphorus compounds such as phosphates, phosphonates, phosphinates and phosphine oxides have been used for solvent extraction of metal ions for the extraction and recovery of actinides from liquid and solid matrices.8–10 These compounds have wide range of applications in nuclear industry from mining of nuclear materials to reprocessing of the spent nuclear fuel. The extraction power of these molecules was found to be increasing in the order: phosphates < phosphonates < phosphinates < phosphine oxides.11 Among these, trialkyl phosphate based molecules have been used for the metal ion extraction.12 Further, among trialkyl phosphates, tributyl phosphate (TBP) is widely used as an extractant in various steps of nuclear fuel reprocessing.13,14 A wide range of other trialkyl phosphates such as triisobutyl phosphate (TiBP), triisoamyl phosphate (TiAP), triamyl phosphate (TAP) and trihexyl phosphate (THP) have also examined for the extraction of actinides.15–17 SFE of metal ions such as heavy metals, lanthanides and actinides from different matrices using organophosphorus compounds was carried out.4,5,7,18,19 SFE based methods were developed for the extraction of actinides from various matrices with organophosphorus compounds.20–24
The determination of solubility of organophosphorus ligands in SCCO2 is crucial towards designing a SFE method for recovery of a metal ion. The solubility of a variety of complexing agents and metal complexes in SCCO2 has been reviewed.25–30 However, the literature on the solubilities of organophosphorus compounds in SCCO2 is scarce. The solubilities of TBP,27,31 triphenyl phosphate (TPP), triphenyl phosphine (TPPh), triphenyl phosphine oxide (TOPO) and other paraffinic hydrocarbon have already been determined.30 But the solubility behavior of other trialkyl phosphates has not been studied.
The experimental determination of solubilities of compounds in supercritical fluid (SCF) is difficult and time consuming. Mathematical models have been used to correlate the solubility data.32 There are certain types of models such as equation of state based models, neural network models33–35 and semi-empirical models that can be used to correlate and predict the solubilities of compounds in SCF. The equation of state based models require the knowledge of pure component properties that are not readily available and require group contribution theory methods.32,36 Similarly, neural network models has a disadvantage of time requirement to train the nets.37 Thus, empirical or semi-empirical models are preferably used for solubility determination. Several empirical models are available in the literature.38–47 Density based models are the most commonly used semi-empirical equations. Many of these models correlate the solubilities of solids. However, the models that correlate the solubility of liquid solutes in supercritical fluids are scarce. A semi-empirical equation for correlating the liquid solubilities in supercritical fluids based on solution theory coupled with Wilson activity coefficient model was developed.48 Recently, several correlations based on association/solution theories using different activity coefficients have been developed.49
The solubilities of various trialkyl phosphates in SCCO2 were experimentally determined at different temperatures and pressures. These solubilities were correlated with various semi-empirical correlations such as the Chrastil,38 Méndez-Santiago and Teja43 models. The solubilities were also correlated by a recently developed association model based on van Laar activity coefficient.50 A key result found in this study was that the model parameters of the association model based on van Laar activity coefficient varied linearly with the carbon number of the trialkyl phosphates.
2. Experimental
2.1. Materials
Carbon dioxide with a purity of 99.9% was used for the solubility measurements. Trimethyl phosphate (TMP) (Koch Light Laboratories Ltd.), triethyl phosphate (TEP) (99%, Sigma Aldrich) and tributyl phosphate (TBP) (99%, Alfa), were used as such without any purification. The compounds, triamyl phosphate (TAP) and trihexyl phosphate (THP) were synthesized by the condensation reaction between POCl3 and stoichiometric equivalent of corresponding alcohol in the presence of pyridine with n-heptane as the reaction medium.16 TAP and THP were purified by vacuum distillation followed by washing with concentrated sodium hydroxide and water. The characterization of TAP and THP was carried out using infrared (IR) spectroscopy, elemental analysis and 31P NMR. The purity of these compounds was determined by gas chromatography (GC) with flame ionization detector (FID) and the purity was found to be ∼99%. All other chemicals used were of analytical grade.2.2. Procedure
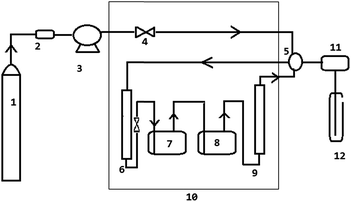
The schematic of continuous flow apparatus used in this study for measuring the solubility in supercritical carbon dioxide is shown in Fig. 1. The experimental setup consisted of a carbon dioxide cylinder (1), a high pressure reciprocating CO2 pump (JASCO-PU-2080-CO2) (3), 10 mL CO2 tank (6), 50 mL twin high pressure equilibrium cells (7 & 8), thermostat (JASCO-CO-156) (10), and a back pressure regulator (JASCO-880-81-BP) (11). The uncertainties in the temperature and pressure measurements are ±0.1 K and ±0.1 MPa, respectively.An appropriate amount of trialkyl phosphate was loaded into the equilibrium cells (7 & 8). The outlet of the first vessel (7) was connected as inlet for the second vessel (8). The saturated carbon dioxide stream from the second vessel (8) flows through an entrainer column (9) that traps the entrained liquid. Two equilibrium cells and entrainer column were placed in a thermostat (10) to maintain a constant temperature. The system pressure was regulated and controlled by a back pressure regulator.
Carbon dioxide from the gas cylinder (1) was passed through a silica gel column (2) to remove traces of water and then fed into a CO2 pump (3) where it was liquefied by using a Peltier element. Liquid carbon dioxide was pressurized and sent to the CO2 tank (6) placed inside the thermostat to reach the supercritical state prior to its entry into the equilibrium cells (7 & 8). At a fixed experimental temperature, the equilibrium cells were pressurized with SCCO2 until the desired pressure was reached. The system was kept at the desired temperature and pressure for an hour to reach the equilibrium. After equilibration, SCCO2 was allowed continuously to flow through the system at a constant flow rate and the concentration of solute in the SCCO2 stream was monitored continuously. The exiting CO2 stream from equilibrium cells was introduced into a collection vessel (12), where the pressure was reduced to atmospheric pressure. Saturation solubility was achieved and it was observed by periodically collecting the solute and quantifying the same. It was found that the solubility did not vary with the time and outlet CO2 stream was saturated with the solute, which ensures the equilibrium.
The primary criterion for the accurate measurement of solubilities in SCCO2 is that the exiting stream has to be saturated with the solute. Repeated measurements were carried out at different flow rates of CO2 between 0.1 and 1 mL min−1, to ensure saturation of solute in SCCO2 medium. It was found that the solubilities did not vary with flow rates up to 0.3 mL min−1. When the flow rate was increased beyond 0.4 mL min−1, the concentration of solute in the exiting stream decreased with the flow rate, indicating that the exiting stream has not been saturated with the solute. Hence, a CO2 flow rate of 0.1 mL min−1 was employed to ensure that the exiting CO2 was saturated with the trialkyl phosphate. The exiting stream was trapped and collected in collection vessel containing n-hexane, at regular intervals of time. Subsequently, n-hexane was evaporated and the amount of solute collected was determined gravimetrically using an analytical balance (±0.1 mg). However, quartz wool was also used as a trap to collect the solute in the collection vessel and the collection efficiency was found to be similar to that of n-hexane. The precision of the gravimetric determination was 0.5%. The reliability of the experimental set-up and procedures were tested by measuring the solubility of tributyl phosphate and trioctyl amine in SCCO2 medium. The results were in good agreement with the literature data.25,27
The mole fraction solubility (y2) and solubility in g L−1 (S) is calculated using the expressions
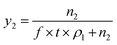 | (1) |
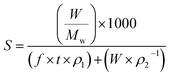 | (2) |
In eqn (1) and (2), n2 is number of moles of compound collected, f is the flow rate in mL min−1 of the CO2 at CO2 pump, t represents the collection time in min and ρ1 gives the molar density of CO2 at pump head, W is the amount of compound collected in g, Mw is the molecular weight of the compound and ρ2 is the density of the compound at experimental temperature.
The solubilities were measured three times at each experimental conditions. The uncertainty of experimental measurements was found to be ±5%. The density data used in this study was from NIST Web Book.
3. Models and correlations
3.1. Méndez–Teja (MT) model
Méndez-Santiago and Teja43 derived an expression that can be used for checking the consistency of the experimental data of solubility of solutes in supercritical carbon dioxide. This model represents the solubility in terms of temperature, pressure and density as
T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Py2) = A1 + B1ρ + C1T ln(Py2) = A1 + B1ρ + C1T
| (3) |
In eqn (3), y2 is the solubility in mol mol−1, P is the pressure in MPa, T is the temperature in K and A1, B1 and C1 are the temperature independent constants. Thus a plot of T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Py2) − C1T and ρ would be linear with all the isotherms collapsing on to a single straight line.
ln(Py2) − C1T and ρ would be linear with all the isotherms collapsing on to a single straight line.
3.2. Chrastil model
The Chrastil model38 relates the solubility of solute and density of the pure supercritical fluid (SCF) as follows
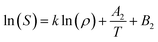 | (4) |
In eqn (4), S is the solubility of solute in SCF in g L−1; ρ is the density of the SCF in g L−1; k is the association number that describes the number of solvent molecules associated with the complex; A2 is a function of enthalpy of vaporization and enthalpy of solvation; T is the temperature in K; B2 depends on the association number and molecular weight of solute and supercritical fluid. Thus a plot of ln(S) with ln(ρ) will be linear at a constant temperature.
3.3. Association model with van Laar activity coefficient model
An association model, such that a molecule of solute A (liquid) associates with k molecules of solvent B (SCCO2) to form a solvate complex, ABk was developed50 with the assumption of formation of solvato complex which is in equilibrium with the supercritical phase. An expression in terms of densities of both phases, fugacities, activity coefficients, pressure and temperature was obtained as
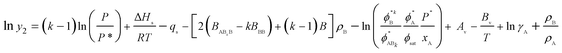 | (5) |
The above expression was simplified and the activity coefficient was modeled using a van Laar activity coefficient model and the following expression was obtained,
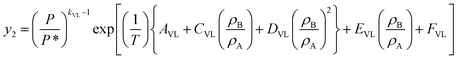 | (6) |
In eqn (6), y is solubility, P is pressure in MPa, P* is reference pressure, T is temperature in K, ρB, ρA and xB, xA are the molar densities in kg m−3 and mole fractions of solvent (B) and solute (A), respectively. kVL represents association number and AVL, BVL, CVL, DVL, EVLand FVL are temperature independent constants. Eqn (6) was used for correlating the solubilities of trialkyl phosphates in SCCO2.
4. Results and discussion
The solubilities of various trialkyl phosphates: TMP, TEP, TBP, TAP and THP were measured at temperatures of 313, 323 and 333 K in the pressure range of 10 to 25 MPa. The consistency of the solubility data was checked by the MT model (eqn (3)) as shown in Fig. 2. The constants A1, B1, and C1 in the eqn (3) were obtained by the multiple linear regression of the experimental data and given in Table 2. The plot of T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Py2) − C1T and ρ was linear with all experimental data fitting onto single straight line and this indicates that the data is self-consistent.
ln(Py2) − C1T and ρ was linear with all experimental data fitting onto single straight line and this indicates that the data is self-consistent.
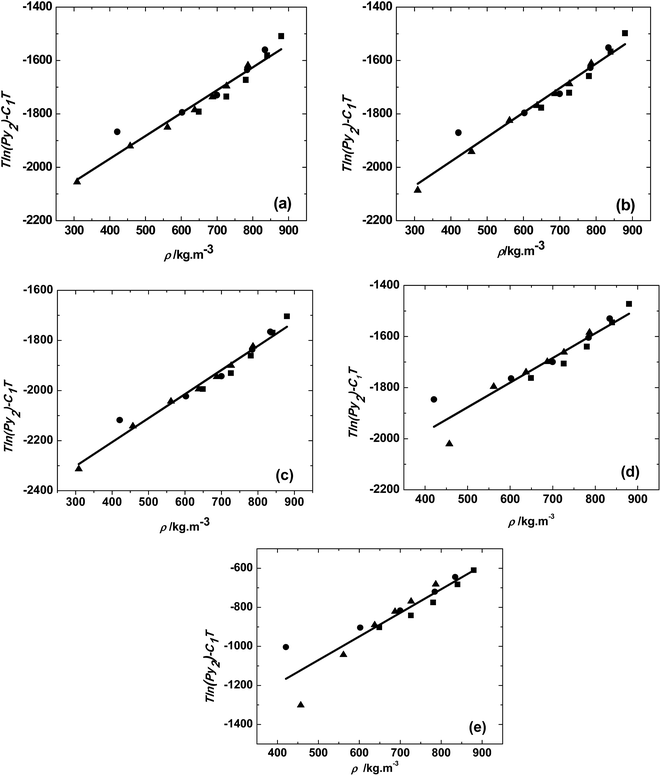 | ||
| Fig. 2 Solubility of (a) trimethyl phosphate, (b) triethyl phosphate, (c) tributyl phosphate, (d) triamyl phosphate, (e) trihexyl phosphate at different temperatures, ■, 313 K; ●, 323 K; ▲, 333 K. Solid line represents the MT model fit (eqn (3)). | ||
| T (K) | P (MPa) | Densitya (kg m−3) | Solubility y2 (mol mol−1) | ||||
|---|---|---|---|---|---|---|---|
| TMP | TEP | TBP | TAP | THP | |||
| a Density values taken from http://www.webbook.nist.gov/chemistry/fluid/ | |||||||
| 313 | 8.3 | 320.54 | 0.188 | 0.160 | 0.105 | 0.097 | 0.075 |
| 10.3 | 651.49 | 0.191 | 0.162 | 0.110 | 0.099 | 0.081 | |
| 12.3 | 727.57 | 0.191 | 0.163 | 0.113 | 0.099 | 0.082 | |
| 15 | 781.32 | 0.192 | 0.163 | 0.116 | 0.101 | 0.083 | |
| 20 | 840.61 | 0.193 | 0.163 | 0.117 | 0.102 | 0.084 | |
| 25 | 880.15 | 0.194 | 0.163 | 0.115 | 0.103 | 0.085 | |
| 323 | 10.3 | 423.74 | 0.180 | 0.145 | 0.092 | 0.091 | 0.065 |
| 12.3 | 604.62 | 0.189 | 0.152 | 0.103 | 0.098 | 0.074 | |
| 15 | 701.08 | 0.190 | 0.156 | 0.108 | 0.098 | 0.079 | |
| 20 | 785.16 | 0.191 | 0.158 | 0.113 | 0.099 | 0.080 | |
| 25 | 834.89 | 0.192 | 0.160 | 0.113 | 0.100 | 0.081 | |
| 333 | 10.3 | 309.89 | 0.122 | 0.090 | 0.062 | 0.014 | 0.005 |
| 12.3 | 458.89 | 0.153 | 0.116 | 0.087 | 0.054 | 0.024 | |
| 14 | 563.09 | 0.165 | 0.144 | 0.102 | 0.092 | 0.046 | |
| 16 | 638.84 | 0.177 | 0.150 | 0.104 | 0.096 | 0.064 | |
| 18 | 688.34 | 0.182 | 0.153 | 0.107 | 0.096 | 0.070 | |
| 20 | 724.63 | 0.185 | 0.154 | 0.110 | 0.097 | 0.074 | |
| 25 | 787.28 | 0.186 | 0.155 | 0.111 | 0.098 | 0.077 | |
| Model | Model Parameters | TMP | TEP | TBP | TAP | THP |
|---|---|---|---|---|---|---|
| MT model | A1 | −2313 ± 36 | −2358 ± 35 | −2593 ± 30 | −2363 ± 60 | −2052 ± 60 |
| B1 | 0.85 ± 0.05 | 0.92 ± 0.05 | 0.96 ± 0.04 | 0.97 ± 0.08 | 0.94 ± 0.08 | |
| C1 | 6.4 ± 0.5 | 6.26 ± 0.5 | 6.54 ± 0.54 | 5.7 ± 0.5 | 4.54 ± 0.4 | |
| R2 | 0.942 | 0.954 | 0.967 | 0.885 | 0.913 | |
| AARD (%) | 7 | 7 | 6 | 9 | 10 | |
| Chrastil model | A2 | −1.56 ± 0.01 | −1.75 ± 0.02 | −1.50 ± 0.01 | 0.53 ± 0.02 | −1.84 ± 0.01 |
| B2 | 514 ± 4 | 433 ± 4 | 392 ± 4 | 106 ± 1 | 546 ± 3 | |
| k | 0.890 ± 0.03 | 0.957 ± 0.04 | 0.929 ± 0.01 | 0.758 ± 0.01 | 0.896 ± 0.01 | |
| R2 | 0.937 | 0.954 | 0.968 | 0.997 | 0.973 | |
| AARD (%) | 6 | 7 | 5 | 3 | 4 | |
| Association model based on van Laar activity coefficient model | kVL | 1 | 1 | 1 | 1 | 1 |
| AVL | 2369 ± 27 | 3169 ± 40 | 4400 ± 150 | 5520 ± 105 | 6250 ± 150 | |
| CVL | −3295 ± 18 | −3885 ± 23 | −5192 ± 27 | −6110 ± 61 | −6980 ± 48 | |
| DVL | −118 ± 5 | −176 ± 5 | −289 ± 6 | −376 ± 12 | −390 ± 20 | |
| EVL | 10.9 ± 0.4 | 13 ± 0.1 | 17.8 ± 0.6 | 21 ± 1.2 | 24 ± 0.8 | |
| FVL | −9.3 ± 0.1 | −12.1 ± 0.12 | −16.6 ± 0.13 | −20.3 ± 0.4 | −23 ± 0.5 | |
| R2 | 0.90 | 0.87 | 0.92 | 0.70 | 0.84 | |
| AARD (%) | 3 | 3 | 3 | 7 | 5 |
In general, the solubilities of trialkyl phosphates were found to be high in the investigated region and are shown in Table 1. The variation of solubilities with temperature and pressure is shown in Fig. 3 for different trialkyl phosphates. Across all the isotherms (313, 323 and 333 K) the solubilities of trialkyl phosphates increases with the pressure. We have included the solubility data for TBP from existing literature27 and compared it with the present data in Fig. 3 and the agreement is reasonable. Increasing the pressure at isothermal conditions increases the density of SCCO2 that improves the specific interactions between CO2 and solute molecules, enhancing the solvating power and leading to higher solubility. The reverse behavior was observed with temperature and the solubilities of trialkyl phosphates decreases with temperature in the entire pressure region. The effect of temperature on the solubility is not straight forward and there are two competing factors that can influence the solubility. The vapor pressure of the solute generally increases with the temperature whereas density of SCCO2 decreases with increase in temperature.49 However, the vapor pressure of the trialkyl phosphates in the investigated temperature region of 313 to 333 K is low and hence making density as the dominating factor. The decrease of SCCO2 density with temperature results in reduced solubility at 333 K compared to that obtained at 313 K, as depicted by Fig. 3.
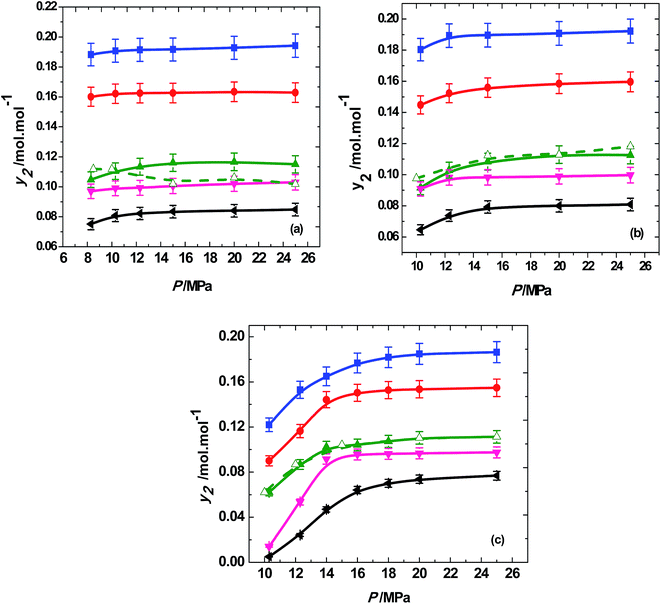 | ||
| Fig. 3 Variation of solubility of trialkyl phosphates (■, trimethyl phosphate; ●, triethyl phosphate; ▲, tributyl phosphate; ▼, triamyl phosphate; ◀, trihexyl phosphate) with pressure at different temperatures of (a) 313 K; (b) 323 K; (c) 333 K. Solid symbols and solid lines represent the present work. Open symbols and dash line represent the tributyl phosphate (TBP) data by Meguro et al.27 | ||
From the solubility data, it was observed that TMP has highest solubility among its homologous series investigated in the present study. The solubilities of TMP ranged from 0.122 to 0.194 mol mol−1. THP has relatively lower solubilities, ranging from 0.005 to 0.085 mol mol−1. All other trialkyl phosphates show intermediate solubility in comparison to TMP and THP. It was found that the solubility is inversely related to the number of carbon atoms present in the trialkyl phosphate. The vapor pressure is a parameter influencing the solubility behavior and is directly dependent on the molecular weight of the compound. For a homologous series, the solubility of a solute decreases with increase in carbon number where generally, the vapor pressure decrease with increase in carbon chain.51,52 In Fig. 4, experimental solubilities of trialkyl phosphates were plotted against their carbon number at 20 MPa with temperature ranging from 313 to 333 K. It was found that, in the homologous series of trialkyl phosphates, the solubility decreases with its molecular weight or carbon number at all isotherms. The solubility of trialkyl phosphates decreases with increase in the temperature as the density of SCCO2 decreases with the temperature.
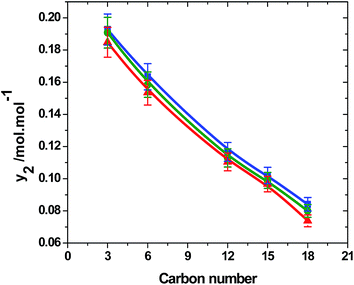 | ||
| Fig. 4 Variation of solubility of trialkyl phosphates with their carbon number at 20 MPa, with temperatures ■, 313 K; ●, 323 K; ▲, 333 K. | ||
The interaction and solubility of trialkyl phosphates in SCCO2 is mainly due to Lewis acid (LA)–Lewis-base (LB) interactions and weak C–H–O hydrogen bonding.53 Because of large quadrupole moment of CO2, there will be a charge separation between carbon and oxygen atoms and electron density moves towards oxygen. Therefore, the carbon atom has partial positive charge acting as a LA and oxygen atoms having negative charge act as a LB. The phosphoryl group of the trialkyl phosphate acts as LB and interacts with the CO2 through LA–LB interactions.53 The partial negative charge on oxygen atom induces the electrostatic interaction with –C–H group present in the trialkyl phosphate to form a weak H-bonding. Kim et al. performed the quantum mechanical calculations for the CO2–TMP complex and found that the LA–LB interaction energy was much higher than the weak H-bonding and it could be the main driving force for the higher solubility in CO2.53 The high solubilities in the investigated pressure and temperature range may be due to the complete miscibility of the trialkyl phosphates with SCCO2. Meguro et al. reported high solubility behavior of TBP in SCCO2 due to the formation of single phase TBP–SCCO2.27
Chrastil equation has been employed in the present study to correlate the solubility data of trialkyl phosphates in SCCO2. The experimental solubilities were fitted using non-linear curve fitting with eqn (4) to obtain the model parameters k (association number), A2 and B2 and were given in Table 2. The logarithm of solubility (g L−1) data was plotted against the logarithm of density (g L−1) of SCCO2. These plots represent straight lines for different isotherms and are shown in Fig. 5. The slopes of the different isotherms are close; however, the slope shows a small increase at higher temperature.
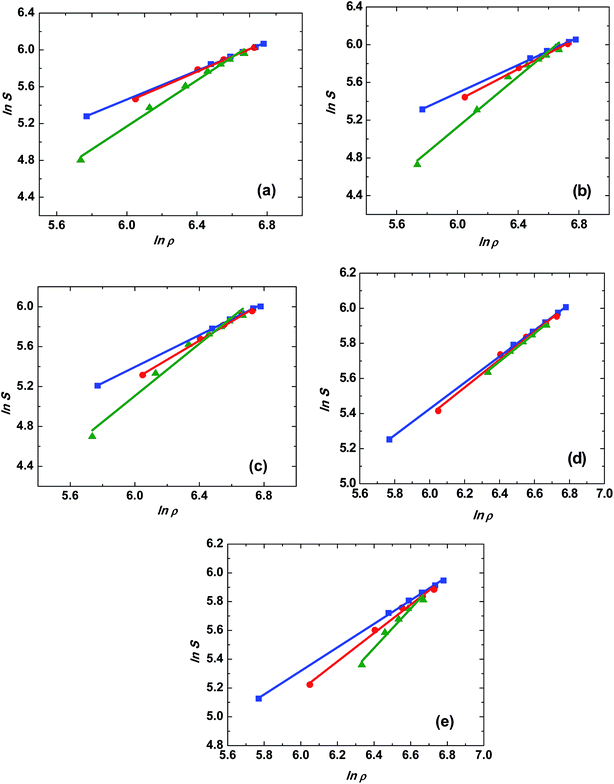 | ||
Fig. 5 Correlation plots of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S vs. ln S vs. ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ (eqn (4)) for trialkyl phosphates in the pressure range of 10 to 25 MPa, and the temperature of ■, 313 K; ●, 323 K; ▲, 333 K; (a) trimethyl phosphate, (b) triethyl phosphate, (c) tributyl phosphate, (d) triamyl phosphate, (e) trihexyl phosphate. ρ (eqn (4)) for trialkyl phosphates in the pressure range of 10 to 25 MPa, and the temperature of ■, 313 K; ●, 323 K; ▲, 333 K; (a) trimethyl phosphate, (b) triethyl phosphate, (c) tributyl phosphate, (d) triamyl phosphate, (e) trihexyl phosphate. | ||
Assuming the association number, kVL, to be unity in eqn (6), this equation can be rewritten as,
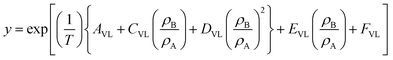 | (7) |
Eqn (7) was used to determine the solubility by the model and was compared with the experimental solubilities. The model parameters were obtained by non-linear curve fitting and represented in Table 2. The solubilities correlated by the model are depicted by Fig. 6. The deviation of the experimentally measured solubilities from the solubilities derived from the model was estimated by calculating the average absolute relative deviation (AARD%) and is given by eqn (8),
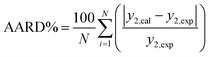 | (8) |
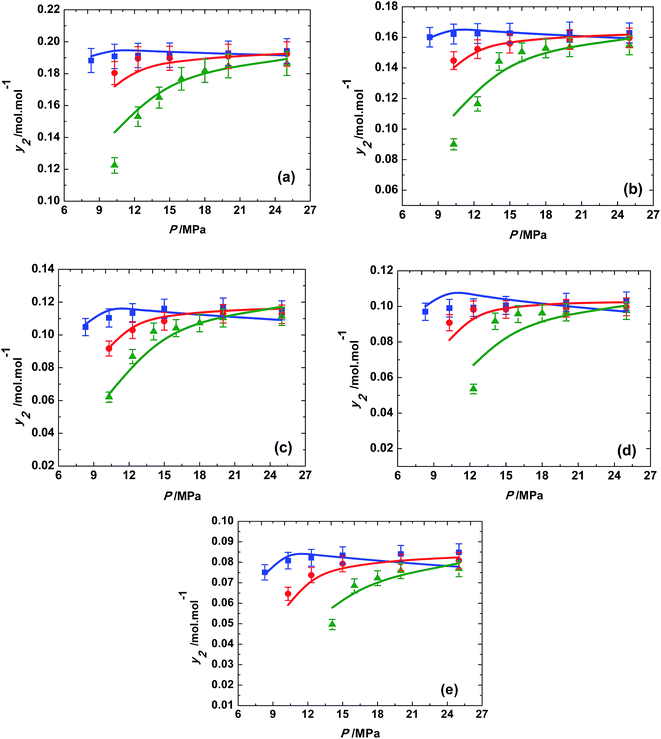 | ||
| Fig. 6 Variation of solubility of trialkyl phosphates with pressure at different temperatures; ■, 313 K; ●, 323 K; ▲, 333 K; in supercritical carbon dioxide. (a) Trimethyl phosphate, (b) triethyl phosphate, (c) tributyl phosphate, (d) triamyl phosphate, (e) trihexyl phosphate; the solid line represents the association model based on van Laar activity coefficient model (eqn (7)). | ||
While correlating the solubilities of alkanes in supercritical carbon dioxide, it was observed that the adjustable binary interaction parameters in the model vary linearly with the chain length of the n-alkanes.54 Other studies have indicated that the vapor pressure is an important physicochemical parameter influencing the solubility behavior and gives a direct correlation on the solubilities in supercritical fluids.51 Based on the above observations, the boiling points of the trialkyl phosphates55,56 were correlated with the carbon number of the trialkyl phosphates. This relationship is linear as observed in the inset of Fig. 7(c). Therefore, the model parameters of the all three models used in the present study were correlated with the carbon number of the trialkyl phosphates. The model parameters of the MT and Chrastil model did not show any particular trend with the carbon number, as shown in Fig. 7(a) and (b). However, the five model parameters of the association model based on van Laar activity coefficient model successfully correlated with the carbon number of the trialkyl phosphates. A linear relationship was observed, as shown in Fig. 7(c). These equations reveal the anticipated trend of solubility with the molecular weight of the trialkyl phosphates. All the three models discussed in this study gave average AARD values ranging from 4% to 8%. However, the association model gave a linear relationship between the model parameters and the carbon number of the trialkyl phosphates. This provides an easy method to calculate the unknown solubilities of other members of the trialkyl phosphate series as well as predict the solubilities of these compounds at different temperatures and pressures.
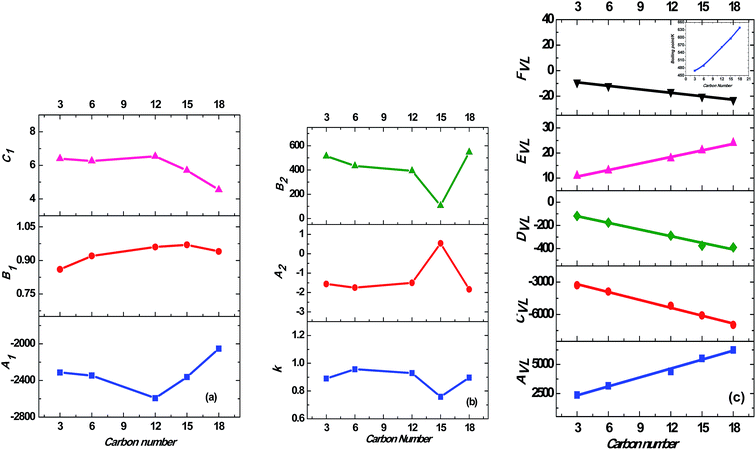 | ||
| Fig. 7 Correlation of model parameters with carbon number of trialkyl phosphates; (a) MT model (eqn (3)); model parameters are represented by the symbols, ■, A1; ●, B1; ▲, C1; (b) Chrastil model (eqn (4)); model parameters are represented by the symbols, ■, k; ●, A2; ▲, B2; (c) association model based on van Laar activity coefficient model (eqn (7)); model parameters are represented by the symbols, ■, AVL; ●, CVL; ◆, DVL; ▲, EVL; ▼, FVL. The inset of this figure represents the relation between carbon number and normal boiling point of the trialkyl phosphates. | ||
5. Conclusions
The solubilities of a series of trialkyl phosphates were determined in supercritical carbon dioxide (SCCO2). All the trialkyl phosphates examined in the present study are highly soluble in SCCO2 and can be employed as ligands in the SFE of metal ions. The solubility of trialkyl phosphates increases with the pressure at constant temperature and it decreases with the temperature in the investigated pressure range. At constant temperature and pressure, solubility of trialkyl phosphates decreases with increase in molecular weight. The experimental results were successfully correlated using MT model, Chrastil and an association model based on van Laar activity coefficient model. The least AARD% of 4% was obtained for the association model based on van Laar activity coefficient model. The model parameters of the association model (eqn (7)) followed a linear relationship with the carbon number (and boiling point) of the trialkyl phosphates and thus can be used to predict the solubilities of a homologous series of trialkyl phosphates.Acknowledgements
The authors would like to thank M. Joseph, IGCAR for his constant encouragement and support. Giridhar Madras thanks the department of science and technology (DST), India for the J. C. Bose fellowship.References
- Properties of supercritical fluids relevant to extraction and chromatography, ed. A. A. Clifford, Harwood Academic Publishers, Amsterdam, 1999 Search PubMed.
- M. A. McHugh and V. J. Krukonis, Supercritical fluid extraction: principles and practice, Butterworth-Heinemann, Boston, MA, 2nd edn, 1994 Search PubMed.
- X. Zhang, S. Heinonen and E. Levänen, RSC Adv., 2014, 4, 61137–61152 RSC.
- C. M. Wai, Anal. Sci., 1995, 11, 165–167 CrossRef CAS.
- K. E. Laintz, C. M. Wai, C. R. Yonker and R. D. Smith, Anal. Chem., 1992, 64, 2875–2878 CrossRef CAS.
- C. Erkey, J. Supercrit. Fluids, 2000, 17, 259–287 CrossRef CAS.
- Y. Lin, N. G. Smart and C. M. Wai, Trends Anal. Chem., 1995, 14, 123–133 CAS.
- L. L. Burger, Nucl. Sci. Eng., 1963, 16, 428–439 CAS.
- T. H. Siddall, Ind. Eng. Chem. Res., 1959, 51, 41–44 CrossRef CAS.
- T. H. Siddall, J. Inorg. Nucl. Chem., 1960, 13, 151–155 CrossRef CAS.
- L. L. Burger, J. Phys. Chem., 1958, 62, 590–593 CrossRef CAS.
- P. R. V. Rao, Miner. Process. Extr. Metall. Rev., 1998, 18, 309–331 CrossRef CAS.
- The purex process, ed. H. A. C. Mckay, J. H. Miles and J. L. Swanson, CRC Press, Boca Raton, Florida, USA, 1990 Search PubMed.
- The Thorex process, ed. W. D. Bond, CRC Press, Boca Raton, Florida, USA, 1990 Search PubMed.
- A. Suresh, T. G. Srinivasan and P. R. V. Rao, Solvent Extr. Ion Exch., 1994, 12, 727–744 CrossRef CAS.
- A. Suresh, T. G. Srinivasan and P. R. V. Rao, Solvent Extr. Ion Exch., 2009, 27, 258–294 CrossRef CAS.
- B. Sreenivasulu, A. Suresh, S. Subramaniam, K. N. Sabharwal, N. Sivaraman, K. Nagarajan, T. G. Srinivasan and P. R. V. Rao, Solvent Extr. Ion Exch., 2015, 33, 120–133 CrossRef CAS.
- Y. Lin, R. D. Brauer, K. E. Laintz and C. M. Wai, Anal. Chem., 1993, 65(18), 2549–2551 CrossRef CAS.
- B. J. Mincher, R. V. Fox, R. G. G. Holmes, R. A. Robbins and C. Boardman, Radiochim. Acta, 2001, 89, 613–617 CrossRef CAS.
- R. Kumar, N. Sivaraman, K. Sujatha, T. G. Srinivasan and P. R. V. Rao, Radiochim. Acta, 2007, 95, 577–584 CAS.
- R. Kumar, N. Sivaraman, E. S. Vadivu, T. G. Srinivasan and P. R. Vasudeva Rao, Radiochim. Acta, 2003, 91, 197–201 CrossRef CAS.
- K. Sujatha, K. C. Pitchaiah, N. Sivaraman, T. G. Srinivasan and P. R. V. Rao, Am. J. Anal. Chem., 2012, 3, 916–922 CrossRef.
- K. Sujatha, K. C. Pitchaiah, N. Sivaraman, K. Nagarajan, T. G. Srinivasan and P. R. V. Rao, Desalin. Water Treat., 2013, 52, 470–475 CrossRef.
- K. C. Pitchaiah, K. Sujatha, C. V. S. B. Rao, S. Subramaniam, N. Sivaraman and P. R. V. Rao, Radiochim. Acta, 2015, 103, 245–255 CrossRef CAS.
- H. S. Ghaziaskar and M. Kaboudvand, J. Supercrit. Fluids, 2008, 44, 148–154 CrossRef CAS.
- R. B. Gupta and J.-J. Shim, Solubility in supercritical carbon dioxide, CRC Press, Boca Raton, Florida, 1st edn, 2006 Search PubMed.
- Y. Meguro, S. Iso, T. Sasaki and Z. Yoshida, Anal. Chem., 1998, 70, 774–779 CrossRef CAS.
- N. G. Smart, T. Carleson, T. Kast, A. A. Clifford, M. D. Burford and C. M. Wai, Talanta, 1997, 44, 137–150 CrossRef CAS PubMed.
- C. M. Wai and S. Wang, Anal. Chem., 1996, 68, 3516–3519 CrossRef CAS PubMed.
- W. J. Schmitt and R. C. Reid, Chem. Eng. Commun., 1988, 64, 155–176 CrossRef CAS.
- S. J. Nejad, R. Mohammadikhah, H. Abolghasemi, M. A. Moosavian and M. G. Maragheh, Can. J. Chem. Eng., 2009, 87, 930–938 CrossRef CAS.
- H. S. Yeoh, G. H. Chong, N. M. Azahan, R. A. Rahman and T. S. Y. Choong, Eng. J., 2013, 17, 67–78 CrossRef.
- A. N. Sarve, M. N. Varma and S. S. Sonawane, RSC Adv., 2015, 5, 69702–69713 RSC.
- M. Li, X. Huang, H. Liu, B. Liu, Y. Wu and L. Wang, RSC Adv., 2015, 5, 45520–45527 RSC.
- S. K. Jha and G. Madras, Ind. Eng. Chem. Res., 2005, 44, 7038–7041 CrossRef CAS.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The properties of gases and liquids, McGraw-Hill, New York, 5th edn, 2001 Search PubMed.
- D. M. Himmelblau, Korean J. Chem. Eng., 2000, 17, 373–392 CrossRef CAS.
- J. Chrastil, J. Phys. Chem., 1982, 86, 3016–3021 CrossRef CAS.
- Y. Adachi and B. C.-Y. Lu, Fluid Phase Equilib., 1983, 14, 147–156 CrossRef CAS.
- J. M. D. Valle and J. M. Aguilera, Ind. Eng. Chem. Res., 1988, 27, 1551–1553 CrossRef.
- K. D. Bartle, A. A. Clifford, S. A. Jafar and G. F. Shilstone, J. Phys. Chem. Ref. Data, 1991, 20, 713–757 CrossRef CAS.
- M. D. Gordillo, M. A. Blanco, A. Molero and E. M. D. L. Ossa, J. Supercrit. Fluids, 1999, 15, 183–190 CrossRef CAS.
- J. Méndez-Santiago and A. S. Teja, Fluid Phase Equilib., 1999, 158, 501–510 CrossRef.
- C. Garlapati and G. Madras, Fluid Phase Equilib., 2009, 283, 97–101 CrossRef CAS.
- C. Garlapati and G. Madras, J. Chem. Thermodyn., 2010, 42, 193–197 CrossRef CAS.
- X. Bian, Z. Du and Y. Tang, Thermochim. Acta, 2011, 519, 16–21 CrossRef CAS.
- D. L. Sparks, R. Hernandez and L. A. Estévez, Chem. Eng. Sci., 2008, 63, 4292–4301 CrossRef CAS.
- R. C. Narayan, J. V. Dev and G. Madras, J. Supercrit. Fluids, 2015, 101, 87–94 CrossRef CAS.
- N. Lamba, R. C. Narayan, J. Raval, J. Modak and G. Madras, RSC Adv., 2016, 6, 17772–17781 RSC.
- N. Lamba, R. C. Narayan, J. Modak and G. Madras, J. Supercrit. Fluids, 2016, 107, 384–391 CrossRef CAS.
- M. D. A. Saldaña, B. Tomberli, S. E. Guigard, S. Goldman, C. G. Gray and F. Temelli, J. Supercrit. Fluids, 2007, 40, 7–19 CrossRef.
- F. Temelli, J. Supercrit. Fluids, 2009, 47, 583–590 CrossRef CAS.
- K. H. Kim and Y. Kim, Bull. Korean Chem. Soc., 2007, 28, 2454–2458 CrossRef CAS.
- S. K. Jha and G. Madras, Fluid Phase Equilib., 2004, 225, 59–62 CrossRef CAS.
- R. S. Edmundson, Dictionary of organophosphorous compounds, Chapman and Hall Ltd, New York, London, 1988 Search PubMed.
- K. Paneerselvam, M. P. Antony, T. G. Srinivasan and P. R. V. Rao, Thermochim. Acta, 2010, 511, 107–111 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |