Influence of temperature on molecular interactions of imidazolium-based ionic liquids with acetophenone: thermodynamic properties and quantum chemical studies†
Indra Bahadur*a,
Masilo Kgomotsoa,
Eno E. Ebensoa and
Gan Redhib
aDepartment of Chemistry and Materials Science Innovation, Modelling Research Focus Area, School of Mathematical and Physical Sciences, Faculty of Agriculture, Science and Technology, North-West University (Mafikeng Campus), Private Bag X2046, Mmabatho 2735, South Africa. E-mail: bahadur.indra@gmail.com; bahadur.indra@nwu.ac.za; Tel: +27 18 389 2870
bDepartment of Chemistry, Durban University of Technology, P O Box 1334, Durban, 4000, South Africa
First published on 27th October 2016
Abstract
The physicochemical properties namely: densities (ρ), sound velocities (u), viscosities (η), and refractive indices (nD) of a series of alkyl imidazolium-based ionic liquids (ILs) with same cation and different anion and vice versa of ILs: 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM]+[BF4]−, 1-butyl-3-methylimidazolium hexafluorophosphate [BMIM]+[PF6]−, 1-ethyl-3-methylimidazoium ethyl sulphate [EMIM]+[EtSO4]− and 1-ethyl-3-methylimidazolium tetrafluoroborate [EMIM]+[BF4]−, with acetophenone over the wide range of composition and at (293.15, 303.15, 313.15, 323.5 and 333.15) K under atmospheric pressure is reported in this study. The excess molar volumes, (VEm), deviation in isentropic compressibilities (Δκs), deviation in viscosities (Δη) and deviation in refractive indices (ΔnD) were derived from experimental results. The VEm, Δκs and ΔnD values for the mentioned systems are both negative and positive over the entire composition range while the Δη values are negative under the same experimental conditions. The derived properties were fitted to the Redlich–Kister polynomial equation to check the accuracy of experimental results. Furthermore, the inter-ionic interactions between the cations and anions of the ILs both in vacuo and in acetophenone (using continuum solvation) were confirmed using quantum chemical technique such as [Density Functional Theory (DFT)]. The quantum chemical results are in good agreement with the experimental results suggesting that there exist appreciable interactions between the ILs and acetophenone. The theoretical and measured data were interpreted in terms of intermolecular interfaces and structural effects between similar and dissimilar molecules upon mixing in order to obtain more information on the thermophysical and thermodynamic properties of ILs and their binary mixtures. This study will contribute to the data bank of thermodynamic properties of IL mixtures, so as to establish principles for the molecular design for chemical separation processes and to enhance the applications of ILs in certain aspects of research or industrial application.
1. Introduction
Ionic liquid (IL) is a term which is used to describe a broad group of salts which have an extensive liquid range.1 This includes organic or inorganic molten salts, fused salts, non-aqueous ILs and liquid organic salts.2,3 As compared to traditional molecular solvents, ILs are liquids at ambient temperatures and are composed entirely of ions referring to cations and anions, and are held together by columbic forces.4–6 The melting point of ILs is relatively low and/at below 100 °C, therefore they remain as liquids within a broad temperature window.1–4 The low melting point of ILs is due to its chemical composition,7,8 the relatively large size of either the anion or the cation in ILs and low symmetry which also explains the lower melting points of these ILs.1 ILs that melt at room temperature are said to be room temperature ionic liquids (RTILs).9 The ILs possess more favourable properties than organic molecular solvents, which includes broad liquid range, negligible vapour pressure therefore most unlikely to evaporate under normal conditions, high thermal stability, non-flammable and found to be stable at room temperature.3,10,11 ILs have high polarity, miscible and soluble with water and other organic solvents.3,7 Ionic interaction within ILs enables them to be miscible with polar substances, miscibility with water and organic solvents depends on the side chain lengths on the cation and the anion combinations,8,10 and also allows a large variety of interactions and applications.12–14Acetophenone is an important industrial chemical, widely used as an ingredient of flavour and fragrance in soaps, detergents, cosmetics creams, lotions, and perfumes.15 It has also been used as an important intermediate for pharmaceuticals and agrochemicals.15 Furthermore, it is used as a plasticizer, as a solvent in resins, for cellulose ethers, as a hypnotic (induces sleep),16 in organic syntheses as a photosensitizer and as a catalyst for the polymerization of olefins.17 The thermodynamic properties of systems containing acetophenone are helpful to better understand molecular interaction and to design and simulate the different processes of separation.15 Unlike other ketones like acetone and 2-pyrrolidone, acetophenone can be used for medical purposes in, whereby it can be used to kill cancer cell. In comparison to simple alcohol like methanol, acetophenone play a role in animal metabolite whereas methanol plays a role in bacterial metabolite.
The thermophysical and thermodynamics properties of ILs mixtures allow for new correlations and/or predictive models to test the solution theories for ILs and their binary mixtures with organic solvents18–25 as well as provide information about molecular interactions such as solute–solute, solute–solvent and solvent–solvent that occur in binary mixtures specifically where hydrogen bonding takes place. Thus a more systematic study of thermodynamic and thermophysical properties of ILs and their mixtures with solvents is required in chemical and separation processes. Furthermore, accurate knowledge about the thermophysical and thermodynamic data is critical in order to transfer the ILs from laboratory to industry, designing future processes and equipment involving these ionic compounds.26–30
Density Functional Theory (DFT)31 (a quantum chemical method) focuses on the electron density of the system, which depends on only three variables. DFT method have turned out to be exceptionally well known recently because of their accuracy that is similar to other techniques in less time and with a smaller investment from the computational perspective. In most recent years, theoretical quantum chemical calculations have turn out to be complementary for experimental methods in many fields.32–44
The volumetric, acoustic and transport properties of liquids and liquid mixtures are utilised to study the molecular interactions between the several components of the mixtures45 and also to understand engineering applications concerning heat transfer, mass transfer and fluid flow. Thus, data on some of the properties associated with the liquids and liquid mixtures such as density, viscosity, sound velocity and refractive index find extensive application in solution theory and molecular dynamics. Such results are essential for elucidation of data obtained from thermochemical, electrochemical, biochemical and kinetic studies. To the best of our knowledge, few work has been done on studied ILs with other solvents in literature (Rao et al.;46 Zafarani-Moattar and Shekaari;47 González et al.48 and Bhagour et al.49) but no literature data are available in literature on thermophysical or thermodynamics properties of these ionic liquids under study in acetophenone with quantum chemical calculation. This therefore emphasises the novelty of the present investigation.
In the present work, a new inclusive record for the density, sound velocity, viscosity, and refractive index, of alkyl imidazolium based ionic liquids, which include 1-butyl-3-methylimidazolium tetrafluoroborate [BMIM]+[BF4]−, 1-butyl-3-methylimidazolium hexafluorophosphate [BMIM]+[PF6]−, 1-ethyl-3-methylimidazoium ethyl sulphate [EMIM]+[EtSO4]−, 1-ethyl-3-methylimidazolium tetrafluoroborate [EMIM]+[BF4]−, and their binary mixture with acetophenone at various temperatures and concentrations together with quantum chemical calculation is introduced. The results are used to derive other thermodynamic data namely; excess molar volume, deviation in isentropic compressibility, deviation in refractive indexes and deviation in viscosity. The intermolecular interactions in the ILs and their binary mixtures were evaluated. Furthermore, the influence in temperature and concentration, as well as the variance in the anion, cation and alkyl group of the IL and their binary mixtures were discussed. The present work is a part of the comprehensive and extensive investigations on-going in our research group on physicochemical properties of alkyl imidazolium/ammonium-based ILs with solvents at different temperatures and incorporation of the quantum chemical studies to support experimental data.50–61
2. Experimental procedure
2.1. Materials
Imidazolium based ILs used in the present study namely 1-butyl-3-methylimidazolium tetra fluoroborate [BMIM]+[BF4]−, 1-butyl-3-methylimidazolium hexafluorophosphate [BMIM]+[PF6]− and 1-ethyl-3-methylimidazolium tetra fluoroborate [EMIM]+[BF4]− were obtained from Ionic Liquids Technologies Inc., 1-ethyl-3-methylimidazoium ethyl sulphate [EMIM]+[EtSO4]− was purchased from Sigma-Aldrich with the purity of ≥98%. The solvent acetophenone was supplied by Sigma-Aldrich. Deionised water was used in the experiments. The purity and the investigated thermophysical properties of acetophenone and ILs are presented in Table 1 together with literature62–66 reported at 303.15 K. The mass percent water content was determined using a Metrohm 702 SM Titrino Metter before the experiments, and was found to be ≤0.06% in the chemicals used (Table 2).| Solvent | Supplier | MW/g mol−1 | % purity | ρ/g cm−3 |
|---|---|---|---|---|
| [BMIM]+[BF4]− | Ionic Liquids Technologies Inc. | 226.022 | 99 | 1.20129 (ref. 62) |
| [BMIM]+[PF6]− | Ionic Liquids Technologies Inc. | 284.182 | 99 | 1.36240 (ref. 63) |
| [EMIM]+[BF4]− | Ionic Liquids Technologies Inc. | 197.970 | 98 | 1.28174 (ref. 64) |
| [EMIM]+[EtSO4]− | Sigma-Aldrich | 236.289 | ≥98 | 1.23425 (ref. 65) |
| Acetophenone | Sigma-Aldrich | 120.148 | >99 | 1.01942 (ref. 66) |
| T/K | A0 | A1 | A2 | A3 | A4 | σ | |
|---|---|---|---|---|---|---|---|
| {[BMIM]+[BF4]− (x1) + acetophenone (x2)} | |||||||
| VEm/cm3 mol−1 | 293.15 | 18.852 | −0.637 | −3.972 | −1.029 | 0.131 | 0.106 |
| 303.15 | 19.631 | −0.803 | −4.373 | −3.110 | 3.022 | 0.103 | |
| 313.15 | 20.449 | −1.587 | −6.059 | −4.431 | 8.210 | 0.113 | |
| 323.15 | 21.333 | −1.755 | −6.516 | −7.050 | 11.654 | 0.119 | |
| 333.15 | 22.574 | −2.933 | −13.007 | −9.821 | 22.630 | 0.170 | |
| Δκs/TPa−1 | 293.15 | 237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 330 330 |
−22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 085 085 |
89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 050 050 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
543 |
| 303.15 | 233![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685 685 |
−20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053 053 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 521 521 |
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 867 867 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 297 297 |
411 | |
| 313.15 | 225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243 243 |
−18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 051 051 |
111![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 467 |
−44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 855 855 |
831 | |
| 323.15 | 214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 378 378 |
−32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 887 |
34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 326 326 |
146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
−104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 398 398 |
644 | |
| 333.15 | 203![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
−320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978 978 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 486![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 978 978 |
−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 228 228![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 338 338 |
1373 | |
| Δη/mPa s | 293.15 | −131.150 | 136.112 | −70.256 | 466.800 | −482.503 | 0.786 |
| 303.15 | −72.971 | 51.551 | −47.655 | 248.928 | −191.642 | 0.436 | |
| 313.15 | −59.012 | 39.132 | 25.249 | 168.289 | −202.855 | 1.134 | |
| 323.15 | −37.538 | 14.851 | 14.935 | 125.530 | −133.040 | 0.537 | |
| 333.15 | −25.400 | 13.596 | 34.790 | 90.037 | −133.621 | 0.839 | |
| Δn | 293.15 | −0.0560 | −0.0085 | −0.0128 | −0.0697 | 0.1364 | 0.0002 |
| 303.15 | −0.0552 | −0.0192 | 0.0022 | −0.0415 | 0.1291 | 0.0002 | |
| 313.15 | −0.0510 | −0.0209 | −0.0051 | −0.0416 | 0.1159 | 0.0003 | |
| 323.15 | −0.0474 | −0.0249 | −0.0077 | −0.0349 | 0.1213 | 0.0004 | |
| 333.15 | −0.0443 | −0.0242 | 0.0211 | −0.0349 | 0.1100 | 0.0004 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| {[BMIM]+[PF6]− (x1) + acetophenone (x2)} | |||||||
| VEm/cm3 mol−1 | 293.15 | 25.867 | −19.539 | −13.925 | −5.802 | 17.259 | 0.058 |
| 303.15 | 26.252 | −19.848 | −14.239 | −6.323 | 18.098 | 0.060 | |
| 313.15 | 26.668 | −20.117 | −14.717 | −7.167 | 19.465 | 0.062 | |
| 323.15 | 27.111 | −20.513 | −14.953 | −7.661 | 20.216 | 0.065 | |
| 333.15 | 27.629 | −20.878 | −15.365 | −8.669 | 21.732 | 0.069 | |
| Δκs/TPa−1 | 293.15 | 169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167 167 |
−254![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 159 159 |
−217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 659 659 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 317 317 |
92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
656 |
| 303.15 | 169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 169 169 |
−254![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 157 157 |
−217![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 677 |
−58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 338 338 |
92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 944 944 |
656 | |
| 313.15 | 138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
−290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681 681 |
−137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 488 488 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 475 |
−64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 931 931 |
610 | |
| 323.15 | 115![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
−259![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 106 106 |
−185![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
−213 | −50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 674 |
998 | |
| 333.15 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
−306![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 315 315 |
−225![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 102 102 |
151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 424 |
−95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 946 946 |
983 | |
| Δη/mPa s | 293.15 | −352.733 | 273.914 | −283.830 | 959.770 | −847.274 | 2.253 |
| 303.15 | −204.106 | 110.791 | −83.038 | 637.389 | −652.417 | 2.346 | |
| 313.15 | −110.457 | 54.423 | −77.853 | 323.853 | −272.339 | 0.794 | |
| 323.15 | −67.379 | 19.187 | −13.282 | 214.549 | −217.628 | 0.915 | |
| 333.15 | −43.425 | 17.276 | 29.925 | 139.596 | −211.452 | 0.928 | |
| Δn | 293.15 | −0.1436 | −0.0381 | 0.0072 | 0.0221 | 0.0241 | 0.0002 |
| 303.15 | −0.0479 | −0.0154 | 0.0554 | −0.0678 | 0.0526 | 0.0004 | |
| 313.15 | −0.0455 | −0.0195 | 0.0534 | −0.0686 | 0.0716 | 0.0005 | |
| 323.15 | −0.0396 | −0.0178 | 0.0443 | −0.0757 | 0.0959 | 0.0005 | |
| 333.15 | −0.0365 | −0.0181 | 0.0681 | −0.0841 | 0.0657 | 0.0003 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| {[EMIM]+[BF4]− (x1) + acetophenone (x2)} | |||||||
| VEm/cm3 mol−1 | 293.15 | 7.762 | −21.213 | 4.294 | −4.592 | 6.467 | 0.056 |
| 303.15 | 10.164 | −21.110 | 1.146 | −12.883 | 15.145 | 0.113 | |
| 313.15 | 10.587 | −21.508 | 0.805 | −14.441 | 17.417 | 0.125 | |
| 323.15 | 11.046 | −21.924 | 0.418 | −16.138 | 19.923 | 0.140 | |
| 333.15 | 11.393 | −22.981 | 3.878 | −18.262 | 18.181 | 0.155 | |
| Δκs/TPa−1 | 293.15 | 261![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 467 467 |
−238![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 721 |
−123![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
−234![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 443 443 |
264![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715 715 |
1010 |
| 303.15 | 220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921 921 |
−167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 349 349 |
−133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 613 613 |
−134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309 309 |
8675 | 794 | |
| 313.15 | 182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 119 119 |
−172![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 264 264 |
−155![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579 579 |
−23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 923 923 |
−39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 482 482 |
521 | |
| 323.15 | 143![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344 344 |
−135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
−81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
−41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407 407 |
−200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615 615 |
793 | |
| 333.15 | 121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 550 550 |
−182![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 071 071 |
−169![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 015 |
925 | −98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
1058 | |
| Δη/mPa s | 293.15 | −43.545 | 28.300 | −48.306 | 89.442 | −62.857 | 0.112 |
| 303.15 | −27.540 | 12.528 | −11.914 | 59.761 | −63.258 | 0.195 | |
| 313.15 | −18.761 | 12.249 | −8.344 | 34.175 | −40.769 | 0.193 | |
| 323.15 | −13.309 | 11.7670 | −14.720 | 20.466 | −16.561 | 0.135 | |
| 333.15 | −8.046 | 2.827 | −7.386 | 10.065 | −5.082 | 0.119 | |
| Δn | 293.15 | −0.0302 | −0.0235 | 0.0974 | −0.0083 | −0.0432 | 0.0002 |
| 303.15 | −0.0272 | −0.0256 | 0.0949 | 0.0086 | −0.0374 | 0.0003 | |
| 313.15 | −0.0246 | −0.0258 | 0.0826 | −0.1185 | −0.0157 | 0.0001 | |
| 323.15 | −0.0227 | −0.0243 | 0.0900 | −0.0176 | −0.0207 | 0.0001 | |
| 333.15 | −0.0201 | −0.0277 | 0.0804 | −0.0130 | −0.0043 | 0.0002 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| {[EMIM]+[EtSO4]− (x1) + acetophenone (x2)} | |||||||
| VEm/cm3 mol−1 | 293.15 | −6.429 | 2.560 | 12.560 | −13.367 | 1.413 | 0.047 |
| 303.15 | −5.957 | 2.654 | 12.016 | −17.958 | 7.353 | 0.048 | |
| 313.15 | −5.445 | 2.573 | 11.513 | −21.042 | 11.573 | 0.042 | |
| 323.15 | −4.893 | 2.374 | 11.120 | −24.136 | 15.689 | 0.052 | |
| 333.15 | −4.267 | 2.165 | 10.760 | −27.585 | 20.393 | 0.025 | |
| Δκs/TPa−1 | 293.15 | −88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 019 |
−262![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006 |
706 |
| 303.15 | −98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 751 751 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880 880 |
187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 116 116 |
−262![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 214 214 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
583 | |
| 313.15 | −109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 962 962 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012 012 |
173![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 265 |
−265![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 702 702 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 968 968 |
782 | |
| 323.15 | −117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 269 269 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
148![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 852 852 |
−246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 001 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 707 707 |
941 | |
| 333.15 | −88![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 483 483 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 626 626 |
230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 019 |
−262![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 334 334 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006 |
706 | |
| Δη/mPa s | 293.15 | −139.733 | 50.296 | −22.440 | 200.521 | −190.369 | 1.098 |
| 303.15 | −76.920 | 31.738 | 1.307 | 110.531 | −131.677 | 0.030 | |
| 313.15 | −44.822 | 26.386 | −17.842 | 71.022 | −60.353 | 0.348 | |
| 323.15 | −27.050 | 10.696 | −46.834 | 51.453 | −0.645 | 0.340 | |
| 333.15 | −16.167 | 1.901 | −19.639 | 28.183 | −6.702 | 0.279 | |
| Δn | 293.15 | −0.0188 | 0.0002 | 0.0055 | −0.0102 | 0.0707 | 0.0000 |
| 303.15 | −0.0175 | 0.0000 | 0.0090 | −0.0090 | 0.0694 | 0.0001 | |
| 313.15 | −0.0166 | −0.0014 | 0.0161 | −0.0040 | −0.0612 | 0.0000 | |
| 323.15 | −0.0149 | −0.0008 | 0.0178 | −0.0032 | 0.0613 | 0.0000 | |
| 333.15 | −0.0138 | −0.0028 | 0.0166 | 0.0014 | 0.0676 | 0.0001 | |
2.2. Methods and procedure
The binary mixtures were prepared by transferring via syringe the pure liquids into stoppered bottles to prevent evaporation. The components were filled directly into the air-tight Stoppard 10 cm3 glass vial and then weighed. For the determination of mass of each component, Radwag analytical mass balance was used with a precision of ±0.0001 g. The mixtures were shaken in order to ensure complete homogeneity of the compounds. After mixing the sample, the bubble-free homogeneous samples were injected into the vibration tube or sample cell of the densitometer, sound velocity analyzer, viscometer and refractor meter slowly using a medical syringe to avoid formation of bubbles inside the vibration tubes or sample cell. The chemicals were used without any further purification.2.3. Density and sound velocity measurements
Density and sound velocity for various ILs, acetophenone and mixture of ILs with acetophenone were measured using a digital vibrating-tube densitometer and sound velocity analyzer (Anton Paar DSA 5000M) with an accuracy of ±0.02 K. The instrument measured simultaneously density in the range of (0 to 3) g cm−3 and sound velocity from (1000 to 2000) m s−1 in temperature range of (293.15 to 333.15) K with pressure variation from (0 to 0.3) MPa. The sound velocity was measured using a propagation time technique.53 The samples were mediated between two piezoelectric ultrasound transducers. One transducer emits sound waves through the sample-filled cavity (frequency around 3 MHz) and the second transducer receives those waves.67 Thus, the sound velocity was determined by dividing the known distance between transmitter and receiver by the measured propagation time of the sound waves.53 The instrument was calibrated with dry air and freshly distilled degassed water once a day. The estimated error in density and speed of sound was less than ±2 × 10−4 g cm−3 and ±1 m s−1, respectively. The estimated error in excess molar volume and deviation in isentropic compressibility was ±0.005 cm3 mol−1 and ±1 TPa−1, respectively.2.4. Viscosity measurements
The viscosities measurements for pure components and their binary mixtures were determined using an Anton Paar Stabinger Viscometer (SVM 3000) fitted with jacketed small sample adapter (SSA) and a thermosel spindle (SC4-18) with an accuracy of ±0.02 K. Prior to each experimental run, the cell was firstly cleaned with deionised water (liquid 1) and then dried with acetone (liquid 2) using a fully automatic X-sample 452 Module which performed a cleaning routine after each measurement X-sample 452 performs a cleaning routine after each measurement. The estimated error in viscosity was less than ±0.05 mPa s. The instrument measured viscosity at temperature range of (293.15 to 333.15) K.2.5. Refractive index measurements
Measurement of the refractive index for pure components and their binary mixtures were measured by a digital automatic refractometer (Anton Paar RXA 156) with an accuracy of ±0.03 K. The estimated error in refractive index was less than ±0.005. The instrument measured refractive index at temperature range of (293.15 to 333.15) K.2.6. Quantum chemical studies
In other to rationalize our experimental results, quantum chemical calculations were used to investigate the inter-ionic interactions between the cations and anions of the ionic liquids both in gaseous state and in continuum solvation with acetophenone by utilizing the integral formalism variant of the polarized continuum model (IEFPCM).68Geometry optimizations of the molecular structures of [BMIM]+[BF4]−, [BMIM]+[PF6]−, [EMIM]+[BF4]− and [EMIM]+[EtSO4]− were done using the Density Functional Theory (DFT) method. The Perdew–Wang hybrid exchange–correlation functional (B3PW91)69,70 and Pople-type split-valence triple-zeta basis set71 augmented with diffuse and polarization functions on both the hydrogen and heavier atoms (6-311++G (d,p)) were selected for all the calculations. The B3PW91 (/6-311++G (d,p)) was selected because its adequate prediction of ionic liquids properties has been reported.72–75 Frequency calculations were carried out on the optimized structures and the absence of imaginary frequencies confirmed that the optimized structures are true energy minima. Both geometry optimizations and frequency calculations were performed with ultrafine grid (99 radical and 590 angular points) to increase the accuracy of the results.71 All the quantum chemical calculations were performed using Windows based Gaussian 09 suite version D.01.76
3. Results and discussion
3.1. Thermophysical and thermodynamics studies
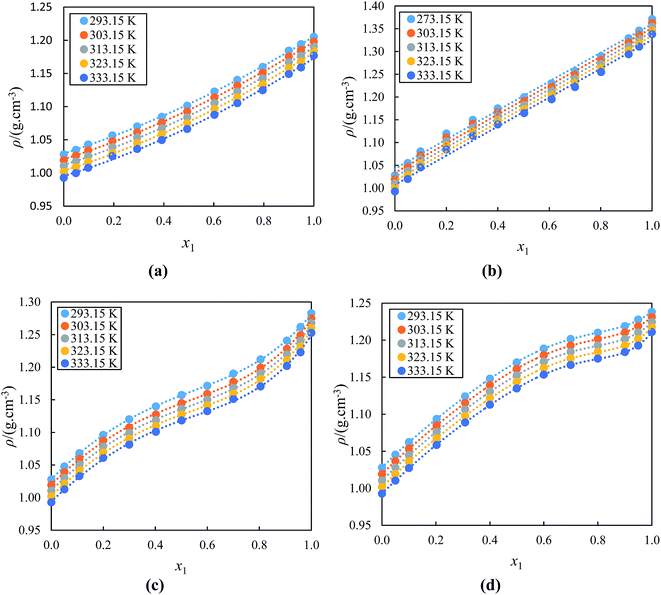
In order to understand the influence of acetophenone on the thermophysical properties of the alkyl imidazolium-based ILs, the values of ρ, u, η and nD for the binary mixtures of (ILs + acetophenone) systems were measured at temperature range (293.15 to 333.15) K under atmospheric pressure. Table 1 gives a clear indication that the studied ILs have higher ρ values than acetophenone at 303.15 K. The experimental values, ρ, u, η and nD for the binary mixtures of alkyl imidazolium-based ionic liquids with acetophenone at temperature range (293.15 to 333.15) K as a function of IL concentration are presented in Table 1S (ESI†).The values of ρ against the mole fraction of the IL at different temperature have been plotted in Fig. 1(a)–(d) for acetophenone and its binary mixtures with [BMIM]+[BF4]− or [BIMIM]+[PF6]− or [EMIM]+[BF4]− or [EMIM]+[EtSO4]−, respectively. Results in Fig. 1(a)–(d) reveals that the ρ values for all studied binary mixtures increases as concentration of the IL in acetophenone increase and decreases with temperatures. In this study, ILs were completely miscible in acetophenone (ε = 18.00 at 298.15 K),77 since acetophenone is a high dielectric liquid. The increase in the values of ρ for IL with acetophenone mixtures is as a result of an increase in the ion pair interactions between the IL and acetophenone. Increasing the temperature of the mixtures results in thermal agitation and causes molecules in the mixture to speed up and spread slightly further apart, occupying a larger volume hence decreasing the density. The thermophysical properties of ILs are dependent on the alkyl chain of the cation and nature of the structure of ions. The lower the alkyl chain length cation of the IL, the more dense compared to the higher alkyl chain length of the ILs, for example (1.20129 g cm−3 for [BMIM]+[BF4]− and 1.28174 g cm−3 for [EMIM]+[BF4]− at 293.15 K). This is mainly due to increase in dispersive interactions in ILs with increase in chain length, resulting in a nanostructured organization in polar and non-polar regions. The nonpolar regions are build-up of alkyl chains whereas the polar regions contain the cationic head groups and the anions. When the chain length of cation is enhanced, the nonpolar regions increase and take up more and more space, resulting in lower density in ILs with higher alkyl chain length.78–80 Results obtained gives a proper indication that the ρ of the binary mixtures depend on the size of the cation and anion of the alkyl imidazolium-based ILs and the composition of the entire binary mixture. The ρ values at all temperatures of the alkyl imidazolium-based ILs with acetophenone follow the order: [BMIM]+[PF6]− > [EMIM]+[BF4]− > [EMIM]+[EtSO4]− > [BMIM]+[BF4]−. This result show a clear indication of effect of cation and anion on ρ.81 This order displays the highest ρ values due to the increased size of the anion with the same cation and vice versa.
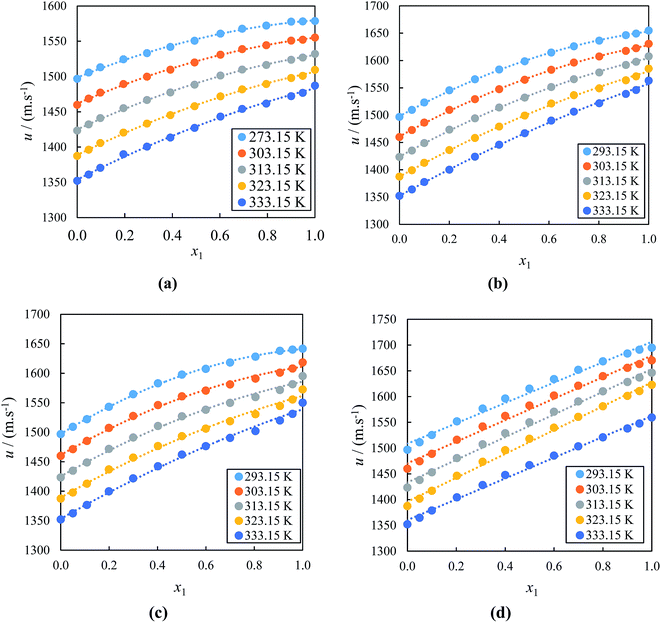
The sound velocity of the (IL + acetophenone) mixtures presented in Fig. 2(a)–(d), shows that the size of the ions and the content of the acetophenone has an effect on the values of u for the studied binary mixtures. Practically, the u values of ILs mainly depend on the nature and structure of ions and the alkyl chain length of the cation. It can be clearly seen from Fig. 2(a)–(d) that at a given temperature, u values increased as the concentration of IL increased in the mixture and decreased as the temperature is increased for all studied systems. The u values at T = 333.15 K of the alkyl imidazolium-based ILs with acetophenone follow the order: [BMIM]+[PF6]− > [EMIM]+[EtSO4]− > [EMIM]+[BF4]− > [BMIM]+[BF4]−. This order shows at the highest u values is due to the increased size of the anion. Further, the u values decrease as the cation alkyl chain length of ILs increases as seen in results with same anion. This is mainly due to anion accommodation closer to the cation. Apparently, ILs with higher cation side chain is accompanied by lower ρ and lower u. Therefore, our result demonstrates the influence of the cation and anion significantly affect the alkyl imidazolium-based ILs with acetophenone interactions. This may be also due to the stronger molecular interactions decreasing with increasing size of alkyl chain length of the cation of alkyl imidazolium-based ILs with acetophenone.81
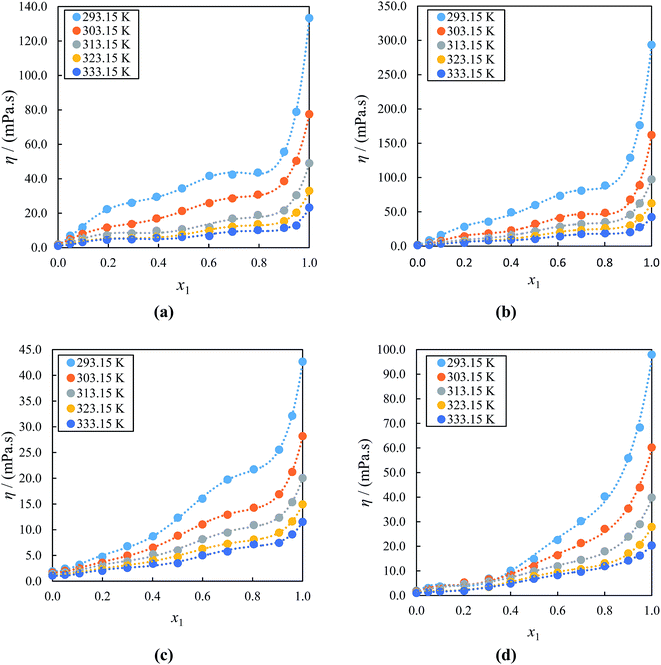
With regard to the viscosity, the results displayed in Fig. 3(a)–(d) indicates that the values η for all studied binary mixtures increases as concentration of the IL in acetophenone increase due to the strong coulombic interactions between the ions of ILs. These are strengthened upon mixing with acetophenone, leading to lower mobility of ions which is partially based on smaller sizes of ions of ILs and also decreases with temperatures mainly due to increased Brownian motion of the constituent molecules of ILs.81 It is clearly indicated that the (IL + acetophenone) mixtures are less viscous than pure ILs yet more viscous than acetophenone. In contrast to the ρ which increases with a decrease in the alkyl chain length of the cation, the values of η increases with an increase in alkyl side chain length of the cation if the system have a common anion. The η values for ([BMIM]+[BF4]− + acetophenone) binary mixture are higher compared to ([EMIM]+[BF4] + acetophenone) binary mixture. This results from an increase in the van der Waals interactions between alkyl side chains of the cation and the proportion of the charged species in an entire mixture. It is clear that these results possibly imply that the cation size has an effect on the variation of the thermophysical properties of ILs in mixture with acetophenone. Furthermore, it can be seen that η values for ([EMIM]+[EtSO4]− + acetophenone) binary mixture are higher compared to ([EMIM]+[BF4] + acetophenone) binary mixture. This is mainly due to the nature of the anion which also affects the η of ILs with same cation, particularly through relative basicity and the ability to form the hydrogen bonding. The η values at all temperatures of the alkyl imidazolium-based ILs with acetophenone follow the order: [BMIM]+[PF6]− > [BMIM]+[BF4]− > [EMIM]+[EtSO4]− > [EMIM]+[BF4]− with may be due to the increased alkyl chain of the cation.
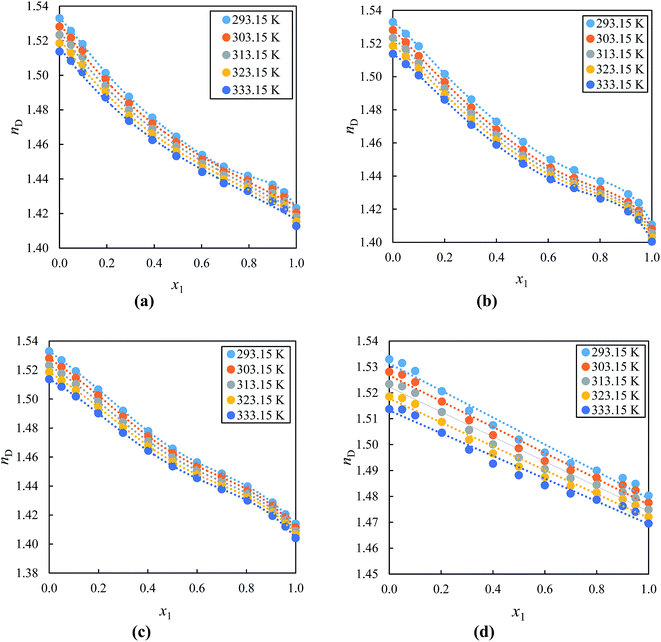
Fig. 4(a)–(d) shows the measured values of nD for alkyl imidazolium-based ILs with acetophenone at (293.15, 303.15, 313.15, 323.15 and 333.15) K over the entire composition range plotted against the mole fraction of the IL. The values of nD decreased with increasing concentration and temperature of IL in the mixture due to the ion–ion pair interactions between the IL and acetophenone The nD values at T = 293.15 K of the alkyl imidazolium-based ILs with acetophenone follow the order: [EMIM]+[EtSO4]− > [BMIM]+[BF4]− > [EMIM]+[BF4]− ≈ [BMIM]+[PF6]−. This order clearly shows that [EtSO4]− anion has higher nD values with same cation [EMIM]+ IL as compared to [BF4]− anion due to the ions arrangement and an efficient packing of ions of ILs.77 This result also indicated that the alkyl chain of cation decreases as nD values increases with the same anion but different cation. There are no previous, ρ, u, η and nD data reported in the literature for studied systems at various temperatures for comparison.
The obtained experimental thermo-physical properties; ρ, u, η and nD of the alkyl imidazolium-based ILs and their mixtures with acetophenone were further used to obtain the derived thermodynamics properties; VEm, Δκs, Δη and Δn using the standard equations in order to give an excellent estimation of the strength of unlike molecular interactions in the solution. These properties were fitted to the Redlich–Kister82 polynomial equation to check the accuracy of experimental results.
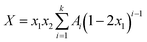 | (1) |
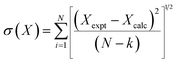 | (2) |
| ILs | Gaseous state | Acetophenone | ||
|---|---|---|---|---|
| ΔEint (kJ mol−1) | ΔG (kJ mol−1) | ΔEint (kJ mol−1) | ΔG (kJ mol−1) | |
| [BMIM]+[BF4]− | −337.79 | −294.80 | −22.04 | 11.93 |
| [BMIM]+[PF6]− | −310.62 | −273.16 | −14.05 | 13.01 |
| [EMIM]+[BF4]− | −338.10 | −297.64 | −25.91 | 4.27 |
| [EMIM]+[EtSO4]− | −350.71 | −302.36 | −24.92 | 11.44 |
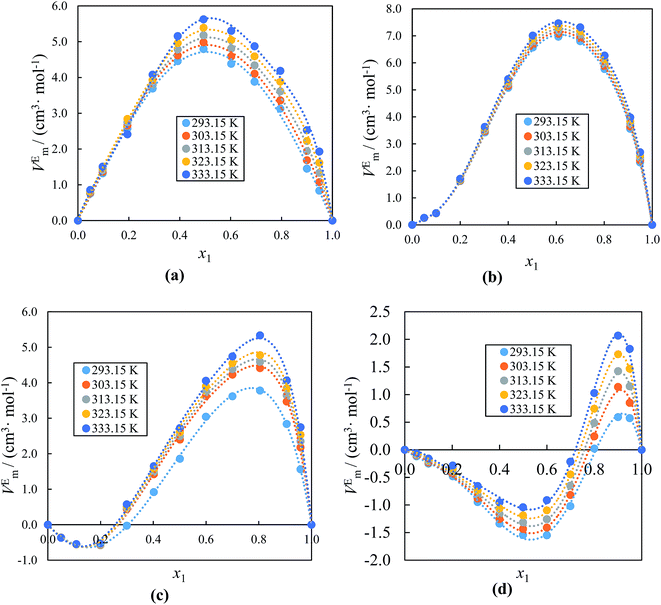
The obtained values of VEm, Δκs, Δη and Δn for the binary mixtures of alkyl imidazolium-based ILs with acetophenone at (293.15 to 333.15) K as a function of IL concentration are also presented in Table 1S.† Fig. 5(a) and (b) which are the VEm graphs of ILs with acetophenone, depicts positive values over the entire mole fraction range at (293.15 to 333.15) K for binary systems ([BMIM]+[PF6]− or [BMIM]+[BF4]− + acetophenone), while both positive and negative values for the systems ([EMIM]+[BF4]− or [EMIM]+[EtSO4]− + acetophenone) with negative values up to x1 ≈ 0.3000, and ≈0.8000 and positive values over the remaining mole fraction indicated in Fig. 5(c) and (d), respectively. As the mole fraction of IL increases the negative VEm increases sharply up to x1 ≈ 0.2000, and 0.6000, while with further addition of the ILs there is a decrease in the excess molar volume graph at all temperature ranges as seen in Fig. 5(c) and (d). This may reveal that more efficient packing is due to the differences in size and shape of molecules in the mixtures or attractive interaction occurs in the region of low mole fraction of IL. Furthermore, the negative VEm values of acetophenone-rich region of ([EMIM]+[BF4]− or [EMIM]+[EtSO4]− + acetophenone) becomes positive VEm values at higher IL concentration region. This inconsistency may be due to the variation from IL to IL (depending on the cation/anion size) as well as solvent to solvent and also depend on the nature of the structural arrangement of ILs and acetophenone. The positive values shows that there is a volume expansion mixing of IL. There is less volume contraction due to the interactions between unlike molecules which are weaker. The negative values shows that more attractive interactions in the mixtures than in the pure components and the systems have a strong packing effect by associations between ILs and acetophenone molecules through hydrogen bonding. The dependency of VEm on temperature and composition for the mixture can be described as the difference in intermolecular forces between the compounds or the variation in the molecular packing, which results from the differences in size and shape of the molecules forming a binary mixture with other compounds.83 The results in Fig. 5 show that the VEm values increase with increasing temperature for all systems at a fixed composition, indicating the deviation from ideal behavior to become pronounced as the temperature is increased. These observations can be attributed to the natural complexity of the IL with acetophenone systems as far as interactions with in the system are concerned. From Fig. 5, it can be noted that the magnitude of VEm values for ILs with acetophenone at studied temperature follow the order: [BMIM]+[PF6]− > [BMIM]+[BF4]− > [EMIM]+[BF4]− > [EMIM]+[EtSO4]−. From this order, it can be seen that the increase of the alkyl chain length of cation on the IL from [BMIM]+ to [EMIM]+ strongly affect the VEm values of the solutions. At T = 333.15 K, the positive VEm values for ([BMIM]+[BF4]− + acetophenone) (VEm = 5.623 cm3 mol−1 at x1 = 0.4936) are more positive than for the system ([EMIM]+[BF4]− + acetophenone) (VEm = 2.721 cm3 mol−1 x1 = 0.5011) while having the same anion [BF4]−, therefore VEm values become more positive in higher alkyl length of the IL cation under the same experimental condition. The more positive VEm values for ([BMIM]+[PF6]− + acetophenone) serves as an evidence that higher alkyl chain molecules decrease the hydrogen bonding tendency between [BMIM]+ with acetophenone. On the other hand, the ([EMIM]+[EtSO4]− + acetophenone) mixture reveals less positive values of VEm than other studied systems, which imply that [EMIM]+[EtSO4]− ion–dipole interactions and packing effects with acetophenone are stronger than those in the other systems. Clearly, it is also shown that the nature of interactions in ILs with acetophenone systems is highly dependent on nature of the ions as well as anion. It is quite clear from Fig. 5 that anion structure in alkyl imidazolium-based ILs strongly affects the VEm values. It was found that [PF6]− anion exhibit more positive VEm values than the corresponding [BF4]− anion with same cation [BMIM]+ and also [BF4]− anion more than [EtSO4]− anion with same cation [EMIM]+. It has been shown that the values of VEm also depend on the basicity as well as size of the anion.
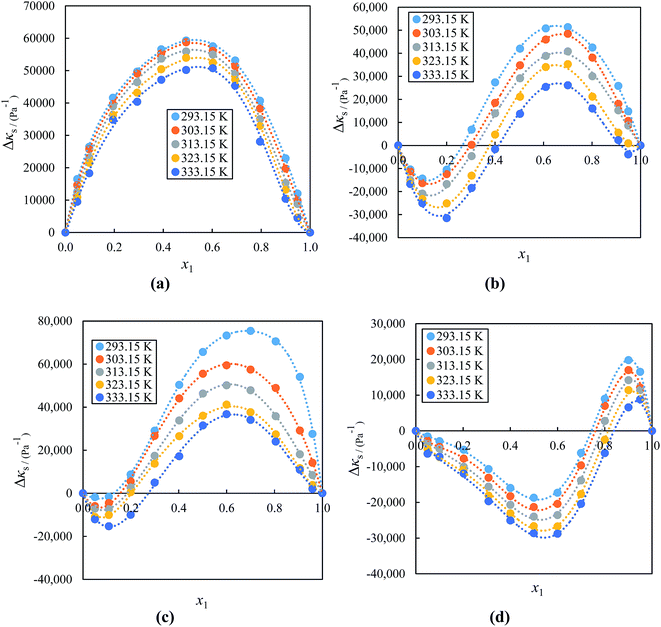
Fig. 6(a)–(d) shows the graphs for Δκs against the mole fraction at (293.15 to 333.15) K. As seen in Fig. 6(a), the values for Δκs are all positive for the whole compositions for the system ([BMIM]+[BF4] + acetophenone) and both positive and negative for the systems ([BMIM]+[PF6] or [EMIM]+[BF4]− or [EMIM]+[EtSO4]− + acetophenone) negative up to x1 ≈ 0.3000, ≈0.4000 and ≈0.8000 and positive over the remaining mole fraction indicated in Fig. 6(b)–(d), respectively at all temperatures. The negative Δκs values are attributed to the strong attractive interactions of the ions in the mixture due to the solvation of the ions in the acetophenone. The negative values of the Δκs of an alkyl imidazolium-based ILs with acetophenone implies that acetophenone molecules around the ILs are less compressible than the solvent molecules in the bulk solutions. As the mole fraction of IL increases, the negative deviation increases sharply up to x1 ≈ 0.1000, 0.0500, and 0.5000, while with further addition of the ILs there is a decrease in the compressibility graph at all temperature ranges. This might be due to a decrease in attraction of acetophenone and IL molecules in the IL-rich concentration region, since the interaction between the IL to IL increases and that between IL to acetophenone decreases. On the other hand, the negative Δκs values of acetophenone-rich region of ([BMIM]+[PF6] or [EMIM]+[BF4]− or [EMIM]+[EtSO4]− + acetophenone) becomes positive Δκs values at higher IL concentration region. These inconsistencies vary from IL to IL (depending on the cation/anion size) and solvent to solvent as well as also depend on the nature of the structural arrangement of IL and solvent. The positive values of Δκs for binary mixtures of IL with acetophenone are possibly attributed to the repulsive forces due to the electric charge of components and therefore, the molecular interactions between IL and acetophenone molecules weaken. The results in Fig. 6 show that the Δκs values decrease with increasing temperature for all systems at a fixed composition. These results are in good agreement with those obtained from the volumetric studies. On the other hand, the values followed the order [EMIM]+[EtSO4]− > [EMIM]+[BF4]− > [BMIM]+[BF4]− > [BMIM]+[PF6]−. The Δκs values decreases as alkyl chain length of cation increases and have higher values for [EMIM]+[EtSO4]−. These results reveal that Δκs values also depend on size of anion with the same cation.
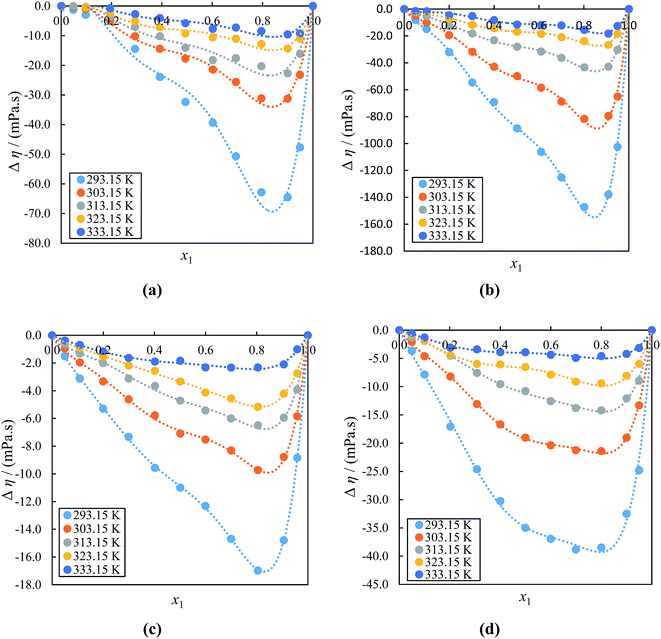
Fig. 7(a)–(d) which shown the Δƞ graphs of ILs with acetophenone, reveals that the values are all negative and become less negative with increasing temperature over a wide mole fraction range at (293.15 to 333.15) K under atmospheric pressure, and the minimum existed at IL region; i.e., x1 ≈ 0.8000–0.9000 and these curves are asymmetric. The minimum Δη values are −64.48 mPa s (at x1 ≈ 0.8999), −147.27 mPa s (at x1 ≈ 0.8017), −16.98 mPa s (at x1 ≈ 0.8050) and −38.83 mPa s (at x1 ≈ 0.6992) for ([BMIM]+[BF4]− or [BMIM]+[PF6] or [EMIM]+[BF4]− or [EMIM]+[EtSO4]− + acetophenone) systems, respectively. The negative Δη values may be attributed to the formation of weak hydrogen bonding interactions between the ions of ILs with acetophenone. These results clearly show that the Δη data is more affected with anions of alkyl imidazolium cation of ILs, which indicates that the interactions become weak between the ions of ([BMIM]+[PF6] + acetophenone) than ([BMIM]+[BF4]− + acetophenone) and ([EMIM]+[EtSO4]− + acetophenone) than ([EMIM]+[BF4]− + acetophenone) systems due to weakening of the dipolar association by ILs. The negative Δη values of [BMIM]+ cation with same anion is higher than [EMIM]+ cation due to the steric hindrance of alkyl chain groups in [BMIM]+ cations. When acetophenone is added to the IL, the viscosities of the mixtures decreases faster, mainly at lower temperatures. The strong coulomb interaction between the anions and cations becomes upon adding acetophenone, which in turn leads to a higher mobility of the ions and hence a lower viscosity of the mixtures.83 Therefore the values of Δη are negative in all cases.
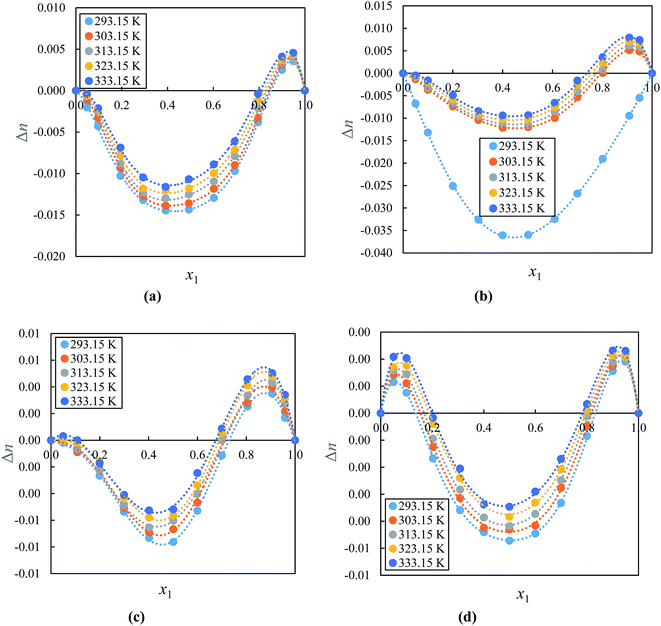
The “ΔnD” values can be used to determine of the electronic polarizability of a molecule and provide useful information about the intermolecular interactions between molecules. However, an accurate ΔnD data for ILs with molecular solvents are still scarce. Fig. 8(a)–(d) show ΔnD for binary mixture of alkyl imidazolium-based ILs with acetophenone and indicates that both negative and positive values for ΔnD over a wide mole fraction range at (293.15 to 333.15) K under atmospheric pressure show curves that are asymmetric with minimum and maximum reaching near to 0.4000–0.6000 and 0.9000 mole fraction of IL, respectively. The ΔnD values increases as temperature increased. The positive values of ΔnD may be due to the stronger interactions of ions of ILs with acetophenone and negative values attributed to weaker interaction ions of ILs with acetophenone. The values for ΔnD are dependent mainly on the difference in intermolecular interactions occurring between the two components. It can be seen that positive or negative VEm values corresponded to negative or positive ΔnD values; the minimum or maximum of both values exist at almost the same mole fraction of IL of corresponding systems. On the other hand, the values followed the order: [EMIM]+[BF4]− > [EMIM]+[EtSO4]− > [BMIM]+[PF6]− > [BMIM]+[BF4]−. These results reveal that ΔnD values also depend on size of anion with the same cation. The opposite signs between VEm and ΔnD can be attributed to less free volume available (if VEm is negative) and more free volume available (if VEm is positive) than in an ideal solution and photons will be more likely to interact with molecules or ions constituting the compound.84–87 These results are in good agreement with those obtained from the volumetric and acoustic studies.
3.2. Quantum chemical studies
Quantum chemical calculations have been employed complement our experimental findings on the interactions existing between the ionic liquids studied and acetophenone. Isolated structures of the anions ([PF6]−, [BF4]− and [EtSO4]−) and cations ([BMIM]+ and [EMIM]+) as well as molecular structures of the ionic liquids were optimized. Optimized structures of ionic systems are shown in Fig. 9. The interaction energies (ΔEint) for the ionic liquid systems were calculated from the stabilization energy difference according to eqn (3):| ΔEint = E(ac) − (E(a) + E(c)) | (3) |
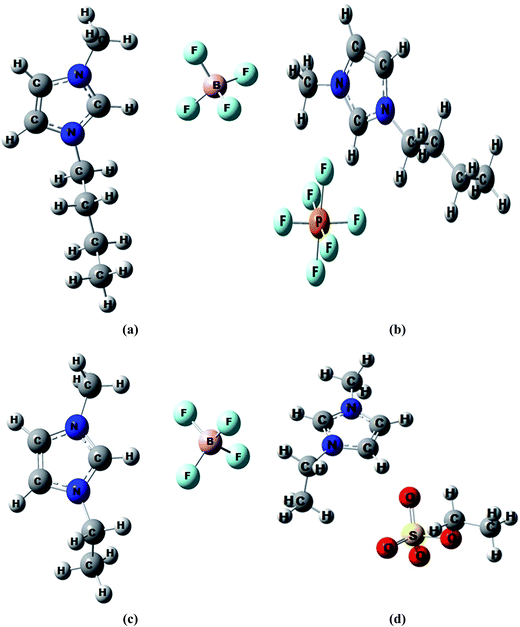 | ||
| Fig. 9 Optimized structures of ionic liquids (a) [BMIM]+[BF4]−, (b) [BMIM]+[PF6]−, (c) [EMIM]+[BF4]−, (d) [EMIM]+[EtSO4]−. | ||
Frequency calculations were also done on the optimized structures from which the change in Gibb's free energy (ΔG) for the cation–anion interaction was calculated. The interaction energies and change in Gibb's free energies are given in Table 3.
More negative ΔEint is an indication of stronger interaction when comparing interactions between two or more systems.89,90 As shown in the Table 3, ΔEint of the ionic systems in the presence of acetophenone remarkably increased (less negative) as compared to when they were without the solvent. This is an indication of appreciable decrease in the cation–anion interaction in the presence of the solvent.91 This can be attributed to the separate interactions of the cations and anions of the ionic liquids with the acetophenone molecules (i.e. ion–solvent interactions) rather than with each other (i.e. cation–anion interactions).69,90 The ion–solvent interaction reduces the cation–anion interaction by reducing the number of anion–cation pairs that are available for the cation–anion interaction.91,92
The ΔEint of the studied ionic liquid in solvent system, followed the order [BMIM]+[PF6]− > [BMIM]+[BF4]− > [EMIM]+[EtSO4]− > [EMIM]+[BF4]−. This trend shows that the extent of the solvent–ion interactions in ionic liquids follows the same order because the lower the cation–anion interaction (i.e. less negative ΔEint), the greater the ion–solvent interaction. The change in Gibb's free energy (ΔG) of the ionic systems also follows the similar trend as ΔEint indicates a reduced spontaneity of the cation–anion interactions in the presence of the acetophenone in the order [BMIM]+[PF6]− > [BMIM]+[BF4]− > [EMIM]+[EtSO4]− > [EMIM]+[BF4]− because of energetically more favourable solvent–ion interaction. The [BMIM]+[PF6]− system has the highest ΔG (13.01 kJ mol−1) which means the cation–anion interaction is least favourable and automatically the solvent–ion interaction is most favourable in this system relative to other systems of study.
4. Conclusions
This study report on new data for densities (ρ), sound velocities (u), viscosities (η), and refractive indices (nD) of binary mixtures of four alkyl imidazolium-based ionic liquids which have same anion and different anion and vice versa; [BMIM]+[BF4]−, [BMIM]+[PF6]−, [EMIM]+[BF4]− and [EMIM]+[EtSO4]−, with acetophenone over the wide composition range at (293.15 to 333.15) K under atmospheric pressure. The study illustrated the effect of temperature, concentration as well as cation/anion of ILs on the molecular interaction behavior of alkyl imidazolium-based IL with acetophenone. From experimental data, excess and derived properties such as VEm, Δκs, Δη and ΔnD were calculated and fitted to Redlich–Kister equation to check the accuracy of experimental results and found to be in good agreement with experimental results. Our results reveal that the values of, ρ, u and η increases as concentration of the IL increases whereas opposite trend was observed for nD and all the other measured properties decreases with temperatures. Results obtained indicates that the ρ, u and ΔnD values decrease with increase in the cation alkyl chain length, however an opposite trend was observed, in which the values of η increase when the number of carbon atoms in the alkyl chain length of cation of ILs increases. The experimental data indicate that cation and anion of ILs have a strong influence on the excess and deviation properties, especially on excess molar volume. Quantum chemical studies confirm the interactions of acetophenone with the ILs and also show that the solvent–ion interaction is highest in [BMIM]+[PF6]− system and lowest in [EMIM]+[BF4]− thereby confirming the experimental results.Acknowledgements
The authors acknowledge funding from North-West University, Department of Science and Technology and the National Research Foundation (DST/NRF) South Africa for M. Kgomotso and Dr I. Bahadur, respectively.References
- P. Sun and D. W. Armstrong, Anal. Chim. Acta, 2010, 661, 1–16 CrossRef CAS PubMed.
- K. N. Marsh, J. A. Boxall and R. Lichtenthaler, Phys. Chem. Chem. Phys., 2004, 219, 93–98 CAS.
- M. Freemantle, An introduction to ionic liquids, Royal Society of Chemistry, Cambridge, 2010, ch. 1, pp. 1–10 Search PubMed.
- Z. Yang and W. Pan, Enzyme Microb. Technol., 2005, 37, 19–28 CrossRef CAS.
- V. H. Alvarez, S. Mattedi, M. Martin-Pastor, M. Aznar and M. Iglesias, J. Chem. Thermodyn., 2011, 43, 997–1010 CrossRef CAS.
- A. E. Andreatta, A. Arce, E. Rodil and A. Soto, J. Chem. Eng. Data, 2009, 54, 1022–1028 CrossRef CAS.
- S. Keskin, D. Kayrak-Talay, U. Akman and O. Hortac, J. Supercrit. Fluids, 2007, 43, 150–180 CrossRef CAS.
- G. Laus, G. Bentivoglio, H. Schottenberger, V. Kahlenberg, H. Kopacka, T. Röder and H. Sixta, Lenzinger Ber., 2005, 84, 71–85 CAS.
- Y. Xu, J. Yao, C. Wang and H. Li, J. Chem. Eng. Data, 2012, 57, 298–308 CrossRef CAS.
- D. Han and K. H. Row, Molecules, 2010, 15, 2405–2426 CrossRef CAS PubMed.
- D. Shao, X. Lu, W. Fang, Y. Guo and L. Xu, J. Chem. Eng. Data, 2012, 57, 937–942 CrossRef CAS.
- H. Yao, S. Zhang, J. Wang, Q. Zhou, H. Dong and X. Zhang, J. Chem. Eng. Data, 2012, 57, 875–881 CrossRef CAS.
- Y. Zhong, H. Wang and K. Diao, J. Chem. Thermodyn., 2007, 39, 291–296 CrossRef CAS.
- V. V. Singh, K. Nigam, A. Batra, M. Boopathi, B. Singh and R. Vijayaraghavan, Int. J. Electrochem., 2012, 2012, 1–19 Search PubMed.
- M. Almasi and H. Iloukhani, J. Chem. Eng. Data, 2010, 55, 1416–1420 CrossRef CAS.
- M. N. Roy, B. K. Sarkar and R. Chanda, J. Chem. Eng. Data, 2007, 52, 1630–1637 CrossRef CAS.
- M. Sittig, Handbook of Toxic and Hazardous Chemicals and Carcinogens, Noyes Publications, Park Ridge, NJ, 2nd edn, 1985 Search PubMed.
- J. M. Prausnitz, Fluid Phase Equilib., 1999, 95, 158–160 Search PubMed.
- P. B. Mandal, K. Madhusree and S. S Bandyopadhyay, J. Chem. Eng. Data, 2003, 48, 703–707 CrossRef.
- M. J. Dávila, S. Aparicio and R. Alcalde, Ind. Eng. Chem. Res., 2009, 48, 10065–10076 CrossRef.
- Y. Maham, L. Lebrette and A. E. Mather, J. Chem. Eng. Data, 2002, 47, 550–553 CrossRef CAS.
- P. Abrman and I. Malijevská, Fluid Phase Equilib., 1999, 166, 47–52 CrossRef CAS.
- Z. Zhou, Y. Shi and X. Zhou, J. Phys. Chem. A, 2004, 108, 813–822 CrossRef CAS.
- W. Dongqing, J. F. Truchon, S. Sirois and D. Salahub, J. Chem. Phys., 2002, 116, 6028–6038 CrossRef.
- G. F. Velardez, J. C. Ferrero, J. A. Beswick and J. A. Dudey, J. Phys. Chem. A, 2001, 105, 8769–8774 CrossRef CAS.
- S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem., 2006, 35, 1475–1517 CAS.
- B. González, N. Calvar, E. González and A. Domínguez, J. Chem. Eng. Data, 2008, 53, 881–887 CrossRef.
- A. B. Pereiro, J. L. Legido and A. Rodríguez, J. Chem. Thermodyn., 2007, 39, 1168–1175 CrossRef CAS.
- G. Annat, M. Forsyth and D. R. MacFarlane, J. Phys. Chem. B, 2012, 116, 8251–8258 CrossRef CAS PubMed.
- M. Deetlefs, K. R. Seddon and M. Shara, Phys. Chem. Chem. Phys., 2006, 8, 642–649 RSC.
- A. Kovács, R. J. M. Konings, J. K. Gibson, I. Infante and L. Gagliardi, Chem. Rev., 2015, 115, 1725–1759 CrossRef PubMed.
- A. Jardy, A. L. Lasalle-Molin, M. Keddam and H. Takenouti, Electrochim. Acta, 1993, 37, 2195–2201 CrossRef.
- D. Tromans, J. Electrochem. Soc., 1998, 145, L42–L45 CrossRef CAS.
- R. Walter, Corrosion, 1973, 29, 290–298 CrossRef.
- V. Brusic, M. A. Frisch, B. N. Eldridge, F. P. Novak, F. B. Kaufman, B. M. Rush and G. S. Frankel, J. Electrochem. Soc., 1991, 138, 2253–2259 CrossRef CAS.
- S. L. F. da Costa, S. M. L. Agostinho and K. Nobe, J. Electrochem. Soc., 1993, 140, 3483–3488 CrossRef CAS.
- D. Tromans and R. Sun, J. Electrochem. Soc., 1991, 138, 3235–3244 CrossRef CAS.
- T. E. Shubina and M. T. M. Koper, Electrochim. Acta, 2002, 47, 3621–3628 CrossRef CAS.
- N. Lopez and F. Illas, J. Phys. Chem. B, 1998, 102, 1430–1436 CrossRef CAS.
- S. Biing-Ming, S. Zhang and Z. C. Zhang, J. Phys. Chem., 2004, 108, 19510–19517 CrossRef.
- B. O. Roos and K. P. Lawley, Adv. Chem. Phys, Wiley-Chichester, Inc., England, 1987 Search PubMed.
- J. S. Wilkes, J. Mol. Catal. A: Chem., 2004, 214, 11–17 CrossRef CAS.
- S. Zhang, X. Lu, Y. Zhang, Q. Zhou, J. Sun, L. Han, G. Yue, X. Liu, X. Cheng and S. Li, Springer-Verlag, 2008, DOI:10.1007/430.
- I. G. Cruz, D. Valencia, T. Klimova, R. O. Roa, J. M. Magadan, R. D. Balderas and F. Illas, J. Mol. Catal. A: Chem., 2008, 281, 79–84 CrossRef.
- A. Ali, A. K. Nain and M. Kamil, Thermochim. Acta, 1996, 274, 09–21 CrossRef.
- S. G. Rao, T. M. Mohan, T. V. Krishna and B. S. Rao, J. Chem. Thermodyn., 2016, 94, 127–137 CrossRef.
- M. T. Zafarani-Moattar and H. Shekaari, J. Chem. Eng. Data, 2005, 50, 1694–1699 CrossRef CAS.
- E. J. González, B. González, N. Calvar and Á. Domínguez, J. Chem. Eng. Data, 2007, 52, 1641–1648 CrossRef.
- S. Bhagour, S. Solanki, N. Hooda, D. Sharma and V. K. Sharma, J. Chem. Thermodyn., 2013, 60, 76–86 CrossRef CAS.
- N. Deenadayalu, I. Bahadur and T. Hofman, J. Chem. Thermodyn., 2010, 42, 726–733 CrossRef CAS.
- N. Deenadayalu, I. Bahadur and T. Hofman, J. Chem. Eng. Data, 2010, 55, 2636–2642 CrossRef CAS.
- N. Deenadayalu, I. Bahadur and T. Hofman, J. Chem. Eng. Data, 2011, 56, 1682–1686 CrossRef CAS.
- I. Bahadur and N. Deenadayalu, J. Solution Chem., 2011, 40, 1528–1543 CrossRef CAS.
- I. Bahadur, N. Deenadayalu, Z. Tywabi, S. Sen and T. Hofman, J. Chem. Thermodyn., 2012, 49, 24–38 CrossRef CAS.
- I. Bahadur and N. Deenadayalu, Thermochim. Acta, 2013, 566, 77–83 CrossRef CAS.
- I. Bahadur and N. Deenadayalu, S. Afr. J. Chem., 2013, 66, 200–206 CAS.
- V. Govinda, P. M. Reddy, I. Bahadur, P. Attri, P. Venkatesu and P. Venkateswarlu, Thermochim. Acta, 2013, 556, 75–88 CrossRef CAS.
- I. Bahadur, T. M. Letcher, S. Singh, G. G. Redhi, P. Venkatesu and D. Ramjugernath, J. Chem. Thermodyn., 2015, 82, 34–46 CrossRef CAS.
- S. Singh, I. Bahadur, G. G. Redhi, D. Ramjugernath and E. E. Ebenso, J. Mol. Liq., 2014, 200, 160–167 CrossRef CAS.
- S. Singh, I. Bahadur, G. G. Redhi, E. E. Ebenso and D. Ramjugernath, J. Chem. Thermodyn., 2015, 89, 104–111 CrossRef CAS.
- S. Singh, I. Bahadur, G. G. Redhi, E. E. Ebenso and D. Ramjugernath, J. Mol. Liq., 2014, 199, 518–523 CrossRef CAS.
- R. Gomes de Azevedo, J. M. S. S. Esperança and V. Najdanovic-Visak, J. Chem. Eng. Data, 2005, 50, 997–1008 CrossRef.
- M. T. Zafarani-Moattar and H. Shekaari, J. Chem. Eng. Data, 2005, 50, 1694–1699 CrossRef CAS.
- Y. A. Sanmamed, D. González-Salgado, J. Troncoso, L. Romani, A. Baylaucq and C. Boned, J. Chem. Thermodyn., 2010, 42, 553–563 CrossRef CAS.
- E. Gómez, B. González, N. Calvar, E. Tojo and Á. Domìnguez, J. Chem. Eng. Data, 2006, 51, 2096–2102 CrossRef.
- K. Saravanakumar, R. B. Askran and T. R. Kubendran, Asian J. Chem., 2011, 23, 2643–2647 CAS.
- T. J. Fortin, A. Laesecke, M. Freund and S. Outcalt, J. Chem. Thermodyn., 2013, 57, 276–285 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Phys. Chem., 1997, 107, 3032–3041 CrossRef CAS.
- J. P. Perdew, Electronic Structure of Solids, Akademie Verlag, Berlin, 1991, pp. 11–20 Search PubMed.
- K. Burke, J. P. Perdew and Y. Wang, Electronic density functional theory: recent progress and new directions, New York, 1998, p. 81 Search PubMed.
- R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 542, 724–728 CrossRef.
- D. Singh, V. Singh, N. Islam and R. L. Gardas, RSC Adv., 2016, 6, 623–631 RSC.
- V. H. Álvarez, D. Serrão, J. L. da Silva Jr, M. R. Barbosa and M. Aznar, Ionics, 2013, 19, 1263–1269 CrossRef.
- D. Keshapolla and R. L. Gardas, Fluid Phase Equilib., 2014, 383, 32–42 CrossRef CAS.
- B. A Marekha, M. Bria, M. Moreau, I. De Waele, F.-A. Miannay, Y. Smortsova, T. Takamuku, O. N. Kalugin, M. Kiselev and A. Idrissi, J. Mol. Liq., 2015, 210, 227–237 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, G09a: GAUSSIAN 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- J. A. Riddick, W. B. Bunger and T. K. Sakano, Organic solvents, Wiley-Interscience, New York, 4th edn, 1986 Search PubMed.
- C. Kolbeck, J. Lehmann, K. R. J. Lovelock, T. Cremer, N. Paape, P. Wasserscheid, A. P. Fröba, F. Maier and H.-P. Steinrück, J. Phys. Chem. B, 2010, 114, 17025–17036 CrossRef CAS PubMed.
- Y. T. Wang and G. A. Voth, J. Am. Chem. Soc., 2005, 127, 12192–12193 CrossRef CAS PubMed.
- J. N. A. C. Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef PubMed.
- V. Govinda, P. Venkatesu and I. Bahadur, Phys. Chem. Chem. Phys., 2016, 18, 8278–8326 RSC.
- O. Redlich and A. Kister, Ind. Eng. Chem., 1948, 40, 345–348 CrossRef.
- M. M. Taib and T. Murugesan, J. Chem. Eng. Data, 2012, 57, 120–126 CrossRef CAS.
- L. Cammarata, S. G. Kazarian, P. A. Salterb and T. Welton, Phys. Chem. Chem. Phys., 2001, 3, 5192–5200 RSC.
- M. A. Iglesias-Otero, J. Troncoso, E. Carballo and L. Romani, J. Chem. Thermodyn., 2008, 40, 949–956 CrossRef CAS.
- M. Anouti, A. Vigeant, J. Jacquemin, C. Brigouleix and D. Lemordant, J. Chem. Thermodyn., 2010, 42, 834–845 CrossRef CAS.
- Y. Tian, X. Wang and J. Wang, J. Chem. Eng. Data, 2008, 53, 2056–2059 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- N. Cheng, P. Yu, T. Wang, X. Sheng, Y. Bi, Y. Gong and L. Yu, J. Phys. Chem. B, 2014, 118, 2758–2768 CrossRef CAS PubMed.
- W. Xu, T. Wang, N. Cheng, Q. Hu, Y. Bi, Y. Gong and L. Yu, Langmuir, 2015, 31, 1272–1282 CrossRef CAS PubMed.
- Y. Zhao, J. Wang, H. Wang, Z. Li, X. Liu and S. Zhang, J. Phys. Chem. B, 2015, 119, 6686–6695 CrossRef CAS PubMed.
- M. Bešter-Rogač, A. Stoppa and R. Buchner, J. Phys. Chem. B, 2014, 118, 1426–1435 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra15476j |
| This journal is © The Royal Society of Chemistry 2016 |