First-principles study on quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In) with large spin-flip gap

Abstract

First-principles calculations were used to systematically investigate the structural, electronic and half-metallic properties of newly designed quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In). The calculated results show that these three compounds have an excellent half-metallicity in their ferrimagnetic ground state. ZrFeVZ (Z = Al, Ga, In) compounds exhibit the large spin-flip gaps of 0.348 eV, 0.428 eV and 0.323 eV at their equilibrium lattice constants, respectively. The total spin magnetic moment is 2 μ_B for all the three compounds, which is in agreement with the M_t = Z_t − 18 rule. The half-metallic properties of these three compounds are quite robust to the hydrostatic and tetragonal strain, and can also be kept when the electron correlation (U) is considered. For the ZrFeVIn compound, the spin-flip band gap achieves the maximum value (0.57 eV) under a small strain. The calculated Curie temperatures based on the mean field approximation (MFA) method are 818.04 K, 826.66 K, and 751.70 K for the ZrFeVAl, ZrFeVGa, and ZrFeVIn compounds, respectively. We hope that our current work may trigger Heusler compounds containing 4d transition metal elements and with quite large spin-flip band gaps for application in future spintronics devices.

---

1. Introduction

Since the first half-metallic (HM) material NiMnSb, a half-Heusler compound, was reported by Groot et al.,¹ a lot of Heusler compounds have been predicted to be HM materials. The half-metallic Heusler compounds can be regarded as highly-spin-polarized materials due to their special electronic structures near the Fermi level. Up to date, much attention has been paid to investigating the novel physical properties of the half-metallic Heusler compounds.^2–20

Most of the reported half-metallic compounds with Heusler structure have a very small spin-flip band gap (or named as half-metallic gap). The spin-flip band gap refers to the minimum energy value in the bottom of minority spin conduction bands with respect to the Fermi level and the absolute value of the top energy of minority spin valence bands.^21,22 For example, CoFeMnZ (Z = Al, Si, Ga, Ge), NiFeMnGa, and NiCoMnGa compounds reported by Felser's team have a small spin-flip gap of almost 0 eV, except for CoFeMnSi.^23–26 It is well known that the small spin-flip band gap indicates that the half-metallicity is not stable, because the defect or temperature can easily destroy the small gap and the half-metallicity, and further affect the applications of half-metallicity in spintronics devices. Recently, some half-metallic Heusler compounds with a large spin-flip band gap have been predicted by the first-principles calculation. For example, quaternary Heusler compounds CoFeTiSi, CoFeTiAs and CoFeVSb²² studied by Xiong et al. are half-metallic ferromagnets with considerable spin-flip band gaps of 0.31 eV, 0.18 eV and 0.17 eV, respectively; Wang et al.⁴ observed that quaternary Heusler ZrVTiZ (Z = Al and Ga) compounds are half-metallic materials both with a spin-flip band gap of 0.19 eV; Gao et al. predicted that CoFeCrAl and CoFeCrSi exhibit excellent half-metallic ferromagnetism with the large spin-flip band gaps of 0.16 and 0.28 eV;²¹ ZrFeTiZ (Z = Al, Si, Ge) and ZrNiTiAl compounds³⁵ investigated based on the GGA calculation are proved to be half-metallic ferromagnets with spin-flip gaps of 0.56 eV, 0.92 eV, 0.86 eV and 0.65 eV, respectively, which are quit large compared to other reported half-metallic materials; another series of Zr-based Heusler compounds ZrCoTiZ (Z = Al, Ga, Si and Ge)³⁶ have a robust half-metallic gap to the hydrostatic and tetragonal and they can be regard as good candidates for applications in some complex environment.

Motivated by above-mentioned information, it is important to search for new HM materials with a large spin-flip band gap in the quaternary Heusler compounds for spintronics applications. In this work, we focus on the study of a new series of quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In). It is predicted that the newly designed quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In) are half-metallic ferrimagnets and exhibit larger spin-flip band gaps than similar Zr-based Heusler compounds ZrVTiZ (Z = Al, Ga)⁴ and ZrTiCrZ (Z = Al, Ga, In, Si, Ge, Sn)²⁷ reported previously. Furthermore, we also discuss the origin of the band gap and test the structural stability and the sensitivity of half-metallicity to the hydrostatic and tetragonal strain.

2. Computational details

The CASTEP code based on the pseudopotential method with a plane-wave basis set^28,29 is used to calculate the magnetic and electronic properties of the ZrFeVZ (Z = Al, Ga, In) compounds. The interaction between the atom core and valence electrons is described by the ultrasoft pseudopotential.³⁰ The generalized gradient approximation (GGA)³¹ was selected in the Perdew–Burke–Ernzerhof scheme for the exchange-correction functional and we adopted a cutoff energy of 400 eV and a mesh of 12 × 12 × 12 k-points to ensure good convergence. Otherwise, the calculation continue to ensure good convergence until the energy deviation is less than 1 × 10⁻⁶ eV per atom. We apply 1.34 eV, 2.0 eV and 1.8 eV on the V, Zr and Fe atoms respectively to calculate the property of electron correlation of the ZrFeVZ (Z = Al, Ga, In) compounds based on the GGA+U calculation method.

3. Results and discussion

Full-Heusler compounds with Cu₂MnAl-type or Hg₂CuTi-type structure have the same chemical formula: X₂YZ, where the X and Y are transition metal elements and the Z is s–p element. The difference of the two structures is that the two X elements occupy the A (0, 0, 0), C (0.5, 0.5, 0.5) and the A (0, 0, 0), B (0.25, 0.25, 0.25) positions in the Cu₂MnAl-type and Hg₂CuTi-type structures, respectively. When one of X atoms is replaced by another transition metal element M, a quaternary Heusler compounds X–M–Y–Z is obtained.^32,33 In our calculations, X is V atom, Z is a main group element, M and Y are Zr and Fe atoms, respectively. As shown in Fig. 1, there are three possible atomic arrangement fashions for X–M–Y–Z with quaternary Heusler structure. We also list the three types of atomic arrangement in Table 1 to give more detailed and intuitive information.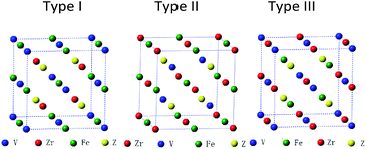

Fig. 1 Three possible atomic arrangement fashions of quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In).

Table 1 The atomic occupation of the three types of quaternary Heusler compounds ZrFeVZ (Z = Al, Ga and In): 4a = (0, 0, 0)a, 4b = (0.25, 0.25, 0.25)a, 4c = (0.5, 0.5, 0.5)a, and 4d = (0.75, 0.75, 0.75)a, where a is the optimized lattice parameter

Type	4a (0, 0, 0)	4b (0.25, 0.25, 0.25)	4c (0.5, 0.5, 0.5)	4d (0.75, 0.75, 0.75)
Type I	V	Zr	Fe	Z
Type II	V	Fe	Zr	Z
Type III	Zr	V	Fe	Z

---

In order to achieve the equilibrium lattice constants of ZrFeVZ (Z = Al, Ga, In) compounds, the geometry optimization was firstly performed in the three different atomic arrangement fashions by calculating the total energy as a function of the volume of per unit cell. The geometry optimization curves are plotted in Fig. 2. It can be seen that the type I atomic arrangement fashion has the lowest total energy in the ferrimagnetic state. That is, the ZrFeVZ (Z = Al, Ga, In) compounds with quaternary Heusler structure prefer to crystal in the type I structure, which is similar to the previous studies of Zr-based Heusler compounds.³ The calculated equilibrium lattice constants are 6.22 Å, 6.20 Å, and 6.47 Å for the ZrFeVAl, ZrFeVGa and ZrFeVIn compounds. Next, we only focus on the ZrFeVZ (Z = Al, Ga, and In) compounds with type I atomic arrangement fashion in ferrimagnetic state.

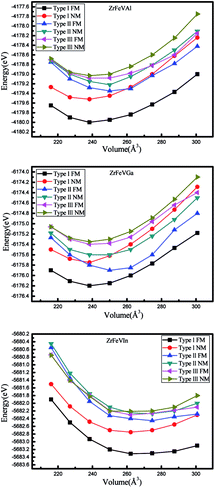Fig. 2 Total energy as a function of lattice constants in both the non-magnetic and ferrimagnetic states for ZrFeVZ (Z = Al, Ga, In) compounds with three possible atomic arrangement fashions.

The formation energy is a key parameter to theoretically investigate the structure stability and analyze the possibility of synthesis. The calculation formula of formation energy is that: E_f = (E_total − mE_Zr − nE_V − pE_Fe − qE_Z) (E_f is the formation energy, E_total is the calculated energy of per formula unit based on equilibrium lattice constants and the E_Zr, E_V, E_Fe and E_Z correspond to the total energy of per atom for the Zr, Fe, V, and Z (Z = Al, Ga, In) bulks, respectively. In addition, m, n, p and q are the percentage of Zr, V, Fe and Z elements occupied in the compound.). The calculated formation energies are listed in the Table 2. It can be seen that the E_f are negative for all those ZrFeVZ (Z = Al, Ga, In) compounds with type I atomic arrangement fashion, which indicates that the thermodynamic stability of those compounds.

Fig. 3 shows the calculated band structures of ZrFeVZ (Z = Al, Ga, In) compounds at their equilibrium lattice constants with type I atomic arrangement fashion. It can be seen that the Fermi level crosses some of the majority-spin bands, and the ZrFeVZ (Z = Al, Ga, In) compounds exhibit a metallic nature in the majority-spin channel. While the Fermi level lies in a indirect band gap, and therefore the ZrFeVZ (Z = Al, Ga, In) compounds exhibit a semiconductive behavior in the minority-spin channel. That is, ZrFeVZ (Z = Al, Ga, In) compounds are half-metallic materials with 100% spin-polarized ratio of conduction electron. More importantly, the spin-flip band gaps of these three compounds are 0.348 eV, 0.428 eV and 0.323 eV, respectively, which are larger than other Zr-based half-metallic materials and many 3d-transition-metal-element-based quaternary Heusler compounds. Usually, the larger spin-flip band gap, the more robust half-metallic behavior to lattice deformation and temperature. So the ZrFeVZ (Z = Al, Ga, In) compounds reported in this work can be regarded as the good candidates for spintronics devices due to their large spin-flip gaps and robust half-metallicity.

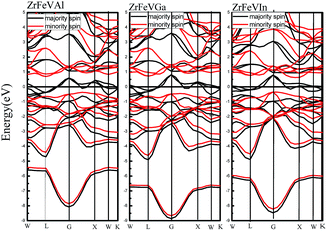Fig. 3 Calculated band structures of ZrFeVZ (Z = Al, Ga, In) compounds at their equilibrium lattice constants with type I structure.

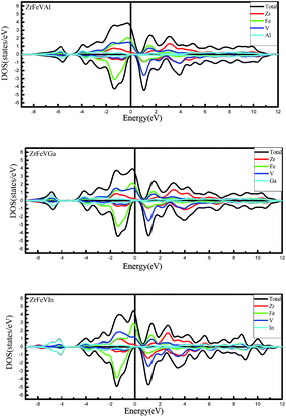
Furthermore, we calculated the total density of states (TDOS) and partial density of states (PDOS) of ZrFeVZ (Z = Al, Ga, In) compounds at their respective equilibrium lattice constants to further study their electronic structures. As is shown in Fig. 4, the significant contributions to the total DOS in the energy range between −2 eV and 1 eV come from 3d states of Fe and V atoms hybridized with 4d states of Zr atom in the majority-spin channel. In the minority-spin channel, the hybridization between the lower-energy 3d states of the high-valence transition-metal Fe atom and the higher-energy 3d states of the lower-valence transition-metal V atom leads to the formation of bonding and antibonding states. The bonding states are mainly localized at the high-valence transition-metal Fe atom site, while the unoccupied antibonding states are mainly localized at the lower-valence transition-metal V atom site. The Fermi level is located at the band gap between the antibonding and bonding states in the minority-spin channel for ZrFeVZ (Z = Al, Ga, In) compounds. Therefore, the band gap of ZrFeVZ (Z = Al, Ga, In) compounds in the minority-spin channel is mainly caused by the formation of bonding and antibonding states.

Fig. 4 Calculated total and partial density of states (DOS) for ZrFeVZ (Z = Al, Ga, In) compounds.

The Table 2 also gives the values of the total magnetic moments and the atomic magnetic moments of the ZrFeVZ (Z = Al, Ga, In) compounds. The results show that the total spin moments of the three compounds are 2.00 μ_B. The integral value of total spin moment is one of essential features of half-metallic compounds.^7,8 The hybridization schematic reported in ref. 34 explain the relationships between the total number of the valance electrons and the magnetic moment in per unit cell for full-Heusler compounds. The number of total valence electrons in per unit cell are 20 for ZrFeVZ (Z = Al, Ga, In) compounds and obviously the ZrFeVZ (Z = Al, Ga, In) obey the s–p formula M_t = Z_t − 18 rather than M_t = Z_t − 24 (the M_t and Z_t represent for the number of total valence electrons in per unit cell and the total magnetic moment, respectively).³⁷ It is well known that the p–d hybridizations between the transition element and the s–p element determine the degree of p–d orbital occupation and then tune the location of the Fermi level.³⁸ In order to understand why ZrFeVZ (Z = Al, Ga, In) compounds follow the M_t = Z_t − 18 rule, the key is to describe counts of occupied states in the spin channel where the half-metallic gap appears. From Fig. 3, it can be seen that there are 9 bands below the Fermi level in minority spin channel. Among these 9 bands, one s band and three p bands originate from the Z atom.³⁹ Corresponding to the DOS patterns as shown in Fig. 4, it can be seen that in minority spin channel, a set of 2 × e_g bands and a set of 3 × t_2g bands between −3 to −1 eV originate from the transition metal elements, which finally determines five d bands below the Fermi level. So, it is very clear that there are 5 occupied d states in minority spin channel, together with the s and p ones, totally 9 occupied bands in ZrFeVZ (Z = Al, Ga, In) compounds. Based on the following formula: M_total = (N ↑ − N ↓)μ_B = (Z_total − 2N ↓)μ_B = (Z_total − 18)μ_B, the relationship between M_t and Z_t is M_t = Z_t − 18. The atomic magnetic moments of Zr/V are 0.18 μ_B/2.88 μ_B, 0.08 μ_B/2.62 μ_B, and 0.52 μ_B/3.28 μ_B, and the atomic magnetic moments of Fe/Z are −0.90 μ_B/−0.16 μ_B, −0.52 μ_B/−0.16 μ_B, and −1.60 μ_B/−0.20 μ_B, respectively. Table 2 shows the major contributions to the total magnetic moments arise from Fe and V atoms while the Zr and Z atoms contributions are minor. The atomic magnetic moment of Zr/V is antiparallel to that of Fe/Z atoms, and therefore, these three compounds are half-metallic ferrimagnets.^40–43

Table 2 The calculated equilibrium lattice constants, the total and atomic magnetic moments (M_t), the maximum of the valence band (VBM), the minimum of the conduction band (CBM), the spin-flip/half-metal gap (HM Gap) and the formation energy (E_f) of the ZrFeVZ (Z = Al, Ga, In) compounds based on the GGA and the GGA+U calculation method

	a (Å)	Calculation method	Mtotal (μB)	MZr (μB)	MV (μB)	MFe (μB)	MZ (μB)	VBM (eV)	CBM (eV)	Gap (eV)	HM gap (eV)	Ef (eV)
ZrFeVAl	6.22	GGA	2.00	0.18	2.88	−0.90	−0.16	−0.35	0.85	1.20	0.35	−2.77
		GGA+U	2.00	0.70	3.98	−2.50	−0.18	−0.33	0.50	0.83	0.33
ZrFeVGa	6.20	GGA	2.00	0.08	2.62	−0.52	−0.16	−0.43	0.74	1.17	0.43	−2.91
		GGA+U	2.00	1.22	4.10	−2.98	−0.36	−0.06	0.17	0.24	0.06
ZrFeVIn	6.47	GGA	2.00	0.52	3.28	−01.60	−0.20	−0.32	0.63	0.95	0.32	−3.06
		GGA+U	2.00	1.08	4.10	−2.90	−0.28	−0.01	0.27	0.28	0.01

---

To test the effect of the electron correlation to the half-metallic properties for the ZrFeVZ (Z = Al, Ga, In) compounds, the calculations with GGA+U are also performed. The results are shown in the Table 2. For ZrFeVZ (Z = Al, Ga, In) compounds, although the half-metallic gap reduces when the electron correlation is considered in the calculations, the compounds are still half-metallic ferrimagnet. Especially, the ZrFeVAl compound remains to keep a large half-metallic gap. The total magnetic moment of the unit cell for the ZrFeVZ (Z = Al, Ga, In) compounds have not changed but the atomic magnetic moments of Zr and V atoms have a substantial increase and those of Fe and Z (Z = Al, Ga and In) atoms have a greatly decrease when the electron correlation is considered in the calculations.

For practical application, it is necessary to know the sensitivity of the half-metallicity of ZrFeVZ (Z = Al, Ga, In) compounds to the external strains and lattice thermal expansion. The usual method to simulate the effect of the external stress and lattice thermal expansion is to change the lattice constants. Therefore, we investigated the effects of two kinds of strain, i.e., hydrostatic strain and tetragonal strain on the half-metallicity. The effect of the change of the lattice constant on the half-metallic properties were shown in the Fig. 5. We used the conduction band minimum (CBM) and the valence band maximum (VBM) in the minority-spin channel to characterize the half-metallic nature. Obviously, the half-metallicity can be kept in a quit large range of 5.2–6.8 Å for ZrFeVAl compound, 5.1–6.8 Å for ZrFeVGa compound and 4.9–6.5 Å for ZrFeVIn compound.

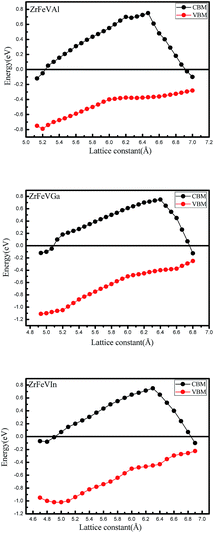Fig. 5 The values of valence band maximums (VBM) and conduction band minimums (CBM) in the minority-spin channel as a function of lattice constants for the ZrFeVZ (Z = Al, Ga, In) compounds.

The curves of the spin-flip band gaps versus the lattice constant for ZrFeVZ (Z = Al, Ga, In) compounds are shown in Fig. 6. From Fig. 6, it can be seen that the spin-flip band gaps of the ZrFeVZ (Z = Al, Ga, In) compounds achieve the maximum value (0.46 eV, 0.55 eV and 0.57 eV) at their strained lattice constants (5.85 Å, 5.84 Å, and 5.83 Å). In Fig. 7, we show the energies of the CBM and VBM as functions of c/a ratio of ZrFeVZ (Z = Al, Ga, In) compounds. Here, a and c are the lattice constants in different direction of 3D coordinate system and the c/a indicates the degree of the tetragonal distortion of those compounds. Calculated results show that their half-metallic nature can be kept when the c/a ratio are changed in the range of 0.81–1.12 for ZrFeVAl, 0.77–1.16 for ZrFeVGa and 0.82–1.18 for ZrFeVIn, respectively. It also can be seen that these three compounds possess their largest large spin-flip gaps when c/a = 1. The absolute values of spin-flip gaps decrease monotonically with both positive and negative tetragonal strains (that is, the increasing and decreasing the c/a ratio).

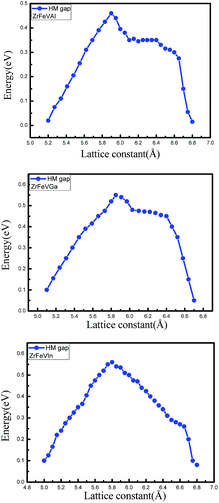Fig. 6 The spin-flip/half-metal gaps of the minority-spin channel as a function of lattice constants for the ZrFeVZ (Z = Al, Ga, In) compounds.

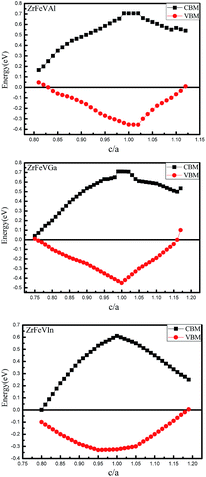Fig. 7 CBM and VBM in minority-spin channel as a function of c/a ratio for the ZrFeVZ (Z = Al, Ga, In) compounds.

Fig. 8 shows the magnetic moment dependence on the lattice constants for ZrFeVZ (Z = Al, Ga, In) compounds. The magnetic moments of the Zr, Fe, and V atoms are sensitive to the change of the lattice constants while those of the Z (Z = Al, Ga, In) atoms are not. For these three compounds, the magnetic moments of Zr and V atoms increase while the magnetic moment of Fe atom gradually decrease with the increasing lattice constants. In addition, it should be noted that the effect of tetragonal strain on the magnetic properties is inconspicuous. The value of the total or atomic magnetic moment is almost a constant in the whole investigated range of c/a ratio for ZrFeVZ (Z = Al, Ga and In) compounds.

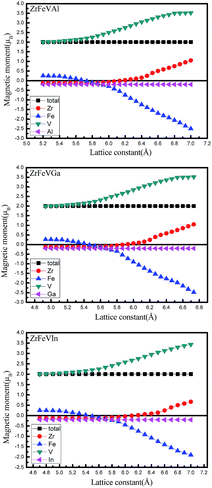Fig. 8 The total and atomic magnetic moments as a function of lattice constants for ZrFeVZ (Z = Al, Ga, In) compounds.

Finally, we come to estimate the Curie temperature T_c of ZrFeVZ compounds (Z = Al, Ga, In) from the energy difference: ΔE = E_AFM − E_FM by means of a mapping on the Heisenberg model in a mean field approximation (MFA), where the E_AFM and E_FM are the total energies of ZrFeVZ (Z = Al, Ga, In) compounds in AFM and FM states. The estimation of Curie temperature T_c is given as formula: 3K_BT_C = ΔE, and the calculated results are 818.04 K, 826.66 K, and 751.70 K for ZrFeVAl, ZrFeVGa, and ZrFeVIn, respectively. Obviously, the Curie temperature T_c of all these compounds are higher than the room temperature, and therefore, these compounds are suitable for spintronics and magnetic electronics applications.

4. Conclusions

In this work, we employed the first-principles calculation to investigate the electronic, magnetic and half-metallic properties of quaternary Heusler compounds ZrFeVZ (Z = Al, Ga, In). It is found that ZrFeVZ (Z = Al, Ga, In) compounds with the type I atomic arrangement fashion exhibit a typical half-metallic characteristic and have a quite large spin-flip gap in the minority-spin channel. The total magnetic moment (M_t) of the ZrFeVZ (Z = Al, Ga, In) compounds is 2 μ_B, which is in line with the Slater–Pauling curve of M_t = Z_t − 18 in half-metal system. The origin of the half-metallic gap in the minority-spin channel is attributed to the formation of the bonding and antibonding states which mainly comes from the Fe and V atoms. The half-metallicity can be kept in a changing region of the hydrostatic and tetragonal strain, which declares the good stability in half-metallic properties for ZrFeVZ (Z = Al, Ga, In) compounds. In addition, the ZrFeVGa and ZrFeVIn compounds exhibit a larger spin-flip band gap than 0.5 eV in its strained lattice constants. The calculated Curie temperatures of the three compounds based on the mean field approximation are higher than the room temperature. All of those indicate that those newly designed quaternary Heusler compounds can be regarded as good candidates for spintronics devices.

Acknowledgements

This work is supported by the Natural Science Foundation of Hebei Province (No. E2016202383), the Program for Leading Talents in Science and Technology Innovation of Chongqing City (No. cstckjcxljrc19), and the Basic and Frontier Research Project of Chongqing City (No. cstc2014jcyja50005), Xiaotian Wang thanks the financial support from the China Scholarship Council and the Graduate-level Innovation Project Funded by Hebei Province.

References

1. R. A. de Groot, F. M. Mueller, P. G. Van Engen and K. H. J. Buschow, Phys. Rev. Lett., 1983, 50, 2024.
2. X. T. Wang, X. F. Dai, L. Y. Wang, X. F. Liu, W. H. Wang, G. H. Wu, C. C. Tang and G. D. Liu, J. Magn. Magn. Mater., 2015, 378, 16–23.
3. X. T. Wang, Y. T. Cui, X. F. Liu and G. D. Liu, J. Magn. Magn. Mater., 2015, 394, 50–59.
4. X. T. Wang, Z. X. Cheng, J. L. Wang, L. Y. Wang, Z. Y. Yu, C. S. Fang, J. T. Yang and G. D. Liu, RSC Adv., 2016, 6, 57041.
5. X. T. Wang, Z. X. Cheng, J. L. Wang, X. L. Wang and G. D. Liu, J. Mater. Chem. C, 2016, 23, 45–49.
6. X. T. Wang, Z. X. Cheng, J. L. Wang, H. Rozale, L. Y. Wang, Z. Y. Yu, J. T. Yang and G. D. Liu, J. Alloys Compd., 2016, 686, 549–555.
7. L. Zhang, X. T. Wang, H. Rozale, Y. C. Gao, L. Y. Wang and X. B. Chen, Curr. Appl. Phys., 2015, 15, 1117.
8. G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 014424.
9. G. D. Liu, X. F. Dai, S. Y. Yu, Z. Y. Zhu, J. L. Chen, G. H. Wu, H. Zhu and J. Q. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 74, 054435.
10. A. Birsan and V. Kuncser, J. Magn. Magn. Mater., 2016, 406, 282.
11. Z. Y. Deng and J. M. Zhang, J. Magn. Magn. Mater., 2016, 409, 28.
12. H. H. Xie, Q. Gao, L. Li, G. Lei, G. Y. Mao, X. R. Hu and J. B. Deng, Comput. Mater. Sci., 2015, 103, 52.
13. S. Kervan and N. Kervan, Curr. Appl. Phys., 2013, 13, 80.
14. F. Ahmadian and A. Salary, Intermetallics, 2014, 46, 243.
15. I. Galanakis, P. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 134428.
16. G. H. Fecher, H. C. Kandpal, S. Wurmehl, C. Felser and G. Schonhense, J. Appl. Phys., 2006, 99, 08J106.
17. S. Skaftouros, K. Özdoğan, E. Şaşıoğlu and I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024420.
18. I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 012413.
19. I. Galanakis, K. Özdoğan and E. Şaşıoğlu, J. Phys.: Condens. Matter, 2014, 26, 379501.
20. H. Y. Jia, X. F. Dai, L. Y. Wang, R. Liu, X. T. Wang, P. P. Li, Y. T. Cui and G. D. Liu, J. Magn. Magn. Mater., 2014, 367, 33.
21. G. Y. Gao, L. Hu, K. L. Yao, B. Luo and N. Liu, J. Alloys Compd., 2013, 551, 539–543.
22. L. Xiong, L. Yi and G. Y. Gao, J. Magn. Magn. Mater., 2014, 360, 98–103.
23. X. Dai, G. Liu, G. H. Fecher, C. Felser, Y. Li and H. Liu, J. Appl. Phys., 2009, 105, 07901.
24. P. Klaer, B. Balke, V. Alijani, J. Winterlik, G. H. Fecher, C. Felser and H. J. Elmers, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 144413.
25. V. Alijani, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 224416.
26. V. Alijani, J. Winterlik, G. H. Fecher, S. S. Naghavi and C. Felser, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 84428.
27. P. L. Yan, J. Phys. D: Appl. Phys., 2016, 49, 255002.
28. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoolous, Rev. Mod. Phys., 1992, 64, 1065.
29. M. D. Segall, P. L. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717.
30. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
32. Q. Gao, H. H. Xie, L. Li, G. Lei, J. B. Deng and X. R. Hu, Superlattices Microstruct., 2015, 85, 536.
33. J. M. Khalaf Al-zyadi, G. Y. Gao and K.-L. Yao, J. Magn. Magn. Mater., 2015, 378, 1–6.
34. R. J. Pan, T. T. Lin, Y. H. Chang, L. Y. Wang, Z. M. Wu, P. Yu, Y. T. Cui and G. D. Liu, J. Supercond. Novel Magn., 2016, 29, 1963.
35. S. Berri, M. Ibrir, D. Maouche and M. Attallah, J. Magn. Magn. Mater., 2014, 371, 106–111.
36. S. Berri, M. Ibrir, D. Maouche and M. Attallah, Condens. Matter, 2014, 1, 26–31.
37. I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429.
38. S. Skaftouros, K. Ozdogan, E. Sasioglu and I. Galanakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024420.
39. I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429.
40. M. Rostami, M. Afshari and M. Moradi, J. Alloys Compd., 2013, 575, 301.
41. K. Sato, P. H. Dederichs, H. Katayama-Yoshida and J. Kudrnovsky, J. Phys.: Condens. Matter, 2004, 16, S5491.
42. A. Rohrbach, J. Hafner and O. K. Andersen, J. Phys.: Condens. Matter, 2003, 15, 979.
43. X. M. Zhang, X. F. Dai, G. F. Chen, H. Y. Liu, H. Z. Luo, Y. Li, W. H. Wang, G. H. Wu and G. D. Liu, Comput. Mater. Sci., 2012, 59, 1.

---