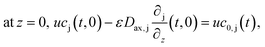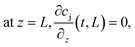Model-based development of an on-column PEGylation process
David
Pfister
,
Oliver
Ingold
and
Massimo
Morbidelli
*
Institute of Chemical and Bioengineering, Department of Chemistry and Applied Biosciences, ETH, Zurich, 8093 Zurich, Switzerland. E-mail: massimo.morbidelli@chem.ethz.ch
First published on 4th November 2015
Abstract
Considering the high production cost of therapeutic proteins, post-translational modifications such as PEGylation have to be highly efficient and optimized so as not to waste the valuable protein to be modified. Among the different processes available, on-column PEGylation appears as an interesting alternative to the classical solution reaction for more selective synthesis of the targeted mono-PEGylated protein since it has the potential to restrict the coupling reaction to fewer reaction sites. In this work, the on-column PEGylation of α-lactalbumin using a strong anion-exchange resin is investigated. The influence of pH, reaction time, PEG to protein ratio and protein load is investigated. The on-column PEGylation process is shown to be more selective for lower degrees of PEGylation than the classical solution PEGylation reaction. Finally, the experimental results are described by a mathematical model in order to gain a more complete understanding of the mechanisms involved and develop a tool for process design and development.
Introduction
The PEGylation of therapeutic proteins is a hot topic in the pharmaceutical industry which is eager to improve the efficacy and stability of protein-derived drugs.1 Indeed, thanks to the incomparable increase of the in vivo circulation half-life of the conjugated drug, PEGylated biopharmaceuticals are already on the market and used for the treatment of diseases such as hepatitis C, leukemia, Crohn's disease and neutropenia, among others.2 In 2012, their total sales amounted to 7 billion US$ per year.3The advantages of the PEGylated protein compared to its native counterpart include reduced immunogenicity, increased water solubility, higher thermal stability, reduced aggregation propensity and longer circulation half-life due to the diminished proteolysis and reduced renal clearance.4 While the secondary and tertiary structures of the protein seem to remain substantially unaltered upon PEGylation, its biological activity is often weakened due to the presence of the polymer at the protein surface. However, the improved circulation half-life often outweighs this loss of specific activity.5 There is therefore a trade-off between the pharmacokinetic and pharmacodynamic properties of such conjugated drugs and most frequently the conjugate of choice is the mono-PEGylated protein since it typically offers the best compromise between activity-loss and increased circulation half-life.
PEGylation is always carried out with the purified, and a fortiori expensive, therapeutic protein; so a viable PEGylation process should deliver the desired product at high yield and high purity together with the highest possible conversion of the protein.6 Different chemistries were developed over the past decades, targeting various residues more or less selectively, if not exclusively in the most successful cases. Some of them use highly selective coupling reactions which specifically target functional groups such as N-terminal residues, disulfide bridges or free thiol groups. New strategies even involve the incorporation of non-natural amino acids into the protein sequence with orthogonal reactivities compared to the natural amino acid analogues.7
However, to date, PEGylation of amino groups remains the most frequently used coupling method. Among the PEGylated proteins brought to the market so far, half of them are still derived from non-selective amine PEGylation.7 In contrast with more selective methods, this strategy is a quite versatile tool since it can be used for practically any protein as lysine is one of the most abundant residues (accounting for about 10% on average of all the amino acids present in proteins). On the other hand, the large abundance of this amino acid causes selectivity issues. Lysine-directed PEGylation reactions lead to complex mixtures containing conjugates with different degrees of PEGylation as well as various positional isomers for a given degree of PEGylation.7 Even though a certain degree of selectivity can be achieved by optimizing the pH, temperature, reaction time and PEG to protein molar ratio, positional isomers are always formed in solution PEGylation processes. Different reaction engineering approaches have been proposed to increase the yield towards the mono-PEGylated protein and integrated processes, combining reaction and separation, appear as promising options.
For instance, Fee et al. developed an integrated size-exclusion reactive chromatography process for the PEGylation of α-lactalbumin and β-lactoglobulin with mPEG-SPA.8 Protein and mPEG-SPA solutions were injected into a SEC column successively and since the PEGylated species formed are significantly larger than the reactants, i.e. the protein and the functionalized PEG, the products elute faster thus inhibiting the consecutive reactions leading to the formation of multi-PEGylated proteins. Consequently, this process does not only allow a simultaneous reaction and separation, but also increases the selectivity towards the desired mono-PEGylated product.
Alternatively, Lee et al.9 proposed an on-column PEGylation process using an ion-exchange stationary phase. They reported the attachment of PEG aldehyde to the N-terminal position of recombinant interferon α-2a on a cation-exchange resin. The protein was first adsorbed on the resin, followed by the injection of the functionalized PEG at a low flow rate. Once adsorbed to the stationary phase, the reactivity of some of the functional groups strongly decreases due to steric hindrance, while others may be more easily exposed. This effect is expected to avoid the formation of multi-PEGylated species by reducing the number of reactive sites and to lead to the selective formation of specific positional isomers. The mono-PEGylated product yield was in the range between 51 and 62% (depending on the PEG molecular weight) at a protein conversion of 68%. Even though the mono-PEGylated protein yield was not significantly higher than in the corresponding batch solution process (60%), this method opened the door to integrated and potentially more selective PEGylation processes.
Huang et al.10 immobilized keratinocyte growth factor 1 on a Heparin-Sepharose resin, followed by the PEGylation at the N-terminal position by reductive alkylation and purification on an SP Sepharose ion-exchange resin. The reported yield of 40% was, however, not compared to the batch solution PEGylation. A similar study was performed with recombinant human fibroblast growth factor 2.11
More recently, hemoglobin was PEGylated using succinimidyl carbonate by both solution and on-column PEGylation by Suo et al.12 The on-column PEGylation was performed on a CM Sepharose Fast Flow resin. The final mono-PEGylated protein yield was in the range from 68 to 75% (depending on the molecular weight of the PEG), which clearly surmounted the batch solution process (never exceeding 38%).
Alternatively, Shang et al. immobilized the functionalized PEG on hydrophobic membranes. The reactant was then placed in contact with a protein solution, which after coupling with the polymer remained adsorbed on the membrane. The elution was then obtained by lowering the conductivity of the buffer solution. This process has the great potential to exclusively lead to the formation of mono-PEGylated proteins.13,14
Herein, the PEGylation of α-lactalbumin by a similar process using an anion-exchange stationary phase is reported. The covalent attachment of PEG to the lysine amino groups of the protein using a succinimidyl ester functionalized PEG was considered. The batch solution reaction kinetics is investigated and the kinetic rate constants are estimated. The PEGylation of the protein in the adsorbed state was then investigated experimentally and the performance of the on-column PEGylation process was compared to the classical solution PEGylation process. The influence of pH, PEG to protein molar ratio, protein load and residence time was thoroughly scrutinized. The collected information was incorporated into a reactive chromatography model, enabling the simulation of the on-column PEGylation process and the model-based optimization of the operating conditions.
Experimental section
Materials
α-Lactalbumin (85%) was purchased from Sigma-Aldrich and the 10 kDa mPEG-SPA was purchased from Jenkem Technology. All the buffer components of reagent grade were purchased from Sigma-Aldrich. The chromatographic resin Q Sepharose HP was purchased from GE Healthcare and packed in a Tricorn column according to the manufacturer's protocol. The final bed dimensions are 143 × 5 mm.Solution PEGylation
The PEGylation of α-lactalbumin with 10 kDa mPEG-SPA was performed at room temperature in a 25 mM phosphate solution adjusted to pH 7.0. A 6 g L−1 protein solution was mixed with 1, 3 and 6-fold molar excess of mPEG-SPA in a 2.5 mL batch reactor agitated with a magnetic stirrer. Samples were taken regularly and quenched by dropping the pH below 3.0 so as to stop the reaction and thus follow the kinetics of PEGylation. See our previous work for more details about the kinetic study.15On-column PEGylation
The on-column PEGylation reaction was performed on a Q Sepharose HP resin using an Agilent 1200 Series HPLC system. Before loading the reactants in the chromatographic column, the ion-exchange resin was equilibrated with a 25 mM Tris-HCl buffer solution adjusted to pH 7.0, 8.0 or 9.0 and maintained at 25 °C. Then, 1 mg of protein solubilized in 2.5 mL of the 25 mM Tris-HCl solution adjusted to the desired pH (i.e. 7.0, 8.0 or 9.0) was loaded into the column by means of a manual injection valve fitted with a 2.5 mL external loop (Rheodyne). The resin was washed with 5 mL of the equilibration buffer solution at 1 mL min−1. After this, 2.5 mL of a mPEG-SPA solution (in the same buffer solution) containing 4, 8 or 16-fold molar excess of the functionalized PEG with respect to the loaded protein was injected into the external loop. The content of the loop was then slowly injected into the column at a flow rate of 0.03 mL min−1. In order to limit the waste of functionalized PEG by hydrolysis of the N-hydroxysuccinimide before it actually enters the column, the loop was placed in ice cold water. After complete injection of the PEG solution, the column was washed with 10 mL of the 25 mM Tris-HCl buffer solution at pH 7.0 to get rid of the NHS, unreacted PEG and hydrolyzed PEG.For the elution of the products, a salt (NaCl) gradient was applied using a 25 mM Tris-HCl buffer solution at pH 7.0 containing 1 M NaCl. The flow rate was set to 1 mL min−1. The salt concentration was suddenly increased to 50 mM NaCl and maintained at this level for 10 minutes. The linear salt gradient was then applied until 400 mM NaCl over 25 minutes. During the elution, fractions were collected and analyzed by SEC. The recovery was computed to make sure that all the protein was recovered at the end of the fractionation. After 25 minutes, the salt concentration was maintained at the maximum concentration (1 M NaCl) for 5 minutes. The resin was then re-equilibrated with the loading buffer at the desired pH value.
Characterization
Size exclusion chromatography analyses were performed using a Tricorn Superdex 200 10/300 GL high performance column (GE Healthcare). The mobile phase was a 25 mM Na2HPO4/100 mM Na2SO4 solution adjusted to pH 7.0.The active moiety of functionalized mPEG-SPA is known to undergo hydrolysis in aqueous solution. The hydrolysis of the ester bond between the propionic acid and the NHS is usually modeled by a pseudo-first order reaction for which the kinetic rate constant accounts for all deactivation sources, mostly pH, water and the buffer solution components. The overall hydrolysis rate constant, kd, is estimated from independent experiments for which the UV absorbance at 260 nm of a 1 mg mL−1 mPEG-SPA solution in 25 mM Tris-HCl buffer adjusted to the desired pH value (i.e. 7.0, 8.0 or 9.0) and maintained at 0 °C was monitored. By doing so, the released NHS concentration increase could be monitored. The values of kd at the same pH values and at room temperature are also reported.
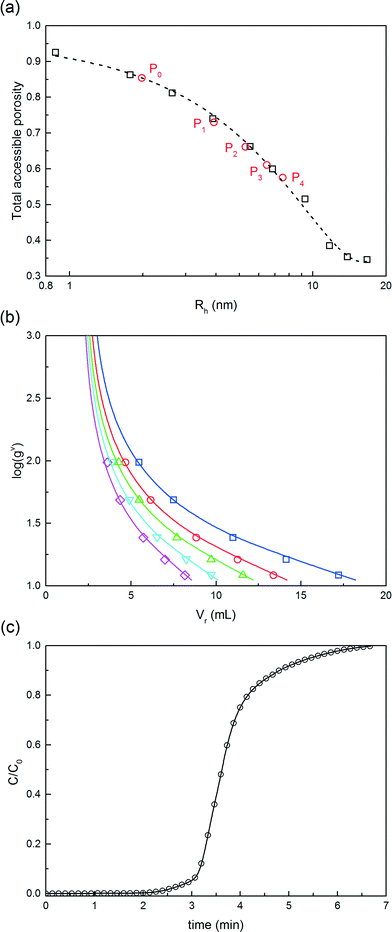
The model parameters of the chromatographic column model were estimated for each solute, i.e. for the native protein, the PEGamers until the tetra-PEGylated one and the PEG polymer. Pure solutes, only presenting a single degree of PEGylation, were obtained by fractionating the SEC chromatogram. The model parameters were divided into four groups estimated independently: (i) the size related parameters (external bed porosity, ε and steric factor, K∞), (ii) the parameters of the linear adsorption isotherm (α and β), (iii) the saturation capacity (qsat), and (iv) the mass transfer coefficients and hydrodynamic dispersion coefficients (km and Dax).
(i) These parameters were estimated by inverse size exclusion chromatography as described by DePhillips and Lenhoff.16 Dextran tracers with a wide range of molecular weights (1, 5, 12, 50, 150, 270, 410, 670 and 2000 kDa) were considered in order to measure the accessible volume fraction of the packing material as a function of the tracer hydrodynamic radius. This selection of tracers with radii from 0.84 nm to 37.2 nm enables to screen the entire pore size distribution. The radii of the dextrans were estimated by R = 0.845 × M0.498n (nm), Mn being the molecular weight of the dextran polymer in kDa. The protein and PEGylated conjugates were eluted under non-adsorbing conditions (eluent containing 1 M NaCl).
(ii) The parameters of the linear adsorption isotherm were estimated from independent pulse injection experiments under diluted conditions according to the method developed by Pfister et al.17 Linear gradient elution experiments were performed with gradient slopes ranging from 12.5 mM of NaCl min−1 to 100 mM min−1. The adsorption parameters were obtained by measuring the retention volumes and comparing them with the following equation:
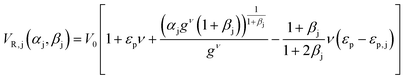 | (1) |
(iii) The saturation capacity of α-lactalbumin on this resin was estimated by breakthrough analysis with a mini-column. To do so, a small column (7 × 5 mm) packed with the Q Sepharose HP resin, was loaded with a 5 mg mL−1 protein solution in the 25 mM Tris-HCl solution at pH 7.0. The protein was loaded at 0.5 mL min−1 and the breakthrough profile was recorded by UV spectroscopy at 300 nm. The equilibrium binding capacity (EBC) was computed as follows:
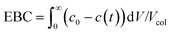 | (2) |
| qsat,0 = (EBC − εtc0)/(1 − ε) | (3) |
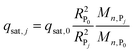 | (4) |
(iv) The axial dispersion coefficients as well as the overall mass transfer coefficients for the PEG were estimated from literature correlations.18 For the protein, the overall mass transfer coefficient was estimated according to the method developed by Pfister and Morbidelli based on pulse injections of pure solutes under diluted conditions.19 The same linear gradient elution experiments used in (ii) were used to estimate the mass transfer coefficient, km,j, from the measured HETP as follows:
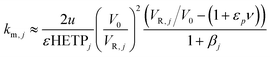 | (5) |
The estimation given in eqn (5) was used as a first guess value and the mass transfer coefficients were then further fitted on different experimental chromatograms.
Model description
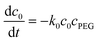 | (6) |
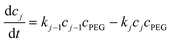 | (7) |
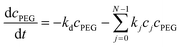 | (8) |
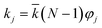 , N being the number of PEGylation sites and
, N being the number of PEGylation sites and 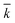 is the average PEGylation rate constant of the lysine residues and the subscript j designates the degree of PEGylation. c0 is the concentration of native protein while cj is the concentration of PEGamer conjugated to j PEG polymers. The parameter φ is defined as follows:
is the average PEGylation rate constant of the lysine residues and the subscript j designates the degree of PEGylation. c0 is the concentration of native protein while cj is the concentration of PEGamer conjugated to j PEG polymers. The parameter φ is defined as follows: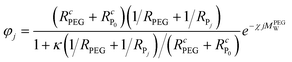 | (9) |
In the case where the protein reacts in the adsorbed state, such as in the on-column PEGylation process, kj is considered as a fitting parameter.
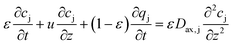 | (10) |
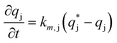 | (11) |
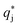 is the solute concentration in the stationary phase at equilibrium with the solution. The local equilibrium between the mobile phase and the stationary phase is modeled by a multicomponent Langmuir isotherm:
is the solute concentration in the stationary phase at equilibrium with the solution. The local equilibrium between the mobile phase and the stationary phase is modeled by a multicomponent Langmuir isotherm: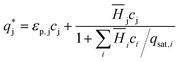 | (12) |
The Henry coefficient, 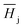 , is described in the frame of the stoichiometric displacement model.21 The expression of the Henry coefficient is given by the following equation:
, is described in the frame of the stoichiometric displacement model.21 The expression of the Henry coefficient is given by the following equation:
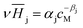 | (13) |
The boundary conditions of eqn (10) are the following:
Finally, the initial conditions are defined as follows:
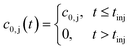 | (14) |
The column model was discretized with the finite difference method along the column length. The resulting set of ordinary differential equations was integrated in time using the FORTRAN routine ODEPACK. The number of grid point was set to 100 while the number of time steps was set to 1500 after checking that numerical convergence has been achieved.
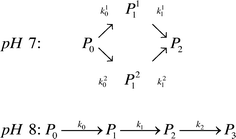
Kinetic scheme. The derivation of a simplified kinetic scheme (compared to the solution PEGylation process) was motivated by two important experimental observations: (1) at pH 7.0, two different mono-PEGylated PEGamers (i.e. two distinct groups of multiple positional isomers conjugated to a single PEG chain) were observed while only one was detected at pH 8.0 and (2) no traces of tri-PEGylated protein were detected at pH 7.0 while they were present at pH 8.0. Accordingly, in order to properly describe these observations, two kinetic schemes were considered as a function of pH:
 | (15) |
Reactive chromatography modeling. The solution of mPEG-SPA is slowly injected into the column by means of a 2.5 mL external loop. The injection loop is modeled as a plug flow reactor in which the only reaction taking place is the hydrolysis of the functionalized PEG at 0 °C. Once the mPEG-SPA solution enters the chromatographic column, the hydrolysis rate constant is changed to the one measured at 25 °C. The on-column PEGylation model is based on the previous chromatographic model given in eqn (10)–(14). As the protein and the PEGylated proteins are assumed to react with the functionalized PEG only in the adsorbed state, the reaction term is added to the stationary phase mass balance eqn (11) as follows:
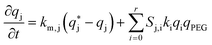 | (16) |
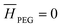 ).
).
It is worth noting that the mPEG-SPA is not only consumed by all PEGylation reactions, but it also undergoes hydrolysis, so the mass balance equation for the PEG has to be modified as follows:
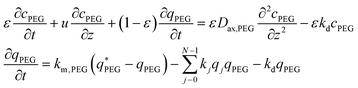 | (17) |
Results and discussion
Solution PEGylation in a homogeneous batch reactor
The kinetic model, described by eqn (6)–(9) was implemented in Matlab® and integrated numerically. A non-linear regression method was used to determine the three kinetic model parameters: 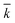 , χ and κ. For the least-square regression, only the experiments with the PEG to protein ratios ϕ = 1 and ϕ = 6 were used. The last condition (ϕ = 3) was used to validate the model. The experimental data and the model predictions are compared in Fig. 2b–d for the set of parameter values
, χ and κ. For the least-square regression, only the experiments with the PEG to protein ratios ϕ = 1 and ϕ = 6 were used. The last condition (ϕ = 3) was used to validate the model. The experimental data and the model predictions are compared in Fig. 2b–d for the set of parameter values 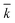 = 1.88 mL mol−1 min−1, χ = 1.9 × 10−5 Å2 and κ = 60.3 mol g−1. It can be seen that the model is in fairly good agreement with the experimental data and is capable of providing excellent predictions for the PEGylation process in aqueous solution.
= 1.88 mL mol−1 min−1, χ = 1.9 × 10−5 Å2 and κ = 60.3 mol g−1. It can be seen that the model is in fairly good agreement with the experimental data and is capable of providing excellent predictions for the PEGylation process in aqueous solution.
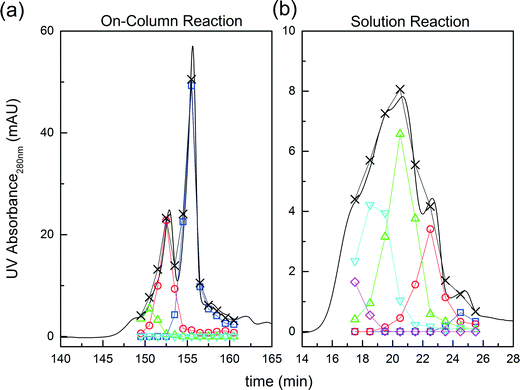 | ||
Fig. 3 Comparison between on-column and solution PEGylation in terms of the product distributions. Analytics performed by size exclusion chromatography: ( ) P0, ( ) P0, ( ) P1, ( ) P1, ( ) P2, ( ) P2, ( ) P3 and ( ) P3 and ( ) P4. ) P4. | ||
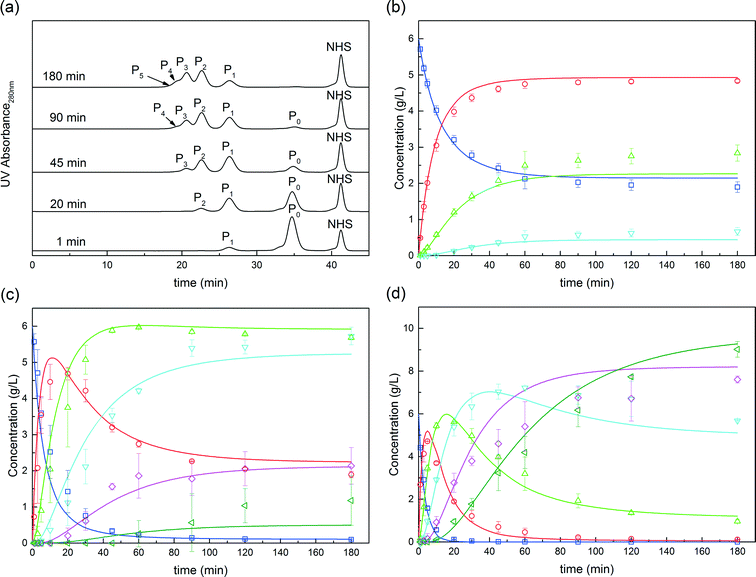
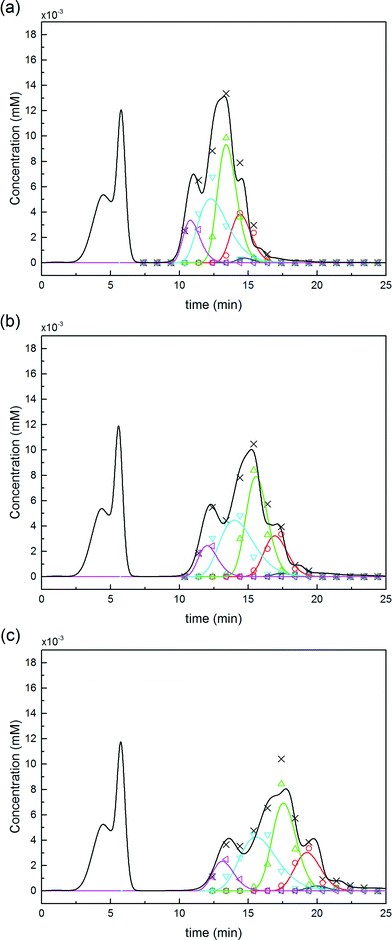
Further experiments were performed with the aim of improving this limited conversion for the protein. To do so, reactions at pH 7.0 and 8.0 were considered with various PEG/protein ratios and different reaction times. The obtained results are shown in Fig. 4. The first interesting result is the presence at pH 7.0 of two distinct groups of mono-PEGylated protein positional isomers while only one peak is observed at pH 8.0. The work of Dismer et al.22 on the adsorption of lysozyme on strong cation-exchange resins showed that the protein adsorption is not only orientation selective, but the most probable orientation is driven by pH. Indeed, the pH of the buffer solution affects the electrostatic potential at the protein surface and therefore its most favorable binding site as well. Therefore it can potentially be that the orientation of the adsorbed α-lactalbumin at pH 7.0 and 8.0 is different leading to the formation of different positional isomers.
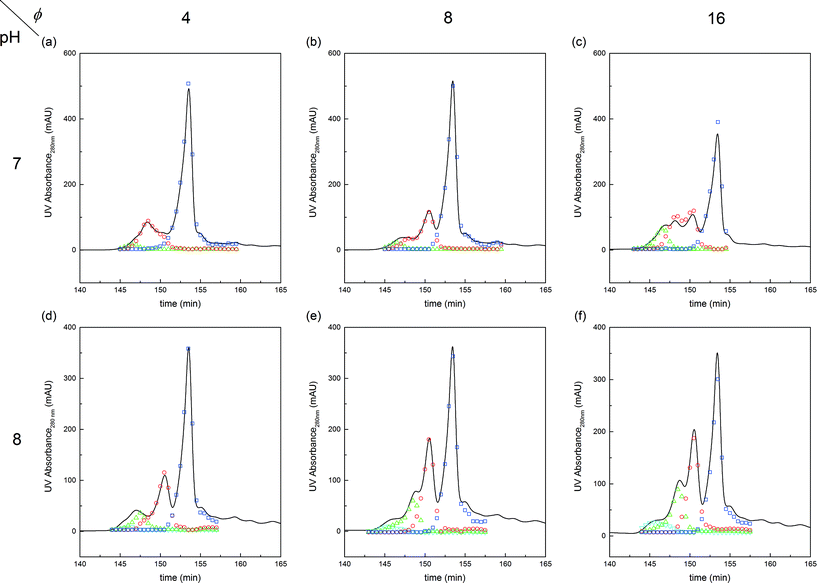 | ||
Fig. 4 Chromatograms illustrating the effect of pH and PEG to protein molar ratio, ϕ, on the on-column PEGylation products. Analytics performed by SEC: ( ) P0, ( ) P0, ( ) P1, ( ) P1, ( ) P2 and ( ) P2 and ( ) P3. ) P3. | ||
On the other hand, it is interesting to note that the two peaks of the mono-PEGylated protein observed at pH 7.0 were never found in solution PEGylation for which only one peak was observed when analyzed by IEC. When PEGylated in solution, more PEGylation sites are potentially accessible which lead to a more complex distribution of positional isomers. In the end, the positional isomers are probably too similar to be separated by ion-exchange chromatography.
Following the work of Richardson and Brew,23 presented in Fig. 5 are all the different PEGylation sites of α-lactalbumin (i.e. lysine residues and N-terminal) accessible in solution with their reactivity towards acetylation. Since the reaction of the amino groups with acetic anhydride is similar to the PEGylation reaction, these data provide valuable information also about their reactivity towards PEGylation.
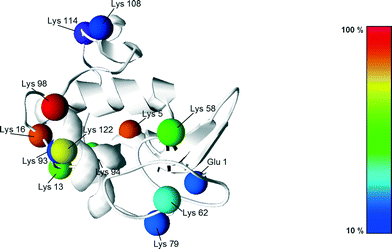 | ||
| Fig. 5 Structure of the α-lactalbumin with indication of the reactive residues with respect to acetylation, with the colours indicating their reactivity extent. The reactivity values were taken from Richardson and Brew23 and scaled with respect to the most reactive residue (Lys 98). | ||
It can be seen that half of the residues are poorly reactive (low pKa, buried amines), and only 3, out of 13 are very reactive: Lys98, 5 and 16. This is revealing a rather heterogeneous distribution of the residue reactivity, similar to what has previously been observed for lysozyme.15 Since the on-column PEGylation process promotes the PEGylation of fewer residues, which are the most accessible ones, such a distribution of reactivities explains the different positional isomers obtained at pH 7.0 and 8.0, which can be better resolved by IEC. This site selectivity has been clearly evidenced for lysozyme in the recent work of Maiser et al.24
When comparing pH 7.0 and pH 8.0, it can be seen that the reaction is faster at higher pH. It is well-acknowledged that the reactivity of the amino groups depends on their ionization state.7 Considering that the pKa of an ε-amine is in the range from 9 to 10, the closer we get to these values, the more reactive are the residues.
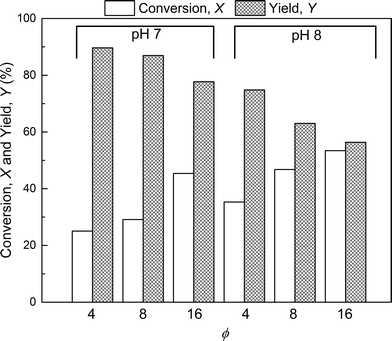
The effect of PEG to protein ratio was also investigated. As expected, the higher ϕ, the higher the conversion of the protein and average degree of PEGylation. However, the quantity of PEG needed to obtain conversions equivalent to the ones observed in solution is much higher for both pH values. On the other hand, when compared with the solution experiments, the amount of multi-PEGylated species is much lower with the on-column PEGylation process, revealing a better selectivity for smaller degrees of PEGylation.
In the following, the performance of the process will be assessed by considering the conversion, X, and yield, Y, with respect to the protein defined as follows:
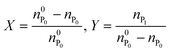 | (18) |
Modeling and simulation
In this section, we finalize the estimation of the required model parameters: at first for the chromatographic model alone (i.e. ε, K∞, α, β, qsat, km and Dax for the different solutes) and then for the on-column PEGylation model (i.e. k0, k11 and k21 at pH 7.0 and k0, k1 and k2 at pH 8.0). These parameters were estimated using suitable experimental data as described in the Experimental section. The validity of these parameters will then be assessed by comparing the results of the simulations with the experimental data.The validity of the model parameters determined from independent experiments was assessed by comparing the chromatographic model (eqn (10)–(14)) predictions with three chromatographic experiments of pure separation (i.e. without on-column reaction) of a mixture of PEGamers produced by solution PEGylation.
For this reaction in solution, a 6-fold molar excess of mPEG-SPA was used. 100 μL of the as-prepared product mixture was injected into the column and eluted at three different modifier gradient slopes: 25 mM min−1, 16.6 mM min−1 and 12.5 mM min−1 of NaCl. The first chromatogram (i.e. with the 25 mM of NaCl min−1 gradient slope) was used to refine the model parameters (only β and km) by proper data fitting. The two other chromatograms were purely predictive and used to confirm the validity of the chromatographic model. It is worth noting that the model predictions are in good agreement with the experimental data as it appears from the comparison shown in Fig. 8. The corresponding values of the chromatographic model parameters are summarized in Table 1.
| K ∞ | log10 (α) | β | q sat | k m | D ax | |
|---|---|---|---|---|---|---|
| — | — | — | mg mL−1 | min−1 | cm2 min−1 | |
| a Estimated from the correlation by Athalye et al.25 | ||||||
| P0 | 1.47 | 8.6 ± 1.1 | 3.7 ± 0.5 | 218 | 10.5 ± 1.1 | 0.31 |
| P11 | 1.11 | 7.3 ± 0.9 | 3.14 ± 0.5 | 95 | 5.9 ± 4 | 0.35 |
| P21 | 1.11 | 6.8 ± 0.9 | 3.11 ± 0.5 | 95 | 5.9 ± 4 | 0.35 |
| P1 | 1.11 | 7.3 ± 0.9 | 3.2 ± 0.5 | 95 | 5.9 ± 4 | 0.35 |
| P2 | 0.91 | 6.7 ± 1.3 | 3.0 ± 0.6 | 73 | 5.8 ± 3 | 0.37 |
| P3 | 0.76 | 5.6 ± 1.3 | 2.6 ± 0.7 | 63 | 1.9 ± 0.8 | 0.38 |
| P4 | 0.66 | 5.1 ± 1.1 | 2.6 ± 0.6 | 58 | 4.5 ± 1.7 | 0.39 |
| PEG | 1.27 | — | — | — | 42.6 | 0.34 |
| NaCl | 1.53 | — | — | — | 200 | 1.15 |
Moreover, the scheme presented in eqn (15) shows two different mono-PEGylated PEGamers, P11 and P21. These two groups of mono-PEGylated positional isomers observed at pH 7.0 were considered independently, so that different adsorption isotherm parameters were used as summarized in Table 1.
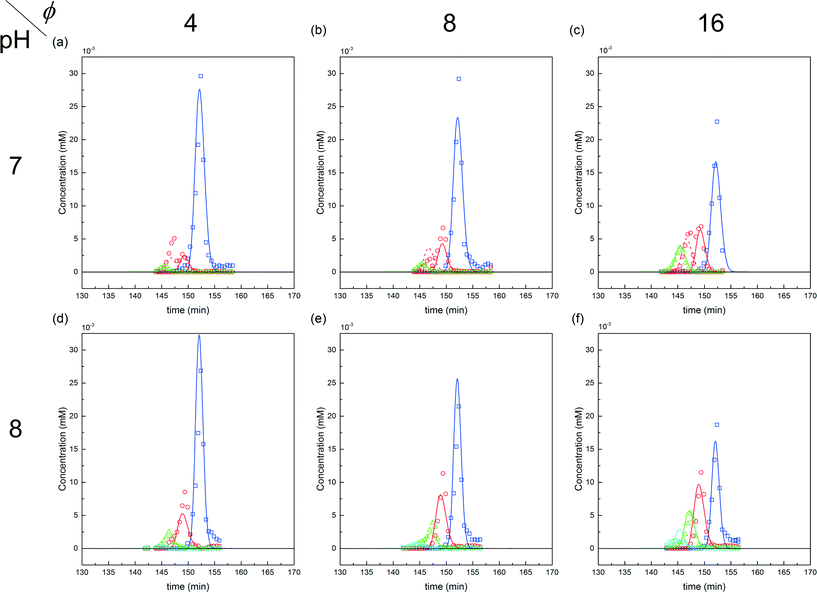 | ||
Fig. 9 Comparison between experiments (( ) P0, ( ) P0, ( ) P1, ( ) P1, ( ) P2 and ( ) P2 and ( ) P3) and simulations for the on-column PEGylation process at various ϕ values for both pH (7.0 and 8.0). ) P3) and simulations for the on-column PEGylation process at various ϕ values for both pH (7.0 and 8.0). | ||
The corresponding values of the fitted kinetic parameters are summarized in Table 2. As expected, the rate constants at pH 8.0 are larger than at pH 7.0, due to the increased nucleophilicity of the amine residues at higher pH. When compared with the kinetic rate constants observed in solution at pH 7.0, they are found to be about five times smaller for the on-column PEGylation reaction (k0 (solution) = 123 mL mol−1 min−1). This is due to the reduction of the number of accessible sites caused by the hindrance of the resin surface. As discussed above, in the present case much fewer sites seem to react (no degrees of PEGylation above 2 are observed at pH 7.0 and 3 at pH 8.0), which when compared to the 13 available sites in solution shown in Fig. 5, lead to a dramatic reduction of the protein overall reactivity. Moreover, contrary to the reaction in solution, the assumption of ‘iso-reactivity’ cannot be used any longer since the few sites accessible once the protein is adsorbed on the resin are probably too dissimilar, as illustrated by the heterogeneous reactivity distribution shown in Fig. 5.
| pH 7.0 | pH 8.0 | ||
|---|---|---|---|
| k 0 | 22.8 | k 0 | 110.3 |
| k 11 | 17.9 | k 1 | 137.9 |
| k 21 | 24.0 | k 2 | 125.5 |
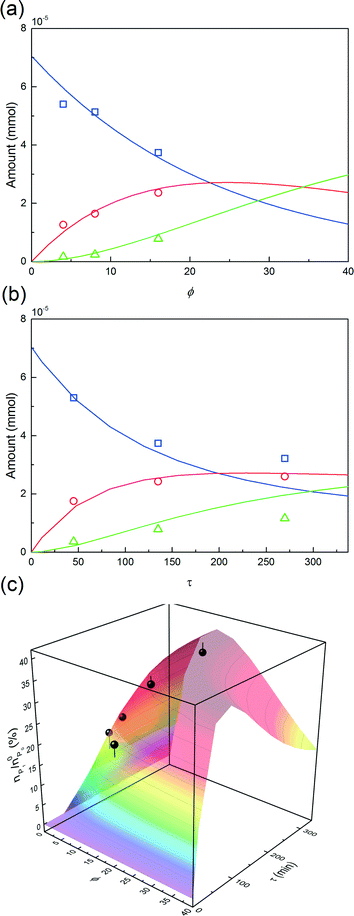
The first parameter to be varied was ϕ for a given amount of protein and the given reaction time (i.e. ωP0 and τ were fixed at 3 × 10−3 and 135 minutes, respectively). The selected values were the following: ϕ = 4, 8 and 16. The experimental concentration profiles are shown in Fig. 10a and compared with the model predictions. As expected, the increase in the mPEG-SPA concentration led to a higher conversion of the protein. The concentration of mono-PEGylated protein is also increasing until a certain value (ϕ = 28, estimated from the model) at which the mono-PEGylated protein is consumed faster than it is formed. Meanwhile, the quantity of di-PEGylated protein keeps on increasing. More important is that at pH 7.0, no traces of tri-PEGylated protein were observed, even at the highest ϕ value confirming the hindrance of the PEGylation sites by the ion-exchange resin surface.
In order to investigate the influence of the rate of mPEG-SPA addition, τ was varied by keeping ϕ constant at 16. Fig. 10b shows the comparison between the experimental concentration profiles and the model predictions. The slower and longer the mPEG-SPA is fed, the higher the conversion of the adsorbed protein. However, it is also clear that adding the mPEG-SPA solution at an extremely low flow rate leads to a decrease in the PEG yield because the mPEG-SPA mainly gets hydrolyzed before it even enters the column. It is seen in Fig. 10b that the model slightly overestimates the protein conversion at long reaction times, as can be seen at τ = 268 minutes. However, the mono-PEGylated protein amount formed by on-column PEGylation is correctly predicted.
Finally, the mole fraction of the mono-PEGylated protein estimated from these different experiments together with the model predictions are summarized in Fig. 10c. It can be seen that the agreement between the model predictions and the experimental data is satisfactory and for all the different (ϕ, τ) values considered.
From the results of our simulations, it clearly appeared that the PEG is underused and mostly undergoes hydrolysis. In the best case only 10% of the PEG is really incorporated in the mono-conjugated protein. This phenomenon is even worse when the pH is increased since the hydrolysis reaction gets faster (see Fig. 1). In order to improve the PEG usage, a solution would be to accelerate the rate of PEGylation with respect to the rate of hydrolysis. To do so, the protein load was increased so as to favor the second order coupling reaction with respect to the first order hydrolysis of mPEG-SPA.
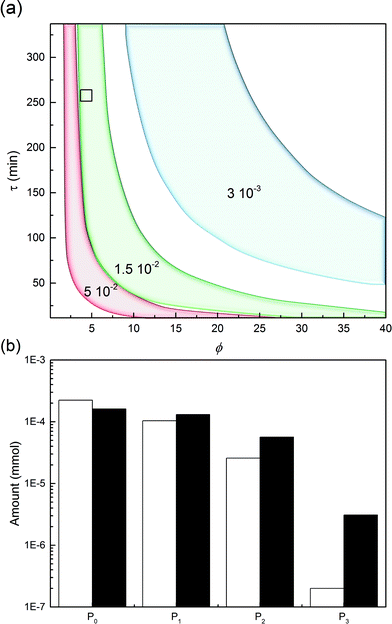
This leads us to the last parameter to be varied, ωP0. The model was used to compute the design space of a process delivering a minimal mole fraction of mono-PEGylated protein, nP1/n0P0, of 35% and considering ϕ and τ as tuning variables. The design space thus obtained is shown in Fig. 11. It can be seen in this figure that the operating area is shrinking when increasing ωP0, thus underlining the increasing difficulty of controlling the process at higher protein load. Moreover, it can be seen that by increasing the protein load fraction, the required amount of PEG to obtain a certain quantity of mono-PEGylated protein, given by the parameter ϕ, is decreasing. As expected we are now favoring the coupling reaction with respect to the hydrolysis of the functionalized PEG, so less PEG is needed to obtain similar performance.
One experiment was performed with ωP0 = 1.5 × 10−2, ϕ = 4.3 and τ = 270 minutes. The results are presented in Fig. 11 together with the model predictions. The model is overestimating the protein conversion revealing some phenomena that are not accounted for. Among these phenomena, the pore blockage due to the protein adsorption, and a fortiori to the PEGylation of the protein at the pore inlet, might explain the observed discrepancy. The adsorbed protein is known to reduce the effective pore size and therefore affect the diffusivity of the polymer inside the particles.26 The use of a more detailed chromatographic column model accounting for the pore shrinking due to protein adsorption and PEGylation would certainly lead to a better description of the diffusion of the reactants in the porous particles. More accurate predictions could be obtained but this would require a much more computationally demanding model.26 In the end, the measured value of nP1/n0P0 was 29.4%, to be compared with the 35% fixed to compute the design space shown in Fig. 11a. The distribution of PEGamers corresponding to these experiments is shown in Fig. 11b. It can be concluded that the model-based approach still offers a fairly good estimation of the process performance even when used at higher protein load fractions and is an interesting tool to gain some deeper understanding of the elementary mechanisms involved in the on-column PEGylation.
Conclusion
The on-column PEGylation of α-lactalbumin was successfully carried out on an anion-exchange stationary phase. The chromatographic separation of the product of the reaction (i.e. unreacted protein and PEGamers up to the tri-PEGylated α-lactalbumin) was performed right after the on-column reaction by linear gradient elution chromatography. Thus, the PEGylation reaction and the separation were performed in a single unit.The influence of pH, reaction time, protein load and PEG to protein molar ratio was assessed experimentally. The on-column kinetic scheme was shown to be pH dependent since different mono-PEGylated PEGamers were formed at pH 7.0 and 8.0. The rate of PEGylation was observed to be substantially reduced when performed in the adsorbed state. This slowing down could be explained by the reduction of the number of active sites since those facing the ion-exchange media cannot react any longer. In the end, the on-column PEGylation process was observed to be more selective for smaller degrees of PEGylation than the classical solution PEGylation process. When compared with the reaction in solution, it was observed that under similar conditions the conversion of the protein was lower with the on-column process. Therefore, the on-column PEGylation process would become economically interesting by implementing a recycling of the unreacted protein.
Finally, a mathematical model was derived in order to get a better understanding of the effect of the operating conditions on the process yield and produce an efficient tool for process design and development. This process is an interesting example of process integration and has to be regarded as a proof of concept for a future implementation of the on-column PEGylation reaction in a continuous multi-column chromatographic process.
Acknowledgements
This work was financially supported by Sanofi, Vitry sur Seine, France and by ETH Research Grant ETH-22 13-1.References
- F. M. Veronese, A. Mero and G. Pasut, in PEGylated Protein Drugs: Basic Science and Clinical Applications, Springer, 2009, pp. 11–31 Search PubMed.
- J. R. Molek, PhD Thesis, The Pennsylvania State University, 2008 Search PubMed.
- H. Zhao, presented in part at the International Conference and Exhibition on Biowaivers & Biosimilars, Hilton San Antonio Airport, 2012 Search PubMed.
- G. Pasut and F. M. Veronese, J. Controlled Release, 2012, 161, 461–472 CrossRef CAS PubMed.
- P. Bailon and C. Y. Won, Expert Opin. Drug Delivery, 2009, 6, 1–16 CrossRef CAS PubMed.
- C. J. Fee and J. A. Van Alstine, Chem. Eng. Sci., 2006, 61, 924–939 CrossRef CAS.
- D. Pfister and M. Morbidelli, J. Controlled Release, 2014, 180, 134–149 CrossRef CAS PubMed.
- C. J. Fee, Biotechnol. Bioeng., 2003, 82, 200–206 CrossRef CAS PubMed.
- B. K. Lee, J. S. Kwon, H. J. Kim, S. Yamamoto and E. Lee, Bioconjugate Chem., 2007, 18, 1728–1734 CrossRef CAS PubMed.
- Z. F. Huang, G. H. Zhu, C. C. Sun, J. G. Zhang, Y. Zhang, Y. T. Zhang, C. H. Ye, X. J. Wang, D. Ilghari and X. K. Li, PLoS One, 2012, 7 CAS.
- Z. Huang, C. Ye, Z. Liu, X. Wang, H. Chen, Y. Liu, L. Tang, H. Zhao, J. Wang, W. Feng and X. Li, Bioconjugate Chem., 2012, 23, 740–750 CrossRef CAS PubMed.
- X. Suo, X. Lu, T. Hu, G. Ma and Z. Su, Biotechnol. Lett., 2009, 31, 1191–1196 CrossRef CAS PubMed.
- X. Shang and R. Ghosh, J. Membr. Sci., 2014, 451, 177–184 CrossRef CAS.
- X. Shang, D. Yu and R. Ghosh, Biomacromolecules, 2011, 12, 2772–2779 CrossRef CAS PubMed.
- D. Pfister, E. Bourgeaux and M. Morbidelli, Chem. Eng. Sci., 2015, 137, 816–827 CrossRef CAS.
- P. DePhillips and A. M. Lenhoff, J. Chromatogr. A, 2000, 883, 39–54 CrossRef CAS PubMed.
- D. Pfister, F. Steinebach and M. Morbidelli, J. Chromatogr. A, 2015, 1375, 33–41 CrossRef CAS PubMed.
- G. Guiochon, A. Felinger, D. G. Shirazi and A. M. Katti, Fundamentals of Preparative and Nonlinear Chromatography, Academic Press, 2006 Search PubMed.
- D. Pfister and M. Morbidelli, J. Chromatogr. A, 2015, 1375, 42–48 CrossRef CAS PubMed.
- R. M. Nicoud, Chromatographic Process: modeling, simulation and design, 2015 Search PubMed.
- G. Carta and A. Jungbauer, Protein chromatography: process development and scale-up, John Wiley & Sons, 2010 Search PubMed.
- F. Dismer and J. Hubbuch, J. Chromatogr. A, 2010, 1217, 1343–1353 CrossRef CAS PubMed.
- R. H. Richardson and K. Brew, J. Biol. Chem., 1980, 255, 3377–3385 CAS.
- B. Maiser, K. Baumgartner, F. Dismer and J. Hubbuch, J. Chromatogr., B, 2015, 1002, 313–318 CrossRef CAS PubMed.
- A. M. Athalye, S. J. Gibbs and E. N. Lightfoot, J. Chromatogr. A, 1992, 589, 71–85 CrossRef CAS.
- B. C. de Neuville, A. Tarafder and M. Morbidelli, J. Chromatogr. A, 2013, 1298, 26–34 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2016 |