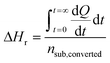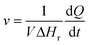Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The application of reaction engineering to biocatalysis
R. H.
Ringborg
and
J. M.
Woodley
*
CAPEC-PROCESS Research Center, Department of Chemical and Biochemical Engineering, Technical University of Denmark, DK-2800 Lyngby, Denmark. E-mail: jw@kt.dtu.dk
First published on 13th January 2016
Abstract
Biocatalysis is a growing area of synthetic and process chemistry with the ability to deliver not only improved processes for the synthesis of existing compounds, but also new routes to new compounds. In order to assess the many options and strategies available to an engineer developing a new biocatalytic process, it is essential to carry out a systematic evaluation to progress rapidly and ensure decisions are made on firm foundations. In this way, directed development can be carried out and the chances of implementation of a commercially successful process can be much improved. In this review we outline the benefits of reaction engineering in this development process, with particular emphasis of reaction kinetics. Future research needs to focus on rapid methods to collect such data at sufficient accuracy that it can be used for the effective design of new biocatalytic processes.
Introduction
In recent decades a growing branch of synthetic chemistry has been established which uses enzymes to catalyze interesting reactions for the production of valuable molecules.1,2 Such an approach is termed biocatalysis and today finds application in the synthesis of many chemical products, ranging from bulk commodities to pharmaceutical intermediates.3–6 Several hundred industrial processes have already been implemented, mostly in the pharmaceutical industry, with more in development.3,7 The motivation for the application of such catalysts stems from their ability to perform highly selective chemistry under mild conditions in water based solutions, making them attractive as ‘green’ catalysts.8 In the last decade the ability to alter the properties of the enzyme via protein engineering9–11 has enabled the synthesis of entirely new molecules and reactions (without precedent in nature).10,12 Multi-step sequences of enzymes, operating sequentially or in tandem,13,14 as well as chemo-enzymatic combinations15,16 have now also been established. In short, biocatalysis provides a valuable tool to complement many established synthetic approaches. Despite these scientific developments biocatalysis is still often limited in application due to a poor transition from the laboratory to the process plant. There are several good reasons for this, but amongst the most important is the complexity of enzyme kinetics, combined with the fact that the enzymes need to carry out synthetic reactions under conditions far away from those found in Nature. This makes the collection of parameters in kinetic models especially difficult. For conventional chemical reactions (including catalytic conversions), reaction engineering has long provided an efficient and effective methodology for the design and sizing of appropriate reactors in which to synthesize valuable industrial chemicals.17–20 At the heart of the discipline lies the determination of rate laws, collection of kinetic parameters and the application of these models to mass balances to enable in silico prediction of product concentration and reactant conversion as a function of residence time. It is an essential activity to inform chemical engineers charged with the design of pilot-scale or full scale plant. The time is now right for the development of such a paradigm for biocatalytic reactions where suitable methods are established for deriving kinetic expressions, not solely aimed at the mechanistic understanding required by biochemists, but now also of appropriate accuracy to be used by (bio)chemical engineers to design (bio)reactors. Such design should also include options for defining suitable biocatalyst loadings and operating schemes to make optimal use of existing equipment, which is often the requirement in the pharmaceutical industry. Likewise such design should also enable considerations for improvement of the enzyme itself21 (via protein engineering) as well as the process plant and operation to be considered.In order for the new biocatalytic synthesis routes to reach industrialization it is necessary to have models describing the kinetic properties of the biocatalyst. Chemical engineering tools can then be used to scale and design facilities. Ideally, for the biocatalyst to reach this stage several requirements need to be met.
• An enzyme has been developed to thrive in the operational conditions required in the industrial process, frequently much harsher than those found in Nature. For example, a process for pharmaceutical synthesis, requires product concentrations of >50 g L−1,3,6,22,23 with a biocatalyst yield of 10–100 gProduct gImmobilized Biocatalyst−1.22,23
• The enzyme has been characterized comprehensively in terms of kinetics and stability.
• A model has been fitted to describe the rate of reaction in the full conversion range.
• A process concept has been made to define targets for the performance of the enzyme.
These four requirements are often attained in an iterative manner, leading to inefficiencies. Systematic procedures would be far more preferable to give the opportunity to assess the feasibility of processes quickly and where appropriate design optimum development strategies. Enzyme kinetics lies at the center of this procedure.
Today processes are developed first with an emphasis on protein engineering to broaden substrate scope, and secondly by process engineering to enable implementation. However, it is our contention that investigation of potential processes should be considered much earlier in the development procedure, so that it is possible to use reaction engineering as a guide for protein engineering such that biocatalytic properties match the process requirements. Indeed, without such guidance there is even a danger of ‘over’-engineering an enzyme. We believe judicious use of process engineering in concert with protein engineering may ultimately prove more effective.
With this background to the importance of kinetics, we will in this review describe different kinetic models of enzymes important to synthesis and production, and describe methods available for determination of rate laws (and associated kinetic parameters). Importantly, we will describe the application of such models in process evaluation and design and give a future outlook, emphasizing where they can be used to assist the targeted improvement of the biocatalysts themselves.
Biocatalytic process features
As described in numerous texts, chemical reaction engineering is built around the determination of a rate law (defining the relationship of the rate of reaction with the concentration of reactants and catalyst, under given conditions). Although in essence the rate law is similar whether an enzymatic or a chemical catalyst is used (e.g. Michaelis–Menten kinetics are equivalent to Langmuir–Hinshelwood), in reality extra terms are required in enzyme catalysis to account for reactant and product inhibition at the extraordinarily high concentrations required for an industrial process, compared to those found in Nature. This added complexity needs to be built into the rate law and becomes particularly important when multiple reactants are used and/or products produced. Hence the rate law may prove particularly complex and while the estimation of macro-kinetic parameters is difficult, the estimation of micro-kinetic parameters is in many cases impossible due to problems of identifiability.A second feature of enzyme reactions is that they usually take place in the liquid phase. This means that operating a simple continuous plug flow reactor for catalyst characterization, is frequently limited due to high pressure drops. The many chemical reactions that take place in a gas phase can easily overcome such problems, due to much lower viscosities and higher diffusion rates. Additionally, enzyme reactions in Nature mostly take place in an aqueous environment, and while many enzymes have the ability to work in organic media (to a greater or lesser extent), clearly the kinetics are affected.24 In many cases the requirement for addition of an organic solvent is essential based on the poor water-solubility of many of the most interesting industrial compounds. The complex structure of an enzyme also means that the protein is subject to unfolding under exposure to extremes of pH, temperature, ionic strength and interfacial effects.25 In general, conditions such as the solvent, pH and temperature will therefore be predefined, but in principle this also provides room for optimization, provided suitable kinetic data is available as a function of these variables. In itself this also implies a vast space of reaction conditions.
The third important feature of biocatalysis, with respect to reaction engineering, concerns thermodynamics. The early days of biocatalysis focused in particular on hydrolytic reactions, in the presence of water. Since then we now know that the amount of water required to maintain structure is minimal (although essential) meaning such reactions can be run in reverse.26,27 Biocatalysts lowers the activation energy for both directions of a reaction and thermodynamics determines the favourable direction. Nonetheless, it can be desirable to operate reactions in the unfavourable direction for synthetic purposes. Specific products, low cost substrates or natural substrates can be the motivator for such a direction of reaction, but makes the process considerable more difficult to design. Substrate and consequently product pairs can however be chosen so that the direction of the reaction will be overall favourable. This has been shown for amine transaminases28 and can also be obtained by coupling the main reaction with enzymatic cascades.29 In cases where reactions are operated against the thermodynamically favourable direction it is necessary to collect thermodynamic data to establish the reaction equilibrium as well as the kinetic data. Unlike chemical catalysts where the variables of pressure and/or temperature can be used to shift equilibrium, for biocatalysis other methods are required such as use of an excess of a reactant (provided it is beneath its inhibitory threshold) and in situ product removal (ISPR technologies).30,31 This also needs consideration in reaction engineering.
For all these reasons we argue that biocatalysis is deserving of a separate treatment in reaction engineering. The variables available to improve the process metrics, as well as the targets required, are quite different depending on whether one develops a chemo-catalytic reaction or a biocatalytic reaction. For example, the operational temperature for chemo-catalysts can span hundreds of degrees and investigation of rate constants can be extrapolated by activation energies to describe this change. The different activation energies of parallel reactions can then be used to tune selectivity. In contrast, the temperature range for enzymes is rather limited and selectivity rarely a concern.
Operational window for kinetic studies
Historically and still today for biocatalysis, activity assays are used for the investigation of enzyme kinetics. These preliminary studies include an investigation of the effect on reaction rate of changes in temperature, pH, ionic strength, enzyme and component concentration. The results have not always been presented in a rate law, but have most often provided a useful starting point for more detailed studies by fixing some of the environmental variables such as ionic strength, pH and temperature. Experiments have usually been carried out by mixing all components together at the same time and thereafter monitoring the development of the individual component concentrations. The rate of reaction has then been defined as either the disappearance or production of a component over time. The initial testing of enzymes usually includes an investigation of the linear activity/enzyme concentration range and the optimal pH. After this has been established, enzyme concentration can be fixed so as to obtain subsequently measured initial rates in a reasonable time period. pH is then also fixed in accordance with the highest activity observed, which usually also represents the most stable condition for the enzyme. Care should however be taken here to investigate the protonation of the different compounds in solution. The activity dependence on temperature for enzymes is similar to that of chemo-catalysts. Here also the empirical rule of a 10 °C increase in temperature resulting in a two-fold increase in rate holds true.32 However, with enzymes, denaturation can also occur at higher temperatures, resulting in a trade-off of activity and stability – most usually reported as an optimum temperature. The temperature at which an enzyme is fully denatured is termed its melting temperature.33 Technology for measuring this is available and can be done either with differential scanning calorimetry (DSC)34 or the recently developed thermal shift methodology.35 At temperatures beneath the melting temperature, denaturation will still occur but at a slower rate, and can easily be mistaken for inhibition. An optimal temperature will require a minimum enzyme stability and will therefore lie significantly below the melting temperature. In order to avoid stability issues, experiments are therefore often carried out at ambient temperatures similar to these in their natural environment. After fixing the enzyme concentration, pH and temperature, the concentration of the different compounds can be investigated. To put the above analysis into perspective the general workflow for developing a kinetic model for an enzyme can be represented diagrammatically as shown on Fig. 1, without the dashed processes. An overview of the different analysis methods are given later in the article.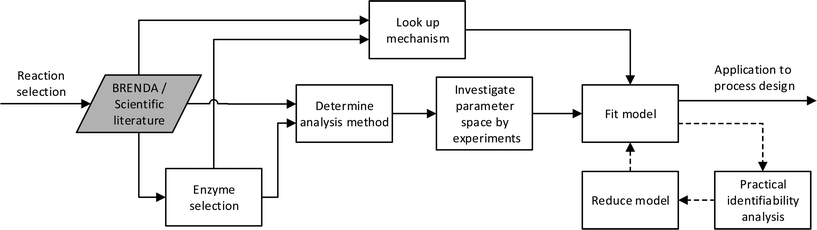 | ||
| Fig. 1 Proposed workflow for developing a kinetic model, here BRENDA refers to the data base.115 The dashed line introduces statistical analysis of the model applied. | ||
The determination of the rate law is the last part of such a workflow. Modelling chemo-catalytic reactions can be done by fitting or testing zero, first or second order rate laws which are relatively straight forward since these will remain constant under specific conditions.17,36 However, for biocatalytic reactions, the identification of rate laws is more complex since they display mixed order kinetics. The strategy has therefore been to elucidate reaction mechanisms and in turn develop models, prior to parameter estimation based on rigorous experimental data. Not surprisingly, the field of biocatalytic model construction has therefore produced several textbooks covering the common mechanisms.37,38 Enzyme classification has long been based on the reaction catalysed and according to the convention of the International Union of Biochemistry and Molecular Biology, IUBMB, an agreed nomenclature falls into 6 Enzyme Commission (EC) groups, each of which have a further 3 levels of sub-classes. In this way each enzyme can be characterized by a 4 digit number (e.g. transketolase is EC 2.2.1.1). The generalized reactions that are carried out by these enzymes in the 6 groups are summarized in Table 1.
| Group | Reaction catalyzed | Typical reaction | Enzyme example(s) with trivial name |
|---|---|---|---|
| EC 1 oxidoreductases | To catalyze oxidation/reduction reactions; transfer of hydrogen and oxygen atoms | A + B ⇌ P + Q | Dehydrogenase, oxidase |
| A + O2 ⇌ P + H2O2 | |||
| EC 2 transferases | Transfer of a functional group from one substance to another. The group may be methyl-, acyl, amino- or phosphate | A + B ⇌ P + Q | Transaminase, transketolase |
| EC 3 hydrolases | Formation of two products from a substrate by hydrolysis | A + H2O ⇌ P + Q | Lipase, amylase, peptidase |
| EC 4 lyases | Non-hydrolytic addition or removal of groups from substrates. C–C, C–N, C–O or C–S bonds may be cleaved | A ⇌ P + Q | Aldolase decarboxylase |
| EC 5 isomerase | Intramolecular rearrangement, i.e. isomerization changes within a single molecule | A ⇌ P | Isomerase, mutase |
| EC 6 ligases | Join together two molecules by synthesis of new C–O, C–S, C–N or C–C bonds with simultaneous breakdown of ATP | A + B + ATP ⇌ P + ADP + Pi | Synthetase |
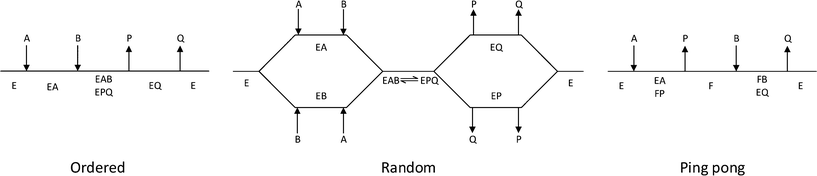
The third column of Table 1 indicates the general reaction equation of these conversions. This is important in order to identify the basic structure of the rate law. For synthetic purposes, the emphasis lies with EC groups 1–4,1,2,5,6 where typical reaction schemes involve two reactants and two products (with the exception of EC 4 that in the synthesis direction only has a single product). General models for EC groups 1–3 are summarized in Fig. 2 and represent so-called ordered, random and ping pong bi–bi mechanisms, reflecting the order in which multiple substrates and products are bound to or released from the enzyme complex, respectively. Enzymes in EC group 4 will also follow these models but in a reduced form since this group has a reaction equation with one less specie. Examples of synthetically useful enzymes from these different EC categories are listed in Table 2. It is well known that the three mechanisms listed do not represent all enzymes, and both more complex as well as simpler mechanisms exist. Nonetheless, for synthetic purposes these are the most common and further discussion will therefore be based on the identification and parameter fitting of these models in particular.
| EC category | Sub EC # | Reactive group | Case enzyme | Kinetic mechanism | Ref. |
|---|---|---|---|---|---|
| EC 1 oxidoreductases | Acting on | ||||
| 1.1 | Alcohol groups | Alcohol dehydrogenase | Random bi–bi, ordered bi–bi, theorell-chance | 39–41 | |
| 1.1 | Alcohol groups | Galactose oxidase | Ping pong bi–bi | 42 | |
| 1.2 | Aldehyde or oxo groups | Pyruvate dehydrogenase | Ping pong bi–bi | 43 | |
| 1.4 | Amino groups | Mono amino oxidase | Ping pong bi–bi | 44 | |
| EC 2 transferases | Transferring | ||||
| 2.7 | Phosphorous-containing groups | Non-specific protein-tyrosine kinase | Random bi–bi | 45 | |
| 2.4 | Glycosyl groups | Glycogen phosphorylase | Random bi–bi | 46 | |
| 2.1 | One-carbon groups | Thymidylate synthase | Ordered bi–bi | 47 | |
| 2.3 | Acyl groups | Histone acetyltransferases | Ordered bi–bi | 48 | |
| 2.6 | Nitrogenous groups | Transaminases | Ping pong bi–bi | 49–51 | |
| 2.2 | Carbon–carbon | Transketolase | Ping pong bi–bi | 52, 53 | |
| EC 3 hydrolases | Acting on | ||||
| 3.1 | Ester bonds | Lipase | Ping pong bi–bi | 26 | |
| 3.2 | Glycosyl bonds | Amylase | Ping pong bi–bi | 54 | |
| 3.5 | Carbon–nitrogen bonds | Amidase | Ping pong bi–bi | 55, 56 | |
| EC 4 lyases | Acting on | ||||
| 4.1 | Keto acid | Aldolase | Random bi–uni ordered bi–uni | 57 | |
| 4.3 | Carbon–nitrogen | Methylaspartate ammonia-lyase | Ordered bi–uni | 58 |
Mechanistic models
In cases where no mechanism has previously been determined for an enzymatic catalyst of interest, it can be determined by an inhibition study. The initial rates are studied under the conditions where one substrate is varied while the other is kept constant. The mechanism can hereafter be identified by plotting them in a Lineweaver–Burk plot, see Fig. 3. The relative position of the intercept depends on whether the substrates hinder or favour one another, resulting in an intercept above or below the abscissa, respectively. Commonly, the intercept will appear to the left of the ordinate above the abscissa. If both substrates bind independent of one another then the intercept should lie on the abscissa, indicating a random mechanism. When parallel lines are observed, then a ping-pong mechanism is inferred. As can be observed in Fig. 3, the enzyme is either in the form of one or other complex (EX) or alternatively activated enzyme (F). Experiments need to be designed such that the substrate concentration greatly exceeds that of the enzyme. This is not required in order to saturate the enzyme but rather to have a negligible amount of the substrate bound to the enzyme.59 The required sensitivity of the analysis method for measuring the different enzymatic species can thereby only be achieved by the sensitive fluorescence methods. Aside for mechanistic studies, for reaction engineering the inability to measure the species restricts model fitting substantially and estimation of micro-kinetic constants will therefore only make sense in cases where the individual species can be measured. The necessary simplification of the models is achieved primarily by the steady state assumption, which states that the concentration of enzymatic species reaches steady state after milliseconds of reaction. Additionally, the rate constants are collected together in the form of equilibrium-like constants, K, which are termed macro-kinetic constants. For example the model for the ping pong bi–bi mechanism without dead-end inhibition37 is shown in eqn (1)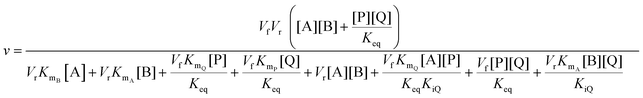 | (1) |
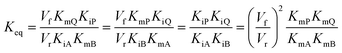 | (2) |
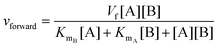 | (3) |
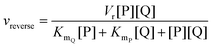 | (4) |
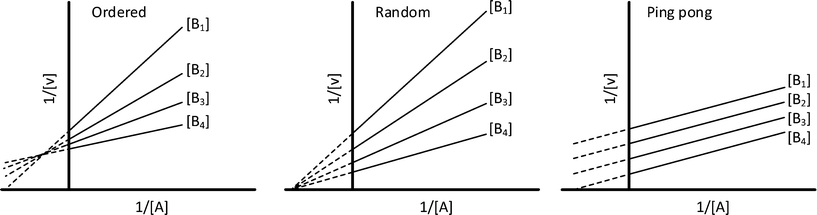 | ||
| Fig. 3 Lineweaver–Burk plots for the determination of ordered, random and ping pong bi–bi mechanisms. | ||
In the scientific literature, makrokinetic reaction networks with sequential, competitive or consecutive steps are models recognized to have highly correlated parameters.60 This causes problems with finding a global minimum for the objective function, and therefore a unique solution. The estimated parameters from the previously described method rely on “independent estimation”, first fitting the forward rate, then fitting the backward rate and finally fitting the remaining parameters. However, because correlation persists further measures need be taken. Model-based design of experiments (MBDoE), uses the model to design new experiments which will yield information in terms of reducing uncertainty or correlation.60,61 In order for this method to be applicable it is necessary to have a good initial guess of the individual model parameters. The stepwise approach is currently the best way of fitting the data and thus the best “initial-guess” available. MBDoE aims at devising experiments that will yield the most informative data, in a statistical sense, for use in parameter estimation and model validation. The method applies the maximization of the Fisher information matrix (FIM) or minimization of the covariance matrix, which is the inverse of the FIM. The calculated experimental conditions required to reach this point can then be identified and tested. Specific, anti-correlation criteria for experimental design have been described by Franceschini et al.62 In the case where correlation cannot be eliminated, the parameters should be collapsed into a new variable. This variable may lose physical meaning but, as with the case of the rate and equilibrium constants described previously, it is better to have an practically identifiable model.
Methods for obtaining kinetic data
The term ‘reaction progress kinetic analysis’, coined by Blackmond,17,36 stresses the importance of on- or in-line analysis to elucidate mechanisms of catalytic systems. Ideally, this would also be routinely applied to the study of enzyme kinetics and Johnson63 has reported an excellent case applying this to determine the micro-kinetic parameters for the rate law of invertase and the more complex case of EPSP synthase.64 The goal of that research was to investigate the structure–activity relationship, which is quite different from the process engineering objective, which is the primary target addressed in this paper. In principle, for process design and development all that is desired is a sufficiently accurate model that can describe the kinetic dynamics of a biocatalytic reaction. The stepwise fitting procedure presented in the mechanistic model section is heavily reliant upon initial rates. For this reason determination of macro-kinetic parameters is probably more practical, although correlation remains a challenge. A suitable technology and methodology for determining enzyme kinetics would therefore be very desirable. Ideally it could be used to reliably determine initial rates at low conversion and likewise have the possibility of conducting high conversion experiments. Recent developments include exciting new ways of collecting data at microscale,65–68 although the associated FT-IR and Raman spectroscopy do not yet deliver the required sensitivity. All the methods are summarized in Table 3.| Micro wells | Spectrophotometric assays | Batch | Continuous flow | Stopped-flow | Isothermal titration calorimetry | |
|---|---|---|---|---|---|---|
| Detector | UV-plate reader | UV-vis | HPLC | NIR, IR, Raman | — | Heat flow |
| HPLC | ||||||
| Advantages | Automated | In-line | Omnipotent | Automated batch kinetics | Studying reactions in the millisecond range | Direct non-destructive measurement |
| Mixing | Cheap | Mixing | Controlled environment | Constant error | ||
| Running many reactions in parallel | Running many reactions in parallel | Determination of ΔHr | ||||
| Disadvantages | Generally not sealed | Generally not sealed | Manual handling | Long term experiments | Long term experiments | Expensive |
| No mechanical mixing | External validation for ΔHr | |||||
| Fitting of heat flow | ||||||
| Examples of application | Oxygen dependent systems | Kinetics at benign conditions | Long term experiments | Exo and endothermic reactions | Very fast reactions | Complex and opaque solutions |
| Small quantity of consumables | Small quantity of consumables | Assays | ||||
| Time range | Seconds–hours | Seconds–few hours | Minutes–days | Few minutes–few hours | Millisecond–few minutes | Second–few hours |
| Time resolution | Single wavelenght: 1/10 Hz for 96 wells | Up to 100 Hz | Minutes | 1-1/15 Hz | Up to 300 Hz | Up to 100 Hz |
| Data acquisition | Parallel-semicontinuous | Single-continuous | Parallel-discontinouos | Single-continuous | Single-continuous | Single-continuous |
| Ref. | 75–77 | 40, 41, 43, 49, 50, 78–81 | 51, 53, 54, 57, 76 | 65–68 | 39, 44, 82–86 | 87–90 |
Spectrophotometric assays
Proteins and enzymes are in general detectable by UV-vis absorption spectroscopy, and can in this way be quantified, although the absorption maxima of many substances, e.g., carbonyl groups or peptide bonds, lie in the far-UV region (122–200 nm), which is not easily accessible. From the perspective of synthesis, many small molecules are used which absorb in the mid-UV region (200–300 nm). Therefore, for determination of enzyme kinetics, both the absolute absorption and spectral changes must be considered. In fact, in many cases the spectral differences in solutions with enzyme, substrate(s) and product(s) are not very large and only small shifts can be observed. Even with curve resolution techniques, the quantification of small molecules proves to be very dependent upon local calibration. Historically, this has been circumvented by determination of the cofactor NAD(P)+, which upon reduction to NAD(P)H forms a new absorption band at 340 nm.69 This is not only an easily accessible region but has the great advantage that the oxidized form does not absorb at this wavelength, meaning any observed change in absorption is directly proportional to the reaction rate. This technique is directly applicable to dehydrogenases39–41,43 and these enzymes can also be coupled with other reactions in cascades.70–72 The reaction conditions of such ‘coupled assays’ are rather complex to ensure that the test reaction and not the ‘indicator’ reaction becomes limiting. In general, coupled assays are helpful for the determination of enzyme activity, but cannot be recommended for enzyme kinetic studies for this exact reason. In an analogous way, oxidases can be used to produce hydrogen peroxide which can then oxidize phenol red73 or xylenol orange74 detected at 610 and 560 nm, respectively.Batch reactors
The slowest and most labor intensive method for collecting kinetic data is in batch mode. However, this is also the most robust in terms of wide applicability. Vessels can range from micro wells to laboratory scale equipment, although vessels are commonly chosen in the scale of a few mLs. Such reactors can fit into thermoshakers and aliquots can be drawn without affecting the reaction. The samples can then be measured off-line, most commonly by HPLC. The frequency of sampling is usually quite high for measuring initial rates and 5–10 points can be collected within an hour. Many batch experiments can be carried out in parallel and for a prolonged time, making them ideal for the measuring of progress curves. Here the sampling frequency is in the order of hours.Flow reactors
More recently systems based on the principles of flow chemistry have been developed to ensure rapid, low-volume and high precision analysis. This can replace many tedious and high volume requirements of conventional analysis. Use of flow systems implies the use of pumps and this environment leads quite naturally towards automation. The implications of computer controlled liquid handling can give rapid characterization throughputs and cost savings. Furthermore, automated operation can remove manual errors and in principle will give more reliable results.Flow strategies can best be classified dependent upon how the reacting stream is manipulated after merging of the reactant and enzyme. The different types considered here are “continuous flow” which is a non-interrupted flow from introduction to waste, “stopped flow” which holds the mixture in a chamber fit for spectrophotometric measurements and “quench flow” which involves either physically or chemically stopping the reaction at the exit of the system and thereafter analyzing the samples off-line.
Generally flow systems struggle to circumvent the problem of laminar flow, which introduces dispersion into the system. Dispersion elongates the flow profile and hence time required to reach steady state. This is a problem because the concentration profile in the reactor will change over time until steady-state is reached. A comparison of different performance under non-steady state reactor conditions should therefore only be made when the flow conditions are exactly the same, such as constant residence time and Reynolds number. Flow injection analysis (FIA) solves this to some extent by measuring pulses of samples. Here the distribution of the sample is followed over time and the area of the pulse is measured. This method is very similar to that of an HPLC and it is calibrated likewise. What further complicates things for enzymes are their size, which in solution translates to a factor 100 slower diffusivity compared to small molecules (10−11 to 10−9 m2 s−1).91,92 The dispersion of enzymes will therefore be much more pronounced, meaning they are more dispersed through the channel compared to the small molecule reactants and resulting products. Homogeneity of the pulses is therefore questionable for FIA applied to enzyme catalysis. The effect of enzyme diffusion in 83–283 μm wide channels with side-by-side flow has been investigated by Swarts and co-workers.93 A Michaelis–Menten model was constructed for a β-galactopyranoside enzyme (Vmax = 20.9 μmol s−1 g enzyme−1, KM = 1.04 mM), the model was combined with a computational fluid dynamics (CFD) model. The pure model and the CFD model were subsequently compared to understand the effects of diffusion. Even though the enzyme only occupies half of the reactor volume, the reaction rate was not limiting due to the short characteristic mixing time of the reactant. Consequently, only at high enzyme concentrations (>1 g L−1) in this case would rate limiting effects be observed. Clearly, this is very dependent on the kinetic constants of the enzyme of interest. The investigation was assumed to have been carried out at steady-state, and so the impact of enzyme diffusion on non-steady state methods is yet to be described.
Microfluidic flow reactors
Developments towards carrying out chemical reactions in flow micro-reactors has in recent years received much attention.94–98 This can also be applied to the collection of kinetic data. In many cases it is likely this will replace the traditionally used flasks or stirred vessels operated in batch mode. The small scale makes it possible to conduct experiments with low material input but yielding the same degree of information about the reaction performance. There are three methods reported in the scientific literature used for conducting such investigations, namely: (1) steady-state, (2) measurements at multiple positions at steady-state and (3) non-steady state. The measurements at non-steady-state are made possible by reconsidering low disperse flow99 that was originally described by Taylor100 and Aris.101 Low-disperse flow behaves similar to that of plug flow but at relatively small flow rates. What makes this so interesting is that a plug-flow reactor has the same integrated mass balance model as a batch reactor. Sampling from an ideal batch reactor will provide concentration over time data and such data is exactly what is used for kinetic modelling. Low-disperse flow reactors can therefore also be used to obtain this type of data without correction for flow dynamics.Stopped-flow techniques
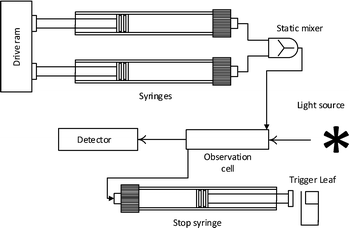
This technique has been developed for the study of reactions in the millisecond to minutes time range. Transient kinetics can be measured in the lower time range102–104 if the method is in place. The system can otherwise be used to study steady-state kinetics with the common assays as described previously. Experiments can be carried out by rapidly injecting solutions into a mixing device. The liquid is then led into the flow cell from the mixer, replacing the previous sample, the displaced liquid then fills a stop syringe moving the plunger towards the trigger leaf. After hitting the leaf the flow is stopped and measurement begins. The flow cell is illuminated and data is collected over time. The usual properties exploited are absorbance and fluorescence measurements, as well as application of light scattering, turbidity and fluorescence anisotropy technologies see Fig. 4. In the absence of a spectrophotometric method, quench flow can be applied. Directly after mixing, the solution is be chemically quenched, which can be used to study reactions in the millisecond range. Instead of holding the solution in an observation cell the quenched sample is collected and analyzed elsewhere (e.g. by HPLC).Isothermal titration calorimetry (ITC)
In contrast to spectral methods, measurements performed with ITC, are independent of the optical properties of the solution. ITC instruments have the objective of keeping the temperature constant in the reaction chamber, achieved either by heating or cooling the chamber. The required energy added or subtracted is logged and can be directly translated into reaction rate by relating the heat flow (dQ/dt) to the enthalpy change of reaction (ΔHr).105 From a practical perspective this is usually done with a single injection experiment where reactant is inserted into the reaction chamber. In the chamber it is possible to follow the burst of energy as the reaction initiates. From this point the reaction will follow a 1st order reaction development until the return to steady state (zero energy flow). It is necessary to know the exact amount of reactant converted by performing an independent concentration determination. The enthalpy change of reaction can thereafter be calculated by dividing the total heat transferred to the measurement cell by the total number of moles of substrate converted, nsub,converted.The reaction rate can thereafter be determined by
where V denotes the volume of the reaction chamber.
The technique of ITC is particularly potent since it can essentially measure any event occurring in a reaction chamber. This is also its problem, since dilution, binding events, interaction of impurities and buffer protonation effects106 will influence the readout. Pure formulations and materials for experiments are therefore required to ensure accurate measurements. Furthermore, dialysis of macromolecular solutions is also recommended, and preparation of small molecule solutions should be made from dialysate. After satisfying the rather high entrance requirements, it is necessary to match the energy development (rate of reaction) with the lower and upper detection limits. The enthalpy changes for most enzyme-catalyzed reactions range from −40 to −400 kJ mol−1, allowing reaction rates from 10 to 100 pmol s−1 to be accurately measured.107 Despite the fact that ITC has been used to measure enzymatic activity87,89,90 and that the technology dates back to 1965,108,109 the method is not found to be frequently applied in the field of enzyme kinetics. The advantage of a direct non-invasive measurement is though obvious and could be applied to a greater extent.
Application of kinetic data for process development
A powerful tool in assessing how a process can be developed is by coupling mass balances in a process design. This can only be carried out if kinetic and thermodynamic models for all the different parts of the process are available. Biocatalytic processes most often deal with the relatively low reaction rates prior to any biocatalyst engineering and this emphasizes the importance of having a reliable kinetic model. Theoretical evaluation is thereafter possible and requirements for the different elements of a process can be set. In the development of new processes one of the most difficult parts is to assess where the bottleneck lies. Moreover, it is not expected that biocatalyst engineering alone will be able to overcome all problems in relation to carrying out reactions at industrial conditions. Today, process engineering is most often only carried out at the end of a protein engineering development phase, where the biocatalyst engineer hands over the enzyme to the chemical engineer. It would be hugely advantageous were process engineers able to be involved earlier such that they could obtain enzymatic kinetic data and fit the different mechanisms (as they do for chemo-catalytic processes) prior to setting targets for enzyme development.Recent reviews on the application of biocatalytic models,110,111 show that models are applied to find performance limitations, to define optimal operating conditions, different reactor choices and compare different process configurations. Example: Berendsen and co-workers112 combined models of two enzymes to optimize the enantiomeric excess as a function of conversion. Schaber and co-workers113 carried out an economic assessment of a full process. It is therefore clear that these models can be applied to obtain this kind of information, and from a development perspective it is necessary to use these for identification of the bottleneck. For example enzymatic reactions are often hampered by product inhibition at high product concentrations. The introduction of ISPR to the simulation could here reveal targets for a given removal method, which would assist process engineering in terms of improving the method as well as protein engineering in terms of increasing tolerance.
Hence the input from the process engineering gives direction for protein engineering, which in turn drives a better process. While the order of the necessary tasks in process development is still not fixed22 it remains certain that in order to move the field forward collaboration between chemical engineers and protein engineers must be emphasized.
Discussion
Many spectrophotometric assays require alterations to the original reaction in order to be carried out effectively. This is can be achieved either by derivatization of the reactant with a chromophore or by an analytical enzyme cascade. The widely used indirect spectrophotometric assays rely on the stability of not only the target enzyme but also the assay enzyme and cofactors (e.g. NAD(P)H). Testing rather harsh conditions also requires a robust assay and this should therefore be carefully considered in the experimental planning phase. The industrial development environment is rarely able to conduct comprehensive investigations, so both speed and resources are important factors, driving automated and flexible methods similar to those that have been developed for classic organic synthesis.66,68 However, more sensitive concentration measurement methods are required and preferably in the order of 0.1 mM. The UV-vis spectrophotometer-based assays are therefore still advantageous, and if these fail one can turn to classic chromatographic measurements.The microfluidic FT-IR method developed by Moore and Jensen68 can be further developed to automatically propose experiments in the parameter space (e.g. concentration, temperature) based on the Fisher information matrix.114 However, focus in the paper by Schaber and co-workers was to have a fluid dynamic model of the reactor to circumvent the problems of dispersion. We propose that focus should rather be on fitting more complex models while applying the low-disperse flow regime.99 Having this in mind one can envisage automation of the kinetic models for enzymes. This may be possible after the realization of a versatile and sensitive on-line method.
The different parts of the development required could conceivably be combined into a methodology as proposed in Fig. 1, including the dashed processes. The theory and methods have already been developed, but appropriate models are yet to be produced as a basic step in biocatalytic process development.
Conclusion
In order to find the real bottleneck for the development of a new biocatalytic process, it is necessary to have a kinetic model of the reaction. The increasing interest in biocatalytic processes and the constant change of catalysts justifies a more streamlined development. Here, the common bi-substrate mechanisms covering most enzymes for synthetic purposes have been shown, the models for these can be found in textbooks and a method for fitting them has been presented. Methods for collecting kinetic data are available and assays can be found for almost any enzyme. The general methods of stopped flow, quenched flow or ITC in combination with HPLC provide an almost universal detection method. Analytical tools coupled with microfluidics are rapidly developing and it can be assumed that a method for enzymatic systems will be available in the near future. The entry barrier of fitting biocatalytic kinetic models is therefore lowered, this enables others to find bottlenecks, quantify the process problem and conduct a fast feasibility analysis of what is at hand. In this way the application of validated models will therefore be able to drive the field biocatalytic process development, as a whole, forward.Nomenclature
In this article, reactants are designated by the letters A and B in the order in which they are added to the enzyme. Products are designated the letters P and Q in the order in which they leave the enzyme. Stable enzyme forms are designated E and F, complexes between e.g. E and A are designated EA. KiX is the dissociation constant of EX, KMX is the Michaelis–Menten constant for the individual compound X. The number of kinetically important reactants in a given direction is indicated by the prefix or postfix uni, bi, ter and quad. A reaction with two reactants and two products is therefore termed a bi–bi reaction.Acknowledgements
R. H. Ringborg kindly acknowledges that he is funded by the European Union Seventh Framework Programme (FP7/2007-2013) BIOINTENSE under grant agreement no. 312148 and the Technical University of Denmark.References
- K. Faber, W.-D. Fessner and N. J. Turner, Science of Synthesis: Biocatalysis in Organic Synthesis, Georg Thieme Verlag KG, 2015 Search PubMed.
- K. Drauz, H. Groger and O. May, Enzyme Catalysis in Organic Synthesis, Third, Completely Revised and Enlarged Edition, WILEY-VCH Verlag, 3rd edn, 2012 Search PubMed.
- D. J. Pollard and J. M. Woodley, Trends Biotechnol., 2007, 25, 66–73 CrossRef CAS PubMed.
- B. M. Nestl, B. A. Nebel and B. Hauer, Curr. Opin. Chem. Biol., 2011, 15, 187–193 CrossRef PubMed.
- H.-P. Meyer, E. Eichhorn, S. Hanlon, S. Lütz, M. Schürmann, R. Wohlgemuth and R. Coppolecchia, Catal. Sci. Technol., 2012, 3, 29–40 Search PubMed.
- G. W. Huisman and S. J. Collier, Curr. Opin. Chem. Biol., 2013, 17, 284–292 CrossRef CAS PubMed.
- A. Schmid, J. S. Dordick, B. Hauer, A. Kiener, M. Wubbolts and B. Witholt, Nature, 2001, 409, 258–268 CrossRef CAS PubMed.
- Y. Ni, D. Holtmann and F. Hollmann, ChemCatChem, 2014, 6, 930–943 CrossRef CAS.
- N. J. Turner and M. D. Truppo, Curr. Opin. Chem. Biol., 2013, 17, 212–214 CrossRef CAS PubMed.
- G. A. Strohmeier, H. Pichler, O. May and M. Gruber-Khadjawi, Chem. Rev., 2011, 111, 4141–4164 CrossRef CAS PubMed.
- U. T. Bornscheuer, G. W. Huisman, R. J. Kazlauskas, S. Lutz, J. C. Moore and K. Robins, Nature, 2012, 485, 185–194 CrossRef PubMed.
- J. B. Siegel, A. Zanghellini, H. M. Lovick, G. Kiss, R. Abigail, J. L. S. Clair, J. L. Gallaher, D. Hilvert, M. H. Gelb, B. L. Stoddard, K. N. Houk, F. E. Michael and D. Baker, Science, 2011, 329, 309–313 CrossRef PubMed.
- E. Ricca, B. Brucher and J. H. Schrittwieser, Adv. Synth. Catal., 2011, 353, 2239–2262 CrossRef CAS.
- R. C. Simon, N. Richter, E. Busto and W. Kroutil, ACS Catal., 2014, 4, 129–143 CrossRef CAS.
- H. Gröger and W. Hummel, Curr. Opin. Chem. Biol., 2014, 19, 171–179 CrossRef PubMed.
- A. Bruggink, R. Schoevaart and T. Kieboom, Org. Process Res. Dev., 2003, 7, 622–640 CrossRef CAS.
- D. G. Blackmond, J. Am. Chem. Soc., 2015, 137, 10852–10866 CrossRef CAS PubMed.
- V. Hessel, D. Kralisch, N. Kockmann, T. Noël and Q. Wang, ChemSusChem, 2013, 6, 746–789 CrossRef CAS PubMed.
- J. P. McMullen and K. F. Jensen, Annu. Rev. Anal. Chem., 2010, 3, 19–42 CrossRef CAS PubMed.
- S. G. Newman and K. F. Jensen, Green Chem., 2013, 15, 1456–1472 RSC.
- J. M. Woodley, Curr. Opin. Chem. Biol., 2013, 17, 310–316 CrossRef CAS PubMed.
- P. Tufvesson, J. Lima-Ramos, N. Al Haque, K. V. Gernaey and J. M. Woodley, Org. Process Res. Dev., 2013, 17, 1233–1238 CrossRef CAS.
- J. Lima-Ramos, W. Neto and J. M. Woodley, Top. Catal., 2014, 57, 301–320 CrossRef CAS.
- A. M. Klibanov, Nature, 2001, 409, 241–246 CrossRef CAS PubMed.
- C. R. Thomas and D. Geer, Biotechnol. Lett., 2011, 33, 443–456 CrossRef CAS PubMed.
- A. L. Paiva, V. M. Balcão and F. X. Malcata, Enzyme Microb. Technol., 2000, 27, 187–204 CrossRef CAS PubMed.
- P. J. Halling, Enzyme Microb. Technol., 1994, 16, 178–206 CrossRef CAS PubMed.
- R. J. Meier, M. T. Gundersen, J. M. Woodley and M. Schürmann, ChemCatChem, 2015, 7, 2594–2597 CrossRef CAS.
- R. Abu and J. M. Woodley, ChemCatChem, 2015, 7, 3094–3105 CrossRef CAS.
- J. M. Woodley, M. Bisschops, A. J. J. Straathof and M. Ottens, J. Chem. Technol. Biotechnol., 2008, 83, 121–123 CrossRef.
- W. van Hecke, G. Kaur and H. De Wever, Biotechnol. Adv., 2014, 32, 1245–1255 CrossRef PubMed.
- H. Bisswanger, Perspect. Sci., 2014, 1, 41–55 CrossRef.
- C. Vieille, G. J. Zeikus and C. Vieille, Microbiol. Mol. Biol. Rev., 2001, 65, 1–43 CrossRef PubMed.
- G. Bruylants, J. Wouters and C. Michaux, Curr. Med. Chem., 2005, 12, 2011–2020 CrossRef PubMed.
- C. G. Alexander, R. Wanner, C. M. Johnson, D. Breitsprecher, G. Winter, S. Duhr, P. Baaske and N. Ferguson, Biochim. Biophys. Acta, Proteins Proteomics, 2014, 1844, 2241–2250 CrossRef PubMed.
- D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320 CrossRef PubMed.
- I. H. Segel, Enzyme kinetics: behavior and analysis of rapid equilibrium and steady-state enzyme systems, John Wiley & Sons, 1975, vol. 2 Search PubMed.
- W. W. Cleland, in The enzymes, vol II: kinetics and mechanism, ed. P. D. Boyer, Academic Press, 3rd edn, 1970, pp. 1–61 Search PubMed.
- H. W. Adolph, P. Maurer, H. Schneider-bernlöhr, C. Sartorius and M. Zeppezauer, Eur. J. Biochem., 1991, 201, 615–625 CrossRef CAS PubMed.
- P. W. Heinstra, G. E. Thörig, W. Scharloo, W. Drenth and R. J. Nolte, Biochim. Biophys. Acta, 1988, 967, 224–233 CrossRef CAS.
- K. Dalziel and F. M. Dickinson, Biochem. J., 1966, 100, 34–46 CrossRef CAS PubMed.
- K. J. Humphreys, L. M. Mirica, Y. Wang and J. P. Klinman, J. Am. Chem. Soc., 2009, 131, 4657–4663 CrossRef CAS PubMed.
- C. S. Tsai, M. W. Burgett and L. J. Reed, J. Biol. Chem., 1973, 248, 8348–8352 CAS.
- H. Suzuki, Y. Ogura and H. Yamada, J. Biochem., 1972, 72, 703–712 CAS.
- J. A. Adams, Chem. Rev., 2001, 101, 2271–2290 CrossRef CAS PubMed.
- V. T. Maddaiah and N. B. Madsen, J. Biol. Chem., 1966, 241, 3873–3881 CAS.
- C. W. Carreras and D. V. Santi, Annu. Rev. Biochem., 1995, 64, 721–762 CrossRef CAS PubMed.
- S. Y. Roth, J. M. Denu and C. D. Allis, Annu. Rev. Biochem., 2001, 70, 81–120 CrossRef CAS PubMed.
- C. P. Henson and W. W. Cleland, Biochemistry, 1963, 3, 338–345 CrossRef.
- J. S. Shin and B. G. Kim, Biotechnol. Bioeng., 1998, 60, 534–540 CrossRef CAS PubMed.
- N. Al-Haque, P. A. Santacoloma, W. Neto, P. Tufvesson, R. Gani and J. M. Woodley, Biotechnol. Prog., 2012, 28, 1186–1196 CrossRef CAS PubMed.
- M. Gyamerah and A. J. Willetts, Enzyme Microb. Technol., 1997, 20, 127–134 CrossRef CAS.
- B. H. Chen, E. G. Hibbert, P. A. Dalby and J. M. Woodley, AIChE J., 2008, 54, 3–5 Search PubMed.
- B. A. van der Veen, G. J. W. M. van Alebeek, J. C. M. Uitdehaag, B. W. Dijkstra and L. Dijkhuizen, Eur. J. Biochem., 2000, 267, 658–665 CrossRef CAS PubMed.
- M. Maestracci, A. Thiery, A. Arnaud and P. Galzy, Agric. Biol. Chem., 1986, 50, 2237–2241 CrossRef CAS.
- D. Fournand, F. Bigey and A. Arnaud, Appl. Environ. Microbiol., 1998, 64, 2844–2852 CAS.
- W. Wang, P. Baker and S. Y. K. Seah, Biochemistry, 2010, 49, 3774–3782 CrossRef CAS PubMed.
- N. P. Botting and D. Gani, Biochemistry, 1992, 31, 1509–1520 CrossRef CAS PubMed.
- R. Schulz, A, Enzyme Kinetics, Cambridge University Press, 1994 Search PubMed.
- G. Franceschini and S. Macchietto, Chem. Eng. Sci., 2008, 63, 4846–4872 CrossRef CAS.
- D. Telen, F. Logist, E. van Derlinden, I. Tack and J. van Impe, Chem. Eng. Sci., 2012, 78, 82–97 CrossRef CAS.
- G. Franceschini and S. Macchietto, AIChE J., 2008, 54, 1009–1024 CrossRef CAS.
- K. A. Johnson, FEBS Lett., 2013, 587, 2753–2766 CrossRef CAS PubMed.
- K. S. Anderson, J. A. Sikorski and K. A. Johnson, Biochemistry, 1988, 27, 7395–7406 CrossRef CAS PubMed.
- S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608 CrossRef CAS PubMed.
- S. Schwolow, F. Braun, M. Rädle, N. Kockmann and T. Röder, Org. Process Res. Dev., 2015, 19, 1286–1292 CrossRef CAS.
- J. Fagaschewski, D. Sellin, C. Wiedenhöfer, S. Bohne, H. K. Trieu and L. Hilterhaus, Bioprocess Biosyst. Eng., 2015, 38, 1399–1405 CrossRef CAS PubMed.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- H. B. Burch, M. E. Bradley and O. H. Lowry, J. Biol. Chem., 1967, 242, 4546–4554 CAS.
- J. V. Passonneau and O. H. Lowry, Enzym. Anal. A Pract. Guid., 1993, pp. 229–305 Search PubMed.
- H. Bisswanger, Practical Enzymology, Wiley-VCH Verlag GmbH & Co. KGaA, 2nd edn, 2011 Search PubMed.
- D. L. Purich and R. D. Allison, The enzyme reference: a comprehensive guidebook to enzyme nomenclature, reactions, and methods, 1st edn, 2003 Search PubMed.
- E. Pick and Y. Keisari, J. Immunol. Methods, 1980, 38, 161–170 CrossRef CAS PubMed.
- O. Erel, Clin. Biochem., 2005, 38, 1103–1111 CrossRef CAS PubMed.
- L. Rios-Solis, N. Bayir, M. Halim, C. Du, J. M. Ward, F. Baganz and G. J. Lye, Biochem. Eng. J., 2013, 73, 38–48 CrossRef CAS.
- L. Rios-Solis, P. Morris, C. Grant, A. O. O. Odeleye, H. C. Hailes, J. M. Ward, P. A. Dalby, F. Baganz and G. J. Lye, Chem. Eng. Sci., 2015, 122, 360–372 CrossRef CAS.
- F. Galgani, Y. Cadiou and G. Bocquene, Biotechnol. Bioeng., 1991, 38, 434–437 CrossRef CAS PubMed.
- S. Schätzle, M. Höhne, E. Redestad, K. Robins and U. T. Bornscheuer, Anal. Chem., 2009, 81, 8244–8248 CrossRef PubMed.
- L. A. DeLouise and B. L. Miller, Anal. Chem., 2005, 77, 1950–1956 CrossRef CAS PubMed.
- Y. Kim, K. G. Tanner and J. M. Denu, Anal. Biochem., 2000, 280, 308–314 CrossRef CAS PubMed.
- P. Baker, D. Pan, J. Carere, A. Rossi, W. Wang and S. Y. K. Seah, Biochemistry, 2009, 48, 6551–6558 CrossRef CAS PubMed.
- B. J. Burke and F. E. Regnier, Anal. Chem., 2003, 75, 1786–1791 CrossRef CAS PubMed.
- B. Faller, M. Cadène and J. G. Bieth, Biochemistry, 1993, 32, 9230–9235 CrossRef CAS PubMed.
- B. Kintses, Z. Simon, M. Gyimesi, J. Tóth, B. Jelinek, C. Niedetzky, M. Kovács and A. Málnási-Csizmadia, Biophys. J., 2006, 91, 4605–4610 CrossRef CAS PubMed.
- S. K. Hartwell and K. Grudpan, J. Anal. Methods Chem., 2012, 2012 Search PubMed.
- L. P. Saunders, W. Cao, W. C. Chang, R. A. Albright, D. T. Braddock and E. M. De La Cruz, J. Biol. Chem., 2011, 286, 30130–30141 CrossRef CAS PubMed.
- M. J. Todd and J. Gomez, Anal. Biochem., 2001, 296, 179–187 CrossRef CAS PubMed.
- G. D. Watt, Anal. Biochem., 1990, 187, 141–146 CrossRef CAS PubMed.
- I. Haq and B. Hill, Microcal, LLC Appl. note, 2002, p. 44 Search PubMed.
- M. L. Bianconi, Biophys. Chem., 2007, 126, 59–64 CrossRef CAS PubMed.
- E. L. Cussler, Diffusion: Mass Transfer in Fluid Systems, 1997, vol. Second Search PubMed.
- M. E. Young, P. A. Carroad and R. L. Bell, Biotechnol. Bioeng., 1980, 22, 947–955 CrossRef.
- J. W. Swarts, R. C. Kolfschoten, M. C. A. A. Jansen, A. E. M. Janssen and R. M. Boom, Chem. Eng. J., 2010, 162, 301–306 CrossRef CAS.
- K. Jähnisch, V. Hessel, H. Löwe and M. Baerns, Angew. Chem., Int. Ed., 2004, 43, 406–446 CrossRef PubMed.
- C. Wiles and P. Watts, Green Chem., 2012, 14, 38 RSC.
- R. L. Hartman and K. F. Jensen, Lab Chip, 2009, 9, 2495–2507 RSC.
- R. Wohlgemuth, I. Plazl, P. Žnidaršič-Plazl, K. V. Gernaey and J. M. Woodley, Trends Biotechnol., 2015, 33, 302–314 CrossRef CAS PubMed.
- J. I. Yoshida, H. Kim and A. Nagaki, ChemSusChem, 2011, 4, 331–340 CrossRef CAS PubMed.
- K. D. Nagy, B. Shen, T. F. Jamison and K. F. Jensen, Org. Process Res. Dev., 2012, 16, 976–981 CrossRef CAS.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1953, 219, 186–203 CrossRef CAS.
- R. Aris, Proc. R. Soc. London, Ser. A, 1956, 235, 67–77 CrossRef.
- D. L. Zechel, L. Konermann, S. G. Withers and D. J. Douglas, Biochemistry, 1998, 2960, 7664–7669 CrossRef PubMed.
- S. L. Lawson, W. W. Wakarchuk and S. G. Withers, Biochemistry, 1997, 36, 2257–2265 CrossRef CAS PubMed.
- J. P. Huddleston, G. K. Schroeder, K. A. Johnson and C. P. Whitman, Biochemistry, 2012, 51, 9420–9435 CrossRef CAS PubMed.
- J. A. Thomson and J. E. Ladbury, in Biocalorimetry 2: Application of Calorimetry in the Biological Sciences, ed. J. E. Ladbury and M. L. Doyle, 2004 Search PubMed.
- H. Fukada and K. Takahashi, Proteins: Struct., Funct., Genet., 1998, 33, 159–166 CrossRef CAS.
- M. W. Freyer and E. A. Lewis, Methods Cell Biol., 2008, 84, 79–113 CAS.
- J. J. Christensen, R. M. Izatt, L. D. Hansen and J. A. Partridge, J. Phys. Chem., 1966, 70, 2003–2010 CrossRef CAS.
- L. D. Hansen, J. J. Christensen and R. M. Izatt, Chem. Commun., 1965, 36–38 RSC.
- D. Vasić-Rački, Z. Findrik and A. Vrsalović Presečki, Appl. Microbiol. Biotechnol., 2011, 91, 845–856 CrossRef PubMed.
- G. Sin, J. M. Woodley and K. V. Gernaey, Biotechnol. Prog., 2009, 25, 1529–1538 CrossRef CAS PubMed.
- W. R. Berendsen, G. Gendrot, A. Freund and M. Reuss, Biotechnol. Bioeng., 2006, 96, 883–892 CrossRef PubMed.
- S. D. Schaber, D. I. Gerogiorgis, R. Ramachandran, J. M. B. Evans, P. I. Barton and B. L. Trout, Ind. Eng. Chem. Res., 2011, 50, 10083–10092 CrossRef CAS.
- S. D. Schaber, S. C. Born, K. F. Jensen and P. I. Barton, Org. Process Res. Dev., 2014, 18, 1461–1467 CrossRef CAS.
- M. Scheer, A. Grote, A. Chang, I. Schomburg, C. Munaretto, M. Rother, C. Söhngen, M. Stelzer, J. Thiele and D. Schomburg, Nucleic Acids Res., 2011, 39, 670–676 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2016 |