Use of a card sort task to assess students' ability to coordinate three levels of representation in chemistry
Stefan M.
Irby
ab,
Andy L.
Phu
a,
Emily J.
Borda
*a,
Todd R.
Haskell
c,
Nicole
Steed
a and
Zachary
Meyer
a
aDepartment of Chemistry, Western Washington University, Bellingham, WA, USA. E-mail: bordae@wwu.edu
bDepartment of Chemistry, Purdue University, West Lafayette, IN, USA
cDepartment of Psychology, Western Washington University, Bellingham, WA, USA
First published on 25th January 2016
Abstract
There is much agreement among chemical education researchers that expertise in chemistry depends in part on the ability to coordinate understanding of phenomena on three levels: macroscopic (observable), sub-microscopic (atoms, molecules, and ions) and symbolic (chemical equations, graphs, etc.). We hypothesize this “level-coordination ability” is related to the formation and use of principle-based, vs. context-bound, internal representations or schemas. Here we describe the development, initial validation, and use of a card sort task to measure the level-coordinating ability of individuals with varying degrees of preparation in chemistry. We have also developed a novel method for generating two-dimensional sorting coordinates which were used to arrange participants along a hypothetical progression of level-coordination ability. Our findings suggest the card sort task shows promise as a tool to assess level-coordination ability. With the exception of graduate students, participant groups on average progressed from sorting by level of representation toward sorting by underlying principle. Graduate students unexpectedly sorted primarily by level of representation. We use these data to form initial hypotheses about a typical process for the development of level-coordination ability and schema formation. In doing so, we demonstrate the usefulness of our task paired with sorting coordinate analysis as a tool to explore the space between novice and expert behavior. Finally, we suggest potential uses for the task as a formative assessment tool at the classroom and program levels.
Introduction
Since the introduction of the “chemistry triplet” over three decades ago (Johnstone, 1982), expertise in chemistry has been associated with the ability to coordinate understanding on three levels: macroscopic, submicroscopic, and symbolic (Gilbert and Treagust, 2009; Taber, 2013). Chemistry “experts” transition readily between these three levels (Johnstone, 1982; Kozma et al., 2000), but this process is not necessarily intuitive to novices (Rappoport and Ashkenazi, 2008). A lack of fluency with the chemistry triplet may be related to difficulty in developing conceptual understanding (Johnstone, 1982; Rappoport and Ashkenazi, 2008) and over-reliance on algorithmic procedures while solving chemistry problems (Nakhleh, 1992; Cracolice et al., 2008). Little is known about how individuals develop “level-coordination ability,” and what factors are necessary in its development. The purpose of this study is to design a tool to diagnose an individual's level-coordination ability and to use this tool to arrange individuals along a hypothetical progression for its acquisition. The information gathered from such a tool could help track the development of level-coordination ability in students and explore factors that may be correlated with its development.Literature review
Coordinating the three levels of representation
The three “worlds” of chemistry were first identified by Johnstone (1982) as a potential source of difficulty for students learning chemistry. These worlds are: (1) macroscopic, which describes observable phenomena; (2) submicroscopic, which consists of atomic and molecular models; and (3) symbolic, in which the submicroscopic models and observable data are expressed symbolically, e.g., through chemical equations and graphs (Gilbert and Treagust, 2009; Taber, 2013). Often called “Johnstone's triangle” or the “chemistry triplet,” this framework has become a powerful way to conceptualize the challenges and affordances of chemistry as a discipline, as well as to guide approaches to teaching and learning chemistry. The development of expertise in chemistry has been suggested to hinge, to some degree, on students' ability to link the corners of the chemistry triplet (Gabel, 1999; Gilbert and Treagust, 2009). For example, in a study by Jaber and BouJaoude (2012), students performed well on problems expressed on the symbolic level, but poorly on problems that required integration between two or more levels of representation.The ability to decode external representations in chemistry is a skill in itself. Research suggests decoding is not straightforward, particularly from the symbolic to the submicroscopic level (Kern et al., 2010). However, students' difficulty in coordinating the apexes of the chemistry triplet may not entirely be a matter of decoding representations or translating one external representation into another. Talanquer (2011), Taber (2013), and Johnstone (1982) argue the different forms of representation are different ways of understanding a chemical phenomenon, and that each level is associated with a different purpose. Others add to this idea by describing an interplay between external representations and students' internal, or mental, representations (Rapp and Kurby, 2008). Such internal representations, often called schemas, have been described as “a large unit of organized information” (Galotti, 2014, p. 177) and “well-integrated chunks of knowledge” (Eysenck and Keane, 2005, p. 383). According to Revlin (2012), schemas change with the acquisition of new knowledge and experiences. Early in a learning experience, our schemas tend to be dominated by superficial or context-bound characteristics, whereas later they become more abstract and principle-based. Schemas appear to become more principle-based the more experience students have with varied types of learning tasks, and principle-based schemas predict better success in problem solving (Chen, 1999).
One aspect of generating a more principle-based schema is called re-representation (Gentner, 2005), in which a new, more abstract idea is constructed to capture similarities between concepts that are not similar on their surface. Relevant abstract ideas in chemistry might include the concepts “reactant” and “product” when coordinating a chemical equation and a small particle representation showing the same reaction. On this view, expertise in chemistry requires not just the ability to translate between different levels of external representation, but the development of internal schemas that are not directly present in a single component of the chemistry triplet.
When individuals' conceptual frameworks are well organized and guided by general principles, they are able to more easily retrieve and apply concepts appropriately (Simon and Newell, 1972; Chi, 2006). This claim is supported by a study in which participants were asked to sort cards depicting a variety of physics problems. While physics graduate students categorized the problems based on underlying principles such as conservation of momentum, introductory physics students sorted them based on surface features such as the presence of an inclined plane (Chi et al., 1981). Other studies suggest symbolic representations such as chemical equations and graphs can serve as distractors, becoming over-relied upon when conceptual understanding is under-developed (Kozma, 2000; Rappoport and Ashkenazi, 2008), and causing students to rely on algorithmic approaches to problem solving (Kozma and Russell, 1997; Kozma, 2000).
In this study we use the chemistry triplet in two discrete, but related, ways. For the purposes of creating a card sort task similar to that used in Chi et al. (1981), we conceptualize the triplet as describing levels of external representation in which the three levels are present as drawings, cartoons, or equations on the cards. However, we use this card sort task to investigate individuals' internal representations, or schemas. Thus, we interpret an individual's external level-coordination ability, as measured by this card sort task, as evidence of the generality of his or her schemas: the grouping of different types of external representations under a single underlying principle is evidence of a principle-based schema.
While the importance of coordinating chemistry understanding on the three levels in Johnstone's triangle is generally acknowledged among chemistry education researchers, only one instrument is known by the authors to assess this construct as of the publication of this article. The Representational Systems and Chemical Reaction Diagnostic Instrument (RSCRDI, Chandrasegaran et al., 2007) requires students to choose between different explanations for chemical observations. The instrument was built from secondary students' responses during tasks and interviews meant to elicit the three levels of representation in students' reasoning.
Evaluating expertise
The idea of context-bound vs. principle-based schemas is related to the idea of expertise, which is defined in the cognitive science literature as the degree to which knowledge is organized in a coherent and useful way (Bédard and Chi, 1992). Card sort tasks, in which individuals group cards depicting a variety of problems and then describe their sorts in an interview (Chi et al., 1981; Hardiman et al., 1989; Mason and Singh, 2011; Wolf et al., 2012a, 2012b), are commonly used for evaluating expertise, and have been conducted in physics (e.g.Chi et al., 1981), biology (Smith et al., 2013), and chemistry (Kozma and Russell, 1997) contexts. In the latter study, chemistry experts sorted problems based on underlying principles, whereas novices sorted according to the most prominent type of representation.Other types of classification tasks have also been used to measure expertise in chemistry. Stains and Talanquer explored the categories college students created when classifying chemical substances (Stains and Talanquer, 2007) and reactions (Stains and Talanquer, 2008). With one exception (first term general chemistry), students' categories referred to fewer “explicit” (surface) features and more “implicit” (principle-based) features with more chemistry preparation. Further, Taber (1994) asked A-level (secondary) chemistry students to discriminate between cards in a three-card set (triad) depicting different chemical species. Students' responses were evidence of their “personal constructs” (p. 5), proposed to be similar to concepts. While some students focused on features of the representations in their personal constructs, others focused on more abstract, chemically meaningful features.
Analyses of card sort or other types of categorization tasks are often focused on looking for differences between pre-defined novice and expert groups (Chi et al., 1981; Hardiman et al., 1989; Smith et al., 2013). However, deciding how to categorize study participants has been problematic. For example, graduate students (the “experts” in Chi et al., 1981's study) have behaved in other studies more like novices when compared to faculty (Rappoport and Ashkenazi, 2008; Mason and Singh, 2011). Other classification systems consisting of intermediate classes between novice and expert (Dreyfus and Dreyfus, 1986; Chi, 2006; Rappoport and Ashkenazi, 2008), or in which groupings were determined based on performance on some other measure (Heyworth, 1999) have been proposed. However, most novice/expert or novice/intermediate/expert studies focus on differences between these groups; fewer studies focus on processes by which expertise is acquired (Lajoie, 2003; Stains and Talanquer, 2008).
Study description and motivation
The greater capability of “experts” compared to “novices” in coordinating the corners of the chemistry triplet, along with the importance of this skill in gaining expertise in chemistry, has been well established (e.g.Gilbert and Treagust, 2009). However, few tools exist to investigate its development. Without knowledge about how this skill develops over time, it is difficult to develop instructional interventions aimed at facilitating its acquisition. Here we take a first step toward exploring the development of “level-coordination ability” using a card sort task. We define level-coordination ability as an individual's ability to recognize underlying principles expressed through different levels of representation.We hypothesize an individual can recognize the principles behind a problem without necessarily having the skills to solve it. Thus, we aim to develop an instrument to assess level-coordination ability as an isolated construct, inasmuch as it can be separated from factual knowledge and problem-solving skills. The RSCRDI (Chandrasegaran et al., 2007), which is scored on correct responses to specific questions, assesses level-coordination ability alongside these more technical types of knowledge and skills, which could increase with more preparation even if level-coordination ability does not. Therefore, it is critical to have a tool that measures one's ability to represent problems in an abstract fashion, independently (to the degree possible) of content knowledge. Our task accomplishes this by asking participants only to categorize problems; not solve them. The absence of problem solving in our task also allows us to access a population with minimal experience in chemistry.
Our study takes advantage of the well-established use of card sort tasks to investigate expertise. We take the card sort a step further first by organizing our task specifically around the chemistry triplet. Although a card sort task has been used to investigate how students use certain chemistry-based representations (Kozma and Russell, 1997), this study did not characterize the representations in terms of the chemistry triplet, a widely-valued framework in chemistry. Secondly, we have developed a novel method for using card sort data to arrange individuals drawn from six groups representing a range of formal preparation in chemistry (Table 1) along a hypothetical progression. Similar to Stains and Talanquer (2007, 2008), we did not begin with the assumption that each group is assigned to a specific level of expertise, such as the five levels defined by Dreyfus and Dreyfus (1986). Rather, we hypothesized these groups would be well positioned to generate data that would place them differently along a continuum of expertise.
| Participant group | n (card sort) | n (RSCRDI) |
|---|---|---|
| a Representational systems and chemical reaction diagnostic instrument (Chandrasegaran et al., 2007). All RSCRDI participants were part of the card-sort sample. | ||
| No chemistry (NC) | 11 | 3 |
| High school (HS) | 28 | 10 |
| General chemistry (GC) | 17 | 6 |
| Upper-division (UD) | 5 | 2 |
| Graduate student (GS) | 4 | 4 |
| College faculty (CF) | 5 | 4 |
| Total | 70 | 29 |
Underpinning the creation of the card sort task is the hypothesis that translating between the levels of external representation to identify a common idea is evidence of principle-based internal schemas. As such, we consider the levels of external representation (macro, submicro, symbolic) on our cards to be to be surface features. While it is necessary to decode these representations to understand the problem, such decoding does not mean the underlying principles leading to a solution have been recognized. The recognition and decoding of external representations is therefore a learned skill that is necessary, yet insufficient, for the development of principle-based schemas. Thus, organization of the cards by level of representation is indicative of a lower level of expertise, rather than absence of expertise. In reality, we do not see these two modes of categorization (representation- vs. principle-based) as mutually exclusive, nor do we see representations as surface features in chemistry writ large. We engineered our card sort to force one categorization at the expense of the other to allow us to investigate to what extent individuals could coordinate the levels of representation to recognize the underlying principle. Stains and Talanquer (2008) took a similar approach, considering both particle rearrangement and chemical behavior-type classifications of chemical reactions to be meaningful, but chemical behavior-type classifications more productive.
In sum, the novelty of the present study rests on the use of a well-established technique, a card sort task, to evaluate a specific component of expertise in chemistry: level-coordination ability. A tool for evaluating level-coordination ability as an isolated construct, and that can be accessed by a broad population, is needed. Finally, we describe a novel use of card sort data to “map” sorts along a hypothetical progression of development of level-coordination ability, which sets the stage for the exploration of the development of this skill over time.
Research questions and hypotheses
Two questions have guided this research:(1) Can a card sort task validly assess level-coordination ability?
(2) Can card sort data be used to distinguish individuals from each other along a hypothesized progression of level-coordination ability?
For question #1, evidence of validity consists of: (a) recognizability of the representations and principles present in the cards to individuals with a range of preparation in chemistry, (b) consistency with previous observations of increased recognition of underlying principles with increasing chemistry preparation (e.g.Kozma and Russell, 1997; Stains and Talanquer, 2008), (c) consistency between participants' sorts and their verbal justifications in post-sort interviews, and (d) consistency between sorts and scores on a validated instrument that measures level-coordination ability (Chandrasegaran et al., 2007). For question #2, we formulated a hypothetical progression which builds upon prior research showing the abandonment of surface features and adoption of principle-based categories with increasing chemistry preparation (Kozma and Russell, 1997; Stains and Talanquer, 2008). Our progression assumes the development of level-coordination ability in a linear fashion, where representation-based schemas are abandoned and principle-based schemas are adopted gradually and at the same rate throughout one's chemistry preparation. We then use card sort data to arrange participants with respect to this progression.
Methods
Participants
All research participants were drawn from a mid-sized regional university in the Pacific Northwest. Participants were grouped into six categories (Table 1) based on their level of chemistry preparation: No Chemistry (NC), students with no formal chemistry education (n = 11); High School (HS), students having completed only secondary-level chemistry coursework (n = 28); General Chemistry (GC), students having completed 1–3 terms of a 3-term undergraduate general chemistry sequence (n = 17); Upper Division (UD), students having completed one or more course beyond general chemistry (n = 5); Graduate Student (GS), master's-level graduate students (the university in this study does not grant doctoral degrees) (n = 4); and College Faculty (CF), chemistry professors (n = 5). The total number of participants was 70. All NC, HS, and GC subjects were solicited using a psychology research subject pool and received credit toward their psychology course for participating. Subjects in the UD, GS, and CF participant groups volunteered to participate. All participants consented to the study under the approved human subjects protocol. A sub-sample of each group also completed the Representational Systems and Chemical Reaction Diagnostic Instrument (Chandrasegaran et al., 2007). This task was not part of the original study solicitation and was completed voluntarily after it was added.Instruments
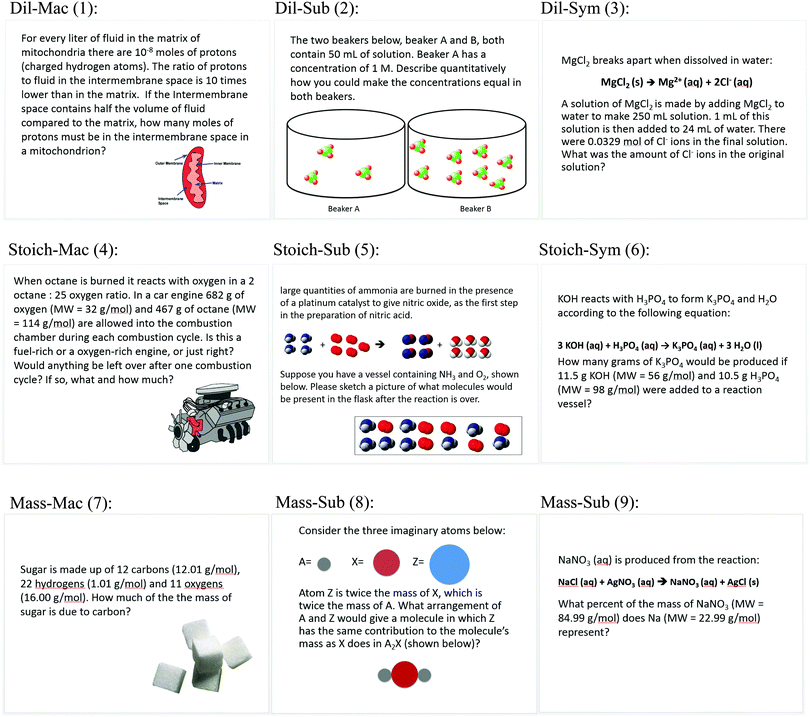
The nine cards in the card sort task (Table 2) crossed the type of external representation (macroscopic, submicroscopic, symbolic) with principle(s) needed to solve the problems (dilution, stoichiometry, percent mass). The principles represent content from the first of a three-course general chemistry sequence at the institution of this study. They were chosen because of their prevalence in secondary and tertiary general chemistry curricula and likelihood that they would take place near the beginning of a general chemistry sequence. The principles are also not straightforward to distinguish from one another on the basis of representation, as opposed to, for example, a question on atomic structure vs. one about stoichiometry.| Topic (principle(s) needed to solve problem) | Level of representation | ||
|---|---|---|---|
| Macroscopic | Sub-microscopic | Symbolic | |
| Dilution (Concentration is defined by a ratio of solute to solution. Changing the amount solute or solvent changes the concentration.) | Dil-Mac | Dil-Sub | Dil-Sym |
| Limiting reactant stoichiometry (The reactant present in smallest stoichiometric abundance limits the amount of product that can be formed in a chemical reaction. Stoichiometric coefficients can be used to relate the amounts of any two substances in a chemical reaction.) | Stoich-Mac | Stoich-Sub | Stoich-Sym |
| Percent mass (Each atom type has a unique mass. The number and type of each atom in a molecule determines to what extent the mass of the molecule is represented by a single element.) | Mass-Mac | Mass-Sub | Mass-Sym |
All macroscopic (Mac) cards depicted a visually observable object: a car engine, sugar cubes, and a mitochondrion (considered “macroscopic” for our purposes, because it represents bulk, rather than small particle, behavior). All submicroscopic (Sub) cards depicted space-filling models of atoms and molecules with no associated elemental symbols. All symbolic (Sym) cards displayed chemical equations. Chemical formulas were present only on the Sym cards. On all other cards, names of chemical substances were spelled out. Further, the questions themselves were written to emphasize the use of one of the levels in solving the problem. For example, the Mass-Mac question asks about the bulk percentage of carbon in sugar, while the Mass-Sub question asks about the percent mass represented by individual atoms in a molecule, and the Mass-Sym question is phrased in terms of units in a chemical formula. Sample card sorts are shown in the results section. The complete card set is provided in Appendix 1.
Problems were initially adapted from a widely-used general chemistry textbook (Ebbing and Gammon, 2013). The final card set was developed through five rounds of piloting and editing. Modifications consisted of eliminating potentially leading language, making all the stoichiometry questions contain a limiting reactant, and modifying the prompt to maximize understanding of the task while simultaneously avoiding leading individuals toward a particular sort. The final version of the prompt asked participants to sort the cards as if they were incorporating practice problems into a general chemistry textbook, based on the concepts students are expected to use to solve them.
The Representational Systems and Chemical Reaction Diagnostic Instrument (RSCRDI), administered to 41% of our study sample, is a questionnaire designed to assess level-coordination ability at the general chemistry level (Chandrasegaran et al., 2007). This questionnaire is a two-tiered instrument, in which each question assessing a concept is paired with another question asking the individual to choose an explanation that matches his or her choice. The intent of using the RSCRDI is to add information about the validity of the card-sort task by determining whether, and to what extent, performance on the two assessments is correlated. A discrimination index test revealed that 12 of 15 items were considered acceptable (Chandrasegaran et al., 2007).
Data collection and analysis
Before engaging in the card-sort task, participants from the RSCRDI subgroup (Table 1) were instructed to complete the instrument individually, in the absence of the researcher. All participants were then given the cards, read the prompt, and told to limit their sort to 2–8 mutually exclusive groups. While participants sorted the cards, the researcher again left the work area to minimize perceived pressure and to avoid unintentionally leading the participant. After participants sorted the cards, the researcher returned and asked them to describe and justify their sorts. All post-sort interviews were video and audio recorded then transcribed. Participants were given as much time as they wanted to complete each task.To analyze general sorting patterns, the number and distribution of “canonical groups,” 3-card groups that contained all of one representation or principle to the exclusion of the rest, as well as the number of pairings of each card with each other card (whether or not in a larger group), were recorded. As a measure of the recognizability of the representations and principles, the fraction of unexpected pairings (pairings that shared neither a representation nor a principle) was calculated for each participant group. The card pairing data were then used to determine the number of representation-based, principle-based, and unexpected pairings. To allow for comparison, each of these numbers was divided by the maximum number of possible pairs of a single type our study sample could have made. For each pair type (e.g. macroscopic), 3 opportunities to make that pair (Mac-Dil/Mac-Stoich, Mac-Dil/Mac-Mass, Mac-Stoich/Mac-Mass) times 70 participants is 210 total opportunities. The number of each type of pairing divided by the maximum number of possible pairings is called “percent of maximum possible pairings.”
To facilitate the investigation of sorts along a progression, a procedure was created to represent each participant's sorting in two dimensions, where the first dimension represents the extent to which the participant sorts according to representation and the second represents the extent to which he or she sorts according to principle. To compute the value on the representation dimension, we first considered each possible pair and determined whether or not those cards would be grouped together in a canonical representation-based sort. We then examined the participant's actual sort and counted the pairs that were grouped differently from the canonical sort (either grouped together when the canonical sort has them in different groups, or placed in different groups when the canonical sort has them grouped together). This computation was repeated for the principle dimension. This protocol generates two “coordinates,” similar to “edit distances” described in Smith et al. (2013). The first coordinate describes the “distance” from sorting solely by representation, and the second describes the “distance” from sorting solely by principle (see Appendix 2 for a detailed example). When plotted such that the former is on the x-axis and the latter on the y-axis, the coordinate (0,18) represents a complete representation-based sort, whereas (18,0) represents a sort entirely by principle. These two sorts are called “anchor sorts.” After participants' 2-dimensional sorting coordinates were computed, the individual and average coordinates for each group were plotted to reveal any trends in sorting.
Sorting coordinates were also compared to a “canonical sort line” that connects the anchors. This line represents a hypothetical progression of development of level-coordination ability in which adoption of principle-based sorts takes place at the same “rate” as abandonment of representation-based sorts. Because all coordinates on this line add up to 18, the sum of the two coordinates minus 18 is a measure of the degree of unexpected sorting. This value, called the canonical sort distance, was calculated for each group.
The RSCRDI was scored according to percentage of correct answers on the 12 acceptable items, where the participant must have answered both parts of each two-tiered item correctly for the item to be considered correct. The RSCRDI scores were plotted against y-axis sorting coordinates (distance from underlying principle), and a Pearson's r was calculated to evaluate the strength and direction of the relationship, if any, between the two. The second coordinate was used instead of the first because it is more indicative of expert performance: an individual can avoid sorting the cards by representation but still may not recognize the underlying principles.
In order to further investigate the validity of the card-sort task, transcripts from all post-card sort interviews were blinded, shuffled and coded. The transcripts were then searched for phrases the researchers felt could be unambiguously associated with a single level of representation or underlying principle. Ambiguous phrases or phrases that indicated some other type of organizing scheme were coded as “Other.” Phrases indicating no scheme (e.g. “I don't know”) were not given a code. The coding rubric that emerged from this process was then applied to all transcripts by two researchers (NS and ZM), who coded each phrase that expressed a reason for grouping two or more cards together (descriptions of individual cards were not coded). Representation, Principle, and Other codes were not mutually exclusive; a phrase could receive more than one code. Coding proceeded iteratively, such that the two researchers coded 5–10 transcripts, discussed discrepancies and reached a consensus set of codes, then coded 5–10 more transcripts, and so on. Overall interrater reliability was 68%. The master list associating ID numbers to membership in the six participant groups was consulted only after all final codes were assigned, at which point the distribution of codes between participant groups was recorded.
Results
Sorting patterns
A total of 283 card groups were created by the study participants. Samples of the most common sorts are shown in Fig. 1, which aligns the sorts with sample justifications and their codes (Representation, Principle, or Other). Because the data were blinded before coding, codes from verbal justifications did not always match the sorts themselves. At least one quote representing each code assigned for each sort is shown. | ||
| Fig. 1 Sample card sorts with sample verbal justifications. Codes, principle-based (P), representation-based (R), and O (other), followed by participant group, are in parentheses after each quote. | ||
Canonical representation-based groups, in which all three cards with the same representation were grouped together and combined with no other cards (e.g. Dil-Sym/Stoich-Sym/Mass-Sym), were observed 26 times (6 NC, 12 HS, 4 GC, 4 GS). Canonical principle-based groups (e.g. Mass-Mac/Mass-Sub/Mass-Sym) were observed 32 times (1 NC, 9 HS, 5 GC, 3 UD, 14 CF). The most frequently observed canonical representation-based sort was symbolic (observed 18 times), while the most frequently observed canonical principle-based sort was by mass percent (observed 13 times). The most frequently observed unexpected sorts consisted of Mass-Mac being grouped with all three symbolic cards (observed 9 times) and Dil-Mac being grouped with Mass-Sub (observed 7 times).
As a measure of the recognizability of the representations and principles, the fraction of unexpected pairings was calculated for each participant group. Because the probability of “expected” (representation + principle-based) and unexpected pairs are equal (18 each), the fraction of unexpected pairs would be 50% for random sorting. This fraction was 21% overall: 16% for NC, 21% for HS, 29% for GC, 18% for UD, 24% for GS, and 0% for CF.
Categorization of card pairs (Table 3) reveals about the same frequency of representation- and principle-based pairings, whereas unexpected pairings were much less frequent. Further analysis of each of the first two categories reveals over half of the representation-based pairings were based on symbolic representations. Principle-based pairings were divided more evenly between the three different sub-types; however, there was still an uneven distribution. Mass percent and stoichiometry were the most and least frequent principle-based pairings, respectively.
| Number of pairings | Percent of maximum possible pairings (%) | |
|---|---|---|
| Macroscopic | 43 | 20 |
| Submicroscopic | 52 | 25 |
| Symbolic | 132 | 63 |
| Total representation | 227 | 36 |
| Dilution | 68 | 32 |
| Stoichiometry | 58 | 28 |
| Mass percent | 82 | 39 |
| Total principle | 208 | 33 |
| Unexpected | 115 | 9 |
Sorting coordinates
The purpose of generating sorting coordinates is to discriminate between sorting patterns along a hypothesized progression. Fig. 2 shows plots of individual participants' coordinates, in which the y-axis represents the distance from sorting entirely by underlying principle and the x-axis represents the distance from sorting entirely by level of representation. “Anchor” representation-based sorts (all nine cards sorted by our three types of representation) were observed three times, twice from HS participants and once from a GS participant, while anchor principle-based sorts were observed four times, all by CF participants. Variation in sorting patterns was observed within each sample, and in some cases spanned much of the “distance” between representation- and principle-based sorts.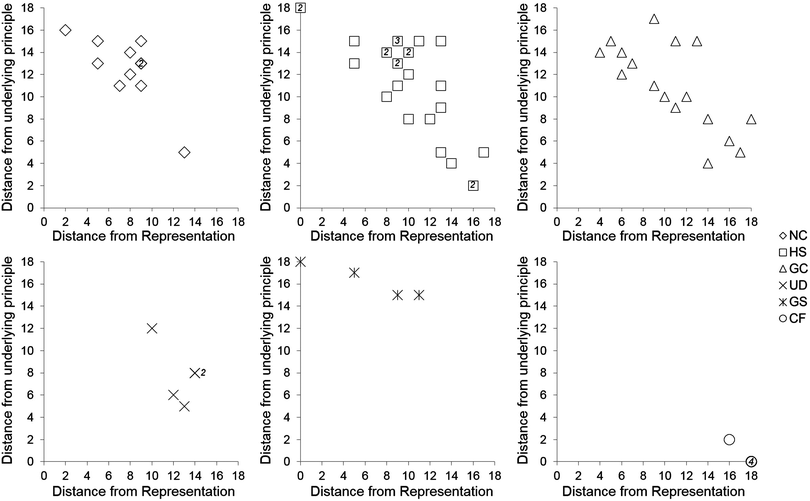 | ||
| Fig. 2 Plots of individual sorting coordinates by participant group. Each symbol represents an individual, except when it is accompanied by the number of individuals sharing the sorting coordinate. | ||
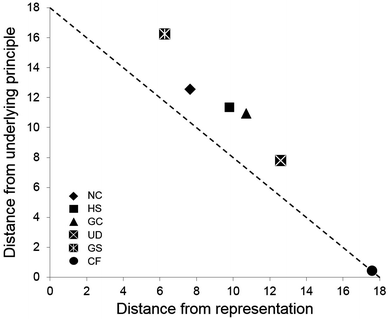
On average, CF participants sorted closest to underlying principle, while NC participants displayed an average sorting pattern closer to level of representation than underlying principle. In between these two groups, the HS, GC, and UD participants' average sorts progressed away from representation and toward underlying principle. Interestingly, the GS participants sorted most closely, on average, to the level of representation anchor point than any other group (Fig. 3). The only discernable pattern in canonical sort distance involves increased distances with increasing chemistry preparation, with the exception of the UD and CF groups (Table 4).
| Classification | Average sorting coordinates | Mean canonical sort distance | Mean RSCRDI score, % (SD) | |
|---|---|---|---|---|
| Distance from representation (SD) | Distance from underlying principle (SD) | |||
| a Only 2 UD participants completed the questionnaire, and received the same score. | ||||
| NC | 7.6 (2.9) | 12.6 (3.0) | 2.2 | 13.9 (4.8) |
| HS | 9.8 (4.1) | 11.4 (4.5) | 3.2 | 11.7 (13.7) |
| GC | 10.7 (4.3) | 10.9 (3.9) | 3.6 | 34.7 (11.1) |
| UD | 12.6 (1.7) | 7.8 (2.7) | 2.4 | 41.7 (0.0)a |
| GS | 6.3 (4.9) | 16.3 (1.5) | 4.6 | 50.0 (34.0) |
| CF | 17.6 (0.9) | 0.4 (0.9) | 0 | 87.5 (10.8) |
RSCRDI
Scores on the RSCRDI paralleled level of chemistry preparation (Table 4). When individual RSCRDI scores were plotted against individual distance from underlying principle scores (second coordinate), a statistically significant, moderate, negative correlation was observed, such that greater distance from the principle anchor was associated with lower RSCRDI scores, r(27) = −0.57, p = 0.001, R2 = 0.32. When the anomalous GS group is removed from this analysis, the correlation is strong, statistically significant, and negative: r(23) = −0.79, p < 0.001, R2 = 0.62.Qualitative data
In coding the transcripts, we encountered several phrases that were either ambiguous or that referenced an unexpected dimension of categorization (e.g. problem difficulty). These were given the code “other.” The phrase “balancing equations” was placed in this category because it was impossible to determine whether it was meant as an expression of the symbolism present on the cards (after the codes were matched with the participants, we discovered several students who had a symbol-based group used this phrase to describe it), as a tool needed to solve the problem, or as an expression of an underlying principle, such as the conservation of mass. The codes placed in the “Representation” or “Principle” category were only those that could be categorized as such with fairly little ambiguity (Table 5).| Code | Description (key phrases) | Sample quote |
|---|---|---|
| R-Submicro | Entities and phenomena impossible to directly observe (atoms, molecules, ions, dissociating) | “… my general theme for this chapter would be drawing molecules.” |
| R-Macroscopic | Observable properties or processes (physical changes, burning, engines) | “It had to do with … why combustion engines work.” |
| R-Symbolic | Abstract symbols (chemical formulas, chemical equations) | “… they have reaction models, I guess. Or equations.” |
| P-Dilution | Ratio between units of solute and units of solution (molarity, concentration) | “They are all describing the number of particles or target particles per unit volume” |
| P-Stoichiometry | Quantities of substances related by a chemical reaction (limiting reagent, amount of substance, change in mass) | “These two have to do with the amount of something in a substance before and after a reaction.” |
| P-Percent mass | Ratio between mass of a part to mass of the whole (percent mass, mass ratio) | “… problems involving the amount of mass involved in an equation of a certain compound.” |
| Other | Sorts not based on representation or principle (word problem, difficulty, application problem, calculation, qualitative, mathematical, conceptual) | “… this seemed like pretty basic information that would go at the beginning of the textbook.” |
| Unclear whether the justification was made on the basis of a representation or principle (reaction, chemical, biology, osmosis, combustion, dimensional analysis, unit conversion, ratio, balancing equations) | “… using a lot of molarity and molecular weight ratios.” | |
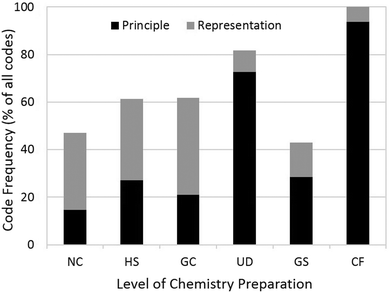
A total of 265 codes were assigned, 85 Representation, 79 Principle, and 101 Other. Examination of the distribution of code sub-categories revealed a low percentage of R-Mac codes (7%) when compared to R-Sub (42%) and R-Sym (49%). This is likely due to ambiguity in language: it was difficult to find words or phrases in the transcripts that we could confidently assign to this level of representation to the exclusion of the either the other two levels or a principle. We suspect some of the words or phrases in the “other” category (e.g. biology, application problem) might be attempts to describe some of the macroscopic “cover stories” of these problems. Therefore, this level of representation might be under-represented in our coding system. The distribution of Principle-based codes was more even: 38% P-Dil, 34% P-Stoich, and 28% P-Mass. The lower frequency of the latter code, especially compared to the higher frequency of percent mass sorts compared to other principle-based sorts, is likely due to under-specificity when the word “mass” was used. Because mass played a part in other questions, we were careful to assign P-Mass only when this word was used alongside an expression of a fraction (e.g. “percent,” “ratio”). Therefore, P-Mass might also be under-represented.
With the exception of the GS group, the frequency of categorizable (R- or P-) phrases increased with increasing level of preparation in chemistry (Fig. 4). Further, the majority of the categorizable codes for the three lower-preparation groups (NC, HS, and GC) were by representation, while for the UD, GS, and CF groups the majority of categorizable codes were by principle.
Discussion
Card-sort task as an assessment of level-coordination ability
Initial results suggest our card sort task shows promise as a method of assessing level-coordination ability for undergraduates with a range of chemistry preparation. Although canonical representation- and principle-based card groupings were rare (26 and 32, respectively, out of 283), and few individuals demonstrated anchor representation (3) or principle (4)-based sorts, the frequency of representation- or principle-based pairings was much higher than unexpected pairings (Table 3). Furthermore, the fraction of unexpected sorts was less than 30% for all participant groups, and even lower (16% and 21%) for participants with the least amount of chemistry preparation, the NC and HS participants, respectively. These data suggest our intended representations and principles (Table 2) were recognizable to our study participants.Although small sample sizes prohibit the use of inferential statistics to determine between-group effects, quantitative data suggest a higher degree of principle-based sorting with increased chemistry preparation, with the exception of the GS group. The distribution of canonical card groupings suggests that, with the exception of GS, representation-based sorts decrease and principle-based sorts increase with increasing chemistry preparation. Sorting coordinates also reflect this trend, and further suggest participants with intermediate (UD) and high (CF) chemistry preparation appear to sort primarily by underlying principles, whereas those with less chemistry preparation (NC) appear to sort primarily by level of representation. Further, results from the RSCRDI (Chandrasegaran et al., 2007) add evidence that the card sort validly assesses level-coordination ability for all but the GS group: we observed a strong negative correlation between the distance from principle coordinate and RSCRDI scores when this group was excluded.
Verbal justifications were roughly consistent with the quantitative data for all groups but GS. For the three groups with less chemistry preparation (NC, HS, and GC), the majority of categorizable codes were representation-based, whereas for the higher-preparation groups (UD, GS, and CF) they were principle-based. For the GS group, these data conflict with the highly representation-positioned average sorting coordinates. Finally, the distribution of codes for the HS and GC groups were similar, mirroring their close positions on the 2D plot and similar RSCRDI scores. These data suggest the card sort task may not discriminate well between these two groups. In sum, consistency between the qualitative and quantitative data add validity to the card-sort task as a measure of level-coordination ability.
Use of card-sort data to arrange participants along a hypothetical progression
Our novel use of sorting coordinates enabled us to arrange participants along a hypothetical linear progression for the development of level-coordination ability. The sorting coordinates suggest that, on average, participants with more chemistry preparation are closer to the principle-based anchor than those with less chemistry preparation, with the exception of the GS group. This result is consistent with previous studies (Kozma and Russell, 1997; Stains and Talanquer, 2007, 2008) suggesting the adoption of more principle-based categories or schemas with more chemistry preparation. Although the observed trend from the sorting coordinates does not precisely match the trends we observed in the verbal justifications, both sets of data converge on the observation that, on average, NC, HS, and GC participants sorted mostly by representation and UD and CF participants sorted mostly by underlying principle. Again, graduate students did not follow this trend, showing a majority of principle-based justifications but representation-based sorting coordinates.While we can describe a general trend using the average sorting coordinates, a notable result is the large variability of sorts within the NC, HS, and GC groups (Fig. 2, Table 3 SD values). Stains and Talanquer (2007, 2008) gathered similar results, noting a range of formal chemistry preparation in each level of expertise they defined from their results. Variability and overlap between groups serves as evidence that level-coordination ability is probably only one facet of expertise in chemistry, other possibilities being factual knowledge and problem-solving skills, to the extent they are separable from level-coordination ability. Furthermore, we might expect level-coordination ability to vary widely within a population due to variability of instruction in this skill. The ability of the card sort task to distinguish between individuals in a single group is evidence for its potential as a formative assessment tool.
Finally, it is noteworthy that the average sorting coordinates for all groups except CF were some distance from the canonical sort line (Fig. 3). This line represents a linear progression from representation- to principle-based sorting, in which the former is abandoned at the same rate as the latter is adopted. The frequency of unexpected sorts and “other” codes in the verbal justifications could indicate that some students were: (a) able to recognize the underlying principles but reluctant to give up representation-based groupings, or (b) able to recognize representation as a surface feature but had difficulty recognizing the underlying principles. Results from Taber's (1994) “triad” study support the latter possibility, suggesting some students were able to recognize representation-based features but chose not to express them due to their perceived triviality. The extent to which these potential explanations are true probably depends upon the sample: participants with less chemistry experience might be expected to fit the latter typology, while those with emerging expertise might be expected to fit the former. Using “framed” card sorts, Smith et al. (2013) established that when told what the underlying principles were, expert participants shifted toward more sorting by underlying principle, whereas novices shifted toward more unexpected sorting patterns.
Canonical sort distances reflect differential rates of abandonment of representation-based sorts and adoption of principle-based sorts, producing “hybrid” sorts, or entirely different sorting criteria, producing “unexpected” sorts. In our study, canonical sort distances increase with increasing chemistry experience with the exception of UD and CF participants. This trend may have been produced by chance, or it may be indicative of participants recognizing representations as surface features earlier than they were able to identify our underlying principles. The decrease in uncategorizable verbal justifications with increasing chemistry preparation, with the exception of the GS group, conflicts to some degree with the apparent pattern in canonical sort distances, suggesting the “other” codes were due in large part to imprecise language, making participants' sorting systems simply unrecognizable to the research team. Although additional research should be done to further dissect the meaning of canonical sort distances, the present study demonstrates the novel analyses that can be conducted with card sort data when sorting coordinates are used to quantify results.
Graduate students
Our data suggest the card sort task may not be a valid measurement tool for graduate students. The GS group did not take the “position” in the hypothetical progression that we expected (Fig. 3), instead sorting the cards mostly according to level of representation. Mason and Singh (2011) gathered similar results, concluding graduate students should not be categorized with experts. However, our results stand in contrast to results from a classification task in which graduate students were observed at an advanced level of expertise, with more principle-based classifications compared to several undergraduate groups among whom differentiation was difficult (Stains and Talanquer, 2008). It is possible that our small GS sample was biased toward poor level-coordination ability due to chance. On the other hand, these individuals may have approached the task from a relatively new instructor perspective (all GS participants were teaching assistants in general chemistry labs), and sorted according to how they might help a student employ the representations during problem-solving. Some of the GS participants' justifications, though not systematically coded for this element, did include ideas about how they would help a student solve the problem(s). Another possibility is that GS participants were undertaking a large-scale reorganization of their knowledge as first year master's students, compared to a more gradual reorganization in undergraduates. This idea of strong versus weak restructuring has been proposed in the conceptual change literature (Hewson, 1981; Carey, 1987). That the GS group had the largest canonical sort distance (Table 3), suggesting a high degree of hybrid or unexpected sorting, supports this hypothesis. If this strong restructuring hypothesis is true, the development of level-coordination ability may be less linear than we think, including the possibility that students fall back on surface features while attempting to manage a large-scale conceptual restructuring. This interpretation is consistent with results from a chemical reactions classification task, in which Stains and Talanquer (2008) found general chemistry students to perform at an anomalously high level and hypothesized that “… advanced levels of expertise in chemical classification do not necessarily evolve in a linear and continuous way with academic training” (p. 790).The majority of categorizable codes from GS participants' verbal justifications were principle-based, which appears to conflict with their representation-based sorting coordinates. It is possible that most of the “other” codes reflect representation-based justifications. On the other hand, these data could represent a choice to sort by representation, due to the graduate students' teaching roles, while reflecting a value on principle-based sorts as the GS participants gain competence in chemistry. According to Dreyfus and Dreyfus (1986), the third of five steps toward expertise, called “competence,” involves choosing an organizing plan for a task, rather than rote application of learned skills and knowledge. If the GS group were placed at this level, their anomalous results could be indicative of an attempt to choose different plans for their different roles.
Finally, GS participants performed on the RSCRDI as one might expect, between UG and CF (Table 3), suggesting either that their representation-based sorts were a conscious choice, as above, or that they may have used their content knowledge in place of level-coordination ability to respond to RSCRDI items. That our card sort task was able to identify the GS students as potentially anomalous where the RSCRDI did not is evidence of its potential for assessing level-coordination ability outside of content knowledge. In any case, our data suggest our GS participants should not be considered “experts” as in Chi et al. (1981), and identify an interesting area for future study.
Schema induction
In the literature review, we suggested coordination of the three levels of the chemistry triplet might involve a process of creating schemas that are more abstract than any single level. Qualitative results from our study are consistent with this theory: NC, HS, and GC participants were more likely to reference representations than principles when justifying their sorts. Conversely, UD and CF participants seemed to have more abstract, principle-based justifications. Further investigation of a possible relationship between level-coordination ability and the abstractness of one's schemas, possibly through think-aloud interviews, is required.Card pairing data revealed the symbolic level of representation was used as a sorting criterion more than twice as often (58%) as each of the other two representations. This observation is consistent with research indicating heavy reliance on symbolic representations by undergraduates (Rappoport and Ashkenazi, 2008). Many of the verbal justifications for these sorts referenced mathematical tools or processes, such as ratios, percentages, or numerical equations, suggesting the chemical equations cued schemas related to mathematical problem solving. Another possible explanation is that symbolic external representations are used more frequently in instruction than the other two representation types, causing this level to be a stronger cue to undergraduates than the other two. The three general principles, on the other hand, were much more evenly distributed in the card pairs. The higher percentage (39%) of mass percent pairings compared to dilution (33%) and stoichiometry (28%) might be due to chance. On the other hand, it could be due to a perceived wider applicability of this concept outside of chemistry. More data from a larger participant group are needed to investigate these possibilities.
If we were to use our cross-sectional data to describe the progression of level-coordination development a single student might experience, our hypothetical student would re-formulate and combine schemas to become progressively more abstract throughout her undergraduate studies, while still retaining elements of representation-based features. These features would play an important role in her schemas and may even return to become the primary organizing features for some length of time during her graduate studies, as her more abstract schemas continue to shift and evolve. Ultimately she would gain a level of expertise comparable to a college faculty member and primarily adopt principle-based schemas.
Implications
From the arrangement of the six participant groups on the 2D plot (Fig. 3), it appears the ability to coordinate the three levels of representation in chemistry is a learned skill that develops over time, but may not necessarily be a straightforward, linear process. The unit of time over which we separated participant groups in our cross-sectional study was not a lesson, or even an individual course, but rather a year or more of coursework. However, there may be ways of speeding up the progression if level-coordination skills are taught explicitly. Other types of chemistry experience, such as research and teaching, may also move participants along the progression and may explain the larger gaps from GC to UD and UD to CF. Our results therefore suggest teaching students to meaningfully link the three levels of representation at the undergraduate level must be coordinated across multiple courses and experiences.The putative ability of the card sort task to separate at least five groups from each other, paired with the variability we observed within groups, suggests it has potential to evaluate the effectiveness of treatments designed to help students develop level-coordination ability. Consistent with research showing the benefit of variety in practice problem types for the development of principle-based schemas (Chen, 1999), use of multiple representations in practice problems and instruction might help students develop level-coordination ability in chemistry. In this case, the card sort task could be administered as a pre- and post-assessment measure. Our highly variable GC data (Fig. 2) suggest differences within a single quarter might be observable through the card sort task. This variability also suggests the card sort task could be used to identify students who need extra support and who could be directed toward multimedia resources designed to develop level-coordination ability (e.g.Chiu and Wu, 2009). As a program assessment tool, the task could be used to track level-coordination ability through a student's undergraduate coursework and identify high-impact courses as well as those needing improvement.
One NC and several HS students sorted close to the underlying principle anchor, while several GS students sorted close to the representation anchor, suggesting level-coordination ability is, to some extent, separable from content knowledge. Thus, this card-sort task is well suited to investigate cognitive skills related to level-coordination ability that might also be somewhat independent of content knowledge. Examples are reasoning skills and metacognition. One might expect, for example, an individual with well-developed logical reasoning skills to distinguish between underlying principles, even though he or she may not be familiar with the content. The RSCRDI would not be expected to distinguish between this individual and one with limited content knowledge and poor level-coordination skills, as success on this instrument requires correct responses to content-specific questions.
Finally, the use of sorting coordinates adds to the card sort literature by providing a method for distinguishing between levels of a construct, in our case level-coordination ability, rather than differentiating between two dichotomous anchor points. Although others have used methods for quantifying card sort data along an interval scale (Smith et al., 2013), our method allows for the mapping of individuals against a hypothesized progression. Research suggests intermediate levels between “novice” and “expert” may exist (Dreyfus and Dreyfus, 1986), and these may be identifiable and further operationalized through sorting coordinates in other card sort tasks assessing some facet of expertise.
Limitations and future study
This study was exploratory in nature, using relatively small sample sizes and a cross-sectional sampling approach, and the results should be interpreted with caution. Larger sample sizes are required to investigate between-group differences, especially between HS and GC. In addition, although there is precedent for the use of cross-sectional data to construct (Stevens et al., 2010) and test (Johnson and Tymms, 2011) learning progressions, longitudinal studies must be conducted to add validity to any claim about the development of level-coordination ability. Our cross-sectional samples may differ from each other in factors that might affect individuals' sorts, such as academic ability or career aspirations.Graduate students' performance on this task needs to be further investigated. This group was the smallest and consisted only of master's students. A follow-up study at an institution housing a large doctoral program would generate a clearer picture of the level-coordination ability of a more representative group. Secondly, more in-depth studies of graduate students' problem solving approaches through think-aloud interviews or other qualitative methods can help identify whether their sorts are related to teaching roles, shifts in knowledge structures, some other factor, or a combination. Graduate students could also be given the card sort task at the beginning and end of their first teaching assignment to determine to what extent a new teaching role factors into their sorting patterns. Finally, a framed condition, in which participants re-sort the cards having been given the underlying principles (Smith et al., 2013), an approach requiring a subject to choose a card to relate to a given card or card group (Hardiman et al., 1989), or the use of triads to evoke concepts differentiating the cards (Taber, 1994), may help to further characterize this group. It could be that the representation-based sorts were more of a preference than a reflection of the graduate students' expertise, and that they would be more likely than undergraduates to create principle-based groups under different conditions.
The difficulty in coding some of our participants' verbal justifications also limits the extent to which we can understand their sorting behavior. The prevalence of “other” codes in some groups might reflect surface- or principle-level justifications that were not recognized as such, and thus calls into question the reliability of the relative code frequencies, especially for NC, HS, GC, and GS participants. The use of already-formed sorts in interviews may help “calibrate” the task by building a bank of words and phrases that are used to describe known sorting systems.
Another limitation of this study is the number of tasks used to measure level-coordination ability. Subjects' sorts, justifications, and, for some, RSCRDI results were used to characterize their level-coordination ability. Some of the conditions discussed above would give more insight into an individual's level-coordination ability. For example, some sorts and “other” codes might reflect entirely different sorting criteria than the two we expected. As an assessment tool, the combination of unframed and framed conditions might therefore more accurately diagnose one's level-coordination ability than the use of the unframed condition alone.
Finally, any card sort task is limited by the content represented on the cards. An individual's sorting criteria may be influenced by the content of their formal chemistry preparation. Although we chose what we thought was representative introductory content accessible by most groups (this accessibility is supported by relatively low fractions of unexpected pairings), the content does not span the entirety of a chemistry preparation program, or even one general chemistry course. Non-zero fractions of unexpected pairings for some participant groups suggest the representations and/or principles may still be unrecognizable for some participants. Multiple sorting tasks, using different underlying principles from those used in this study, could be used to generate a better understanding of participants' schemas.
Appendix 1. card sort task
Prompt: You are editing a general chemistry textbook. The following cards represent practice problems you need to incorporate into the textbook. Please organize the cards so that they represent different chapters or sub-sections of the textbook. The textbook is organized in terms of concepts, so the cards should be placed together according to similar concepts you would need to solve each problem. The chapters/sub-sections don't need to be sorted by order in which they may appear within the text book. You need not actually solve these problems. There must be between 2–8 chapters/sub-sections, but you may choose to put any number of cards into each chapter/sub-section. There is not one particular, correct, way to sort the cards. After you finish grouping the cards you will be asked to explain why you grouped the cards the way you did.The full set of cards is shown in Fig. 5, both with the acronyms used in the article, and with numbers used in our original data processing and referred to in Appendix 2.
Appendix 2. generation of sorting coordinates
Assume a hypothetical participant sorted the set of cards into three groups as shown in Table 6. Group 1 includes cards 7, 8, and 9, which are paired together by underlying principle. The other two groups contain cards 1, 2, 5 and 3, 4, 6 respectively. These two groups have cards grouped together by underlying principle (1 with 2 and 3 with 4) and cards grouped together by level of representation (2 with 5 and 3 with 6).| Group 1 | Group 2 | Group 3 |
|---|---|---|
| 7, 8, 9 | 1, 2, 5 | 3, 4, 6 |
To calculate the two coordinates, distance from representation and distance from underlying principle, a covariance matrix (Fig. 6) is generated to represent all the possible card pairs. Within the matrix, “1” represents the two cards that cross at that location being paired together. The non-shaded region shows that there are 36 unique pairings, which will be used in calculating the distances.
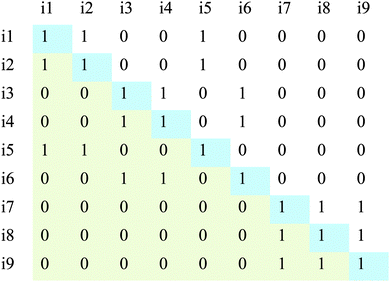 | ||
| Fig. 6 A sample covariance matrix for the hypothetical sort shown in Table 6. Here, i1 = card 1, i2 = card 2, and so on. The green region represents redundant pairings and the blue regions represent cards paired with themselves. Only the non shaded region is considered when calculating the sorting coordinates. | ||
Card pairings are then compared to the canonical sorts. The difference between the participant's sort, as recorded in the covariance matrix, and each canonical sort is calculated to generate the sorting coordinates (Tables 7 and 8). For the case of the hypothetical participant described above (Table 6), the coordinates are (8,14), to represent a difference of 8 from the canonical underlying principle sort and a distance of 14 from the canonical representation sort.
| 1–2 | 1–3 | 1–4 | 1–5 | 1–6 | 1–7 | 1–8 | 1–9 | 2–3 | 2–4 | 2–5 | 2–6 | 2–7 | 2–8 | 2–9 | 3–4 | 3–5 | 3–6 | 3–7 | 3–8 | 3–9 | 4–5 | 4–6 | 4–7 | 4–8 | 4–9 | 5–6 | 5–7 | 5–8 | 5–9 | 6–7 | 6–8 | 6–9 | 7–8 | 7–9 | 8–9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Underlying Principle | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Difference = 8 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1–2 | 1–3 | 1–4 | 1–5 | 1–6 | 1–7 | 1–8 | 1–9 | 2–3 | 2–4 | 2–5 | 2–6 | 2–7 | 2–8 | 2–9 | 3–4 | 3–5 | 3–6 | 3–7 | 3–8 | 3–9 | 4–5 | 4–6 | 4–7 | 4–8 | 4–9 | 5–6 | 5–7 | 5–8 | 5–9 | 6–7 | 6–8 | 6–9 | 7–8 | 7–9 | 8–9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| Representation | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| Difference = 14 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
References
- Bédard J. and Chi M. T. H., (1992), Expertise, Curr. Dir. Psychol. Sci., 1(4), 135–139.
- Carey S., (1987), Conceptual change in childhood, Cambridge: MIT Press.
- Chandrasegaran A. L., Treagust D. F. and Mocerino M., (2007), The development of a two-tier multiple-choice diagnostic instrument for evaluating secondary school students' ability to describe and explain chemical reactions using multiple levels of representation, Chem. Educ. Res. Pract., 8(3), 293–307.
- Chen Z., (1999), Schema induction in children's analogical problem solving, J. Educ. Psychol., 91(4), 703–715.
- Chi M. T. H., (2006), Methods to assess the representations of experts' and novices' knowledge, in Ericsson K. A., Charness N., Feltovich P. J. and Hoffman R. R. (ed.), The Cambridge Handbook of Expertise and Expert Performance, New York: Cambridge University Press.
- Chi M. T. H., Feltovich P. J. and Glaser R., (1981), Categorization and representation of physics problems by experts and novices, Cognitive Sci., 5(2), 121–152.
- Chiu M.-H. and Wu H.-K., (2009), The roles of multimedia in the teaching and learning of the triplet relationship in chemistry, in Gilbert J. K. and Treagust D. F. (ed.), Multiple Representations in Chemical Education, UK: Springer.
- Cracolice M. S., Deming J. C. and Ehlert B., (2008), Concept learning versus problem solving: a cognitive difference, J. Chem. Educ., 85(6), 873–878.
- Dreyfus H. L. and Dreyfus S. E., (1986), Five steps from novice to expert, Mind over machine: the power of human intuition and expertise in the era of the computer, New York: Free Press, pp. 16–51.
- Ebbing D. D. and Gammon S. D., (2013), General Chemistry, Belmont, CA: Brooks/Cole.
- Eysenck M. W. and Keane M. T., (2005), Cognitive Psychology: A Student's Handbook, New York: Psychology Press.
- Gabel D., (1999), Improving teaching and learning through chemistry education research: a look to the future, J. Chem. Educ., 76(4), 548–554.
- Galotti K. M., (2014), Cognitive Psychology In and Out of the Laboratory, Los Angeles: Sage Publications.
- Gentner D., (2005), The development of relational category knowledge, in Gershkoff-Stowe L. and Rakison D. H. (ed.), Building object categories in developmental time, Hillsdale N.J.: Erlbaum.
- Gilbert J. K. and Treagust D. F. (ed.), (2009), Multiple Representations in Chemical Education, U.K.: Springer.
- Hardiman P. T., Dufresne R. and Mestre J. P., (1989), The relation between problem categorization and problem-solving among experts and novices, Mem. Cognition, 17(5), 627–638.
- Hewson P. W., (1981), A conceptual change approach to learning science, Eur. J. Sci. Educ., 3, 383–396.
- Heyworth R. M., (1999), Procedural and conceptual knowledge of expert and novice students for the solving of a basic problem in chemistry, Int. J. Sci. Educ., 21(2), 195–211.
- Jaber L. Z. and Boujaoude S., (2012), A Macro-Micro-Symbolic Teaching to Promote Relational Understanding of Chemical Reactions, Int. J. Sci. Educ., 34(7), 973–998.
- Johnson P. and Tymms P., (2011), The Emergence of a Learning Progression in Middle School Chemistry, J. Res. Sci. Teach., 48(8), 849–877.
- Johnstone A. H., (1982), Macro- and micro-chemistry, Sch. Sci. Rev., 64, 377–379.
- Kern A. L., Wood N. B., Roehrig G. H. and Nyachwaya J., (2010), A qualitative report of the ways high school chemistry students attempt to represent a chemical reaction at the atomic/molecular level, Chem. Educ. Res. Pract., 11(3), 165–172.
- Kozma R. B., (2000), The use of multiple representations and the social construction of understanding in chemistry, in Jacobson M. J. and Kozma R. B. (ed.), Innovations in science and mathematics education: advanced designs for technologies of learning, Mahwah, N.J.: Erlbaum.
- Kozma R. B. and Russell J., (1997), Multimedia and understanding: expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 34(9), 949–968.
- Kozma R., Chin E., Russell J. and Marx N., (2000), The Roles of Representations and Tools in the Chemistry Laboratory and Their Implications for Chemistry Learning, J. Learn. Sci., 9(2), 105–143.
- Lajoie S. P., (2003), Transitions and Trajectories for Studies of Expertise, Educ. Res., 32(8), 21–25.
- Mason A. and Singh C., (2011), Assessing expertise in introductory physics using categorization task, Phys. Rev. ST Phys. Educ. Res., 7(2), 020110.
- Nakhleh M. B., (1992), Why some students don't learn chemistry, J. Chem. Educ., 69(3), 191–196.
- Rapp D. N. and Kurby C., (2008), The ‘ins’ and ‘outs’ of learning: internal representations and external visualizations, in Gilbert J., Reiner M. and Nakhleh M. B. (ed.), Visualization: Theory and Practice in Science Education, New York: Springer.
- Rappoport L. T. and Ashkenazi G., (2008), Connecting levels of representation: emergent versus submergent perspective, Int. J. Sci. Educ., 30(12), 1585–1603.
- Revlin R., (2012), Cognition: Theory and Practice, New York: Worth Publishers.
- Simon H. A. and Newell A., (1972), Human problem solving, Englewood Cliffs, N.J.: Prentice-Hall.
- Smith J. I., Combs E. D., Nagami P. H., Alto V. M., Goh H. G., Gourdet M. a. A., Hough C. M., Nickell A. E., Peer A. G., Coley J. D. and Tanner K. D., (2013), Development of the Biology Card Sorting Task to Measure Conceptual Expertise in Biology, CBE-Life Sci. Educ., 12(4), 628–644.
- Stains M. and Talanquer V., (2007), Classification of chemical substances using particulate representations of matter: an analysis of student thinking, Int. J. Sci. Educ., 29(5), 643–661.
- Stains M. and Talanquer V., (2008), Classification of chemical reactions: stages of expertise, J. Res. Sci. Teach., 45(7), 771–793.
- Stevens S. Y., Delgado C. and Krajcik J. S., (2010), Developing a Hypothetical Multi-Dimensional Learning Progression for the Nature of Matter, J. Res. Sci. Teach., 47(6), 687–715.
- Taber K. S., (1994), Can Kelly's triads be used to elicit aspects of chemistry students' conceptual frameworks? 20th Annual British Educational Research Association Conference, Oxford.
- Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14(2), 156–168.
- Talanquer V., (2011), Macro, Submicro, and Symbolic: The Many Faces of the Chemistry “Triplet”, Int. J. Sci. Educ., 33(2), 179–195.
- Wolf S. F., Dougherty D. P. and Kortemeyer G., (2012a), Empirical approach to interpreting card–sorting data, Phys. Rev. ST Phys. Educ. Res., 8(1), 010124.
- Wolf S. F., Dougherty D. P. and Kortemeyer G., (2012b), Rigging the deck: Selecting good problems for expert-novice card-sorting experiments, Phys. Rev. ST Phys. Educ. Res., 8(2), 020116.
| This journal is © The Royal Society of Chemistry 2016 |