The nature of students' chemical reasoning employed in scientific argumentation in physical chemistry
A.
Moon
a,
C.
Stanford
b,
R.
Cole
b and
M.
Towns
*a
aDepartment of Chemistry, Purdue University, 560 Oval Drive, West Lafayette, Indiana, USA. E-mail: mtowns@purdue.edu
bDepartment of Chemistry, University of Iowa, Iowa city, Iowa, USA
First published on 2nd February 2016
Abstract
Recent science education reform efforts have emphasized scientific practices in addition to scientific knowledge. Less work has been done at the tertiary level to consider students' engagement in scientific practices. In this work, we consider physical chemistry students' engagement in argumentation and construction of causal explanations. Students in two POGIL physical chemistry classrooms were videotaped as they engaged in discourse while solving thermodynamics problems. Videos were transcribed and transcripts were analyzed using the Toulmin Argument Pattern (TAP). Arguments were then characterized using the modes of reasoning in a learning progression on chemical thinking (CTLP) (Sevian and Talanquer, 2014). Results showed that students used primarily relational reasoning, in which no causal explanation is generated, rather a single relationship between variables was used to justify a claim. We discuss all types of reasoning present in students' arguments.
Introduction
Recent science education reform efforts have emphasized explicitly teaching scientific practices in addition to scientific knowledge (NRC, 2012a, 2012b; Cooper et al., 2015). Scientific practices include the means by which scientific knowledge is generated. One of these fundamental scientific practices, argumentation, requires students to make claims based on evidence (Driver et al., 2000; Bell, 2000; Bell, 2004; Garcia-Mila and Andersen, 2007; Berland and Reiser, 2009; NRC, 2012a, 2012b). In addition to modeling authentic scientific discourse, facilitating argumentation in the classroom has also shown to promote learning content knowledge (Zohar and Nemet, 2002; Asterhan and Schwarz, 2007; von Aufschnaiter et al., 2008). To improve students' abilities to engage in building scientific arguments, instructors must explicitly teach argumentation (Berland and Reiser, 2011; Christodoulou and Osborne, 2014). In this study, we aim to consider how physical chemistry students engaged in this scientific practice. To identify and consider arguments, Toulmin's Argument Pattern (TAP) was used to extract arguments constructed in two POGIL physical chemistry classrooms. In order to characterize the reasoning in students' arguments, we use the framework of chemical thinking (Sevian and Talanquer, 2014). Chemical thinking refers to the “development and application of chemical knowledge and practices with the main intent of analyzing, synthesizing, and transforming matter for practical purposes.” (Sevian and Talanquer, 2014). Considering the students' reasoning equips us to move past only evaluating students' content knowledge to evaluating their ability to think and argue like a scientist (Berland and Reiser, 2011; Evagorou and Osborne, 2013). Motivated to consider upper-level undergraduate students' participation in the scientific practices of argumentation, this study aimed to answer the following research question:What is the nature of students' chemical reasoning as evidenced by their argumentation across two different POGIL chemistry classrooms?
To answer this question, a qualitative discourse analysis method was used in which arguments were identified in classroom talk using Toulmin's Argument Pattern (Cole et al., 2012). Rather than exclusively investigating the presence and construction of arguments, we aimed to evaluate the content of the arguments to assess the quality of causal reasoning students were employing.Background
Argumentation
Argumentation is the practice of generating, considering, and comparing arguments. Arguments are composed of a claim or conclusion supported with evidence (Toulmin, 1958; Garcia-Mila and Andersen, 2007). There has been growing interest in incorporating argumentation into the science classroom (Bricker and Bell, 2008), as explicitly teaching and facilitating argumentation invites students to participate in scientific discursive practices, which is highlighted as an objective in science education (Duschl et al., 2007; Kelly, 2008; NRC, 2012a, 2012b). It also serves as an insightful platform for identifying patterns in students' reasoning, as building arguments requires students to articulate causal explanations for phenomena (Berland and Reiser, 2009).Little work in argumentation has been published at the tertiary level. In chemistry, argumentation has served as a lens for describing reasoning patterns in a POGIL physical chemistry classroom (Becker et al., 2013). Becker et al. (2013) found that a sociochemical norm emerged in the classroom in which arguments were justified using particulate-level reasoning. In a separate analysis, Becker and colleagues also found that the instructor served an important role in promoting reasoning across multiple levels (macroscopic, submicroscopic, and symbolic). In comparing the small group and whole class discourse, they found that small group discourse centered largely on the symbolic level, while the whole class discourse, which included more instructor discursive moves, helped elicit reasoning across multiple levels (Becker et al., 2015).
In introductory chemistry, Kulatunga and Lewis (2013) explored students and peer leaders' verbal behaviors in a general chemistry course incorporating peer-led guided inquiry sessions. Researchers compared two small groups to identify differences in frequency of individual arguments versus collaboratively constructed arguments and patterns in the individual contributions to collaboratively constructed arguments. Without peer leader intervention, students were largely able to construct arguments with their peers that included evidence and justification. Further, if an argument included an incorrect claim, students corrected it and achieved resolution through argumentation (Kulatunga et al., 2013). By distinguishing between different peer leader verbal behaviors, researchers identified patterns in two peer leaders' interactions with their small groups. The evidence provided in students' arguments largely resulted from short questions, which targeted facts, while the justifications in arguments were frequently generated in response to probing and clarifying questions, which generally take the form of “why” or “how” (Kulatunga and Lewis, 2013).
There are examples of inquiry into university students' argumentation in other disciplines, such as oceanography (Kelly and Takao, 2002; Takao and Kelly, 2003) and engineering (Erduran and Villamanan, 2009). These studies evaluated students' written arguments generated in response to a writing scaffold that included a data set. Kelly and Takao (2002) constructed a rubric that evaluated arguments using epistemic criteria. Epistemic levels were proposed that ranged from one level including references to specific data to another level that included references to general geological principles. These levels were used to characterize students' arguments. Erduran and Villamanan (2009) illustrated the difficulty that tertiary engineering students experienced with using experimental evidence to support their arguments.
With dialogic argumentation in the context of chemistry, the instructor or facilitator plays an important role in eliciting arguments and promoting scientific reasoning. With written argumentation in other disciplines, the task and data set inform the quality of resulting arguments. In both written and dialogic argumentation, support is necessary to help students learn to interpret experimental data, construct coherent arguments drawing on data, and employ reasoning across multiple representational levels. Little work has been done to understand how tertiary students use cause and effect reasoning to construct arguments. This is especially relevant in the context of chemical thermodynamics, which has the potential to answer “why” and “how” many chemical processes occur.
Scientific reasoning
In considering student reasoning, the next generation science standards (NGSS) framework for K-12 science education in the United States identifies crosscutting concepts that span scientific inquiry (NRC, 2012a, 2012b). Of these concepts, the most relevant for this study was building arguments using cause and effect, or mechanisms. Cause and effect descriptions serve to answer the “why” and “how” scientific questions. The framework highlights how cause and effect mechanisms range in complexity depending on the system being investigated. This capacity to generate mechanisms that use cause and effect is also important to explicitly teach at the undergraduate level as research suggests chemistry experts possess this skill (Sevian and Talanquer, 2014).This study considers the overall scientific reasoning and use of causal models in classroom arguments. Research shows that more expert-like causal models are dynamic, integrated, and complex (Perkins and Grotzer, 2005; Brown et al., 2010). However, the causal models that students or novices generate and draw upon tend to be linear and oversimplified (Grotzer, 2003; Perkins and Grotzer, 2005). Further, novices can focus on single salient features of a problem or phenomenon and assign them total causal agency (Smith et al., 1985; Perkins and Grotzer, 2005; Sevian and Talanquer, 2014). However, explicitly teaching different causal models results in students using more complex models in their explanations (Perkins and Grotzer, 2005).
This body of literature largely focuses on primary and secondary students. Less work has been done with upper level science, technology, engineering, and mathematics (STEM) students to evaluate their scientific reasoning and use of scientific mechanism (Taber and Watts, 2000). Though expectations for chemistry undergraduate students' skills vary across institutions, this lack of research in the post-secondary chemistry classroom is indeed a gap considering that students nearing the end of their degree should ideally possess competencies essential to being a professional chemist (ACS CPT, 2015). In one study, Sevian and Talanquer (2014) interviewed chemists ranging from undergraduate students to chemistry faculty members (representing a novice to expert range) using the GoKart question (Szteinberg et al., 2014). One goal of their work was to elicit the types of reasoning employed by the participants and describe a learning progression for chemical thinking that characterizes qualitatively different levels of reasoning about chemical processes. This learning progression is valuable for characterizing students' reasoning, specifically students' use of causal reasoning. For this reason, it is used in this study to characterize physical chemistry students' reasoning as evidenced by their arguments. As this progression is grounded in a theoretical commitment to a focus on disciplinary [chemistry] core practices, it serves as a domain-specific measure of argument quality.
Process oriented guided inquiry learning (POGIL) approach
Student reasoning was explored in two classrooms in which the Process-Oriented Guided Inquiry Learning (POGIL) pedagogy was used. POGIL classrooms emphasize the development of process skills through small group discourse, providing an ideal space for considering students' participation in practices of constructing arguments and explanations. Use of the process-oriented guided inquiry learning (POGIL) approach at the undergraduate level has been shown to improve student attitudes (Chase et al., 2013), performance on ACS standardized examinations (Hein, 2012), and grades (Conway, 2014). While the use of POGIL in the classroom has been widely studied, the effect of the POGIL approach on student learning or reasoning at the physical chemistry level has received less attention (Becker et al., 2013; Becker et al., 2015). The National Research Council's report on discipline based education research has called for evaluation of the POGIL approach and research in upper-level courses, such as physical chemistry (NRC, 2012a, 2012b).The POGIL approach applies social constructivist theories of learning to develop curricular materials and facilitation strategies that prompt students to co-construct and apply knowledge. A POGIL classroom involves a significant portion of collaborative small group work intended to promote higher order thinking and application of knowledge (Moog and Spencer, 2008). Students are guided through a process of exploration, concept development, and application. In the thermodynamics workbook used in both of the classrooms under study, each activity poses a focus question for which students do not typically have the chemical knowledge to answer. Students then work through a series of critical thinking questions (CTQs) that build on previous units and help them construct models specific to the activity. Final CTQs typically ask students to describe and explain the concepts they have been constructing throughout the activity (Moog and Spencer, 2008). Each activity concludes with exercises that provide further opportunity to apply concepts constructed in the activity. Though POGIL provides curricular materials and a general approach, it leaves room for the instructor to make decisions about the actual implementation and facilitation based on their classroom's needs.
Methods
Theoretical orientation
This work was shaped by the sociocultural perspective (John-Steiner and Mahn, 1996). The primary tenet of the sociocultural perspective is that knowledge is co-constructed by individuals in a social and cultural context through the medium of language (Geelan, 1997). The social construction and individual construction of knowledge occur simultaneously and are interdependent (John-Steiner and Mahn, 1996). Vygotsky theorizes that intermental (social) activity in fact promotes intramental (individual) learning (Mercer et al., 2004). This occurs through a process of internalization by the individual. The learning process is housed in discourse. Therefore, the success or failure of an educational intervention may be attributed to the quality of the discourse rather than simply the students' or teacher's capabilities (Mercer, 2004). Argumentation is one form of discourse we have chosen to evaluate, as it is a core scientific practice.The sociocultural perspective theoretically supports this work in its justification of the use of POGIL for facilitating small group and whole class discourse as a means of supporting individual understanding. It further supports the method of analysis used in this study. As learning is mediated by language, analyzing the classroom discourse is the most appropriate method for identifying instances of learning or discursive moves that hindered learning.
Analytic framework: toulmin argument pattern
The widely used Toulmin Argument Pattern (TAP) presented in Fig. 1 was used to identify, model, and organize arguments (Erduran, et al., 2004; Jimenez-Aleixandre and Erduran, 2008). The core of the argument includes a conclusion, some data or evidence supporting the claim, and an explanation connecting the data to the claim. In certain instances, backings are required to justify or support a warrant. Qualifiers provide the limitations or restrictions to the core of the argument. In the context of physical chemistry, qualifiers often appear as a description of limitations for a formula or model. Rebuttals identify a shortcoming in an argument by undermining either the use of a component in the core argument or the content of a component in the core argument.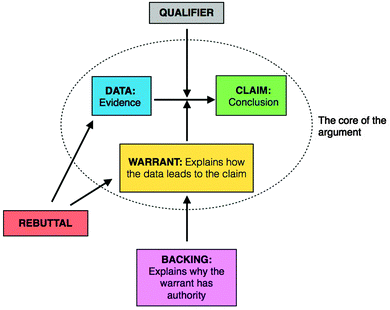 | ||
| Fig. 1 Toulmin Argument Pattern (Adapted from Erduran et al., 2004). | ||
To identify arguments using TAP, transcripts from the whole class videos were analyzed for claims, which often took the form of the answer to a POGIL prompt. The presence of evidence or data to support the claim qualified the unit of text as an argument. Perhaps the most challenging step in using TAP was distinguishing between claims, data, warrants, and backings (Erduran, 2007; Kaya, 2013). Indicator words such as “so” or “because” were useful for identifying what was being concluded (claim) or why the conclusion was drawn (warrant). For arguments concerning phenomena or empirical data, warrants frequently served an explanatory function. For arguments concerning mathematical derivations or problems, warrants tend to be more algorithmic, describing steps taken to move from the data to the claim (Rasmussen and Stephan, 2008). Both of these types of arguments are present in physical chemistry discourse.
Participants and data collection
Institutional review board approval was obtained to protect human subjects prior to data collection and analysis in this study. Two classrooms using the POGIL Physical Chemistry curriculum were explored in this study. Table 1 describes the settings and participants of the two classrooms.| 2010 | 2013 | |||
|---|---|---|---|---|
| Instructor: Dr Black | Instructor: Dr Green | |||
| Instructor experience | 10 years of implementing POGIL | 7 years of implementing POGIL | ||
| Setting | Public University, ∼14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 students 000 students |
Private college, ∼1000 students | ||
| Thermodynamics | Physical Chemistry I & II | |||
| Spencer, Moog, & Farrell POGIL materials | Spencer, Moog, and Farrell POGIL materials | |||
| Number of participants | 18 students | 5 Females | 10 students | 3 Females |
| 13 Males | 7 Males | |||
| Participant demographics | Third & fourth years | Second through fourth years | ||
| At least 1 semester of calculus | 2 semester of Calculus (except 1) | |||
| Class time | 1/3 to 1/2 class small group work, rest whole class discussion | 1/2 to 2/3 time small group work and 1/3 to 1/2 lecture | ||
Some of the key differences between the two implementations were the instructors' experiences with implementing POGIL, the physical chemistry topics covered, and the presence of whole class discussion. Both instructors became involved with the larger POGIL project since first using it in their classroom, with Dr Black focusing on instructor facilitation and Dr Green focusing on developing POGIL materials. While Dr Black iteration covered exclusively thermodynamics, Dr Green iteration covered all traditional physical chemistry topics. While the order and timing of the use of activities differed, for the purpose of this study we analyzed classroom discourse while students completed the same set of chemistry topics. In the 2010 implementation, class time was split between small group discussion and whole class discussions with very little lecture. In the 2013 implementation, time was split primarily between small group work and lecture. Though there were instances of students asking questions during the lectures during the 2013 implementation, they were not frequent. Video data of entire class periods were collected with cameras aimed at collecting small group interactions and whole classroom interactions (Cole et al., 2012).
Data analysis
The videos of each class period were transcribed verbatim. The classroom transcripts were then analyzed using Toulmin's Argument Pattern (TAP). To extract arguments, researchers carefully read through transcripts to identify the presence of claims. Usually, these were responses to prompts in the POGIL activities. If a claim was joined by any evidence, it was extracted as an argument. There were instances when the data was implied based on context, rather than being explicitly verbalized. Discourse surrounding the claim and data were analyzed for fit to a component of Toulmin's model (e.g. warrant, backing, qualifier). Two separate graduate student chemistry education researchers independently generated argument logs, lists of arguments organized according to the TAP, for each transcript. After this, the entire research team, made up of the two graduate students and their faculty advisors, met and discussed discrepancies until complete consensus was reached. The product of this step was an argument log for each class period that included every argument along with its corresponding POGIL question. When extracting arguments, discourse was often paraphrased to fit into the TAP model. This served to condense large amounts of text into a concise form. When paraphrasing contributed to a loss of meaning, the original text was used in the argument log. Italics were used to indicate original quotes from students. These argument logs were used for all further analysis. Below is an excerpt to illustrate the layout and function of an argument log.10.13.10 Argument log
Whole class discussion
[00:01–02:42] ChemActivity T9, CTQ 4a
Claim: dA = dU − TdS (Elliot)
Data: A = U − TS (given in book)
Warrant: Apply state function to data (Elliot)
Rebuttal: Why did T come out? Did you chain rule? (Quentin)
Resolved claim: dA = dU − TdS − SdT (Jerome, Elliot, Caprice)
Data: dA = dU − d(TS) (Caprice)
Warrant: Use the chain rule (Jerome)
The second stage in analysis involved coding these arguments with the modes of reasoning in the Chemical Thinking Learning Progression (CTLP). This level of analysis allowed us to characterize the modes of reasoning used within each argument as a whole adding further dimensions of analysis. Ultimately it was used to reveal the types of reasoning students use within arguments. Additionally, the modes of reasoning in the CTLP allow for the consideration of the entire argument as a unit, rather than consideration of its individual components. Arguments were labeled as descriptive, relational, linear causal, or multicomponent based on the features described in Table 2.
| Mode | Features |
|---|---|
| Descriptive |
• Salient properties are recognized
• Explicit properties are verbalized • Phenomenon is instantiation of reality • Reasoning based on experiences from daily life |
| Relational |
• Explicit and implicit properties are highlighted
• Spatial and temporal relations are noticed • Phenomenon is effect of single variable (no mechanism) |
| Linear | • Mechanisms proposed that involve linear cause-effect relationships |
| Multi-component | • Mechanism weighs effects of several variables |
In order to categorize arguments, the first author read arguments along with the corresponding POGIL prompt. If the argument only provided information present in the prompt in order to respond to the prompt, it was assigned a descriptive code. Arguments that consisted of statements that described the phenomenon or question, it also received a descriptive code. Relational codes were assigned to arguments that highlighted a single relationship between variables to justify a claim or if the claim was made assuming a relationship between variables (e.g. “work was done because the piston went up”). Linear arguments included steps linking variables together in a linear cause and effect sequence used to achieve some outcome. The multicomponent code was assigned to arguments that explicitly considered more than one variable as simultaneously contributing to an outcome.
The first author presented a description of these codes to two chemistry education graduate students and they each coded an argument log for one class period. The codes for each argument were discussed until the three coders reached a complete consensus. This discussion prompted the first author to refine the code descriptions and code all of the arguments again. This round of coding resulted in only assigning a few arguments new codes.
It is important to note that the modes of reasoning used in this work are only one aspect of this learning progression. We considered the disciplinary crosscutting concepts in so far as we identified chemical mechanism, chemical identity, and structure–property relationships as the most widely used in both of the classrooms studied (Sevian and Talanquer, 2014).
Results
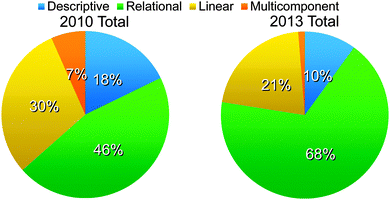
Examples were found for each type of student reasoning: descriptive, relational, linear, and multicomponent. Fig. 2 shows that the classrooms differed in their chemical thinking distribution; however, the overall reasoning patterns are similar. It is important to note that because argumentation is a process skill, valid arguments consisting of claims grounded in evidence can be made by students irrespective of the complexity of reasoning. Because of this, arguments using all levels of reasoning reflect positively on students' skills in constructing arguments.Descriptive
Descriptive arguments did not contribute new information. Rather, they were repetitive, focusing solely on superficial features of the prompt. Table 3 shows an example of a POGIL prompt eliciting descriptive reasoning. In this argument, the student is interpreting the reaction as listed in the problem. The student correctly identifies that one mole of A(g) and one mole of B(g) means that there are two moles of reactants. However, this argument indicates only consideration of explicit features of the problem, that is, the chemical reaction. This argument is not surprising, considering the prompt specifically asked the students to elaborate on what information the symbolic representation of the chemical reaction provides.| POGIL prompt | 2013 |
|---|---|
|
The chemical reaction of A and B goes to completion:
A(g) + B(g) → C(g) + 2D(g) ΔrH = 0 Before the chemical reaction occurs, what is the total number of moles in the container? |
Claim: There are two moles of gas before the chemical reaction occurs (Elliot) |
| Data: Model 2 information (book) | |
| Warrant: 1 mole of gas A and 1 mole of gas B (Rosalind) |
Table 4 shows the students in 2010 and 2013 making different claims, but using the same data and reasoning. It is clear that they are describing reactants in order to respond to the prompt. The claims they are generating rely on identifying reactants as molecules or elements as they are written. Similar to the previous example, the question is prompting the students to describe features of the problem to make a claim. The prompt provides seemingly explicit conditions for identifying an enthalpy of formation reaction and yet the students from 2010 and 2013 do not generate the same claim. The practice of generating arguments revealed areas of possible confusion on the part of the students. Though it seems like they are not using complex reasoning or generating new information, the arguments they constructed to make descriptive claims reveal their reasoning and interpretation of the problem.
| POGIL prompt | 2010 | 2013 |
|---|---|---|
|
Mg(s) + CO(g) + O2(g) → MgCO3(s)
MgO(s) + CO2(g) → MgCO3(s) Mg(s) + C(s) + 3/2 O2(g) → MgCO3(s) BaCO3(s) → BaO(s) + CO2(g) CO(g) + 1/2O2(g) → CO2(g) C(s) + O2(g) → CO2(g) In which of the above reactions is the product the result of the reaction of the elements that compose it, each of the elements being in their stable states at 1 bar? |
Claim: C and F are a result of the reaction of the elements that compose it (Jerome/Jamal/Book) | Claim: In reaction F, the product is the result of the reaction of the elements that compose it (Mark) |
| Data: Reactions from the book (book) | Data: Model 4 chemical reactions (Mark) | |
| Warrant: All the other reactions have molecules (Jerome/Jamal) |
Relational
The students in both 2010 and 2013 primarily used relational reasoning. Arguments using relational reasoning relied on a relationship without providing any sort of causal justification. Table 5 provides examples of this type of argument. Excluding Dr Green's backing in 2013, student arguments took the form “If this variable is dependent upon another variable that is a state function, then it is a state function.” Rather than considering the nature of enthalpy or internal energy in order to make claims about whether or not the variables were state functions, students exclusively considered the relationship between all the variables. Dr Green's backing inputs reasoning based on how pressure and volume change in a system in order to decide if they should be state functions. The backing provided by Dr Green illustrates a more complex causal model in which more thorough justifications indicating an understanding of pressure and volume are used to support the claim that pressure and volume are state functions.| POGIL prompt | 2010 | 2013 |
|---|---|---|
| Recall that energy, U, is a state function (or that dU is an exact differential). Is PV a state function? Is H a state function? | Claim: H is a state function (Class) | Claim: PV a state function (Garrett/Mark) |
| Data: H = U + PV (book) | Data: U is a state function (Mark) | |
| Warrant: It is a sum of state functions P, V, and U (Jake) | Warrant: Because it's a measure of energy, which is a state function (Garrett) | |
| Backing: The pressure is what it is, it doesn't matter what path the system took to get there. And the same with the volume (Dr Green) |
In another example, Table 6 shows students' use of the relationship between the total entropy change and spontaneity of a system. In both iterations, students claimed that the total change in entropy would be positive for the process because the process is spontaneous. Dr Black aims to move students past only considering spontaneity and entropy change as mathematical values to considering them as variables that describe a process. Earlier arguments from this activity reveal that this justification is grounded in the definition for a spontaneous process provided in the POGIL information. Table 7 includes Jamal's argument when prompted to consider a process in which the final total entropy was larger than the initial total entropy.
| POGIL prompt | 2010 | 2013 |
|---|---|---|
| Imagine tossing a hot brick into cold water in an adiabatic enclosure. Assume that the resulting process does not affect the volume of the brick or the water. Can you determine the sign and/or magnitude of ΔStot for this process? If so, provide this information. If not, explain why not. | Claim: ΔS total is positive. (Callum) | Claim: ΔS total for the process has a positive sign (Garrett) |
| Data: Because it's spontaneous (Callum) | Data: Because it is spontaneous (Garrett) | |
| Warrant: Yeah, the change has to be spontaneous, ΔS system has to be spontaneous, so then the total has to be spontaneous. (Tice) | ||
| Clarifier: So the total can't be spontaneous, the process can be spontaneous, but the math can't be spontaneous.(Dr Black) |
| 2010 |
|---|
| Claim: Yes, the process is spontaneous (Jamal) |
| Data: (Stot) final > (Stot) initial (Book) |
| Warrant: That was part of the definition of spontaneous (Jamal) |
Caprice uses the same reasoning for the reverse process, shown in Table 8. All of these arguments draw on the relationship between spontaneity and total entropy change to justify claims. None of the arguments indicate an understanding of spontaneity, entropy, or the phenomenon (hot brick in cold water). There were no instances of students making sense of this relationship. This is partially due to the description of this concept in the POGIL curriculum in which a spontaneous event is defined as having a positive total entropy change. However, this indicates that Caprice and Nathan are simply quoting the POGIL text with no evidence of interpretation or sense making. More complex causal arguments would ideally incorporate reasoning about entropy and spontaneity, as well as the phenomenon at hand, to justify and predict an outcome. What these two arguments above suggest is that the relationship between spontaneity and total entropy change was assumed to be sufficient justification for claims without a supporting explanation or interpretation.
| 2010 |
|---|
| Claim: No the process is not spontaneous (Caprice) |
| Data: (Stot) final < (Stot) initial (Book) |
| Warrant: Because of the definition of spontaneous (Caprice) |
Relational reasoning is particularly useful for revealing how students use relationships to justify claims. However, relational arguments often lack evidence of students' understanding of a certain relationship. More complex argumentation, including more robust warrants and more frequent rebuttals, can serve to prompt students to make explicit their understanding of scientific relationships.
Linear
Students in both groups demonstrated linear reasoning, which included some linear cause and effect mechanism. These arguments tended to take one of two forms, mathematical or conceptual. The structure of mathematical arguments usually included a linear, stepwise description of the mathematical operations students completed to move from the data, or initial equations, to claim, or final output.The arguments in Table 9 show the sequential reasoning employed by the students to arrive at some mathematical product. In both cases, students list mathematical steps taken to complete the derivation. This is most frequently how students discussed any mathematical reasoning. This is noteworthy because one of the only times we see students use linear, stepwise reasoning with ease is when they are describing their mathematics. The burden to use linear reasoning is not a priority when explaining phenomena. In that case, relational reasoning without explanation is often considered sufficient.
There were instances of linear causal arguments for phenomena and concepts, but they did not follow as consistent of a structure as that observed in the mathematical arguments. In response to the prompt in Table 10 that required them to compare the final temperatures for neon and nitrogen upon the addition of the same amount of heat, Qi generated a linear argument to justify his claim.
| POGIL prompt | 2013 |
|---|---|
|
Consider 1 mole samples of Ne and N2 at the same temperature T. Equal amounts of heat are added to each sample under otherwise identical conditions.
Predict whether the final temperatures of the two samples will be the same or different. If different, predict which will have the higher final temperature. Explain clearly |
Claim: Neon would have a higher temperature than N2 upon input of the same amount of energy (Qi) |
| Data: It has like bonds (Qi) | |
| Warrant: So the bonds would absorb some energy (Qi) |
Qi argues neon would have higher temperature exclusively from the perspective of nitrogen, explaining that because nitrogen has bonds that would absorb energy, it will have a lower temperature. It is important to note that there are features that are implicitly included in this argument. The reason that we can conclude that they are present is because they provide the connection between features that were made explicit (in contrast to relational reasoning where sequential reasoning was not employed and mechanistic steps were not made explicit). In order for Qi to draw the conclusion that he did, she had to assume that having more energy contributes to higher temperature. Providing a mechanism in an argument is revealing of steps the students thought important to verbalize and the steps that they assume are implicit.
Some linear arguments were a hybrid between mathematical and conceptual arguments. This hybrid type was particularly prevalent in arguments concerning Hess' law. Students in both groups used reasoning about the chemical process to inform how they completed the mathematical operation. These arguments still assume a linear description of steps taken to reach a mathematical output, but they include justifications grounded in the chemical process. Table 11 shows similar arguments generated in both classrooms to calculate the enthalpy change for vaporization of water.
| POGIL prompt | 2010 | 2013 |
|---|---|---|
| Use these data [enthalpies of formation for gaseous and liquid water] and Hess' law to calculate ΔrH for the following reaction H2O(l) → H2O(g) | Claim: ΔH for H2O(l) → H2O(g) = difference between two heats of formation (44.01 kJ mol−1) (Jerome/Quentin) | Claim: The ΔH of reaction is 44.01 kJ mol−1 (implied) |
|
Data: H2(g) + ½O2(g) → H2O(l)
ΔrHo = −285.83 kJ mol−1 H2(g) + ½O2(g) → H2O(g)ΔrHo = −241.82 kJ mol−1 (Text) |
Data: heat of formation reactions and ΔH values (book) | |
| Warrant: The top equation needs to be flipped because you start with liquid water, flip it so the net equation would end with gas (Jerome/Liam) | Warrant: you add the reverse reaction, because you are going from H2 liquid to H2 gas, so you want to add the reverse (Stephanie) | |
| Backing: A positive value makes sense since you are vaporizing the water. (Liam/Quentin) |
In the arguments presented in Table 11, students determine an enthalpy of reaction for the vaporization of water equaling 44.01 kJ mol−1. Using Hess' law, they warrant switching the sign of the enthalpy of formation of liquid water and adding the enthalpy values to determine the total enthalpy change for the reaction. Particularly noteworthy in this argument is Liam and Quentin's explicit evaluation of the output value in which they rationalize the positive value based on the phenomenon. Students draw from the phenomenon to provide conceptual justifications for the mathematical steps taken to calculate an output value.
In another example of a hybrid structure argument, Dr Black builds on Sam's claim with a conceptual explanation, shown in Table 12. Dr Black explained the mathematical substitution (−PdV for dw in the first law equation) with a more conceptual description of the energy change sourcing from the work change. Dr Black was intentional about modeling how mathematical, linear reasoning is meaningful for understanding thermodynamic concepts. Linear arguments are distinct in their inclusion of cause and effect reasoning. In the arguments presented above, the students propose a mechanism in which one step (mathematical or phenomenal) leads to another and eventually an outcome.
| POGIL prompt | 2010 |
|---|---|
| Use your answer to CTQ 8 and parts a and b above to provide an equation relating dUsys to pressure and volume for an adiabatic, reversible process. | Claim: dUsys = −PdV (Sam) |
| Data: In an adiabatic system, dU = dq + dw, dq = 0, dw = −PdV (CTQ8, 10a, 10b) | |
| Warrant: So for an adiabatic system where dq = 0, then the change in energy comes from changes due to work (Dr Black) |
Multicomponent
Multicomponent arguments were the least frequent indicating the difficulty of considering multiple variables as contributing to an outcome. During the discussion of neon and nitrogen, two different groups from the 2010 implementation generated multicomponent arguments shown in Table 13.| POGIL prompt | 2010 | 2010 |
|---|---|---|
|
Consider 1 mole samples of Ne and N2 at the same temperature T. Equal amounts of heat are added to each sample under otherwise identical conditions.
Predict whether the final temperatures of the two samples will be the same or different. If different, predict which will have the higher final temperature. Explain clearly |
Claim: Ne is hotter (Reed's board) | Claim: Neon would be hotter than N2 (Quentin) |
| Data: Because neon is lighter. (Reed) | Data: Neon doesn't have any bonds (Quentin) | |
| Warrant: it'll move faster with the same amount of heat added. And because there's triple bond between nitrogen. The amount of heat given in the system, part of it will be considered to break the bonds. (Reed/Elliot) | Warrant: Nitrogen has bonds, bonds can devote energy to stretching, straining, and you've also got rotational and those other types of motion. Whereas the Neon just has translational (Quentin) |
In response to this problem, we see two different responses using multicomponent thinking. Reed concludes that neon would be hotter as it is lighter so it will move faster while nitrogen has bonds that heat will be used to break, so there is less energy to go into increasing temperature. The warrant that the heat added would break nitrogen bonds indicates an incorrect understanding of bond energies. However, he was correct in considering nitrogen's bonds and the difference in mass between nitrogen and neon as significant. Quentin's argument builds on Reed's by explicitly considering both neon and nitrogen, specific vibrational modes, rotational, and translational modes. Both of these arguments indicate that students recognize that multiple variables (i.e. mass difference, bond difference, etc.) give rise to neon ultimately having the higher temperature. The warrants in multicomponent arguments tend to be the most complete and thorough, making consideration of multiple variables explicit. In the argument shown in Table 14, the students are considering entropy by discussing multiple facets of the concept.
| POGIL prompt | 2010 |
|---|---|
| As the temperature associated with the system is raised above 0 K, do you expect that the entropy of the system will increase or decrease? Explain your reasoning. | Claim: As temperature increases, entropy increases because of molecular movement (Jerome/Summer) |
| Data: Definition of a solid is no molecular movement | |
| Warrant: Because the lower you go [temperature], the less movement there is (Summer) | |
| Backing: Because you have more distributed energy states (Thaddeus) |
This argument provides evidence of students making sense of the concept of entropy by considering the definition of a solid, molecular motion, temperature, and energy states. Multicomponent arguments are especially complex, but are most apt for making sense of complex concepts such as entropy, which is inherently multifaceted. Because of this complexity, multicomponent arguments were by far the least frequent. These constitute quite sophisticated arguments, including thorough and complete justifications, in which students make their reasoning clear.
Conclusions
We used modes of reasoning in the CTLP to analyze and classify arguments generated by students in POGIL physical chemistry classrooms. Results showed that physical chemistry students did not frequently use descriptive reasoning, the least complex mode of reasoning. Students primarily used relational reasoning across both classrooms. Relational arguments draw on a relationship without explaining the relationship as sufficient justification for an outcome. These arguments were frequently generated in response to conceptual problems, indicating a possible comfort with drawing only from relationships to make sense of phenomena. Students did propose mechanisms in the form of linear and multicomponent arguments. Linear arguments generally took one of three forms, mathematical, conceptual, or hybrid. In the context of physical chemistry, students were frequently required to perform a derivation or calculate a value. These tasks elicited mathematical linear causal arguments that often follow a pattern of claim (output equation or value), data (starting equation), and warrant (how starting equation leads to final output). This pattern of argument serves to answer the question of “how” a mathematical output was computed. Employing causal reasoning to construct arguments in response to conceptual problems occurred less frequently, evidenced by the lower percentage of linear and multicomponent arguments.The results from our study demonstrate that students can construct arguments without necessarily including a causal mechanism. This counters what was expected based on previous work highlighting the usefulness of argumentation for prompting students to articulate their reasoning (Berland and Reiser, 2009). In this work, linear and multicomponent arguments that included evidence of cause and effect reasoning were more complete and thorough than the relational and descriptive arguments. That is, linear and multicomponent arguments were indicative of students verbalizing more of their reasoning and understanding; whereas relational arguments included little evidence of the students' understanding of relevant concepts. This points to an important relationship between how thorough an argument is and the type of reasoning used. Generating an argument that is clear, coherent, and comprehensive often requires students to employ cause and effect reasoning to sufficiently justify a claim.
Our analysis suggests that a link exists between the nature of the question or problem and the mode of reasoning that students use. There was a clear link between problems requiring the student to derive an equation or provide an expression and linear causal arguments that took a mathematical form that resulted. However, other links were less strong. For example, some multicomponent arguments were generated in response to questions prompting students to make some sort of prediction. Relational arguments, on the other hand, resulted from every question type. Although there appears to be a link between the question and the resulting argument, more research is needed to fully understand these relationships. One complicating factor is the role of instructor facilitation and the learning environment. Although examples of each type of reasoning was found in both cases, the degree to which they were used differed. Even though the students used the same instructional materials in both cases, the order of activities, use of whole class discussion, and other aspects of implementation varied. A more thorough investigation of these differences in facilitation has been conducted and will be detailed in a forthcoming publication.
Using the modes of reasoning in the learning progression on chemical thinking (CTLP) equipped us to distinguish arguments based on complexity of reasoning. This is the first instance of the CTLP being used to analyze classroom discourse. The CTLP was especially useful for characterizing arguments aimed at explaining an outcome of a phenomenon. It was not as insightful for characterizing arguments that included mathematical derivations or calculations, though these types of arguments are especially frequent in the context of physical chemistry.
Implications for teaching and research
One desired outcome of advanced chemistry coursework is the ability to generate robust arguments that use sophisticated causal models. To support students in developing this skill, instructors can use student argumentation as a platform for identifying and evaluating students' causal reasoning skills. Providing students with an argument model and making time in the classroom for students to build arguments offers the instructor exposure to students' reasoning. Throughout the course, explicitly prompting students to construct arguments can establish argumentation as a normative form of discourse in the classroom. Having students create arguments is not enough, however, instructors must also be attentive to the reasoning students are employing in their arguments.We recognize that different levels of reasoning are likely to be appropriate for considering different problems. In the context of physical chemistry, as students are constructing an understanding of thermodynamic concepts and relationships, they might rely primarily on relational reasoning. In some cases, this may be sufficient for sense-making. However, reliance on this reasoning may limit students' growth as they move forward in thermodynamics. For concepts that are abstracted from observable variables, such as entropy or Gibbs energy, a coherent understanding requires synthesizing an understanding of mathematical derivations with an understanding of chemical and physical implications. In order to make sense of chemical phenomena or solve complex problems, one must be able to consider multiple variables and how they interact with each other.
We propose two approaches instructors may use as they help students develop reasoning skills for understanding complex phenomena. Instructors can support students in developing this ability by modeling more complex causal reasoning in their lectures. Perkins and Grotzer (2005) found that explicitly teaching complex causal models improved students' causal reasoning. Using the modes of reasoning applied in this work, instructors are encouraged to explicitly discuss linear causal and multicomponent models, provide examples of each, and model these modes of reasoning in the arguments and explanations in their lectures. By explicitly modeling this reasoning, students are better equipped to apply it in their own reasoning. Instructors can also collaboratively construct arguments with their students to contribute variables students may not have included. This contribution can come in the form of core argument components (i.e. providing data or a warrant) or other components (i.e. rebutting or qualifying a student's argument). The benefits of collaboratively constructing arguments with students is two-fold. It supports students' causal reasoning by including variables students may not have considered. It also supports students' argumentation by building more comprehensive arguments.
In this work, we have demonstrated the utility of the modes of reasoning in the CTLP as an analytical tool and we have used it to describe the types of reasoning used in two POGIL physical chemistry classrooms. More research is needed to understand when students employ certain types of reasoning and how to scaffold these reasoning skills with students. This will involve elucidating the relationship between the types of reasoning students use and the problems being solved. An understanding of this relationship can be used to design and evaluate interventions for improving students' causal reasoning and argumentation.
Acknowledgements
We would like to thank the physical chemistry students who participated in this study.Notes and references
- Asterhan C. S. C. and Schwarz B. B., (2007), The effects of monological and dialogical argumentation on concept learning in evolutionary theory, J. Educ. Psychol., 99(3), 626–639.
- Becker N., Rasmussen C., Sweeney G., Wawro M., Towns M. and Cole R., (2013), Reasoning using particulate nature of matter: an example of a sociochemical norm in a university-level physical chemistry class, Chem. Educ. Res. Pract., 14, 81.
- Becker N., Stanford C., Towns M. and Cole R, (2015), Translating across macroscopic, submicroscopic, and symbolic levels: the role of instructor facilitation in an inquiry-oriented physical chemistry class, Chem. Educ. Res. Pract., 16, 769–785.
- Bell P., (2004), Promoting Students' Argument Construction and Collaborative Debate in the Science Classroom, in Linn M., Davis E. and Bell P. (ed.), Internet environments for science education, New Jersey: Lawrence Erlbaum, pp. 115–143.
- Bell P., (2000), Scientific arguments as learning artifacts: Designing for learning from the web with KIE, Int. J. Sci. Educ., 22, 797–817.
- Berland L. K and Reiser B., (2009), Making sense of argumentation and explanation, Sci. Educ., 93, 26–55.
- Berland L. K. and Reiser B. J., (2011), Classroom communities' adaptations of the practice of scientific argumentation, Sci. Educ., 95(2), 191–216.
- Bricker L. A. and Bell P., (2008), Conceptualizations of argumentation from science studies and the learning sciences and their implications for the practices of science education, Sci. Educ., 92, 473–498.
- Brown N. J. S., Nagashima S. O., Fu A., Timms M. and Wilson M., (2010), A Framework for Analyzing Scientific Reasoning in Assessments, Educ. Assess., 15(3–4), 142–174.
- Chase A., Pakhira D. and Stains M., (2013), Implementing Process-Oriented, Guided-Inquiry Learning for the first time: adaptations and short-term impacts on students' attitude and performance, J. Chem. Educ., 90(4), 409–416.
- Christodoulou A. and Osborne J., (2014), The science classroom as a site of epistemic talk: A case study of a teacher's attempts to teach science based on argument, J. Res. Sci. Teach., 51(10), 1275–1300.
- Cole R., Becker N., Towns M., Sweeney G., Wawro M. and Rasmussen C., (2012), Adapting a methodology from mathematics education research to chemistry education research: documenting collective activity, Int. J. Sci. Math. Educ., 10(1), 193–211.
- Committee on Professional Training, (2015), Undergraduate Professional Education in Chemistry: ACS Guidelines and Evaluation Procedures for Bachelor's Degree Programs, Washington, DC: American Chemical Society.
- Conway C., (2014), Effects of guided inquiry versus lecture instruction on final grade distribution in a one-semester organic and biochemistry course, J. Chem. Educ., 91, 480–483.
- Cooper M., Caballero M., Elbert-May D., Fata-Hartley C., Jardaleza S., Krajcik J., Laverty J., Matz R., Posey L. and Underwood, (2015), Challenge faculty to transform STEM learning: focus on core ideas, crosscutting concepts, and scientific practices, Science, 350(6258), 281.
- Driver R., Newton P. and Osborne J., (2000), Establishing the norms of scientific argumentation in classrooms, Sci. Educ., 84, 287–312.
- Duschl R., Schweingruber H. and Shouse A., (2007), Taking science to school: Learning and teaching science in grades K-8, Washington, DC: National Academy Press.
- Erduran S., (2007), Methodological foundations in the study of argumentation in science classrooms, in Erduran S. and Jimenez-Aleixandre M. (ed.), Argumentation in science education: Perspectives from classroom-based research, Dordrecht, The Netherlands: Springer, pp. 47–69.
- Erduran S. and Villamanan R., (2009), Cool argument: engineering students' arguments about thermodynamics in the context of Peltier effect in refrigeration, Educ. Quim., 20(2), 119–125.
- Erduran S., Simon S. and Osborne J., (2004), TAPping into argumentation: developments in the application of Toulmin's argument pattern for studying science discourse, Sci. Educ., 88(6), 915–933.
- Evagorou M. and Osborne J., (2013), Exploring young students' collaborative argumentation within a socioscientific issue, J. Res. Sci. Teach., 50(2), 209–237.
- Garcia-Mila M. and Andersen C., (2007), Cognitive Foundations of Learning Argumentation, in Erduran S. and Jiménez-Aleixandre M. (ed.), Argumentation in Science Education, Netherlands: Springer, vol. 35, pp. 29–45.
- Geelan D.R., (1997), Epistemological anarchy and the many forms of constructivism, Sci. Educ., 6, 15–28.
- Grotzer T. A., (2003), Learning to understand the forms of causality implicit in scientifically accepted explanations, Stud. Sci. Educ., 39, 1–74.
- Hein S., (2012), Positive impacts using POGIL in Organic Chemistry, J. Chem. Educ., 89(7), 860–864.
- Jimenez-Aleixandre M. and Erduran S., (2008), Argumentation in science education: An overview, in Erduran S. and Jimenez-Aleixandre M. (ed.), Argumentation in science education: perspectives from classroom-based research, Dordrecht, The Netherlands: Springer, pp. 3–27.
- John-Steiner V. and Mahn H., (1996), Sociocultural approaches to learning and development: a Vygotskian framework, Educ. Psychol., 31(3–4), 191–206.
- Kaya E., (2013), Argumentation practices in classroom: preservice teachers' conceptual understanding of chemical equilibrium, Int. J. Sci. Educ., 35(7), 1139–1158.
- Kelly G. J., (2008), Inquiry, activity and epistemic practice, in Duschl R. A. and Grandy R. E. (ed.), Teaching scientific inquiry: recommendations for research and implementation, Rotterdam: Sense Publishers, pp. 99–117.
- Kelly G. and Takao A., (2002), Epistemic levels in argument: an analysis of university oceanography students' use of evidence in writing, Sci. Educ., 86(3), 314–342.
- Kulatunga U. and Lewis J., (2013), Exploration of peer leader verbal behaviors as they intervene with small groups in college general chemistry, Chem. Educ. Res. Pract., 14(4), 576–588.
- Kulatunga U., Moog R. S. and Lewis J. E., (2013), Argumentation and participation patterns in general chemistry peer-led sessions, J. Res. Sci. Teach., 50(10), 1207–1231.
- Mercer N., (2004), Sociocultural discourse analysis: analyzing classroom talk as a social mode of thinking, J. Appl. Linguist., 1(2), 137–168.
- Mercer N., Dawes L., Wegerif R. and Sams C., (2004), Reasoning as a scientist: ways of helping children to use language to learn science, Br. Educ. Res. J., 30, 359–377.
- Moog R.S. and Spencer J.N., (2008), Process-Oriented Guided Inquiry Learning, Washington, DC: American Chemical Society.
- National Research Council, (2012a), A Framework for K-12 Science Education: Practices, Crosscutting Concepts, and Core Ideas, Washington, DC: National Academies Press.
- National Research Council, (2012b), Discipline-Based Education Research: Understanding and Improving Learning in Undergraduate Science and Engineering, Washington, DC: National Academies Press.
- Perkins D. N. and Grotzer T., (2005), Dimensions of Causal Understanding: The Role of Complex Causal Models in Students' Understanding of Science, Stud. Sci. Educ., 41(1), 117–165.
- Rasmussen C. and Stephan M., (2008), A methodology for documenting collective activity, in Kelly A. E., Lesh R. A. and Baek J. Y. (ed.), Handbook of innovative design research in science, technology, engineering, mathematics (STEM) education, New York: Taylor and Francis, pp. 195–215.
- Sevian H. and Talanquer V., (2014), Rethinking chemistry: a learning progression on chemical thinking, Chem. Educ. Res. Pract., 15(1), 10–23.
- Smith C., Carey S. and Wiser M., (1985), On differentiation: a case study of the development of the concepts of size, weight, and density, Cognition, 21, 177–237.
- Szteinberg G., Balicki S., Banks G., Clinchot M., Cullipher S., Huie R., Lambertz J., Lewis R., Ngai C., Weinrich M., Talanquer V. and Sevian H., (2014), Collaborative Professional Development in Chemistry Education Research: Bridging the Gap between Research and Practice, J. Chem. Educ., 91(9), 1401–1408.
- Taber K. S. and Watts M., (2000), Learners' explanations for chemical phenomena, Chem. Educ.: Res. Pract. Eur., 1(3), 329–353.
- Takao A. Y. and Kelly G. J., (2003), Assessment of Evidence in University Students' Scientific Writing, Science & Education, 12, 341–363.
- Toulmin S., (1958), The uses of argument, Cambridge: Cambridge University Press.
- Von Aufschnaiter C., Erduran S., Osborne J. and Simon S., (2008), Arguing to learn and learning to argue: case studies of how students' argumentation relates to their scientific knowledge, J. Res. Sci. Teach., 45(1), 101–131.
- Zohar A. and Nemet F., (2002), Fostering students' knowledge and argumentation skills through dilemmas in human genetics, J. Res. Sci. Teach., 39(1), 35–62.
| This journal is © The Royal Society of Chemistry 2016 |