View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5RP00215J (Paper) Chem. Educ. Res. Pract., 2016, 17, 296-308

Characterizing high school chemistry teachers' use of assessment data via latent class analysis†

Jordan Harshman and Ellen Yezierski *
Department of Chemistry and Biochemistry, Miami University, 501 East High Street, Oxford, OH 45056, USA. E-mail: yeziere@miamioh.edu

Received 30th November 2015 , Accepted 6th January 2016

First published on 14th January 2016

Abstract

In this study, which builds on a previous qualitative study and literature review, high school chemistry teachers' characteristics regarding the design of chemistry formative assessments and interpretation of results for instructional improvement are identified. The Adaptive Chemistry Assessment Survey for Teachers (ACAST) was designed to elicit these characteristics in both generic formative assessment prompts and chemistry-specific prompts. Two adaptive scenarios, one in gases and one in stoichiometry, required teachers to design and interpret responses to formative assessments as they would in their own classrooms. A national sample of 340 high school chemistry teachers completed the ACAST. Via latent class analysis of the responses, it was discovered that a relatively small number of teachers demonstrated limitations in aligning items with chemistry learning goals. However, the majority of teachers responded in ways consistent with a limited consideration of how item design affects interpretation. Details of these characteristics are discussed. It was also found that these characteristics were largely independent of demographics such as teaching experience, chemistry degree, and teacher education. Lastly, evidence was provided regarding the content- and topic-specificity of the characteristics by comparing responses from generic formative assessment prompts to chemistry-specific prompts.

Introduction

According to the Department of Education, teachers are expected to “use student data as a basis for improving the effectiveness of their practice” (Means et al., 2011). For high school chemistry teachers, there is rarely a shortage of available student data, as teachers have access to homework, quizzes, lab reports, classroom observations, activities, and exams. However, the design of the tools used to collect data and what the teachers do with data have not been investigated thoroughly. This paper will present select quantitative findings from a study that has previously been reported on qualitatively (Harshman and Yezierski, 2015a; Sandlin et al., 2015). We want to explicitly note that we are advocates for high school chemistry teachers and believe that all teachers can improve their skills in using data to improve their instruction. Any limitations in assessment practices discussed here are therefore presented as targets for professional development opposed to an affront to teachers.

Background

In educational literature, the process by which a teacher designs/administers an assessment and interprets the students' results to guide his/her instruction is called data-driven inquiry (Harshman and Yezierski, in press). Our extensive literature review covers the details available to data-driven inquiry (DDI), but we provide the four main steps here (italicized). First, a teacher needs to set goals that go beyond the traditional student learning objectives by incorporating instructionally-centered goals, viewing the data as having the potential to answer several inquiries (Copland, 2003; Knapp et al., 2006; Hamilton et al., 2009; Means et al., 2011). After designing, administering, and collecting an assessment, the teacher then examines evidence within the students' responses to the assessment items. Based on evidence, both from the assessment and from other sources (previous experiences, classroom observations, etc.), teachers then make (a) conclusion(s) about a variety of different things related to both students and teachers. Finally, based on the conclusions made, teachers will determine the best course of pedagogical action to address issues and support positive findings. From this description, it should be apparent that DDI is very similar to the practices of scientific inquiry that researchers employ throughout their studies.

In our literature review, we found that while suggestions for effectively carrying out DDI were plentiful and valuable, previous literature did not provide adequate specificity for how to successfully carry out DDI in content-specific classrooms and did not present many empirical studies for how DDI is actually carried out in classrooms (Harshman and Yezierski, in press). Both of these points were the basis for investigating the details of how chemistry teachers specifically guide their instruction via assessment results. In our previous qualitative study (Harshman and Yezierksi, 2015; Sandlin et al., 2015), we found that several teachers (out of 19 interviewed) did not design/choose assessment items that aligned well with their targeted learning goals, used evidence of various degrees of validity to make conclusions, and primarily made conclusions about students' level of understanding as opposed their own impact/effectiveness as teachers. A few different authors have investigated components of DDI processes in science and more specifically chemistry (Ruiz-Primo and Furtak, 2007; Tomenek et al., 2008; Izci, 2013; Haug and Ødegaard, 2015), but we were unable to find a related set of studies that provides examples of how teachers enact DDI in a high school chemistry classroom.

A number of the findings of this paper focus on setting content-specific learning objectives and designing assessment items that align with those learning objectives (goals). The literature divides goals into two components: learning goals set a priori and goals only set after data is collected. Here, we focus on the learning and teaching goals set before an assessment is designed so that we can characterize how teachers align their goals with their assessment items (Calfee and Masuda, 1997; Hamilton et al., 2009). This alignment between teaching and learning goals is critically important, because proper alignment is required to make valid conclusions regarding teaching and learning. This work also derives from an existing discussion of instructional sensitivity, which is the extent to which assessment results can be used to determine instructional effectiveness (Popham, 2007; Polikoff, 2010; Ruiz-Primo et al., 2012).

In setting the scope for this paper, we focus only on written formative assessments. Formative assessment is better defined as what a teacher does with the assessment results than design features of specific sets of items or timing of administration (Wiliam, 2014). For this project, if the assessment results could be used to inform/guide teaching, it was considered within the purview of the study. We focused on formative assessments because formative assessments usually warrant examination of results for purposes other than evaluation. While teachers certainly can and do enact other types of assessments in non-written mediums (such as through reflection, Schön, 1987), we focused solely on how teachers use written student responses. Additionally, a comprehensive study in every topic typically taught in high school chemistry is well beyond the scope of this article; we focus on two common topics, gases and stoichiometry.

Theoretical assumptions

Because teachers' assessment practices, and not students' learning, is being investigated, we have outlined a theory of how teachers use data to inform their instruction in DDI. Thus, we assume that high school teachers purposefully design items on their assessments (or choose them from existing resources) to provide information which they can use to make inferences about student understanding and inform their actions based on those inferences. The assumption that this occurs to some degree, whether consciously or sub-consciously, is not in question, but rather to what fidelity this process is enacted is in question.

Research questions

The purpose of the study reported here is to describe the characteristics of a national sample of high school chemistry teachers in terms of use of their assessment data to inform instructional practices. This paper addresses the chemistry-specific findings from two scenarios, but the responses to more generic formative assessment prompts are only briefly discussed here. (For additional information, see Chapters 3 and 5 of Harshman, 2015). The research questions that guided this study are:

(1) What characteristics can be identified in responses of a national sample of high school chemistry teachers to chemistry scenarios that mimic designing assessment items and interpreting assessment results?

(2) To what degree do teacher demographics predict characteristics observed in these chemistry-scenarios?

(3) To what degree are the characteristics determined by chemistry-specific prompts different than response patterns from generic formative assessment prompts?

Methods

Development of the adaptive chemistry assessment survey for teachers

To assess DDI practices of high school chemistry teachers, we designed a survey called the Adaptive Chemistry Assessment Survey for Teachers (ACAST) based on previous qualitative results (Harshman and Yezierski, 2015a) and relevant literature. This survey consists of two main portions: one that elicits self-reported beliefs and practices related to DDI in a general sense and one that presents teachers with two chemistry scenarios where teachers are asked to choose formative assessment items that would assess particular content goals and interpret hypothetical student results. The two scenarios were on the topics of stoichiometry and gases. These topics were chosen because they both have conceptual and algorithmic components and are commonly found in the high school curriculum. Items found on the ACAST were designed in one of two ways. The generic formative assessment prompts (12 items, labels start with “I”) were designed based on previous qualitative results (as suggested by Cresswell, 2003; Towns, 2008; Brandriet and Bretz, 2014; Luxford and Bretz, 2014). For example, I9a–d in Fig. 1 resulted from specific quotes from interviews that asked teachers what they did and did consider when choosing/making their assessment items.
image file: c5rp00215j-f1.tif
Fig. 1 I9a–d on the ACAST.

Refer to Appendix A (ESI†) for a summary of all the items on the ACAST. We highly advise the reader to review the full online survey at http://tinyurl.com/otxc8sp to better understand the two scenarios. Back buttons have been added to allow the reader to investigate how the survey adapts to different responses. While the chemistry-specific scenarios were also informed by the qualitative results, they were designed around overarching themes as opposed to individual teacher quotes. For example, several teachers demonstrated misalignment between learning goals and the items they would use to assess those goals, so we designed a scenario that would allow teachers to align or misalign items with learning goals. These scenarios in gases and stoichiometry were adaptive to teachers' responses, meaning that the prompt a teacher received was dependent on how that teacher responded to the previous prompt.

The gases scenario

In the gases scenario (labels start with “G”), teachers responded to three phases. In the first phase, teachers choose the most important goal to assess if they were building a formative assessment about gases content from five options. In the second phase, teachers choose any item(s) from seven that they believed assessed the goal they selected in the previous phase. The items and corresponding student tasks are listed in Table 1.
Table 1 Items and student tasks for gases scenario
Item Item Student task
G1 If a fixed-volume container of an ideal gas is cooled, its pressure decreases. Which gas law best describes this behavior? Recall name of scientist that defined P–V relationship
G2 According to Charles' law, what will happen to the volume of a balloon filled with an idea gas if temperature is decreased? Recall what happens to V given change in T according to Charles' Law
G3 If you were to maintain temperature and number of moles, how would an increase in pressure affect the volume of an ideal gas? Explain change in volume given change in pressure
G4 Describe and draw (a) gas molecules in a balloon and (b) the same molecules after a decrease in temperature assuming constant pressure and moles. Determine effect of doubling pressure on volume
G5 Assuming that temperature and number of moles is constant, what effect would doubling the pressure have on the volume of an ideal gas? Calculate Tf given Ti, Pi, and Pf
G6 An ideal gas in a closed container (fixed volume and number of moles) has a pressure of 1.3 atm at 298 K. If the pressure is decreased to 0.98 atom, what will the final temperature be? Predict increase/decrease in V given Ti and Tf
G7 If the volume of an idea gas is 3.4 L at 298 K, will the volume be larger or smaller if the temperature is raised to 315 K? Describe and draw particle diagram before and after change in T

Lastly, for every item chosen, teachers were prompted to determine what content, in addition to the content it was originally chosen to assess, their chosen item(s) assess(es). As an example series of responses, a teacher that believes that particulate level PVnT relationships are the most important to assess may select G7 to assess that goal, and then select what additional content is assessed by G7.

The seven items in the gases scenario were designed so that teachers' responses could be analyzed in two ways. The first analysis, curricular alignment, assessed the degree to which an item assessed the goal chosen by the teacher. For example, if a teacher wanted to determine PVnT relationships on a particulate level, only G7 (and possibly G3 and G4) assess particulate relationships while the other items do not. The second way responses were analyzed was considering the item's validity of evidence of understanding. This validity of evidence of understanding (VEU) was determined by the authors and six additional chemistry education experts in a novel validity evaluation called meta-pedagogical content validity (see “Validity” sub-section) and is best described via an example: If a teacher wished to determine students' understandings of PVnT relationships (particulate, macroscopic, or symbolic domains), all items assess PVnT relationships (except G1 and G2, which likely assess rote memorization more so than actual understanding; although this depends on what “understanding” entails). However, if one considers the results students will produce in responding to items, those results, or data, have different levels of validity in the determination of students' understanding. G5 and G6, for example, can be solved using algorithms “without any understanding or reflection of the meaning of calculations,” in the words of one of our chemistry education experts. Because of this, when a teacher sees the correct answer to these items, s/he cannot validly determine, based on the evidence available to him/her, the degree to which the student understands the relationship as opposed to being able to get the right answer due to sufficient algebraic skills. As such, our six experts largely agreed that G5 and G6 would have lower VEU compared to G3, G4, and G7. In these latter items, the level of understanding will be easier to detect, making for more valid determination of students' understanding, meaning G3, G4, and G7 have higher VEU. As such, G3, G4, and G7 are referred to as the “expert recommended” items in the gases scenario.

The general structure of the gases scenario (select goal, then select items, etc.) was informed largely by the process that teachers generally discussed during the qualitative interviews and accurately reflected how they thought about designing their assessments. Each of the seven questions was chosen based on typical questions that could be found in high school textbooks and to ensure a collection of items that assessed a variety of features of a topic. This variety in item selection would ensure that teachers would have items available to them that they would normally have in the classroom setting.

The stoichiometry scenario

Teachers responded to the stoichiometry scenario which consists of five phases (labels start with “S”). First, teachers choose which one of four items best assessed mole-to-mole ratios only. S1 and S2 were designed with 1[thin space (1/6-em)]:[thin space (1/6-em)]1 mole ratios and S3 and S4 were designed with 3[thin space (1/6-em)]:[thin space (1/6-em)]1 ratios. Additionally, S1 and S3 assessed multiple concepts (required students to know nomenclature, write/balance a chemical equation, and convert from grams to moles) whereas S2 and S4 assessed only mole-to-mole ratios (balanced equation given and starting information was in moles). Some teachers did not see a difference between some items during response-process validation interviews. For this reason, we added “either S1 or S3” and “either S2 or S4” as response options. The exact wording of these items can be found in Table 2.
Table 2 Items and what is assessed in each for stoichiometry scenario
Item Item Assessed
S1 If 2.34 g of sodium chloride reacts with excess silver nitrate, how much (in moles) silver chloride would be produced? Multiple concepts assessed, 1[thin space (1/6-em)]:[thin space (1/6-em)]1 mole-to-mole ratio
S2 If 0.0155 mol barium chloride reacts with excess sodium sulfate, how much (in moles) barium sulfate would be produced? Balanced equation is:

BaCl2(aq) + Na2SO4(aq) → BaSO4(s) + 2NaCl(aq)

 Single concept assessed, 1[thin space (1/6-em)]:[thin space (1/6-em)]1 mole-to-mole ratio
S3 If 2.34 g of calcium chloride reacts with excess sodium phosphate, how much (in moles) calcium phosphate would be produced? Multiple concepts assessed, 3[thin space (1/6-em)]:[thin space (1/6-em)]1 mole-to-mole ratio
S4 If 0.00788 mol of barium bromide reacts with excess lithium phosphate, how much (in moles) barium phosphate would be produced? Balanced equation is:

3BaBr2(aq) + 2Li3PO4(aq) → Ba3(PO4)2(s) + 6LiBr(aq)

 Single concept assessed, 3[thin space (1/6-em)]:[thin space (1/6-em)]1 mole-to-mole ratio assessed

Once teachers chose the item (or pair of items) they thought would best assess mole-to-mole ratios, they chose what format of results (total number correct/incorrect or individual student work) they would examine to determine students' understanding of mole-to-mole ratios. Based on the item and format of results chosen, teachers were then given (a) hypothetical student response(s) and asked to determine if the student(s) response(s) provided evidence demonstrating understanding of mole-to-mole ratios, dimensional analysis, writing/balancing equations, and calculating molar mass. Because not all of these topics are assessed by all of the items and formats, teachers were given the option “cannot determine.” Regardless of the ratio in the item teachers chose, the example of student work was always a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 setup. Once teachers determined the (mis)understanding demonstrated in his/her hypothetical results, they were prompted to choose from a number of pedagogical responses to address any content deficiencies.

Finally, the teachers were given an item that they did not originally choose, a hypothetical response to that item, and were asked to determine understanding and choose pedagogical actions for this new item and data. The new item was assigned to teachers based on a simple algorithm: if a teacher originally chose S4, they were given S1. If a teacher chose any response other than S4, they were given S4 for the last phase of the scenario. This was to ensure that every teacher made conclusions using data from S4. According to the chemistry education experts and authors, S4 had the highest VEU and should be considered alongside individual student results as opposed to aggregated scores so that more information is available to lead to valid conclusions. As an example series of responses, a teacher might select S3 as being the best item to assess mole-to-mole ratios and would analyze the results of S3 by looking at individual student work. This teacher would then be given an example student response displaying a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio and ask to mark what the student does (not) understand.

The general structure of the stoichiometry scenario questions (choose an item, response format, and conclusions) was guided by the DDI framework. The process of allowing teachers to select a hypothetical assessment and interpret hypothetical data seemed to be the best way to capture most of the DDI process as a whole. The wording of the items, response choices, and conclusions were derived from actual words used in the previous qualitative studies with teachers or constructed to match typical questions found in high school chemistry texts.

Validity

As mentioned previously, a meta-pedagogical content validity evaluation was employed. The nomenclature of this technique derives from the goal of meta-cognitively thinking about what pedagogical inferences can be made about teachers given their responses to prompts. The content of these prompts are used to evaluate the validity associated with the inferences made. First, assertions were made by the authors regarding what inference(s) would be made given certain response patterns. As an example, the following assertion was made regarding selection of G5 and G6: “Knowing that students can solve mathematical equations without understanding the concepts behind them, [G5 and G6] cannot [validly] determine students' understanding of the relationships between pressure, volume, temperature, and/or moles.” Thus, the inference we would make about teachers that chose G5 or G6 was they either had not considered students' ability to solve problems correctly without understanding the concepts, or did not think it affects interpretations in a significant way. Six chemistry education experts then responded to each assertion, stating their (dis)agreements. In essence, these experts served as “preemptive journal reviewers” so that adjustments could be made to the ACAST prior to data collection.

Teachers could respond to items throughout the ACAST in contradictory/nonsensical ways, so the frequency and severity of these possible contradictions were examined (idea based on discriminant validity, Barbera and VandenPlas, 2011). No significant issues were detected as a result. Lastly, 14 high school teachers participated in response-process interviews (American Educational Research Association, 1999, 2014; Desimone and Le Floch, 2004). For response-process and meta-pedagogical content validation, a summary of all issues discovered and respective changes made can be found in Appendix B (ESI†).

Reliability

Evidence for reliability of data produced by the ACAST was examined in another publication (Harshman and Yezierski, 2015). For nominal and dichotomous items on the ACAST, the method described by Brandriet and Bretz (2014) was used. For this, we calculated the percentage of teachers who were and were not consistent from the test to the retest administration and subsequently tested those for significance via a chi-square goodness of fit. With appropriate effect size analysis, this yielded evidence that teachers responded consistently for most nominal level items. For interval and ordinal items, a novel method was proposed as an alternative to traditional test–retest correlations (Harshman and Yezierski, 2015b). A summary of the evidence for reliability can be found in Appendix C (ESI†). This method entailed defining a range of measurement error called the zeta-range. This range for each item was defined in earlier response–process validation interviews. Given the actual test and retest responses of 62 teachers, we calculated a 95% confidence interval to estimate the proportion of teachers that would fail to respond within measurement error via a bootstrap analysis. Several items not discussed in this paper showed evidence that teachers did not respond in a reliable manner from the calculation of this confidence interval. As opposed to deeming individual items or the ACAST as a whole reliable or unreliable, inferences made from items that produced less reliable data are discussed in less certain terms while greater certainty is applied to inferences made on items that produced more reliable data.

Participants

High school chemistry teachers were recruited via national and state National Science Teachers Association and American Association of Chemistry Teachers listservs. Additional recruitment occurred at the 2014 Biennial Conference for Chemical Education. Complete data from 340 chemistry teachers were collected. This included teachers who did not respond to at most six items (10% of the ACAST) and were subjected to imputation via mean (interval) or mode (ordinal and nominal). While this treatment of missing data is severely limited (Brandriet and Holme, 2015), only 0.5% of the data were imputed in this manner. Of these 340 teachers, 62 took the ACAST a second time within 10–14 days after completing it originally as a part of the test–retest study. Teachers were incentivized to participate by offering a $50 Amazon gift card with a lottery. All data were analyzed via R version 3.1.2 (R Core Team., 2014).

Latent class analysis

Modeling via latent class analysis (LCA) is a robust means of discovering latent characteristics given participant responses to nominal and ordinal prompts (Hagenaars and McCutheon, 2002; Collins and Lanza, 2009). In this data-mining technique, a number of classes (groups of participants with the same latent characteristics) are determined by modeling probabilities that they respond to an input variable in a certain way (i.e., 75% probability of choosing option A, 25% probability of choosing option B) for one of the input variables. The “fit” of the model is the degree to which the model accurately predicts the actual data. In this study, the final models were determined based on empirical evidence (fit statistics, convergence, clarity of global maxima, and most diametric posterior probabilities) and theoretical evidence (meaningful inferences, aligned with theory, and minimum number of teachers in nonsensical or interpretable classes). Fit statistics result from 25 random-start repetitions with a maximum iteration of 104 and a tolerance of 10−10 for convergence. All models discussed in this paper converged on a maxima.

It is important to note that LCA carries an assumption of local independence (Hagenaars, 1998; Ubersax, 2009), which is clearly violated by the adaptive chemistry scenarios. Violation of this assumption has an unpredictable effect on the results and leaves the researcher with either more theoretically sensible models with heightened potential for misspecification or empirically superior models that are much more difficult to make sense of theoretically (Reboussin et al., 2008). To minimize the risk of misspecification, we have corroborated all findings with other models, descriptive statistics, validation interviews, previous qualitative results, and emphasize the presence of characteristics over the exact proportion of teachers that exhibit each characteristic.

Results and discussion

This section is broken into four sub-sections. In the first sub-section, the demographics are displayed. In the next sub-section, we describe the assessment characteristics of chemistry teachers based on the two chemistry scenarios (research question 1). Next, we explore the demographic composition of teachers that have certain characteristics (research question 2). Lastly, we present evidence for the content- and topic-specificity of the characteristics measured (research question 3).

Demographics

Table 3 and Fig. 2 show the demographics of the sample. In Table 3, “Education Degree” refers to a teacher who went through a formal teacher preparation program as a part of their bachelor degree and the four options listed in “Science Degree” were determined by the individual teachers' degree. School location (not shown) was made according to Common Core of Data classification system (National Center for Educational Statistics, 2015).
Table 3 Demographics of national sample
Demographic Count Demographic Count
Sex Education Degree
Male 103 Education 75
Female 237 No Education 265
School Type Science Degree
Public 277 Chemistry 131
Private 56 Biology 64
Other 7 Both 113
Neither 32


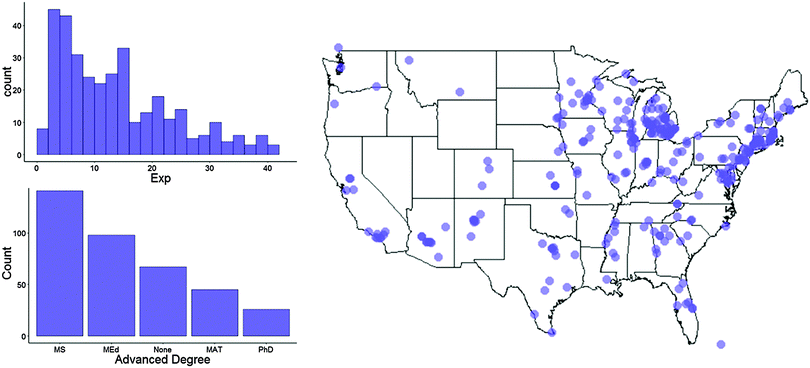image file: c5rp00215j-f2.tif
Fig. 2 Shows years of teaching experience (top left), post baccalaureate degrees (bottom left), and location (right) of national sample.

According to a recent census of high school chemistry teachers (Smith, 2013), our sample demographics closely matched those of the national population of chemistry teachers with the exception of biological sex (our sample was over-representative of females).

Assessment characteristics of chemistry teachers

The gases scenario. Due to the adaptive nature of the ACAST, it is difficult to display the descriptive results to the scenario items efficiently. As an attempt to display this information, Fig. 3 shows the distribution of the responses to the gases scenario.
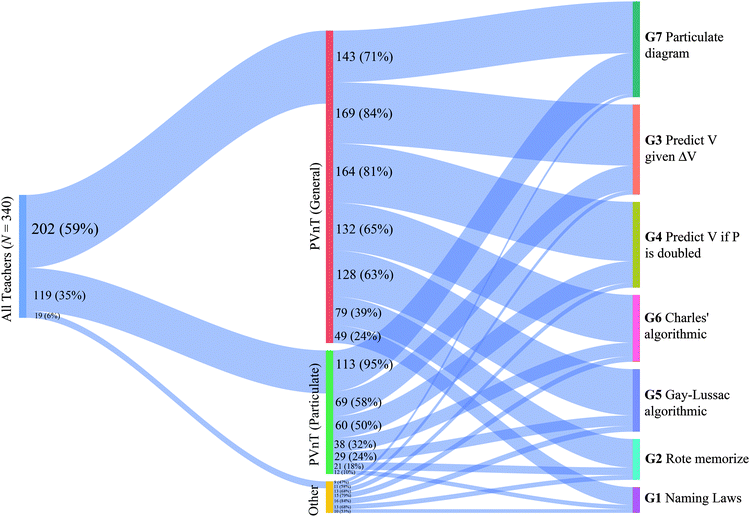
image file: c5rp00215j-f3.tif
Fig. 3 Distribution of gases scenario responses.

The national sample of teachers were largely split between focusing on particulate PVnT relationships (35%) or PVnT relationships with no domain specified (59%). The other 6% of teachers chose one of the other three options. From Fig. 3, it is apparent that regardless of which of the two common goals chosen, particulate versus no specific domain PVnT relationships, meaningful proportions of teachers selected a variety of items they would use to assess that goal. This indicates that a smaller proportion (10–32%) of our sample of teachers did not demonstrate curricular alignment by choosing items that do not assess their chosen goal.

While examining aggregated results is insightful, answering our first research question required investigation of groups of items that were chosen together by individual teachers, for which we modeled using LCA. A total of 57 models were considered using various input responses. However, only six models (four in the gases scenario, two in the stoichiometry) were empirically and theoretically viable, and as such, we based all inferences on those six models. The fit statistics for all six are presented in Table 4.

Table 4 Fit statistics for six models
Scenario Model Classes χ 2 p (χ2) G2 p (G2) AIC BIC
a In LCA, a p-value greater than 0.05 is preferred because it indicates no significant differences from observed proportions to those predicted by the model.
Gases 1 5 126.8 0.004 104.4 0.112 2534 2684
Gases 2 6 91.0 0.189 78.8 0.515 2524 2705
Gases 3 4 402.2 <0.001 216.4 0.557 3091 3287
Gases 4 7 153.8 0.983 129.1 0.999 3057 3402
Stoichiometry 5 4 15.1 0.515 15.39 0.496 1601 1766
Stoichiometry 6 4 297.2 0.007 72.1 1.000 1916 2135

Models 1 and 2 (gases) modeled the selection of items; Models 3 and 4 (gases) modeled selection of goals and items; Model 5 (stoichiometry) modeled item selection, response format, and determination of understanding; Model 6 (stoichiometry) was the same as Model 5 with the addition of determination of understanding made in the second iteration. For space concerns, the results from two of these models (Models 4 and 6) will be presented. Results of models not discussed here can be found in Appendix D (ESI†). LCA that modeled the last phase in the gases scenario (selection of additional content assessed by items) and the pedagogical outcomes in the stoichiometry scenario did not converge, likely due to the large number of variables present in these models. As such, we based no inferences on responses from the last phase of the gases scenario.

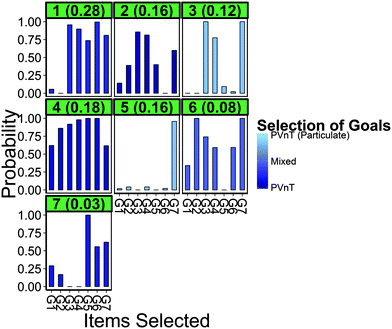
Results for Model 4 are shown in Fig. 4 and identified characteristics are consistent with those results observed in Models 1–3. Due to the large amount of information that results from LCA models shown in Fig. 4, we provide an example interpretation. Teachers in Class 5 (center graph, second row) are predicted to represent 15.7% of the population of chemistry teachers. These teachers have a very high probability of choosing particulate PVnT goals (light blue), a very high probability of selecting G7 to assess this goal, but very low probabilities of selecting any of the other items (seven bars in the bar graph). Thus, the model predicts that based on the 340-teacher sample, 15.7% ± 2.1% (errors not shown in Fig. 4) of the population of chemistry teachers will respond in this manner, which reflects a high degree of curricular alignment (due to the high selectivity of G7) and exemplar consideration of the VEU of items (due to the low selectivity of other items).


image file: c5rp00215j-f4.tif
Fig. 4 Model 4 predicted class memberships. Shows the probability (y-axis) that teachers in a certain class (arbitrarily numbered 1–7 in green bars with rounded proportions in parentheses) choose the seven items (x-axis) and the probability they choose a certain goal (color gradient, light/dark blue means high probability for particulate/nonspecific domain PVnT goal).

Classes 2 and 3 exhibit a similar signal by having higher probabilities of choosing G3, G4, and G7, the expert recommended items. However, these classes differ in two ways. First, Class 3 has a high probability of selecting particulate-focused PVnT goals where Class 2 is not likely to specify the particulate domain. Model 4 provides evidence that this difference in goal selection leads to another observed difference – the heightened signal-to-noise ratio of Class 3 over Class 2 (where the signal is the probability of selecting the expert recommended items and the noise is that of selecting any of the other items). This is an interesting finding as it suggests that goal selection, which is dependent on chemistry content knowledge and curricular values, may be driving selectivity of items and teachers' consideration of VEU of items. Teachers in Class 3 are predicted to choose the more specific goal and not choose items with lower VEU as frequently as those in Class 2, who do not specify the domain of their PVnT relationship goal. While we do not want to rely on precise quantification, Models 1–4 predicted that approximately 25–35% of teachers do not include items with lower VEU, implying that the majority of teachers are likely to include these items on their classroom formative assessments. This is clearly observed in the two largest classes, Classes 1 and 4. These response patterns alone indicate that in addition to the expert recommended items, a predicted 45.8% of chemistry teachers are likely to include items with lower VEU and possibly items that do not align at all with their learning goals. Classes 6 and 7 are smaller classes that have no meaningful interpretation.

Stoichiometry scenario. Two plots that display the response patterns of the teachers for the stoichiometry scenario can be found in Appendix E (ESI†). Models 5 and 6 easily converged due to the high degree of homogeneity in the responses (72% of the sample decided either S2 or S4 would best assess mole-to-mole ratios). The results of Model 6 are shown in Fig. 5.
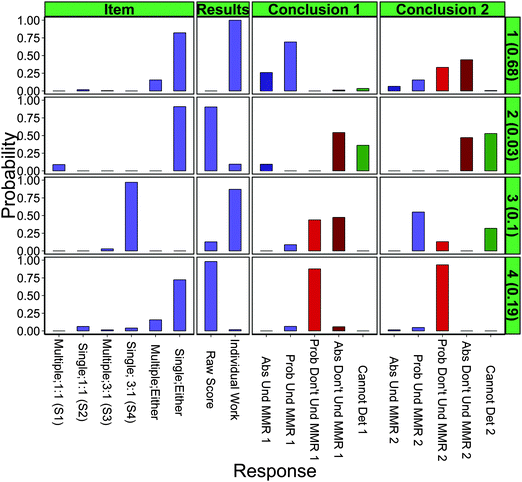
image file: c5rp00215j-f5.tif
Fig. 5 Model 6 predicted class memberships show the probability (y-axis) that teachers in a certain class (arbitrarily numbered 1–4 in green bars on right with rounded proportions in parentheses) respond in a certain way (x-axis) to each phase of the stoichiometry scenario (green bars on top). Colors only used as reference in text.

As an example interpretation of Class 3 (third row), which is predicted to represent 10.1% ± 1.7% of chemistry teachers, these teachers were very likely to select S4 (expert recommended, single concept, 3[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio) as the item that best assesses mole-to-mole ratios (“Item” column). They also exhibited a high probability of examining individual responses as opposed to aggregated scores (“Results” column). As a consequence, most of these teachers were presented with a hypothetical student response that showed an incorrect use of a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 mole ratio instead of a 3[thin space (1/6-em)]:[thin space (1/6-em)]1 mole ratio, which lead the majority of the teachers to determine that the student either absolutely or probably did not understand mole-to-mole ratios (red bars in “Conclusion 1” column). After making their determinations, these teachers determined appropriate pedagogical actions (not shown in Fig. 5 and not included in models). Finally, these teachers repeated the interpretation of student results, this time being given Item 1 (multiple concepts, 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio). They were shown an example of a student using a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio, and many concluded that the student probably understood, but some could not determine understanding of mole-to-mole ratios (green and blue bars in “Conclusions 2” column). Characteristics of this group align very well with DDI theory, as they recognize the impact that the change in mole-to-mole ratio will have on the validity of their findings and as a result, make a decision to focus only on the 3[thin space (1/6-em)]:[thin space (1/6-em)]1 item, choose to examine the most evidence, and make appropriate conclusions. However, this model predicted that these characteristics will only be present in about a tenth of chemistry teachers.

The vast majority (67.9 ± 2.5%) of teachers were predicted to possess the characteristics outlined in Class 1. These teachers did not choose one item and instead selected pairs of items. As was suggested by our response–process interviews, choosing item pairs as opposed to just one item indicated these teachers either did not recognize the difference in mole-to-mole ratios in the two items or recognized it, but did not think the change would make a substantial difference in interpretation of student results. Approximating how many teachers were thinking each of these possible ideas was done by comparing their first round of conclusions that used an item with a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio with their second round of conclusions that used an item with a 3[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio. From the first to the second determination of understanding, about 20% claimed that the example student (using a 1[thin space (1/6-em)]:[thin space (1/6-em)]1 ratio) demonstrated understanding for both the 1[thin space (1/6-em)]:[thin space (1/6-em)]1 and 3[thin space (1/6-em)]:[thin space (1/6-em)]1 items, indicating that these teachers did not notice the change in mole-to-mole ratio. Alternatively, approximately 75% changed their response in the second determination to account for the change in mole ratio of the item, indicating that this group of teachers noticed the change in ratios, but did not originally think it would affect the results. If they did, they would have chosen one item over the other. These specific proportions (20% and 75%) are estimates of probabilities of a probability with known error, but are informative even with a relatively high degree of uncertainty in the specific quantification.

The other two classes are difficult to interpret. Class 2 is a very small random-pattern group while Class 4 represents a sizeable portion of the national sample of teachers (18.7 ± 2.2%). The selection of an item for Class 4 is scattered, making it difficult to infer any characteristics from this group. However, the group appears to be quite homogenous in what format of results they choose to examine. Therefore, we can infer that this group of teachers chooses to analyze aggregated scores over individual work, but little else.

Predicting membership based on demographics

The LCA results provided strong evidence for the existence of characteristics in teachers' response patterns to the ACAST scenarios that imply varying levels of chemistry content, pedagogical, and pedagogical content knowledge. Therefore, we investigated the degree to which these characteristics, identified by class membership, were predicted by demographics collected. For the years of teaching experience (interval measure), this was tested using an ANOVA, shown in Table 5.
Table 5 ANOVA results (dependent variable: years of teaching experience; between-subjects factor: class membership with differing numbers of levels, 4–7 depending on the model tested)
Model Classes df F P η 2
1 5 4 2.71 0.030 0.03
2 6 5 2.23 0.052 0.03
3 4 3 2.03 0.109 NA
4 7 6 2.73 0.013 0.05
5 4 3 0.46 0.701 NA
6 4 3 0.92 0.433 NA

From these results, it is very clear that the years of teaching experience is not related to class membership in any of the six models for our national sample of teachers. The assumptions for ANOVA were tested prior to analysis. While some of the groups displayed non-normal distributions (tested by Anderson–Darling), ANOVAs are generally robust to deviations from normality and no visual differences were detected by examination of graphs of descriptive statistics. While results from models 1, 2, and 4 show a significant p-value, the effect sizes are very small, indicating that these differences detected are either spurious or indicative of very weak associations. For nominal-level demographics (sex, education degree, school type, location, and chemistry emphasis in bachelor), a chi-square analysis would be appropriate, but potentially misleading due to limitations in post hoc testing, cell-size restrictions, and overall sample size. As an alternative, we have plotted the expected (by probabilistic calculation, incorporating standard errors to give a range of expected values) versus observed memberships by demographic for all six models and every demographic. An example of these plots is displayed in Fig. 6.


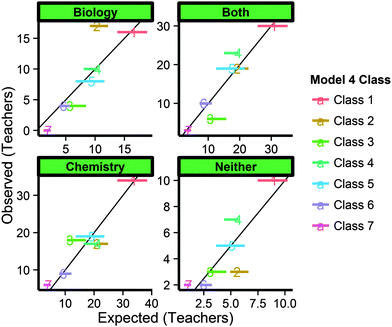image file: c5rp00215j-f6.tif
Fig. 6 Range of expected (horizontal lines) versus observed frequencies for class membership in Model 4.

These plots provide much more information than a chi-square statistic can give because instead of just focusing on overall change across 28 cells (four demographic categories for seven classes), this graphic displays expected versus observed frequencies for each class. For example, 18.4% of the 321 teachers included in Model 4 majored in a biology-related field only. Additionally, Model 4 predicted that 15.5% to 20.7% of teachers belong to Class 2. When class assignments were made by the model, 17.4% of the teachers were assigned to Class 2. Therefore, the range of expected teachers that would have biology-only degrees and belong to Class 2 would be from 2.9% (9.2 teachers) to 3.8% (12.2 teachers), and based on how many were actually assigned to Class 4, 3.2% (10.3 teachers) of Class 2 would be expected to have biology-only degrees. In Fig. 6, the orange line of the “Biology” facet displays the range of expected values (9.2–12.2 teachers) where the label “2” marks the expected value given actual class assignments (10.3). The positioning at y = 17 indicates that 17 teachers in the sample were members of Class 2 with biology-only degrees, indicating a slight overrepresentation of biology-only degrees in Class 2. However, this difference of approximately five to eight teachers out of over three hundred is not meaningful, nor did this trend appear in the other models. In interpreting these plots, it is helpful to note that any range of expected values that does not intersect with the diagonal line (where expected is equal to observed) suggests over- (above/left of diagonal) or under- (below/right of diagonal) represented class membership for that demographic. However, the absolute number of teachers in the over-/under-represented demographic as well as whether or not a similar trend was observed in similar models should be considered before drawing inferences.

This visual display was used to compare expected versus observed frequencies qualitatively for every model and every nominal-level demographic. In this investigation, it was found that not a single demographic resulted in consistent and meaningful over- and under-representation in any of the classes with one exception. Male chemistry teachers were consistently 1.2–1.6 times as likely as female teachers to demonstrate characteristics similar to Classes 4 and 1 in Model 4. Without pertinent theory to explain this trend, we do not make any inferences based on it. With no other meaningful trends observed, it was determined that bachelor education preparation, chemistry emphasis in bachelor degree, and other demographics were independent of the characteristics reported earlier. While it seems contrary to conventional wisdom that content-specific training and teaching experience will lead to improved data-driven inquiry, our results indicate that bachelor education preparation, chemistry emphasis in bachelor degree, and other demographics were independent of the characteristics reported earlier.

Content- and topic-specificity of data-driven inquiry

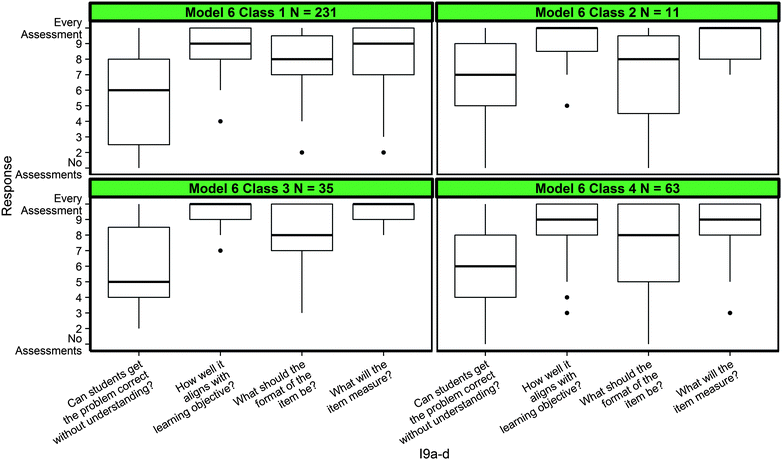
While this paper has focused exclusively on the chemistry scenarios, it is necessary to briefly mention the twelve generic formative assessment items used to gauge content and topic specificity of DDI practices. These items were designed to be analogous to the chemistry-based prompts. For example, I9 (Fig. 1) asks teachers how often they think about the alignment between assessment items and learning goals, the format items should be in (multiple choice, free response, etc.), and whether or not the student responds correctly without understanding the concepts. These three ideas are either directly or indirectly present in the gases and/or the stoichiometry scenarios and characteristics discovered were based on some of these ideas (i.e. Classes 3 and 5 in Model 4 demonstrated exemplar alignment between items and goals). Therefore, if sensible patterns between teachers' responses to generic formative assessment prompts and class membership based on chemistry-specific prompts were found, that would provide evidence that these DDI characteristics are similar in each setting. The opposite (no patterns between the responses to different prompts) would indicate that DDI characteristics are intrinsically different in generic formative assessment contexts versus chemistry-specific contexts. Therefore, we produced graphs of responses to the twelve generic items broken down by each class of the six modeled solutions and compared them side-by-side to qualitatively detect any differences. An example of I9a–d broken down by classes found in Model 6 is provided in Fig. 7.
image file: c5rp00215j-f7.tif
Fig. 7 Shows the responses to I9a–d broken down by Classes identified in Model 6.

In Fig. 7, no meaningful differences were observed between the characteristics identified in Model 6 to the responses of I9a–d. This was consistent when breaking down all responses to generic formative assessment items (12 items) by all possible class groupings (30 classes in total), providing strong evidence that the generic formative assessment prompts elicited different characteristics than the chemistry-specific prompts.

With evidence that elicitation of DDI characteristics was different depending on the context, we used the same visualization as with the demographics (Fig. 6) to determine if members of classes identified in the gases scenario were also members of certain classes identified in the stoichiometry scenario. As an example, teachers who demonstrated strong content alignment in the gases scenario (Classes 3 and 5 in Model 4) would be expected to demonstrate strong content alignment in stoichiometry (Class 3 in Model 6) if the general skill of aligning items with goals was independent on the specific chemistry topic. However, Fig. 8 shows that this is not the case, as teachers categorized into Classes 3 or 5 in Model 4 and Class 3 in Model 6 is as expected if the teachers were completely randomly distributed.


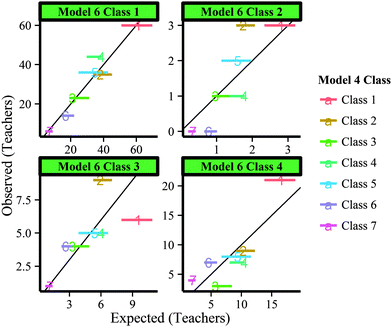image file: c5rp00215j-f8.tif
Fig. 8 Range of expected (horizontal lines) versus observed frequencies for class membership in from Model 6 to Model 4 classes.

Similar to the demographics analysis, this graphic was produced for every possible pairwise model from gases to stoichiometry scenarios, but no meaningful differences were found. This provides some evidence that DDI skills are dependent not only on content area, but also the specific topic. However, since only two topics were modeled, we cannot claim that this is the case across all chemistry topics.

Conclusions

Primarily through LCA of responses to two chemistry scenarios, we identified several characteristics related to how high school chemistry teachers design assessments and interpret student results. While we express less certainty in the exact quantification of teachers possessing each characteristic, it was found that a relatively small proportion displayed problems with content alignment, while the majority of teachers demonstrated at least some level of limited consideration of the VEU an item has in a chemistry-specific setting. The most prevalent lack of consideration was identification of how nuanced details, such as a stoichiometric ratio or item phrasing that implies a dichotomous response, could potentially affect how students' responses would be interpreted by the teachers. The extent of consideration for VEU and content alignment was not predicted by teacher or chemistry education, experience as a teacher, sex, or school location. Additionally, responses from chemistry teachers to generic formative assessment prompts bore little relationship to the characteristics clearly identified in chemistry-specific prompts. Further, few relationships between class membership for gases and class membership for stoichiometry were found, suggesting that DDI characteristics are not only content-specific but also topic-specific (Park and Oliver, 2008). Further work is required to validate both findings.

Implications

For teachers and administrators

While our study may seem to paint chemistry teachers' ability to design and interpret assessments in a negative light, we do not believe that these teachers are at all “unable” to do this. Rather, it is unlikely that they (a) have received chemistry-specific education for considerations such as VEU and alignment, (b) are encouraged from stakeholders to prioritize such detailed decisions in assessment design and interpretation, or (c) have anywhere near enough time to properly design and analyze formative assessments for instructional improvement. Therefore, the main implication for administrators is the realization that for inferences to be made about teachers based on student data, a large amount of time and expertise needs to be dedicated to designing assessments that measure student ideas with high VEU, which requires discipline-specific professional development. While this may carry practical and financial barriers, the payoff is developing teachers who are independent experts in using data from their own students in their own classrooms to guide their development as educators.

For chemistry teachers, the relatively large portion of teachers that do not show as much consideration for VEU of items in assessment design should cause heightened awareness among teachers about how the structure and content of item design can have huge effects on the interpretation of student results. To date, we are not aware of any professional development opportunities or graduate courses that will assist in developing and interpreting formative assessments specifically regarding chemistry. However, sometimes simply subjecting assessment items to critical feedback from colleagues, experts, or even oneself is enough to see potential limitations of one assessment item over another. In textbooks and online resources, there are often end-of-unit problem sets where it is not uncommon to find 5–20 items under the same heading, giving the impression that they all assess the same thing. However, we encourage teachers to consider how these items will likely assess slightly different things depending on how the question is worded and what content it requires to not just respond correctly to the question, but also to provide students with an opportunity to actually display what they understand about a concept or idea. It is this latter goal that is often missed in chemistry formative assessments.

Limitations

As mentioned previously, LCA carries an assumption of local independence, which was violated by the dependent-nature of the ACAST. However, with an emphasis on describing (as opposed to strictly quantifying) different characteristics, the existence of the classes discussed were corroborated by other models, validation interviews, previous qualitative results, and relevant literature. Under the assumption that few, if any, teachers had undergone development specific to designing and interpreting chemistry assessments, we did not collect demographics regarding previous professional development. Teachers could have had development in generic formative assessment that could lead to the responses observed. However, this is unlikely given the independence of previous educational experiences on response patterns. Finally, the two ACAST chemistry scenarios were not designed to be of analogous format. While few teachers expressed any confusion or misinterpretation in either scenario, the conclusions regarding content- and topic-specificity would have been strengthened if the only thing changed from the gases to stoichiometry scenario was the topic, as opposed to altering the format as well. Even so, characteristics discovered in LCA models were similar (VEU, item alignment, etc.) across the two scenarios.

Acknowledgements

We greatly appreciate all high school chemistry teachers who took time out of their day to complete our survey. We also wish to thank the six chemistry education research experts who helped us with our meta-pedagogical validity.

References

  1. American Educational Research Association, American Psychological Association, National Council on Measurement in Education, & Joint Committee on Standards for Educational and Psychological Testing (U.S.), (1999), Standards for Educational and Psychological Testing, Washington, DC: American Educational Research Association.
  2. American Education Research Association; American Psychological Association; National Council on Measurement in Education; Joint Committee on Standards for Educational and Psychological Testing and Psychological Testing of the American Educational Research Association (U.S.), (2014), Standards for Educational and Psychological Testing, Washington, DC: American Educational Research Association.
  3. Barbera J. and VandenPlas J. R., (2011), All Assessment Materials are not Created Equal: The Myths about Instrument Development, Validity, and Reliability, in Bunce D. (ed.), Investigating Classroom Myths through Research on Teaching and Learning, Washington, DC: American Chemical Society.
  4. Brandriet A. R. and Bretz S. L., (2014), The development of the Redox Concept Inventory as a measure of students' symbolic and particulate redox understandings and confidence, J. Chem. Educ., 91, 1132–1144.
  5. Brandriet A. and Holme T., (2015), Methods for addressing missing data with application from ACS exams, J. Chem. Educ., 92(12), 2045–2053.
  6. Calfee R. C. and Masuda W. V., (1997), Classroom assessment as inquiry, in Phye G. D. (ed.), Handbook of classroom assessment. Learning, adjustment, and achievement, San Diego: Academic Press.
  7. Collins L. M. and Lanza S. T., (2009), Latent Class Analysis and Latent Transition Analysis: With Applications in the Social, Behavioral, and Health Sciences, Hoboken, NJ: John Wiley and Sons, Inc.
  8. Copland M. A., (2003), The Bay Area School Collaborative: Building the capacity to lead, in Murphy J. and Datnow A. (ed.), Leadership lessons from comprehensive school reform, Thousand Oaks, CA: Corwin Press.
  9. Cresswell J. W., (2003), Research design: Qualitative, Quantitative, and Mixed Methods Approaches, 2nd edn, Sage: Thousand Oaks, CA.
  10. Desimone L. M. and Le Floch K. C., (2004), Are we asking the right questions? Using cognitive interviews to improve surveys in educational research, Educ. Eval. Pol. Anal., 26(1), 1–22.
  11. Hagenaars J. A., (1998), Categorical causal modeling: latent class analysis and directed log-linear models with latent variables, Soc. Methods Res., 26(4), 436–486.
  12. Hagenaars J. A. and McCutheon A. L., (2002), Applied Latent Class Analysis, Cambridge, MA: Cambridge University Press.
  13. Hamilton L., Halverson R., Jackson S., Mandinach E., Supovitz J. and Wayman J., (2009), Using student achievement data to support instructional decision making (NCEE 2009-4067), Washington, DC: National Center for Education Evaluation and Regional Assistance, Institute of Education Sciences, U.S. Department of Education.
  14. Harshman J., (2015), Characterizing high school chemistry teachers' use of formative assessment data to improve teaching, Doctoral dissertation, Miami University.
  15. Harshman J. and Yezierski E., (2015a), Guiding teaching with assessments: high school chemistry teachers' use of data-driven inquiry, Chem. Educ. Res. Pract., 16, 93–103.
  16. Harshman J. and Yezierski E., (2015b), Test-Retest reliability of the Adaptive Chemistry Assessment Survey for Teachers: measurement error and alternatives to correlation, J. Chem. Educ. DOI: http://10.1021/acs.jchemed.5b00620.
  17. Harshman J. and Yezierski E., (in press), Assessment DDI: a review of how to use assessment results to inform chemistry teaching, Sci. Educ..
  18. Haug B. S. and Ødegaard M., (2015), Formative assessment and teachers' sensitivity to student responses, Int. J. Sci. Educ., 37(4), 629–654.
  19. Izci K., (2013), Investigating High School Chemistry Teachers' Perceptions, Knowledge and Practices of Classroom Assessment, PhD Dissertation for the University of Missouri – Columbia.
  20. Knapp M. S., Swinnerton J. A., Copland M. A. and Monpas-Huber J., (2006), Data-Informed leadership in education, Center for the Study of Teaching and Policy.
  21. Luxford C. J. and Bretz S. L., (2014), Development of the Bonding Representations Concept Inventory to identify student misconceptions about covalent and ionic bonding representations, J. Chem. Educ., 91, 312–320.
  22. Means B., Chen E., DeBarger A. and Padilla C., (2011), Teachers' ability to use data to inform instruction: Challenges and supports, Office of Planning, Evaluation and Policy Development, U.S. Department of Education.
  23. National Center for Educational Statistics, (2015), Identification of Rural Locales, http://https://nces.ed.gov/ccd/rural_locales.asp#justification, accessed June 9, 2015.
  24. Park S. and Oliver J. S., (2008), Revisiting the conceptualisation of pedagogical content knowledge (PCK): PCK as a conceptual tool to understand teachers as professionals, Res. Sci. Educ., 38(3) 261–284.
  25. Polikoff M. S., (2010), Instructional sensitivity as a psychometric property of assessments, Educational Measurement: Issues and Practice, 29(4), 3–14.
  26. Popham W. J., (2007), Instructional insensitivity of tests: Accountability's dire drawback, Phi Delta Kappan, 89(2), 146–155.
  27. R Core Team., (2014), R: A Language and Environment for Statistical Computing, Vienna, Austria: R Foundation for Statistical Computing.
  28. Reboussin B. A., Ip E. H. and Wolfson M., (2008), Locally dependent latent class models with covariates: an application to under-age drinking in the USA, J. R. Stat. Soc Ser. A: Stat. Soc., 171(4), 877–897.
  29. Ruiz-Primo M. A. and Furtak E. M., (2007), Exploring teachers' informal formative assessment practices and students' understanding in the context of scientific inquiry, J. Res. Sci. Teach., 44(1), 57–84.
  30. Ruiz-Primo M. A., Li M., Wills K., Giamellaro M., Lan M. C., Mason H. and Sands D., (2012), Developing and evaluating instructionally sensitive assessments in science, J. Res. Sci. Teach., 49(6), 691–712.
  31. Sandlin B., Harshman J. and Yezierski E., (2015), Formative assessment in high school chemistry teaching: investigating the alignment of teachers' goals with their items, J. Chem. Educ., 92(10), 1619–1625.
  32. Schön D.A., (1987), Teaching artistry through reflection-in-action. In Schön Educating the Reflective Practitioner, San Francisco, CA: Jossey-Bass Publishers.
  33. Smith P. S., (2013), 2012 National Survey of Science and Mathematics Education: Status of high school chemistry, Chapel Hill, NC: Horizon Research, Inc.
  34. Tomenek D., Talanquer V. and Novodvorsky I., (2008), What do science teachers consider when selecting formative assessment tasks? J. Res. Sci. Teach., 45(10), 1113–1130.
  35. Towns M. H., (2008), Mixed methods designs in chemical education research, in Bunce D. M. and Cole R. S. (ed.), Nuts and Bolts of Chemical Education Research, Washington, DC: Oxford University Press.
  36. Ubersax J. S., (2009), A Practical Guide to Conditional Dependence in Latent Class Models. Latent Structure Analysis, http://john-uebersax.com/stat/condep.htm.
  37. Wiliam D., (2014), Formative assessment and contingency in the regulation of learning processes, paper presented at Annual Meeting of American Educational Research Association, Philadelphia, PA.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5rp00215j
This journal is © The Royal Society of Chemistry 2016
Click here to see how this site uses Cookies. View our privacy policy here.