Using Rasch measurement to validate an instrument for measuring the quality of classroom teaching in secondary chemistry lessons
Peng
He
a,
Xiufeng
Liu
b,
Changlong
Zheng
*a and
Mengying
Jia
a
aNortheast Normal University, College of Chemistry, 130024, Changchun, Jilin, China. E-mail: zhengcl@nenu.edu.cn
bUniversity at Buffalo, SUNY, Department of Learning and Instruction, 14228, Buffalo, NY, USA
First published on 10th February 2016
Abstract
This study intends to develop a standardized instrument for measuring classroom teaching and learning in secondary chemistry lessons. Based on previous studies and interviews with expert teachers, the progression of five quality levels was constructed hypothetically to represent the quality of chemistry lessons in Chinese secondary schools. The measurement instrument was revised from the Evaluation Scale of Effectiveness of Primitive System of Classroom Teaching (ESEPrSCT). 90 videotaped chemistry lessons were collected and measured to validate the instrument in the pilot and field stage. By means of Rasch modeling, the instrument consisting of 18 items with five response categories was finally validated in this study. The results provide the validity and reliability evidence for using this measurement instrument to assess the quality of chemistry lessons.
Introduction
Teacher professional development has been a concern in China and other countries. In 2011, the Chinese government released the Outline of the National Plan for Medium and Long-Term Education Reform and Development (2010–2020) (shortened to “Education Plan Outline”). The Education Plan Outline states that teachers' professional development and teaching ability is one of the most important aspects to meet the national educational goal (The State Council of the People's Republic of China, 2010). In order to improve the quality of teachers around the whole nation, in 2007 the Chinese Ministry of Education (MOE) implemented the Government-Sponsored Normal Students Program (GSNSP) for pre-service teachers, and in 2010 implemented the National Teacher Training Program (NTTP) for in-service teachers.In Mainland China, the new science curriculum reform initiated in 2001 called for promoting students' scientific literacy, and aimed to change traditional teacher-centered classrooms into inquiry-based student-centered classrooms (Ministry of Education, 2001a, 2001b, 2001c, 2001d). In order to meet the goals of the new science curriculum reform, science teachers confront a great challenge as they improve their professional skills and abilities. As the development of teacher professionalization is a concern for educators worldwide, research on the traits of effective teachers and the characteristics of effective teaching has been continuously conducted over the past three decades. Research on measuring teachers' teaching quality has been strongly influenced by the ideas of performance-based teacher education (Gage, 1972). To establish consolidated evidence for teacher performance criteria, researchers have conducted thorough reviews of existing literature to identify the key indicators of the quality of effective teaching (Rosenshine and Furst, 1971; Heath and Nielson, 1974). The main focus of the current study is the measurement of effective classroom teaching in chemistry lessons in secondary schools.
Literature review
Major factors for effective classroom teaching
During the past three decades, studies on dimensions of effective teaching have made great progress in the measurement of the quality of classroom teaching (Feldman, 1989; Muijs and Reynolds, 2000; Meijnen et al., 2003). Based on different purposes and specific methods used in their studies, researchers identified varying characteristics of effective teaching. For example, using meta-analysis, Fraser and his colleagues (1987) reported that the five teaching features with highest effect sizes are reinforcement, acceleration, reading training, cues and feedback, and science mastery. Scheerens and Bosker (1997) claimed reinforcement, feedback, cooperative learning, differentiation/adaptive instruction, and time on task to have the highest effect sizes of student outcomes.To identify major factors of effective classroom teaching, five features have been selected by summarizing previous studies and interviewing chemistry educators (Wayne and Youngs, 2003; ÇMER, 2006; Goldhaber and Anthony, 2007; Gurney, 2007; Seidel and Shavelson, 2007). For measuring the quality of effective teaching by these key features, we have proposed a hypothesized progression of classroom teaching (see Fig. 1) by interviewing chemistry educators and expert teachers in Mainland China. Following the hypothesized progression, five main traits are identified as: (1) using teaching resources and technology effectively; (2) the quality of instructional practices; (3) the rationality of teaching and learning content; (4) teachers' choices of instructional strategies; and (5) the rationality of teaching time.
Using effective teaching resources and technology such as ICT technology, lab experiments and scientific models can be treated as the first trait of effective classroom teaching. New technologies offer a wealth of information and resources for both teachers and students. ICT materials are particularly important for dealing with science in everyday life and it is proven to enhance student learning through a positive impact on student motivation and engagement (Cowie and Jones, 2009). However, the study conducted by Office of Technology Assessment (OTA) shows evidence that school teachers do not use computers frequently for their instruction even though those technologies are available in their schools. Some reasons are attributed to this situation, for example, lacking of access to equipment, training, and time to learn software, different attitudes toward use of technology, pedagogical beliefs and practices of teachers (Office of Technology Assessment, 1995). Hands-on activities provide students with opportunities to gather their own data for developing their competencies of using scientific evidence to draw conclusions in science classrooms (OECD, 2007). Baumert and Koeller (2000) emphasized that hands-on experiments have a positive impact on students' scientific literacy. Scientific models have been used in science classrooms for over 40 years, and it has been claimed that models can serve as key tools for students' understanding of science concepts (Schwarz et al., 2009; Gobert et al., 2011) and explaining real-world phenomena (White, 1998; Schwarz and White, 2005).
The quality of instructional practices is regarded as the second feature that affects the quality of classroom teaching. Some essential features of instructional practices include the clarity of presentation, questioning, immediate practice after presentation, evaluation of goal achievement, and corrective instruction (Werf et al., 2000). Questions should be designed to involve students in sustained discussion and to deep understanding of key ideas, whereas group discussion should be provided with opportunities for all students' engagement (Good et al., 2009). Interactions in class work are found to be related to motivational affective development (Seidel et al., 2005). Mortimer and Scott (2003) believed that student–teacher interaction is correlated with student outcomes. Cowie (2012) suggested that mutual trust and respect are central to students' active participation in formative interactions when they are working at the edges of their understanding. In order to achieve social goals, students work to develop positive social identities and to establish positive interpersonal relationships with peers and teachers.
The rationality of teaching and learning content serves as the third trait for considering the quality of classroom teaching. The curriculum and its implementation in teaching and learning is a key factor for considering the quality of classroom teaching (Creemers, 1994). Good and his colleagues (2009) emphasized that curriculum alignment and coherent content are two general principles of high quality classroom teaching. To be specific, content should be aligned to create a visible and coherent plan for achieving curriculum goals, and teachers should carefully differentiate between more and less important content. Furthermore, content should be organized and explained in sufficient depth for students to learn it meaningfully (Good et al., 2009).
The fourth vital feature is teachers' choices of instructional strategies. Since instructional strategies play an important role in the relationship between teaching styles and student outcomes (Brekelmans and Wubbels, 2012), teachers need to be concerned about students' learning characteristics and cognition so that they can make a decision on which instructional strategies should be utilized in their lessons. Good and Brophy (2008) have argued that the implementation of a variety of teaching strategies should be related to teaching targets and students' needs; a certain type of teaching strategy may be appropriate in particular situations, but cannot be applied for all purposes optimally. Therefore, teachers' use of suitable instructional strategies should be in accordance with the domain-specific content needs, students' learning characteristics, school resources and other factors.
The last feature of effective classroom teaching refers to the rationality of teaching time. Carroll (1963) and Walberg (1981) suggested that the time spent in the classroom teaching process is important to students' learning experience. According to the core idea of Carroll's (1963) model of school teaching and learning, using time properly is regarded as important to students' active engagement in the instructional process (Anderson, 1981). Fraser and his colleagues (1987) emphasized the strongest factor of teaching quality to be the time in questioning and answering and in students' hands-on activities.
Measuring classroom teaching quality
For evaluating classroom processes, the most widely-used measurements are classroom observation protocols. Previous studies on developing instruments to measure classroom teaching quality are considered in the current study. In order to improve the preparation of science and mathematics teachers in elementary and secondary schools, the program of the Arizona Collaborative for Excellence in the Preparation of Teachers (ACEPT) developed an observational instrument of the Reformed Teaching Observation Protocol (RTOP) to measure “reformed” teaching (Piburn et al., 2000). The Horizon Research, Inc. (HRI) developed the Inside Classroom Observation and Analytic Protocol (ICOAP) for measuring the quality of observed K-12 science or mathematics classroom lessons in the core evaluation of National Science Foundation's Local Systemic Change Initiative (Weiss et al., 2003). To provide scores for assessing teachers' teaching quality, Hill and her colleagues developed the Mathematical Quality of Instruction (MQI) instrument (Hill et al., 2008). Based on constructivist and social constructivist theories of science instruction, Minner and Delisi (2010) developed the Inquiring into Science Instruction Observation Protocol (ISIOP) to assess the quality of teaching practices in the science classroom. The Classroom Assessment Scoring System (CLASS) focused on the quality of classroom interactional processes in preschool and in the early elementary grades (Pianta et al., 2008). Based on Johnstone's triangle of macroscopic, symbolic, and submicroscopic representations of matter (Johnstone, 1991, Gilbert and Treagust, 2009), Philipp and her colleagues developed their protocol specific to Representations in Chemistry Instruction (RICI) (Philipp et al., 2014). Although those researchers have provided the reliability and validity of these instruments based on the data collected from a variety of lessons, few of them attend to the content characteristics of lessons, a domain-specific approach to observing lessons.Videotaped lesson studies on classroom teaching
Video recording and analysis is offered as a new technology-based approach to analyze classroom teaching. By using video analysis, preserved classroom activity can be viewed several times to get a detailed examination of the complex teaching and learning process taking place in classrooms. Video recording improves the quality of the observation data because indicators can be reviewed carefully to get valid and reliable scores. Therefore, observers' ratings of all indicators in the instrument are gathered (Liu, 2012). Research on the quality of classroom teaching receives a major revival with the TIMSS (Stigler, 1999) and LPS study (Clarke, 2002). In the TIMSS Video Study, the analysis of mathematics and science lessons covers the content of the lessons, the teachers' aims as well as teachers' and students' manuals, verbal activities, and the materials used (Stigler and Hiebert, 1997; Hiebert, 2003). The LPS study is designed to examine teaching practice and student achievement with an in-depth analysis of eighth grade mathematics classroom (Clarke, 2002; Clarke et al., 2006). Another video study of science teaching quality is conducted by the Institute for Science Education (IPN) in Kiel, Germany (Seidel et al., 2007). Based on the results of research on teacher and teaching effectiveness, they employ a “complex mediating process from instructional activities to student learning” (Seidel et al., 2005) as a theoretical framework to investigate science classroom activity patterns, and survey aspects of instructional quality.Using the video recording approach, the current study employs the Classroom Teaching and Learning System (CTLS) theory as a theoretical framework to observe and analyze classroom teaching in chemistry lessons (Zheng et al., 2014). The CTLS theory regards a chemistry lesson as a four-hierarchy system and proposes a CPUP system model (Class-Plate-Unit-Primitive). The Primitive System is the smallest teaching and learning segment that cannot be further divided. Zheng and his colleagues have developed an instrument for assessing the effectiveness of primitive systems in chemistry lessons under the CPUP model. To further identify the quality of classroom teaching within an entire chemistry lesson, the instrument of ESEPrSCT (Evaluation Scale of Effectiveness of Primitive System of Classroom Teaching) is revised in the current study to form a standardized instrument for measuring the quality of chemistry lessons in Chinese secondary schools. The specific research questions in this study are: what is the validity and reliability evidence supporting the use of this instrument to measure classroom teaching in chemistry lessons? What further improvements are needed to increase its validity and reliability?
Method
Instrumentation
The instrument of ESEPrSCT (Evaluation Scale of Effectiveness of Primitive System of Classroom Teaching) was developed specifically for assessing effectiveness of primitive systems in chemistry lessons (Zheng et al., 2014). The initial ESEPrSCT was a 20-item Likert-type instrument (Likert, 1932) with a six-point scale (i.e. “strongly disagree”, “disagree”, “slightly disagree”, “slightly agree”, “agree”, and “strongly agree”) for each item. Exploratory factor analysis and confirmatory factor analysis revealed five distinct factors as subscales in the instrument. Reliability of the above five subscales ranged from 0.69 to 0.91. The five distinct factors identified in the ESEPrSCT instrument described above were used as the five significant features of chemistry lessons in this study. Table 1 presents descriptions of the five significant features. These five significant features were named as Teaching Resources and Technology (TRT), Quality of Instructional Behaviors (QIB), Logicality of Teaching Contents (LTC), Choice of Instructional Strategies (CIS), and Rationality of Teaching Time (RTT). TRT pertains to teachers' utilization of school resources and educational technology for enhancing the effectiveness of each primitive system; QIB pertains to the quality of a certain instructional practice model implemented by teachers in each primitive system. LTC pertains to teachers' mastery of teaching and learning contents in each primitive system; CIS pertains to teachers' selection of teaching methods in each primitive system; and RTT pertains to teachers' usage of time in each primitive system. In this study, we employed the ESEPrSCT instrument as an initial instrument to measure the quality of an entire chemistry lesson. Five-point Likert scale was adopted with all indicators in this initial measurement (i.e. “very good”, “good”, “barely acceptable”, “poor”, and “very poor”).| Levels | Items (in initial instrument) | Items (in revised instrument) | Treatments |
|---|---|---|---|
| Note: items with bold abbreviation (e.g.TRT-a) both in the second and third column represent that this item was revised (e.g.TRT-a*) or deleted in the revised instrument; the others with regular signs (e.g. QIB-b) represent that they did not change (e.g. QIB-b) both in initial and revised instruments. | |||
| Level 5: Teaching Resource and Technology (TRT) | TRT-a: These experimental materials are used to attract students' attention properly; | TRT-a*: These experimental materials are used to engage students in class participation. | Revised (a big gap exists in Fig. 2 between TRT-a and TRT-c) |
| TRT-b: These content materials are rich and innovative; | TRT-b: These content materials are rich and innovative; | ||
| TRT-c: These object materials are provided properly (or model, writing on the blackboard, multimedia, etc.) to assist students' understanding; | TRT-c1*: The computer-based technology is used properly to enhance students' understanding; | Revised (a big gap exists in Fig. 2 between TRT-a and TRT-c) | |
| TRT-c2*: Physical models are demonstrated properly to enhance students' understanding; | |||
| Level 4: Quality of Instructional Behaviors (QIB) | QIB-a: The teacher is encouraging students to make self-evaluation; | QIB-a*: The teacher is encouraging students with positive feedback and evaluation; | Revised (disorder in the level of TRT in Fig. 2) |
| QIB-b: The questions are designed for triggering students' thinking deeply; | QIB-b: Questions are designed for triggering students' thinking deeply; | ||
| QIB-c: All students are participating fully in teaching and learning activities (discussion and communication, questioning and answering, etc.); | QIB-c: All students are participating fully in teaching and learning activities (discussion and communication, questioning and answering, etc.); | ||
| QIB-d: The teacher and students are communicating fully with each other; | QIB-d: The teacher and students are communicating fully with each other; | ||
| QIB-e: This classroom activity is wrapped up properly; | QIB-e*: This classroom activity is wrapped up simply and explicitly; | Revised (disordered in the levels of CIS and RTT in Fig. 2) | |
| Level 3: Logicality of Teaching Contents (LTC) | LTC-a: The breadth and depth of this content are in students' zone of proximal development; | LTC-a: The breadth and depth of this content is in students' zone of proximal development; | |
| LTC-b: This content is in accordance with the curriculum standards and textbooks; | LTC-b*: This content is integrated effectively with the current curriculum standards and textbooks; | Revised (mixed up with the level of CIS in Fig. 2) | |
| LTC-c: The depth and width of this content are reasonable; | LTC-c*: This content is taught scientifically and accurately by the teacher; | Revised (mixed up with the level of CIS in Fig. 2) | |
| Level 2: Choice of Instructional Strategies (CIS) | CIS-a: The type of this teaching behavior chain is consistent with the characteristics of the content; | CIS-a: The type of this teaching behavior chain is consistent with the characteristics of the content; | |
| CIS-b: The type of this teaching behavior chain is consistent with the learning characteristics of students; | Deleted (poor INFIT and OUTFIT values of item fit statistic) | ||
| CIS-c: The type of this teaching behavior chain is consistent with the school resources; | CIS-c: The type of this teaching behavior chain is consistent with the school resources; | ||
| CIS-d: The type of this teaching behavior is utilized well by the teacher; | CIS-d: The type of this teaching behavior is utilized well by the teacher; | ||
| Level 1: Rationality of Teaching Time (RTT) | RTT-a: There is no time consumption on unreasonable generation of classroom teaching; | Deleted (poor INFIT and OUTFIT values of item fit statistic) | |
| RTT-b: There is no time consumption on lack of clarity; | RTT-bc*: There is no time wasted on unclear questions or illustrations; | Revised (a big gap exists in the below of the map in Fig. 2 after deleting item RTT-a) | |
| RTT-c: There is no time consumption on making mistake or repeated presentation; | |||
| RTT-d: The teaching time is allocated properly according to the characteristics of this content; | RTT-d: The teaching time is allocated properly according to the characteristics of this content; | ||
| RTT-e: The teaching process is organized in a well-sequenced manner | RTT-e: The teaching process is organized in a well-sequenced manner | ||
In the stage of constructing the hypothesized progression of chemistry lessons, three chemistry educators and five expert chemistry teachers were group interviewed. Three major issues were explored in the interview process: according to the nature of teaching and learning chemistry, what are the stages of professional development of chemistry teachers? What are the significant features specific for chemistry teachers in these professional development stages? What are the significant features for each level in the hypothesized progression of chemistry lessons?
A high agreement was reached on three stages of professional development specific for chemistry teachers, which are categorized as the developing stage, basic stage and excellent stage. In the developing stage, chemistry teachers always pay great attention on how to manage teaching time properly so that they can finish their lesson plan; they rarely consider how to select a suitable instructional strategy or how to organize their teaching content coherently, much less think about the quality of their instructional behaviors and the rational use of resources and technology. In the basic stage, chemistry teachers can handle teaching time well, and start to focus on the selection of appropriate instructional strategies and the logicality of teaching content, but the quality of their instructional behaviors and the usage of teaching resources and technology still need further improvement. Chemistry teachers in the excellent stage are experts in dealing with teaching time, choice of instructional strategies and logicality of teaching content; they would hold themselves accountable with high quality of all instructional behaviors they performed in classroom, and would attempt to use various teaching resources and educational technology to improve their lesson qualities.
Lesson sampling
In order to study chemistry lessons, we established a videotaped lesson database that have over 500 secondary chemistry lessons varying from different high schools in Mainland China. All contents of these lessons are derived from Grade 10 in the General High School Chemistry Curriculum Standard (Ministry of Education, 2003b). Wright and Tennant (1996) suggested that with a reasonable targeted sample of 50 participants, there is a 99% confidence that the estimated item difficulty is within ±1 logit of its stable value when each participant takes ten or more items in Rasch analysis. Therefore, 50 chemistry lessons were extracted from the database in the pilot study. 25 lessons (50%) were well designed and were taught in national teaching ability competitions; other lessons (50%) were ordinary lessons and were taught in routine classrooms. Twenty one lessons (42%) were taught by male teachers, while 29 lessons (58%) were taught by female teachers. The videotaped lessons from the national teaching ability competitions were public open-resources for all chemistry teachers who intend to improve their teaching skills and abilities and for all chemistry education research programs, especially for improving the effectiveness of chemistry classroom teaching; whereas, the videotaped lessons from routine classrooms were collected by the members of our research team; the chemistry teachers of those lessons were volunteers, and were told in advance that their videotaped lessons would be anonymously used for the research purpose of effective classroom teaching.Elements of chemistry teaching and learning
In this study, a meaningful element of teaching and learning is regarded as a certain primitive system in chemistry lessons. As the smallest system within a class system, the primitive system cannot be divided further into any parts; otherwise there is no value of teaching and learning in this element.As an example, the following element of teaching and learning is retrieved from a chemistry lesson of “chemical and physical properties of sulfur dioxide”. The lesson was taught by a chemistry teacher in a national teaching ability competition. This element is about investigating the properties of sulfur dioxide when the gas of SO2 was put into water. Using the observation instrument, the two raters would give their scores based upon reviewing the transcript of the lesson and observing the videotape of this lesson. The use of the instrument to evaluate the quality of this particular element will be demonstrated as an example of how the scoring procedure was conducted for the study. For the item of “these experimental materials are used to engage students in class participation” (see item TRT-a* in Table 1), the performance of the teacher on this indicator was judged to be “excellent”, so the raters both gave him the score of 5 (very good) on this item. In this element, the experimental equipment (bottle of water and collection of gas) is simple and easy to handle, so all students can fully participate in this activity. Another example can be shown with the item of “the teacher and students are communicating fully with each other” (see item QIB-d in Table 1), the performance of the teacher on this indicator was judged to be “good”, so the raters both gave him the score of 4 (good) on this item. In this element, the teacher guided a group representative to report his findings with a designed set of five questions and then provided opportunities for other groups to share their ideas. Students within a lab group interacted actively with each other, which can be evidenced from the videotaped segment. However, the teaching and learning in this element would be better if other group representatives would share their findings with the representative and the teacher, and would generate a deep understanding of the properties of sulfur dioxide.
[Teacher] Let's put the gas (SO2) into the bottle (SO2 dissolves in water) according to the experiment design proposed by the first student. The specific procedure of this experiment you can follow in the PowerPoint.
[All Students] (Student groups work on experiments)
[Teacher] One group has already done, oh, your groups also have finished. After your experiments, you can compare the color of the solution with the color chart on your table.
[Teacher] Ok! Almost all groups have finished the experiments. I'd like someone tell us what phenomenon did you see in your experiment? What findings did you get? You please!
[Student] The pH test strip turned red, and compared with the color chart, the pH value of the SO2 solution is 2, ah…1.
[Teacher] Between 1 and 2.
[Student] 1 to 2.
[Teacher] Hum! What else? How about blue litmus test? Anything changes?
[Student] The blue litmus paper turned red.
[Teacher] Turned red!
[Teacher] At the beginning of your experiment, after you added water into your bottle, what did you find?
[Student] The bottle was squashed.
[Teacher] Squashed! Do you know the reason why the bottle turned flat?
[Student] I guess it is because SO2 reacted with water.
[Teacher] Because of the reaction, the bottle turned flat. Are there any other possible reasons?
[Student] SO2 dissolved into water.
[Teacher] Yea! A great quantity of SO2 molecules dissolved into water. Very good! Sit down please!
[Teacher] Anybody who wants give additional comments? Have you seen a similar phenomenon with him? Ah, the similar phenomenon. At the end, we saw the bottle turn flat, SO2 dissolve into water, and react with water.
Data analysis
Bond and Fox (2007) stated that the data in the Likert scale can be more easily collected, and the total scale score can be calculated from individual item scores. However, values such as 1–5 assigned to five choices of a statement do not have the same origin and interval unit because they are not on a ratio scale; therefore, the total score cannot meaningfully be calculated from individual item scores (Liu, 2012). In order to address this issue, Liu (2012) recommends that Rasch modeling should be employed as a better way to convert raw scores into ratio scores so that person abilities (i.e., chemistry lesson quality in this study) can be measured on a ratio scale. Numerous studies on using Rasch modeling to validate their instruments can be regarded as support for the application of Rasch modeling in this study (e.g.Herrmann-Abell and Deboer, 2011; Wren and Barbera, 2014; Taskin et al., 2015).Rasch modeling allows the estimation of both item difficulty and person ability for a test (Bond and Fox, 2007; Liu, 2010). Based on the observed responses to the items, the purpose of the current study is to estimate an internal trait for the quality of classroom teaching in chemistry lessons. Rasch modeling can be estimated for items coded dichotomously, as well as in rating scales (Andrich, 1978). According to Bond and Fox (2007), items and item responses are examined in Rasch modeling for their degree of fit between the person responses and the measurement model. The mean square residual (MNSQ) and the standardized mean square residual (ZSTD) are typically used as the fit indices to examine how well each item is coherent with the Rasch model. In general, items have acceptable fit if their MNSQs fall into the range from 0.6 to 1.4 for rating scale (Linacre, 2013), while ZSTD values are within the range from −2 to +2 (Liu, 2010). The point measure correlation (PTMEA) is the correlation between the observations in the data and the measures of the items (or persons) producing them (Linacre, 2013). Wolfe and Smith (2006) suggest that the PTMEA values should be positive. Item difficulties and response-option difficulties can be explored further with person and item estimate maps and category probability curves. A person and item estimate map plots the persons' ability estimates and the items' difficulty estimates on the same logit scale. When a person and an item are at the same position on the logit scale, then the person has a 50% probability of answering the item correctly (Bond and Fox, 2007). A variance greater than or equal to 50% explained by the Rasch dimension can be regarded as evidence that the scale is unidimensional (Linacre, 2013), and scale unidimensionality can be assumed if the second dimension (first contract) has the strength of less than 3 items (in terms of eigenvalues) and the unexplained variance by the first contrast is less than 5% (Oon and Subramaniam, 2011). As Rasch modeling is a probabilistic model of measurement, there is always some anticipated variation in the ordering of responses; so both too-high and too-low fit statistics of the data to the model would be the cause for concern with the instrument (Bond and Fox, 2007). Winsteps computer software was utilized to conduct the Rasch analysis in this study.
Inter-rater reliability
In order to ensure the rating reliability, we recruited two raters in this study. The first rater was an expert teacher who has more than 20 years of teaching experience, and the second rater was a chemistry educator with a doctoral degree in chemistry education. Both of the two raters had a sufficient theoretical and practical knowledge on teaching chemistry lessons effectively. We calculated the inter-rater agreement with Cohen' kappa coefficient, and the value was 0.747, indicating that these two raters have an acceptable reliability on using this instrument to rate chemistry lessons (Cohen, 1968).Pilot-study
According to the results of the pilot test, person separation was 4.10 (reliability = 0.94) and item separation was 6.43 (reliability = 0.98), and both were acceptable. In terms of the fit statistics for all 20 items, 14 items had infit and outfit of MNSQs with the acceptable range from 0.6 to 1.4, and infit and outfit of ZSTD from −2 to +2. The items with poor fit were items RTT-a, RTT-c, QIB-a, CIS-b, TRT-a, LTC-c (see Table 1). All PTMEA values ranged from 0.46 to 0.85, suggesting that these 20 items contribute to measuring chemistry lesson quality.The item category frequencies had a good spread, which meets the expectation; each category count satisfied the criterion for minimum counts of 10 observations (Linacre, 2002; Wolfe and Smith, 2006). Probability curves of good rating scales showed that each peak stands alone, indicating that persons with different performance abilities could be distinguished easily by those categories (Royal et al., 2010).
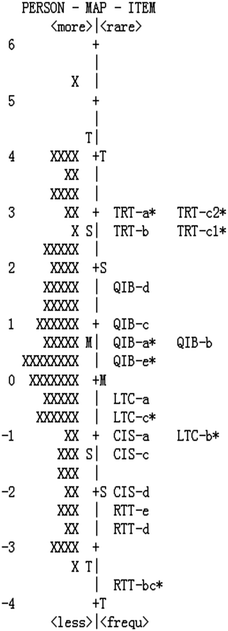
The person and item estimate map in the pilot test (see Fig. 2) showed the quality of chemistry lessons had a wide range of variations. The hypothesized progression of chemistry lessons can be seen from the map. However, two gaps can be seen clearly from the map, indicating that some items should be revised or added to fill with the gaps and to meet with the hypothesized progression in the next validation stage.
Instrument revisions
According to the results in the pilot study, some improvements were made to form a revised instrument in the next validation stage. Finally, 18 items were included in the revised instrument (see Table 1). From the fit statistics of items and the person and item estimate map in Fig. 2, 10 items in the initial instrument might not fit well with the hypothesized progression of chemistry lessons. Because of the high separation and reliability of person and item, even if there exist some big gaps in the person and item estimate map (see Fig. 2), more items do not need to be added in the revision stage. The items of RTT-a and CIS-b were deleted for the poor item fit statistics; the items of TRT-a, TRT-c, RTT-b, and RTT-c were revised for the gaps exist in the map; the items of QIB-a, QIB-e, LTC-b, and LTC-c were revised for disorders and mixtures between levels.According to the person and item estimate map in the pilot test (see Fig. 2), 40 more chemistry lessons from routine classrooms were added and finally 90 chemistry lessons were scored by the same two raters in the field study. The new data were subjected to the Winsteps program again to run the rating scale Rasch analysis.
Results
The person and item estimate map
Fig. 3 presents the person and item estimate map of the revised instrument. The left side of vertical line is the distribution of chemistry lessons from low levels (bottom) to high levels (top). The right side of the map is the distribution of items from easy (bottom) to difficult (top) endorsement. It can be seen that the distribution of chemistry lessons spread widely from −3.30 logits to 5.22 logits, while the revised item measures ranged from −3.75 logits to 3.04 logits. From the map in Fig. 3, the items within a hypothesized level were close to each other, and all items were distributed in an orderly way to match with the hypothesized progression of chemistry lessons. To be specific, the items in the highest level (TRT) were presented on the top of the map, whereas the items in the lowest level (RTT) were located at the bottom of the map. Compared with the gaps in Fig. 2, the range lengths among those gaps in Fig. 3 were decreased, indicating that the revision work contributed a positive effect on the quality of this instrument.Item category structure
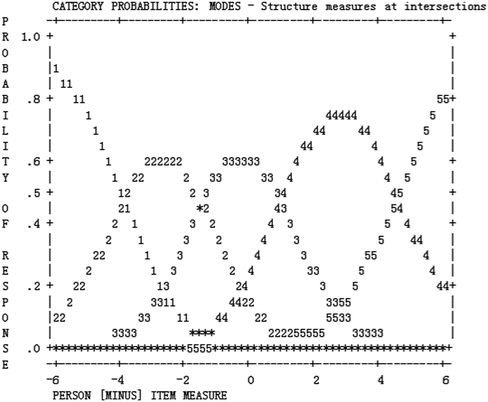
Table 2 presents the statistics of item category structure. The five-point rating scale (i.e. “very good”, “good”, “barely acceptable”, “poor”, and “very poor”) was used for all items in the revised instrument. Those five categories can be seen as walking along steps from a low level to a high level of difficulty endorsement. As can be seen from Table 2, the average category measures were ordered, increasing monotonically from −4.07 logits to 4.50 logits. The outfit MNSQs ranged from 0.78 to 1.08, indicating expected category usage (Linacre, 2002). Furthermore, the category threshold calibrations increased monotonically with categories, and the distances were all more than 1.1 logits, meeting the guidelines suggested by Linacre (2002). According to the category probability curves in Fig. 4, we can see that each category represented a distinct region of the underlying construct.| Category | Observed count | Observed (%) | Average measure | Infit MNSQ | Outfit MNSQ | Step calibrations |
|---|---|---|---|---|---|---|
| Note: category 1 stands for “very poor”; category 2 stands for “poor”; category 3 stands for “barely acceptable”; category 4 stands for “good”; and category 5 stands for “very good”. | ||||||
| 1 | 125 | 8 | −4.07 | 0.78 | 0.80 | None |
| 2 | 295 | 18 | −2.07 | 0.94 | 1.00 | −5.07 |
| 3 | 475 | 29 | 0.00 | 0.95 | 0.95 | −1.77 |
| 4 | 544 | 34 | 2.21 | 1.05 | 1.05 | 1.51 |
| 5 | 181 | 11 | 4.50 | 1.08 | 1.06 | 5.33 |
Item fit statistics
Table 3 shows the fit statistics for the final 18 items in the revised instrument. We can see that infit MNSQs ranged from 0.62 to 1.31, whereas the outfit MNSQs ranged from 0.65 to 1.26; both were regarded as acceptable except the item of TRT-c2* (infit and outfit MNSQ = 1.51, 1.67). Infit ZSTDs and outfit ZSTDs ranged from −2.0 to +2.0 with the exception of items of TRT-c2*, QIB-a*, QIB-b and QIB-d. All items exhibited strong positive point-measure correlations (PTMEA) and ranged from 0.66 to 0.85. Together, these MNSQ and ZSTD statistics indicate that these chemistry lessons' responses to items show appropriate fit to the model and are consistent with the Rasch measurement model's formulation of a unidimensional construct of person ability (Bond and Fox, 2007).| Item | Measure | S.E. | Infit | Outfit | PTMEA | ||
|---|---|---|---|---|---|---|---|
| MNSQ | ZSTD | MNSQ | ZSTD | ||||
| Note: RTT refers to the rationality of teaching time; CIS refers to the choice of instructional strategies; LTC refers to the logicality of teaching contents; QIB refers to the quality of instructional behaviors; TRT refers to the teaching resource and technology. | |||||||
| TRT-a* | 3.04 | 0.18 | 0.99 | 0.0 | 0.99 | 0.0 | 0.77 |
| TRT-b | 2.51 | 0.18 | 0.92 | −0.5 | 0.90 | −0.6 | 0.82 |
| TRT-c1* | 2.79 | 0.18 | 1.07 | 0.6 | 1.05 | 0.4 | 0.80 |
| TRT-c2* | 2.94 | 0.18 | 1.51 | 3.0 | 1.67 | 3.6 | 0.72 |
| QIB-a* | 0.54 | 0.18 | 0.67 | −2.5 | 0.68 | −2.4 | 0.81 |
| QIB-b | 0.64 | 0.17 | 0.62 | −3.0 | 0.65 | −2.6 | 0.83 |
| QIB-c | 1.09 | 0.17 | 0.96 | −0.2 | 0.98 | −0.1 | 0.75 |
| QIB-d | 1.51 | 0.17 | 0.69 | −2.3 | 0.74 | −1.9 | 0.85 |
| QIB-e* | 0.24 | 0.18 | 1.31 | 1.9 | 1.26 | 1.7 | 0.73 |
| LTC-a | −0.43 | 0.18 | 0.80 | −1.4 | 0.84 | −1.1 | 0.77 |
| LTC-b* | −0.93 | 0.18 | 0.79 | −1.5 | 0.77 | −1.6 | 0.80 |
| LTC-c* | −0.79 | 0.18 | 0.87 | −0.9 | 0.87 | −0.9 | 0.74 |
| CIS-a | −1.10 | 0.19 | 1.12 | 0.8 | 1.15 | 1.0 | 0.66 |
| CIS-c | −1.24 | 0.19 | 1.11 | 0.8 | 1.19 | 1.2 | 0.68 |
| CIS-d | −2.05 | 0.20 | 0.99 | 0.0 | 1.02 | 0.2 | 0.68 |
| RTT-bc* | −3.75 | 0.22 | 1.08 | 0.6 | 0.98 | 0.0 | 0.73 |
| RTT-d | −2.52 | 0.20 | 1.12 | 0.8 | 1.19 | 1.1 | 0.69 |
| RTT-e | −2.48 | 0.20 | 0.91 | −0.6 | 0.98 | −0.1 | 0.71 |
Local independence of items
Item fit residual and item residual correlation are two key indices to evaluate the local dependency of items (Marais and Andrich, 2008). The criteria for examining item redundancy are the standardized fit residual value (ZSTD) less than −2.0 (Smith, 2005) or the correlation coefficient of residuals higher than 0.7 (Linacre, 2013). Table 3 shows that the ZSTD values of items QIB-a*, QIB-b, and QIB-d are below −2.0, indicating that those three items are possibly over-discriminating, may be correlated with each other in a similar manner. The correlation coefficients of residuals for all pairs of items were smaller than 0.7; the largest value was 0.59 between items RTT-d and RTT-e. The above results suggested that most of the items in this revised instrument are local independent, though a few items in the QIB level should be reconsidered in future research.Separation and reliability
As can be seen in Table 4, the person separation index is 4.35, with an equivalent Cronbach's reliability coefficient (α value) of 0.95. The item separation index is 10.35, and the corresponding Cronbach's α value was 0.99, indicating reliable item and person estimation. In Rasch modeling, we examine how reliable we can differentiate these teachers according to their abilities using a separation reliability coefficient, which shows how consistently our estimates of teacher ability match the observed data. The number can be interpreted similarly to a Cronbach's α coefficient in classical analyses. Separation reliability is also applicable for the items, to see how well the model can differentiate the items on their difficulty. The results showed better reliability for the items than for persons, which is typically the case (Liu, 2010). The high item reliability indicates that the items of varying difficulty can be differentiated under the model. As DeVellis (2012) notes, a scale reliability of 0.65–0.70 is ‘minimally acceptable’ and between 0.70 and 0.85 is ‘respectable’ for instruments to be used for research purposes. Furthermore, Rasch measurement produces a standard error (S.E.) as an additional measure of reliability for each individual person and item measure. Persons and items with measures closer to their means have smaller S.E.s than those farther from the means. From Table 3, the S.E. values for persons and items were small, ranging from 0.17 to 0.22.| Measure | Error | INFIT | OUTFIT | Separation | Reliability | |||
|---|---|---|---|---|---|---|---|---|
| MNSQ | ZSTD | MNSQ | ZSTD | |||||
| Persons | 0.55 | 0.41 | 0.98 | −0.1 | 1.00 | 0.0 | 4.35 | 0.95 |
| Items | 0.00 | 0.18 | 0.97 | −0.2 | 1.00 | −0.1 | 10.35 | 0.99 |
Dimensionality
Principal component analysis (PCA) was applied to the standardized residuals to identify possible dimensions existing in the scale (Oon and Subramaniam, 2011). Measures resulting from the revised measurement accounted for 73.1% of total variance, 4.6% higher than the value in initial measurement, and also higher than the expected norm. The second dimension had an eigenvalue of 3.5 and accounted for 19.2% (previously it was 4.0 and 19.8%) of the variance, indicating that unidimensionality of items was still not ideal. The items RTT-d, RTT-e, CIS-c, QIB-e* and TRT-c1* had the largest contrast loadings (higher than 0.50), suggesting that they might measure an additional dimension.Application of the instrument
Table 5 presents the conversion table of raw scores to Rasch scale scores. The Rasch scores were estimated on a scale so that this instrument had a mean of 0 and standard deviation of 1. There were no raw scores lower than 18 or greater than 90. Using this conversion table, we do not need to conduct Rasch analysis every time to get the Rasch scale scores when we apply this instrument to assess the quality of chemistry lessons. From the table, for example, if a chemistry lesson scores 30 points, that the lesson's Rasch scale score is −4.07.| Raw score | Ability estimate | S.E. | Raw score | Ability estimate | S.E. | Raw score | Ability estimate | S.E. |
|---|---|---|---|---|---|---|---|---|
| 18 | −9.50 | 1.88 | 43 | −1.83 | 0.39 | 68 | 2.13 | 0.42 |
| 19 | −8.15 | 1.10 | 44 | −1.67 | 0.39 | 69 | 2.31 | 0.43 |
| 20 | −7.26 | 0.82 | 45 | −1.52 | 0.39 | 70 | 2.50 | 0.43 |
| 21 | −6.69 | 0.71 | 46 | −1.37 | 0.39 | 71 | 2.69 | 0.44 |
| 22 | −6.24 | 0.64 | 47 | −1.22 | 0.39 | 72 | 2.88 | 0.44 |
| 23 | −5.87 | 0.59 | 48 | −1.07 | 0.39 | 73 | 3.08 | 0.45 |
| 24 | −5.54 | 0.55 | 49 | −0.92 | 0.39 | 74 | 3.28 | 0.45 |
| 25 | −5.25 | 0.53 | 50 | −0.77 | 0.39 | 75 | 3.49 | 0.46 |
| 26 | −4.98 | 0.51 | 51 | −0.62 | 0.39 | 76 | 3.70 | 0.47 |
| 27 | −4.74 | 0.49 | 52 | −0.47 | 0.39 | 77 | 3.92 | 0.48 |
| 28 | −4.50 | 0.48 | 53 | −0.32 | 0.39 | 78 | 4.16 | 0.49 |
| 29 | −4.28 | 0.46 | 54 | −0.16 | 0.39 | 79 | 4.40 | 0.50 |
| 30 | −4.07 | 0.45 | 55 | −0.01 | 0.39 | 80 | 4.66 | 0.52 |
| 31 | −3.87 | 0.44 | 56 | 0.14 | 0.39 | 81 | 4.93 | 0.53 |
| 32 | −3.68 | 0.44 | 57 | 0.30 | 0.40 | 82 | 5.23 | 0.55 |
| 33 | −3.49 | 0.43 | 58 | 0.46 | 0.40 | 83 | 5.55 | 0.58 |
| 34 | −3.31 | 0.42 | 59 | 0.62 | 0.40 | 84 | 5.90 | 0.61 |
| 35 | −3.13 | 0.42 | 60 | 0.78 | 0.40 | 85 | 6.29 | 0.64 |
| 36 | −2.96 | 0.41 | 61 | 0.94 | 0.40 | 86 | 6.73 | 0.68 |
| 37 | −2.79 | 0.41 | 62 | 1.10 | 0.41 | 87 | 7.23 | 0.74 |
| 38 | −2.62 | 0.41 | 63 | 1.27 | 0.41 | 88 | 7.84 | 0.84 |
| 39 | −2.46 | 0.40 | 64 | 1.43 | 0.41 | 89 | 8.73 | 1.09 |
| 40 | −2.30 | 0.40 | 65 | 1.60 | 0.41 | 90 | 10.06 | 1.87 |
| 41 | −2.14 | 0.40 | 66 | 1.78 | 0.42 | |||
| 42 | −1.98 | 0.39 | 67 | 1.95 | 0.42 |
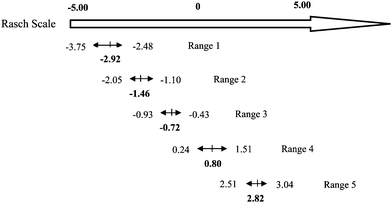
Table 6 shows the items and the item difficulty range grouped by the levels of the quality of chemistry lessons. The levels of chemistry lessons can be identified by using the ranges of Rasch scores. Fig. 5 presents the levels of the quality of chemistry lessons and the ranges along the Rasch scale (Liu, 2007). The top arrow shows the Rasch scale scores, and the five arrows underneath represent five ranges. The bar at the middle of each arrow represents the mean Rasch scale score for that range. Using the above means, the Rasch scale scores of chemistry lessons can be transformed into the levels of the quality of chemistry lessons. According to Fig. 5, the Rasch score of a chemistry lesson is below −2.92, the quality of this lesson is below level 1; if the Rasch score of a chemistry lesson is between −2.92 and −1.46, the quality of this lesson is at level 1; if the Rasch score of a chemistry lesson is between −1.46 and −0.72, the quality of this lesson is at level 2; if the Rasch score of a chemistry lesson is in the range of −0.72 and 0.80, the quality of this lesson is at level 3; if the Rasch score of a chemistry lesson is between 0.80 and 2.82, the quality of this lesson is at level 4; and finally, if a chemistry lesson's Rasch score is higher than 2.82, the quality of this lesson is at level 5.
| Levels | Items | Minimum | Maximum | Average |
|---|---|---|---|---|
| Note: RTT refers to the rationality of teaching time; CIS refers to the choice of instructional strategies; LTC refers to logicality of teaching contents; QIB refers to the quality of instructional behaviors; TRT refers to the teaching resource and technology. | ||||
| 1 | RTT-bc*, RTT-d, RTT-e | −3.75 | −2.48 | −2.92 |
| 2 | CIS-a, CIS-c, CIS-d | −2.05 | −1.10 | −1.46 |
| 3 | LTC-a, LTC-b*, LTC-c* | −0.93 | −0.43 | −0.72 |
| 4 | QIB-a*, QIB-b, QIB-c, QIB-d, QIB-e* | 0.24 | 1.51 | 0.80 |
| 5 | TRT-a*, TRT-b, TRT-c1*, TRT-c2* | 2.51 | 3.04 | 2.82 |
Discussion and conclusion
The ESEPrSCT instrument we used as an initial instrument was validated by the Classical Test Theory (CTT) in the previous study (Zheng et al., 2014). Because a number of fundamental limitations exist when CTT is applied to the development of measurement instruments in science education (Liu, 2010), we used Rasch measurement to further develop and validate this initial instrument. In the pilot study, the results showed a good reliability and validity of this initial instrument; however, six items in the initial instrument had poor fit statistics, so they need to be revised at the next stage. The person and item estimate map suggested that the distribution of items cannot perfectly match with the hypothesized progression of chemistry lessons, indicating that some items need to be revised at the next stage. According to the suggestions of the Rasch analysis, we removed two items, revised eight items into eight new items, and formed 18 items in the revised instrument. In the final Rasch analysis, the fit statistics for all items were acceptable except item TRT-c2*, indicating that item TRT-c2* needs to be improved in the future validation process. The person and item estimate map was presented to illustrate the items in revised instrument spread perfectly to match with the hypothesized progression. The thresholds of responses on the five-point Likert scale proved to be meaningful through the analysis of category structure. The item and person separation index and Cronbach's α value indicated good reliable items and person estimations. The PCA method indicated that the dimensionality of the revised instrument is acceptable, and some items need to be improved to further enhance the accounted total variance. Overall, the results indicated that the revised instrument has moderately good functioning as a standardized instrument for measuring the quality of classroom teaching in secondary chemistry lessons.Compared with previous instruments, the current instrument for measuring the quality of classroom teaching is based on CTLS theory. The previous instruments, such as RTOP (Piburn et al., 2000), ICOAP (Weiss et al., 2003), and ISIOP (Minner and Delisi, 2010), measured the quality of classroom teaching through a holistic perspective of entire lesson. However, this study applied the analytical perspective to assess the quality of classroom teaching. To be specific, the entire lesson is divided into several segments, known as PrS (Zheng et al., 2014), and then the quality of PrS is measured by the current instrument. This analytical perspective provides a new methodology to measure the quality of classroom teaching in science education.
Interviewing chemistry educators and expert teachers, the hypothesized progression of chemistry classroom teaching represents the mainstream ideas of chemistry classroom teaching in China. Therefore, this hypothesized progression is predicated on the context of the current real status in Chinese chemistry education. The results of data analysis showed the evidence that the quality of classroom teaching in Chinese chemistry lessons has a very good fit with the hypothesized progression, with a high separation and reliability for the item difficulty estimates and the high quality of classroom teaching estimates.
Some issues still need to be considered in future research. Although the above results suggest that measures of the final instrument possess high validity and reliability, some improvements are still necessarily with regard to some items. For using the instrument in other disciplines or in other countries, further improvement and validation are required. Suggested by some other related studies (Liu, 2010; Wei et al., 2012, 2013), it is essential to collect additional data using the revised instrument to conduct new rounds of validation when researchers employ the Rasch measurement model to develop a standardized instrument. In addition, this study provides another example to demonstrate how Rasch measurement can be applied to validating the measurement instruments in science education.
Based on the iterative process of using Rasch measurement to develop instruments, the final stage is developing documentation (Liu, 2010). In order to support users to apply this instrument, important information should be included in the documentation, such as the intended uses of the measurement, construct definition, developing process, score rubric, and reporting individual scores (Wei et al., 2012). Reviewing the documentation of this measurement instrument, researchers can learn how to use this instrument as a measurement tool to assess the quality of chemistry lessons and further to identify the levels of chemistry lessons. Using this instrument, researchers can conduct some comparison studies to find if there exist any differences in the quality of chemistry lessons among genders, grade levels, and teacher professional levels. This instrument also can be applied as a promising observation tool in teacher professional development programs to see if intervention promotes teachers’' teaching abilities of chemistry lessons. However, some cautions need to be mentioned for utilizing this instrument. Because we construct the hypothesized progression and data collection based on the background of Chinese chemistry lessons, the fitness for other countries and other disciplines should be further investigated; and this instrument is developed for assessing the new content lessons, for other types of lessons need to be explored in future studies.
References
- Anderson L. W., (1981), Instruction and time-on-task: a review, J. Curric. Stud., 13, 289–303.
- Andrich D., (1978), Rating formulation for ordered response categories, Psychometrika, 43(4), 561–573.
- Baumert J. and Koeller O., (2000), Lesson design, insightful learning and multiple target achievement in mathematics and science classrooms in higher secondary education, in Baumert J., Bos W. and Lehman R. (ed.) TIMSS/III the third international mathematics and science study – mathematics and science competency at the end of schooling, volume 2: mathematics and science competency at the end of upper secondary education, Opladen, Germany: Leske+Budrich, pp. 271–315.
- Bond T. G. and Fox C. M., (2007), Applying the Rasch model: fundamental measurement in the human sciences, 2nd edn, Mahwah, NJ: Lawrence Erlbaum.
- Brekelmans M. and Wubbels T., (2012), Teacher-student relationship in the classroom, in Second International Handbook of Science Education, Netherlands: Springer, pp. 1241–1255.
- Carroll J. B., (1963), A model of school learning, Teach. Coll. Rec., 64(8), 723–733.
- ÇMER A., (2006), Effective teaching in science: a review of literature, Turk. Sci. Educ., 4(1), 20.
- Clarke D., (2002), The learner's perspective study: exploiting the potential for complementary analyses, in American Education Research Association Annual Meeting, New Orleans, USA.
- Clarke D., Keitel C. and Shimizu Y., (ed.), (2006), Mathematics classrooms in twelve countries: the insider's perspective, vol. 1, Sense publishers.
- Cohen J., (1968), Weighted kappa: nominal scale agreement provision for scaled disagreement or partial credit, Psychol. Bull., 70(4), 213.
- Cowie B., (2012), Focusing on the classroom: assessment for learning, in Second International Handbook of Science Education, Netherlands: Springer, pp. 679–690.
- Cowie B. and Jones A., (2009), Teaching and learning in the ICT environment, in International Handbook of Research on Teachers and Teaching, USA: Springer, pp. 791–801.
- Creemers B. P., (1994), The effective classroom, London: Cassell.
- DeVellis R. F., (2012), Scale development: theory and applications, 3rd edn, Thousand Oaks, CA: SAGE.
- Feldman K. A., (1989), The association between student ratings of specific instructional dimensions and student achievement: refining and extending the synthesis of data from multisection validity studies, Res. High. Educ., 30(6), 583–645.
- Fraser B. J., Walberg H. J., Welch W. W. and Hattie J. A., (1987), Syntheses of educational productivity research, Int. J. Educ. Res., 11(2), 147–252.
- Gage N. L., (1972), Teacher effectiveness and teacher education, Palo Alto, Calif.: Pacific Books.
- Gilbert J. K. and Treagust D. F., (2009), Multiple representations in chemical education, vol. 2, Dordrecht: Springer.
- Gobert J. D., O'Dwyer L., Horwitz P., Buckley B., Levy S. and Wilensky U., (2011), Examining the relationship between students' understanding of the nature of models and conceptual learning in Biology, Physics, and Chemistry, Int. J. Sci. Educ., 33(5), 653–684.
- Goldhaber D. and Anthony E., (2007), Can teacher quality be effectively assessed? National Board Certification as a Signal of Effective Teaching, Rev. Econ. Stat., 89(1), 134–150. DOI: http://10.1162/rest.89.1.134.
- Good T. and Brophy J., (2008) Looking in classrooms, 10th edn, Boston: Allyn and Bacon.
- Good T. L., Wiley C. R. and Florez I. R., (2009), Effective teaching: an emerging synthesis, in International handbook of research on teachers and teaching, USA: Springer, pp. 803–816.
- Gurney P., (2007), Five factors for effective teaching, New Zeal. J. Teach. Work, 4(2), 89–98.
- Heath R. W. and Nielson M. A., (1974), The research basis for performance-based teacher education, Rev. Educ. Res., 44(4), 463–484. DOI: http://10.2307/1170103.
- Herrmann-Abell C. F. and DeBoer G. E., (2011), Using distractor-driven standards-based multiple-choice assessments and Rasch modeling to investigate hierarchies of chemistry misconceptions and detect structural problems with individual items, Chem. Educ. Res. Pract., 12(2), 184–192.
- Hiebert J., National Center for Education Statistics and Institute of Education Sciences (U.S.), (2003), Teaching mathematics in seven countries: results from the TIMSS 1999 video study, Washington, DC: National Center for Education Statistics.
- Hill H. C., Blunk M. L., Charalambous C. Y., Lewis J. M., Phelps G. C., Sleep L. and Ball D. L., (2008), Mathematical knowledge for teaching and the mathematical quality of instruction: an exploratory study, Cognition Instruct., 26(4), 430–511.
- Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Learn., 7(2), 75-83.
- Likert R., (1932), A technique for the measurement of attitudes, Archieves of Psychology, 22, 5–53.
- Linacre J. M., (2002), Optimizing rating scale category effectiveness, J. Appl. Meas., 3(1), 85–106.
- Linacre J. M., (2013), A user's guide to Winsteps ministep Rasch-model computer programs, version 3.80.0, Chicago, IL: Winsteps.com.
- Liu X., (2007), Elementary to high school students' growth over an academic year in understanding concepts of matter, J. Chem. Educ., 84(11), 1853–1856.
- Liu X., (2010), Using and developing measurement instruments in science education: a Rasch modeling approach, Iap.
- Liu X., (2012), Developing measurement instruments for science education research, in Second International Handbook of Science Education, Netherlands: Springer, pp. 651–665.
- Marais I., and Andrich D., (2008), Effects of varying magnitude and patterns of local dependence in the unidimensional Rasch model, J. Appl. Meas., 9(2), 105–124.
- Meijnen G. W., Lagerweij N. W. and Jong P. F., (2003), Instruction characteristics and cognitive achievement, Sch. Eff. Sch. Improv., 14(2), 159–187.
- Ministry of Education (MOE) of PRC, (2001a), Full-time compulsory education biology curriculum standard (trial), Beijing, PRC: Beijing Normal University Press (in Chinese).
- Ministry of Education (MOE) of PRC, (2001b), Full-time compulsory education physics curriculum standard (trial), Beijing, PRC: Beijing Normal University Press (in Chinese).
- Ministry of Education (MOE) of PRC, (2001c), Full-time compulsory education chemistry curriculum standard (trial), Beijing, PRC: Beijing Normal University Press (in Chinese).
- Ministry of Education (MOE) of PRC, (2001d), Full-time compulsory education science curriculum standard for elementary school (trial), Beijing, PRC: Beijing Normal University Press (in Chinese).
- Minner D. and Delisi J., (2010), Inquiring into science instruction observation protocol (ISIOP) Grades 9–12, Newton, MA: Education Development Center.
- Mortimer E. and Scott P., (2003), Meaning making in the secondary science classroom, Milton Keynes, UK: Open University Press.
- Muijs D. and Reynolds D., (2000), School effectiveness and teacher effectiveness in mathematics: some preliminary findings from the evaluation of the mathematics enhancement programme (primary), Sch. Eff. Sch. Improv., 11(3), 273–303.
- Office of Technology Assessment, (1995), Teachers and technology: making the connection, Washington, DC: U.S. Congress, Government Printing Office.
- Oon P. T. and Subramaniam R., (2011), Rasch modeling of a scale that explores the take-up of physics among school students from the perspective of teachers, in Applications of Rasch measurement in learning environments research, Sense Publishers, pp. 119–139.
- Organisation for Economic Cooperation and Development (OECD), (2007), PISA 2006: science competencies for tomorrow's world, vol. 1: analysis, Paris: OECD.
- Philipp S. B., Johnson D. K. and Yezierski E. J., (2014), Development of a protocol to evaluate the use of representations in secondary chemistry instruction, Chem. Educ. Res. Pract., 15(4), 777–786.
- Pianta R. C., La Paro K. M. and Hamre B. K., (2008), Classroom assessment scoring system, Baltimore: Paul H. Brookes.
- Piburn M., Sawada D., Turley J., Falconer K., Benford R., Bloom I. and Judson E., (2000), Reformed teaching observation protocol (RTOP) reference manual, Tempe, Arizona: Arizona Collaborative for Excellence in the Preparation of Teachers.
- Rosenshine B. and Furst N., (1971), Research on teacher performance criteria, in Smith B.O. (ed.) Research in teacher education: a symposium, Englewood Cliffs, N.J.: Prentice-Hall.
- Royal K. D., Ellis A., Ensslen A. and Homan A., (2010), Rating scale optimization in survey research: an application of the Rasch rating scale model, J. Appl. Quant. Method., 5(4), 607.
- Scheerens J. and Bosker R., (1997), The foundations of educational effectiveness, Oxford: Pergamon.
- Schwarz C. V. and White B. Y., (2005), Metamodeling knowledge: developing students' understanding of scientific modeling, Cognition Instruct., 23(2), 165–205.
- Schwarz C. V., Reiser B. J., Davis E. A., Kenyon L., Acher A., Fortus D., Shwartz Y., Hue B. and Krajcik J., (2009), Developing a learning progression for scientific modeling: making scientific modeling accessible and meaningful for learners, J. Res. Sci. Teach., 46(6), 632–654.
- Seidel T. and Shavelson R. J., (2007), Teaching effectiveness research in the past decade: the role of theory and research design in disentangling meta-analysis results, Rev. Educ. Res., 77(4), 454–499.
- Seidel T., Rimmele R. and Prenzel M., (2005), Clarity and coherence of learning goals as a scaffold for student learning, Learn. Instruct., 15, 539–556.
- Seidel T., Prenzel M., Rimmele R., Herweg C., Kobarg M., Schwindt K., et al., (2007), Science teaching and learning in German physics classrooms, in Prenzel M. (ed.) Studies on the educational quality of schools, Münster, Germany: Waxmann, pp. 79–99.
- Smith Jr E. V., (2005), Effect of item redundancy on Rasch item and person estimates, J. Appl. Meas., 6(2), 147–163.
- Stigler J. W., (1999), The TIMSS videotape classroom study: methods and findings from an exploratory research project on eighth-grade mathematics instruction in Germany, Japan, and the United States: DIANE Publishing.
- Stigler J. and Hiebert J., (1997), Understanding and improving classroom mathematics instruction: an overview of the TIMSS video study, Insights from TIMSS, 52.
- Taskin V., Bernholt S. and Parchmann I., (2015), An inventory for measuring student teachers' knowledge of chemical representations: design, validation, and psychometric analysis, Chem. Educ. Res. Pract., 16(3), 460–477.
- The State Council of the People's Republic of China, (2010), Outline of China's National Plan for Medium and Long-Term Education Reform and Development (2010–2020), Resource document (in Chinese), Retrieved from http://www.moe.gov.cn/publicfiles/business/htmlfiles/moe/moe_838/201008/93704.html.
- Walberg H. J., (1981), A psychological theory of educational productivity, in Farley F. H. and Gordon N. (ed.) Psychology and Education: The State of the Union, Berkeley, CA: McCutchan, pp. 81–108.
- Wayne A. J. and Youngs P., (2003), Teacher characteristics and student achievement gains: a review, Rev. Educ. Res., 73(1), 89–122.
- Wei S., Liu X., Wang Z. and Wang X., (2012), Using Rasch measurement to develop a computer modeling-based instrument to assess students' conceptual understanding of matter, J. Chem. Educ., 89(3), 335–345.
- Wei S., Liu X. and Jia Y., (2013), Using Rasch measurement to validate the instrument of students' understanding of models in science (SUMS), Int. J. Sci. Math. Educ., 1–16.
- Weiss I. R., Pasley J. D., Smith P. S., Banilower E. R. and Heck D. J., (2003), Looking inside the classroom: a study of K-12 mathematics and science education in the United States, Horizon Research, Inc.
- Werf G. V. D., Creemers B., Jong R. D. and Klaver E., (2000), Evaluation of school improvement through an educational effectiveness model: the case of Indonesia's PEQIP project, Comp. Educ. Rev., 44(3), 329–355.
- White B. Y., (1998), Computer microworlds and scientific inquiry: an alternative approach to science education, in Fraser B. J. and Tobin K. G. (ed.) International handbook of science education, Dordrecht: Kluwer Academic Publishers, pp. 295–315.
- Wolfe E. W. and Smith Jr E. V., (2006), Instrument development tools and activities or measure validation using Rasch models: part II – validation activities, J. Appl. Meas., 8(2), 204–234.
- Wren D. and Barbera J., (2014), Psychometric analysis of the thermochemistry concept inventory, Chem. Educ. Res. Pract., 15(3), 380–390.
- Wright B. D. and Tennant A., (1996), Sample size again, Rasch Meas. Trans., 9(4), 468.
- Zheng C., Fu L. and He P., (2014), Development of an Instrument for Assessing the Effectiveness of Chemistry Classroom Teaching, J. Sci. Educ. Technol., 23(2), 267–279.
| This journal is © The Royal Society of Chemistry 2016 |