Open Access Article
Open Access ArticleSupramolecular aggregates of single-molecule magnets: exchange-biased quantum tunneling of magnetization in a rectangular [Mn3]4 tetramer†
Tu N.
Nguyen
a,
Wolfgang
Wernsdorfer
b,
Muhandis
Shiddiq
c,
Khalil A.
Abboud
a,
Stephen
Hill
 c and
George
Christou
*a
c and
George
Christou
*a
aDepartment of Chemistry, University of Florida, Gainesville, Florida 32611-7200, USA. E-mail: christou@chem.ufl.edu
bInstitut Néel-CNRS, 38042 Grenoble Cedex 9, France
cNational High Magnetic Field Laboratory and Department of Physics, Florida State University, Tallahassee, Florida 32310, USA
First published on 16th November 2015
Abstract
The syntheses and properties of four magnetically-supramolecular oligomers of triangular Mn3 units are reported: dimeric [Mn6O2(O2CMe)8(CH3OH)2(pdpd)2] (3) and [Mn6O2(O2CMe)8(py)2(pdpd)2](ClO4)2 (4), and tetrameric [Mn12O4(O2CR)12(pdpd)6](ClO4)4 (R = Me (5), tBu (6)). They were all obtained employing 3-phenyl-1,5-di(pyridin-2-yl)pentane-1,5-dione dioxime (pdpdH2), either in direct synthesis reactions involving oxidation of MnII salts or in metathesis reactions with the preformed complex [Mn3O(O2CMe)6(py)3](ClO4) (1); complex 6 was then obtained by carboxylate substitution on complex 5. Complexes 3 and 4 contain two [MnIII2MnII(μ3-O)]6+ and [MnIII3(μ3-O)]7+ units, respectively, linked by two pdpd2− groups. Complexes 5 and 6 contain four [MnIII3(μ3-O)]7+ units linked by six pdpd2− groups into a rectangular tetramer [MnIII3]4. Solid-state dc magnetic susceptibility studies showed that the Mn3 subunits in 3 and 4 have a ground-state spin of S = 3/2 and S = 2, respectively, while the Mn3 subunits in 5 and 6 possess an S = 6 ground state. Complexes 5 and 6 exhibit frequency-dependent out-of-phase (χ′′M) ac susceptibility signals indicating 5 and 6 to be tetramers of Mn3 single-molecule magnets (SMMs). High-frequency EPR studies of a microcrystalline powder sample of 5·2CH2Cl2 provided precise spin Hamiltonian parameters of D = −0.33 cm−1, |E| = 0.03 cm−1, B04 = −8.0 × 10−5 cm−1, and g = 2.0. Magnetization vs. dc field sweeps on a single crystal of 5·xCH2Cl2 gave hysteresis loops below 1 K that exhibit exchange-biased quantum tunneling of magnetization (QTM) steps with a bias field of 0.19 T. Simulation of the loops determined that each Mn3 unit is exchange-coupled to the two neighbors linked to it by the pdpd2− linkers, with an antiferromagnetic inter-Mn3 exchange interaction of J/kB = −0.011 K (Ĥ = −2JŜi·Ŝj convention). The work demonstrates a rational approach to synthesizing magnetically-supramolecular aggregates of SMMs as potential multi-qubit systems for quantum computing.
Introduction
Single-molecule magnets (SMMs) are individual molecules that function as single-domain nanoscale magnetic particles,1,2,3,4,5 and they bring the advantages of molecular chemistry to the field of nanoscale magnetism, such as crystallinity, monodispersity, solubility, and a shell of organic ligands that can be readily varied. Different from molecule-based magnets, which require intermolecular interactions and long-range ordering,6,7,8,9 SMMs are a class of metal clusters that display superparamagnetic behavior down to a characteristic blocking temperature, TB, below which they exhibit slow magnetization dynamics. For Mn and most 3d transition metal SMMs, this behavior arises from the combination of a large ground-state spin (S) and Ising-type magnetoanisotropy (negative zero-field splitting parameter, D), which leads to a significant energy barrier to the thermal equilibration of the molecular magnetic moment. Experimentally, an SMM exhibits frequency-dependent out-of-phase ac magnetic susceptibility signals, and hysteresis in a plot of magnetization vs. applied dc magnetic field. The significant advantage of the single-molecule approach to nanomagnetism is the ability to investigate “particles” that are naturally identical and have well-defined sizes and electronic levels. Moreover, the possibility to modify the ligand sphere by standard solution chemistry methods allows for exquisite tuning of structures and magnetic properties of the molecules. Various families of SMMs have been discovered; the majority of which are Mn-based complexes with Mn84 being the largest among them.10SMMs have also been shown to display interesting quantum phenomena such as quantum tunneling of magnetization (QTM),11,12 quantum phase interference (QPI),13,14,15 spin–spin cross relaxation,16 and quantum entanglement.17,18,19 Consequently, they have been proposed as qubits for quantum computation20–23 and as components in molecular spintronics devices,24,25 which would exploit their quantum tunneling properties. For such applications, weak couplings of two or more SMMs to each other or to other components of a device are essential, while maintaining the intrinsic single-molecule properties of each SMM, and this represents the main goal of this study. The report of supramolecular C–H⋯Cl hydrogen-bonded pairs of [Mn4O3Cl4(O2CEt)3(py)3] (S = 9/2) demonstrated such coupling between two SMMs for the first time, manifested as exchange-biased QTM steps, quantum superposition states, and quantum entanglement of the two SMMs.17,18,19,26 Several supramolecular dimers, chains, and 3D networks of weakly coupled SMMs connected by hydrogen-bonds have since been reported.27–33 Disadvantages of linkage by hydrogen-bonds, however, are (i) de-aggregation into monomeric units on dissolution, and (ii) the major loss of synthetic control, with all the previously mentioned supramolecular aggregates being discovered serendipitously. A superior approach is connection of SMMs via covalent bonds. Such covalent linkage of SMMs has already been explored extensively, invariably leading to chains or 2- or 3D networks.34–50 Discrete, magnetically-supramolecular51,52 oligomers of magnetic molecules comprising two or more covalently linked subunits are relatively rare.53–64 Several studies have provided important insights into tailoring exchange interactions when connecting non-SMM subunits, such as the linking of two Cr7Ni wheel molecules65,66 or two lanthanide ions,67,68,69,70,71 resulting in weak antiferromagnetic (AF) or ferromagnetic (F) interactions. Only a few of these exhibit SMM behavior and none display exchanged-biased QTM steps in hysteresis loops, probably due to the SMM subunits interacting too strongly causing the oligomer to behave magnetically like a single molecule,54 or individual SMM subunits having low lying excited states that interfere with the quantum tunneling process, resulting in stepless hysteresis loops even when the interactions between the subunits are weak.60
An ideal magnetically-supramolecular aggregate of SMMs should possess two features: (i) each subunit is a ‘good’ SMM showing hysteresis loops with clear QTM steps; and (ii) the exchange-coupling through the connecting ligands is very weak so as to represent merely a small perturbation of the single-molecule properties of the constituent SMM subunits. Moreover, a better understanding can be achieved if the properties of the aggregate can be compared to those of the corresponding monomer from which it is constructed, thus requiring the SMM monomer to be available to function as a control for independent structural and magnetic characterization. The desired oligomers might be obtainable by direct synthesis from simple reagents but there are many potential problems and no guarantee that the desired magnetic properties will be obtained this way. A more rational and controllable route would be to apply a building-block approach of linking SMMs together using suitably-designed linker groups that will result in weak inter-SMM interactions, while ensuring that molecular oligomers rather than polymers are obtained.
Our group has therefore initiated a program to link covalently two or more SMMs to give non-polymeric, magnetically-supramolecular ‘aggregates-of-SMMs’ exhibiting very weak inter-SMM exchange interactions. The objective is to obtain materials exhibiting exchange-biased QTM and, in some cases, allow detailed study of quantum superposition states and related phenomena. For these reasons we are targeting small oligomers at this stage, in order to better detect the signatures of these nebulous and fragile effects. In the present work, we report the synthesis and properties of four oligomeric aggregates of Mn3 units; two [Mn3]2 dimers and two [Mn3]4 tetramers, all containing dioximate inter-Mn3 linker groups. We shall describe their structures and magnetic properties and, for one of the [Mn3]4 tetramers, the detailed analysis of high-frequency EPR and micro-SQUID magnetic data. Some preliminary results have been previously communicated.72
Experimental section
Syntheses
All manipulations were performed under aerobic conditions using chemicals and solvents as received unless otherwise stated. [Mn3O(O2CMe)6(py)3](ClO4) (1) was prepared as described elsewhere;73 the dioxime pdpdH2 was synthesized as previously reported.72Caution! Although no such behavior was observed during the present work, perchlorate compounds are potentially explosive; such compounds should be synthesized and used in small quantities, and treated with utmost care at all times.
[Mn6O2(O2CMe)8(pdpd)2(MeOH)2] (3)
A solution of Mn(O2CMe)2·4H2O (0.25 g, 1.0 mmol) in 15 mL of MeCN/MeOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was treated with NEt3 (0.14 mL, 1.0 mmol) and pdpdH2 (0.18 g, 0.50 mmol). The solution was stirred for 1 hour at room temperature, filtered and the dark brown filtrate left undisturbed to concentrate slowly by evaporation. X-ray quality crystals of 3·xMeOH·yMeCN slowly formed over one week. These were collected by filtration, washed with Et2O, and dried under vacuum. The yield was 75% based on Mn. Anal. calcd (found) % for 3·4H2O (Mn6O28C60H76N8): C 42.72 (42.39); H 4.54 (4.18); N 6.64 (6.25). Selected IR data (KBr, cm−1): 1600 (s), 1471 (m), 1397 (s), 1338 (m), 1182 (m), 1107 (w), 1035 (w), 784 (w), 760 (w), 700 (m), 658 (m), 614 (m), 542 (w), 421 (w).
1 v/v) was treated with NEt3 (0.14 mL, 1.0 mmol) and pdpdH2 (0.18 g, 0.50 mmol). The solution was stirred for 1 hour at room temperature, filtered and the dark brown filtrate left undisturbed to concentrate slowly by evaporation. X-ray quality crystals of 3·xMeOH·yMeCN slowly formed over one week. These were collected by filtration, washed with Et2O, and dried under vacuum. The yield was 75% based on Mn. Anal. calcd (found) % for 3·4H2O (Mn6O28C60H76N8): C 42.72 (42.39); H 4.54 (4.18); N 6.64 (6.25). Selected IR data (KBr, cm−1): 1600 (s), 1471 (m), 1397 (s), 1338 (m), 1182 (m), 1107 (w), 1035 (w), 784 (w), 760 (w), 700 (m), 658 (m), 614 (m), 542 (w), 421 (w).
[Mn6O2(O2CMe)8(pdpd)2(py)2](ClO4)2 (4)
A brown solution of complex 1 (0.44 g, 0.50 mmol) in 15 mL of MeCN/MeOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was treated with pdpdH2 (0.18 g, 0.50 mmol). The solution was stirred for 1 hour at room temperature and then evaporated under vacuum to obtain black powder. The powder was dissolved in CH2Cl2 (25 mL) and the resulting solution was layered with Et2O (50 mL). X-ray quality crystals of 4·xEt2O·yCH2Cl2 slowly formed over 2 days. The crystals were collected by filtration, washed with Et2O and dried under vacuum. The yield was 80% based on Mn. Anal. calcd (found) % for 4·3H2O (Mn6O33C68H76N10Cl2): C 41.63 (41.79); H 3.90 (3.62); N 7.14 (6.77). Selected IR data (KBr, cm−1): 1600 (s), 1474 (m), 1392 (s), 1339 (m), 1182 (w), 1108 (m), 1030 (w), 937 (w), 784 (w), 760 (w), 698 (w), 661(m), 625 (w).
1 v/v) was treated with pdpdH2 (0.18 g, 0.50 mmol). The solution was stirred for 1 hour at room temperature and then evaporated under vacuum to obtain black powder. The powder was dissolved in CH2Cl2 (25 mL) and the resulting solution was layered with Et2O (50 mL). X-ray quality crystals of 4·xEt2O·yCH2Cl2 slowly formed over 2 days. The crystals were collected by filtration, washed with Et2O and dried under vacuum. The yield was 80% based on Mn. Anal. calcd (found) % for 4·3H2O (Mn6O33C68H76N10Cl2): C 41.63 (41.79); H 3.90 (3.62); N 7.14 (6.77). Selected IR data (KBr, cm−1): 1600 (s), 1474 (m), 1392 (s), 1339 (m), 1182 (w), 1108 (m), 1030 (w), 937 (w), 784 (w), 760 (w), 698 (w), 661(m), 625 (w).
[Mn12O4(O2CMe)12(pdpd)6](ClO4)4 (5)
A brown solution of complex 1 (0.044 g, 0.050 mmol) in 25 mL of CH2Cl2 was treated with pdpdH2 (0.036 g, 0.10 mmol). The solution was stirred for 1 hour at room temperature, filtered, and the black filtrate left undisturbed. X-ray quality crystals of 5·xCH2Cl2 slowly formed over 2 days. The crystals were collected by filtration, washed with CH2Cl2 and dried under vacuum. The yield was 35% based on Mn. Anal. calcd (found) % for 5·2CH2Cl2 (ref. 74) (Mn12O56C152H148N24Cl8): C 43.99 (43.58); H 3.59 (3.54); N 8.10 (7.75). Selected IR data (KBr, cm−1): 1600 (s), 1574 (s), 1474 (m), 1388 (s), 1337 (m), 1183 (m), 1162 (m), 1109 (s), 1088 (m), 1047(w), 781 (w), 758 (w), 700 (m), 661(m), 623 (m).[Mn12O4(O2CtBu)12(pdpd)6](ClO4)4 (6)
A brown solution of complex 5 (0.21 g, 0.050 mmol) in 30 mL of MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EtOH (2
EtOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) was treated with pivalic acid (0.12 g, 1.2 mmol), and the solution was stirred overnight at room temperature. Toluene (10 mL) was added and the solvent was removed under vacuum. After three cycles of toluene addition and removal, the residue was dissolved in CH2Cl2 (25 mL) and the resulting solution was layered with hexanes (50 mL). X-ray quality crystals of 6·xCH2Cl2 slowly formed over 3 days. The crystals were collected by filtration, washed with hexanes, and dried under vacuum. The yield was 50% based on Mn. Anal. calcd (found) % for 6·2CH2Cl2 (ref. 74) (Mn12O56C188H220N24Cl8) C 48.51 (48.83); H 4.76 (4.92); N 7.22 (6.95). Selected IR data (KBr, cm−1): 1601 (s), 1584 (s), 1561 (s), 1516 (w), 1478 (s), 1440 (w), 1400 (s), 1384 (m), 1348 (s), 1219 (s), 1188 (m), 1165 (w), 1096 (s), 783 (m), 756 (w), 700 (m), 663 (m), 622 (s), 449 (m).
1 v/v) was treated with pivalic acid (0.12 g, 1.2 mmol), and the solution was stirred overnight at room temperature. Toluene (10 mL) was added and the solvent was removed under vacuum. After three cycles of toluene addition and removal, the residue was dissolved in CH2Cl2 (25 mL) and the resulting solution was layered with hexanes (50 mL). X-ray quality crystals of 6·xCH2Cl2 slowly formed over 3 days. The crystals were collected by filtration, washed with hexanes, and dried under vacuum. The yield was 50% based on Mn. Anal. calcd (found) % for 6·2CH2Cl2 (ref. 74) (Mn12O56C188H220N24Cl8) C 48.51 (48.83); H 4.76 (4.92); N 7.22 (6.95). Selected IR data (KBr, cm−1): 1601 (s), 1584 (s), 1561 (s), 1516 (w), 1478 (s), 1440 (w), 1400 (s), 1384 (m), 1348 (s), 1219 (s), 1188 (m), 1165 (w), 1096 (s), 783 (m), 756 (w), 700 (m), 663 (m), 622 (s), 449 (m).
X-ray crystallography
X-ray intensity data were collected at 100 K on a Bruker DUO diffractometer using MoKα radiation (λ = 0.71073 Å) and an APEXII CCD area detector. Suitable crystals of 3·xMeOH·yMeCN, 4·xEt2O·yCH2Cl2, 5·xCH2Cl2 and 6·xCH2Cl2 were attached to glass fibers using silicone grease and transferred to a goniostat where they were cooled to 100 K for data collection. Raw data frames were read by the program SAINT and integrated using 3D profiling algorithms. The resulting data were reduced to produce hkl reflections, their intensities and estimated standard deviations. The data were corrected for Lorentz and polarization effects, and numerical absorption corrections were applied based on indexed and measured faces. The structures were solved and refined in SHELXTL6.1,75 using full-matrix least-squares refinement cycles. The non-H atoms were refined with anisotropic thermal parameters and all of the H atoms were calculated in idealized positions and refined as riding on their parent atoms. Unit cell data and structural refinement details for the four compounds are listed in Table 1. More details are provided in ESI.†76| a Including solvate molecules. b Graphite monochromator. c I > 2σ(I). d R 1 = ∑(||Fo| − |Fc||)/∑|Fo|. e wR2 = [∑[w(Fo2 − Fc2)2]/∑[w(Fo2)2]]1/2 where w = 1/[σ2(Fo2) + (m × p)2 + n × p], p = [max(Fo2, 0) + 2 × Fc2]/3, m and n are constants. | ||||
|---|---|---|---|---|
| Parameter | 3·xMeOH·yMeCN | 4·xC4H10O·yCH2Cl2 | 5·xCH2Cl2 | 6·xCH2Cl2 |
| Formulaa | C65H86Mn6N10O26 | C82H98Cl10Mn6N10O32 | C150.25H144Cl4.50Mn12N24O56 | C206H252Cl44Mn12N24O48 |
| FWa, g mol−1 | 1753.08 | 2419.84 | 4000.70 | 6051.40 |
| Crystal system | Monoclinic | Triclinic | Monoclinic | Monoclinic |
| Space group | C 2/c |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
P 21/c | C 2/c |
| a, Å | 16.0232(17) | 16.7797(18) | 34.190(4) | 42.112(3) |
| b, Å | 41.093(4) | 16.9615(18) | 32.890(4) | 26.4980(16) |
| c, Å | 13.0506(14) | 20.538(4) | 44.013(5) | 30.5334(18) |
| α, ° | 90 | 93.849(3) | 90 | 90 |
| β, ° | 110.908(2) | 105.068(3) | 110.320(3) | 127.707(1) |
| γ, ° | 90 | 116.263(2) | 90 | 90 |
| V, Å3 | 8027.2(15) | 4948.4(11) | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413(9) 413(9) |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956(3) 956(3) |
| Z | 4 | 2 | 8 | 4 |
| T, K | 100(2) | 100(2) | 100(2) | 100(2) |
| λ, Åb | 0.71073 | 0.71073 | 0.71073 | 0.71073 |
| ρ calc, g cm−3 | 1.451 | 1.624 | 1.145 | 1.491 |
| μ, mm−1 | 0.995 | 1.097 | 0.748 | 1.048 |
| R 1 , | 0.0460 | 0.0732 | 0.0740 | 0.0505 |
| wR2e | 0.1276 | 0.2028 | 0.1617 | 0.1218 |
Physical and spectroscopic measurements
Infrared spectra were recorded in the solid state (KBr pellets) on a Nicolet Nexus 670 FTIR spectrometer in the 400–4000 cm−1 range. Elemental analyses (C, H, and N) were performed by the in-house facilities of the University of Florida, Chemistry Department. Variable-temperature direct current (dc) and alternating current (ac) magnetic susceptibility data were collected at the University of Florida using a Quantum Design MPMS-XL SQUID magnetometer equipped with a 7 T magnet and operating in the 1.8–300 K range. Samples were embedded in solid eicosane to prevent torquing. Magnetization vs. field and temperature data were fit using the program MAGNET.77a Pascal's constants were used to estimate the diamagnetic correction, which was subtracted from the experimental susceptibility to give the molar paramagnetic susceptibility (χM). Low-temperature (<1.8 K) hysteresis loop and dc relaxation measurements were performed at Institut Néel using an array of micro-SQUIDS.78 The high sensitivity of this magnetometer allows the study of single crystals of SMMs of the order of 10–500 μm. The field can be applied in any direction by separately driving three orthogonal coils. High-frequency EPR (HF-EPR) powder spectra were collected at the Electron Magnetic Resonance facility of the U.S. National High Magnetic Field Laboratory using a broadband (10 to 700 GHz) transmission probe in which microwaves are propagated into and out of a 17 T superconducting magnet through cylindrical light pipes.79 Tunable microwave radiation was generated using a phase-locked Virginia Diodes solid-state source operating at 13 ± 1 GHz, followed by a chain of solid-state multipliers and amplifiers. Field modulation was employed in conjunction with a phase-sensitive homodyne detection scheme using a cold bolometer, yielding derivative mode spectra. Temperature control was achieved using helium gas flow cryostats.Results and discussion
Syntheses
The synthetic strategies employed in this work are based on the report in 2007 that the use of the mono-oxime methyl-2-pyridyl ketone oxime (mpkoH; Fig. 1) in MnIII carboxylate chemistry gives the triangular complex [Mn3O(O2CMe)3(mpko)3](ClO4) (2), which has an S = 6 ground state and is an SMM.80 The cation of 2 has C3 symmetry with the acetate and mpko− ligands on opposite sides of the Mn3 plane (Fig. 1). This tripodal arrangement of the three oximates made this Mn3 SMM attractive to us for our present objectives because it suggested that their replacement with dioximates to link multiple Mn3 units together might give molecular oligomers rather than polymers.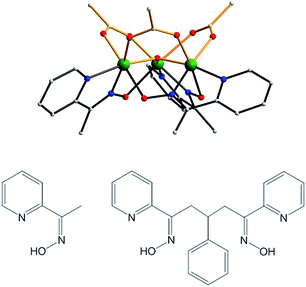 | ||
| Fig. 1 Structure of the cation of complex 2 (top), mpkoH (bottom left) and pdpdH2 (bottom right). Colour code: Mn green; N blue; O red; C grey. | ||
After some planning, we settled on the dioxime 3-phenyl-1,5-di(pyridin-2-yl)pentane-1,5-dione dioxime (pdpdH2) for this work. It was designed taking into consideration the established binding modes of mpkoH, which has been well investigated in transition metal chemistry by many groups,81–89 and the decision to have a three-carbon linker between the two ends to impart sufficient length and flexibility to yield any potential oligomeric product without steric problems. The Ph ring at the central carbon atom was included to facilitate the synthesis, which comprised the reaction of two equivalents of 2-acetylpyridine with benzaldehyde to give the dione90 followed by a standard conversion to the dioxime with hydroxylamine. We recognized that the overall flexibility of pdpdH2 meant that it was not ‘pre-programmed’ to yield any particular degree of oligomerization or product topology, but this was as desired at this initial stage in order to explore various possibilities.
Two procedures to 2 had been used80 that could now be employed with pdpdH2: (i) direct synthesis with simple reagents involving comproportionation between MnII acetate and MnO4− in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio in the presence of MeCO2H and mpkoH, the Mn3+
1 ratio in the presence of MeCO2H and mpkoH, the Mn3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn7+ ratio of 3
Mn7+ ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 giving a Mn3.25+ average; and (ii) reaction of mpkoH with the non-SMM [Mn3O(O2CMe)6(py)3](ClO4) (1) in a 3
1 giving a Mn3.25+ average; and (ii) reaction of mpkoH with the non-SMM [Mn3O(O2CMe)6(py)3](ClO4) (1) in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio (eqn (1)). Analogues of 2 with other carboxylates were also available from these methods using the corresponding starting materials.
1 ratio (eqn (1)). Analogues of 2 with other carboxylates were also available from these methods using the corresponding starting materials.
| [Mn3O(O2CR)6(py)3]+ + 3mpkoH → [Mn3O(O2CR)3(mpko)3]+ + 3RCO2H + 3py | (1) |
The reactions between pdpdH2 and a series of manganese salts were screened under a variety of conditions: solvent, stoichiometry, presence or absence of base, etc. Reaction of Mn(O2CMe)2, pdpdH2 and NEt3 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio in MeCN
2 molar ratio in MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH (2
MeOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) led to [Mn6O2(O2CMe)8(pdpd)2(MeOH)2] (3) (eqn (2)).
1 v/v) led to [Mn6O2(O2CMe)8(pdpd)2(MeOH)2] (3) (eqn (2)).
The oxidation of MnII to MnIII is by atmospheric O2, facilitated by the basic conditions imparted by the NEt3. In the absence of NEt3, the reaction is much slower and the yield of 3 is much lower. The MnII![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pdpdH2 reaction ratio of 2
pdpdH2 reaction ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 means the dioxime is in excess, but reactions with 3
1 means the dioxime is in excess, but reactions with 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 still gave the same product in comparable yield. The cleanest, most crystalline product was obtained with the 2
1 still gave the same product in comparable yield. The cleanest, most crystalline product was obtained with the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, as in the Experimental section.
1 ratio, as in the Experimental section.
| 6Mn(O2CMe)2 + 2pdpdH2 + 2MeOH + 4NEt3 + O2 → [Mn6O2(O2CMe)8(pdpd)2(MeOH)2] + 4MeCO2− + 4Et3NH+ + 4H2O | (2) |
3 is mixed-valence (2MnII, 4MnIII) indicating incomplete oxidation of MnII under these conditions. To explore whether an all-MnIII analogue was obtainable, we used the preformed MnIII complex 1. Indeed, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction of pdpdH2 with 1 in MeCN
1 reaction of pdpdH2 with 1 in MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH (2
MeOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) successfully gave [Mn6O2(O2CMe)8(pdpd)2(py)2](ClO4)2 (4), the all-MnIII version of 3 (eqn (3)). In both 3 and 4, each pdpd2− oxime group clips onto the same edge of each of the two Mn3 triangular units, the other edges being bridged by only acetate groups (vide infra).80
1 v/v) successfully gave [Mn6O2(O2CMe)8(pdpd)2(py)2](ClO4)2 (4), the all-MnIII version of 3 (eqn (3)). In both 3 and 4, each pdpd2− oxime group clips onto the same edge of each of the two Mn3 triangular units, the other edges being bridged by only acetate groups (vide infra).80
| 2[Mn3O(O2CMe)6(py)3]+ + 2pdpdH2 → [Mn6O2(O2CMe)8(py)2(pdpd)2]2+ + 4MeCO2− + 4pyH+ | (3) |
We now turned our attention to obtaining analogues of 2 with dioximate linkers bound to all edges of the triangular core rather than mpko−. Given our observations with 3 and 4, we decided to employ preformed 1 rather than MnII salts. Thus, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 reaction of 1 and pdpdH2 in CH2Cl2 was explored and this led to [Mn12O4(O2CMe)12(pdpd)6]4+ (5) (eqn (4)).
2 reaction of 1 and pdpdH2 in CH2Cl2 was explored and this led to [Mn12O4(O2CMe)12(pdpd)6]4+ (5) (eqn (4)).
| 4[Mn3O(O2CMe)6(py)3]+ + 6pdpdH2 → [Mn12O4(O2CMe)12(pdpd)6]4+ + 12MeCO2− + 12pyH+ | (4) |
The excess of pdpdH2 was beneficial, the stoichiometric 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio of eqn (4) giving a much lower yield. Ratios higher than 1
3 ratio of eqn (4) giving a much lower yield. Ratios higher than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 did not improve the yield further. The CH2Cl2 solvent was crucial for obtaining good crystals, the MeCN
2 did not improve the yield further. The CH2Cl2 solvent was crucial for obtaining good crystals, the MeCN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH (2
MeOH (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) medium, as used for 3 and 4, also giving 5 but as crystals unsuitable for crystallography.
1 v/v) medium, as used for 3 and 4, also giving 5 but as crystals unsuitable for crystallography.
With 5 attained and characterized (vide infra), it was of importance for the magnetic studies to determine if its ligation could be modified in a controlled fashion. We have previously shown that the acetate groups of, for example, the [Mn12O12(O2CMe)16(H2O)4] SMM can be substituted with numerous other carboxylates,5 the substitution being driven to completion by removal of MeCO2H as its toluene azeotrope under vacuum. This controlled modification has been crucial for many studies on SMMs.91–97 We have now found that a similar carboxylate substitution using pivalic acid is possible for 5, without breaking any of the dioximate linkages, to give 6 (eqn (5)). This mild carboxylate substitution augurs well that controlled modification of supramolecular aggregates of many types will be possible in the future to optimize them for particular studies or attachment to functional units or surfaces.
| [Mn12O4(O2CMe)12(pdpd)6]4+ + 12tBuCO2H → [Mn12O4(O2CtBu)12(pdpd)6]4+ + 12MeCO2H | (5) |
Description of structures
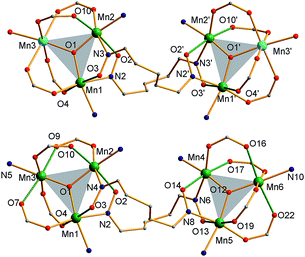
The structures of 3 and the cation of 4 are shown in Fig. 2 and 3, and selected interatomic distances and angles are listed in ESI.†76 The compounds are essentially isostructural. Their cores (Fig. 3) consist of two [MnIIMnIII2(μ3-O)]6+ (3) or [MnIII3(μ3-O)]7+ (4) triangular subunits linked by two pdpd2− groups to give [Mn3]20/2+ dimers. The O2− ions lie only slightly out of the Mn3 planes in both complexes (d = 0.002–0.017 Å). Interestingly, both pdpd2− linkers attach to the same Mn3 edge so that these edges are bridged by two pyridyloximate groups whereas the other edges are bridged by two acetate groups each. This is distinctly different from 2 (Fig. 1) where each edge is bridged by one mpko− and one acetate. The ligation is completed by terminal MeOH groups on the MnII atoms (Mn3, Mn3′) in 3 and pyridine groups on the MnIII ions at the corresponding positions in 4. The Mn oxidation states were deduced from charge balance considerations and the MnIII Jahn–Teller distortions (Fig. 3), and confirmed by bond valence sum (BVS) calculations. BVS calculations also confirmed that the μ3-O atoms are O2− ions.76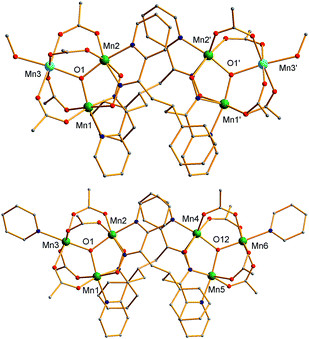 | ||
| Fig. 2 Complete structure of 3 (top) and the cation of 4 (bottom) with H atoms omitted for clarity. Colour code: MnIII green; MnII sky blue; O red; N blue; C grey. | ||
The Mn3 triangles are far from equilateral, with Mn⋯Mn separations and Mn–O2−–Mn angles for the edges bridged by two oximate groups being noticeably smaller than those for edges bridged by two acetates. This is a characteristic of a diatomic N–O oximate bridge vs. a triatomic O–C–O carboxylate bridge. The triangles are crystallographically scalene but isosceles within the 3σ criterion. Overall, both dimers have C2 symmetry, either crystallographic (3) or virtual (4). Inspection of short contacts reveals that each [Mn3]2 dimer molecule of 3 connects to two neighbors by two hydrogen-bonds to each (Oacet⋯OMeOH = 2.752(4) Å) to form a {[Mn3]2}n zig-zag chain (Fig. S1†).76
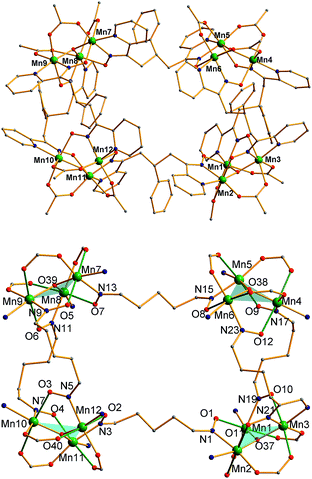
The structure of the cation of 5 is shown in Fig. 4. The cation of 6 (Fig. S2†) is very similar and will not be described separately. Selected [Mn3(μ3-O)] core distances and angles for the cation of 5 are listed in Table 2, and fuller listings for both cations are available in ESI.†76 The asymmetric unit of 5 consists of two essentially superimposable [Mn3]44+ cations (only the one shown in Fig. 4 will be discussed further), eight ClO4− anions, and large amounts of disordered CH2Cl2 solvent; the asymmetric unit of 6 contains only one cation. The cation consists of four [Mn3(μ3-O)]7+ units linked by six pdpd2− groups to give a rectangular [Mn3]4 supramolecule with each Mn3 unit at a corner. One of the two μ-MeCO2− ligands bridging each edge of 1 has been replaced by a bridging oximate from a pdpd2− group. The long and short sides of the rectangle are bridged by one and two pdpd2− groups, respectively (Fig. 4). In addition, the pdpd2− pyridyl groups have replaced the terminal pyridine ligands of 1. Each of the μ3-O2− ions lies slightly above the Mn3 plane (d ∼ 0.3 Å), and all the Mn–N–O–Mn torsion angles are relatively large (ϕ ∼ 8–20°) (Table 3), as in 2. Thus, the local structure of each Mn3 unit of 5 (and 6) is very similar to that of 2. Also as in 2, the three bridging oximate groups are on the same side of the Mn3 plane, and this facilitates the formation of a molecular tetramer rather than a polymer. The flexibility of pdpd2−, however, is likely why a rectangular rather than tetrahedral [Mn3]4 topology, as might be expected from four tripodal units and stiff linkers, has been obtained. The elemental analysis data for vacuum-dried 5 and 6 both indicate two CH2Cl2 molecules, and this is consistent with the observation of two CH2Cl2 molecules encapsulated within the central cavity of the Mn12 cations, with no opening big enough for them to escape (Fig. S3†).74
| Distance (Å) | Angle (°) | ||
|---|---|---|---|
| Mn1⋯Mn3 | 3.184(2) | Mn1–O37–Mn3 | 115.3(2) |
| Mn1⋯Mn2 | 3.212(2) | Mn1–O37–Mn2 | 118.3(3) |
| Mn2⋯Mn3 | 3.201(2) | Mn2–O37–Mn3 | 118.6(3) |
| Mn4⋯Mn5 | 3.189(2) | Mn4–O38–Mn5 | 116.5(3) |
| Mn4⋯Mn6 | 3.173(2) | Mn4–O38–Mn6 | 116.9(3) |
| Mn5⋯Mn6 | 3.216(2) | Mn5–O38–Mn6 | 118.2(3) |
| Mn7⋯Mn8 | 3.180(2) | Mn7–O39–Mn8 | 116.3(3) |
| Mn7⋯Mn9 | 3.206(2) | Mn7–O39–Mn9 | 118.0(3) |
| Mn8⋯Mn9 | 3.205(2) | Mn8–O39–Mn9 | 118.7(3) |
| Mn10⋯Mn11 | 3.185(2) | Mn10–O40–Mn11 | 118.5(3) |
| Mn10⋯Mn12 | 3.197(2) | Mn10–O40–Mn12 | 116.6(3) |
| Mn11⋯Mn12 | 3.218(2) | Mn11–O40–Mn12 | 119.3(3) |
| Complex 5 | Complex 6 | ||||||
|---|---|---|---|---|---|---|---|
| a Displacement (Å) of μ3-oxide atom from the Mn3 plane. b Mn–N–O–Mn torsion angle ϕ (°). | |||||||
| Triangle | d | Torsion angleb | ϕ (°) | Triangle | d | Torsion angleb | ϕ (°) |
| Mn1Mn2Mn3 | 0.31 | Mn1–N19–O10–Mn3 | 17.98 | Mn1Mn2Mn3 | 0.31 | Mn1–N2–O3–Mn3 | 14.38 |
| Mn2–N1–O1–Mn1 | 14.49 | Mn2–N4–O4–Mn1 | 10.60 | ||||
| Mn3–N21–O11–Mn2 | 10.90 | Mn3–N6–O5–Mn2 | 13.30 | ||||
| Mn4Mn5Mn6 | 0.32 | Mn4–N17–O9–Mn5 | 19.82 | Mn4Mn5Mn6 | 0.31 | Mn5–N10–O7–Mn4 | 18.31 |
| Mn5–N15–O8–Mn6 | 10.75 | Mn6–N12–O8–Mn5 | 12.64 | ||||
| Mn6–N28–O12–Mn4 | 18.28 | Mn4–N8–O6–Mn6 | 10.96 | ||||
| Mn7Mn8Mn9 | 0.29 | Mn7–N13–O7–Mn8 | 15.88 | ||||
| Mn8–N11–O6–Mn9 | 9.97 | ||||||
| Mn9–N9–O5–Mn7 | 15.73 | ||||||
| Mn10Mn11Mn12 | 0.26 | Mn10–N7–O4–Mn11 | 15.57 | ||||
| Mn11–N3–O2–Mn12 | 8.09 | ||||||
| Mn12–N5–O3–Mn10 | 12.59 | ||||||
As seen also for 2, the Mn⋯Mn separations and Mn–O2−–Mn angles span a small range and lead to each triangle being virtually isosceles within the 3σ criterion. Interestingly, both types of distortion from equilateral to isosceles are seen, i.e., short/long/long and short/short/long Mn⋯Mn separations, and corresponding small/large/large and small/small/large Mn–O–Mn angles. There are two of each type of Mn3 unit in the cation in Fig. 4 and Table 2. The MnIII oxidation states were confirmed by BVS calculations, and their JT elongation axes (green bonds in Fig. 4) are aligned in a propeller fashion, again as in 2. Overall, the cations of both 5 and 6 have virtual D2d symmetry, i.e., the four Mn3 units are virtually symmetry equivalent.
Magnetochemistry
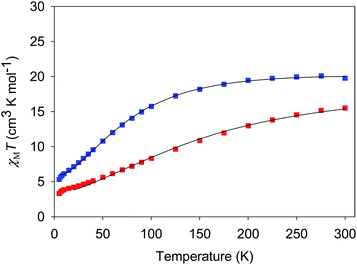 | ||
| Fig. 5 χ M T vs. T for complexes 3·4H2O (red) and 4·3H2O (blue). The solid lines are the fits of the data from 20–300 K (3) and 6.5–300 K (4); see Table 4 for the fit parameters. | ||
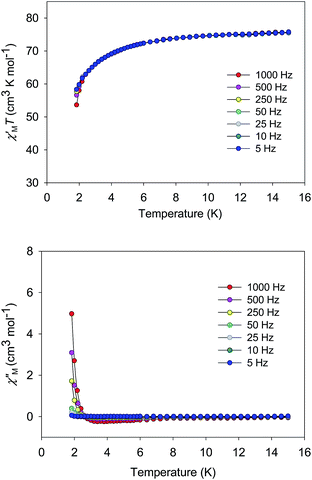
The χMT vs. T plots for 5·2CH2Cl2 and 6·2CH2Cl2 are essentially identical (Fig. 6), as expected from their near-identical structures. χMT for 5·2CH2Cl2 increases from 48.25 cm3 K mol−1 at 300 K to a plateau value of 76.55 cm3 K mol−1 at 20 K, and then decreases slightly to 70.62 cm3 K mol−1 at 5.0 K. For 6·2CH2Cl2, χMT is 46.34 cm3 K mol−1 at 300 K, increasing to 76.57 cm3 K mol−1 at 25 K before slightly decreasing to 70.97 cm3 K mol−1 at 5.0 K. The overall profiles are extremely similar to that of monomer 2, indicating each of the four Mn3 units of 5 and 6 to still be ferromagnetically coupled with S = 6 ground states. Indeed, the 300 K values of 5·2CH2Cl2 and 6·2CH2Cl2 are much larger than the spin-only (g = 2) value for twelve MnIII atoms (36 cm3 K mol−1), and the peak values are as expected for four ostensibly non-interacting S = 6 units with g slightly less than 2.0 (spin-only value 84 cm3 K mol−1). The decreases below 20 K can be attributed to zero-field splitting (ZFS) within the S = 6 ground states, weak inter-Mn3 interactions, and any Zeeman effects from the applied field.
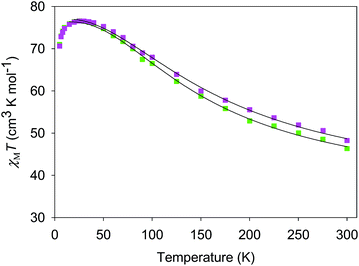 | ||
| Fig. 6 χ M T vs. T for complexes 5 (purple) and 6 (green). The solid lines are the fits of the data from 20–300 K (5) and 10–300 K (6); see Table 4 for the fit parameters. | ||
The data were fit to the theoretical χMT vs. T expressions to obtain the exchange interaction parameters (Jij) between MniMnj pairs. We assumed the interaction through the bridging pdpd2− to be too weak to affect the data except at the lowest temperatures, and thus fit the data assuming non-interacting Mn3 units; however, the H-bonding between different dimers of 3 should give somewhat stronger inter-Mn3 interactions (vide infra). For complexes 3/4 and 5/6, the theoretical χMT is the sum for two and four independent Mn3 units, respectively. In accord with the mixed-valence nature of 3 and the Mn3 structural parameters for 4–6, we used an isosceles triangle model for each Mn3 unit. For convenience, we label this triangle in a general way as Mn1Mn2Mn2′, with Mn2Mn2′ being the unique edge. The Heisenberg–Dirac–van Vleck (HDVV) spin Hamiltonian is then given by eqn (6), where J = J12 = J12′ and J′ = J22′. Using the
| Ĥ = −2J(Ŝ1·Ŝ2 + Ŝ1·Ŝ2′) − 2J′Ŝ2·Ŝ2′ | (6) |
| Ĥ = −J(ŜT2 − ŜA2 − Ŝ12) − J′(ŜA2 − Ŝ22 − Ŝ2′2) | (7) |
| E(ST, SA) = −J[ST(ST + 1) − SA(SA + 1)] − J′[SA(SA + 1)] | (8) |
| Complex | J (cm−1) | J′ (cm−1) | g | S |
|---|---|---|---|---|
| 3·4H2O | −9.9 ± 0.5 | 10.4 ± 3.9 | 1.96 ± 0.04 | 3/2 |
| 4·3H2O | −4.9 ± 0.1 | 28.4 ± 2.0 | 1.99 ± 0.01 | 2 |
| 5·2CH2Cl2 | 16.8 ± 0.6 | 1.5 ± 0.7 | 1.91 ± 0.01 | 6 |
| 7.2 ± 0.7 | 21.4 ± 0.6 | 6 | ||
| 6·2CH2Cl2 | 13.5 ± 0.8 | 3.8 ± 1.0 | 1.91 ± 0.01 | 6 |
| 6.8 ± 1.0 | 17.6 ± 0.8 | 6 |
For both 3 and 4, J and J′ are AF and F, respectively. The J vs. J′ error surfaces for the fits, obtained with the program GRID,77b showed them to be unique (Fig. S5 and S6†).76 The obtained J and J′ reveal 3 to have an S = 3/2 ground state with an S = 5/2 first excited state at 49.7 cm−1. 4 has an S = 2 ground state and an S = 3 first excited state at 29.6 cm−1. The presence of both F and AF interactions is as expected from the structures of 3 and 4. The bis-acetate-bridged edges correspond to the AF J interactions, while the bis-oximate-bridged edge corresponds to the F J′ interaction. This is consistent with previous studies of (i) [Mn3O(O2CR)6L3]0,+ complexes (2MnIIIMnII and 3MnIII),73 where all couplings are AF, and (ii) mono-oximate bridged 2, where all couplings are F.80 In 3 and 4, two oximates now bridge the J′ (MnIII2) edge and the coupling is again F, consistent with the non-zero oximate Mn–O–N–Mn torsion angles in 3 (av 17.1°) and 4 (av 15.7°), one of the recognized effects that promote F coupling between MnIII atoms.100,101 Interestingly, on conversion of the MnII atoms in 3 to MnIII in 4, and the shortening of the resulting Mn–O2− bond, the J′ coupling increases by nearly a factor of three even though its Mn–O–N–Mn torsion angles decrease to 15.7°. This emphasizes the importance of not just the torsion angles but also of perturbations to coupling pathways through the central O2− ion to the overall F J′ coupling in 3 and 4, and other O2−-bridged Mn3 triangles, as we have discussed elsewhere.102
For 5 and 6, both J and J′ are F. However, the error surface for 5 in Fig. 7 (and for 6 in Fig. S8†) show two minima of near-equivalent quality located either side of the J vs. J′ line. These two minima are assigned to the two different distortions from equilateral to isosceles, as discussed above. Since the crystal structure of the cation of 5 shows that both distortions are present, we conclude that both J/J′ pairs are present and contribute to the observed magnetic properties. In our previous study of monomer 2 and its other carboxylate analogues,80 only one type of isosceles triangle was observed crystallographically and therefore only the best fit J/J′ pairs were reported (J = 12.1–18.6 cm−1 and J′ = 1.5–6.7 cm−1), which are very similar to one of the fits in the present work.80 Further, the two fits for 5 and 6 each have the same average within the fit uncertainties: Jav = 11.8 ± 0.1 cm−1 for 5, and Jav = 10.3 ± 0.1 cm−1 for 6. In all cases, the Mn3 units have an S = 6 ground state, with an S = 5 first excited state. The first excited states lie 79.5 and 84.1 cm−1 above the ground states of 5 and 6, respectively, and the ground states are thus well-isolated.
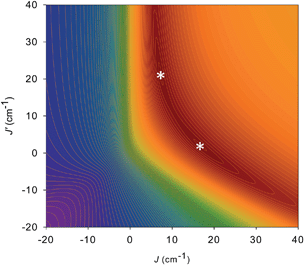 | ||
| Fig. 7 2-D contour plot of the error surface for the J vs. J′ fit of the dc χMT vs. T data for complex 5. The darkest-brown region has the lowest error, where the two fits (asterisks) of comparable quality are located, and the blue region has the highest error. See Table 4 for the fit parameters. | ||
The ground states of the Mn3 units in 5 and 6 were confirmed by fits of magnetization (M) data collected in the 0.1–7 T and 1.8–10 K ranges. The data, plotted as M/NμBvs. H/T in Fig. S9† (N is Avogadro's number and μB is the Bohr magneton) were fit, as described for 2,80 using the program MAGNET77a by diagonalization of the spin Hamiltonian matrix assuming only the ground state is populated, incorporating axial anisotropy (DŜz2) and Zeeman terms, and employing a full powder average.103,104 We assumed each Mn3 to be acting independently, i.e., that any inter-Mn3 interactions through pdpd2− linkers were too weak to have a noticeable effect at these fields and temperatures. In support of the latter, we obtained excellent fits with S = 6, g = 1.92(1), D = −0.30(2) cm−1 for 5 and S = 6, g = 1.89(1), D = −0.30(2) cm−1 for 6. These are very similar to those for 2 (S = 6, D = −0.34 cm−1, and g = 1.92). The gvs. D error surfaces (Fig. S10†) revealed alternative fits with positive D but of much poorer quality.
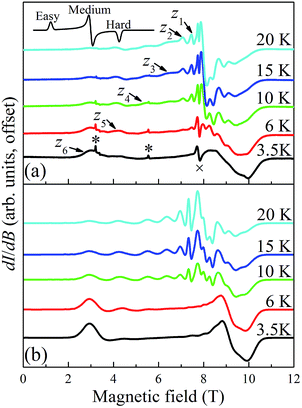
Temperature dependent EPR spectra collected at 217.6 GHz are presented in Fig. 9. The two very sharp features (indicated by asterisks) at 3.2 and 5.5 T have been well characterized and are attributed to paramagnetic oxygen impurities trapped in the KBr pellet. The sharp feature observed around the isotropic g = 2.00 position (marked by “×” at 7.77 T) corresponds to an impurity phase within the powder, possibly containing MnII; this is often found to be the case in Mn-containing polynuclear clusters. The spectra were recorded in field-derivative mode (dI/dB, where I denotes the absorption intensity), making it relatively easy to determine which peaks correspond to which components of the spectrum. The inset to Fig. 9a displays a trivial example of a T = 0 derivative mode powder spectrum for a biaxial S = 1/2 system with three distinct g-tensor components: the onset of absorption appears as a peak in the derivative mode spectrum, and corresponds to the easy-axis of magnetization (largest g component); the cessation of absorption thus appears as a dip in the derivative, corresponding to the hard-axis (smallest g component); meanwhile, the intermediate component of the g-tensor occurs at the maximum in absorption and, therefore, looks like the derivative of the z-component. The same general behavior is expected for high-spin systems that experience zero-field splitting (zfs) interactions, and examination of the resonances on the low (high) field side of g = 2.00 in Fig. 9a indicates that they are indeed peaks (dips). In the case of a uniaxial zfs tensor, the parallel (B∥z) component of the powder spectrum typically extends about twice as far from the g = 2.00 position, compared to the perpendicular (B⊥z) component, with the extent of the deviation from g = 2.00 being directly proportional to the magnitude of the axial D parameter. On this basis, the multiple low-field features in Fig. 9a can be attributed to resolved parallel (B∥z) excitations. Careful inspection of the 20 K spectrum reveals six such peaks (z1 to z6) on the low field side of g = 2.00. This is an indication of an S = 6 ground state for the Mn3 triangle units. The peaks correspond to the following fine-structure transitions within the ground S = 6 spin multiplet: mS = −6 → −5 (z6), mS = −5 → −4 (z5), …, and mS = −1 → 0 (z1). The fact that the spectral weight associated with the parallel spectrum shifts to the low field, mS = −6 → −5 (z6), transition upon cooling provides confirmation of the negative sign of D, i.e., the mS = −6 state is lowest in energy when B∥z.
In contrast to the parallel spectrum, the fine structure transitions within the perpendicular spectrum are not resolved. There are several possible reasons for this. First of all, the relevant peaks should be much more closely spaced (two perpendicular components, each with half the separation of the parallel spectrum) and, therefore, more difficult to resolve. Nevertheless, this alone cannot account for the observed spectrum. Another compounding factor is the existence of the two distinct isosceles triangles (with short/short/long and long/long/short edges) within the tetramer (vide supra), which one would expect to have different zfs parameters, with the difference likely being more pronounced for the transverse 2nd-order anisotropy parameter, E. The transverse anisotropy results from a projection of the anisotropies of the individual MnIII ions onto the plane of the triangle. The 2nd-order projection is strictly zero (E = 0) for the perfectly equilateral case, i.e., there is an exact cancelation. However, for the isosceles case, the projections onto the plane of the triangle do not cancel, and the value of E can be expected to be extremely sensitive to the distortion away from a perfect equilateral triangle. This contrasts the case for the axial molecular zfs parameter, D, which results from an addition of the single-ion anisotropies. The effect of the two triangular topologies is therefore likely to be quite similar to a disorder that disproportionately affects the transverse anisotropy parameter, E. This type of disorder is well known in other MnIII containing clusters,105 including the Mn12-acetate SMM,106,107 where it has been shown to significantly impact the perpendicular spectrum without affecting the parallel components significantly. These influences can be taken into consideration when simulating spectra using a program such as EasySpin.108 We note that the temperature dependent studies (Fig. 9) do not provide any strong indications that there are low-lying states with S = 5, 4, etc., i.e., no additional peaks emerge upon raising the temperature that cannot be accounted for via simulations that assume an isolated S = 6 ground state.
Fig. 9b displays the simulation obtained from the spin Hamiltonian in eqn (9), where Ŝ and Ŝi (i = x, y, z) are spin operators,
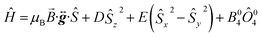 | (9) |
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) is the applied magnetic field vector,
is the applied magnetic field vector, 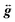 is the Landé g tensor, D and E are the second-order axial and rhombic zfs parameters, respectively, and the final term represents an axial fourth-order zfs interaction.108 The parameters used for the simulation are S = 6, D = −0.33 cm−1, |E| = 0.030 cm−1, B04 = −8.0 × 10−5 cm−1, and gx = gy = gz = 2.00. As can be seen, the relevant parallel and perpendicular portions of the simulations agree with the experiments very well, and the obtained D value is consistent with that deduced from the magnetic studies. Gaussian distributions of the D and E parameters (σD = 8%, σE = 40%) were employed in order to reproduce the observed line broadening. As expected, the strain in E is much more pronounced than that of D, which explains the almost complete loss of resolution of the transverse part of the EPR spectrum.
is the Landé g tensor, D and E are the second-order axial and rhombic zfs parameters, respectively, and the final term represents an axial fourth-order zfs interaction.108 The parameters used for the simulation are S = 6, D = −0.33 cm−1, |E| = 0.030 cm−1, B04 = −8.0 × 10−5 cm−1, and gx = gy = gz = 2.00. As can be seen, the relevant parallel and perpendicular portions of the simulations agree with the experiments very well, and the obtained D value is consistent with that deduced from the magnetic studies. Gaussian distributions of the D and E parameters (σD = 8%, σE = 40%) were employed in order to reproduce the observed line broadening. As expected, the strain in E is much more pronounced than that of D, which explains the almost complete loss of resolution of the transverse part of the EPR spectrum.
In order to obtain tighter constraints on the spin Hamiltonian parameters for complex 5·xCH2Cl2, the positions of parallel component peaks obtained at multiple frequencies are displayed on a 2D frequency vs. field plot in Fig. 10. The combined data set was then simulated using the Hamiltonian of eqn (9); the solid lines in Fig. 10 represent the best simulation using the same parameters as those used in Fig. 9b. We note that the fourth-order B04Ô04 term is absolutely essential to the simulations, accounting for the uneven field spacing of the resonances. One can estimate a kinetic barrier (U) to magnetization relaxation of ∼12 cm−1 from the S and D values or ∼15 cm−1 if the effect of the significant B04 is included.
 | ||
| Fig. 10 2-D plot of frequency vs. the field locations of powder EPR spectral features observed for 5·xCH2Cl2 at multiple frequencies in the 52.4 to 422.4 GHz range. Simulated transition curves employing eqn (9) are included for B∥x (blue), y (green) and z (red). See the text for the simulation parameters. | ||
We conclude this section by discussing the interaction between the four Mn3 units in the tetramer. EPR spectra for the powder sample suggest that the Mn3 units are essentially uncoupled, or the coupling is too weak to detect by EPR. Hysteresis loop data suggest an antiferromagnetic coupling of −0.0076 cm−1 (vide infra) between adjacent Mn3 units within the tetramer. This coupling is smaller than the D and E strains (σD = 0.026 cm−1 and σE = 0.012 cm−1), which means that the spectral broadening (FWHM = 2.35σ) is likely to far exceed any additional splittings of the EPR spectra induced by the inter-SMM exchange. Consequently, it cannot be detected by EPR.
The picture that emerges from the combined magnetic and HF-EPR studies on 5 and 6 described above is that magnetically-supramolecular aggregates of the Mn3 SMMs with S = 6 can be obtained using the dioximate pdpd2−, and that these do indeed contain Mn3 units that still retain the structural and magnetic properties of the monomeric analogue 2. Any inter-Mn3 exchange interactions through the dioximate groups are either zero or too weak to affect the magnetic data collected above 1.8 K. The tetramers 5 and 6 therefore behave as an assembly of independent Mn3 units and their data can be fit as such to give fit parameters that are essentially identical with those previously obtained for 2. The crucial question now needing to be addressed is whether there are indeed any inter-Mn3 interactions present, and if so what is their effect? The answers to these questions required studies at even lower temperatures.
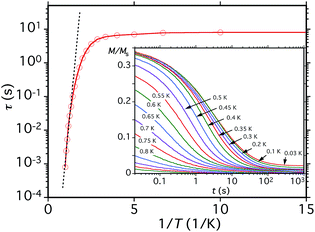
Before analysing the QTM step pattern, we describe the determination of the effective relaxation barrier (Ueff) from magnetization decay measurements. A large dc magnetic field was applied to the crystal at ∼5 K to saturate the magnetization in one direction, and T decreased to a chosen value in the 0.03–1.0 K range. The field was then removed and M measured as a function of time (Fig. 12, inset). From these data, relaxation time (τ) vs. T data were extracted and used to construct an Arrhenius plot based on eqn (10) (Fig. 12), where k is the Boltzmann constant. Below ∼0.3 K, τ is temperature-independent
| ln(τ) = ln(τ0) + Ueff/kT | (10) |
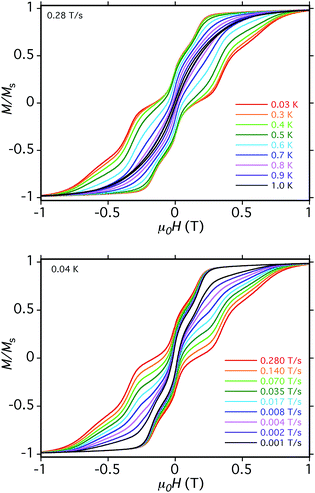
We now address whether the four Mn3 SMM units in 5·xCH2Cl2 are weakly interacting with each other. The answer is clearly yes because the hysteresis loops show an exchange-bias (shift) of the QTM steps. The first step in the hysteresis loop of an SMM on scanning from negative to positive fields is normally at zero field, where the mS levels on either side of the anisotropy barrier are in resonance and QTM can occur, reversing the orientation of the magnetization vector. The presence of an AF exchange-coupled neighbor provides a bias field that shifts the QTM step (resonance tunneling) to a new field position before zero. This was first seen for the hydrogen-bonded [Mn4]2 dimer of S = 9/2 SMMs,26 and a related explanation is valid for 5, except that each Mn3 SMM will be seen to be exchange-coupled to two neighboring Mn3 SMMs via the bridging pdpd2− groups.
The loops for 5·xCH2Cl2 in Fig. 11 show the first QTM step before zero field, confirming weak AF interactions between the Mn3 subunits. However, there is still a step at zero field and at a slow sweep rate of 0.001 T s−1, a third step is evident after zero field giving a three-step pattern with equal step separations that is symmetric about zero field. This is unlike anything seen previously in exchange-biased dimers. At faster sweep rates, the step patterns change markedly, the symmetric three-step pattern being lost and new steps appearing. The overall loop profiles and their sweep-rate dependence point to a more complicated exchange-coupled system than any encountered previously and which needed to be carefully explained.
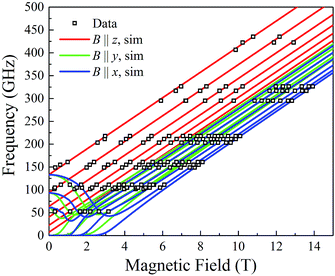
To obtain a simplified spin Hamiltonian to model the [Mn3]4 tetramer, each Mn3 SMM can be treated as a giant spin of S = 6 with easy-axis anisotropy. The spin Hamiltonian (Ĥ) for each Mn3 is given by eqn (11), where i = 1–4 refers to the four Mn3 SMMs of the tetramer (Fig. 13), μ0 is the vacuum permeability,
| Ĥi = DŜz,i2 + Ĥtrans,i + gμBμ0Ŝzi·Hz | (11) |
| Ĥ = ∑Ĥi − ∑2JijŜi·Ŝj | (12) |
 | ||
| Fig. 13 Labelling scheme used in the spin Hamiltonians of eqn (11)–(15), and the QTM transitions described in the text. | ||
Since 5 is a rectangular [Mn3]4 aggregate, and assuming the interactions are superexchange couplings through the pdpd2− linkers (this assumption will be confirmed later), there should be two different inter-Mn3 interactions, J1 and J2, which are likely to be comparable but not identical in magnitude; the diagonal interaction (J13) should be essentially zero and can be ignored. Therefore, the spin Hamiltonian is given in eqn (13).
| Ĥ = Ĥ1 + Ĥ2 + Ĥ3 + Ĥ4 − 2J1(Ŝ1·Ŝ2 + Ŝ3·Ŝ4) − 2J2(Ŝ1·Ŝ4 + Ŝ2·Ŝ3) | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 561 energy states is allowed by the small transverse anisotropy Ĥtrans,i and the transverse coupling terms containing Ŝxi and Ŝyi operators. Calculating the energy states of [Mn3]4 by exact diagonalization would be a major undertaking, and for convenience we instead neglect all transverse anisotropy terms. The spin Hamiltonian in eqn (13) can then be rewritten as eqn (14).
561 energy states is allowed by the small transverse anisotropy Ĥtrans,i and the transverse coupling terms containing Ŝxi and Ŝyi operators. Calculating the energy states of [Mn3]4 by exact diagonalization would be a major undertaking, and for convenience we instead neglect all transverse anisotropy terms. The spin Hamiltonian in eqn (13) can then be rewritten as eqn (14).| Ĥ ≈ Ĥ1 + Ĥ2 + Ĥ3 + Ĥ4 − 2J1(Ŝ1zŜ2z + Ŝ3zŜ4z) − 2J2(Ŝ1zŜ4z + Ŝ2zŜ3z) | (14) |
| E = D(mS12 + mS22 + mS32 + mS42) + gμBμ0Hz(mS1 + mS2 + mS3 + mS4) − 2J(mS1mS2 + mS3mS4 + mS1mS4 + mS2mS3) | (15) |
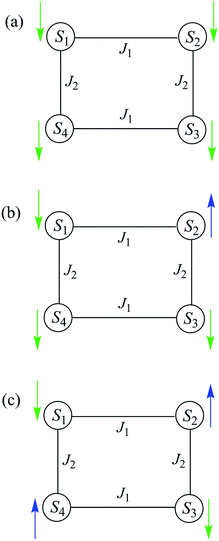
The spin-state energy vs. applied dc field was calculated using eqn (15) for all the states of 5. It was then adjusted by varying the magnitude of J and D to simulate the experimental hysteresis loop at 0.001 T s−1. The resulting plot (Fig. 14, top) was obtained with J = −0.0076 cm−1 (J/kB = −0.011 K) (Ĥ = −2JŜi·Ŝj convention) and D = −0.33 cm−1. When the spin Hamiltonian contains transverse terms (Ĥtrans), the level crossings can be ‘avoided level crossings’. The spin S is ‘‘in resonance’’ between two states when the local longitudinal field is close to an avoided level crossing, and tunneling may occur. The plot shows all avoided level crossings at which QTM transitions could be seen, and we can now explain the three-step hysteresis loop at 0.001 T s−1 in Fig. 11, bottom.
 | ||
| Fig. 14 (Top) simulation with J = −0.0076 cm−1 (J/kB = −0.011 K), (Ĥ = −2JŜi·Ŝj convention) and D = −0.33 cm−1 of the spin state energies vs. applied dc field for an [Mn3]4 tetramer of S = 6 SMMs using eqn (15): red = spin states involving only the mS = ±6 states of the four Mn3 sub-units; blue = spin states involving both mS = ±6 states and one mS = ±5 state; black = other states. (Bottom) spin states involving only the mS = ±6 states and their identity. * = multiple spin flips (2, 3 or 4) at the same time. The green arrows are the avoided level crossings at which QTM leads to the three steps at 0.001 T s−1 in Fig. 11. | ||
At the lowest T of 0.04 K, only the lowest energy states involving mS = ±6 states will be populated (red lines in Fig. 14). As the field is scanned from −1 T, where the four Mn3 magnetization vectors will have all been polarized into the mS = −6 orientation (Fig. 13a), the following is seen:
(a) the first QTM step corresponds to tunneling of a Mn3 vector from the mS = −6 to the mS = +6 state; this occurs at −0.19 T, which thus represents the total bias field from two mS = −6 neighbours. In the format (mS1, mS2, mS3, mS4), where i = 1–4 are the four Mn3 SMMs within 5, the −0.19 T step corresponds to the (−6, −6, −6, −6) to (−6, +6, −6, −6) tunneling transition (Fig. 13b); for convenience, other possible equivalent product states, (+6, −6, −6, −6), (−6, −6, +6, −6), and (−6, −6, −6, +6), are not shown;
(b) the second step at zero field is assigned to tunneling of molecules with −6, +6 neighbors (S1 and S3 in Fig. 13b), which therefore experience a zero bias (if J1 = J2, or a small bias related to |J1 − J2| if J1 ≠ J2). The step at zero field is thus the (−6, +6, −6, −6) to (−6, +6, +6, −6) tunneling transition, which will then have some probability of undergoing a spin flip-flop relaxation to the (−6, +6, −6, +6) ground state since J is AF (Fig. 13c);
(c) If enough vectors have tunnelled in the first two steps to +6 (i.e., if the sweep rate is slow enough), then a third step is expected for Mn3 vectors tunneling in the presence of a +6, +6 bias field (S1 and S3 in Fig. 13c). This would be symmetrically located with respect to the first step, and should thus occur at +0.19 T.
The three-step pattern at 0.001 T s−1 sweep rate (in Fig. 11, bottom) is thus as predicted at this slow scan rate, which is required to see situation (c). Note that the avoided level crossings at positions marked with asterisks might at first glance be predicted to give additional QTM steps, but these involve multiple (2, 3, or 4) tunneling transitions at the same time, e.g. (−6, −6, −6, −6) to (−6, +6, +6, −6), (−6, −6, −6, −6) to (−6, +6, +6, +6), etc. They thus have a very low probability of occurring and in fact we see no evidence for their occurrence. Note that double tunneling transitions also occur at ±0.19 T and 0 T, i.e., at the avoided level crossings where the single transitions are seen as steps in the loops.
At faster scan rates, the three-step hysteresis loop changes markedly. On scanning from −1 T at 0.28 T s−1, the first step has now decreased in size, as has the second step at zero field, and the third step has disappeared completely. This is as expected from standard Landau–Zener theory,109,110 which predicts that the tunneling probability decreases with increasing field scan rate, i.e. fewer molecules are in resonance long enough for their spins to tunnel. As these steps decrease or disappear, new steps appear in the 0.0–1.0 T range as the magnetization relaxes via alternative tunnelling pathways; some steps appear and disappear as the scan rate increases (e.g. at 0.35 T), and by 0.28 T s−1 two broad features at ∼0.4 T and ∼0.6 T are evident. We assign these tunneling transitions to levels involving one mS = ±5 state, i.e., at positions involving avoided level crossings of red and blue lines in Fig. 14. These include (−6, −6, −6, −6) to (−6, +6, −6, −5) at ∼0.1 T, (−6, +6, −6, −6) to (−6, +6, +6, −5) at ∼0.2 T, (−6, +6, −6, −6) to (−6, +6, +6, −5) at ∼0.4 T, (−6, +6, −6, +6) to (−6, +6, +5, +6) at ∼0.6 T, and others.
It should be noted that all the steps in Fig. 11 are rather broad compared with, e.g., those for monomer 2 (Fig. S14†). This is due to the two independent cations in the asymmetric unit having different orientations, and the four Mn3 planes within each cation not being coplanar (Fig. 4, bottom). As a result, the applied field will be at a range of angles to the z-axes (easy-axes) of the eight Mn3, leading to step broadening. This is unfortunate because had the steps been sharper, we might have been able to resolve the different tunneling transitions that occur at different sweep rates in the hysteresis loops. We did attempt to collect micro-SQUID data on single crystals of 6·xCH2Cl2 but they were more fragile than those of 5·xCH2Cl2 and we could not get satisfactory data.
As a further test of the validity of the above model and Fig. 14, we carried out hysteresis minor-loop sweeps from −1 T to various fields up to zero and then reversed the sweep direction. The objective was to scan through the avoided level crossing centered at −0.19 T to allow some molecules to tunnel from (−6, −6, −6, −6) to (−6, +6, −6, −6), i.e., step (a) above, and then on reversing the sweep to see the (−6, +6, −6, −6) to (−6, −5, −6, −6) QTM transition at just under −0.55 T (Fig. 15, inset). The separation between these two QTM steps is proportional to the energy difference between the (−6, −6, −6, −6) and (−6, −5, −6, −6) states, i.e., it depends on D. The desired step was observed, although broad due to the factors discussed above. Nevertheless, a field separation of ΔH ≈ 0.4 T could be estimated. Using eqn (16) gives D ≈ −0.37 cm−1 with g = 2.0, in satisfying agreement with values obtained from the magnetization and HF-EPR fits, and thus supporting the overall validity of the model and the analysis of the hysteresis loops. The value of D suggests the population of Mn3 units sampled in the minor-loop scans had an average angle between their z-axes and the applied field of ∼28°.
| |D| = gμBΔH | (16) |
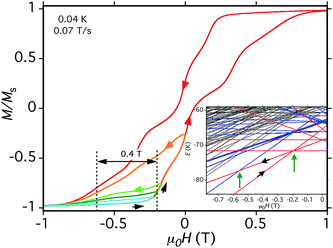 | ||
| Fig. 15 Hysteresis loop and minor loops at the indicated T and sweep rate. The field was swept from −1.0 T and then reversed at various field positions to probe the separation of the (−6, +6, −6, −6) to (−6, −5, −6, −6) QTM step from the (−6, −6, −6, −6) to (−6, +6, −6, −6) step, which depends on D. The different colors are to distinguish different sweeps. (Inset) portion of the spin state energy plot of Fig. 14, showing with green arrows the two avoided level crossings and associated QTM transitions being probed. | ||
It could be argued that the pdpd2− linkers are not the superexchange pathways through which the Mn3 interact. Might the interactions instead be dipolar between a Mn3 and nearby neighbors (intra- or inter-tetramer), or via inter-tetramer π-stacking or weak H-bonds? However, 5·xCH2Cl2 contains no significant inter-tetramer contacts, other than some C–H⋯π and π⋯π contacts involving the central Ph ring of the pdpd2− group, and many C–H⋯Cl H-bonds to the solvent molecules. Nevertheless, we compared inter-tetramer distances and contacts in 5·xCH2Cl2 crystals with those in 2·3CH2Cl2. Shortest inter-Mn3 Mn⋯Mn distances are comparable (Fig. S4†), ∼6.0 and ∼6.6 Å in 5 and 2, respectively, and similar C–H⋯π, π⋯π, and C–H⋯Cl contacts are present in both. In fact, 2 contains π⋯π stacking between the pyridyl rings on neighboring Mn3 units (5 does not) and thus might be expected to give stronger inter-Mn3 exchange couplings than in 5. Thus, if the inter-Mn3 couplings that give the exchange-biased QTM in 5 were dipolar in origin or superexchange through any of the mentioned contacts, we would expect to see similar (or even larger) shifts of the QTM steps in 2. In fact, the hysteresis loops of 2·3CH2Cl2 show no discernible shift of the zero field step (Fig. S14†). We thus conclude that the only significant inter-Mn3 coupling leading to the exchange-biased QTM in 5·xCH2Cl2 is indeed superexchange through the pdpd2− linkers.
The rectangular structure of 5 suggests J1 ≠ J2, although both should be very weak. We therefore calculated what might be expected in this case, and whether we might be able to identify this difference experimentally. A representative energy plot calculated with a reasonable J1/J2 = 0.7 ratio is shown in Fig. S15,† where it is also compared with the J1 = J2 plot. The only change to the three-step hysteresis loop of the J1 = J2 situation is the step at zero-field splitting into two, with splitting proportional to ∣J1 − J2∣. The other steps still occur symmetrically about zero at ±(J1 + J2). With better step resolution, we might have been able to pick up a splitting in the zero-field peak, but the broadness of the steps due to the range of magnetic field alignments, as described above, precludes this. We thus conclude that even though it is likely that J1 ≠ J2, the difference must be too small to have a noticeable effect on the hysteresis loops within the experimental step broadness.
Conclusions
We summarize below the main results and conclusions of this study:(1) Employment of a designed dioxime group has allowed the isolation from straightforward procedures of two non-SMM [Mn3]2 and two SMM [Mn3]4 aggregates; the latter serve to achieve the overall objective of this work, to obtain covalently-linked oligomers of SMMs to extend previous work beyond the dimeric systems studied in the past. The dioxime was not pre-programmed to give any particular oligomer topology, and a rectangular one was obtained.
(2) Each Mn3 SMM subunit in [Mn3]4 tetramers has retained the structure and magnetic properties of the monomeric analogue, encouraging us that the oligomerization methodology has the potential for general application to a range of linkers without damage to the units or their SMM properties.
(3) Carboxylate substitution on preformed [Mn3]4 tetramer 5 has been accomplished without rupture of the oligomer linkages, providing a convenient means for post-synthetic modification of oligomers for comparative studies or certain applications.
(4) Lower dioxime![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Mn ratios afford [Mn3]2 dimers at two oxidation levels, [MnIIMnIII2]2 and [MnIII3]2, with asymmetric ligation not previously observed, leading to a mix of F and AF exchange interactions in both complexes.
Mn ratios afford [Mn3]2 dimers at two oxidation levels, [MnIIMnIII2]2 and [MnIII3]2, with asymmetric ligation not previously observed, leading to a mix of F and AF exchange interactions in both complexes.
(5) The magnetic analysis confirms that each Mn3 unit is still ferromagnetically-coupled with an S = 6 ground state, and there is no evidence in the data at 1.8 K and above for any inter-Mn3 exchange-interactions. In addition, both types of distortion of the Mn3 triangles from equilateral to isosceles have been seen and magnetically analyzed, characterizing two best-fit minima in the error surface and the degree of difference caused to the constituent J values.
(6) Detailed multi-frequency HF-EPR spectra at a range of temperatures, and their simulations, have provided the important spin Hamiltonian parameters to fourth order, confirming that the oligomerization has minimal effect on the intra-Mn3 magnetic properties, and addressing the difficulty of detecting by HF-EPR very weak inter-Mn3 interactions.
(7) Hysteresis loops obtained on a single crystal of 5·xCH2Cl2 established that the four Mn3 SMMs are each weakly coupled to two neighbors, and this interaction is manifested as an exchange-bias of the QTM steps, with the exact positions of the latter determined by the spin alignments at these two neighbors. The exchange-biased hysteresis loops at 0.04 K and 0.001 T s−1 scan rates have been explained by identification of the ground state quantum transitions taking place.
(8) Equally important, the large changes in QTM step locations at higher scan rates have been explained as a function of decreasing tunneling probability with increasing scan rate, resulting in relaxation via QTM transitions involving higher energy levels.
(9) Using the hysteresis loop of the analogous Mn3 monomer as a control, a crucial conclusion has been reached that the inter-Mn3 interaction is via superexchange through the bridging dioximate linkers. This shows that intra-oligomer couplings and quantum effects can be studied in the solid state without complications from dipolar or other inter-oligomer pathways.
(10) The validity of the overall model used to describe the quantum behavior has been tested by simulations of the 1- or 2-J coupling model, and also by hysteresis minor-loop studies that have been shown to give a Mn3D value comparable to those from the magnetization fits and HF-EPR studies.
Overall, the described work represents a rational approach to obtaining covalently-connected multiple Mn3 SMMs that is now being extended to other oligomers with various structural topologies and quantum mechanical couplings in order to assess their potential for use as multi-qubit assemblies and other systems based on SMMs.
Acknowledgements
This work was supported by the USA National Science Foundation (GC: CHE-0910472, DMR-1213030; SH: DMR-1309463) and by the Air Force (SH: AOARD grant #134031). WW acknowledges grants FP7-ICT-2013-10-610449 MoQuaS and ANR-13-BS10-0001-03 MolQuSpin. T. N. N thanks the Vietnam Education Foundation for a fellowship. Work performed at the NHMFL is supported by the USA National Science Foundation (DMR-1157490) and the State of Florida.References
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- G. Christou, D. Gatteschi, D. N. Hendrickson and R. Sessoli, MRS Bull., 2000, 25, 66–71 CrossRef CAS.
- G. Christou, Polyhedron, 2005, 24, 2065–2075 CrossRef CAS.
- R. Bagai and G. Christou, Chem. Soc. Rev., 2009, 38, 1011–1026 RSC.
- V. I. Ovcharenko and R. Z. Sagdeev, Russ. Chem. Rev., 1999, 68, 345–363 CrossRef CAS.
- J. S. Miller and A. J. Epstein, MRS Bull., 2000, 25, 21–30 CrossRef CAS.
- S. J. Blundell and F. L. Pratt, J. Phys.: Condens. Matter, 2004, 16, R771–R828 CrossRef CAS.
- J. S. Miller, Chem. Soc. Rev., 2011, 40, 3266–3296 RSC.
- A. J. Tasiopoulos, A. Vinslava, W. Wernsdorfer, K. A. Abboud and G. Christou, Angew. Chem., Int. Ed., 2004, 43, 2117–2121 CrossRef CAS PubMed.
- J. R. Friedman, M. P. Sarachik, J. Tejada and R. Ziolo, Phys. Rev. Lett., 1996, 76, 3830–3833 CrossRef CAS PubMed.
- L. Thomas, L. Lionti, R. Ballou, D. Gatteschi, R. Sessoli and B. Barbara, Nature, 1996, 383, 145–147 CrossRef CAS.
- W. Wernsdorfer and R. Sessoli, Science, 1999, 284, 133–135 CrossRef CAS PubMed.
- W. Wernsdorfer, M. Soler, G. Christou and D. N. Hendrickson, J. Appl. Phys., 2002, 91, 7164–7166 CrossRef CAS.
- W. Wernsdorfer, N. E. Chakov and G. Christou, Phys. Rev. Lett., 2005, 95, 037203 CrossRef CAS PubMed.
- W. Wernsdorfer, S. Bhaduri, R. Tiron, D. N. Hendrickson and G. Christou, Phys. Rev. Lett., 2002, 89, 197201 CrossRef CAS PubMed.
- S. Hill, R. S. Edwards, N. Aliaga-Alcalde and G. Christou, Science, 2003, 302, 1015–1018 CrossRef CAS PubMed.
- A. Wilson, S. Hill, R. S. Edwards, N. Aliaga-Alcalde and G. Christou, AIP Conf. Proc., 2006, 850, 1141–1142 CrossRef CAS.
- R. Tiron, W. Wernsdorfer, D. Foguet-Albiol, N. Aliaga-Alcalde and G. Christou, Phys. Rev. Lett., 2003, 91, 227203 CrossRef CAS PubMed.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- B. Zhou, R. Tao, S.-Q. Shen and J.-Q. Liang, Phys. Rev. A, 2002, 66, 010301 CrossRef.
- M. Affronte, F. Troiani, A. Ghirri, A. Candini, M. Evangelisti, V. Corradini, S. Carretta, P. Santini, G. Amoretti, F. Tuna, G. Timco and R. E. P. Winpenny, J. Phys. D: Appl. Phys., 2007, 40, 2999–3004 CrossRef CAS.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Chem.–Asian. J., 2012, 7, 1154–1169 CrossRef CAS PubMed.
- W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406–409 CrossRef PubMed.
- R. Tiron, W. Wernsdorfer, N. Aliaga-Alcalde and G. Christou, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 140407 CrossRef.
- E.-C. Yang, W. Wernsdorfer, S. Hill, R. S. Edwards, M. Nakano, S. Maccagnano, L. N. Zakharov, A. L. Rheingold, G. Christou and D. N. Hendrickson, Polyhedron, 2003, 22, 1727–1733 CrossRef CAS.
- L. M. Wittick, K. S. Murray, B. Moubaraki, S. R. Batten, L. Spiccia and K. J. Berry, Dalton Trans., 2004, 1003–1011 RSC.
- R. Bagai, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2007, 129, 12918–12919 CrossRef CAS PubMed.
- R. Inglis, L. F. Jones, K. Mason, A. Collins, S. A. Moggach, S. Parsons, S. P. Perlepes, W. Wernsdorfer and E. K. Brechin, Chem.–Eur. J., 2008, 14, 9117–9121 CrossRef CAS PubMed.
- A. Das, K. Gieb, Y. Krupskaya, S. Demeshko, S. Dechert, R. Klingeler, V. Kataev, B. Buchner, P. Muller and F. Meyer, J. Am. Chem. Soc., 2011, 133, 3433–3443 CrossRef CAS PubMed.
- A. E. Thuijs, G. Christou and K. A. Abboud, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 185–187 CAS.
- M. Murugesu, R. Clerac, W. Wernsdorfer, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2005, 44, 6678–6682 CrossRef CAS PubMed.
- C. Coulon, H. Miyasaka and R. Clérac, Struct. Bonding, 2006, 122, 163–206 CrossRef CAS.
- H. Miyasaka, K. Nakata, L. Lecren, C. Coulon, Y. Nakazawa, T. Fujisaki, K. Sugiura, M. Yamashita and R. Clérac, J. Am. Chem. Soc., 2006, 128, 3770–3783 CrossRef CAS PubMed.
- E. E. Moushi, T. C. Stamatatos, W. Wernsdorfer, V. Nastopoulos, G. Christou and A. J. Tasiopoulos, Angew. Chem., Int. Ed., 2006, 45, 7722–7725 CrossRef CAS PubMed.
- H. Miyasaka and M. Yamashita, Dalton Trans., 2007, 399–406 RSC.
- H.-B. Xu, B.-W. Wang, F. Pan, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2007, 46, 7388–7392 CrossRef CAS PubMed.
- L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758 RSC.
- O. Roubeau and R. Clérac, Eur. J. Inorg. Chem., 2008, 4325–4342 CrossRef CAS.
- L. F. Jones, A. Prescimone, M. Evangelisti and E. K. Brechin, Chem. Commun., 2009, 2023–2025 RSC.
- S. K. Langley, N. F. Chilton, B. Moubaraki and K. S. Murray, Dalton Trans., 2011, 40, 12201–12209 RSC.
- T. Shiga, H. Miyasaka, M. Yamashita, M. Morimoto and M. Irie, Dalton Trans., 2011, 40, 2275–2282 RSC.
- G. Wu, J. Huang, L. Sun, J. Bai, G. Li, E. Cremades, E. Ruiz, R. Clérac and S. Qiu, Inorg. Chem., 2011, 50, 8580–8587 CrossRef CAS PubMed.
- I.-R. Jeon and R. Clérac, Dalton Trans., 2012, 41, 9569–9586 RSC.
- Y. Liu, Z. Chen, J. Ren, X.-Q. Zhao, P. Cheng and B. Zhao, Inorg. Chem., 2012, 51, 7433–7435 CrossRef CAS PubMed.
- A. D. Katsenis, R. Inglis, A. Prescimone, E. K. Brechin and G. S. Papaefstathiou, CrystEngComm, 2012, 14, 1216–1218 RSC.
- D. Gatteschi and A. Vindigni, Single-Chain Magnets, in Molecular Magnets-Physics and Applications, ed. J. Bartolome, F. Luis and J. F. Fernandez, NanoScience and Technology Series, Springer, Verlag Berlin Heidelberg, 2014, pp. 191–220 Search PubMed.
- D. P. Giannopoulos, A. Thuijs, W. Wernsdorfer, M. Pilkington, G. Christou and T. C. Stamatatos, Chem. Commun., 2014, 50, 779–781 RSC.
- The term ‘magnetically-supramolecular’ is based on the general definition of supramolecular chemistry as “…chemical systems made up of a discrete number of assembled molecular subunits or components. The forces responsible for the spatial organization may vary from weak (intermolecular forces, electrostatic or hydrogen bonding) to strong (covalent bonding), provided that the degree of electronic coupling between the molecular components remains small with respect to relevant energy parameters of the component.”52 In the present situation, ‘magnetically-supramolecular’ means covalently-linked magnetic molecular components (SMMs) with inter-component exchange interactions that are very weak with respect to the intra-SMM interactions.
- https://en.wikipedia.org/w/index.php?title=Supramolecular_chemistry%26oldid=679393015 .
- G. Wu, R. Clérac, W. Wernsdorfer, S. Qiu, C. E. Anson, I. J. Hewitt and A. K. Powell, Eur. J. Inorg. Chem., 2006, 1927–1930 CrossRef CAS.
- V. A. Grillo, M. Knapp, J. C. Bollinger, D. N. Hendrickson and G. Christou, Angew. Chem., Int. Ed. Engl., 1996, 35, 1818–1820 CrossRef CAS.
- G. Novitchi, W. Wernsdorfer, L. F. Chibotaru, J.-P. Costes, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2009, 48, 1614–1619 CrossRef CAS PubMed.
- R. Inglis, A. D. Katsenis, A. Collins, F. White, C. J. Milios, G. S. Papaefstathiou and E. K. Brechin, CrystEngComm, 2010, 12, 2064–2072 RSC.
- E. C. Sanudo, J. S. Uber, A. P. Balague, O. Roubeau and G. Aromi, Inorg. Chem., 2012, 51, 8441–8446 CrossRef CAS PubMed.
- P. Albores, C. Plenk and E. Renschler, Inorg. Chem., 2012, 51, 8373–8384 CrossRef CAS PubMed.
- H. Kumari, C. L. Dennis, A. V. Mossine, C. A. Deakyne and J. L. Atwood, ACS Nano, 2012, 6, 272–275 CrossRef CAS PubMed.
- J. S. Costa, L. A. Barrios, G. A. Craig, S. J. Teat, F. Luis, O. Roubeau, M. Evangelisti, A. Camon and G. Aromi, Chem. Commun., 2012, 48, 1413–1415 RSC.
- G. F. S. Whitehead, F. Moro, G. A. Timco, W. Wernsdorfer, S. J. Teat and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2013, 52, 9932–9935 CrossRef CAS PubMed.
- J. M. Frost, S. Sanz, T. Rajeshkumar, M. B. Pitak, S. J. Coles, G. Rajaraman, W. Wernsdorfer, J. Schnack, P. J. Lusby and E. K. Brechin, Dalton Trans., 2014, 43, 10690–10694 RSC.
- (a) G. F. S. Whitehead, J. Ferrando-Soria, L. G. Christie, N. F. Chilton, G. A. Timco, F. Moro and R. E. P. Winpenny, Chem. Sci., 2014, 5, 235–239 RSC; (b) J. Ferrando-Soria, A. Fernandez, E. M. Pineda, S. A. Varey, R. W. Adams, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, C. A. Muryn and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 7644–7647 CrossRef CAS PubMed.
- M. Pascu, F. Lloret, N. Avarvari, M. Julve and M. Andruh, Inorg. Chem., 2004, 43, 5189–5191 CrossRef CAS PubMed.
- V. Bellini, G. Lorusso, A. Candini, W. Wernsdorfer, T. B. Faust, G. A. Timco, R. E. P. Winpenny and M. Affronte, Phys. Rev. Lett., 2011, 106, 227205 CrossRef CAS PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, 2015, arXiv:1510.01694.
- (a) G. Aromsı, D. Aguila, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC; (b) D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- K. Katoh, R. Asano, A. Miura, Y. Horii, T. Morita, B. K. Breedlove and M. Yamashita, Dalton Trans., 2014, 43, 7716–7725 RSC.
- C. Y. Chow, H. Bolvin, V. E. Campbell, R. Guillot, J. W. Kampf, W. Wernsdorfer, F. Gendron, J. Autschbach, V. L. Pecoraro and T. Mallah, Chem. Sci., 2015, 6, 4148–4159 RSC.
- R. Sato, K. Suzuki, M. Sugawa and N. Mizuno, Chem.–Eur. J., 2013, 19, 12982–12990 CrossRef CAS PubMed.
- K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Coord. Chem. Rev., 2011, 255, 2124–2148 CrossRef CAS.
- T. N. Nguyen, W. Wernsdorfer, K. A. Abboud and G. Christou, J. Am. Chem. Soc., 2011, 133, 20688–20691 CrossRef CAS PubMed.
- J. B. Vincent, H. R. Chang, K. Folting, J. C. Huffman, G. Christou and D. N. J. Hendrickson, J. Am. Chem. Soc., 1987, 109, 5703–5711 CrossRef CAS.
- Although almost all lattice CH2Cl2 molecules are disordered, the two encapsulated ones are ordered and were included in the refinement cycles.
- SHELXTL6, Bruker-AXS, Madison, Wisconsin, USA, 2008 Search PubMed.
- See ESI†.
- (a) E. R. Davidson, MAGNET, Indiana University: Bloomington, IN, 1999 Search PubMed; (b) E. R. Davidson, GRID, Indiana University: Bloomington, IN, 2000 Search PubMed.
- W. Wernsdorfer, Adv. Chem. Phys., 2001, 118, 99–190 CrossRef CAS.
- A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L. C. Brunel, J. Magn. Reson., 2000, 142, 300–312 CrossRef CAS PubMed.
- T. C. Stamatatos, D. Foguet-Albiol, S.-C. Lee, C. C. Stoumpos, C. P. Raptopoulou, A. Terzis, W. Wernsdorfer, S. Hill, S. P. Perlepes and G. Christou, J. Am. Chem. Soc., 2007, 129, 9484–9499 CrossRef CAS PubMed.
- C. Papatriantafyllopoulou, G. Aromi, A. J. Tasiopoulos, V. Nastopoulos, C. P. Raptopoulou, S. J. Teat, A. Escuer and S. P. Perlepes, Eur. J. Inorg. Chem., 2007, 2761–2774 CrossRef CAS.
- P. Chaudhuri, T. Weyhermuller, R. Wagner, S. Khanra, B. Biswas, E. Bothe and E. Bill, Inorg. Chem, 2007, 46, 9003–9016 CrossRef CAS PubMed.
- C. C. Stoumpos, T. C. Stamatatos, H. Sartzi, O. Roubeau, A. J. Tasiopoulos, V. Nastopoulos, S. J. Teat, G. Christou and S. P. Perlepes, Dalton Trans., 2009, 1004–1015 RSC.
- C. Lampropoulos, T. C. Stamatatos, M. J. Manos, A. J. Tasiopoulos, K. A. Abboud and G. Christou, Eur. J. Inorg. Chem., 2010, 2244–2253 CrossRef CAS.
- C. D. Polyzou, H. Nikolaou, C. Papatriantafyllopoulou, V. Psycharis, A. Terzis, C. P. Raptopoulou, A. Escuer and S. P. Perlepes, Dalton Trans., 2012, 41, 13755–13764 RSC.
- D. Dermitzaki, C. P. Raptopoulou, V. Psycharis, A. Escuer, S. P. Perlepes and T. C. Stamatatos, Dalton Trans., 2014, 43, 14520–14524 RSC.
- A. Chakravorty, Coord. Chem. Rev., 1974, 13, 1–46 CrossRef CAS.
- P. Chaudhuri, Coord. Chem. Rev., 2003, 243, 143–190 CrossRef CAS.
- C. J. Milios, T. C. Stamatatos and S. P. Perlepes, Polyhedron, 2006, 25, 134–194 CrossRef CAS.
- E. C. Constable, J. Lewis, M. C. Liptrot and P. R. Raithby, Inorg. Chim. Acta, 1990, 178, 47–54 CrossRef CAS.
- M. W. Wemple, H.-L. Tsai, K. Folting, D. N. Hendrickson and G. Christou, Inorg. Chem., 1993, 32, 2025–2031 CrossRef CAS.
- H. J. Eppley, H.-L. Tsai, N. de Vries, K. Folting, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1995, 117, 301–317 CrossRef CAS.
- Z. Sun, D. Ruiz, N. R. Dilley, M. Soler, J. Ribas, K. Folting, M. B. Maple, G. Christou and D. N. Hendrickson, Chem. Commun., 1999, 1973–1974 RSC.
- M. Soler, S. K. Chandra, D. Ruiz, E. R. Davidson, D. N. Hendrickson and G. Christou, Chem. Commun., 2000, 2417–2418 RSC.
- B. Fleury, L. Catala, V. Huc, C. David, W. Z. Zhong, P. Jegou, L. Baraton, S. Palacin, P.-A. Albouyd and T. Mallah, Chem. Commun., 2005, 2020–2022 RSC.
- J. J. Henderson, C. M. Ramsey, E. D. Barco, A. Mishra and G. Christou, J. Appl. Phys., 2007, 101, 09E102 CrossRef.
- A. M. Mowson, T. N. Nguyen, K. A. Abboud and G. Christou, Inorg. Chem., 2013, 52, 12320–12322 CrossRef CAS PubMed.
- K. J. Kambe, J. Phys. Soc. Jpn., 1950, 5, 48–51 CrossRef CAS.
- J. H. Van Vleck, The Theory of Electric and Magnetic Susceptibilities, Oxford University Press, 1932 Search PubMed.
- J. Cano, T. Cauchy, E. Ruiz, C. J. Milios, C. C. Stoumpos, T. C. Stamatatos, S. P. Perlepes, G. Christou and E. K. Brechin, Dalton Trans., 2008, 234–240 RSC.
- M. Atanasov, B. Delley, F. Neese, P. L. Tregenna-Piggott and M. Sigrist, Inorg. Chem., 2011, 50, 2112–2124 CrossRef CAS PubMed.
- C. Lampropoulos, K. A. Abboud, T. C. Stamatatos and G. Christou, Inorg. Chem., 2009, 48, 813–815 CrossRef CAS PubMed.
- N. Aliaga-Alcade, R. S. Edwards, S. Hill, W. Wernsdorfer, K. Folting and G. Christou, J. Am. Chem. Soc., 2004, 126, 12503–12516 CrossRef PubMed.
- J. Yoo, A. Yamaguchi, M. Nakano, J. Krzystek, W. E. Streib, L.-C. Brunel, H. Ishimoto, G. Christou and D. N. Hendrickson, Inorg. Chem., 2001, 40, 4604–4616 CrossRef CAS PubMed.
- S.-I. Chen, C. C. Beedle, P.-R. Gan, G.-H. Lee, S. Hill and E.-C. Yang, Inorg. Chem., 2012, 51, 4448–4457 CrossRef CAS PubMed.
- S. Hill, R. S. Edwards, S. I. Jones, N. S. Dalal and J. M. North, Phys. Rev. Lett., 2003, 90, 217204 CrossRef CAS PubMed.
- S. Takahashi, R. S. Edwards, J. M. North, S. Hill and N. S. Dalal, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094429 CrossRef.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- L. Landau, Phys. Z. Sowjetunion, 1932, 2, 46–51 CAS.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic details in CIF format, bond valence sums, bond distances and angles, structural figures, magnetic data, UV-vis spectra. CCDC 869139, 1413392, 1413393, 1413395. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc02599k |
| This journal is © The Royal Society of Chemistry 2016 |