Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of reagent rotation on interferences in the product angular distributions of chemical reactions†
P. G.
Jambrina
 a,
J.
Aldegunde
a,
J.
Aldegunde
 b,
F. J.
Aoiz
b,
F. J.
Aoiz
 *a,
M.
Sneha
c and
R. N.
Zare
*c
*a,
M.
Sneha
c and
R. N.
Zare
*c
aDepartamento de Química Física I, Facultad de Química, Universidad Complutense de Madrid, 28040, Spain. E-mail: aoiz@quim.ucm.es
bDepartamento de Química Física, Universidad de Salamanca, Salamanca, Spain
cDepartment of Chemistry, Stanford University, Stanford, California 94305-5080, USA. E-mail: zare@stanford.edu
First published on 5th October 2015
Abstract
Differential cross sections (DSCs) of the HD(v′, j′) product for the reaction of H atoms with supersonically cooled D2 molecules in a small number of initial rotational states have been measured at a collision energy of 1.97 eV. These DCSs show an oscillatory pattern that results from interferences caused by different dynamical scattering mechanisms leading to products scattered into the same solid angle. The interferences depend on the initial rotational state j of the D2(v = 0, j) reagent and diminish in strength with increasing rotation. We present here a detailed explanation for this behavior and how each dynamical scattering mechanism has a dependence on the helicity Ω, the projection of the initial rotational angular momentum j of the D2 reagent on the approach direction. Each helicity corresponds to a different internuclear axis distribution, with the consequence that the dependence on Ω reveals the preference of the different quasiclassical mechanisms as a function of approach direction. We believe that these results are general and will appear in any reaction for which several mechanisms are operative.
Introduction
The Young's double-slit experiment applied to the interference of single electrons has been considered to be the most beautiful and intriguing experiment in physics1–3 and has become a standard example in quantum mechanics (QM) textbooks for illustrating wave–particle duality. In the experiment, electrons, one at a time, are shot against a screen that contains two small openings (slits). The detection of the transmitted electrons results in an interference pattern, similar to that observed when light waves instead of electrons are used. These results give convincing evidence for the probabilistic nature of the quantum process. Moreover, the experiment has also been carried out using heavier particles,4–9 such as fullerene molecules, leading to similar conclusions and demonstrating the quantum nature of these large and presumably more classical molecules.It might be wondered whether such interference effects occur in chemical reactions and, if so, how they affect the reaction observables. In a recent article,10 we measured state-to-state angular distributions of the HD product reactively scattered at a collision energy, Ecoll, of 1.97 eV, for the benchmark H + D2 → D + HD reaction using the photoloc technique.11,12 The angular distribution, or differential cross section (DCS), represents the cross section as a function of the scattering angle, θ, and its QM value is obtained as the square of a coherent sum of partial waves from the different values of the total angular momentum, J. Hence, this summation contains cross terms from different J values and could possibly give rise to interferences. However, coherences are usually only important between partial waves characterized by very similar values of J and, in many cases, scattering at different angles can be approximately attributed to specific groups of partial waves13 similar to that occurring in quasiclassical trajectory (QCT) calculations. This general behaviour encourages simple pictures to be presented for the scattering process in which the nuclear motions are treated classically with no interference effects.
However, the observed angular distributions at Ecoll = 1.97 eV, obtained for low rotational and vibrational excitation of the HD products were dominated by an oscillatory pattern, resembling that from interferences in the double-slit experiment.10 These results could not be accounted for by the QCT method, wherein the nuclei are treated as classical particles moving on a potential energy surface (PES) originating from quantum electronic motions, even though it usually constitutes a very good approximation for the dynamical description of the H + D2 and many other chemical reactions.14 The fact that the measurements could only be reproduced by exact QM calculations (where both nuclei and electrons are treated quantum mechanically) clearly indicated that the observed oscillatory pattern in the angular distribution was caused by a quantum phenomenon. Oscillations in the energy dependent DCS at given fixed angles had been previously measured and attributed to either partial wave resonances15,16 or to interferences through a network of quantum bottleneck pathways.17 However in this case there are no kinds of resonance and the positions of the peaks do not depend much on small changes on the total energy.
A careful analysis of the reactant's ground rotational state (j = 0) allowed us to unequivocally attribute these oscillations to quantum interferences between different underlying classical mechanisms, characterized by well-defined ranges of the total angular momentum and giving rise to scattering at certain angles. By analogy, the PES acts as an interferometer in which the different mechanisms play the role of the pathways in the classical double-slit experiment; interferences are observed whenever two distinct mechanisms lead to products scattered into the same scattering angle. To understand the nature of these phenomena, we carried out a computational analysis in which we shut down the various scattering mechanisms, one at a time, so as to observe the disappearance of the different peaks in the interference pattern. This procedure is analogous to that of successively blocking the various slits in a multiple-slit experiment.
In the present study we demonstrate that the aforementioned oscillatory pattern observed in the DCS is very sensitive to the rotational state of the D2 reagent. In particular, we will show that interference patterns like those observed for j = 0 collisions are also found in encounters where the reactant molecule is rotationally excited, although the amplitude of the interferences diminishes rapidly with increasing rotational angular momentum of the D2 reactant. In the first instance, this diminishing is a consequence of the larger number of |j, Ω〉 initial states that add incoherently as the reaction occurs, where the helicity Ω is the projection of j on the reactants' approach direction. Although an interference pattern exists for each (j, Ω) combination, the different Ω values contribute incoherently and the interference patterns become blurred. For j = 0, there is only one Ω value (Ω = 0) and the interference pattern is sharp. As j increases, the incoherent sum over different Ω values causes the interference pattern to smooth and diminish in contrast.
We have concentrated on the H + D2 reaction for which we have experimental measurements of the DCSs and strong confidence in the accuracy of the PES. However, we believe that our results apply to all chemical reactions in which more than one classical scattering mechanism contributes to the observed product angular distributions.
The article is structured as follows. The Methods section briefly describes the experimental and theoretical methodologies employed in this work. The Results and discussion section presents the main results and the analysis of the theoretical data. Finally, the Conclusion section summarizes the main findings and future scope of the present work.
Methods
Experiment
We employ a three-dimensional (3D) ion imaging setup and the photoloc technique, the details of which are described in previous publications.11,12 Briefly, a mixture of 3–5% HBr in D2 was co-expanded supersonically into a vacuum chamber through a 10 Hz pulsed valve (General Valve, Series 9), with a typical backing pressure of ∼1300 Torr. This leads to the internal and translational cooling of reactants with D2 being prepared almost exclusively in the (v = 0, j = 0, 1 and 2) internal states with a relative population of 0.39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.31
0.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.29, respectively. The reaction is initiated by photodissociating HBr with a focused, 199 nm UV beam (60 cm lens), which generates translationally hot H atoms with two different collision energies; Ecoll = 1.97 eV and 1.51 eV, referred to as fast channel and slow channel, respectively. These two channels arise from the spin–orbit splitting in bromine, and the ratio of the fast channel to the slow channel is 0.84
0.29, respectively. The reaction is initiated by photodissociating HBr with a focused, 199 nm UV beam (60 cm lens), which generates translationally hot H atoms with two different collision energies; Ecoll = 1.97 eV and 1.51 eV, referred to as fast channel and slow channel, respectively. These two channels arise from the spin–orbit splitting in bromine, and the ratio of the fast channel to the slow channel is 0.84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.16 at the photolysis wavelength of 199 nm. These H atoms react with D2 to form HD(v′, j′) products. After a delay of 15–20 ns, a counter propagating focused UV beam (60 cm lens) is used to probe the HD products state-selectively using a [2 + 1] resonance enhanced multiphoton ionization (REMPI) scheme on the Q branch of the E,F1Σg+–X1Σg+ transition. The lab frame speed of the HD ions is measured using a Wiley–McLaren time-of-flight instrument equipped with a position-sensitive detector and converted into a DCS based on the photoloc technique described elsewhere in detail.12,18 At the photolysis wavelength used here, i.e., 199 nm, the contribution from the slow channel is very small compared to the fast channel and can therefore be ignored18 when converting the speed distribution to DCS.
0.16 at the photolysis wavelength of 199 nm. These H atoms react with D2 to form HD(v′, j′) products. After a delay of 15–20 ns, a counter propagating focused UV beam (60 cm lens) is used to probe the HD products state-selectively using a [2 + 1] resonance enhanced multiphoton ionization (REMPI) scheme on the Q branch of the E,F1Σg+–X1Σg+ transition. The lab frame speed of the HD ions is measured using a Wiley–McLaren time-of-flight instrument equipped with a position-sensitive detector and converted into a DCS based on the photoloc technique described elsewhere in detail.12,18 At the photolysis wavelength used here, i.e., 199 nm, the contribution from the slow channel is very small compared to the fast channel and can therefore be ignored18 when converting the speed distribution to DCS.
Theory
Time-independent quantum mechanics (TIQM) calculations were carried out on the BKMP2 (ref. 19) surface using the coupled-channel hyperspherical method implemented in the ABC code.20 To simulate the experimental conditions, the S matrix was obtained for 90 different collision energies in the 1.85–2.12 eV range for j = 0, and similarly for j = 1 and 2 (Etot = Ecoll + Ev,j = 2.04 − 2.31 eV) to fully cover the experimental Gaussian distribution centred at Ecoll = 1.97 eV, with 0.1 eV FWHM, and the averaging over the initial rotational states populated in the D2 molecular beam. The propagation was performed in 250 sectors from 0.8 to 24.0 a0, including in the basis all the diatomic energy levels up to 3.15 eV and helicity quantum numbers Ωmax = 18. All the partial waves up to J = 40 were included. The present TIQM calculations do not include the geometric phase effect, which takes into account the change of sign of the wave function when encircling a conical intersection. For the H + H2 reaction, this effect is only expected to show up in the DCSs at energies above Ecoll = 3.5 eV.21 Even at 3.26 eV, well above the conical intersection, the comparison between QM calculations and photoloc experiments for H + D2 renders an excellent agreement,22 providing credibility to calculations without the geometric phase.Regarding the QCT calculations, three batches of 15 million trajectories were run at Ecoll = 1.97 eV for the H + D2(v = 0, j = 0–2) collisions following the procedures described in a previous publication.23 An integration step of 5 × 10−17 s and a maximum impact parameter b = 1.4 Å were used in the integration of the trajectories. The rovibrational energies of the HD product molecules were calculated by semiclassical quantization of the action and their values were fitted to Dunham expansions in (v′ + ½) and j′(j′ + 1). The (real) j′ value was assigned by equating the square of the classical HD rotational angular momentum to j′(j′ + 1)ħ2. Comparison of the internal energy to that given by the rovibrational Dunham expansion for a specific j′ value yields the value of v′.
Two additional batches of 10 million trajectories each were run at Ecoll = 1.97 eV for the H + D2(v = 0, j = 1 and 2) using the J–Ω scheme,24 wherein J and Ω were sampled in discrete, integer values. In this scheme, J is sampled uniformly and, once it has been done, Ω is chosen also uniformly within the range of allowed values −min(J, j) ≤ Ω ≤ min(J, j).
DCS expansion
The QM state-to-state DCS, I(θ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, was obtained using the following equation
θ, was obtained using the following equation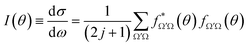 | (1) |
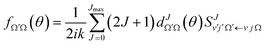 | (2) |
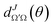 and
and 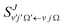 are the elements of the reduced rotation and scattering matrices respectively, where Jmax is the value of J necessary for the convergence of the quantum mechanical calculations. It should be pointed out that the summation over J is coherent while the summation over Ω and Ω′ is incoherent. That means that in the DCS we find crossed products between elements of the scattering matrix corresponding to different values of J but not between elements corresponding to different values of the helicity. Therefore, without any loss of generality, it is possible to express the DCS as
are the elements of the reduced rotation and scattering matrices respectively, where Jmax is the value of J necessary for the convergence of the quantum mechanical calculations. It should be pointed out that the summation over J is coherent while the summation over Ω and Ω′ is incoherent. That means that in the DCS we find crossed products between elements of the scattering matrix corresponding to different values of J but not between elements corresponding to different values of the helicity. Therefore, without any loss of generality, it is possible to express the DCS as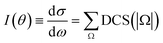 | (3) |
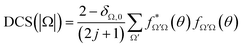 | (4) |
It should be emphasized that, due to the coherences in the summation over J, it is not possible to build the analogous DCS(J) without including crossed terms between different partial waves. Nevertheless, the summation of J in eqn (2) could be restricted to lie within a [J1, J2] interval. These DCS will be denoted as DCS(J1 − J2) and will be very useful to characterize the importance of coherences between groups of J. However, it should be kept in mind that,
| DCS(J1 − J3) ≠ DCS(J1 − J2) + DCS[(J2 + 1) − J3] | (5) |
Results and discussion
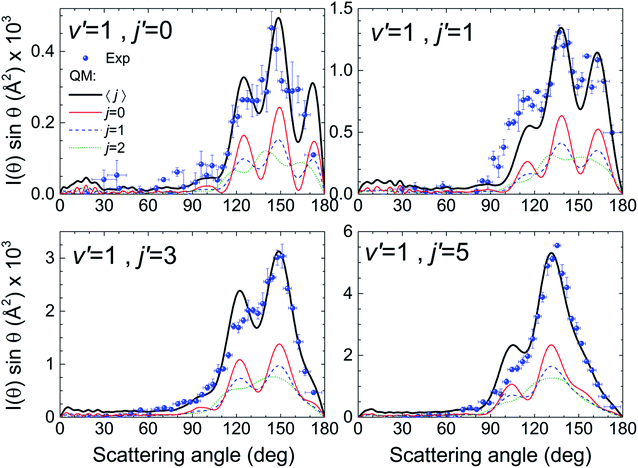
We will base our discussion on the state-to-state DCSs for the H + D2(v = 0, j) → D + HD(v′ = 1, j′) reactive encounters, where (v, j) and (v′, j′) represent the vibrational and rotational quantum numbers for D2 and HD, respectively. As the experiment has been carried out using n-D2 co-expanded through a nozzle, the resulting DCSs contain contributions from the three lowest rotational states populated in the D2 molecular beam (j = 0, 1 and 2). Fig. 1 illustrates the agreement between the experimental results and the QM calculations for the indicated HD rovibrational states. In all cases, to simulate the experimental DCSs, the QM results have been averaged over the experimental collision energy spread and, more importantly, over the D2 experimental rotational distribution (0.39, 0.31 and 0.29 for j = 0, 1 and 2, respectively). The respective contributions of each of the three rotational states are also shown in the figure, such that summing these contributions one obtains the simulated curve. It can be clearly seen that, in all cases, the shapes of the rotational contributions for j = 0 and 1 are quite similar, with the oscillations being more clearly defined for the initial j = 0. It is also worth noticing that the respective maxima for each of these two contributions, the most significant ones, coincide at the same angles. Had it been otherwise – the oscillations being out-of-phase with each other – the interferences would have been unobservable.The dependence of the DCS with j is made more evident in the top panels of Fig. 2, where the DCSs are shown for HD(v′ = 1, j′ = 0) formation at 1.97 eV collision energy (without averaging over the collision energy spread). The angular distributions for j = 0, 1 and 2 bear a common resemblance, with very similar forward and sideways regions and oscillations in the backward region, with maxima at the nearly the same angles (θ ≈ 120, 150, and 175 degrees). However, the most salient feature is the progressive downgrading of the pattern with increasing rotational excitation. While the peak structure is very sharp for j = 0, the finger-like structure seems to smooth out for j = 1 and even more for j = 2. Consequently, the interference effect becomes weaker with rotational excitation.
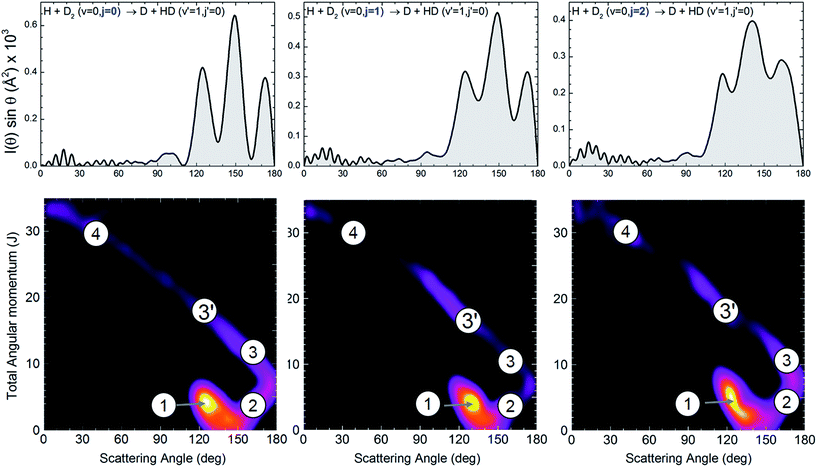 | ||
| Fig. 2 Angular distributions and deflection functions for the H + D2(v = 0, j = 0–2) → D + HD(v′ = 1, j′ = 0) reaction at 1.97 eV collision energy. The top panels show the QM angular distributions for the three rotational states populated in the experiment. The bottom panel shows the state-to-state quasiclassical deflection functions, Dr(J, θ). Although the oscillation pattern is clearly affected by the initial rotational state, the QCT deflection functions are remarkably similar. The quasiclassical mechanisms are labelled in the figure as 1 (ear), 2, 3, 3′ and 4 (the last three form the spiral).25,26 The spiral mechanism displays a clear correlation between J and θ that extends over the whole range of scattering angles. The sketches of the mechanisms that correspond to the labelled regions of Dr(J, θ) are displayed in Fig. S1, ESI.† | ||
The classical deflection function, that is, the joint reaction probability as a function of J and θ, defined as Dr(J, θ) = (2J + 1)Pr(J, θ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where Pr(J, θ) is the reaction probability into a solid angle element defined by θ at a total angular momentum, J, was proven to be an invaluable tool to analyse the interference pattern and to unravel the classical mechanisms behind the quantum interferences.10 Specifically, for initial j = 0, the interference pattern was observed whenever two separated groups of J gave rise to scattering at the same angles. We could therefore expect that the smoothed interference pattern would be associated with a significant change in its QCT deflection function. This is precisely what it is observed for higher j′ states. The gradual smoothing of the oscillations (Fig. 1) with increasing j′ can be traced back to differences in the quasiclassical Dr(J, θ).10 Whereas for j′ = 0 there is a neat separation between the main two mechanisms, they merge at high j′,10 causing the interferences to vanish. Following the double-slit analogy, the two slits merge where j′ is sufficiently high.
θ, where Pr(J, θ) is the reaction probability into a solid angle element defined by θ at a total angular momentum, J, was proven to be an invaluable tool to analyse the interference pattern and to unravel the classical mechanisms behind the quantum interferences.10 Specifically, for initial j = 0, the interference pattern was observed whenever two separated groups of J gave rise to scattering at the same angles. We could therefore expect that the smoothed interference pattern would be associated with a significant change in its QCT deflection function. This is precisely what it is observed for higher j′ states. The gradual smoothing of the oscillations (Fig. 1) with increasing j′ can be traced back to differences in the quasiclassical Dr(J, θ).10 Whereas for j′ = 0 there is a neat separation between the main two mechanisms, they merge at high j′,10 causing the interferences to vanish. Following the double-slit analogy, the two slits merge where j′ is sufficiently high.
However, the calculated Dr(J, θ) for j = 1 and 2, shown in the bottom panels of Fig. 2, appear to be almost identical to that of j = 0, with small differences. Regardless of the initial state, the “ear” (labelled as 1), the mechanism 2 and the “spiral” mechanisms25,26 (labelled as 3, 3′ and 4) coexist; and, accordingly, it could be expected that they behave similarly as far as the interferences between different mechanisms are concerned. The ear mechanism corresponds to trajectories with small impact parameters, attacking angles far from collinearity and a T-shape transition state. The spiral mechanism, in turn, shows a strong J–θ correlation and is associated with nearly collinear transition states (see Fig. S1, ESI†). For the initial and final states displayed in Fig. 2, the magnitude of scattering is dominated by the ear mechanism with smaller contributions from the spiral one, although with a strong imprint via interferences between different types of trajectories, ultimately responsible for the finger-like structures that appear in the QM and experimental DCSs.10 It is evident that the classical deflection functions, as are depicted in the bottom panels of Fig. 2, cannot explain the difference in the amplitude of the oscillation pattern that therefore must be due to a different quantum effect.
As shown in the Methods section, the QM DCS expression comprises two kinds of summation: one coherent over the different partial waves contributing to scattering, and a second, incoherent, over the reagent D2 and product HD helicity quantum states, Ω and Ω′. The complete characterization of the asymptotic states of a closed-shell diatomic molecule, such as the D2 molecule, requires the helicity. Internal states with different values of Ω are asymptotically degenerate and cannot be isolated in typical scattering experiments. On the other hand, the different Ω states are associated with different distributions of the internuclear axis. For j ≠ 0, small values of |Ω| imply head-on collisions, whereas values of |Ω| close to j involve side-on approaches. Therefore, it can be expected that various Ω states will not necessarily behave alike during the collision process. Thus, they give rise to stereodynamical preferences.
The number of Ω states for a given j is 2j + 1, which implies that, for j = 0, the only possible projection of the total angular momentum onto the approach direction (in the body-fixed frame) is Ω = 0 and, hence, j = 0 corresponds to a pure state. For j = 1 and 2 there are three and five Ω states, respectively. In the absence of a field that breaks the degeneracy and of any specific preparation of the reactants, the asymptotic rovibrational states for j ≠ 0 reactant molecules are given by an incoherent mixture of the possible |v, j, Ω〉 states – which are associated with different internuclear axis distributions – where each element carries the same weight.
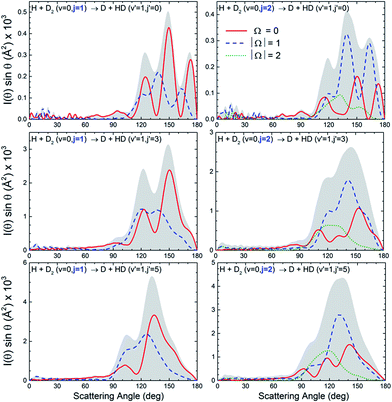
At this point, it seems pertinent to examine the DCS, and particularly the backward structures, attributable to a single reactant's states, |v, j, Ω〉. Addressing this question implies the consideration of the DCS resolved in |Ω| values. Since DCS(Ω) = DCS(−Ω), we need to consider only the possible absolute values of the helicity. Such functions, which will be indicated as DCS(|Ω|), are presented in Fig. 3 for selected state-to-state processes. As can be seen, the position of the peaks and the overall shape of the DCS(|Ω|) depend strongly on Ω. For all the final (v′, j′) states examined, the finger-like pattern is sharper for Ω = 0, less so for |Ω| = 1, and almost absent for |Ω| = 2. But more importantly, as the global DCS is the incoherent sum of the DCS(|Ω|), averaging over Ω washes out the oscillation pattern to a considerable extent, and this is the main reason for the apparent progressive downgrading of the interference pattern with increasing j. An additional reason is the vanishing of the oscillation patterns for larger values of Ω.
More information about the underlying mechanisms causing the observed behaviour for different Ω can be obtained from the inspection of the respective quasiclassical deflection function resolved in Ω, Dr(J, θ; |Ω|). The results for j = 2 are shown in the top panels of Fig. 4. For Ω = 0 both the spiral and ear mechanisms coexist and have a similar importance. As will be explained below, this causes interferences that lead to three peaks of similar height. For |Ω| = 1, the sideways scattering part of the spiral has essentially vanished and the peak closer to the sideways region shrinks and survives as a shoulder. For |Ω| = 2, only the ear mechanism remains and, therefore, there are no interferences and the angular distribution is essentially characterized by a single peak at around 120 degrees. Similar results are obtained when the Dr(J, θ; Ω) are calculated for j = 1 (see Fig. S2, ESI†). Note that the piecewise decomposition of the deflection function in various Ω allows us to unravel the preferred mechanism for the associated internuclear axis distributions. Summation over Ω, which gives rise to an isotropic axis distribution, leads to deflection functions remarkably similar to that found in the j = 0 case, as shown in the bottom panels of Fig. 2.
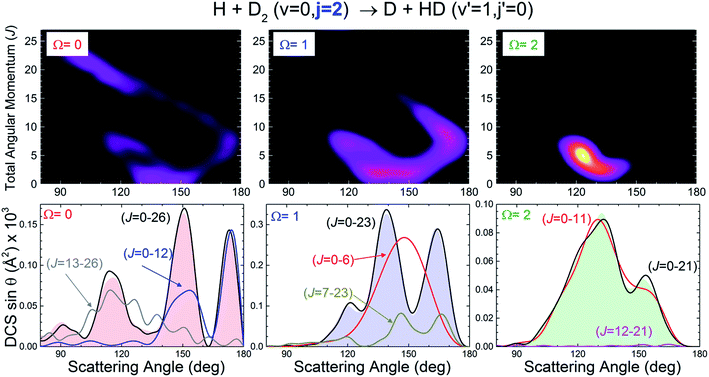 | ||
Fig. 4 Origin of multiple peaks in backward scattering of HD(v′ = 1, j′ = 0, Ω) products for initial j = 2. The top panels show the joint QCT J–θ deflection function resolved in Ω, (2J + 1) Pr(J, θ; Ω) sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, analogous to that displayed in panel (b) of Fig. 1. The bottom panels show the decomposition of the QM angular distributions from the contributions of various sets of J. The notation DCS(J1 − J2) means that the DCS is constructed by including partial waves in the range [J1, J2] including the respective cross terms. The global DCS(|Ω|) is depicted as a shaded background. θ, analogous to that displayed in panel (b) of Fig. 1. The bottom panels show the decomposition of the QM angular distributions from the contributions of various sets of J. The notation DCS(J1 − J2) means that the DCS is constructed by including partial waves in the range [J1, J2] including the respective cross terms. The global DCS(|Ω|) is depicted as a shaded background. | ||
The breakdown of the DCS(|Ω|) in contributions from different partial waves is shown in the lower panels of Fig. 4. For Ω = 0 the situation is similar to that observed for j = 0. The most backward peak results from the interference of mechanisms (2) and (3). The peak appearing at 150 degrees is caused by the interference of mechanisms (1) and (3′). Finally, the third peak at 115 degrees, is an outcome of the interference of mechanisms (1) (with J ≥ 5) and (4). For |Ω| = 1, only two clear peaks remain. The outmost backward peak has the same origin as in the case of Ω = 0, while the second one comes from the interference of the lowest J values of mechanism (1) with some residual scattering in (3′). The stump at 120 degrees has the same origin as that observed at 115 degrees for Ω = 0. Finally, for |Ω| = 2, practically all scattering is caused by the ear mechanism, although the shoulder at 155 degrees is the result of the interference between two very weak sources which would be the remnants of mechanisms (2) and (3). The fact that the shape of the DCS(|Ω|) and, in particular, that the amplitude of the interferences depends strongly on Ω means that the amplitude of those interferences can be potentially controlled in experiments such as those suggested in ref. 27. The presence of interferences cannot modify the total reactive flux (area of the DCS). Hence, the presence of a sharp peak that stems from interferences between two mechanisms should also give rise to troughs, such as that appearing at 150 degrees for |Ω| = 1 where all relevant partial waves are included (J = 0–23).
In contrast, we examine the behaviour displayed for HD products in a v′ = 3 state, where no oscillations were experimentally observed and no interferences could be found in the angular distribution for j = 0. For the initial D2(v = 0, j = 0) state, no interferences were observed in the backward region.10 It serves as a counter-example because it represents a typical situation where the different features of the angular distributions can be attributed to the contribution of different groups of partial waves without interferences between them. In this case, the peaks observed in the sideways and backward directions could be reproduced by QCT calculations and attributed to groups of partial waves. Fig. 5 demonstrates that the rotational excitation of D2 barely has any effect on the shape of the angular distribution. This behaviour is not surprising because the scattering in the v′ = 3 manifold is only due to the spiral mechanism and, therefore, the evolution of the DCS(|Ω|) functions agrees point by point with the features of this mechanism: collinear approaches and a progressive tilting of the internuclear axis as the scattering moves from the backward to the forward directions. Accordingly, backward scattering mainly correlates with Ω = 0 collisions and the preeminent character of the DCS(Ω = 0) contribution is transferred to DCS(|Ω|) functions corresponding to increasingly larger values of the helicity as scattering moves into the forward hemisphere.
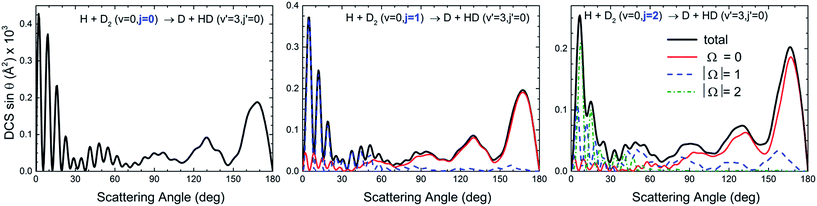 | ||
| Fig. 5 QM DCS(|Ω|) and angular distributions and deflection functions for the H + D2(j = 0–2) → D + HD(v′ = 3, j′ = 0) reaction. | ||
Conclusions
Whenever different classical scattering mechanisms coexist, each of them characterized by different sets of total angular momentum and leading to similar scattering angles, they will interfere with each other giving rise to a characteristic oscillation pattern in the angular distribution, similar to what is found in the multiple-slit experiment. We have shown that the rotational excitation of the reactants has a strong influence on the sharpness of the oscillatory patterns. However, the ultimate reason is not the progressive disappearance of interferences with increasing j, but rather the incoherent sum of contributions from different helicity states of the reagents, associated with different internuclear axis distributions.The oscillations become much more evident when the DCSs from different helicity states are analysed separately. In particular, we have found that the shape of the angular distributions depends on Ω, causing the oscillation pattern to be most prominent for small values of Ω (head-on collisions) where the spiral and the ear mechanisms coexist. For large values of Ω (side-on encounters) only the ear mechanism survives and thus oscillations are no longer observed.
In turn, the appearance or disappearance of certain mechanisms for selected values of the helicity stems from their different stereodynamical requirements. As only those mechanisms that correlate with the same value of Ω can interfere, we can conclude that it is the stereodynamics that lies behind the structure of the DCS(Ω) functions or, in other words, the stereodynamics determines the extent and nature of the interferences between mechanisms when j ≠ 0.
An important conclusion of this work is that, whereas the analysis of the interferences with rotationless reactants serves to reveal the existence of competing mechanisms, their analysis and decomposition in helicities in the case of j ≠ 0 makes it possible to determine the stereodynamical preferences of each of those mechanisms, that is, their preferences for certain approach directions.
We have also examined the behaviour of collisions leading to HD(v′ = 3, j′) where only one mechanism is observed. An increase in the rotational energy of the reactants has no effect on the shape of the DCS. Moreover, the different values of Ω tend to correlate with scattering into different regions of the angular distribution, according to the stereodynamical requirements of the single mechanism that is operative.
The calculations presented here are for the H + D2(v = 0, j = 0, 1 and 2) → HD(v′, j′) + D reaction for which we have experimental measurements of the differential cross sections that can be compared to fully quantum calculations using a highly accurate PES. This comparison gives us confidence in the conclusions we have stated above. However, the same behaviour is expected for any elementary chemical reaction in which we have more than one scattering mechanism leading to state-resolved products being scattered into the same solid angle. In this sense, the PES acts as an intrinsic molecular interferometer. According to our calculations, even in the absence of QM state-to-state results for more complex systems, quasiclassical deflection functions could be used to discern whether the QCT DCS might be reliable or if interference phenomena are expected to modify its shape.
Acknowledgements
The authors acknowledge funding by the Spanish Ministry of Science and Innovation (grants CTQ2012-37404-C02 and Consolider Ingenio 2010 CSD2009-00038), and the US National Science Foundation (grants CHE-1151428 and CHE-1464646).Notes and references
- R. P. Crease, Phys. World, 2002, 15, 15–17 Search PubMed.
- C. Jöhnsson, Z. Phys., 1961, 161, 454 CrossRef.
- P. G. M. J. Steeds, G. Pozzi, G. F. Missiroli and A. Tonomura, Phys. World, 2003, 16, 20–21 CrossRef PubMed.
- O. Carnal and J. Mlynek, Phys. Rev. Lett., 1991, 66, 2689–2692 CrossRef.
- M. Arndt, O. Nairz, J. Vos-Andreae, C. Keller, G. van der Zouw and A. Zeilinger, Nature, 1999, 401, 680–682 CrossRef CAS.
- O. Nairz, M. Arndt and A. Zeilinger, Am. J. Phys., 2003, 71, 319–325 CrossRef CAS.
- S. Gerlich, S. Eibenberger, M. Tomandl, S. Nimmrichter, K. Hornberger, P. J. Fagan, J. Tuxen, M. Mayor and M. Arndt, Nat. Commun., 2011, 2, 263 CrossRef PubMed.
- T. Juffmann, A. Milic, M. Mullneritsch, P. Asenbaum, A. Tsukernik, J. Tuxen, M. Mayor, O. Cheshnovsky and M. Arndt, Nat. Nanotechnol., 2012, 7, 297–300 CrossRef CAS PubMed.
- S. Eibenberger, S. Gerlich, M. Arndt, M. Mayor and J. Tuxen, Phys. Chem. Chem. Phys., 2013, 15, 14696–14700 RSC.
- P. G. Jambrina, D. Herráez-Aguilar, F. J. Aoiz, M. Sneha, J. Jankunas and R. N. Zare, Nat. Chem., 2015, 7, 661–667 CrossRef CAS PubMed.
- K. Koszinowski, N. T. Goldberg, A. E. Pomerantz and R. N. Zare, J. Chem. Phys., 2006, 125, 133503 CrossRef PubMed.
- J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline and S. C. Althorpe, J. Chem. Phys., 2013, 138, 094310 CrossRef PubMed.
- A. N. Panda, D. Herráez-Aguilar, P. G. Jambrina, J. Aldegunde, S. C. Althorpe and F. J. Aoiz, Phys. Chem. Chem. Phys., 2012, 14, 13067–13075 RSC.
- F. J. Aoiz, L. Bañares and V. J. Herrero, Int. Rev. Phys. Chem., 2005, 24, 119–190 CrossRef CAS PubMed.
- W. Dong, C. Xiao, T. Wang, D. Dai, X. Yang and D. H. Zhang, Science, 2010, 327, 1501–1502 CrossRef CAS PubMed.
- C. Berteloite, M. Lara, A. Bergeat, S. D. Le Picard, F. Dayou, K. M. Hickson, A. Canosa, C. Naulin, J.-M. Launay, I. R. Sims and M. Costes, Phys. Rev. Lett., 2010, 105, 203201 CrossRef.
- D. Dai, C. C. Wang, S. A. Harich, X. Wang, X. Yang, S. der Chao and R. T. Skodje, Science, 2003, 300, 1730–1734 CrossRef CAS PubMed.
- N. E. Shafer, A. J. Orr-Ewing, W. R. Simpson, H. Xu and R. N. Zare, Chem. Phys. Lett., 1993, 212, 155–162 CrossRef CAS.
- A. I. Boothroyd, W. J. Keogh, P. G. Martin and M. R. Peterson, J. Chem. Phys., 1996, 104, 7139–7152 CrossRef CAS PubMed.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128–135 CrossRef CAS.
- F. Bouakline, S. C. Althorpe and D. Peláez Ruiz, J. Chem. Phys., 2008, 128, 124322 CrossRef PubMed.
- H. Gao, M. Sneha, F. Bouakline, S. C. Althorpe and R. N. Zare, J. Phys. Chem. A, 2015 DOI:10.1021/acs.jpca.5b04573.
- F. J. Aoiz, V. J. Herrero and V. Sáez-Rábanos, J. Chem. Phys., 1992, 97, 7423–7436 CrossRef CAS PubMed.
- F. J. Aoiz, V. Sáez-Rábanos, B. Martínez-Haya and T. González-Lezana, J. Chem. Phys., 2005, 123, 094101 CrossRef CAS PubMed.
- S. J. Greaves, D. Murdock and E. Wrede, J. Chem. Phys., 2008, 128, 164307 CrossRef PubMed.
- S. J. Greaves, D. Murdock, E. Wrede and S. C. Althorpe, J. Chem. Phys., 2008, 128, 164306 CrossRef PubMed.
- J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Sáez-Rábanos and F. J. Aoiz, J. Phys. Chem. A, 2005, 109, 6200–6217 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional figures. See DOI: 10.1039/c5sc03373j |
| This journal is © The Royal Society of Chemistry 2016 |