Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum coherence in a processable vanadyl complex: new tools for the search of molecular spin qubits†
Lorenzo
Tesi
 a,
Eva
Lucaccini
a,
Eva
Lucaccini
 a,
Irene
Cimatti
a,
Irene
Cimatti
 a,
Mauro
Perfetti
a,
Mauro
Perfetti
 a,
Matteo
Mannini
a,
Matteo
Mannini
 a,
Matteo
Atzori
a,
Matteo
Atzori
 a,
Elena
Morra
a,
Elena
Morra
 b,
Mario
Chiesa
b,
Mario
Chiesa
 b,
Andrea
Caneschi
b,
Andrea
Caneschi
 a,
Lorenzo
Sorace
a,
Lorenzo
Sorace
 *a and
Roberta
Sessoli
*a and
Roberta
Sessoli
 *a
*a
aDepartment of Chemistry “Ugo Schiff”, University of Florence & INSTM RU of Florence, Via della Lastruccia 3-13, 50019 Sesto Fiorentino, Italy
bDepartment of Chemistry, University of Turin & NIS Centre, via P. Giuria 7, 10125, Torino, Italy. E-mail: roberta.sessoli@unifi.it; lorenzo.sorace@unifi.it
First published on 11th December 2015
Abstract
Electronic spins in different environments are currently investigated as potential qubits, i.e. the logic units of quantum computers. These have to retain memory of their quantum state for a sufficiently long time (phase memory time, Tm) allowing quantum operations to be performed. For molecular based spin qubits, strategies to increase phase coherence by removing nuclear spins are rather well developed, but it is now crucial to address the problem of the rapid increase of the spin–lattice relaxation rate, T1−1, with increasing temperature that hampers their use at room-temperature. Herein, thanks to the combination of pulsed EPR spectroscopy and AC susceptometry we evidence that an evaporable vanadyl complex of formula VO(dpm)2, where dpm− is the anion of dipivaloylmethane, presents a combination of very promising features for potential application as molecular spin-qubit. The spin–lattice relaxation time, T1, studied in detail through AC susceptometry, decreases slowly with increasing temperature and, more surprisingly, it is not accelerated by the application of an external field up to several Teslas. State-of-the art phase memory times for molecular spin systems in protiated environment are detected by pulsed EPR also in moderate dilution, with values of 2.7 μs at 5 K and 2.1 μs at 80 K. Low temperature scanning tunnel microscopy and X-ray photoelectron spectroscopy in situ investigations reveal that intact molecules sublimated in ultra-high vacuum spontaneously form an ordered monolayer on Au(111), opening the perspective of electric access to the quantum memory of ensembles of spin qubits that can be scaled down to the single molecule.
Introduction
The realization of a quantum computer is expected to trigger a second revolution in information and communication technology,1–4 allowing for unequalled computation capabilities in disparate fields, ranging from structural biology5 to quantum physics.3 Quantum bits, or qubits, are at the basis of quantum computation, and different strategies to realize them are currently explored,6 including ionic traps,7 quantum dots in semiconductors,8,9 photons,10 and superconducting nanostructures.11 Spins, either nuclear12–14 or electronic,15–19 are among the most efficiently addressable targets to build these logical units, as their initialization and read-out can be performed by well-established magnetic resonance techniques. The parameters to be optimized in the design of these qubits are: i) the longitudinal relaxation time, T1, which corresponds to the lifetime of a classical bit that can assume either the |0> or the |1> value; ii) the characteristic time in which the spin loses the memory of the phase of the superposition state in which it has been prepared. A lower estimation of this decoherence time, T2, can be extracted by the memory time, Tm, which is commonly measured with pulsed EPR or NMR: the ratio of Tm over the time necessary for an individual quantum operation has to be larger than 104 to allow for fault tolerant quantum computing.In the field of electron spin-based qubits nitrogen vacancies in diamond20,21 and impurities in silicon and silicon carbide22 exhibit long-lived quantum coherence but present major challenges in the control of their organization and coupling to perform quantum logic operations. Molecular spin based qubits, on the contrary, can be organized on surfaces and the interaction between them tuned at will through a rational synthetic design. After an extensive research on polynuclear transition metal complexes16,23,24 optimized to exhibit a long Tm, the research in this field has recently focused back on the simplest spin S = 1/2 systems constituted either by organic radicals25 or by 3d transition metal ions.26–28 These have relatively long Tm, in particular at high temperature, because there are no excited spin levels that can foster the magnetic relaxation when thermally populated. In these systems the interaction of the electronic spin with the nuclear spins is the most relevant source of decoherence. Outstanding results have very recently been obtained with vanadium(IV) ions assembled with nuclear spin-free ligands.27 When magnetic dilution is made in a nuclear spin-free solvent, such as CS2, Tm approaches one millisecond at low temperature,29 showing that molecular spin systems can be as performant as extended inorganic structures. Unfortunately this remarkable long coherence is rapidly lost on increasing temperature because the spin–lattice relaxation acts as a limiting factor for T2.30 A recent investigation has clearly evidenced that solid crystalline solutions can enhance T1, thus resulting in enhanced coherence time at high temperature26 but the mechanisms of relaxation, as well as strategies to enhance T1, are still poorly investigated.
In this study we have investigated the magnetic relaxation of a simple mononuclear complex of vanadium(IV) by the combination of AC magnetic susceptometry to study spin–lattice relaxation with pulsed EPR spectroscopy to characterize the spin coherence. The two techniques can in fact shed light on different contributions to the relaxation but their association is unprecedented in the search for potential spin-based qubits.
The vanadyl complex VO(dpm)2, where dpm− is the anion of dipivaloylmethane, has been selected because the strong V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond is expected to increase the rigidity of the coordination sphere with a reduction of spin–lattice relaxation efficiency. The presence of β-diketonate ligands in a neutral complex imparts a high volatility that can be exploited to deposit the molecule on surfaces. An unexpected long T1 over wide field and temperature ranges has been found to accompany Tm values that are among the longest ones observed in molecular species surrounded by spin active nuclei. The in situ morphological and spectroscopic characterization of a monolayer deposit of VO2(dpm)2 on Au(111) suggest that the molecules are intact on the surface, making these simple units potential candidates as molecular qubit individually addressable by scanning probe techniques.
O bond is expected to increase the rigidity of the coordination sphere with a reduction of spin–lattice relaxation efficiency. The presence of β-diketonate ligands in a neutral complex imparts a high volatility that can be exploited to deposit the molecule on surfaces. An unexpected long T1 over wide field and temperature ranges has been found to accompany Tm values that are among the longest ones observed in molecular species surrounded by spin active nuclei. The in situ morphological and spectroscopic characterization of a monolayer deposit of VO2(dpm)2 on Au(111) suggest that the molecules are intact on the surface, making these simple units potential candidates as molecular qubit individually addressable by scanning probe techniques.
Results and discussion
The synthesis of crystalline VO(dpm)2 was achieved according to an earlier reported procedure,31 operating under inert atmosphere to avoid oxidation. VO(dpm)2, prepared in the crystalline form and characterized by X-ray diffractometry (see ESI†), presents a typical square pyramidal coordination (Fig. 1) with a short V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond (1.59 Å vs. an average of 1.964 Å for the V–O single bonds). Deviations from tetragonal symmetry are already visible in the first coordination sphere in both bond lengths and bond angles. Given that the system crystallizes in the monoclinic P21 space group, two sets of molecules with the V
O double bond (1.59 Å vs. an average of 1.964 Å for the V–O single bonds). Deviations from tetragonal symmetry are already visible in the first coordination sphere in both bond lengths and bond angles. Given that the system crystallizes in the monoclinic P21 space group, two sets of molecules with the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O directions forming an angle of 64.1° are present in the crystal lattice. The strongly axial ligand field produced by the short V
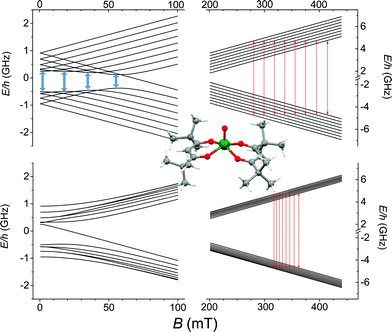
O directions forming an angle of 64.1° are present in the crystal lattice. The strongly axial ligand field produced by the short V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond removes orbital degeneracy with the dxy orbital being the lowest in energy and the only one to be half occupied. Vanadyl systems are therefore well described by a spin S = 1/2 with slightly anisotropic g tensor close to the free electron value. The most abundant isotope of vanadium, 51V (99.75%), is characterized by I = 7/2 thus the S = 1/2 doublet is further split in 16 states by hyperfine interaction as schematized in Fig. 1.
O bond removes orbital degeneracy with the dxy orbital being the lowest in energy and the only one to be half occupied. Vanadyl systems are therefore well described by a spin S = 1/2 with slightly anisotropic g tensor close to the free electron value. The most abundant isotope of vanadium, 51V (99.75%), is characterized by I = 7/2 thus the S = 1/2 doublet is further split in 16 states by hyperfine interaction as schematized in Fig. 1.
Magnetization dynamics
The magnetization dynamics, investigated by AC-susceptometry (see ESI†), of a polycrystalline sample of VO(dpm)2, hereafter 1bulk, revealed no imaginary component of the susceptibility in zero static field down to the lowest investigated temperature (1.9 K). The application of a weak field induced however slow relaxation of the magnetization with the concomitant decrease of the real component χ′ and the appearance of a peak in χ′′ component (ESI Fig. S1†). In a field of 0.2 T the entire magnetization of the system relaxed slowly and this field was selected to investigate the temperature dependence of the relaxation time.Maxima in χ′′ were observed up to 80 K for frequencies lower than 10 kHz, as shown in Fig. 2a (ESI Fig. S2† for χ′), evidencing also a gradual increase in the width of the distribution on lowering the temperature (see ESI and Fig. S3†). Such a high temperature slow relaxation is usually observed in molecules exhibiting strong magnetic anisotropy known as Single-Molecule Magnet (SMMs), for instance in double-decker TbPc2 complexes,32 but clearly it has a different origin here. The data, reproduced with the Debye model,33 allowed to extract the relaxation time of the susceptibility, τ, reported in Fig. 2b. It is evident that τ does not follow the Arrhenius behaviour, in agreement with the lack of electronic/magnetic states that can be thermally populated providing a path for the multiphonon Orbach mechanism of relaxation.34,35 On the contrary the temperature dependence of τ can be reproduced by considering different contributions to the relaxation rate:
| τ−1 = aT + bTn | (1) |
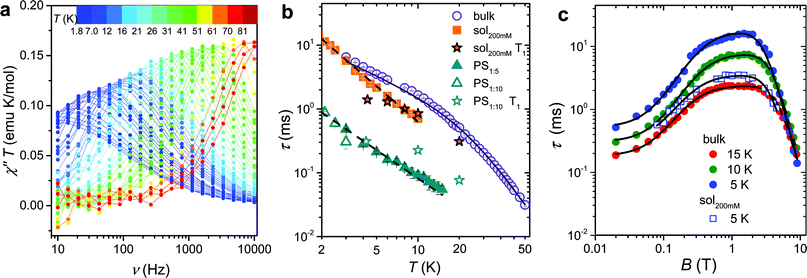 | ||
Fig. 2 (a) Frequency dependence of the imaginary component of the AC susceptibility of 1bulk in Bdc = 0.2 T multiplied by temperature to be readable in the whole 2–80 K temperature range. (b) Temperature dependence of the relaxation time of the magnetic susceptibility measured in Bdc = 0.2 T for the pure and the diluted samples of 1: two dispersions in polystyrene with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and 1 5 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 mass ratio and a 200 mM CH2Cl2 10 mass ratio and a 200 mM CH2Cl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene frozen solution (see legend). The black solid line corresponds to the best-fit of 1bulk data using eqn (1), while the broken lines correspond to simulation with T−n law. T1 for the diluted sample, extracted from pulsed EPR spectra, are shown for comparison. (c) Field dependence of the relaxation time of the magnetic susceptibility of 1bulk and 1sol200 mM frozen solution sample (see legend). The solid lines represent the best fit obtained with eqn (3). Best fit parameters are reported in Table 1. toluene frozen solution (see legend). The black solid line corresponds to the best-fit of 1bulk data using eqn (1), while the broken lines correspond to simulation with T−n law. T1 for the diluted sample, extracted from pulsed EPR spectra, are shown for comparison. (c) Field dependence of the relaxation time of the magnetic susceptibility of 1bulk and 1sol200 mM frozen solution sample (see legend). The solid lines represent the best fit obtained with eqn (3). Best fit parameters are reported in Table 1. | ||
To shed light on the mechanisms of magnetic relaxation the AC susceptibility was investigated in a wide field range, i.e. up to 8.8 T, for three different temperatures, 5, 10, and 15 K. Notice that in this temperature range the direct process dominates as indicated by the almost linear dependence of τ−1 on T. The corresponding relaxation times are reported in Fig. 2c. The initial increase of τ for weak applied field is followed by an almost flat region that extends up to ca. 4 T, followed by a rapid decrease at higher fields. Data of Fig. 2c were reproduced considering different relaxation mechanisms that can be active in S = 1/2 systems. According to the seminal work done by de Vroomen et al. on the Cu2+ Tutton salt,36 two contributions to the relaxation rate can be considered:
| τ−1 = τZ−1 + τint−1 | (2) |
The first term represents the direct mechanism between the two states split by the Zeeman energy, which is expected to vanish in zero field as a result of the Kramers theorem.37 In fact, a pure and isolated S = 1/2 should not be able to relax in zero field. The second term takes into account a sort of internal field whose origin can be either intramolecular (i.e. hyperfine interactions) or intermolecular (i.e. due to dipolar or exchange interactions). The latter is responsible for the efficient relaxation in zero field and presents, for the direct mechanism,38 a field dependence that is similar to the Brons-van Vleck formula developed to describe the Raman process in concentrated systems.39 Summing up the two contributions to the field dependence in eqn (2) the data of Fig. 2c have been reproduced according to:
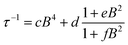 | (3) |
The first term is the typical field dependence of the direct process for a S = 1/2 spin and reflects the fact that the larger is the Zeeman splitting between the states the higher is the density of phonons matching it. In the second one the d term represent the zero field relaxation rate, similar to the tunnelling rate in SMMs,33 the f parameter takes into account the ability of the external field to suppress these mechanisms, while the e parameter, strongly dependent on the concentration of the spin centres, takes into account the field effects on the relaxation of interacting spins.39 The best-fit values obtained with eqn (3) are summarized in Table 1. The c parameter for T = 5 K should be considered with caution because only a small fraction of the susceptibility is detected at such high fields. The field range where the relaxation remains slow is really remarkable, suggesting that the direct mechanism of relaxation is not very efficient.
| T (K) | c (T−4 s−1) | d (s−1) | e (T−2) | f (T−2) |
|---|---|---|---|---|
| 5 | 0.96 ± 0.04 | 2060 ± 180 | 7.6 ± 0.7 | 240 ± 30 |
| 10 | 0.73 ± 0.01 | 3460 ± 150 | 7.6 ± 0.4 | 179 ± 12 |
| 15 | 0.97 ± 0.03 | 5740 ± 270 | 15.1 ± 0.9 | 190 ± 16 |
| 5 | 2.00 ± 0.11 | 3600 ± 550 | 13.7 ± 1.4 | 160 ± 40 |
In ESI Fig. S3 and S4† we also report the temperature and field dependence of the width of the distribution of relaxation rate, respectively. The width is correlated to the parameter α of the extended Debye formula (see ESI†). In general the distribution is quite narrow increasing up to 0.3 at the lowest temperature (ESI Fig. S3†). The decrease of α with increasing fields, see ESI Fig. S4,† is indicative that τint−1 is more sensitive to the local environment, as indeed expected. The non-monotonous trend at low temperature suggests the presence also in this powdered sample of a moderate phonon-bottleneck effect.40
The long spin–lattice relaxation time of VO(dpm)2, above 10 ms at low temperatures, suggests that also decoherence times can be comparatively long. The latter are however accessible only by pulsed EPR techniques and require narrow lines that can be achieved in diluted systems. Unfortunately, extensive efforts to prepare the titanyl-based diamagnetic analogue failed due to the instability of the mononuclear species TiO(dpm)2 in favour of the dimeric one [TiO(dpm)2]2,41 thus precluding the preparation of isomorphous crystalline solid solutions. As an alternative, two dispersions of 1 in polystyrene with mass ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 1PS1
5, 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, and 1
5, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, 1PS1
10, 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, as well as a frozen 200 mM solution of 1 in a 2
10, as well as a frozen 200 mM solution of 1 in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 CH2Cl2
3 CH2Cl2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) toluene mixture (1sol200 mM), were prepared and investigated by AC susceptometry (Fig. S5†). This was aimed at getting information on the relaxation time of the magnetic susceptibility to be compared to T1 extracted from pulsed EPR data. Even if a reduced range of temperature and fields are accessible on the diluted samples for instrumental reasons, it is well evident that also diluted samples show slow relaxation of the magnetization (Fig. 2b): polymeric dispersions are characterized by a relaxation rate which is ca. 20 times faster than bulk sample, with minor difference between the two concentrations, suggesting that matrix effects to the relaxation dominate over those induced by dilutions. On the other hand, the low temperature relaxation rate of the frozen solution is comparable to the bulk phase but increases much faster on increasing temperatures. The almost linear temperature dependence in the log(τ) vs. log(T) plot of Fig. 2b allowed to analyse the data as τ−1 ∝ Tn, with n = 1.49 ± 0.04 for 1PS1
toluene mixture (1sol200 mM), were prepared and investigated by AC susceptometry (Fig. S5†). This was aimed at getting information on the relaxation time of the magnetic susceptibility to be compared to T1 extracted from pulsed EPR data. Even if a reduced range of temperature and fields are accessible on the diluted samples for instrumental reasons, it is well evident that also diluted samples show slow relaxation of the magnetization (Fig. 2b): polymeric dispersions are characterized by a relaxation rate which is ca. 20 times faster than bulk sample, with minor difference between the two concentrations, suggesting that matrix effects to the relaxation dominate over those induced by dilutions. On the other hand, the low temperature relaxation rate of the frozen solution is comparable to the bulk phase but increases much faster on increasing temperatures. The almost linear temperature dependence in the log(τ) vs. log(T) plot of Fig. 2b allowed to analyse the data as τ−1 ∝ Tn, with n = 1.49 ± 0.04 for 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and n = 1.86 ± 0.04 for 1sol200 mM. Exponents larger than one for the direct mechanism are generally attributed to spin–phonon bottleneck effects,34 which are expected to be more relevant for these samples that have a small contact-surface with the helium bath than the ground microcrystalline powder of the bulk sample.40 The field dependence of τ of 1sol200 mM was also investigated at T = 5 K (see Fig. 2c) and revealed the same wide plateau observed in the bulk phase, thus indicating that, despite some matrix effects, this interesting feature is an intrinsic property of the structure of the molecule. Unfortunately, a more direct comparison between the parameters reported in Table 1 for bulk and diluted samples would only be possible for a solid crystalline solution.
5 and n = 1.86 ± 0.04 for 1sol200 mM. Exponents larger than one for the direct mechanism are generally attributed to spin–phonon bottleneck effects,34 which are expected to be more relevant for these samples that have a small contact-surface with the helium bath than the ground microcrystalline powder of the bulk sample.40 The field dependence of τ of 1sol200 mM was also investigated at T = 5 K (see Fig. 2c) and revealed the same wide plateau observed in the bulk phase, thus indicating that, despite some matrix effects, this interesting feature is an intrinsic property of the structure of the molecule. Unfortunately, a more direct comparison between the parameters reported in Table 1 for bulk and diluted samples would only be possible for a solid crystalline solution.
Continuous wave and pulsed EPR spectroscopy
The low temperature CW-EPR X-band spectrum of a frozen 1 mM solution of 1 (1sol1 mM) is shown in Fig. 3a. Similar features are observed for the other investigated samples (1bulk, 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, 1PS1
5, 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, and 1sol200 mM spectra available in ESI Fig. S6†), the effect of concentration being mirrored by the narrowing of the EPR lines when going from pure sample to dispersions and frozen solutions. On the other hand, the position of the lines is not varying, indicating that the spin Hamiltonian parameters, and then the electronic structure, are maintained in different environments.
10, and 1sol200 mM spectra available in ESI Fig. S6†), the effect of concentration being mirrored by the narrowing of the EPR lines when going from pure sample to dispersions and frozen solutions. On the other hand, the position of the lines is not varying, indicating that the spin Hamiltonian parameters, and then the electronic structure, are maintained in different environments.
 | ||
| Fig. 3 (a) Echo detected (black trace) and CW (red trace) experimental EPR spectra of 1sol1 mM, measured at 5 K, and best simulations (dotted traces). The arrow marks the field position of T1 and Tm determination. (b) Temperature dependence of T1 and Tm for 1sol1 mM sample. Full symbols refer to experiments of echo saturation by fast repetition, empty ones to inversion recovery experiments (see ESI† for details). The solid line corresponds to the best-fit of the high temperature data with T1 ∝ T−n. | ||
The spectra clearly show the features due to the anisotropic hyperfine coupling of the electron spin to the I = 7/2 nuclear spin of 51V: at the high and low field extreme region, peaks due to the parallel components of the hyperfine structure are observed, whereas in the centre the closely spaced perpendicular ones are evident, as schematized by the resonant fields in Fig. 1.
Spectral simulations were performed42 on the basis of the following spin Hamiltonian:
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = ηA·Ŝ + μBŜ·g·B = ηA·Ŝ + μBŜ·g·B | (4) |
An echo-detected field-swept EPR spectrum (EDFS) was recorded using the standard Hahn sequence (see ESI†) for 1sol200 mM, 1sol1 mM, and 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 diluted samples (Fig. 3a and ESI Fig. S7†). The observation of a spin-echo is a first indication that quantum coherence is observed in these samples. Further, the same spin Hamiltonian parameters used for the simulation of the CW spectrum yielded good simulations of the EDFS spectrum, confirming that the entire VO(dpm)2 sample is experiencing the detected coherence.
10 diluted samples (Fig. 3a and ESI Fig. S7†). The observation of a spin-echo is a first indication that quantum coherence is observed in these samples. Further, the same spin Hamiltonian parameters used for the simulation of the CW spectrum yielded good simulations of the EDFS spectrum, confirming that the entire VO(dpm)2 sample is experiencing the detected coherence.
Determination of the potential applicability of diluted samples of 1 as molecular qubit was performed by measuring the coherence time, Tm, as a function of temperature and field position for 1sol1 mM to reduce spin–spin interactions. To maximize the observed echo the temperature dependence of Tm has been investigated on the so-called powder like line evidenced by an arrow in Fig. 3a.
The echo decay traces (Fig. 4a) were then fitted using a stretched-exponential equation:
y = y0 + km![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(2t/Tm)βm] exp[−(2t/Tm)βm] | (5) |
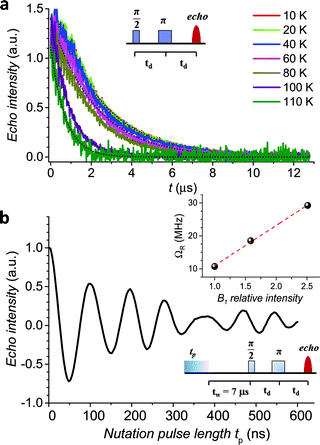 | ||
| Fig. 4 (a) Pulsed EPR Hahn echo decay traces for 1sol1 mM at different temperatures recorded at 343 mT. In the inset the employed pulse sequence. (b) Rabi oscillations for 1sol1 mM recorded at 4.3 K at 10 dB microwave attenuation. The change in oscillations observed at tp > 400 ns is due to the interaction between the electron spin and surrounding protons.48 In the inset the Rabi frequency (ΩR) vs. oscillating field intensity superimposed to the linear best-fit. | ||
It is evident that between 4 K and 80 K the resulting Tm values (Fig. 3b) are almost temperature independent (varying from 2.7 μs to 2.1 μs). Above 80 K the softening of the solvent glassy matrix, and consequently of the tert-butyl groups of the ligands, opens new relaxation pathways leading to the loss of echo above 110 K. The temperature dependence of βm parameter essentially follows the same pattern, being slightly larger than 1 at 5 K and approaching a mono-exponential decay above 80 K (Fig. S8†). This behaviour suggests that decoherence is essentially dominated by physical motions of the magnetic nuclei.45
In agreement with the long coherence time observed at low temperature, Rabi-like oscillations of the echo intensity were observed for 1sol1 mM in nutation experiments performed at different microwave powers as shown in Fig. 4b, where the observed linear dependence of the Rabi oscillation on the intensity of the oscillating field is reported in the inset. This indicates the possibility of creating any arbitrary superposition of states, thus fulfilling one of the two main requirements for creating universal quantum gates.46
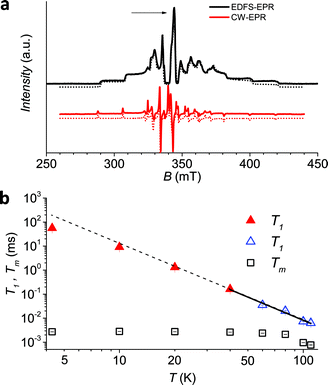
Since earlier studies revealed strong correlation between the spin–lattice relaxation time T1 and Tm for some molecular species candidate for quantum information processing (QIP),26,30 we determined the temperature dependence of T1 between 5 K and 110 K in 1sol1 mM, for which the AC susceptibility technique does not have the necessary sensitivity.
Given the large range of relaxation times two different experimental procedures were applied: at low temperature (5–60 K) the echo saturation by fast repetition, suitable for long relaxation times47 was used, whereas at higher temperature the standard inversion recovery procedure was applied (see ESI† for details). Saturation recovery traces have been fitted using the following equation:
y = y0 + k1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/T1)β1 exp(−t/T1)β1 | (6) |
To have a more quantitative comparison we also measured the temperature dependence of the spin–lattice relaxation time for 1sol200 mM by pulsed EPR: the obtained results are consistent with those obtained by AC susceptibility (Fig. 2b), confirming that the two techniques are actually probing the same process.
As a final test to establish whether this molecule maintains its long decoherence time in a solid matrix not affected by the melting of the frozen solution we measured the temperature dependence of relaxation times for 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10. Remarkably, for this relatively concentrated sample it is possible to observe an echo and measure Tm up to 220 K (Fig. S10†). In particular while Tm is 0.36 μs at 4.3 K, i.e. about one order of magnitude faster than for 1sol1 mM, at the highest measured temperature a Tm value of 0.1 μs could be determined.
10. Remarkably, for this relatively concentrated sample it is possible to observe an echo and measure Tm up to 220 K (Fig. S10†). In particular while Tm is 0.36 μs at 4.3 K, i.e. about one order of magnitude faster than for 1sol1 mM, at the highest measured temperature a Tm value of 0.1 μs could be determined.
Deposition on Au(111) and in situ characterization
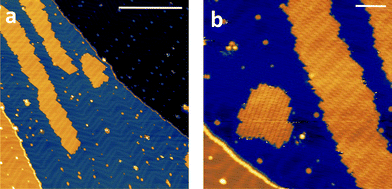
The high volatility of VO(dpm)2 was here exploited to obtain thick films as well as sub-monolayer (ML) deposit assembled on the Au(111) surface. A complete in situ X-ray photoelectron spectroscopy (XPS) and low temperature scanning tunnelling microscopy (STM) characterization was carried out, while the stability of the sample toward oxidation was investigated by exposing a thick film to air. Fig. 5 reports the STM topography obtained at T = 30 K for sub-ML coverage. As observed for other complexes with dpm− ligands,49,50 the molecules weakly interact with the substrate and form patches of variable size constituted by regularly packed molecules. The islands present regular boundaries maintaining the herringbone modulation of the gold substrate. Sub-molecular resolution was hard to achieve inside the patches, though isolated features were visible at the kinks of the herringbone structure.The height of the molecular layer is 0.27 ± 0.02 nm (ESI Fig. S12†), in good agreement with similar deposits obtained with iron β-diketonate complex,49 though no reports are available on VO(dpm)2. By increasing the deposition time full coverage was achieved: regularly packed molecules still revealing the herringbone structure underneath were found (ESI Fig. S13†). Interestingly, as in the case of Fe(dpm)3,49 no additional molecular layer can be deposited at the employed low deposition rates (see ESI†).
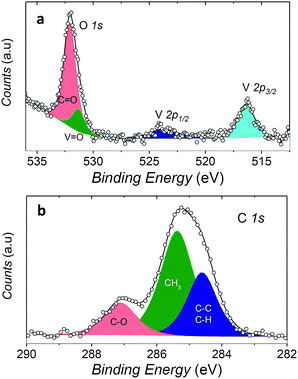
In order to check if the complex is intact on the surface, the full monolayer deposit was investigated by XPS, revealing the presence of the expected elements (see Fig. 6).
The observed broad O 1s peak around 532 eV was reproduced by considering two components. The smaller one at 531.3 eV was attributed to the oxygen of the vanadyl group (OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), in good agreement with what observed for vanadyl phthalocyanine, VOPc, on Ag(111),51,52 while the larger one at 532.1 eV, was associated to the oxygen atoms of the two dpm− ligands (OC
O), in good agreement with what observed for vanadyl phthalocyanine, VOPc, on Ag(111),51,52 while the larger one at 532.1 eV, was associated to the oxygen atoms of the two dpm− ligands (OC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). The ratio of the area of the two peaks is close to 1
O). The ratio of the area of the two peaks is close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, as expected for the stoichiometry of the molecule, thus confirming the integrity of the complex on surface. An analogous analysis allows to distinguish three components contributing to the C 1s region: the carbonylic carbon (287.2 eV), methyl carbon (285.4 eV) and the third one regrouping the remaining carbons (CH, CC, at 284.6 eV).
4, as expected for the stoichiometry of the molecule, thus confirming the integrity of the complex on surface. An analogous analysis allows to distinguish three components contributing to the C 1s region: the carbonylic carbon (287.2 eV), methyl carbon (285.4 eV) and the third one regrouping the remaining carbons (CH, CC, at 284.6 eV).
Even more interestingly the vanadium photoelectron peaks allowed to provide specific hints on the oxidation state of this element and thus on possible interaction with the metal surface. The V 2p3/2 was observed at 516.4 eV, showing a distance to the oxygen peak ΔE(OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O 1s − V 2p3/2) of 14.9 eV which well compares with that observed in VOPc monolayer and multilayers (ΔE(OV
O 1s − V 2p3/2) of 14.9 eV which well compares with that observed in VOPc monolayer and multilayers (ΔE(OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O 1s − V 2p3/2) = 14.6 eV).51 A semi-quantitative analysis of the composition according to the integrated peak signals gave for the three investigated elements the molar composition C = 81 ± 4%, O = 16 ± 1%, V = 2.6 ± 0.6% that well compares with the theoretical one (C = 78.6%, O = 17.9%, V = 3.6%).
O 1s − V 2p3/2) = 14.6 eV).51 A semi-quantitative analysis of the composition according to the integrated peak signals gave for the three investigated elements the molar composition C = 81 ± 4%, O = 16 ± 1%, V = 2.6 ± 0.6% that well compares with the theoretical one (C = 78.6%, O = 17.9%, V = 3.6%).
These observations indicate that the VO(dpm)2 molecules can be deposited intact on the surface and features a weak interaction with the gold substrate as the only occupied d orbital, dxy, is expected to lie flat with limited overlap with the substrate orbitals. A similar scenario was observed for copper(II)phthalocyanine molecules that are known to retain their unpaired electron in the dx2−y2 orbital.53 In the vanadyl derivative VOPc the metal atom is slightly above the plane of the equatorial oxygen atoms; the distance of the metal ion from the surface is therefore further increased thus reducing the interaction with the substrate. It is thus not surprising that synchrotron-based experiments on monolayers of VOPc on Ag(111)51 detected a substantially unchanged magnetism of the S = 1/2 of VIV compared to thicker films. It is therefore reasonable to envisage that VO(dpm)2 molecules retain their paramagnetic nature when in contact with the gold substrate. This system represents therefore an appealing alternative to the use of N-donors phthalocyanine- and porphyrin-based systems for deposition on surfaces, though VO(dpm)2 films resulted somehow instable in air: ex situ prepared thick films of about 150 nm showed a partial surface oxidation as suggested by the decrease in the (ΔE(OV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O 1s − V 2p3/2)) value accompanied by a progressive shift of the V 2p peak (ESI Fig. S14†).
O 1s − V 2p3/2)) value accompanied by a progressive shift of the V 2p peak (ESI Fig. S14†).
Comparison with other molecular spin qubits
AC-susceptometry is currently widely employed to evidence slow relaxation in SMMs characterized by easy axis anisotropy and large magnetic moments; however, Luis et al.54 have recently used this technique to characterize in detail the dynamics of a pseudo spin-doublet resulting from the large easy plane anisotropy of the S = 3/2 of CoII in Co(acac)2(H2O)2.54 The role of hyperfine interaction and of the coupling of the nuclear spins with the phonon bath has been found to contribute to the opening of relaxation pathways otherwise forbidden in zero field for a pure S = 1/2 due to time reversal symmetry. VO(dpm)2 corresponds exactly to the hyperfine-split S = 1/2 model recently developed54 and indeed analogies in the magnetic behaviour of the two molecular systems are observed. In zero static field the hyperfine interaction with the I = 7/2 gives origin to two sets of states characterized by F = |S ± I| with multiplicity 9 and 7, respectively, as can be observed in Fig. 1. The isotropic hyperfine coupling is responsible for the gap between F = 4 and F = 3 states, which are however further split by the anisotropic components of the hyperfine tensor (see eqn (4)). The application of a weak static field has a different effect when applied along the molecular z direction, the one of largest hyperfine interaction corresponding to the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond direction, or perpendicular to it, as also indicated in the eigenvectors composition (ESI Fig. S15†).
O bond direction, or perpendicular to it, as also indicated in the eigenvectors composition (ESI Fig. S15†).
If similar features were already observed in the Co(acac)2(H2O)2pseudo-spin S = 1/2 system, some striking quantitative differences are evident. The first one is that the relaxation time remains long over a wide field range, ca. 30 times larger in VO(dpm)2 compared to the CoII derivative. At 5 K, where the relaxation is still governed by the direct mechanism, the relaxation rate starts to grow above 3 T, to be compared to the drastic 0.1 T upturn observed for CoII at 1.8 K.54 The comparison with early works on the dynamics of CuII spins36 confirms that the field stability of slow relaxation of VO(dpm)2 is unprecedented. This is extremely appealing for technological applications as it allows to exploit higher frequencies to coherently manipulate the spins, e.g. at W-band, corresponding to 95 GHz, with significant improvement of sensitivity. Moreover, working at W-band was also shown to increase Tm in samples of Yb3+ diluted in CaWO4, though at the same time the larger field was found to reduce T1. This serious drawback of the use of high frequencies is not expected for VO(dpm)2.55
The origin of the striking difference between the two compounds can be associated to the reduced efficiency of the direct mechanism of relaxation, which relies on the spin–phonon coupling. The latter is mediated by the spin–orbit coupling, which is significantly lower for such a light transition metal as vanadium. As a result, T1 of VO(dpm)2 remains long over a wide temperature range. For instance, a relaxation time of 2 ms is observed at 6 K for diluted Co(acac)2(H2O)2 but at temperatures as high as 40 K in concentrated VO(dpm)2. The anomaly arises from the small exponent of the Tn dependence of the Raman-like mechanism of relaxation. Such low exponents are relatively common for S = 1/2 states with small orbital contributions comprising light elements and have been associated to the soft character of the molecular lattices.35,56
It is also interesting to compare the measured decoherence times with those of other molecules proposed as potential molecular qubits. Among similarly investigated electron spin-qubits of vanadium, we note that the Tm values observed for a frozen solution of VO(dpm)2 are slightly longer – in the whole investigated temperature range – than those reported for a dispersion in protiated solvents at the same concentration of a vanadium complex with nuclear-spin free ligands:27 this is of particular interest, since in our case an evaporable system containing a large number of protons has been chosen without optimizing the ligand to reduce the number of nuclear spins. We have in fact confirmed that the ligand hydrogen magnetic nuclei play the dominant role in the relaxation by investigating the coherence time of VO(dpm)2 diluted in deuterated solvents. A substantially unchanged Tm was detected (Fig. S11†), in contrast to the improvement of at least an order of magnitude of Tm45,47 expected upon solvent deuteration when nuclei flip-flops of the latter dominate the decoherence process.
The observed decoherence times for VO(dpm)2 are also comparable, despite the higher concentration of our samples, to those reported by Warner et al.28 for a 0.1% diluted film of CuPc (2.1 vs. 1 μs at 80 K, if one consider the frozen solution 1sol1 mM, 0.16 vs. 1 μs if one consider the 1PS1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10). We must stress that the processability and the surface stability of this β-diketonate complex are comparable to those of metal porphyrins, without the drawback of introducing 14N magnetic nuclei. This is not only relevant for reducing the efficiency of decoherence; as suggested by Freedman et al.,27 the well-defined hyperfine states of vanadium ions coordinated by non-magnetic nuclei can be used to investigate multiple quantum coherence. It is interesting to notice that in the Zeeman diagram of Fig. 1 pronounced level anti-crossings with gaps of the order of 0.5–1 GHz are observed at low longitudinal magnetic field. These transitions (in pale blue in Fig. 1), also known as clock transitions, are inherently robust to external perturbations because their effective g is practically zero and therefore are weakly affected by changes in the local field. Enhanced coherence time for these clock transitions have been recently observed in Bi doped silicon enriched in 29Si nuclei.57 Similar effects should be observable at the molecular level in VO(dpm)2 for which clock transitions are expected at fields where the magnetization dynamics is already rather slow.
10). We must stress that the processability and the surface stability of this β-diketonate complex are comparable to those of metal porphyrins, without the drawback of introducing 14N magnetic nuclei. This is not only relevant for reducing the efficiency of decoherence; as suggested by Freedman et al.,27 the well-defined hyperfine states of vanadium ions coordinated by non-magnetic nuclei can be used to investigate multiple quantum coherence. It is interesting to notice that in the Zeeman diagram of Fig. 1 pronounced level anti-crossings with gaps of the order of 0.5–1 GHz are observed at low longitudinal magnetic field. These transitions (in pale blue in Fig. 1), also known as clock transitions, are inherently robust to external perturbations because their effective g is practically zero and therefore are weakly affected by changes in the local field. Enhanced coherence time for these clock transitions have been recently observed in Bi doped silicon enriched in 29Si nuclei.57 Similar effects should be observable at the molecular level in VO(dpm)2 for which clock transitions are expected at fields where the magnetization dynamics is already rather slow.
On the other hand, when Tm of VO(dpm)2 is compared with relaxation times for a copper dithiolate complex with deuterated PPh4+ cation reported by van Slageren et al.26 it is found to be an order of magnitude shorter: this might be attributed both to the larger concentration of the electronic spins in our system as well as to the large number of mobile protons present on the ligand. Further, the use of Q-band frequency, as done by van Slageren et al., is expected to increase Tm of VO(dpm)2 as well as its T1.
Conclusions
We have shown here that a more rational search for potential qubits can significantly benefit from the combination of AC susceptometry with pulsed EPR techniques. This multitechnique approach is of particular relevance to define synthetic strategies because the optimization of T1, in terms of both temperature and field dependence, is mandatory for the realization of molecular spin qubits that can be operated at room temperature. AC susceptibility gives easily access to the field dependence of T1, in contrast to EPR, which relies on the resonance condition. Though T1 extracted with the two techniques are exactly the same only in the case of a S = 1/2 with no hyperfine splitting, a close relation exists also for systems with more than two levels. The simple molecule we have picked up with this approach, though not yet optimized for coherent manipulation of the spin state, presents state-of-the-art phase memory times combined with additional interesting features. The spin–lattice relaxation remains slow even in strong fields, allowing the use of higher frequencies for coherent spin manipulation without losses in performances.A particularly low efficient spin–phonon coupling appears to be at the basis of this behaviour and the potentially positive role played by the strong V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond needs to be further investigated by extending the approach developed here to other and more promising systems.27,29Ab initio modellization of the spin relaxation could also help to identify which structural features can favour long T1, and consequently long Tm, at high temperature.
O bond needs to be further investigated by extending the approach developed here to other and more promising systems.27,29Ab initio modellization of the spin relaxation could also help to identify which structural features can favour long T1, and consequently long Tm, at high temperature.
Even if the crucial aspect of qubits entanglement has not been addressed in this work it can be easily achieved through connection of β-diketonate pockets in more complex architectures.58,59 This approach has already been successfully employed to couple different spin centers60 and to address them individually in resonance experiments in particular in lanthanide polynuclear complexes thanks to their significantly different g-factors.61
Of great relevance is the possibility to obtain monolayers of ordered arrays of intact VO(dpm)2 molecules, retaining their paramagnetic nature thanks to the reduced interaction of the orbital carrying the unpaired electron with the substrate. Metallic nanostructures can be easily decorated with a monolayer of ordered VO(dpm)2 molecules, allowing to investigate the response of an ensemble of identical molecular qubits, whose size can be easily controlled by lithographic exposure of the metallic substrate. Thin films of VO(dpm)2 could be evaporated directly on a μ-SQUID to detect by AC susceptometry the effects of surface confinement on the dynamics of the magnetization, as already done on SMMs.62 Our low temperature STM investigation suggests that VO(dpm)2 could be also a good candidate to investigate quantum coherence at the single molecule level thanks to the recently developed approach based on spin-polarized scanning tunnelling microscopy, employed at very low temperature on single Fe atoms deposited on a MgO surface.63
Combining the optimization of T2 in nuclear spin free environments with the possibility to control the spin–lattice relaxation through a rational synthetic design is foreseen to boost the interest for molecular spin systems as potential qubits.
Acknowledgements
The support of ERC through AdG MolNanoMaS (267746), of Italian MIUR through the project Futuro in Ricerca 2012 (RBFR12RPD1) and of Fondazione Ente Cassa di Risparmio di Firenze is acknowledged. Brunetto Cortigiani and Dr Shengwei Shi are acknowledged for the assistance in the XPS characterization. This paper is dedicated to Prof. Dante Gatteschi on the occasion of his retirement.Notes and references
- R. P. Feynman, Found. Phys., 1986, 16, 507–531 CrossRef.
- P. W. Shor, 35th Annual Symposium on Foundations of Computer Science, 1994 Search PubMed.
- A. M. Steane, Rep. Prog. Phys., 1998, 61, 117–173 CrossRef CAS.
- D. Deutsch, Proc. R. Soc. London, Ser. A, 1985, 400, 97–117 CrossRef.
- P. Ball, Nature, 2011, 474, 272–274 CrossRef CAS PubMed.
- T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O'Brien, Nature, 2010, 464, 45–53 CrossRef CAS PubMed.
- R. Blatt and D. Wineland, Nature, 2008, 453, 1008–1015 CrossRef CAS PubMed.
- R. Hanson and D. D. Awschalom, Nature, 2008, 453, 1043–1049 CrossRef CAS PubMed.
- J. T. Muhonen, J. P. Dehollain, A. Laucht, F. E. Hudson, R. Kalra, T. Sekiguchi, K. M. Itoh, D. N. Jamieson, J. C. McCallum, A. S. Dzurak and A. Morello, Nat. Nanotechnol., 2014, 9, 986–991 CrossRef CAS PubMed.
- E. Knill, R. Laflamme and G. J. Milburn, Nature, 2001, 409, 46–52 CrossRef CAS PubMed.
- J. Clarke and F. K. Wilhelm, Nature, 2008, 453, 1031–1042 CrossRef CAS PubMed.
- I. L. Chuang, L. M. K. Vandersypen, X. Zhou, D. W. Leung and S. Lloyd, Nature, 1998, 393, 143–146 CrossRef CAS.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138 CrossRef CAS PubMed.
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, F. A. Zwanenburg, D. N. Jamieson, A. S. Dzurak and A. Morello, Nature, 2013, 496, 334–338 CrossRef CAS PubMed.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119–3129 RSC.
- G. Aromi, D. Aguila, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- A. Morello, J. J. Pla, F. A. Zwanenburg, K. W. Chan, K. Y. Tan, H. Huebl, M. Mottonen, C. D. Nugroho, C. Yang, J. A. van Donkelaar, A. D. C. Alves, D. N. Jamieson, C. C. Escott, L. C. L. Hollenberg, R. G. Clark and A. S. Dzurak, Nature, 2010, 467, 687–691 CrossRef CAS PubMed.
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, D. N. Jamieson, A. S. Dzurak and A. Morello, Nature, 2012, 489, 541–545 CrossRef CAS PubMed.
- K. Sato, S. Nakazawa, R. Rahimi, T. Ise, S. Nishida, T. Yoshino, N. Mori, K. Toyota, D. Shiomi, Y. Yakiyama, Y. Morita, M. Kitagawa, K. Nakasuji, M. Nakahara, H. Hara, P. Carl, P. Hofer and T. Takui, J. Mater. Chem., 2009, 19, 3739–3754 RSC.
- S. Takahashi, R. Hanson, J. van Tol, M. S. Sherwin and D. D. Awschalom, Phys. Rev. Lett., 2008, 101, 047601 CrossRef PubMed.
- G. Balasubramanian, P. Neumann, D. Twitchen, M. Markham, R. Kolesov, N. Mizuochi, J. Isoya, J. Achard, J. Beck, J. Tissler, V. Jacques, P. R. Hemmer, F. Jelezko and J. Wrachtrup, Nat. Mater., 2009, 8, 383–387 CrossRef CAS PubMed.
- A. M. Tyryshkin, S. Tojo, J. J. L. Morton, H. Riemann, N. V. Abrosimov, P. Becker, H.-J. Pohl, T. Schenkel, M. L. W. Thewalt, K. M. Itoh and S. A. Lyon, Nat. Mater., 2011, 11, 143–147 CrossRef PubMed.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- A. Collauto, M. Mannini, L. Sorace, A. Barbon, M. Brustolon and D. Gatteschi, J. Mater. Chem., 2012, 22, 22272–22281 RSC.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844 CrossRef CAS PubMed.
- M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488 CrossRef CAS.
- C. Schlegel, J. van Slageren, M. Manoli, E. K. Brechin and M. Dressel, Phys. Rev. Lett., 2008, 101, 147203 CrossRef CAS PubMed.
- M. A. K. Ahmed, H. Fjellvåg, A. Kjekshus and B. Klewe, Z. Anorg. Allg. Chem., 2004, 630, 2311–2318 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, Oxford, UK, 2006 Search PubMed.
- K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437–458 CrossRef CAS.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Dover, New York, 1986 Search PubMed.
- A. C. de Vroomen, E. E. Lijphart and N. J. Poulis, Physica, 1970, 47, 458–484 CrossRef CAS.
- H. A. Kramers, Proc. Acad. Sci. Amsterdam, 1930, 33, 959 CAS.
- J. Soeteman, L. Bevaart and A. J. van Duyneveldt, Physica, 1974, 74, 126–134 CrossRef CAS.
- J. H. van Vleck, Phys. Rev., 1940, 57, 426–447 CrossRef CAS.
- J. Soeteman, A. J. van Duyneveldt, C. L. M. Pouw and W. Breur, Physica, 1973, 66, 63–69 CrossRef CAS.
- N. B. Morozova, A. E. Turgambaeva, I. A. Baidina, V. V. Krysyuk and I. K. Igumenov, J. Struct. Chem., 2005, 46, 1047–1051 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- A. J. Fielding, D. B. Back, M. Engler, B. Baruah, D. C. Crans, G. R. Eaton and S. S. Eaton, ACS Symp. Ser., 2007, 974, 364–375 CrossRef CAS.
- J. P. Fackler, J. D. Levy and J. A. Smith, J. Am. Chem. Soc., 1972, 94, 2436–2445 CrossRef CAS.
- G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 136, 63–68 CrossRef CAS PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition, Cambridge University Press, 2011 Search PubMed.
- A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, 2001 Search PubMed.
- S. R. Hartmann and E. L. Hahn, Phys. Rev., 1962, 128, 2042–2053 CrossRef CAS.
- I. Cimatti, S. Ninova, V. Lanzilotto, L. Malavolti, L. Rigamonti, B. Cortigiani, M. Mannini, E. Magnano, F. Bondino, F. Totti, A. Cornia and R. Sessoli, Beilstein J. Nanotechnol., 2014, 5, 2139–2148 CrossRef CAS PubMed.
- L. Malavolti, V. Lanzilotto, S. Ninova, L. Poggini, I. Cimatti, B. Cortigiani, L. Margheriti, D. Chiappe, E. Otero, P. Sainctavit, F. Totti, A. Cornia, M. Mannini and R. Sessoli, Nano Lett., 2015, 15, 535–541 CrossRef CAS PubMed.
- K. Eguchi, Y. Takagi, T. Nakagawa and T. Yokoyama, J. Phys. Chem. C, 2013, 117, 22843–22851 CAS.
- K. Eguchi, T. Nakagawa, Y. Takagi and T. Yokoyama, J. Phys. Chem. C, 2015, 119, 9805–9815 CAS.
- S. Stepanow, A. Mugarza, G. Ceballos, P. Moras, J. C. Cezar, C. Carbone and P. Gambardella, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014405 CrossRef.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300 Search PubMed.
- R. M. Rakhmatullin, I. N. Kurkin, G. V. Mamin, S. B. Orlinskii, M. R. Gafurov, E. I. Baibekov, B. Z. Malkin, S. Gambarelli, S. Bertaina and B. Barbara, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 172408 CrossRef.
- J.-L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1996, 119, 240–246 CrossRef CAS.
- G. Wolfowicz, A. M. Tyryshkin, R. E. George, H. Riemann, N. V. Abrosimov, P. Becker, H.-J. Pohl, M. L. W. Thewalt, S. A. Lyon and J. J. L. Morton, Nat. Nanotechnol., 2013, 8, 561–564 CrossRef CAS PubMed.
- C. Pariya, C. R. Sparrow, C.-K. Back, G. Sandí, F. R. Fronczek and A. W. Maverick, Angew. Chem., Int. Ed., 2007, 46, 6305–6308 CrossRef CAS PubMed.
- J. K. Clegg, F. Li, K. A. Jolliffe, L. F. Lindoy, G. V. Meehan, S. Parsons, P. A. Tasker and F. J. White, Dalton Trans., 2013, 42, 14315–14323 RSC.
- L. A. Barrios, D. Aguilà, O. Roubeau, P. Gamez, J. Ribas-Ariño, S. J. Teat and G. Aromí, Chem.–Eur. J., 2009, 15, 11235–11243 CrossRef CAS PubMed.
- D. Aguila, L. A. Barrios, V. Velasco, O. Roubeau, A. Repolles, P. J. Alonso, J. Sese, S. J. Teat, F. Luis and G. Aromi, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef CAS PubMed.
- E. Bellido, P. Gonzalez-Monje, A. Repollés, M. Jenkins, J. Sesé, D. Drung, T. Schurig, K. Awaga, F. Luis and D. Ruiz-Molina, Nanoscale, 2013, 5, 12565–12573 RSC.
- S. Baumann, W. Paul, T. Choi, C. P. Lutz, A. Ardavan and A. J. Heinrich, Science, 2015, 350, 417–420 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental section and methods. Additional characterization including: AC susceptibility data (Fig. S1–S5); CW- and pulsed EPR results (Fig. S6–S11); STM and XPS of the UHV deposition (Fig. S12–S14); calculated field dependence of the eigenvectors composition (Fig. S15). See DOI: 10.1039/c5sc04295j |
| This journal is © The Royal Society of Chemistry 2016 |