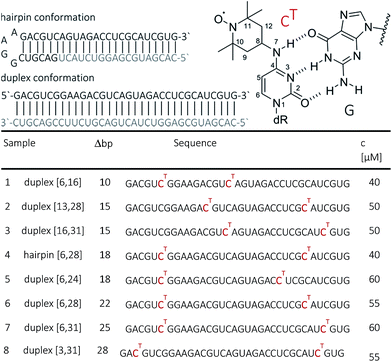
Open Access Article
Open Access ArticleHigh-resolution measurement of long-range distances in RNA: pulse EPR spectroscopy with TEMPO-labeled nucleotides†
Karin
Halbmair
a,
Jan
Seikowski
a,
Igor
Tkach
a,
Claudia
Höbartner
*ab,
Deniz
Sezer
*c and
Marina
Bennati
*ab
aMax Planck Institute for Biophysical Chemistry, 37077 Göttingen, Germany. E-mail: marina.bennati@mpibpc.mpg.de
bDepartment of Organic and Biomolecular Chemistry, University of Göttingen, 37077 Göttingen, Germany
cFaculty of Engineering and Natural Sciences, Sabanci University, 34956 Istanbul, Turkey. E-mail: dsezer@sabanciuniv.edu
First published on 3rd February 2016
Abstract
Structural information at atomic resolution of biomolecular assemblies, such as RNA and RNA protein complexes, is fundamental to comprehend biological function. Modern spectroscopic methods offer exceptional opportunities in this direction. Here we present the capability of pulse EPR to report high-resolution long-range distances in RNAs by means of a recently developed spin labeled nucleotide, which carries the TEMPO group directly attached to the nucleobase and preserves Watson–Crick base-pairing. In a representative RNA duplex with spin-label separations up to 28 base pairs (≈8 nm) we demonstrate that the label allows for a model-free conversion of inter-spin distances into base-pair separation (Δbp) if broad-band pulse excitation at Q band frequencies (34 GHz) is applied. The observed distance distribution increases from ±0.2 nm for Δbp = 10 to only ±0.5 nm for Δbp = 28, consistent with only small deviations from the “ideal” A-form RNA structure. Molecular dynamics (MD) simulations conducted at 20 °C show restricted conformational freedom of the label. MD-generated structural deviations from an “ideal” A-RNA geometry help disentangle the contributions of local flexibility of the label and its neighboring nucleobases and global deformations of the RNA double helix to the experimental distance distributions. The study demonstrates that our simple but strategic spin labeling procedure can access detailed structural information on RNAs at atomic resolution over distances that match the size of macromolecular RNA complexes.
1. Introduction
RNAs have a central role in life being involved in transmission and regulation of genetic information. Besides these classical roles, many additional regulatory and catalytic functions have been recently discovered that depend not only on the tertiary structure but also on its capability to adopt multiple conformational states.1–3 Examples of such functional RNAs include riboswitches that regulate gene expression in response to changes in metabolite concentrations and can be coupled to ribozymes.4 Other non-coding RNAs, such as miRNAs, are also actively involved in regulating gene expression in health and disease,5 and post-transcriptional RNA modifications are currently attracting significant interest for their ability to modulate RNA structures and metabolism.6,7 Thus, detailed investigations of RNA folding and its manipulation upon modification or protein binding are needed to elucidate unknown details about RNA in macromolecular complexes. Spectroscopy and biophysical methods can address the inherent structural flexibility and dynamics in solution state.8 Efficient approaches for solution structure determination of biomolecules and particularly RNAs have been developed based on NMR spectroscopy9 and also in conjunction with small-angle X-ray scattering (SAXS).10 NMR offers the great advantage of atomistic or residue-resolution and permits investigation of dynamic properties in the liquid state, however it is limited by the size (<50 kDa) of the biomolecular complexes. Fluorescence spectroscopy allows investigations in liquid solution on the sub-picosecond time scales with single molecule sensitivity.11 Among the fluorescence-based methods, Förster resonance energy transfer (FRET)12,13 reports on distances between two attached chromophores up to 10 nm but resolution and analysis are aggravated by the size and flexibility of the fluorophores.Pulsed EPR spectroscopy has developed as a powerful method for detection of long-range distances in the 1–10 nm length scale in frozen solution of diluted biomolecules.14–16 The technique, called PELDOR17 (pulse electron–electron double resonance) or DEER,18,19 detects weak dipolar couplings between two paramagnetic species, which can be endogenous20,21 or site-specifically attached to bio-macromolecules via spin labelling techniques.22 Sensitivity and resolution of PELDOR/DEER are both independent of the size of the macromolecular complex. Multiple conformations can be easily detected and disentangled based on their different dipolar frequencies. Therefore the technique delivers structural information often not amenable by other widespread methods.
Several examples for the application of PELDOR/DEER in studies of RNAs have been reported.23–25 RNA secondary structures have been investigated in a hammerhead ribozyme26 as well as in aptamers.27,28 More recently the structure of a 70 kDa protein-RNA complex has been elucidated using an EPR-aided approach that combines distance constraints from EPR as well as NMR.29,30 Another study detected the annealing of a mini-TAR DNA stem loop with the complementary TAR RNA.31 Nevertheless, the availability of spin-labeled RNA and the properties of the spin label itself still pose the major restrictions for the resolution and the application of this powerful technique. Specifically, the label flexibility determines the attainable resolution in distance distributions.32 Labelling procedures for RNA, in which nitroxide radicals are attached either at the ribose,33 the phosphate backbone34,35 or the nucleobase36–38 have been proposed; but the majority employs multi-atom linkers with several degrees of rotational freedom. Rigid nitroxide spin labels conjugated to the nucleobase or to nucleobase analogues have been reported for DNA39 and for RNA.40 Specifically, the so-called Çm label displays excellent performance in combination with orientation studies, as demonstrated by Prisner and coworkers for DNA41 and subsequently by our group for RNA.42,43 However, rigid spin labels have so far only been developed for cytidine, and the building blocks for solid-phase synthesis are not commercially available. Thus, general application and widespread use might be limited.
Some time ago we have introduced TEMPO-based spin labelling for RNA by postsynthetic modification.44 Using convertible nucleosides, the TEMPO group is attached to the exocyclic nucleobase amino groups of cytidines, adenosines and guanosines, resulting in labeled nucleotides denoted CT, AT or GT. We have demonstrated that the label in conjunction with PELDOR/DEER experiments at X-band (9 GHz) frequencies well reports on different secondary structures of RNAs such as duplexes, quadruplexes and hairpins.44 In the present study we take advantage of some recent advances in pulse EPR instrumentation, i.e. the capability to perform PELDOR/DEER at Q-band (34 GHz) frequencies with high microwave power (170 W), to extend the previous study and examine increasingly longer distances in RNAs. For this goal, a longer RNA strand with 34 nucleotides, which contained CT labels at various positions, was synthesized. The RNA strand was annealed to fully or partially complementary sequences to form either a duplex or an extended bi-molecular hairpin secondary structure, resulting in increasing separation between CT-labeled base pairs in a restricted double helical environment. The high sensitivity of the new, commercial, experimental set up combined with the properties of the label has permitted us to measure inter-spin distances up to 8 nm with unprecedented resolution (Δr ≤ 0.5 nm) for RNA concentrations as low as about 50 μM without specific sample requirement except for the use of a 20–50% D8-glycerol/D2O matrix. MD simulations were employed to rationalize the observed high resolution in distance determination with the CT label.
2. Methods
2.1 RNA synthesis and characterisation
RNA strands of 34 nucleotides (nt) were prepared by solid-phase synthesis using O4-chlorophenyl uridine and labeled with TEMPO-NH2 as described previously.44 In this way, seven 34 nt long RNAs were prepared with different combinations of CT site-specifically introduced at nt 3, 6, 13, 16, 24, 28 or 31. All RNAs were purified by PAGE and/or anion exchange HPLC under denaturating conditions, and the quality of the isolated RNAs was examined by analytical HPLC and ESI-MS. HPLC traces of oligonucleotides are provided in the ESI (SI1†). The CT-labeled 34-bp RNA duplexes were also analyzed by thermal melting. Only a minor effect of the spin labels, i.e. reduction of the melting temperatures by ca. 2 °C (at generally high melting temperatures ca. 89 °C) has been observed.Samples for EPR spectroscopy were prepared by annealing of spin-labeled RNA strands with 1.5 equivalents of the 34 nt complementary strand to form the duplex samples, or with 1.5 equiv. of the 18 nt long RNA complementary to the 3′-part of the spin-labeled RNA to form a hairpin containing a GGAA tetra loop and a nicked extended stem. Annealing was performed in 10 mM potassium phosphate/D2o buffer pH 7.0, containing 150 mM NaCl. Labelling efficiency was determined by CW-EPR spectroscopy between 80 and 100% (ESI1†). Samples for PELDOR/DEER were supplemented with 20–50% glycerol to a final concentration of spin-labeled RNA between 40 and 60 μM (Fig. 1). To increase the transverse relaxation time, samples with long inter spin distances (r ≥ 5 nm) contained D8-glycerol.
2.2 PELDOR/DEER experiments
EPR distance measurements were performed using a commercial Bruker ElexSys E580 pulse X/Q-band spectrometer equipped initially with a 3 W Q-band solid state amplifier and later on with a pulsed 170 W Q-band TWT-amplifier (Model 187Ka, Applied Systems Engineering Inc.). For the low-power measurements, the standard Q-band Bruker resonator (EN5107D2) was employed. This resonator under strong overcoupling condition had a typical bandwidth of around 100 MHz. The characteristic π pulse length in the centre of the tuning dip was 48 ns. The achievable frequency separation Δν between pump and detection pulses in the PELDOR/DEER sequence, without a critical loss of sensitivity, was about 50 MHz.With the high-power set up the overcoupled EN5107D2 Bruker resonator delivered a typical π pulse length of 12 ns at the centre of the dip. To increase the signal sensitivity for long distances, the Bruker ER5107QT-II resonator was employed. This resonator in combination with the high-power setup allows for measurements on larger sample volumes (3 mm O.D. vs. 2 mm O.D. in the standard Q-band resonator).
All PELDOR/DEER experiments were performed at 50 K using the four-pulse DEER sequence.18 Usually the pumping frequency was set in the resonator dip centre and the detection frequency at a shift of either 50 or 90 MHz for the low- (3 W) and the high-power (170 W) setups, respectively. The lengths of the detection pulses were adjusted to 56 and 24 ns respectively. Time-delay between the first two pulses in the sequence was set to 400 ns. The dipolar evolution time T (spacing between second and third detection pulses) was set between 3.5 and 18 μs, such as it provided at least 2.5 periods of oscillations for distances of up to 5 nm. The last 100 ns of the traces usually contained artifacts from the pump pulse entering the third detection pulse and were not considered. Typical acquisition time varied in the range from ∼10 h up to ∼24 h. For data analysis, dipolar traces were background corrected using a second order polynomial function. Distance distributions were obtained with the program DEERAnalysis, which uses a fitting procedure based on Tikhonov regularization.45
2.3 Atomistic modeling and MD simulations
CHARMM-compatible force field parameters of the nitroxide TEMPO have been developed previously.46 The energetics of isomerization of TEMPO around the two rotatable bonds connecting it to the cytosine base was examined by performing ab initio calculations on the CT molecular fragment shown in Fig. 1 (top right corner, dR = CH3). The two dihedral angles (C8–N7 and C4–N7) were scanned on a grid of 24 × 24 points (angular increments of 15°) by fixing the angles at the specified values and minimizing the rest of the structure. All ab initio calculations were performed with the package Gaussian47 using B3LYP/6-31G(d) as a level of theory and basis set. The obtained ab initio energy surface was implemented into the CHARMM force field as CMAP.48 The coordinates of a 34-bp A-RNA helix having raise and twist of, respectively, 2.81 Å and 32.7° were generated using the w3dna server.49 This structure, which served as our “ideal” A-form RNA reference, formed the template for two separate constructs, each one simultaneously containing three CT labels. The spin labels were placed at positions 6, 16 and 28 in the first construct, and at positions 6, 16 and 31 in the second. As a result, the first construct mimics samples 1 and 6 (Fig. 1), whereas the second construct mimics samples 1, 3 and 7. The resulting spin-labeled A-RNA structures were immersed in a volume containing 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 waters as well as 130 Na+ and 64 Cl− ions. The ion numbers were chosen to ensure the charge neutrality of the entire solvated RNA system and lead to a salt concentration of approx. 100 mM. MD simulations were performed with the package NAMD50 using the CHARMM36 force field for nucleic acids51 including the recent modification for RNA.52 After gradual equilibration of the two independent systems (6-16-28 and 6-16-31), production runs were carried out for 35 ns with a target temperature of 293 K and pressure of 1 atm. The first 1 ns was not included in the analysis reported in the next section.
000 waters as well as 130 Na+ and 64 Cl− ions. The ion numbers were chosen to ensure the charge neutrality of the entire solvated RNA system and lead to a salt concentration of approx. 100 mM. MD simulations were performed with the package NAMD50 using the CHARMM36 force field for nucleic acids51 including the recent modification for RNA.52 After gradual equilibration of the two independent systems (6-16-28 and 6-16-31), production runs were carried out for 35 ns with a target temperature of 293 K and pressure of 1 atm. The first 1 ns was not included in the analysis reported in the next section.
3. Results and discussion
3.1. Q-band PELDOR/DEER with CT labels: comparison of selective versus broadband excitation
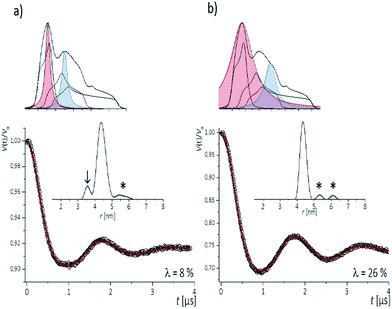
To examine the performance of the DEER experiment at Q-band frequency in conjunction with the CT labels, we have carried out measurements on samples 1–4 under various conditions of pulse excitation band widths as well as excitation positions in the EPR line. As an example, Fig. 2 represents the 34 GHz echo-detected EPR spectra of the CT labels in sample 2. A simulation with EasySpin53 displays the contribution of the individual hyperfine lines, with the mI = +1 hyperfine line resulting in the smallest anisotropy. Therefore, for a most complete spectral excitation the pump pulse was set on the maximum of this line, as also proposed by others,54–56 and detection was performed at a higher field position.The four pulse PELDOR/DEER traces for detection as close as possible to the pump frequency (i.e. optimal S/N but minimal spectral overlap of the pulses) are reported in Fig. 2. The modulation depths are consistent with narrow and wider excitation bandwidths (λ ≤ 0.1 at low power vs. λ ≤ 0.3 at higher power). The trace recorded with selective pulses reflects frequency components due to orientation selection,42 which are also visible when increasing the frequency separation Δν (Fig. S2†). The effect is best recognized in the Fourier transformations of the traces, which show slightly distorted dipolar Pake patterns (Fig. S2†). Variation of the pump and detection positions does not alleviate this effect (Fig. S2†). If this procedure is not performed and individual traces are fit with DeerAnyalysis, which does not account for orientational selectivity, some distortions appear in the distance distribution (marked by the arrow in Fig. 2a). In contrast, the DEER traces recorded with a broadband excitation scheme do not show orientation selection if the pump pulse is kept on the global EPR absorption maximum and the detection frequency at a separation within 90–110 MHz (Fig. S2†). The maximum modulation depth was obtained for Δν ≈ 90 MHz, Fig. 2a. In this case, also the program DEERAnalysis well reproduces the dipolar oscillation with only one frequency contribution and a narrow (Δr = ±0.2 nm) distribution width. Absence of the orientation selection for the broad-band excitation was also confirmed by direct simulations of the time traces (Fig. S2a and b†) that took into account the theoretically predicted (Section 3.3) label conformations. The same result was observed for three other samples with spin labels at other positions in the sequence (Fig. S3†).
The results indicate that the CT labels have restricted conformational freedom, which produces weak orientation selection in Q-band PELDOR/DEER traces if these are recorded with selective pulses. However, broadband excitation can remove the orientation selection and leads to reliable distances. In this case, the restriction of the label due to the zero-length linker to the nucleobase and the tight accommodation in the major groove turns out to be a great advantage as it provides narrow distance distributions. This is of particular interest for detection of longer distances, as demonstrated below.
3.2 Long-range distance measurements
To inspect the capability of the CT label to report on a wide range of distances, PELDOR/DEER experiments were performed on a 34 bp RNA duplex with labels separated by 10 up to 28 bp (Fig. 1). Fig. 3 summarizes the experimental traces and the obtained distance distributions. All traces were recorded with broadband excitation (Fig. 2b) to suppress orientation selection. As compared to our previous experiments at X-band with the CT label,44 the 34 bp RNA sample labelled at [6,16] (1) delivers a trace with a considerable enhancement (≥10) in S/N ratio as expected for the frequency dependence of PELDOR/DEER performance under comparable experimental conditions.54 Analysis of the trace reveals that the asymmetric distance distributions observed at X-band becomes now symmetric with a single Gaussian peak, and ESEEM effects disappear.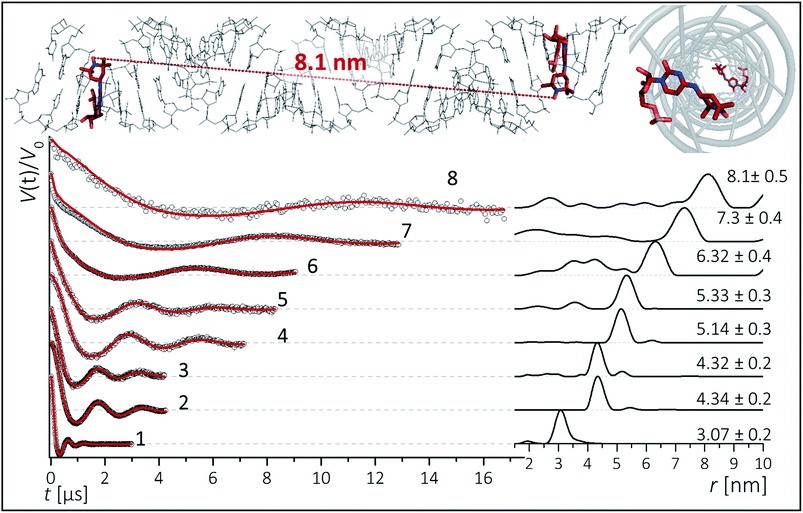 | ||
| Fig. 3 Background corrected Q-band DEER traces (dots) of the 34 bp RNA duplex and hairpin, samples 1–8. Red lines are fits using Deer Analysis. Distance distributions are shown in inset. Experimental conditions: samples 1–6: Δν = 90 MHz, t(π, pump) = 12 ns (π, detect) = 24 ns; 7: Δν = 90 MHz, t(π, pump) = 16 ns (π, detect) = 24 ns. 8: Δν = −90 MHz, t(π, pump) = 26 ns (π, detect) = 16 ns. Modulation depths are normalized and were between 0.3 and 0.2 for samples 1–7 and 0.1 for sample 8. Upper inset: schematic structure of the 34 bp RNA (standard A-form) constructed with PyMOL and illustrating the orientation of the CT labels toward inside of the duplex (side and top views). Labels inserted with dihedral angles of ϕ1 = 77° (C4, N7, C8, C9) and ϕ2 = 11° (C5, C4, N7, C8) (conformation 2, Fig. 5). | ||
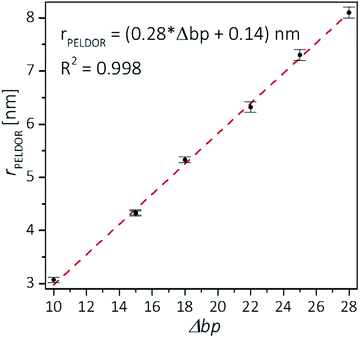
Nevertheless, the previously observed distance between 10 bp in a [6,16] labeled 20 bp RNA duplex and its distribution (r = 3.1 nm Δr = ±0.2 nm, Δr defined here as half width at half height) are reproduced.
In samples 2 and 3 the nitroxides are located 15 bp apart, but the CT nucleotides reside in a different sequence environment, i.e. CT is flanked by different neighboring nucleotides. In both cases a clear oscillation resulted in a single, one-peak inter spin distance of 4.3 nm with Δr = 0.2 nm. Also for the hairpin 4 and duplex 5 we were able to observe sharp oscillations from distances on the order of 5 nm with again very narrow distance distributions Δr = ±0.3 nm. We note that the narrow distribution at these lengths permits to resolve a difference in the oscillation frequency of 4 and 5, which results in 1.9 Å shift in the peak distance. Longer representative traces were also recorded for samples 2 and 5 (Fig. S4†) and the analysis confirmed the distance distribution.
For samples 6–8 only one and a half full oscillation period could be detected, given the low oscillation frequency. Analysis of the traces gives a clear main peak, however the uncertainty in the main distance and its distribution slightly increase due to a more difficult background subtraction. We have illustrated in ESI3† that this leads to an uncertainty of approx. ±0.1 nm in the peak distance and to Δr ≤ ±0.5 nm. In the same samples (6–8), we also observed contributions of short distances that were concentration dependent and pointed to aggregates arising from end-to-end stacking of the helices (Fig. S6†).
The observed distances and distributions are summarized in Table 1. The distances show remarkable agreement with the distances between the two nitroxides extracted from a simple molecular model (PyMOL, Delano Scientific LLC) of the ideal A-form RNA49 using the spin label conformation 2 from the ab initio calculations (i.e. ϕ1 = 77°, ϕ2 = 11°) (Section 3.3).
| Sample | Δbp | Distances [nm] | |||||
|---|---|---|---|---|---|---|---|
| PELDOR | Model A-RNA | MD | |||||
| r | Δr | r | r | Δr | |||
| a Hairpin distance was extracted from a model that contained only the double-stranded helix part of the hairpin, without the loop. | |||||||
| 1 | [6,16]duplex | 10 | 3.07 | 0.2 | 2.82 | 2.80 | 0.17 |
| 2 | [13,28]duplex | 15 | 4.34 | 0.2 | 4.28 | ||
| 3 | [16,31]duplex | 15 | 4.32 | 0.2 | 4.28 | 4.27 | 0.22 |
| 4 | [6,28]hairpin | 18 | 5.14 | 0.3 | 5.11a | ||
| 5 | [6,24]duplex | 18 | 5.33 | 0.3 | 5.11 | ||
| 6 | [6,28]duplex | 22 | 6.32 | 0.4 | 6.19 | 6.07 | 0.25 |
| 7 | [6,31]duplex | 25 | 7.3 | 0.4 | 7.06 | 6.98 | 0.29 |
| 8 | [3,31]duplex | 28 | 8.1 | 0.5 | 7.91 | ||
Plotting the experimental inter-spin distances against the corresponding base-pair separation Δbp leads to a linear dependence (R2 = 0.998) with a rise of 0.28 nm per bp step, which is in agreement with the crystallographic value for A-RNA.49,57 The striking correlation between inter spin distances and the length increment per Δbp is an intrinsic favorable property of the CT label, which sits in the major RNA grove with the NO group residing very close to the symmetry axis of the double helix (Fig. 3, top right corner). Therefore, the relationship in Fig. 4 can be used as a ruler to directly convert measured inter-spin distances to bp separations in RNA duplexes of this length scale without requirement of molecular modeling.
Our observations of narrow distributions are consistent with previous results by Piton et al. who reported distances up to 4 nm on RNA duplexes labeled with the rigid TPA.37 Nevertheless, in their case the distribution was dependent on the label environment, varying between about Δr = ±0.1 and ±0.4 nm. Instead, our results with CT indicate that differences in stacking interactions with upstream or downstream nucleotides play only a minor role in maintaining the conformational preference for the TEMPO substituent in the major groove of the A-form RNA duplex. By comparing our results with distance measurements on RNAs with flexible labels, the CT label offers the substantial advantage of a model-free distance interpretation. In contrast, the popular nucleic acid label R5, which is attached to a thiophosphate group, was reported to lead to more complex distance distributions.58 Molecular modeling, aiming at identifying all accessible conformations of R5 around its three rotatable bonds by taking into account possible clashes with the RNA backbone, is required for the interpretation of the measured frequencies.25 A similar issue is encountered with the spin label attached to 4-thiouridine, where the linker consists of five rotatable bonds and Watson–Crick base-pairing is not preserved.29,36
Although the widths of the obtained distance distributions increase progressively with increasing separation between the spin labels, overall they remain quite narrow in the examined range up to 8 nm (Table 1). This finding is not necessarily expected, as previous PELDOR measurements on B-DNA labeled with rigid Çm spin labels41 showed conformational distribution on the order of ±0.4 nm already for distances around 4 nm. The larger distribution in dsDNA might be due to the fact that the Çm in DNA is more off the helix axis and is therefore more sensitive to the dynamics of the DNA. SAXS data59 on end-to-end distances in B-DNA using gold nanoparticles reported even more pronounced distributions for increasing distances that were assigned to a cooperative DNA stretching.
The narrow distributions that we obtained raise several questions: (1) why does the spin label CT, which connects to cytosine via two rotatable bonds, lead to narrow distributions? (2) Do the observed narrow distance distributions contain information about the global deformations of the RNA helix? If yes, what types of deviations from the ideal A-RNA geometry are consistent with the experimental distributions? To address these questions, we resorted to MD simulations.
3.3 Parametrization and energetics of the spin label CT
The ab initio potential energy landscape of isomerization around the bonds C8–N7 (ϕ1) and C4–N7 (ϕ2) is shown in Fig. 5. It contains four basins of low energy separated by substantial energy barriers. Each of the two broader basins contains two local minima with practically no energy barrier between them. The energies and dihedral angle values of the identified six local energy minima are given in Table S1.† Conformations numbered 4 and 5 are the global energy minima. They are about 2 kcal mol−1 more favorable than conformations 1 and 2. Energy barriers of more than 10 kcal mol−1 separate conformations 1, 2 and 3 from conformations 4, 5 and 6.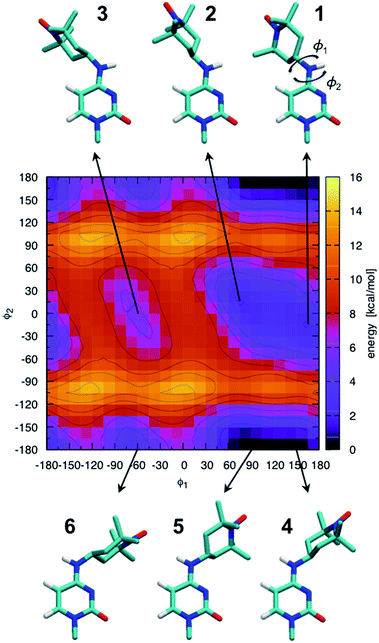 | ||
| Fig. 5 Ab initio scan of the dihedral (ϕ1–ϕ2) potential energy surface and conformations of the six local minima. Some hydrogen atoms are not shown for clarity. The energies of the numbered local minima are given in Table S1.† | ||
It should be stressed that the potential energy surface in Fig. 5 is for the isolated molecular fragment shown in the figure. The actual dihedral free energy surface is expected to be different for a spin-labeled cytosine in the context of the A-RNA double helix. Indeed, a comparison with Fig. 1 (top right corner) makes clear that the nitroxide ring in conformations 4, 5 and 6 will interfere with the Watson–Crick pairing of CT and G, compromising at least one of the hydrogen bonds that keep the two bases together. Therefore, in spite of the fact that they stand out as global energy minima, we expect that conformations 4 and 5 will not be populated when CT is part of the A-RNA double helix. With this understanding, when attaching CT to the A-RNA helices for the subsequent MD simulations, all the spin labels were constructed in conformation 2.
3.4 MD-based modeling of the distance distributions
MD simulations conducted in water at 293 K cannot be expected to faithfully reflect the ensemble of RNA structures present under the experimental PELDOR/DEER conditions (aqueous solution with 20–50% glycerol and frozen at 50 K). Due to the difference in temperature, entropic effects will be more prominent in the MD structural ensemble, whereas enthalpy will dictate the RNA conformations in the experimental ensemble.60 The situation could only be aggravated by limitations of the MD force field, which may be very serious in the case of RNA,61,62 by insufficient MD sampling, and by the inhomogeneous freezing of the sample.60We, therefore, employ MD simulations with two specific goals in mind. The first is to explore the conformational freedom of CT in a systematic way respecting the constraints imposed by the molecular structure and flexibility of its immediate surroundings. Since only the bond C8–N7 is expected to isomerize, C4–N7 being restricted by the base pairing (Fig. 1), sampling of this degree of freedom should be achieved within relatively short simulation time. The second goal is to generate random but feasible deviations of the RNA helix away from the ideal A-form.
The values visited by the two dihedral angles of CT during the simulations are shown in Fig. S7† for the RNA constructs labeled at positions 6-16-28 and 6-16-31. As expected, only conformations 2 and 1 are visited by the spin labels at all labeling sites. The similarity of the isomerization dynamics of 6CT (top) and 16CT (middle) across the two separate simulations indicates that 34 ns simulation time is sufficient to sample the conformational freedom of CT at these two label positions, as well as at the other two positions 28 and 31 (bottom). Having a fair sampling of the conformational freedom of the spin labels, we now turn to the pair-wise distances between them.
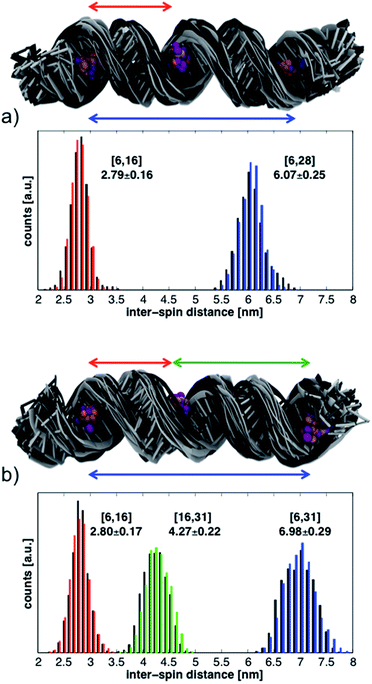
The histograms in Fig. 6 show the distributions of inter-spin distances that were extracted from the MD simulations. Histograms obtained from the first 17 ns are shown in black while those from the last 17 ns are in color. The rather small differences between the first and second half of the simulations suggest convergence in the sampling of small-amplitude structural distortions. Although the histograms could change if the duration of the MD simulations were to be extended, exhaustive sampling of the RNA conformations at 293 K is not our goal.
The conformations of the RNA helices at the end of every ns are shown above the histograms in Fig. 6. Black structures are from the first half of the simulations while lighter (gray) structures are from the second half. The structural ensembles illustrate the magnitude and nature of the deviations from the initial A-RNA that were observed in the MD simulations.
The averages of the inter-spin distances and their standard deviations calculated from the entire 34 ns are written next to the histograms in Fig. 6 and compiled in the MD columns of Table 1. Given the relatively short simulation time, it is not surprising that the average distances are close to the starting values of the ideal A-RNA helix. It is interesting, however, that for every simulated spin-label pair the spread around the average distance closely agrees with the experimental value (Table 1), suggesting that the ensemble of structures generated in the MD runs must reflect fairly well the diversity (or lack thereof) of RNA conformations present in the frozen sample.
Having gained confidence in the relevance of the MD structures, we proceed to disentangle the contributions of local and global flexibility to the observed distance distributions. Utilizing the possibility to perform unrealistic MD “experiments” we remove the global RNA motions by restraining the P and C1′ atoms around their positions in the ideal A-RNA. The resulting distance distributions from the simulations of both 6-16-28 and 6-16-31 are shown in Fig. S8.† We observe that, on the background of the restricted but thermally fluctuating RNA, the conformational freedom of CT accounts for less than ± 0.15 nm of the width of every distance distribution, independently of the label positions. The additional widths observed in the unrestrained MD simulations can, therefore, be ascribed to global deformations of the RNA helix. These are seen to increase linearly with inter-spin separation, similar to the experimental data (Table 1).
The computational analysis allows us to answer the questions that were posed at the end of Section 3.2. By making conformations 4, 5 and 6 (Fig. 5) sterically unfavorable, the Watson–Crick pairing of CT with its complementary base eliminates half of the conformational space of the spin label. Furthermore, as a part of the RNA helix, CT was observed to populate only conformations 2 and 1, both of which lead do very similar positioning of the unpaired electron spin with respect to the labeled base (Fig. S9†). The internal conformational freedom of the spin label was shown to be able to account for at most 0.15 nm of the width of the inter-spin distance distribution, indicating that the widths observed in the experiment report on global distortions of the RNA helix. The overall narrow widths, however, imply relatively small deviations about the ideal A-RNA form, which should be similar to the MD structural ensembles in Fig. 6.
4. Conclusions
We have demonstrated a simple, model-free approach to measure distances at atomic resolution in RNA by pulse EPR spectroscopy. The quality of the measurements relies on the intrinsic capabilities of the label to restrict its conformation in the major grove of duplex RNA by base pairing without requirement of a rigid linker to the backbone. Because of the small conformational contribution of the label to the observed distance distributions, determined here by MD as Δr < 0.2 nm, the method enables to resolve subtle conformational contributions of the RNA itself. Taking this into account, the reported experimental distance distributions in frozen solution give evidence for only small average deviations (Δr < 0.5 nm) of the 34 bp RNA duplex from the ideal A-RNA structure. These are on the order of, or even smaller than, the ones reported on dsDNA by other techniques on a similar length scale (up to 8 nm) such as FRET12,13 or SAXS.59 Recent μs-long MD simulations indicate that the fluctuations of the RNA helix around the A-form remain moderately small, and certainly smaller than the fluctuations of B-DNA, even at 300 K.63 Thus, the narrow distance distributions that we observe are likely an intrinsic property of RNA helices, and not an artifact of the frozen environment.Dispensing with the necessity of rigidly linking the spin label to the backbone substantially simplifies the synthetic approach and permits the use of commercially available convertible nucleosides to which the TEMPO label can be attached with high efficiency. Our labelling strategy will permit to disentangle more complex rearrangements of larger RNAs and RNA-protein interactions. The determination of a high-resolution distance ruler for RNA duplexes might have straightforward interesting applications in studies of natural systems, such as diverse types of non-coding RNAs. For example, new insights can be expected into processing of long double-stranded micro-RNA precursors (pre-miRNA), into functional short micro-RNA of 20–23 bp. Also, conformational changes upon activation of catalytic nucleic acids will be tracked by the application of a high resolution distance ruler. The combined advancements in spectroscopy and label chemistry will make even larger RNA systems accessible64 and provide unparalleled insights into macromolecular assemblies.
Acknowledgements
We would like to acknowledge Giuseppe Sicoli and Thorben Schierhorn for their initial experiments on the RNA samples. This work has been supported by the DFG Collaborative Research Centre (CRC) 803 and by the Max Planck Society.References
- A. Peselis, A. Gao and A. Serganov, Biochimie, 2015, 117, 100–109 CrossRef CAS PubMed.
- A. Serganov and E. Nudler, Cell, 2013, 152, 17–24 CrossRef CAS PubMed.
- R. R. Breaker, Cold Spring Harbor Perspect. Biol., 2012, 4, a003566 Search PubMed.
- R. R. Breaker and G. F. Joyce, Chem. Biol., 2014, 21, 1059–1065 CrossRef CAS PubMed.
- M. Ha and N. V. Kim, Nat. Rev. Mol. Cell Biol., 2014, 15, 509–524 CrossRef CAS PubMed.
- S. R. Jaffrey, Nat. Struct. Mol. Biol., 2014, 21, 945–946 CAS.
- N. Liu and T. Pan, Transl. Res., 2015, 165, 28–35 CrossRef CAS PubMed.
- D. Klostermeier and C. Hammann, RNA Structure and Folding: Biophysical Techniques and Prediction Methods, De Gruyter, 2013 Search PubMed.
- J. R. Bothe, E. N. Nikolova, C. D. Eichhorn, J. Chugh, A. L. Hansen and H. M. Al-Hashimi, Nat. Methods, 2011, 8, 919–931 CrossRef CAS PubMed.
- T. Madl, F. Gabel and M. Sattler, J. Struct. Biol., 2011, 173, 472–482 CrossRef CAS PubMed.
- S. Weisenburger, B. Jing, D. Hanni, L. Reymond, B. Schuler, A. Renn and V. Sandoghdar, ChemPhysChem, 2014, 15, 763–770 CrossRef CAS PubMed.
- S. Kalinin, T. Peulen, S. Sindbert, P. J. Rothwell, S. Berger, T. Restle, R. S. Goody, H. Gohlke and C. A. M. Seidel, Nat. Methods, 2012, 9, 1218–2223 CrossRef CAS PubMed.
- A. K. Wozniak, G. F. Schroder, H. Grubmuller, C. A. M. Seidel and F. Oesterhelt, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18337–18342 CrossRef CAS PubMed.
- G. Jeschke, Annu. Rev. Phys. Chem., 2012, 63, 419–446 CrossRef CAS PubMed.
- P. P. Borbat, J. H. Freed, M. Simon, B. Crane and A. Crane, Methods Enzymol., 2007, 423, 52–116 CAS.
- O. Schiemann and T. F. Prisner, Q. Rev. Biophys., 2007, 40, 1–53 CrossRef CAS PubMed.
- A. D. Milov, A. G. Maryasov and Y. D. Tsvetkov, Appl. Magn. Reson., 1998, 15, 107–143 CrossRef CAS.
- M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340 CrossRef CAS PubMed.
- G. Jeschke, Macromol. Rapid Commun., 2002, 23, 227–246 CrossRef CAS.
- M. Bennati, A. Weber, J. Antonic, D. L. Perlstein, J. Robblee and J. Stubbe, J. Am. Chem. Soc., 2003, 125, 14988 CrossRef CAS PubMed.
- V. P. Denysenkov, D. Biglino, W. Lubitz, T. F. Prisner and M. Bennati, Angew. Chem., Int. Ed. Engl., 2008, 47, 1224 CrossRef CAS PubMed.
- C. R. Timmel and J. R. Harmer, Structural Information from Spin Labels and Intrinsic Paramagnetic Centers in the Bioscience, Springer Verlag, 2014 Search PubMed.
- R. Ward and O. Schiemann, Struct. Bonding, 2014, 152, 249–281 CrossRef.
- T. F. Prisner, A. Marko and S. T. Sigurdsson, J. Magn. Reson., 2015, 252, 187–198 CrossRef CAS PubMed.
- N. S. Tangprasertchai, X. Zhang, Y. Ding, K. Tham, R. Rohs, I. S. Haworth and P. Z. Qin, Methods Enzymol., 2015, 564, 427–453 Search PubMed.
- N. K. Kim, M. K. Bowman and V. J. DeRose, J. Am. Chem. Soc., 2010, 132, 8882–8884 CrossRef CAS PubMed.
- D. Wunnicke, D. Strohbach, J. E. Weigand, B. Appel, E. Feresin, B. Suess, S. Muller and H. J. Steinhoff, RNA, 2011, 17, 182–188 CrossRef CAS PubMed.
- I. Krstić, O. Frolow, D. Sezer, B. Endeward, J. E. Weigand, B. Suess, J. W. Engels and T. F. Prisner, J. Am. Chem. Soc., 2010, 132, 1454–1455 CrossRef PubMed.
- O. Duss, M. Yulikov, G. Jeschke and F. H.-T. Allain, Nat. Commun., 2014, 5, 3669 CAS.
- O. Duss, E. Michel, M. Yulikov, M. Schubert, G. Jeschke and F. H. Allain, Nature, 2014, 509, 588–592 CrossRef CAS PubMed.
- Y. Sun, P. P. Borbat, V. M. Grigoryants, W. K. Myers, J. H. Freed and C. P. Scholes, Biophys. J., 2015, 108, 893–902 CrossRef CAS PubMed.
- G. Jeschke, Prog. Nucl. Magn. Reson. Spectrosc., 2013, 72, 42–60 CrossRef CAS PubMed.
- T. E. Edwards and S. T. Sigurdsson, Nat. Protoc., 2007, 2, 1954–1962 CrossRef CAS PubMed.
- Q. Cai, A. K. Kusnetzow, W. L. Hubbell, I. S. Haworth, G. P. Gacho, N. Van Eps, K. Hideg, E. J. Chambers and P. Z. Qin, Nucleic Acids Res., 2006, 34, 4722–4730 CrossRef CAS PubMed.
- P. Z. Qin, I. S. Haworth, Q. Cai, A. K. Kusnetzow, G. P. Grant, E. A. Price, G. Z. Sowa, A. Popova, B. Herreros and H. He, Nat. Protoc., 2007, 2, 2354–2365 CrossRef CAS PubMed.
- A. Ramos and G. Varani, J. Am. Chem. Soc., 1998, 120, 10992–10993 CrossRef CAS.
- N. Piton, Y. G. Mu, G. Stock, T. F. Prisner, O. Schiemann and J. W. Engels, Nucleic Acids Res., 2007, 35, 3128–3143 CrossRef CAS PubMed.
- O. Schiemann, N. Piton, J. Plackmeyer, B. E. Bode, T. F. Prisner and J. W. Engels, Nat. Protoc., 2007, 2, 904–923 CrossRef CAS PubMed.
- N. Barhate, P. Cekan, A. P. Massey and S. T. Sigurdsson, Angew. Chem., Int. Ed., 2007, 46, 2655–2658 CrossRef CAS PubMed.
- C. Hobartner, G. Sicoli, F. Wachowius, D. B. Gophane and S. T. Sigurdsson, J. Org. Chem., 2012, 77, 7749–7754 CrossRef PubMed.
- A. Marko, V. Denysenkov, D. Margraf, P. Cekan, O. Schiemann, S. T. Sigurdsson and T. F. Prisner, J. Am. Chem. Soc., 2011, 133, 13375–13379 CrossRef CAS PubMed.
- I. Tkach, S. Pornsuwan, C. Hobartner, F. Wachowius, S. T. Sigurdsson, T. Y. Baranova, U. Diederichsen, G. Sicoli and M. Bennati, Phys. Chem. Chem. Phys., 2013, 15, 3433–3437 RSC.
- I. Tkach, K. Halbmair, C. Höbartner and M. Bennati, Appl. Magn. Reson., 2014, 45, 969–979 CrossRef.
- G. Sicoli, F. Wachowius, M. Bennati and C. Hobartner, Angew. Chem., Int. Ed. Engl., 2010, 49, 6443–6447 CrossRef CAS PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
- D. Sezer, J. H. Freed and B. Roux, J. Phys. Chem. B, 2008, 112, 5755–5767 CrossRef CAS PubMed.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian Inc., Wallingford CT, 2009.
- A. D. MacKerell, M. Feig and C. L. Brooks, J. Am. Chem. Soc., 2004, 126, 698–699 CrossRef CAS PubMed.
- G. Zheng, X.-J. Lu and K. Olson, Nucleic Acids Res., 2009, 37, W240–W246 CrossRef CAS PubMed.
- J. C. Philipps, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef PubMed.
- N. Foloppe and A. D. Mackerell, J. Comput. Chem., 2000, 21, 86–104 CrossRef CAS.
- E. J. Denning, U. D. Priyakumar, L. Nilsson and A. D. Mackerell, J. Comput. Chem., 2011, 32, 1929–1943 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- Y. Polyhach, E. Bordignon, R. Tschaggelar, S. Gandra, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10762–10773 RSC.
- P. Hoefer, R. Heilig and D. Schmalbein, Bruker Report, 2003, 152/153, 37–43 Search PubMed.
- H. Ghimire, R. M. McCarrick, D. E. Budil and G. A. Lorigan, Biochemistry, 2009, 48, 5782–5784 CrossRef CAS PubMed.
- S. Arnott, D. W. Hukins, S. D. Dover, W. Fuller and A. R. Hodgson, J. Mol. Biol., 1973, 81, 107–122 CrossRef CAS PubMed.
- Q. Cai, A. K. Kusnetzow, K. Hideg, E. A. Price, I. S. Haworth and P. Z. Qin, Biophys. J., 2007, 93, 2110–2117 CrossRef CAS PubMed.
- R. S. Mathew-Fenn, R. Das and P. A. B. Harbury, Science, 2008, 322, 446–449 CrossRef CAS PubMed.
- B. Halle, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 4793–4798 CrossRef CAS PubMed.
- I. Yildirim, H. A. Stern, S. D. Kennedy, J. D. Tubbs and D. H. Turner, J. Chem. Theory Comput., 2010, 6, 1520–1531 CrossRef CAS PubMed.
- I. Yildirim, S. D. Kennedy, H. A. Stern, J. M. Hart, R. Kierzek and D. H. Turner, J. Chem. Theory Comput., 2011, 8, 172–181 CrossRef PubMed.
- K. Liebl, T. Drsata, F. Lankas, J. Lipfert and M. Zacharias, Nucleic Acids Res., 2015, 43, 10143–10156 Search PubMed.
- L. Büttner, J. Seikowski, K. Wawrzyniak, A. Ochmann and C. Höbartner, Bioorg. Med. Chem., 2013, 21, 6171–6180 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sc04631a |
| This journal is © The Royal Society of Chemistry 2016 |