Open Access Article
Open Access ArticleMultivalence cooperativity leading to “all-or-nothing” assembly: the case of nucleation-growth in supramolecular polymers†
Elkin
Lopez-Fontal
a,
Lilia
Milanesi
b and
Salvador
Tomas
 *a
*a
aInstitute of Structural and Molecular Biology and Department of Biological Sciences, School of Science, Birkbeck University of London, Malet Street, London WC1E 7HX, UK. E-mail: s.tomas@bbk.ac.uk
bSchool of Biological and Chemical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK
First published on 21st March 2016
Abstract
All-or-nothing molecular assembly events, essential for the efficient regulation of living systems at the molecular level, are emerging properties of complex chemical systems that are largely attributed to the cooperativity of weak interactions. The link between the self-assembly and the interactions responsible for the assembly is however often poorly defined. In this work we demonstrate how the chelate effect (multivalence cooperativity) can play a central role in the regulation of the all-or-nothing assembly of structures (supramolecular polymers here), even if the building blocks are not multivalent. We have studied the formation of double-stranded supramolecular polymers formed from Co-metalloporphyrin and bi-pyridine building blocks. Their cooperative nucleation–elongation assembly can be summarized as a thermodynamic cycle, where the monomer weakly oligomerizes linearly or weakly dimerizes laterally. But thanks to the chelate effect, the lateral dimer readily oligomerizes linearly and the oligomer readily dimerizes laterally, leading to long double stranded polymers. A model based on this simple thermodynamic cycle can be applied to the assembly of polymers with any number of strands, and allows for the determination of the length of the polymer and the all-or-nothing switching concentration from the pairwise binding constants. The model, which is consistent with the behaviour of supramolecular polymers such as microtubules and gelators, clearly shows that all-or-nothing assembly is triggered by a change in the mode of assembly, from non-multivalent to multivalent, when a critical concentration is reached. We believe this model is applicable to many molecular assembly processes, ranging from the formation of cell–cell focal adhesion points to crystallization.
Introduction
The regulation of biological systems at the molecular level requires that molecular assembly events respond efficiently to changes in the environment. This responsiveness often rests on the amplification of an input signal (for example, a change in temperature, or the presence of a particular chemical), that leads to an all-or-nothing switch between assembled and de-assembled states. The amplification of the input signal is an emerging property of the system, and can be attributed to the positive cooperativity between the intermolecular interactions involved, resulting in increased stability (above the simple addition of all the pairwise interactions) of assemblies held by multiple interactions.1,2 Cooperativity can be classified as allosteric cooperativity and chelate cooperativity, also termed multivalence cooperativity. In the first, initial binding events lead to changes in the assembled molecules (such as polarization of H-bond donors or conformational changes) that make the binding of additional molecules more efficient. In chelate cooperativity, the formation of the first interaction between two molecules pays the entropic cost of bringing the molecules together, making any subsequent interaction more stable.3–5The linear assembly of molecules leads to the formation of supramolecular polymers, which in biomolecular systems are involved in many vital cellular processes, including cell division (microtubules) or cell motion (actin filaments).6 Supramolecular polymers are also of interest for technological and biomedical applications.7,8 For example, supramolecular polymers produced by the self-assembly of small synthetic molecules have properties that are tuneable through using different components and are interesting for the development of optoelectronic devices.9–11 The crosslinking of nano-filaments leads to the formation of small molecule based gels, with applications ranging from drug delivery to tissue engineering.12–18
In supramolecular polymerization, especially for biological examples such as microtubules, assembly of the building blocks may take place in a cooperative fashion, in what is termed a nucleation–elongation mechanism. This cooperative effect can be quantified,19,20 and has been often explained in terms of allosteric cooperativity, whereby after a few molecules form the nucleus, conformational changes take place that enhance the interaction of subsequent molecules.21–24
The chelate effect, normally seen as a property of complexes formed between two molecules held together by multiple interactions, has not been attributed an explicit role in the assembly of supramolecular polymers, except for the special case of helical polymers.19,25,26 Yet, in most cases, supramolecular polymers are formed by bundles of several strands. Within such structures, the assembly can be interpreted as the combination of two molecular recognition processes: the longitudinal growth of each strand and the lateral assembly between the strands. The latter involves the simultaneous lateral interaction of many building blocks and it is therefore subject to a multivalence cooperativity effect. In other words, the nucleation step would yield a multivalent nucleus, resulting in the amplification of the polymerization process thanks to the chelate effect. Here we study the assembly of a polymer formed from two different building blocks: a cobalt metalloporphyrin and 4,4′-bipyridine. Porphyrin-containing assemblies are intrinsically interesting as they have potential applications for light-harvesting and the development of nano-wires.27–29 In the present work we take advantage of the favourable spectroscopic properties of porphyrins30,31 to carry out a detailed analysis of the role played by the chelate effect in supramolecular polymerization.
Results and discussion
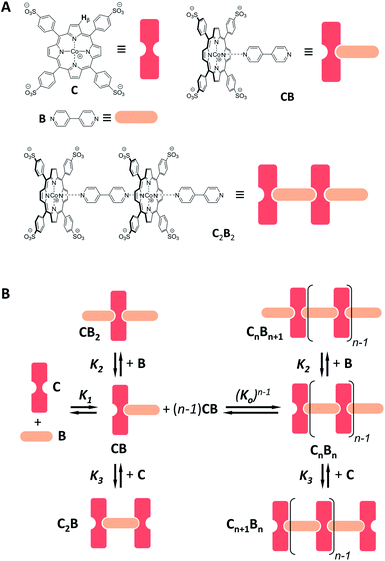
Co metalloporphyrin C was prepared through the metalation of a free-base with cobalt acetate.32 The sharp 1H-NMR signals show that the metal center in C is diamagnetic Co(III) rather than paramagnetic Co(II). The 1H-NMR spectrum of porphyrin C in aqueous buffers (sodium phosphate, 5 to 100 mM, pH 7.2) is independent of the concentration up to 3 mM in our experiments, consistent with the absence of self-aggregation in these conditions. The addition of di-valent bipyridine (B) to di-valent porphyrin C at concentrations between 25 and 200 μM leads to changes in the 1H-NMR spectrum that are consistent with the formation of small oligomeric species with alternating CB building blocks (Fig. 1). Diffusion NMR experiments, together with the changes in the 1H-NMR signal intensity with changing C/B ratios, allowed for the identification of the presence of complexes CB, CB2, C2B, C2B2 and C2B3 (Fig. 2A) (see the ESI, Fig. S1 and Table S1† for details).33K1, K2 and K3 are the stepwise binding constants for the formation of CB, CB2 and C2B, i.e.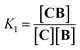 | (1) |
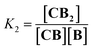 | (2) |
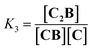 | (3) |
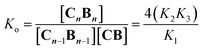 | (4) |
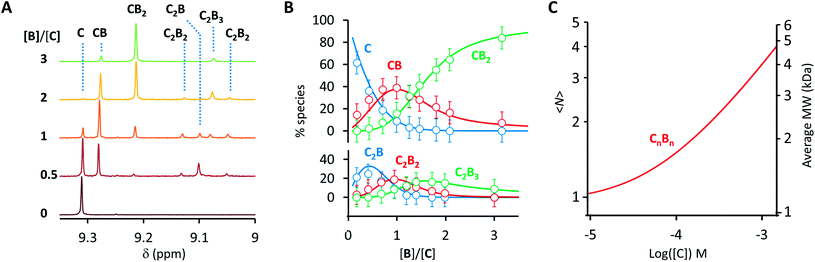 | ||
| Fig. 2 (A) Section of the 1H-NMR spectra of mixtures of B and C, showing the signal assigned to the β hydrogen of the porphyrin ring. The concentration of C is 100 μM in all cases. (B) Speciation plot showing the amount of the various CnBn species as a function of the [B]/[C] ratio determined by integration of the 1H-NMR signals (circles) and modelled using the values of K1, K2 and K3 listed in Table 1 (continuous lines). The error bars are based on the intrinsic error of the NMR integral (ca. 10%). (C) Changes in the average number of CB repeats (i.e.,〈N〉) and average molecular weight of an oligomer CnBn as a function of the total concentration of C (with [C] = [B]), estimated using the equilibria depicted in Fig. 1B and the values of K1, K2 and K3 listed in Table 1. | ||
| K 1 | K 2 | K 3 | K o | |
|---|---|---|---|---|
| a The units for the binding constants are M−1 in all cases. The quoted error is twice the standard deviation of the mean. | ||||
| UV | 1.1 × 106 ± 1.2 × 105 | 9.7 × 104 ± 1.6 × 104 | nd | nd |
| NMR | 1.1 × 106 ± 2.6 × 104 | 1.0 × 105 ± 2.0 × 104 | 2.3 × 104 ± 6.0 × 103 | 8.4 × 103 ± 3.2 × 103 |
Eqn (1)–(4) in combination with the mass balance allow for the modelling of the distribution of species observed in the NMR experiments (Fig. 2A and B). For a mixture of C and B in a 1 to 1 ratio, the length of the oligomer can be expressed by the average number of CB repeats 〈N〉, calculated as follows (see the ESI† for details):
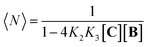 | (5) |
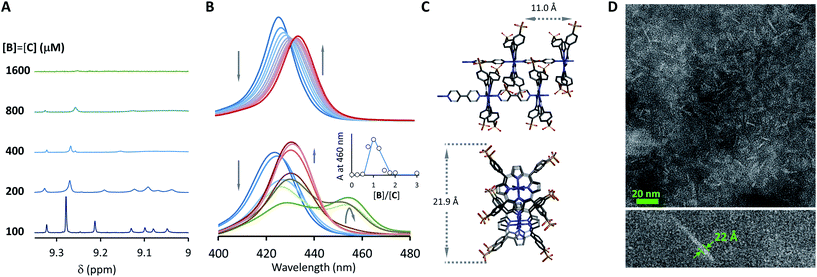 | ||
Fig. 3 Evidence of polymer dimerization. (A) Changes in the 1H NMR signal assigned to the β proton of C as the concentration of the building blocks increases. The buffer used is 5 mM sodium phosphate, pH 7.20. (B) Changes in the Soret band of the UV spectrum of C as the [B]/[C] ratio changes from 0 to 3 in phosphate buffer, 5 mM, pH 7.20. In the top panel the concentration of C was 50 μM and in the bottom panel it was 400 μM. The inset shows the changes in absorbance at 460 nm for the lower panel experiment (empty circles) and the fit to a polymer dimerization model (blue line). (C) 3D model of the dimeric form (CnBn)2 of the oligomer CnBn, based on the crystal structure reported in ref. 34 (see the ESI† for details). (D) Negative stain TEM image of a mixture of C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B in a ratio 1 to 1. The bottom section shows the zoom-in to an isolated single fibre together with the estimated width. The average thickness of the needle-like features is 22 ± 2 A (at a 95% confidence level, see the ESI† for details). B in a ratio 1 to 1. The bottom section shows the zoom-in to an isolated single fibre together with the estimated width. The average thickness of the needle-like features is 22 ± 2 A (at a 95% confidence level, see the ESI† for details). | ||
At concentrations when the 1H-NMR signals start decreasing (i.e., above 100 μM) a new, red-shifted Soret band appears in the UV spectrum (Fig. 3A and B). Red-shifted Soret bands are indicative of the formation of J-type aggregates between porphyrin rings, where the rings are stacked in a staggered fashion.34,35 A possible arrangement that could lead to a J-type aggregate is a dimer of polymers. In the dimer, porphyrin rings intercalate in the space between the two rings of a second polymer, driven by the hydrophobic effect (Fig. 3C).
A number of additional experimental results support this interpretation: (i) crystal structures of C–B complexes described in the literature show the same arrangement (Fig. 3C; see also the ESI and Fig. S3†);36 (ii) electron microscopy experiments, which show the presence of needle-like structures with a thickness that is consistent with the width of the dimeric oligomer (Fig. 3D and S4†) and (iii) the addition of salt to mixtures of C and B at low concentrations, which triggers the rise of the red-shifted band in the UV spectrum (Fig. S5†). With K1, K2 and K3 (and therefore Ko) independent of the salt concentration (see Table 1 and S2†) this behaviour is attributed to the decrease in the electrostatic repulsion between polymers bearing multiple anionic moieties at higher ionic strength, favouring their dimerization. Changes in the 1H-NMR and UV spectra when the concentration of C and B is around 1 mM can be modelled if we take into account the dimerization of the polymers, leading to the double-stranded polymers (CnBn)2, with the lateral association constant Knl (Fig. 4A)
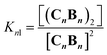 | (6) |
In each strand, the repeating unit CB can be seen as a binding site, so that dimerization of the polymer results from the binding of two multivalent single-stranded polymers. Knl can therefore be expressed as a function of 3 parameters: a lateral association constant per unit repeat (i.e., CB), Kl, the effective molarity EM, a parameter that gives a measure of the local concentration of complementary binding sites in a complex held by multiple interactions, and the number of polymer repeats n in each of the strands:
| Knl = EMn−1Kln | (7) |
For the oligomerization of C and B, the formation of three types of oligomers is taken into account (B capped, C capped and with mixed capping, see Fig. 1B). For the dimerization of the polymer we make two assumptions that considerably simplify the system (Fig. 4A): (i) only mixed capping polymers exist (i.e., with equal C and B units). This assumption is supported by the fact that, for polymers, the average C/B ratio is equal to 1. (ii) The initial concentration of complex CB, [CB]0, is dictated solely by K1. This assumption is supported by the fact that K1 is much larger than all the other association constants (Table 1). Therefore we view the polymerization process as the assembly of equal CB monomers. We call the concentration of B and C that are not involved in the formation of CB [B]x and [C]x, respectively. The polymer can be disassembled by the addition of excess B, that is, increasing [B]x (leading to CB2) or C, that is, increasing [C]x (leading to C2B), as dictated by K2 and K3, respectively (Fig. 4A). The equation that relates all the concentrations is (see the ESI† for the detailed derivation):
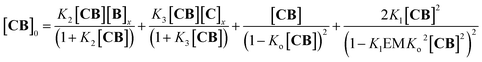 | (8) |
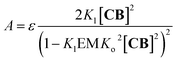 | (9) |
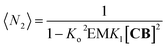 | (10) |
The changes in polymer length (and therefore molecular weight) predicted by eqn (10) are consistent with the changes in the 1H NMR spectrum, where the rapid rise in the polymer average molecular weight and the increase in the overall large polymer population leads to the line broadening observed (Fig. 3A and 4).
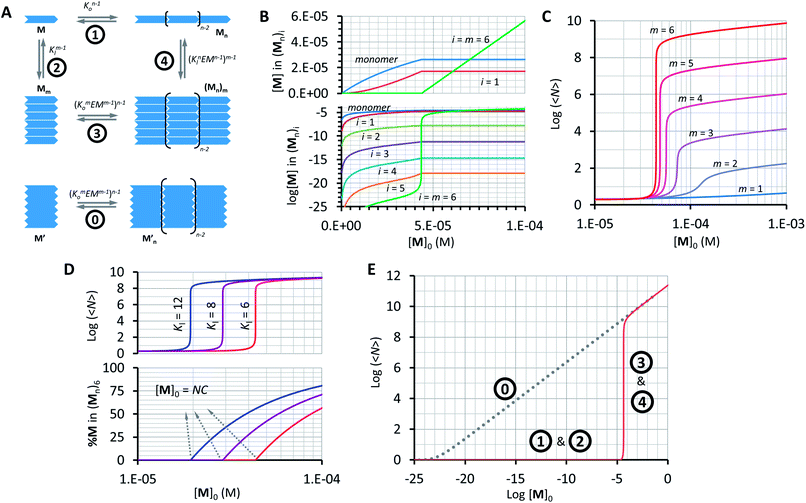
Our model, which accounts for the formation of a double-stranded polymer, can be expanded to the formation of multi-stranded polymers with m strands. Unlike the number of polymer repeats n, which can be very large, m is a discrete number. For simplicity and general applicability, we consider that the polymers are formed by the self-assembly of only one type of building block, that we call M, rather than the two components C and B. Monomer M can assemble in the longitudinal direction, forming single stranded polymers of n units Mn (Fig. 5A, equilibrium 1). The assembly is isodesmic, with the oligomerization constant Ko. The single strand Mn can interact laterally with up to another m − 1 strands to form a multi-stranded polymer of m strands (Mn)m. The lateral assembly is also isodesmic, with the lateral association constant Knl = KlnEMn−1, according to eqn (5) (Fig. 5A, equilibrium 4). We can depict an alternative mechanism for the formation of polymers with m strands (Mn)m, with M first assembling laterally with up to m − 1 molecules of M to produce the complex Mm, following an isodesmic mechanism with the stepwise lateral assembly constant Kl (Fig. 5A, equilibrium 2). The complex Mm then assembles linearly with another n − 1 Mm complexes, following an isodesmic mechanism with the stepwise oligomerization constant Kmo, which is related to Ko as follows:
| Kmo = KomEMm−1 | (11) |
In other words, M can assemble in two orthogonal directions, but the lateral assembly ends at a relatively small number for m while the longitudinal assembly is open ended (Fig. 5A). Irrespective of the route of formation of the multi-stranded polymer, the expression that relates [M]0 and [M] for a polymer composed of a bundle of m strands can be written as:
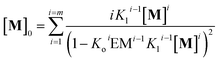 | (12) |
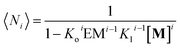 | (13) |
Using eqn (12) and (13) and knowing Ko, the EM and Kl it is possible to determine the changes in the concentration of polymer bundles with any number of strands, and the average number of repeats in the polymer, as the total concentration of the monomer changes. These simulations reveal the following features of the system (Fig. 5): (i) the only species present to any meaningful extent are the monomer, short, single stranded oligomers and the multi-stranded polymer with a maximum number of strands m, while polymers with an i number of strands less than m form only to a very limited extent (Fig. 5B); (ii) the multi-stranded polymer forms following a typical nucleation-growth mechanism, appearing suddenly when a nucleation concentration is reached, with the polymer growing rapidly around this concentration (Fig. 5B and C); (iii) the preferred length of the polymer depends on the maximum number of strands m (Fig. 5C); and (iv) the onset of formation of the multi-stranded polymer is very sensitive to small variations in Kl or Ko (Fig. 5D).
The very high sensitivity of the multi-stranded polymer formation to subtle changes in either the pair-wise binding constants or the concentration of building block M is attributed to the fact that the system switches from the assembly of the monomer (equilibria 1 and 2, Fig. 5A) to the assembly of the nucleus, which is multivalent (equilibria 3 and 4, Fig. 5A) when a critical concentration of M is reached. However, it is not the multivalence on its own that provides the on–off assembly behaviour, but rather the fact that the nucleus is multivalent relative to the monomer. For example, a multivalent monomer M′, analogous to the nucleus Mm, will yield polymers to the same extent as Mm (and to a much larger extent than M) but the assembly process will be isodesmic, showing a smooth dependence of the assembly on the concentration of M′ (equilibrium 0, Fig. 5A and E). By contrast, for M, the assembly is dictated by the properties of Mm only above a certain critical concentration. At this concentration, the length and stability of the polymer formed from the assembly of M building blocks becomes comparable to that formed from M′, giving rise to a sudden increase in the concentration of the assembled species (Fig. 5A and E).
The switching point in the assembly regime occurs at the nucleation concentration, NC. The NC can be written as a function of the constants Kl and Ko, and the maximum number of strands m as follows (see the ESI† for the detailed derivation of the equation):
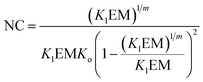 | (14) |
Above the NC, the size of the oligomer can be expressed as a function of Ko, Kl, the EM and the number of strands m as follows:
log〈Nm〉 = 0.5m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ko + 0.5(m − 1)log Ko + 0.5(m − 1)log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EM − 0.5 EM − 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) m + 0.5 m + 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log([M]0 − NC) log([M]0 − NC) | (15) |
A conveniently simple expression can be obtained by combining eqn (14) and (15) for the total concentration of the monomer which is twice that of the NC (see the ESI† for the detailed derivation of the equation):
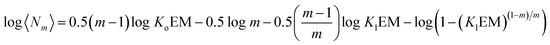 | (16) |
Eqn (16) allows for the calculation of the expected size of a multi-stranded polymer as a function of parameters that are characteristic of the monomer, that is, the association constants, the effective molarity and the number of strands in the polymer.
Conclusions
We have shown that the sequential assembly of cobalt metalloporphyrin C and 4,4′-bipyridine B leads to double stranded polymers, following a nucleation-growth mechanism. The mathematical model derived from the analysis of the spectroscopic data shows that the nucleation-growth mechanism is the consequence of a multivalence cooperative effect.The model was applied to the assembly of multi-stranded polymers with any number of strands. Simulations show that this model accounts well for the all-or-nothing assembly typical of a nucleation-growth mechanism. The overall process can be summarized as a thermodynamic cycle. In the first part of the cycle, monomers assemble into nuclei, following an isodesmic mechanism. In the second part, the nuclei assemble into polymers, also following an isodesmic mechanism. The cooperative behaviour arises from the fact that the assembly of the nuclei is much more efficient than that of the monomers, on account of the multivalence effect. This model offers a simple interpretation of the all-or-nothing assembly observed in many natural (such as microtubules) and artificial (such as small molecule based gelators) polymers. For example, recent studies have found that the assembly of microtubules is better explained as a combination of the lateral and longitudinal binding energies of tubulin, consistent with our model, rather than the classical helicoidal assembly model.38 Moreover, the de-assembly or “catastrophe” following small conformational changes of the tubulin building blocks is also consistent with the all-or-nothing assembly following small changes in the individual pairwise binding constants,6 as predicted by our model. Also consistent with our model, it has been observed that the degree of cooperativity in the assembly of some small molecule based gelators depends on the thickness of the gel fibres, which in turns depends on the number of strands that form the fibre.20
Our model does not exclude the possibility that other cooperative effects of allosteric origin may also play a role in supramolecular polymerization, especially for single-stranded polymers. However, this work shows that for multi-stranded polymers, multivalence cooperativity plays a central role that our model can describe quantitatively. For these polymers, the maximum number of strands m, together with the lateral and oligomerization constants are the key parameters that dictate the preferred size of the oligomer and the nucleation concentration. Since these parameters depend ultimately on the structure of the building blocks, our model is also a useful tool to predict the assembly properties of de novo synthesized molecules. We believe however that our interpretation of the all-or-nothing assembly of supramolecular polymers, whereby the chelate effect is triggered after a multivalent nucleus if formed, can be applied to the formation of any kind of long range assembly that follows a cooperative, all-or-nothing behaviour. Our model can therefore be expanded to include processes as diverse as the crystallization of small molecules or the formation of cell membrane adhesion points. Regarding the latter, previous work from our group has led to an analogous assembly model for membrane embedded receptors.39,40 Current work in our laboratories is directed at demonstrating the general applicability of the model and the specific applicability to cell–cell communication processes involving cell membrane contacts and in the design of multi-stranded supramolecular polymers with predictable assembly properties.
Acknowledgements
We thank Dr Abil Aliev (Department of Chemistry, University College London) for his assistance in performing and analysing the DOSY NMR experiments. We thank the School of Sciences at Birkbeck, University of London, for funding. EM was performed at the School of Crystallography, Birkbeck University of London, supported by a Wellcome Trust program grant to Prof. Helen Saibil.Notes and references
- A. Whitty, Nat. Chem. Biol., 2008, 4, 435 CrossRef CAS PubMed.
- C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488 CrossRef CAS PubMed.
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754 CrossRef.
- J. D. Badjic, A. Nelson, S. J. Cantrill, W. B. Turnbull and J. F. Stoddart, Acc. Chem. Res., 2005, 38, 723 CrossRef CAS PubMed.
- A. Mulder, J. Huskens and D. N. Reinhoudt, Org. Biomol. Chem., 2004, 2, 3409 CAS.
- D. A. Fetcher and R. D. Mullinds, Nature, 2010, 463, 285 Search PubMed.
- T. F. A. De Greef, M. M. J. Smulders, M. Wolffs, A. P. H. J. Schenning, R. P. Sijbesma and E. W. Meijer, Chem. Rev., 2009, 109, 5687 CrossRef CAS PubMed.
- T. Aida, S. I. Stupp and E. W. Meijer, Science, 2012, 335, 813 CrossRef CAS PubMed.
- A. P. H. J. Schenning and E. W. Meijer, Chem. Commun., 2005, 3245 RSC.
- F. J. M. Hoeben, A. P. H. J. Schenning and E. W. Meijer, ChemPhysChem, 2005, 6, 2337 CrossRef CAS PubMed.
- R. Abbel, C. Grenier, M. J. Pouderoijen, J. W. Stouwdam, P. E. L. G. Leclere, R. P. Sijbesma, E. W. Meijer and A. P. H. J. Schenning, J. Am. Chem. Soc., 2009, 131, 833 CrossRef CAS PubMed.
- L. Milanesi, C. A. Hunter, N. Tzokova, J. P. Waltho and S. Tomas, Chem.–Eur. J., 2011, 17, 9753 CrossRef CAS PubMed.
- E. J. Howe, B. O. Okesola and D. K. Smith, Chem. Commun., 2015, 7451 RSC.
- A. R. Hirst, B. Escuder, J. F. Miravet and D. K. Smith, Angew. Chem., Int. Ed., 2008, 47, 8002 CrossRef CAS PubMed.
- A. S. Weingarten, R. V. Kazantsev, L. C. Palmer, M. McClendon, A. R. Koltonow, A. P. S. Samuel, D. J. Kiebala, M. R. Wasielewski and S. I. Stupp, Nat. Chem., 2014, 6, 964 CrossRef CAS PubMed.
- R. N. Shah, N. A. Shah, M. M. D. Lim, C. Hsieh, G. Nuber and S. I. Stupp, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 3293 CrossRef CAS PubMed.
- G. A. Silva, C. Czeislszer, K. L. Niece, E. Beniash, D. A. Harrington, J. A. Kessler and S. I. Stupp, Science, 2004, 303, 1352 CrossRef CAS PubMed.
- J. Boekhoven and S. I. Stupp, Adv. Mater., 2014, 26, 1642 CrossRef CAS PubMed.
- D. H. Zhao and J. S. Moore, Org. Biomol. Chem., 2003, 1, 3471 CAS.
- A. R. Hirst, I. A. Coates, T. R. Boucheteau, J. F. Miravet, B. Escuder, V. Castelletto, I. W. Hamley and D. K. Smith, J. Am. Chem. Soc., 2008, 130, 9113 CrossRef CAS PubMed.
- R. Krishnan and S. L. Lindquist, Nature, 2005, 435, 765 CrossRef CAS PubMed.
- S. L. Bernstein, N. F. Dupuis, N. D. Lazo, T. Wyttenbach, M. M. Condron, G. Bitan, D. B. Teplow, J.-E. Shea, B. T. Ruotolo, C. V. Robinson and M. T. Bowers, Nat. Chem., 2009, 1, 326 CrossRef CAS PubMed.
- P. A. Korevaar, S. J. George, A. J. Markvoort, M. M. J. Smulders, P. A. J. Hilbers, A. P. H. J. Schenning, T. F. A. De Greef and E. W. Meijer, Nature, 2012, 481, 492 CrossRef CAS PubMed.
- P. Jonkheijm, P. van der Schoot, A. P. H. J. Schenning and E. W. Meijer, Science, 2006, 313, 80 CrossRef CAS PubMed.
- F. Oosawa and M. Kasai, J. Mol. Biol., 1962, 4, 10 CrossRef CAS PubMed.
- E. D. Korn, Physiol. Rev., 1982, 62, 672 CAS.
- H. L. Anderson, Chem. Commun., 1999, 2323 RSC.
- Y. Tian, C. M. Beavers, T. Busani, K. E. Martin, J. L. Jacobsen, B. Q. Mercado, B. S. Swartzentruber, F. van Swol, C. F. Medforth and J. A. Shelnutt, Nanoscale, 2012, 4, 1695 RSC.
- M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845 RSC.
- C. A. Hunter and S. Tomas, J. Am. Chem. Soc., 2006, 128, 8975 CrossRef CAS PubMed.
- A. Camara-Campos, C. A. Hunter and S. Tomas, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3034 CrossRef CAS PubMed.
- M. Bhatti, T. D. McHugh, L. Milanesi and S. Tomas, Chem. Commun., 2014, 7649 RSC.
- A. Ortega, D. Amoros and J. Garcia de la Torre, Biophys. J., 2011, 101, 892 CrossRef CAS PubMed.
- O. Ono, Y. Kaizu and H. Kobayashi, J. Chem. Phys., 1993, 99, 4128 CrossRef.
- Y. Gao, X. Zhang, C. Ma, X. Li and J. Jiang, J. Am. Chem. Soc., 2008, 130, 17044 CrossRef CAS PubMed.
- A. Fidalgo-Marijuan, G. Barandika, B. Baza, M.-K. Urtiaga and M. I. Arriortua, CrystEngComm, 2013, 15, 4181 RSC.
- M. C. Misuraca, T. Grecu, Z. Freixa, V. Garavini, C. A. Hunter, P. W. van Leeuwen, M. D. Segarra-Maset and S. M. Turega, J. Org. Chem., 2011, 76, 2723 CrossRef CAS PubMed.
- M. K. Gardner, B. D. Charlebois, I. M. Jánosi, J. Howard, A. J. Hunt and D. J. Odde, Cell, 2011, 146, 582 CrossRef CAS PubMed.
- S. Tomas and L. Milanesi, Nat. Chem., 2010, 2, 1077 CrossRef CAS PubMed.
- A. Grochmal, E. Ferrero, L. Milanesi and S. Tomas, J. Am. Chem. Soc., 2013, 135, 10172 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental methods, including sample preparation for NMR, UV and electron microscopy experiments, the building up of the X-ray derived dimer structure, analysis of the binding of monovalent ligands, additional data on binding constant determination, effect of buffer concentration on polymer dimerization and detailed derivation of the equations. See DOI: 10.1039/c6sc00520a |
| This journal is © The Royal Society of Chemistry 2016 |