Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Stabilizing metastable tetragonal HfO2 using a non-hydrolytic solution-phase route: ligand exchange as a means of controlling particle size†
Gregory R.
Waetzig
a,
Sean W.
Depner
b,
Hasti
Asayesh-Ardakani
cd,
Nicholas D.
Cultrara
b,
Reza
Shahbazian-Yassar
cde and
Sarbajit
Banerjee
 *a
*a
aDepartment of Chemistry and Department of Materials Science and Engineering, Texas A&M University, College Station, TX 77845-3012, USA. E-mail: banerjee@chem.tamu.edu
bDepartment of Chemistry, University at Buffalo, The State University of New York, Buffalo, New York 14260-3000, USA
cDepartment of Mechanical Engineering-Engineering Mechanics, Michigan Technological University, Houghton, Michigan 49933-1295, USA
dDepartment of Physics, University of Illinois at Chicago, Chicago, Illinois 60607-7059, USA
eDepartment of Mechanical and Industrial Engineering, University of Illinois at Chicago, Chicago, Illinois 60607-7059, USA
First published on 3rd May 2016
Abstract
There has been intense interest in stabilizing the tetragonal phase of HfO2 since it is predicted to outperform the thermodynamically stable lower-symmetry monoclinic phase for almost every application where HfO2 has found use by dint of its higher dielectric constant, bandgap, and hardness. However, the monoclinic phase is much more thermodynamically stable and the tetragonal phase of HfO2 is generally accessible only at temperatures above 1720 °C. Classical models comparing the competing influences of bulk free energy and specific surface energy predict that the tetragonal phase of HfO2 ought to be stable at ultra-small dimensions below 4 nm; however, these size regimes have been difficult to access in the absence of synthetic methods that yield well-defined and monodisperse nanocrystals with precise control over size. In this work, we have developed a modified non-hydrolytic condensation method to precisely control the size of HfO2 nanocrystals with low concentrations of dopants by suppressing the kinetics of particle growth by cross-condensation with less-reactive precursors. This synthetic method enables us to stabilize tetragonal HfO2 while evaluating ideas for critical size at which surface energy considerations surpass the bulk free energy stabilization. The phase assignment has been verified by atomic resolution high angle annular dark field images acquired for individual nanocrystals.
Introduction
A particularly powerful aspect of nanoscience that enables much new functionality derives from the greatly altered phase equilibria obtained upon confining materials to nanoscale dimensions.1–4 The increased contributions from surface free energy terms can outweigh bulk free energy considerations and enable the stabilization of crystalline phases under ambient conditions that can otherwise only be stabilized at high temperatures and pressures. As a few notable examples of such metastable phases and their interesting properties: a metallic 1T phase is stabilized upon exfoliating the bulk semiconducting 2H-phases of MoS2 and WS2 to few-layered sheets5,6 and shows greatly improved activity as a catalyst for hydrogen evolution; a γ-MoC phase is stabilized in preference to β-Mo2C for nanostructures of molybdenum carbide and also exhibits promising reactivity for hydrogen evolution;7 the tetragonal phase of ZrO2 is stabilized in preference to the monoclinic phase for particles below a critical size of ca. 30 nm and is used for the transformation toughening of ceramics;8,9 and a metastable LixFePO4 phase is stabilized upon electrochemically delithiating LiFePO4 nanoparticles at high rates within a Li-ion battery and mitigates the need to go through a much slower nucleation and growth process that would result in phase segregation of LiFePO4 and FePO4.10,11 Stabilizing metastable structures requires careful control of particle size and the kinetics of crystallization processes. Low-temperature solution-phase routes for defining structural frameworks are particularly well-suited for preparing kinetically trapped metastable structures since the energetics of these reactions are often too low to allow for coarsening of grain size or overcoming shallow valleys in the potential energy landscape.12–15 In this work, we demonstrate a cross-coupling ligand exchange method for controlling the particle size in the non-hydrolytic sol–gel condensation growth of HfO2 nanocrystals. Precise control of the size of HfO2 nanocrystals enables unequivocal determination of the critical size required to stabilize the tetragonal phase and provides access to well-defined crystals of this technologically important metastable structure that is otherwise stable only above ca. 1720 °C.16Tetragonal ZrO2 has been widely accessible for several decades, even without incorporation of dopant atoms, since the critical size at which the surface free energy terms overcome bulk free energy considerations is relatively large, variously estimated to be ca. 15–30 nm.8,9,17–19 In contrast, stabilization of the tetragonal phase of HfO2 is much more challenging since: (a) the bulk free energy stabilization of the monoclinic phase over the tetragonal phase is almost 40% greater for HfO2 as compared to ZrO2; and (b) the volume expansion accompanying the tetragonal to monoclinic phase transition is much smaller for HfO2 (ca. 2.7%) as compared to ZrO2 (4.0%).20,21 Estimates of the critical size required to stabilize the tetragonal phase of HfO2 vary widely from about 2 to 10 nm but it is clear that this value is substantially smaller than the critical size for ZrO2.16,20,22 Several methods for the preparation of nanometer-sized particles of HfO2 report the stabilization of at least some fraction of tetragonal HfO2; for instance, signatures of the tetragonal phase have been identified in particles obtained by the thermal decomposition of pure Hf(OH)4,16 the oxidation of metallic Hf nanocrystals,23 and a ligand-mediated reaction at the interface of water and oil phases.24 However, the polydispersity and relatively poor crystallinity of the particles obtained by these methods implies that the obtained samples almost always contain only minor proportions of tetragonal phases and a clear delineation of a size-dependent phase diagram has thus far not been possible. Several instances of stabilizing tetragonal domains have also been reported for thin films of HfO2 prepared by methods such as atomic layer deposition in a low-oxygen environment,25 ultra-thin films deposited onto clean Si (100) surfaces by atomic layer deposition,26 and ion-beam-assisted deposition in an oxygen deficient ambient.27 Again, the films usually contain mixtures of multiple crystalline and amorphous phases and exhibit considerable heterogeneity in terms of the dimensions of individual domains.
The stabilization of tetragonal HfO2 is not just an academic curiosity. Indeed, the tetragonal (space group P42/nmc) phase of HfO2 is anticipated to outperform the thermodynamically stable lower-symmetry monoclinic phase (space group P21/c) for almost every application where HfO2 has found use. Perhaps the most important application of HfO2 is in gate dielectric stacks as a high-κ dielectric because of its resistance to silicidation and silicate formation and its much greater dielectric constant as compared to SiO2.20,28–30 First-principles calculations predict a dielectric constant of 18 for monoclinic HfO2, which is far surpassed by the value of almost 70 predicted for tetragonal HfO2.31 The bandgap of the tetragonal phase is also predicted to be larger (ca. 6.11 eV) as compared to the monoclinic phase (5.78 eV).32 Finally, the tetragonal phase is denser and has been experimentally found to have a higher Knoop hardness.27
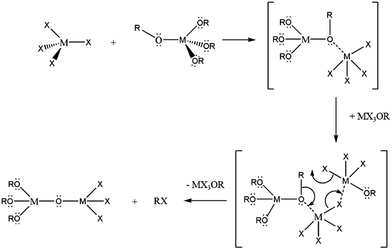
In comparison to aqueous methods, non-hydrolytic methods, often based on formation of oxo-bridges by elimination of small molecules, provide considerable control of the kinetics of condensation.14,15,33 Such control is imperative to precisely control particle size and morphology when growing nanoparticles. In an early work, the condensation of hafnium alkoxides in benzyl alcohol with the elimination of alkyl ethers yielded monoclinic, but not tetragonal, HfO2 nanocrystals.34 Solvothermal processing of various hafnium alkoxides yielded varying morphologies of HfO2 nanocrystals, again crystallized in the monoclinic phase.35 Hyeon and co-workers adapted the alkyl halide elimination route first proposed by Vioux for the growth of nanocrystals and were able to achieve the multigram synthesis of ZrO2 nanocrystals as per:17,36
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) M–X + M–X + ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) M–O–R → M–O–R → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) M–O–M M–O–M![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) + R–X + R–X | (1) |
Brus and co-workers extended this method to prepare HfO2 and solid-solution HfxZr1−xO2 nanocrystals and established considerable control over the relative Hf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr concentrations.19 In previous work, we have demonstrated that the R group of the alkoxide ligand allows for substantial tunability of the size of HfO2 and ZrO2 nanocrystals as well as the relative Hf
Zr concentrations.19 In previous work, we have demonstrated that the R group of the alkoxide ligand allows for substantial tunability of the size of HfO2 and ZrO2 nanocrystals as well as the relative Hf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr ratios of HfxZr1−xO2 nanocrystals.37,38 These studies as well as past work by Vioux have established that upon reacting M(OR)4 and MX4 species, substantial ligand exchange takes place to stabilize haloalkoxides such as M(OR)3Cl, M(OR)2Cl2, and M(OR)Cl3.14,36 The first of these three species has been proposed as a catalyst that brings about transformation of an alkoxo-bridge to an oxo-bridge as per the reaction depicted in Scheme 1.
Zr ratios of HfxZr1−xO2 nanocrystals.37,38 These studies as well as past work by Vioux have established that upon reacting M(OR)4 and MX4 species, substantial ligand exchange takes place to stabilize haloalkoxides such as M(OR)3Cl, M(OR)2Cl2, and M(OR)Cl3.14,36 The first of these three species has been proposed as a catalyst that brings about transformation of an alkoxo-bridge to an oxo-bridge as per the reaction depicted in Scheme 1.
When two different metal precursors are reacted, the composition of the product depends on the relative condensation rates and reactivities. For metals exhibiting comparable reactivity, such as Hf and Zr, the heterocondensation reaction yields solid-solution nanocrystals and can be written as follows:18,19
| mMXn + nM′(OR)m → MmM′nOnm + nmRX | (2) |
However, if the rates of homo- and hetero-condensation are vastly different, the products of the faster reaction are obtained preferentially. In this work, we find that adding a much less reactive precursor, either Ce(OtBu)4 or La(OiPr)3, greatly modifies the concentration of the active monomer depicted in Scheme 1 and thereby retards the kinetics of the homocondensation reaction, yielding considerable control over the size of HfO2 nanocrystals with only minimal incorporation of La and Ce. This unprecedented control of nanocrystal size allows us to explore ultra-small dimensions and determine the critical size for stabilizing the tetragonal phase of HfO2.
Experimental
Synthesis
Hafnium(IV) chloride, cerium(III) chloride, lanthanum(III) chloride, lanthanum(III) iso-propoxide, and tri-n-octylphosphine oxide (TOPO) were purchased from Strem and used without any further purification. Hafnium(IV) tert-butoxide was purchased from Alfa Aesar and used as received. Cerium(IV) tert-butoxide was purchased from Gelest and used without further purification. To synthesize the metal oxide nanocrystals, a metal halide and metal alkoxide are mixed in equimolar amounts with ca. 10 g of TOPO in a three-neck round bottom flask under an Ar ambient within a glovebox. The total concentration of metal precursors is maintained at 4 mmol in all of the reactions. In all of the reactions, 2 mmol of HfCl4 is used as the chloride precursor, whereas the alkoxide precursor is x mmol of La(OiPr)3 or Ce(OtBu)4 and 4 − x mmol of Hf(OtBu)4. CeO2 nanocrystals were obtained by the reaction of equimolar amounts of CeCl3 and Ce(OtBu)4 as reported in our previous work.39 Reducing the amount of the chloride precursor below equimolar amounts solely yields amorphous products as discussed in further detail below.Briefly, the reaction mixture is heated under an argon ambient on a Schlenk line to ca. 60 °C, until the TOPO is melted at which point stirring is initiated. Subsequently, the reaction mixture is heated to 340 °C and kept at this temperature for 2 h. Next, the reaction mixture is cooled to ca. 60 °C and solvent/non-solvent washing is performed alternating acetone and hexanes to remove excess TOPO.
Characterization
A Rigaku Ultima IV diffractometer with a graphite monochromator and a Bruker-AXS D8 Advanced Bragg–Brentano X-ray powder diffractometer, both using Cu Kα radiation (λ = 1.5418 Å), were used for characterization of the samples by powder X-ray diffraction. The crystallinity and size distribution of the nanocrystals was evaluated by high-resolution transmission electron microscopy (HRTEM) using JEOL-2010 and FEI Tecnai G2 F20 ST electron microscopes at an operating voltage of 200 kV. Samples for HRTEM analysis were dispersed in hexanes, drop-cast onto 400-mesh carbon-coated copper grids, and allowed to dry in air. The stoichiometry of the nanocrystals was determined by X-ray fluorescence (XRF) measurements, conducted by Oneida Research Services, Inc. in Whitesboro, NY, by inductively coupled plasma-mass spectrometry (ICP-MS) using a Perkin Elmer DRCII instrument, and by energy dispersive X-ray spectroscopy (EDX) on a JEOL JSM-7500F field emission scanning electron microscope (FE-SEM) operated at an accelerating voltage of 20 kV. Samples for ICP-MS analysis were prepared by acid digestion in an aqueous solution of 67% metals grade HNO3. Further characterization was performed using atomic resolution high-angle annular dark-field (HAADF) imaging. A probe-corrected JEOL JEM-ARM200CF instrument equipped with a cold field-emission gun operated at 200 kV was used with a convergence angle of 22 mrad. The HAADF inner detector angle was 90 mrad.Results
Fig. 1 displays XRD patterns for nanocrystals obtained by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and Ce(OtBu)4. Table 1 lists the actual Hf and Ce atomic concentrations obtained for the different precursor ratios as well as the primary phase identified from analysis of powder XRD patterns. Energy dispersive X-ray spectroscopy (EDX) was also performed on the Hf1−xCexO2 nanocrystals and provides good agreement with the hafnium and cerium concentrations derived by elemental analysis (Fig. S1 and Table S1, ESI†). Decreasing the concentration of HfCl4 below 2 mmol results in the formation of entirely amorphous aggregates and thus Hf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce concentrations with excess cerium in the reaction mixture are not further discussed. Lower alkoxide concentrations further yield amorphous products. HfO2 nanocrystals prepared by the reaction of Hf(OtBu)4 and HfCl4 are clearly monoclinic (P21/c) as delineated by the appearance of sharp (200) and (220) reflections (Joint Committee on Powder Diffraction Standards (JCPDS) 78-0050) indexed in Fig. 1A.37,38 In contrast, CeO2 nanocrystals crystallize in a cubic fluorite structure (Fm
Ce concentrations with excess cerium in the reaction mixture are not further discussed. Lower alkoxide concentrations further yield amorphous products. HfO2 nanocrystals prepared by the reaction of Hf(OtBu)4 and HfCl4 are clearly monoclinic (P21/c) as delineated by the appearance of sharp (200) and (220) reflections (Joint Committee on Powder Diffraction Standards (JCPDS) 78-0050) indexed in Fig. 1A.37,38 In contrast, CeO2 nanocrystals crystallize in a cubic fluorite structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with reflections that can be indexed to JCPDS# 34-0394 (Fig. S2, ESI†). As the concentration of Hf is decreased, or in other words, the relative ratio of Ce(OtBu)4 to Hf(OtBu)4 is increased, the reflections are broadened indicating a pronounced diminution in size even though elemental analysis data presented in Table 1 suggests very little Ce incorporation. In contrast to the rest of the series, reaction between 2 mmol of HfCl4 and 2 mmol of Ce(OtBu)4 preponderantly yields the tetragonal phase of HfO2 characterized by a pronounced (101) reflection centered at 2θ = 30.3° (Fig. 1F). The simulated pattern of tetragonal HfO2 has been generated using coordinates for a relaxed structure of this phase calculated by Perevalov and co-workers and is depicted in blue in Fig. 1 (a complete structure solution is thus far absent for this phase).40 Table S2 in the ESI† lists the atomic coordinates, lattice constants, and angles of the monoclinic and tetragonal phases of HfO2 with the latter set of data being derived from the calculation noted above. Careful examination of Fig. 1E, the XRD pattern for the sample prepared with 1.6 mmol of Ce(OtBu)4, indicates the appearance of a reflection at 2θ = 31° that can be attributed to the (101) reflection of the tetragonal phase and suggests that this set of precursors yields a mixture of tetragonal and monoclinic phases. A reflection at 2θ = ca. 41° in Fig. 1E suggests trace amounts of the monoclinic phase although the tetragonal phase is clearly vastly preponderant.
m) with reflections that can be indexed to JCPDS# 34-0394 (Fig. S2, ESI†). As the concentration of Hf is decreased, or in other words, the relative ratio of Ce(OtBu)4 to Hf(OtBu)4 is increased, the reflections are broadened indicating a pronounced diminution in size even though elemental analysis data presented in Table 1 suggests very little Ce incorporation. In contrast to the rest of the series, reaction between 2 mmol of HfCl4 and 2 mmol of Ce(OtBu)4 preponderantly yields the tetragonal phase of HfO2 characterized by a pronounced (101) reflection centered at 2θ = 30.3° (Fig. 1F). The simulated pattern of tetragonal HfO2 has been generated using coordinates for a relaxed structure of this phase calculated by Perevalov and co-workers and is depicted in blue in Fig. 1 (a complete structure solution is thus far absent for this phase).40 Table S2 in the ESI† lists the atomic coordinates, lattice constants, and angles of the monoclinic and tetragonal phases of HfO2 with the latter set of data being derived from the calculation noted above. Careful examination of Fig. 1E, the XRD pattern for the sample prepared with 1.6 mmol of Ce(OtBu)4, indicates the appearance of a reflection at 2θ = 31° that can be attributed to the (101) reflection of the tetragonal phase and suggests that this set of precursors yields a mixture of tetragonal and monoclinic phases. A reflection at 2θ = ca. 41° in Fig. 1E suggests trace amounts of the monoclinic phase although the tetragonal phase is clearly vastly preponderant.
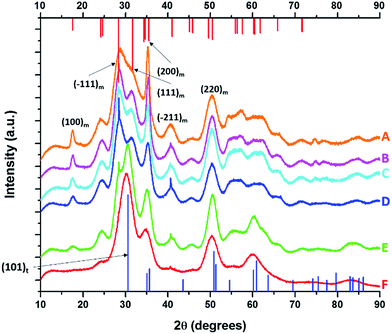 | ||
| Fig. 1 X-ray diffraction patterns of end-member pure HfO2 (A) compared to Hf1−xCexO2 nanocrystals prepared by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and Ce(OtBu)4. The patterns correspond to detected (and precursor) relative Hf concentrations. The precursors are listed in Table 1. (A) 100% (100%), (B) 99.87% (90%), (C) 99.87% (80%), (D) 99.68% (70%), (E) 99.36% (60%) and (F) 97.64% (50%). Vertical bars indicate positions and relative intensities of reflections expected from JCPDS patterns. Reflections of monoclinic HfO2 are indicated in red (JCPDS # 78-0050) and tetragonal HfO2 in blue (XRD pattern simulated as described in the text). | ||
| HfCl4 [mmols] | Hf(O-tBut)4 [mmols] | Ce(O-tBut)4 [mmols] | Precursor Hf concentration [relative at%] | Detected Hf concentration [relative at%] | Detected Ce concentration [relative at%] | Length of nanocrystals [nm] | Phase of nanocrystals |
|---|---|---|---|---|---|---|---|
| 2.0 | 2.0 | 0.0 | 100 | 100.0 | 0 | 12.9 ± 1.8 | Monoclinic |
| 2.0 | 1.6 | 0.4 | 90 | 99.87 | 0.13 | 9.5 ± 2.2 | Monoclinic |
| 2.0 | 1.2 | 0.8 | 80 | 99.87 | 0.13 | 7.8 ± 1.9 | Monoclinic |
| 2.0 | 0.8 | 1.2 | 70 | 99.68 | 0.32 | 5.9 ± 1.0 | Monoclinic |
| 2.0 | 0.4 | 1.6 | 60 | 99.36 | 0.64 | 4.4 ± 0.7 | Monoclinic/tetragonal |
| 2.0 | 0 | 2 | 50 | 97.64 | 2.36 | 3.1 ± 0.4 | Tetragonal |
| 0.0 | 0.0 | 4.0 | 0 | 0 | 100 | 1.5 ± 0.5 | Cubic |
Fig. 2 indicates HRTEM images and size distribution histograms for these nanocrystals. Table 1 lists the dimensions determined by statistical analysis of at least 50 nanocrystals. With increasing concentration of Ce(OtBu)4 in the reaction mixture, the morphology of the obtained nanostructures evolves from elongated nanorods to quasi-spherical particles. The nanorods preferentially grow along the [100] direction of monoclinic HfO2.38 As also suggested by the powder XRD data of Fig. 1, the lengths of the Hf1−xCexO2 nanorods are monotonically diminished with reduced concentration of Hf(OtBu)4 with respect to Ce(OtBu)4. The average length is decreased from 12.9 ± 1.8 nm for monoclinic nanocrystals grown using only Hf(OtBu)4 to 3.1 ± 0.4 nm for tetragonal nanocrystals grown using Ce(OtBu)4 as the only alkoxide precursor. The widths of the Hf1−xCexO2 nanocrystals are not substantially altered and remain around 2.5 ± 0.4 nm. The lattice-resolved HRTEM image in Fig. 2F clearly indicates a lattice separation of 0.292 nm corresponding to the predicted separation between the (101) planes of tetragonal HfO2 (Table S2†),40 corroborating the stabilization of this metastable phase under these conditions.
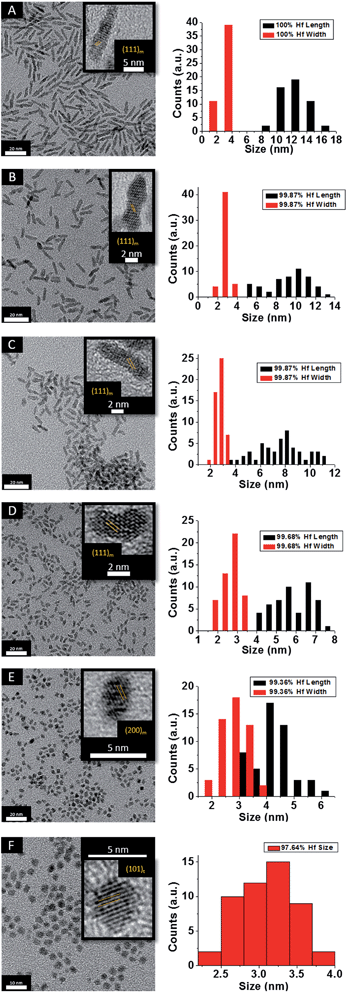 | ||
| Fig. 2 Low-magnification transmission electron microscopy images of HfO2 (A) nanocrystals compared to nanocrystals prepared by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and Ce(OtBu)4. The precursors and calculated dimensions are listed in Table 1. The detected (and precursor) relative Hf concentrations of (A) 100% (100%), (B) 99.87% (90%), (C) 99.87% (80%), (D) 99.68% (70%), (E) 99.36% (60%), and (F) 97.64% (50%). Insets show HRTEM images. The lattice-resolved images indicate separations between the (111) and (200) lattice planes of the monoclinic phase in the insets to (A) to (E). The separation between the (101) lattice planes of the tetragonal phase is indicated in the inset to (F). The accompanying size distribution histograms are shown to the right of each sample illustrating that the length of the nanorods decreases with increasing concentration of Ce(OtBu)4 in the synthesis, whereas the width remains relatively constant. | ||
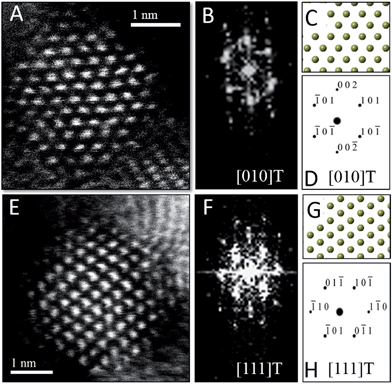
To verify the phase assignment of Hf1−xCexO2 as being tetragonal, atomic-resolution HAADF scanning transmission electron microscopy (STEM) imaging has been performed using an aberration corrected microscope. Fig. 3 indicates HAADF STEM images and fast Fourier transforms (FFT) acquired for two different nanocrystals along the [010] and [111] zone axes. The simulated diffraction patterns for these zone axis assignments using coordinates of the tetragonal structure are an excellent match to the experimental data (as indicated by the reconstructed solid spheres depiction), providing unequivocal corroboration of the tetragonal crystal structure. Fig. S3A and B† indicate the planes of atoms in the tetragonal unit cell that are indexed in the simulated diffraction patterns (Fig. 3D and H) for each image acquired along a specific zone axis.
Fig. 4 displays powder XRD patterns acquired for nanocrystals obtained by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and La(OiPr)3. Table 2 lists the actual Hf and La atomic concentrations obtained for the different precursor ratios as well as the primary phase identified from analysis of powder XRD patterns. EDX was also performed on Hf1−xLaxO2 nanocrystals and the determined hafnium and lanthanum concentrations are in good agreement with the elemental analysis results (Fig. S4 and Table S3†). Again, upon decreasing the Hf![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La ratios such that there is a lower concentration of hafnium precursors as compared to lanthanum precursors, only amorphous aggregates are obtained, and thus we focus our discussion on reaction mixtures with lower concentrations of La(OiPr)3 as listed in Table 2. Lower alkoxide concentrations also yield amorphous aggregates. Notably, the homocondensation of LaCl3 and La(OiPr)3 yields LaOCl nanocrystals crystallized in the matlockite PbFCl-type phase.41–43
La ratios such that there is a lower concentration of hafnium precursors as compared to lanthanum precursors, only amorphous aggregates are obtained, and thus we focus our discussion on reaction mixtures with lower concentrations of La(OiPr)3 as listed in Table 2. Lower alkoxide concentrations also yield amorphous aggregates. Notably, the homocondensation of LaCl3 and La(OiPr)3 yields LaOCl nanocrystals crystallized in the matlockite PbFCl-type phase.41–43
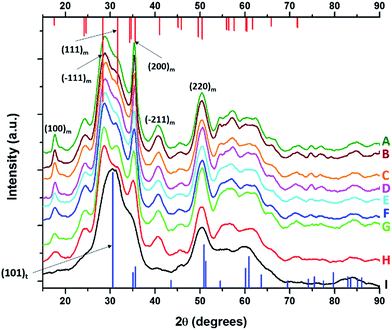 | ||
| Fig. 4 X-ray diffraction patterns of pure HfO2 (A) compared to Hf1−xLaxO2 nanocrystals prepared by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and La(OiPr)3. The patterns correspond to detected (and precursor) relative Hf concentrations. The precursors are listed in Table 2. (A) 100% (100%), (B) 99.98% (97.5%), (C) 99.78% (93.75%), (D) 99.56% (87.5%), (E) 98.87% (75%), (F) 98.68% (62.5%), (G) 98.07% (56.25%), (H) 96.46% (52.5%), and (I) 95.27% (50%). Vertical bars indicate positions and relative intensities of reflections expected from JCPDS patterns. Reflections of monoclinic HfO2 are indicated in red (JCPDS # 78-0050) and tetragonal HfO2 in blue (XRD pattern simulated as described in the text). | ||
| HfCl4 [mmols] | Hf(O-tBut)4 [mmols] | La(O-iPro)3 [mmols] | Precursor Hf concentration [relative at%] | Detected concentration [relative at%] | Detected Ce concentration [relative at%] | Length of nanocrystals [nm] | Phase of nanocrystals |
|---|---|---|---|---|---|---|---|
| 2.0 | 2.00 | 0.00 | 100 | 100.0 | 0.00 | 12.9 ± 1.8 | Monoclinic |
| 2.0 | 1.90 | 0.10 | 97.50 | 99.98 | 0.01 | 11.5 ± 1.26 | Monoclinic |
| 2.0 | 1.75 | 0.25 | 93.75 | 99.78 | 0.22 | 10.1 ± 0.89 | Monoclinic |
| 2.0 | 1.50 | 0.50 | 87.50 | 99.56 | 0.44 | 9.3 ± 1.46 | Monoclinic |
| 2.0 | 1.00 | 1.00 | 75.0 | 98.87 | 1.13 | 8.1 ± 0.98 | Monoclinic |
| 2.0 | 0.50 | 1.50 | 62.50 | 98.68 | 1.32 | 7.0 ± 1.02 | Monoclinic |
| 2.0 | 0.25 | 1.75 | 56.25 | 98.07 | 1.93 | 5.9 ± 0.92 | Monoclinic |
| 2.0 | 0.10 | 1.90 | 52.50 | 96.46 | 3.54 | 4.7 ± 0.79 | Monoclinic |
| 2.0 | 0.00 | 2.00 | 50.00 | 95.27 | 4.73 | 3.3 ± 0.42 | Tetragonal |
Analogous to the above discussion for Ce(OtBu)4, with increasing concentration of La(OiPr)3 in the reaction mixture, the (100) and (200) reflections indexed to the monoclinic phase of pure HfO2 are broadened and diminished in intensity suggesting a pronounced diminution in size. Again, although the powder XRD patterns are substantially altered, the elemental analysis results listed in Table 2 indicate very little incorporation of La in HfO2. For the sample prepared by the reaction of HfCl4 and La(OiPr)3, the (100) monoclinic reflection is no longer observed and the (101) tetragonal reflection becomes the most prominent feature in the powder XRD pattern suggesting stabilization of the tetragonal phase of HfO2 with modest La doping.
HRTEM images and size distribution histograms of this set of nanocrystals are shown in Fig. 5 and the relevant dimensions and standard deviations deduced from statistical analysis are listed in Table 2. With increasing concentration of La(OiPr)3, the Hf1−xLaxO2 nanocrystals again evolve from elongated nanorods to quasi-spherical nanocrystals. The width of the Hf1−xLaxO2 nanocrystals is relatively unchanged at ca. 2.5 ± 0.4 nm for the entire set of samples. However, the length of the nanorods is diminished from 12.9 ± 1.8 nm for monoclinic nanocrystals grown using only Hf(OtBu)4 to 3.3 ± 0.4 nm for Hf1−xLaxO2 tetragonal nanocrystals grown using La(OiPr)3 as the only alkoxide precursor.
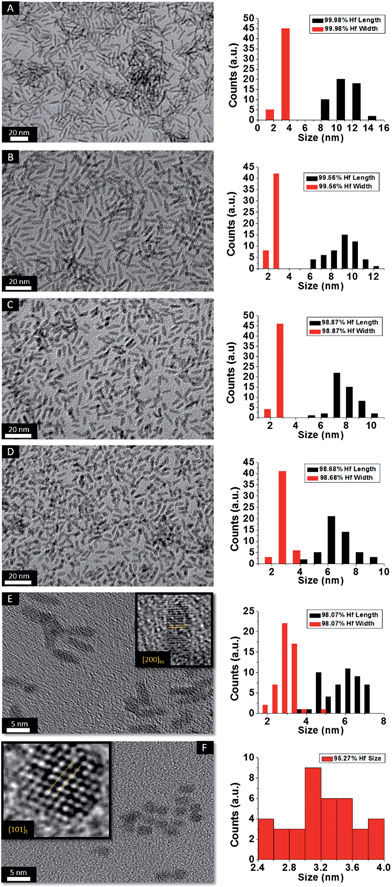 | ||
| Fig. 5 Low-magnification transmission electron microscopy images of nanocrystals prepared by the reaction of HfCl4 with varying proportions of Hf(OtBu)4 and La(OiPr)3. The precursors and calculated dimensions are listed in Table 2. The detected (and precursor) relative Hf concentrations of (A) 99.98% (97.5%), (B) 99.56% (87.5%), (C) 98.87% (75%), (D) 98.68% (62.5%), (E) 98.07% (56.25%), and (F) 95.27% (50%). Insets show HRTEM images. The lattice-resolved images indicate separations between the (200) lattice planes of the monoclinic phase in the inset of (E) and the (101) lattice planes of the tetragonal phase in the inset of (F). The accompanying size distribution histograms are shown to the right of each sample illustrating that the length of the nanorods decreases with increasing concentration of La(OiPr)3 in the synthesis, whereas the width remains relatively constant. | ||
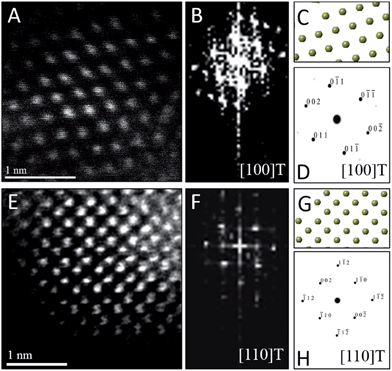
To confirm the phase assignment of Hf1−xLaxO2 nanocrystals as being tetragonal, atomic-resolution HAADF STEM images and fast Fourier transforms (FFT) of the HAADF images were acquired and are depicted in Fig. 6. Images were acquired for different nanocrystals along [100] and [110] zone axes. The simulated diffraction patterns are an excellent match to the Fourier transforms in each case and the reconstructed tetragonal lattice (depicted as solid spheres) is entirely superimposable on the STEM image. Fig. S5A and B† indicate the planes of atoms in the tetragonal unit cell that are indexed in the simulated diffraction patterns (Fig. 6D and H). The STEM data further provides unambiguous confirmation of the tetragonal crystal structure.
The preceding discussion illustrates that the addition of Ce(OtBu)4 and La(OiPr)3 leads to a substantial and monotonic diminution of nanocrystal size even though elemental analysis results indicate that relatively low concentrations of Ce and La are actually incorporated within the lattice. At the smallest dimensions, the tetragonal phase of HfO2 is stabilized over the monoclinic phase. These results lead to two fundamental questions regarding the mechanistic basis for the size control achieved by addition of La and Ce precursors and the origin of the altered phase stability.
Discussion
To understand the origin of the size control achieved by the addition of Ce(OtBu)4 and La(OiPr)3, it is important to consider the overall equation depicted in eqn (1), which results in formation of an oxo-bridge with the elimination of an alkyl halide, as well as the catalytic scheme proposed by Vioux shown in Scheme 1.44,45 Indeed, it is thought that the initial step in a heterocondensation reaction between two metal precursors M and M′ involves ligand exchange and can be written as:| MCln + M′(OR)n → MCln−x(OR)x + M′Clx(OR)n−x, | (3) |
Evidence for such ligand-exchange comes from direct observations of chloroalkoxides by Vioux14,36 as well as the following observations derived from nanocrystal synthesis: (a) reactions of HfCl4 and Zr(OR)4 and ZrCl4 and Hf(OR)4 yield exactly the same compositions of solid-solution HfxZr1−xO2 nanocrystals suggesting that ligand scrambling precedes condensation;37 (b) the reaction of trivalent lanthanide chlorides and lanthanide alkoxides yields lanthanide oxyhalide nanocrystals with well-defined oxyhalide bridges.41–43 The rates of condensation of the chloroalkoxide species produced as per eqn (3) are greatly dependent on the specific metal; precursors with similar reactivities yield solid-solution nanocrystals with a random distribution of two metals, whereas if one species reacts much faster than the second, very little of the second species incorporates within the lattice and the oxide of the first metal is obtained as the primary product.36 Reasonably well-matched precursor pairs such as Hf/Zr and La/Ce yield solid-solution nanocrystals of HfxZr1−xO2 and LaxCe1−xO2, respectively, albeit with compositions that reflect the relative reactivities of the two metal precursors as modified by the alkoxide ligands.18,37,39 However, upon reacting Hf precursors with Ce and La precursors, the homocondensation of the former proceeds much faster than heterocondensation. Indeed, HfO2 with very low dopant concentrations is obtained as the exclusive product upon the reaction of HfCl4 with mixtures of Hf(OtBu)4 and Ce(OtBu)4/La(OiPr)3. The relatively low incorporation of Ce and La within the doped HfO2 lattice, very much lower than the precursor concentrations, corroborates the idea of the lower reactivity of these precursors. Fig. 1, 2, 4, and 5 nevertheless indicate that the addition of Ce(OtBu)4 and La(OiPr)3 allows for substantial tunability of the size of the obtained doped HfO2 nanocrystals. In Scheme 1, the initial step involves the formation of an alkoxo-bridge as a result of a Lewis acid–Lewis base interaction between the oxygen atom of the alkoxide and the metal center of a halide. Subsequently, the MX3OR species (derived from ligand exchange as per eqn (3)) mediates conversion of the alkoxo-bridge to an oxo-bridge with elimination of an alkyl halide. Indeed, Vioux has shown that the presence of MX3OR species is imperative for condensation and that MX2(OR)2 and MX(OR)3 species are much less reactive.36 In other words, the Lewis acid–base complex depicted in Scheme 1 is the “monomer”, whereas the MX3OR species formed by ligand exchange serves as the catalyst. The retention of equimolar amounts of halide and alkoxide precursors ensures that the amount of catalyst is kept essentially the same for all of the reactions listed in Tables 1 and 2 as a result of the ligand exchange reaction depicted in eqn (3) although it must be qualified that the equilibrium constants for formation of the catalyst will be altered for the different alkoxides. Indeed, since formation of an oxo-bridge, and not diffusion of monomers, is thought to be the rate-determining step, in the absence of a sufficient amount of the catalyst, such as at low alkoxide concentrations, only amorphous aggregates are obtained. However, since the Lewis acid–base adducts constituted from HfCl4 and Ce(OtBu)4/La(OiPr)3 are much less reactive as compared to those prepared from HfCl4 and Hf(OtBu)4, the addition of cerium and lanthanum precursors essentially reduces the concentration of the active monomer. In other words, the reaction rate is diminished as a result of the lower reactivity of mixed metal Lewis acid–base adducts towards formation of oxo-bridges. As further corroboration for this idea, Table 1 and Fig. 1 indicate that the homocondensation of hafnium precursors yields pure HfO2 nanocrystals that are 12.9 ± 1.8 nm. In contrast, the homocondensation of cerium precursors yields CeO2 nanocrystals that are 1.5 ± 0.5 nm indicating much slower kinetics of growth (Table 1 and Fig. S2†). Cross-reactions between La and Ce alkoxides indicate even lower reactivities for the La precursors with only ca. 20 at% incorporation of La within solid-solution LaxCe1−xO2 nanocrystals when starting with equimolar concentrations.39 The reduced concentration of the active monomer brings about a systematic and pronounced diminution in the size of the doped HfO2 nanocrystals by inhibiting their growth. In other words, the cross-condensation reaction enables modulation of the concentration of the active monomer, thereby enabling precise control over crystal size.
As a next point, we discuss the origins of the stabilization of the tetragonal phase of HfO2. Indeed, the product of the direct reaction of HfCl4 and Hf(OiPr)4 when ramped at a rate of 15 °C to 500 °C during thermal analysis is monoclinic HfO2, the thermodynamically stable phase, along with an oxygen-deficient orthorhombic HfO2 phase. The inclusion of TOPO still yields monoclinic HfO2, albeit with a smaller size. These results illustrate that direct reaction of the precursors cannot yield the metastable, kinetically trapped phase. The incorporation of the La and Ce alkoxides is imperative to slow the kinetics of crystal growth. Fig. 7 indicates the evolution of size as a function of the measured Hf concentration in the doped nanocrystals and depicts that only below a critical threshold of ca. 3.6–3.8 nm is the tetragonal phase stabilized. Since Tables 1 and 2 indicate that some amount of La and Ce are incorporated within the doped nanocrystals, it is worth considering whether the stabilization of the tetragonal phase results from (a) the size of the La/Ce cations that are displacively doped being different from that of Hf-cations (a strain effect), (b) the creation of oxygen vacancies, or (c) crystal size. Based on the larger size of La3+ cations (110 pm for seven-coordinated and 116 pm for eight-coordinated sites) as compared to Ce3+ (107 pm for seven-coordinated and 114.3 pm for eight-coordinated) or Ce4+ (97 pm for eight-coordinated),46,47 if the effects of cation size were to be of paramount importance, one would expect that incorporation of La would more readily bring about stabilization of the tetragonal phase and one would further expect to see substantial tensile strain. However, Tables 1 and 2 indicate that the amount of detected Ce and La are 2.36 at% and 4.73 at%, respectively, for stabilization of the tetragonal phase and thus size of the cations is likely not the primary driving force for stabilization of the tetragonal phase. Furthermore, the reconstructed HAADF images (Fig. 3 and 6) do not reveal any measurable strain for the tetragonal structure. In other words, if size were the primary factor, relatively lower amounts of La-incorporation would be expected to bring about stabilization of the tetragonal phase (Table 2 indicates that the Hf1−xLaxO2 nanocrystals remain monoclinic even upon incorporation of 3.54 at% of La).
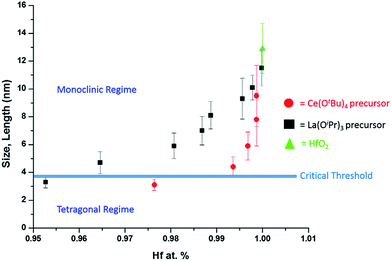 | ||
| Fig. 7 A plot of nanocrystal size versus the relative atomic percentage of Hf detected by elemental analysis (Tables 1 and 2). The line denoted as the critical threshold separates the monoclinic and tetragonal phases of pure HfO2. | ||
The second scenario pertains to the potential role of oxygen vacancies. The substitutional incorporation of trivalent lanthanum cations in the HfO2 lattice will result in creation of half an oxygen vacancy to maintain electrostatic neutrality. The Ce4+/Ce3+ redox couple is readily accessible but since we start with tetravalent cerium precursors, the vacancy concentration generated upon cerium-incorporation is likely to be lower than upon lanthanum incorporation. Again, if oxygen vacancies were to provide the driving force for stabilization of the tetragonal phase, one would expect that lanthanum-incorporation should more readily bring about stabilization of the tetragonal phase as compared to cerium incorporation. Again, Tables 1 and 2 indicate that Hf1−xLaxO2 nanocrystals with 3.54 at% La are monoclinic, whereas Hf1−xCexO2 nanocrystals with only 2.36 at% Ce are tetragonal. The preceding discussion and Fig. 7 thus implies that it is the size of the nanocrystals that is the primary driving force for stabilization of the tetragonal phase. The stabilization of this phase is derived from the surface energy of the tetragonal phase being lower than that of the monoclinic phase (the difference between the two phases is 246 mJ m−2).21 Below the critical size regime, the surface-to-volume ratio of pure HfO2 nanocrystals becomes such that the surface energy term exceeds the bulk energy component of the free energy term (the difference between the two phases is 196 meV for pure HfO2),21 thereby enabling preferentially stabilization of the tetragonal phase at room temperature.1,2,8,9
In 1972, Bailey and co-workers developed an expression for calculating the critical size for stabilizing a metastable state based on a classical thermodynamic treatment of the phase transformation and the competing bulk and surface energy terms. In this formulation, the critical size, d can be expressed as48
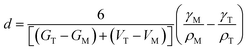 | (4) |
Conclusions
Stabilization of the tetragonal phase of HfO2 has been far more challenging as compared to ZrO2 given the smaller volume expansion accompanying the tetragonal → monoclinic transformation and the relatively greater stabilization enjoyed by the monoclinic phase. Classical thermodynamic models predict that the tetragonal phase should be stable at dimensions smaller than ca. 3.6 nm but the validity of these predictions have been thus far impossible to determine in the absence of synthetic approaches that can access such ultra-small dimensions with precise control of particle size. In this work, we have developed a non-hydrolytic condensation route wherein the concentration of the active monomer is precisely modulated by replacing Hf(OtBu)4 with less reactive Ce(OtBu)4 or La(OiPr)3 precursors. The latter alkoxides exhibit much slower kinetics of condensation and thus are incorporated within the doped HfO2 lattice only to small extents but play a significant role in modifying the growth kinetics by suppressing the concentration of the active monomer. This approach enables precise control of size in ultra-small dimensions and allows for systematic evaluation of the size-dependence of phase stabilities in this system. The much desired metastable tetragonal phase is stabilized at dimensions less than 3.6–3.8 nm, which is in good accord with predictions of thermodynamic models that take into account the competing influences of bulk free energy and specific surface energy.Conflict of interest
The authors declare no competing financial interest.Acknowledgements
The authors gratefully acknowledge support from the National Science Foundation under DMR 1504702. The authors would like to acknowledge that EDX analysis on the FE-SEM were performed at the Texas A&M University Materials Characterization Facility. The authors also want to acknowledge Dr Robert Dennis for help performing the EDX analysis of the nanopowders.Notes and references
- A. Navrotsky, ChemPhysChem, 2011, 12, 2207–2215 CrossRef CAS PubMed.
- T. Waitz, K. Tsuchiya, T. Antretter and F. D. Fischer, MRS Bull., 2009, 34, 814–821 CrossRef CAS.
- M. Grünwald, K. Lutker, A. P. Alivisatos, E. Rabani and P. L. Geissler, Nano Lett., 2013, 13, 1367–1372 Search PubMed.
- S. H. Tolbert and A. P. Alivisatos, Science, 1994, 265, 373–376 CAS.
- M. A. Lukowski, A. S. Daniel, F. Meng, A. Forticaux, L. Li and S. Jin, J. Am. Chem. Soc., 2013, 135, 10274–10277 CrossRef CAS PubMed.
- A. Ambrosi, Z. Sofer and M. Pumera, Chem. Commun., 2015, 51, 8450–8453 RSC.
- C. Wan, Y. N. Regmi and B. M. Leonard, Angew. Chem., Int. Ed., 2014, 53, 6407–6410 CrossRef CAS PubMed.
- R. C. Garvie, J. Phys. Chem., 1965, 69, 1238–1243 CrossRef CAS.
- J. Chevalier, L. Gremillard, A. V. Virkar and D. R. Clarke, J. Am. Ceram. Soc., 2009, 92, 1901–1920 CrossRef CAS.
- H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, P. J. Chupas and C. P. Grey, Science, 2014, 344, 1252817 CrossRef PubMed.
- R. Malik, F. Zhou and G. Ceder, Nat. Mater., 2011, 10, 587–590 CrossRef CAS PubMed.
- J. Gopalakrishnan, Chem. Mater., 1995, 7, 1265–1275 CrossRef CAS.
- J. M. Hodges, K. Kletetschka, J. L. Fenton, C. G. Read and R. E. Schaak, Angew. Chem., Int. Ed., 2015, 54, 8669–8672 CrossRef CAS PubMed.
- P. H. Mutin and A. Vioux, J. Mater. Chem. A, 2013, 1, 11504 CAS.
- P. H. Mutin and A. Vioux, Chem. Mater., 2009, 21, 582–596 CrossRef CAS.
- O. Hunter Jr, R. W. Scheidecker and S. Tojo, Ceramurgia Int., 1979, 5, 137–142 CrossRef.
- J. Joo, T. Yu, Y. W. Kim, H. M. Park, F. Wu, J. Z. Zhang and T. Hyeon, J. Am. Chem. Soc., 2003, 125, 6553–6557 CrossRef CAS PubMed.
- J. Tang, T. Zhang, P. Zoogman, J. Fabbri, S. W. Chan, Y. M. Zhu, L. E. Brus and M. L. Steigerwald, Adv. Funct. Mater., 2005, 15, 1595–1602 CrossRef CAS.
- J. Tang, J. Fabbri, R. D. Robinson, Y. Zhu, I. P. Herman, M. L. Steigerwald and L. E. Brus, Chem. Mater., 2004, 16, 1336–1342 CrossRef CAS.
- W. Zhou, S. V. Ushakov, T. Wang, J. G. Ekerdt, A. A. Demkov and A. Navrotsky, J. Appl. Phys., 2010, 107, 1–7 Search PubMed.
- I. M. Iskandarova, A. A. Knizhnik, E. A. Rykova, A. A. Bagatur'yants, B. V. Potapkin and A. A. Korkin, Microelectron. Eng., 2003, 69, 587–593 CrossRef CAS.
- S. V. Ushakov, A. Navrotsky, Y. Yang, S. Stemmer, K. Kukli, M. Ritala, M. A. Leskelä, P. Fejes, A. Demkov, C. Wang, B.-Y. Nguyen, D. Triyoso and P. Tobin, Phys. Status Solidi B, 2004, 241, 2268–2278 CrossRef CAS.
- B. Matovic, J. Pantic, J. Lukovic, M. Cebela, S. Dmitrovic, M. Mirkovic and M. Prekajski, Ceram. Int., 2016, 42, 615–620 CrossRef CAS.
- J. Qi and X. Zhou, Colloids Surf., A, 2015, 487, 26–34 CrossRef CAS.
- D. Cho, H. S. Jung, I. Yu, J. H. Yoon, H. K. Kim, S. Y. Lee, H. Jeon, S. Han, J. H. Kim, T. J. Park, B. Park and C. S. Hwang, Chem. Mater., 2012, 24, 3534–3543 CrossRef CAS.
- I. MacLaren, T. Ras, M. MacKenzie, A. J. Craven, D. W. McComb and S. De Gendt, J. Electrochem. Soc., 2009, 156, 103 CrossRef.
- R. R. Manory, T. Mori, I. Shimizu, S. Miyake and G. Kimmel, J. Vac. Sci. Technol., A, 2002, 20, 549 CAS.
- G. D. Wilk, R. M. Wallace and J. M. Anthony, J. Appl. Phys., 2001, 89, 5243 CrossRef CAS.
- A. O'Hara, G. Bersuker and A. A. Demkov, J. Appl. Phys., 2014, 115, 183703 CrossRef.
- X. Luo and A. A. Demkov, J. Appl. Phys., 2015, 118, 124105 CrossRef.
- X. Zhao and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 233106 CrossRef.
- H. Jiang, R. I. Gomez-Abal, P. Rinke and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 1–9 Search PubMed.
- R. Deshmukh and M. Niederberger, in The Sol-Gel Handbook-Synthesis, Characterization, and Applications, ed. D. Levy and M. Zayat, Wiley-VCH Verlag GmbH & Co. KGaA., 2015, pp. 29–49 Search PubMed.
- N. Pinna, G. Garnweitner, M. Antonietti and M. Niederberger, Adv. Mater., 2004, 16, 2196–2200 CrossRef CAS.
- T. J. Boyle, L. A. M. Steele, P. D. Burton, S. M. Hoppe, C. Lockhart and M. A. Rodriguez, Inorg. Chem., 2012, 51, 12075–12092 CrossRef CAS PubMed.
- A. Vioux, Chem. Mater., 1997, 9, 2292–2299 CrossRef.
- S. W. Depner, K. R. Kort and S. Banerjee, CrystEngComm, 2009, 11, 841 RSC.
- S. W. Depner, N. D. Cultrara, K. E. Farley, Y. Qin and S. Banerjee, ACS Nano, 2014, 8, 4678–4688 CrossRef CAS PubMed.
- S. W. Depner, K. R. Kort, C. Jaye, D. A. Fischer and S. Banerjee, J. Phys. Chem. C, 2009, 113, 14126–14134 CAS.
- T. V. Perevalov, V. A. Gritsenko, S. B. Erenburg, A. M. Badalyan, H. Wong and C. W. Kim, J. Appl. Phys., 2007, 101, 053704 CrossRef.
- K. R. Kort and S. Banerjee, Inorg. Chem., 2011, 50, 5539–5544 CrossRef CAS PubMed.
- K. R. Kort and S. Banerjee, Small, 2015, 11, 329–334 CrossRef CAS PubMed.
- G. R. Waetzig, G. A. Horrocks, J. W. Jude, L. Zuin and S. Banerjee, Nanoscale, 2016, 8, 979–986 RSC.
- L. Bourget, R. J. P. Corriu, D. Leclercq, P. H. Mutin and A. Vioux, J. Non-Cryst. Solids, 1998, 242, 81–91 CrossRef CAS.
- P. Arnal, R. J. P. Corriu, D. Leclercq, P. H. Mutin and A. Vioux, Chem. Mater., 1997, 9, 694–698 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., 1976, 32, 751–767 CrossRef.
- R. Dronskowski, in Computational Chemistry of Solid State Materials, Wiley-VCH Verlag GmbH & Co. KGaA, 2006, pp. 13–14 Search PubMed.
- J. E. Bailey, D. Lewis, Z. M. Librant and L. J. Porter, Trans. J. Br. Ceram. Soc., 1972, 71, 25–30 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sc01601d |
| This journal is © The Royal Society of Chemistry 2016 |