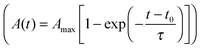Open Access Article
Open Access ArticleDistinct impacts of substrate elasticity and ligand affinity on traction force evolution†
Christina
Müller
and
Tilo
Pompe
*
Faculty of Biosciences, Pharmacy and Psychology, Universität Leipzig, Johannisallee 21-23, 04103 Leipzig, Germany. E-mail: tilo.pompe@uni-leipzig.de
First published on 30th September 2015
Abstract
Cell adhesion is regulated by the mechanical characteristics of the cell environment. The influences of different parameters of the adhesive substrates are convoluted in the cell response leading to questions on the underlying mechanisms, like biochemical signaling on the level of adhesion molecules, or viscoelastic properties of substrates and cell. By a time-resolved analysis of traction force generation during early cell adhesion, we wanted to elucidate the contributions of substrate mechanics to the adhesion process, in particular the impact of substrate elasticity and the molecular friction of adhesion ligands on the substrate surface. Both parameters were independently adjusted by (i) an elastic polyacrylamide hydrogel of variable crosslinking degree and (ii) a thin polymer coating of the hydrogel surface controlling the affinity (and the correlated substrate–ligand friction) of the adhesion ligand fibronectin. Our analysis showed two sequential regimes of considerable force generation, whose occurrence was found to be independent of substrate properties. The first regime is characterized by spreading of the cell and a succeeding force increase. After spreading cells enter the second regime with saturated forces. Substrate elasticity and viscosity, namely hydrogel elasticity and ligand affinity, were both found to affect the kinetics and absolute levels of traction force quantities. A faster increase and a higher saturation level of traction forces were observed for a higher substrate stiffness and a higher ligand affinity. The results complement recent modeling approaches on the evolution of forces in cell spreading and contribute to a better understanding of the dynamics of cell adhesion on viscoelastic substrates.
Introduction
Cells sense the mechanical properties of their microenvironment. This signaling process is facilitated by a complex interplay between transmembrane and intracellular proteins of multicomponent adhesion sites, which links the cytoskeleton with the extracellular matrix (ECM). The adhesion sites contain mechanosensitive proteins enabling the cells to respond to the stiffness of their ECM by applying forces and reorganizing its components.1,2 Viscoelastic properties of the ECM influence cell fate beyond simple adhesive forces. It is known that the proliferation, differentiation and migration of various cell types are affected by the mechanics of the surrounding ECM.3–8 Because of the polymeric nature of the ECM its mechanical properties are governed by the network characteristics, including the density and type of interconnections and the flexibility of network strands.9,10 Furthermore, not only the apparent stiffness of the matrix influences cell behavior, but also the mobility and availability of ligands of cell receptors.9,11–15 Although currently underappreciated in the literature, there are reports stating the impact of viscosity of intracellular components and ECM on cell adhesion and differentiation.8,10 The remodeling of the ECM accompanying cell adhesion and migration implies a continuous molecular friction of adhesion ligands and thus energy dissipation. Time-resolved analyses of cell adhesion processes are needed to decipher the impact of those external mechanical cues on mechanotransduction.16In this context it is known that cell size and shape are important factors controlling the force generation of adherent cells.2,17–20 Early cell adhesion has been intensely studied to reveal common features of cell spreading.21 Different phases of cell spreading were distinguished in correlation with distinct processes within the adhesion apparatus.22,23 The first contact of the cell and the flattening of the cell body are governed by membrane tension and the underlying actin cortex.23–27 It was shown that the initiation of fast spreading by cell protrusions formed by actin polymerization is dependent on the ligand density of the cell culture substrates.24 For the rate of spreading there are different findings. One report demonstrated a universal principle for a lot of cell types and substrate conditions.21 Other studies showed the cell spreading rate to depend on ligand density or substrate stiffness.5,28–31 In particular Nisenholz et al.31 showed that a detailed understanding of the mechanisms correlating cell spreading with traction force evolution is still missing. With the formation of primary small adhesion sites, nascent adhesions, by cell adhesion receptors of the integrin family, cells start to apply increasing forces to the substrate.28 On the other hand it is also known that resistive forces from the substrate are necessary for the formation of adhesion sites.15 At later stages of cell spreading, the increase of adhesive area slows down and cells start to polarize.23,32 At this stage nascent adhesions mature to large focal adhesions and a contractile actin cytoskeleton is developed.2,28,32 Recent findings support the tight sequence of spreading, traction force generation and adhesion formation.33
During the last decade much evidence has been gathered of a stiffness dependent force generation of cells. Traction force microscopy allows for the assignment of traction forces down to the scale of single focal adhesions.34,35 Growth dynamics and corresponding forces of adhesion sites could be resolved on the time scale of seconds.36 In this context, it has been reported that even small nascent adhesions are able to exert considerable forces.37–39 In contrast, other studies state that force magnitude depends linearly on adhesion area, while traction stress correlates with substrate stiffness.40
On the cell level there is an ongoing discussion how the overall cellular traction force is regulated depending on ECM parameters.30,41 The force balance on the cellular length scale and the state of the contractile actin cytoskeleton – and not the force balance at single adhesion sites – are considered as the regulating factors for force homeostasis of cells.20,33,40,42,43 However, the multitude of influencing parameters, including substrate viscoelasticity, ligand density and arrangement, cell type and their limited observation in a single experiment, led to various partly contradicting results and interpretations.13,19,20,44,45 In particular, viscous contributions, like friction at the cell–substrate interface, were hardly addressed up to now, although their impact on cellular traction forces was shown.13 Two very recent studies addressed the importance and options to investigate the friction between the cell surface and the surrounding support.31,46 Hence it is expected that a closer look on the dynamics of traction force generation depending on controlled viscous and elastic properties of the cell culture substrate will help to better understand the underlying mechanisms.
In this study, we addressed this topic by investigating the early cell spreading and the congruent generation of cell traction forces depending on substrate stiffness and ligand affinity, the latter being correlated with a sliding friction of adhesion ligands.14 Within the first 2 h of cell adhesion of human umbilical cord vein endothelial cells (HUVECs), different regimes of spreading and traction force generation could be revealed. In addition to an elasticity dependent traction force response, an additive effect of the ligand affinity on the force generation was found, in agreement with our earlier findings.13,14 Our results agree with recent experimental and theoretical work.30,31 The description of the cell–substrate friction in these modeling approaches can be linked to our controlled variation of ligand affinity. Hence, our work underpins the idea that friction phenomena at the cell–substrate interface are essential for a detailed description of mechanosensitive cell adhesion.
Materials and methods
Preparation of polyacrylamide hydrogels
Polyacrylamide hydrogels with defined ligand affinity and stiffness were prepared for cell traction force measurements as described in more detail elsewhere.13 Briefly, glass coverslips of 22 mm diameter were cleaned by ultrasonication in ultrapure water (MilliQ) and ethanol (p.a., AppliChem GmbH, Darmstadt, Germany). Organic remnants were removed by oxidative cleaning for 10 min in a solution of ultrapure water, 25% ammonium hydroxide (Grüssing GmbH, Filsum, Germany) and 30% hydrogen peroxide (Merck KGaA, Darmstadt, Germany) at a ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 70 °C. After washing in ultrapure water glass coverslips were functionalized by immersion in a solution of 20 mM (3-acryloxypropyl)-trimethoxysilane (Alfa Aeser, Ward Hill, MA, USA) in 20
1 at 70 °C. After washing in ultrapure water glass coverslips were functionalized by immersion in a solution of 20 mM (3-acryloxypropyl)-trimethoxysilane (Alfa Aeser, Ward Hill, MA, USA) in 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethanol (p.a.) and ultrapure water for 2 h. Finally, coverslips were rinsed in ethanol twice, and dried in a nitrogen stream and a drying oven (Heraeus, Thermo Scientific GmbH, Braunschweig, Germany) at 120 °C for 1 h.
1 ethanol (p.a.) and ultrapure water for 2 h. Finally, coverslips were rinsed in ethanol twice, and dried in a nitrogen stream and a drying oven (Heraeus, Thermo Scientific GmbH, Braunschweig, Germany) at 120 °C for 1 h.
Polyacrylamide hydrogels with defined elasticity were prepared from stock solutions of 30% acrylamide and 2% N,N′-methylenebisacrylamide (Carl Roth, Karlsruhe, Germany) in varying ratios, 0.8 wt% tetramethylethylenediamine (AppliChem GmbH), 0.5 wt% ammonium persulfate (Merck) and 0.5 μm green-fluorescent microspheres (Molecular Probes, Life Technologies, Darmstadt, Germany) were embedded. The solution was pipetted on a non-wetting coverslip (coated with Sigmacote, Sigma Aldrich, St. Louis, MO, USA) and subsequently covered by the coverslip. After 20 min polymerization the silanized coverslip with the hydrogel was gently lifted, washed in ultrapure water for 30 min and dried in a vacuum oven (Memmert, Schwabach, Germany) at room temperature and 5 bar for 45 min.
For the preparation of substrate surfaces with a tuned affinity for adhesion ligands, the dried hydrogel layers were spin-coated (Spin 150, SPS Europe B.V., TS Putten, Netherlands) with a solution of maleic anhydride copolymers. Solutions of 0.14 wt% poly(styrene-alt-maleic anhydride) (PSMA, MW = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) in tetrahydrofuran (p.a., AppliChem GmbH) or 0.3 wt% poly(ethene-alt-maleic anhydride) (PEMA, MW = 125
000 g mol−1) in tetrahydrofuran (p.a., AppliChem GmbH) or 0.3 wt% poly(ethene-alt-maleic anhydride) (PEMA, MW = 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) in 1
000 g mol−1) in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 acetone (p.a., AppliChem GmbH) and tetrahydrofuran were used for the spin-coating process. The monomolecular maleic anhydride copolymer film (dry thickness: a few nm)47,48 is attached to the surface of the polyacrylamide hydrogel providing a modulated affinity of adsorbed fibronectin ligands due to the hydrophobicity and polarity of the maleic anhydride copolymer surface13,49,50 (an in-depth chemical analysis of the covalent coupling scheme of the maleic anhydride copolymers to polyacrylamide hydrogels will be published in a forthcoming publication). As the monomolecular polymer layer swells under aqueous conditions the mechanical properties of the bulk hydrogel substrate are not altered.13,48 Finally, coverslips were fixed in punched polystyrene Petri dishes and washed three times in phosphate buffered saline (PBS, Biochrom, Berlin, Germany) to remove non-bound polymers and stored in PBS overnight at 4 °C. Young's modulus of hydrogel layers was determined by scanning force spectroscopy (Nanowizard3, JPK Instruments, Berlin, Germany), ranging from 2.5 kPa to 9 kPa.
2 acetone (p.a., AppliChem GmbH) and tetrahydrofuran were used for the spin-coating process. The monomolecular maleic anhydride copolymer film (dry thickness: a few nm)47,48 is attached to the surface of the polyacrylamide hydrogel providing a modulated affinity of adsorbed fibronectin ligands due to the hydrophobicity and polarity of the maleic anhydride copolymer surface13,49,50 (an in-depth chemical analysis of the covalent coupling scheme of the maleic anhydride copolymers to polyacrylamide hydrogels will be published in a forthcoming publication). As the monomolecular polymer layer swells under aqueous conditions the mechanical properties of the bulk hydrogel substrate are not altered.13,48 Finally, coverslips were fixed in punched polystyrene Petri dishes and washed three times in phosphate buffered saline (PBS, Biochrom, Berlin, Germany) to remove non-bound polymers and stored in PBS overnight at 4 °C. Young's modulus of hydrogel layers was determined by scanning force spectroscopy (Nanowizard3, JPK Instruments, Berlin, Germany), ranging from 2.5 kPa to 9 kPa.
Cell culture of human umbilical cord vein endothelial cells
Human umbilical cord vein endothelial cells (HUVECs) were isolated from umbilical cords of healthy females after informed consent according to a procedure published elsewhere.13 All consent procedures were approved by the local ethics committee. HUVECs were grown in culture medium supplemented with 2% fetal calf serum (Promocell, Heidelberg, Germany). The medium was substituted three times a week and the cells were split when they reached confluence. For experiments cells from the 2nd to the 5th passage were used. Cells were washed with PBS and then detached with a solution of 0.25% trypsin–EDTA (Sigma Aldrich) at 37 °C for 2 min, centrifuged and re-suspended in culture medium for seeding on hydrogel substrates.Traction force microscopy
Prior to experiments hydrogel-coated coverslips were washed with PBS and coated with 50 μg ml−1 fibronectin (purified from human plasma) in PBS for 1 h, as described recently.13 Coverslips were washed again with PBS. Cell medium was added 10 min prior to cell seeding to equilibrate the substrates at 37 °C. Meanwhile the Petri dish with the hydrogel substrate was placed in an incubation chamber (PeCon, Erbach, Germany) of an inverted microscope with scanning stage (AxioObserver.Z1, objective: Plan-Apochromat 20×/0.8, 1.6× Optovar, Carl Zeiss Microscopy, Jena, Germany) at 37 °C and cells were seeded with a density of 3000 cm−2 in order to prevent cell–cell contacts. Cell positions were marked with the microscope software (ZEN 2012, Carl Zeiss Microscopy, Jena, Germany). During the first 2 h of cell adhesion a fluorescence image of the fluorescent microbeads at the topmost hydrogel layer and a DIC image of the cell were taken every 3 min. After 2 h the cells were detached by trypsin–EDTA and a z-stack of fluorescence images of the upper hydrogel layer at intervals of 0.5 μm over 10 μm was taken to account for possible drifts in the z-direction. Z-Drifts were minimized during the experiment by the autocorrection function of the microscope (Definite Focus, Carl Zeiss Microscopy).Image analysis
The open source software ImageJ (NIH, Bethesda, MD, USA) was used for preprocessing of image stacks. Drifts in the lateral direction were corrected with the StackReg plugin.51 The cell border was determined manually from the DIC image. The processed image stacks were imported into a home-built traction force analysis routine written in MATLAB (MathWorks, Ismaning, Germany). The routine relies on Fourier transform traction force cytometry (FTTC) in the unconstrained approach, as introduced by Butler et al.52 with additional improvements and corrections, see also ref. 34 and 53. It is derived from elastic theory and assumed the hydrogel to be linearly elastic. (Although we consider a viscous contribution in our experiments by the sliding friction of the adhesion ligands, the linear elastic approach of the traction force measurement is still valid. The sliding of adhesion ligands occurs on a much larger time scale than the elastic response of the polyacrylamide hydrogel leaving the traction force analysis unaffected by the viscous contribution.) The displacement field![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) was calculated by an iterative crosscorrelation method.53 The displacement field was filtered to decrease noise and render reliable results, see also ref. 34. The traction stress field
was calculated by an iterative crosscorrelation method.53 The displacement field was filtered to decrease noise and render reliable results, see also ref. 34. The traction stress field ![[T with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0054_20d1.gif) was calculated from the displacement field with a Poisson's ratio of ν = 0.48. Although the cell border was determined, we used the unconstrained approach for the traction stress calculation. It is known to better perform concerning traction stress artifacts at the cell border. Furthermore, some cell features were not resolved in the DIC images and a correct cell border analysis is proved to be difficult for the investigated time. For the following analysis a cell border with a small dilation of 4 μm was nevertheless used to set the traction stress field to zero outside of the cell to eliminate small background fluctuations. The pixel size of the reconstructed traction stress field was 3.2 μm.
was calculated from the displacement field with a Poisson's ratio of ν = 0.48. Although the cell border was determined, we used the unconstrained approach for the traction stress calculation. It is known to better perform concerning traction stress artifacts at the cell border. Furthermore, some cell features were not resolved in the DIC images and a correct cell border analysis is proved to be difficult for the investigated time. For the following analysis a cell border with a small dilation of 4 μm was nevertheless used to set the traction stress field to zero outside of the cell to eliminate small background fluctuations. The pixel size of the reconstructed traction stress field was 3.2 μm.
Total traction force Ftot was calculated by summing up the magnitude of all traction stress vectors within the cell border multiplied by cell area. The net contractile moment Mnet was determined as the trace of the first force moment matrix 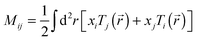 . The strain energy U was calculated by
. The strain energy U was calculated by 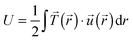 and denotes the energy stored in the hydrogel deformation. Tmax was determined as the maximum traction stress within one traction stress field.
and denotes the energy stored in the hydrogel deformation. Tmax was determined as the maximum traction stress within one traction stress field.
Data analysis
The analysis of the force curves was performed using 55 time-resolved data sets from 10 independent experiments. Curve analysis was performed using the open-source software R (R foundation of Statistical Computing, Vienna, Austria). For analysis of Ftot(t) the force curves were shifted in time to set time point zero at the start of the fast spreading as determined by eye from the area curves. Data smoothing was performed with a non-weighted moving average filter over 5 time points (equal to a time interval of 15 min). The first local maximum was determined from the smoothed curve. The force curves can be divided into two regimes, one with a fast force increase (regime 1, R1) and one with a constant plateau (regime 2, R2). The transition time tR1–R2 between the two regimes was set to be the time point where the total force reached 80% of its value at the local maximum.Other analyses were performed with non-smoothed force curves. In regime 1 a linear fit was applied to the time interval containing force values whose magnitude was between 15% and 80% of the local maximum. For the time interval of regime 2 (between the transition time and the end of measurement after 2 h) the geometric mean of force values was calculated, because the force values in regime 2 follow a log-normal distribution. These values were termed plateau values. Averaged values derived from different curves are shown as arithmetic mean ± standard error unless noted otherwise. Statements of statistical significance were evaluated by means of a multi-way ANOVA test with p < 0.05.
Results and discussion
The present study aimed to reveal the traction force evolution during early cell adhesion under varying conditions of substrate mechanics with the focus on a viscous contribution by a sliding friction of adhesion ligands. In previous work13,14 we introduced a hydrogel layer system with a monomolecular polymeric surface modification to independently adjust the bulk stiffness of the hydrogel substrate and the affinity of surface-bound fibronectin, see Fig. 1. It was demonstrated that the surface modification of the hydrogel layer by a covalently attached maleic anhydride copolymer layer leaves the elastic properties of the hydrogel layer unchanged, but modulates the affinity of adsorbed fibronectin by the hydrophobicity and polarity of the maleic anhydride copolymer surface.13,49,50 Protein exchange experiments and recent adhesion energy measurements using soft colloidal probes proved the high and low affinity of fibronectin for PSMA and PEMA surfaces, respectively.13 The modulated fibronectin affinity leads to an adjustable molecular friction between the adhesion ligands and the hydrogel surfaces in the cell adhesion process. The transport of fibronectin ligands at the cell–substrate interface via the integrin receptors and acto-myosin apparatus was quantitatively described by a molecular friction model based on thermally activated rupture of weak non-covalent bonds under external force.14 This dissipative friction process was demonstrated to control cell traction forces, being a slow dissipation process on the time scale in the order of seconds. On the other site the polyacrylamide hydrogel can be treated as ideally elastic. Thus the experimental setup provides a system with an independent control of elastic and viscous contributions to cell substrate mechanics. Using this setup we now aimed to investigate the time-resolved evolution of spreading and traction forces in cell adhesion depending on substrate elasticity and ligand affinity.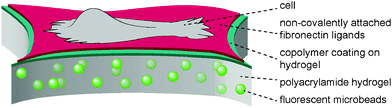 | ||
| Fig. 1 Scheme of substrate design with a polyacrylamide hydrogel layer of varying crosslinking degree and elasticity as well as a surface coating with maleic anhydride copolymers, allowing for the adsorption of adhesion ligands (fibronectin) with varying affinity due to variation in polarity and hydrophobicity of the polymer coating.56 | ||
Regimes of traction force evolution during early cell adhesion
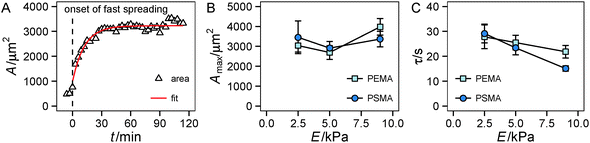
First we looked at the spreading behavior of the cells, as it is correlated with traction force generation.33 After seeding, cells on the substrate remained in a spherical shape for a variable lag phase. Then fast spreading started with a sharp increase in the cell area. After roughly 30 min, spreading slowed down and cell area saturated at a maximum with only weak changes in area during the remaining observation time, see also Fig. S1 (ESI†). Using a simple exponential fit we characterized the time course and the extent of spreading (Fig. 2A). For the range of investigated substrate stiffness we did not find a statistically significant influence of substrate elasticity on the maximum spread area (Fig. 2B and Fig. S1, ESI†). While there are negligible changes at low substrate stiffness (2.5 kPa to 5 kPa), also at higher stiffness (5 kPa to 9 kPa) only a weak tendency of increasing area with increasing stiffness was observed. For the characteristic time τ a decrease with increasing stiffness was found in general, while the high-affinity substrates (PSMA) had a higher slope than the low-affinity substrates (PEMA) (Fig. 2C).The time course of spreading is in accordance with the spreading phases introduced by Dubin-Thaler et al.23 The lag phase corresponds to P(hase)0, fast spreading is related to P1 and P2 is entered as spreading slows down and the maximum area is reached. Referring to the substrate property dependence our findings are somewhat contradictory to studies that state a stiffness dependent cell area for fully spread cells.5,11,44 The weak increase for stiffer substrates found in our work, which did not prove to be statistically significant, might be related to the fact that this behavior depends on the investigated cell type and the range of substrate stiffness. Weng et al.43 reported a severe stiffness sensitivity of HUVECs on PDMS micropost arrays, whose effective stiffness range is in a comparable range to that of our substrates. The reported spread areas at 10 kPa are of the same magnitude (3000 μm2) as in our experiments, but a dramatic decrease of spread area on soft substrates (at around 1 kPa) was reported in the cited study. The negligible effect observed in our experiments may be accounted for the different substrate properties (limited adhesive area on microposts, independent deformation of microposts) or variations in cell culture conditions (cell culture medium). The observation that ligand affinity has no impact on cell area agrees with previous findings: one can assume that the high ligand density used herein enables the cells to reach a fully spread state, because of the high availability of ligands for cell adhesion, masking effects of the substrate affinity on spreading.13 The trend of the characteristic time τ is interesting in the context of recent modeling efforts,29,31 which indicated a similar trend of faster spreading on stiffer substrates. Furthermore, the nonlinear model introduced therein31 suggests a smaller slope for substrates with a lower cell–substrate friction. The friction coefficient of the model was assumed to depend on substrate stiffness as well as on binding/unbinding events and density of ligand–receptors pairs. A lowering of ligand affinity to the underlying substrate, as in our setup, can be interpreted as an increase of the unbinding rate constant in the model leading to a weaker dependence of the friction coefficient on substrate stiffness. This model prediction nicely fits our experimental observations.
The spreading of cells is closely linked to the generation of traction forces. Therefore, we compared the time course of total force Ftot with the development of cell area during cell adhesion as shown for a typical example in Fig. 3A and B (see also Fig. S2, ESI†). After a short, initial phase of very weak forces, a phase of fast, nearly linear increase of Ftot was observed, saturating at later stages. The phase of fast increase of Ftot was delayed relative to the phase of fast increase in cell area by 10 min in the example shown, while average retardation time from all experiments was around 25 min. Hence, the time course of traction force evolution can be subdivided into two distinct regimes. During the very first phase, cells do not exert considerable forces, but start to quickly increase spread area. We refer to this phase as ‘regime 0’, because we focus on regimes with considerable traction forces in our analysis. Regime 0 is followed by a regime with a fast and linear increase in traction force correlated with a further small increase in area. This phase is referred to as ‘regime 1’ in the following (see Fig. 3C). As traction forces and cell area saturate later on, ‘regime 2’ is entered. In regime 2 traction forces do not exceed a certain force level, which is known to be influenced by the cell type's specific contractility and whose magnitude is given by substrate characteristics (see next section). After traction force saturation, fluctuations and relaxation of traction forces were sometimes observed, which were also reported in the literature.19,54 These phenomena were not examined herein.
Little is known about the relationship between spreading and traction force evolution in early cell adhesion. Reinhart-King et al. reported a linear correlation of total cell force and cell area during spreading even at times when actin stress fibers had not yet been assembled.28 Other measurements using cantilever based force sensors showed that the fast increase of contractile forces coincides with the formation of small paxillin stained adhesion sites.33 These reports are in line with our findings. We always observed a time lag between area and traction force increase. Recent experiments and modeling approaches further support these results.30,31
At late time points (regime 2) the traction force increase was low, forces saturated or even decreased. The latter events are often caused by a change in cell behavior. For example, the cell locally retracts its cell edge or reorients its axis, which is accompanied by the assembly and disassembly of adhesion sites. The actin cytoskeleton might account for this drop in cell traction forces. It is known that the adaptation of the contractile actin cytoskeleton in response to external forces leads to a force relaxation,54 too. Fluctuations in forces have also been reported for cells that had enough time to settle and equilibrate their forces.19 In the following, the forces in regime 2 will be treated as fluctuating around a mean value, which is given by the cell's contractility and substrate characteristics, and which describes the force homeostasis of the cell.
Substrate dependent magnitude of traction force
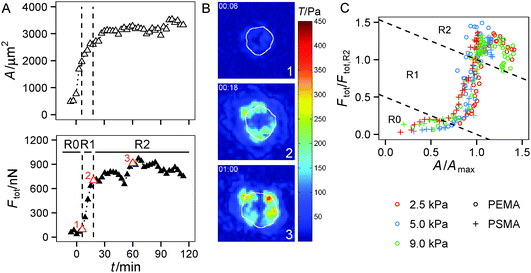
In the following we investigated in more detail if the substrate parameters, i.e. the hydrogel's Young's modulus and the ligand affinity of the polymer coating, differentially affect both regimes of traction force evolution. We used a set of 6 substrate conditions with a variation of Young's modulus of 2.5 kPa, 5 kPa and 9 kPa as well as polymer coatings providing a low (PEMA) and high (PSMA) affinity for the adhesion protein fibronectin. We showed earlier in static measurements13 that the impact of ligand affinity and stiffness on traction force can be decoupled. Therein we found higher maximum traction stress for a higher ligand affinity independent of substrate elasticity. Furthermore, strain energy invested by the cells into the substrate was shown to be indirectly proportional to substrate's Young's modulus. Based on these earlier findings, we restricted our time-resolved investigations to a stiffness range shown to be relevant for HUVECs in our experimental setup.From a brief look a dependence of the slope of Ftot(t) in regime 1 on substrate elasticity was apparent, see Fig. 4A. By a linear fit within the time frame of regime 1, we found a higher rate of traction force increase for stiffer gels, depicted in Fig. 4B. In addition, a slight but constant offset to higher rates of force increase was found for the polymer coating with higher fibronectin affinity (PSMA) at each elasticity. These higher rates correlate with smaller transition times tR1–R2 between regime 1 and regime 2 (Fig. 4C), supporting the above statements. Hence, on stiff hydrogels (9 kPa) the transition to regime 2 occurred at about 35 min, whereas on soft hydrogels (2 kPa) it took about 50 min until traction force saturated. Both effects of faster increase and earlier saturation of Ftot did not completely compensate. Thus, the plateau values of Ftot in regime 2 were not equal for all conditions (Fig. 4D). The plateau values of Ftot increased with the hydrogels' Young's modulus in a nonlinear manner with a weaker increase for higher stiffness. Furthermore, higher ligand affinity (PSMA) resulted in a constant offset to higher plateau values of Ftot.
The same trends (as for Ftot, i.e. faster saturation and higher plateau values) were observed for the first moment of contractile force, the net contractile moment Mnet, which was evaluated, too (data not shown). For the calculation of Mnet the centripetal part of traction forces is weighted by the distance to the cell center, thus cell polarization would be manifested in Mnet. As mentioned earlier, the cells held an almost circular morphology over the observed time period without significant occurrence of polarization and elongation. In addition, the localization of traction forces at cell borders was inherent to cells on all substrates. As a result Ftot and Mnet have similar dynamics during early cell adhesion.
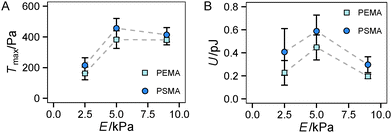
Finally, we had a look on two other indicators of traction forces in regime 2, the maximum traction stress Tmax and strain energy U. While Tmax is in general more noisy due to its restriction to a local point, we previously suggested it as a sensitive measure of force regulation on the length scale of receptors and adhesion sites.13 In our current study, we found a sharp increase of Tmax from 2.5 kPa to 5 kPa but no further increase for stiffer substrates (see Fig. 5A). Thus the saturation of the traction force, which was found for Ftot at high stiffness (Fig. 4D), is more apparent for Tmax with no further increase above the value at 5 kPa. This finding can be related to the difference in the local and global characteristics of Tmax and Ftot, respectively. The cells reach their maximum traction force at single adhesion sites already around a substrate stiffness of 5 kPa, however, an increase of integrated global traction forces can occur by the formation of additional traction force centers distributed over the cell area. The difference in Tmax between the substrates with different affinities is not as pronounced as for the total force Ftot, but again a constant offset to higher traction stress was observed for a higher ligand affinity (PSMA).
Another trend was found for the strain energy U, the energy stored in the gel by the adherent cell (Fig. 5B). A maximum of U was observed for medium stiffness, which can be related to the observed stiffness dependence of Ftot. The increase in strain energy from soft to medium stiffness correlates with the sharp increase in Ftot. At higher stiffness almost no additional increase in traction forces was observed, which results in the observed decrease in U as strain at constant force decreases with increasing stiffness, recall 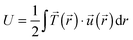 . For the lower stiffness range the strong force increase dominates the impact on U. This leads to the observed behavior of U with a maximum at an intermediate Young's modulus of 5 kPa.
. For the lower stiffness range the strong force increase dominates the impact on U. This leads to the observed behavior of U with a maximum at an intermediate Young's modulus of 5 kPa.
The impact of the cell–substrate friction on traction force evolution
The correlation of cell traction forces with substrate stiffness has been intensely investigated not only on the scale of single focal adhesions, but also for the force homeostasis of whole cells.19,44,54 Similar to our results there are reports on a saturation of forces with increasing stiffness.55 We wanted to decipher the impact of elastic (substrate stiffness) and viscous properties (ligand–substrate friction) of the substrate on the cell's response in early cell adhesion.In agreement with other recent studies31 traction forces are not only higher on stiffer substrates after cells reached a steady state but higher force magnitudes are already apparent at traction force increase during cell spreading. This is interesting, because focal adhesions and stress fibers, as some cellular structures known to be stiffness sensitive, have not yet been assembled to fully functional units at this stage.
The impact of ligand affinity was apparent in all regimes of considerable force generation, implying its direct impact on regulatory cell components. More precisely, increasing ligand affinity caused an increase of traction force (Fig. 4D). This behavior is superimposed onto the elasticity dependence. The higher traction force at higher ligand affinity was already apparent at the early stage of traction force evolution with higher slopes in the total force increase (Fig. 4B).
The affinity between adsorbed ligands and the underlying substrate is known to influence the force balance of cells and thus the formation of adhesion sites.13,14 In this earlier work we demonstrated a direct correlation of modulated ligand–substrate affinity and traction force magnitude, see also the short summary in the beginning of the results section. Additionally, the mobility of adhesion ligands under external forces is known to affect the assembly of mechanosensitive adhesion sites.15
From the above findings and statements we conclude that part of the cell's contractile work is dissipated in the ligand layer due to the substrate–ligand friction. This energy dissipation depends on the ligand affinity and the resulting molecular ligand friction on the underlying polymer. Only a fraction of cellular contractile work is stored as substrate deformation in the underlying hydrogel via the integrin–fibronectin link. Both processes, the elastic hydrogel deformation and the viscous ligand friction, contribute independently to substrate's mechanical properties as the process of hydrogel deformation can be treated as linearly elastic on the time scale of the dissipative friction process (some seconds). One can roughly estimate the dissipated power of the friction process taking Ftot (≈103 nN) and the ligand frictional drag velocity vd (≈10−1 μm s−1).14 An upper estimation of the dissipated power of approx. 10−1 pJ s−1 and the reasonable assumption of a seconds time scale of the traction force generation (e.g. life time of integrin–fibronectin bond) suggest a considerable influence of this viscous contribution on cell behavior when compared with the elastic deformation energy of the substrate U (≈0.5 pJ). This estimation correlates with our findings that an impact of ligand affinity could be observed in the experiments on traction force evolution. Furthermore, this mechanism should already act at early time periods of force evolution as characteristic differences are already found there. Therefore, it can be concluded that matured focal adhesions are not required for traction force generation and affinity-dependent ligand friction occurs on the molecular level of small clusters or single ligand–receptor pairs.
As there are only a few publications available considering the cell–substrate friction as a relevant parameter in cell adhesion, we have to discuss our findings in the light of two recent publications, which deal with the impact of the cell–substrate friction on cell spreading, adhesion and migration. Bergert et al.46 illustrated that the membrane–substrate friction can control cell migration under fluid drag. Their experiments and quantitative modeling showed that a cell–substrate friction coefficient in the order of 104 Pa s m−1 can regulate this process. This value together with a cell area in the order of 103 μm2 corresponds well with an affinity controlled ligand mobility of 105 m N−1 s−1 in our setup as earlier derived by Pompe et al.14
Another model introduced by Nisenholz et al.31 allows us to directly discuss the impact of the cell–substrate friction on the traction force evolution. Although the substrate–ligand friction was not explicitly introduced in the model, the cell–substrate friction is described in terms of binding/unbinding events on the receptor–ligand level, see also the discussion in the first part of the results section. It can be reasonably assumed that a molecular sliding friction of the ligand on the substrate, as introduced by Pompe et al.,14 can be handled in the same framework. An increase of the substrate–ligand friction, like the change from low affinity substrates (PEMA) to high affinity substrates (PSMA), can be described as an effective decrease of the unbinding rate constant in the model of Nisenholz et al., leading to an increase of the effective interfacial friction coefficient ξs. It is very interesting to note that with this assumption the nonlinear model nicely captures our experimental findings of an increase of Ftot, and a steeper negative slope of τ(E) (Fig. 2C) at a higher substrate–ligand affinity. Hence, we suggest both models as good starting points for an explicit description of the substrate–ligand friction.
Conclusion
Two main findings can be derived from this study of traction force evolution during the first two hours of cell adhesion. Firstly, independent of substrate stiffness and ligand affinity, two different regimes can be recognized in the force curves, indicating robust mechanisms behind traction force generation. Secondly, substrate stiffness and ligand affinity influence parameters of traction force evolution. An increasing stiffness of the hydrogel substrate elicits both a faster increase and a higher saturation value of traction force. An increase in ligand affinity imposes an additive effect on the force (i.e. an offset towards higher values) within the investigated stiffness range, which can be accounted for the well-separated elastic (linearly elastic hydrogel) and viscous (ligand friction on the seconds time scale) contributions to substrate mechanics. Thus the contractile work of the cell dissipates in part in the ligand–substrate layer by molecular friction and only parts are stored in the hydrogel.In summary, our study proves that the cell–substrate friction has a considerable influence on the adaption of cells to their surroundings. It demonstrates viscoelasticity of the extracellular environment not only to affect the magnitude of traction forces but also determine the dynamics of force evolution in an additive way, already at early time periods of cell spreading without a fully established focal adhesion and stress fiber apparatus. We expect our experimental findings to stimulate further progress in the description of the dynamic cell behavior in viscoelastic environments.
Acknowledgements
The authors want to acknowledge financial support from the Deutsche Forschungsgemeinschaft (grant: DFG PO713/7-1) and support for a live cell microscope by EFRE and Free State of Saxony (grant: SAB 100144684). C.M. thanks Andreas Müller for helpful discussions.References
- B. Geiger, J. P. Spatz and A. D. Bershadsky, Nat. Rev. Mol. Cell Biol., 2009, 10, 21–33 CrossRef CAS PubMed.
- M. Prager-Khoutorsky, A. Lichtenstein, R. Krishnan, K. Rajendran, A. Mayo, Z. Kam, B. Geiger and A. D. Bershadsky, Nat. Cell Biol., 2011, 13, 1457–1465 CrossRef CAS PubMed.
- C. M. Lo, H. B. Wang, M. Dembo and Y. L. Wang, Biophys. J., 2000, 79, 144–152 CrossRef CAS PubMed.
- M. J. Paszek, N. Zahir, K. R. Johnson, J. N. Lakins, G. I. Rozenberg, A. Gefen, C. A. Reinhart-King, S. S. Margulies, M. Dembo, D. Boettiger, D. A. Hammer and V. M. Weaver, Cancer Cell, 2005, 8, 241–254 CrossRef CAS PubMed.
- T. Yeung, P. C. Georges, L. A. Flanagan, B. Marg, M. Ortiz, M. Funaki, N. Zahir, W. Y. Ming, V. Weaver and P. A. Janmey, Cell Motil. Cytoskeleton, 2005, 60, 24–34 CrossRef PubMed.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Cell, 2006, 126, 677–689 CrossRef CAS PubMed.
- J. P. Fu, Y. K. Wang, M. T. Yang, R. A. Desai, X. A. Yu, Z. J. Liu and C. S. Chen, Nat. Methods, 2011, 8, 184 CrossRef CAS.
- A. R. Cameron, J. E. Frith and J. J. Cooper-White, Biomaterials, 2011, 32, 5979–5993 CrossRef CAS PubMed.
- B. Trappmann, J. E. Gautrot, J. T. Connelly, D. G. T. Strange, Y. Li, M. L. Oyen, M. A. C. Stuart, H. Boehm, B. J. Li, V. Vogel, J. P. Spatz, F. M. Watt and W. T. S. Huck, Nat. Mater., 2012, 11, 642–649 CrossRef CAS PubMed.
- C. Müller, A. Müller and T. Pompe, Soft Matter, 2013, 9, 6207–6216 RSC.
- A. Engler, L. Bacakova, C. Newman, A. Hategan, M. Griffin and D. Discher, Biophys. J., 2004, 86, 617–628 CrossRef CAS PubMed.
- N. D. Gallant, K. E. Michael and A. J. Garcia, Mol. Biol. Cell, 2005, 16, 4329–4340 CrossRef CAS PubMed.
- T. Pompe, S. Glorius, T. Bischoff, I. Uhlmann, M. Kaufmann, S. Brenner and C. Werner, Biophys. J., 2009, 97, 2154–2163 CrossRef CAS PubMed.
- T. Pompe, M. Kaufmann, M. Kasimir, S. Johne, S. Glorius, L. Renner, M. Bobeth, W. Pompe and C. Werner, Biophys. J., 2011, 101, 1863–1870 CrossRef CAS PubMed.
- P. Dillard, R. Varma, K. Sengupta and L. Limozin, Biophys. J., 2014, 107, 2629–2638 CrossRef CAS PubMed.
- V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265–275 CrossRef CAS PubMed.
- C. A. Reinhart-King, M. Dembo and D. A. Hammer, Langmuir, 2003, 19, 1573–1579 CrossRef CAS.
- A. D. Rape, W. H. Guo and Y. L. Wang, Biomaterials, 2011, 32, 2043–2051 CrossRef CAS PubMed.
- S. J. Han, K. S. Bielawski, L. H. Ting, M. L. Rodriguez and N. J. Sniadecki, Biophys. J., 2012, 103, 640–648 CrossRef CAS PubMed.
- P. W. Oakes, S. Banerjee, M. C. Marchetti and M. L. Gardel, Biophys. J., 2014, 107, 825–833 CrossRef CAS PubMed.
- D. Cuvelier, M. Théry, Y. S. Chu, S. Dufour, J. P. Thiéry, M. Bornens, P. Nassoy and L. Mahadevan, Curr. Biol., 2007, 17, 694–699 CrossRef CAS PubMed.
- H. G. Döbereiner, B. Dubin-Thaler, G. Giannone, H. S. Xenias and M. P. Sheetz, Phys. Rev. Lett., 2004, 93, 108105 CrossRef PubMed.
- B. J. Dubin-Thaler, J. M. Hofman, Y. Cai, H. Xenias, I. Spielman, A. V. Shneidman, L. A. David, H. G. Döbereiner, C. H. Wiggins and M. P. Sheetz, PLoS One, 2008, 3, e3735 Search PubMed.
- B. J. Dubin-Thaler, G. Giannone, H. G. Döbereiner and M. P. Sheetz, Biophys. J., 2004, 86, 1794–1806 CrossRef CAS PubMed.
- L. L. Norman, J. Brugués, K. Sengupta, P. Sens and H. Aranda-Espinoza, Biophys. J., 2010, 99, 2715 CrossRef CAS.
- L. Norman, K. Sengupta and H. Aranda-Espinoza, Eur. J. Cell Biol., 2011, 90, 37–48 CrossRef CAS PubMed.
- M. P. Murrell, R. Voituriez, J. F. Joanny, P. Nassoy, C. Sykes and M. L. Gardel, Nat. Phys., 2014, 10, 163–169 CrossRef CAS.
- C. A. Reinhart-King, M. Dembo and D. A. Hammer, Biophys. J., 2005, 89, 676–689 CrossRef CAS PubMed.
- J. J. Li, D. Han and Y. P. Zhao, Sci. Rep., 2014, 4, 3910 Search PubMed.
- Y. Brill-Karniely, N. Nisenholz, K. Rajendran, Q. Dang, R. Krishnan and A. Zemel, Biophys. J., 2014, 107, L37–L40 CrossRef CAS PubMed.
- N. Nisenholz, K. Rajendran, Q. Dang, H. Chen, R. Kemkemer, R. Krishnan and A. Zemel, Soft Matter, 2014, 10, 7234–7246 RSC.
- A. M. Greiner, H. Chen, J. P. Spatz and R. Kemkemer, PLoS One, 2013, 8, e77328 CAS.
- J. Fouchard, C. Bimbard, N. Bufi, P. Durand-Smet, A. Proag, A. Richert, O. Cardoso and A. Asnacios, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13075–13080 CrossRef CAS PubMed.
- B. Sabass, M. L. Gardel, C. M. Waterman and U. S. Schwarz, Biophys. J., 2008, 94, 207–220 CrossRef CAS PubMed.
- J. Stricker, B. Sabass, U. S. Schwarz and M. L. Gardel, J. Phys.: Condens. Matter, 2010, 22, 194104 CrossRef PubMed.
- J. Stricker, Y. Aratyn-Schaus, P. W. Oakes and M. L. Gardel, Biophys. J., 2011, 100, 2883–2893 CrossRef CAS PubMed.
- K. A. Beningo, M. Dembo, I. Kaverina, J. V. Small and Y. L. Wang, J. Cell Biol., 2001, 153, 881–887 CrossRef CAS PubMed.
- N. Q. Balaban, U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi and B. Geiger, Nat. Cell Biol., 2001, 3, 466–472 CrossRef CAS PubMed.
- J. L. Tan, J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju and C. S. Chen, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 1484–1489 CrossRef CAS PubMed.
- L. Trichet, J. Le Digabel, R. J. Hawkins, R. K. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933–6938 CrossRef CAS PubMed.
- H. Wolfenson, T. Iskratsch and M. P. Sheetz, Biophys. J., 2014, 107, 2508–2514 CrossRef CAS PubMed.
- P. Fernández, P. A. Pullarkat and A. Ott, Biophys. J., 2006, 90, 3796–3805 CrossRef PubMed.
- S. N. Weng and J. P. Fu, Biomaterials, 2011, 32, 9584–9593 CrossRef CAS PubMed.
- J. P. Califano and C. A. Reinhart-King, Cell. Mol. Bioeng., 2010, 3, 68–75 CrossRef PubMed.
- Ai. Yip, K. Iwasaki, C. Ursekar, H. Machiyama, M. Saxena, H. Chen, I. Harada, K.-H. Chiam and Y. Sawada, Biophys. J., 2013, 104, 19–29 CrossRef CAS PubMed.
- M. Bergert, A. Erzberger, R. A. Desai, I. M. Aspalter, A. C. Oates, G. Charras, G. Salbreux and E. K. Paluch, Nat. Cell Biol., 2015, 17, 524–529 CrossRef CAS PubMed.
- T. Pompe, S. Zschoche, N. Herold, K. Salchert, M. F. Gouzy, C. Sperling and C. Werner, Biomacromolecules, 2003, 4, 1072–1079 CrossRef CAS PubMed.
- T. Pompe, L. Renner, M. Grimmer, N. Herold and C. Werner, Macromol. Biosci., 2005, 5, 890–895 CrossRef CAS PubMed.
- L. Renner, T. Pompe, K. Salchert and C. Werner, Langmuir, 2005, 21, 4571–4577 CrossRef CAS PubMed.
- S. Martin, H. Q. Wang, L. Hartmann, T. Pompe and S. Schmidt, Phys. Chem. Chem. Phys., 2015, 17, 3014–3018 RSC.
- P. Thevenaz, U. E. Ruttimann and M. Unser, IEEE Trans. Image Process., 1998, 7, 27–41 CrossRef CAS PubMed.
- J. P. Butler, I. M. Tolić-Nørrelykke, B. Fabry and J. J. Fredberg, Am. J. Physiol.: Cell Physiol., 2002, 282, C595–C605 CrossRef CAS PubMed.
- I. M. Tolić-Nørrelykke, J. P. Butler, J. Chen and N. Wang, Am. J. Physiol.: Cell Physiol., 2002, 283, C1254–C1266 CrossRef PubMed.
- K. D. Webster, W. P. Ng and D. A. Fletcher, Biophys. J., 2014, 107, 146–155 CrossRef CAS PubMed.
- M. Ghibaudo, A. Saez, L. Trichet, A. Xayaphoummine, J. Browaeys, P. Silberzan, A. Buguin and B. Ladoux, Soft Matter, 2008, 4, 1836–1843 RSC.
- L. Renner, T. Pompe, K. Salchert and C. Werner, Langmuir, 2004, 20, 2928–2933 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm01706h |
| This journal is © The Royal Society of Chemistry 2016 |