Reordering transitions during annealing of block copolymer cylinder phases

Abstract

While equilibrium block-copolymer morphologies are dictated by energy-minimization effects, the semi-ordered states observed experimentally often depend on the details of ordering pathways and kinetics. Here, we explore reordering transitions in thin films of block-copolymer cylinder-forming polystyrene-block-poly(methyl methacrylate). We observe several transient states as films order towards horizontally-aligned cylinders. In particular, there is an early-stage reorganization from randomly-packed cylinders into hexagonally-packed vertically-aligned cylinders; followed by a reorientation transition from vertical to horizontal cylinder states. These transitions are thermally activated. The growth of horizontal grains within an otherwise vertical morphology proceeds anisotropically, resulting in anisotropic grains in the final horizontal state. The size, shape, and anisotropy of grains are influenced by ordering history; for instance, faster heating rates reduce grain anisotropy. These results help elucidate aspects of pathway-dependent ordering in block-copolymer thin films.

---

Introduction

Block-copolymers (BCP) are self-assembling materials that spontaneously form nanoscale morphologies owing to micro-phase separation.^1,2 That is, the chemical architecture of the polymer chains enforces a particular spatial arrangement of the block materials (forming spheres, cylinders, lamellae, etc.). Although energy-minimization dictates the equilibrium morphology,³ the structures obtained experimentally result from local boundary conditions, processing history, and kinetic trapping.⁴ For instance, BCP phases are typically poly-grain, exhibiting numerous defects and grain boundaries, with the average grain size depending on annealing temperature and time. In thin films, the orientation of the BCP phase depends on many factors, including substrate surface energy,^5–9 roughness,^10–16 and topography,^17–23 as well as film thickness.^13,24–27 Here again, while a preferred orientation can be rationalized in terms of the selectivity and directing forces of interfaces, the actual ordering obtained experimentally may deviate from such considerations owing to pathway-dependent effects. Indeed the orientation and size of grains can depend strongly on thermal annealing conditions,^6,16,27–32 thermal gradients and thermal history,^33–38 and solvent vapor^39–43 exposure. As it is now clear that self-assembly is often regulated by pathway-dependent ordering,^44–46 a deeper understanding of intermediate states, and reordering transitions, is required.

Diblock-copolymer cylinder phases typically orient horizontally (with the cylinder long-axis in the film plane), owing to preferential wetting of one of the blocks at the substrate and free interfaces. Vertical cylinders (cylinder long-axis pointing along film normal) can form under certain conditions,^32,37,47 especially when the substrate is ‘neutral’ (similar interaction strength with both blocks).^7,8 Yet, even when the final ordered state is horizontal, films annealed starting from a disordered as-cast state may exhibit a transient vertical state. Here, we study in detail the thermal annealing of BCP cylinder phases, as they progress from disordered states, to vertical cylinders, and finally to horizontal cylinders. While the coarsening of BCP grains^{28,31,48–50} and order–order transitions^3,51–54 have been well-studied, less attention has been paid to reordering transitions within a particular BCP phase. We demonstrate that the appearance of intermediate states influences the final film structure, including grain size and grain anisotropy. Using zone annealing, we show that the order of the final state is also affected by heating rate. Overall, these results provide context to the pathway-dependent ordering that underlies assembly of BCP phases.

Results and discussion

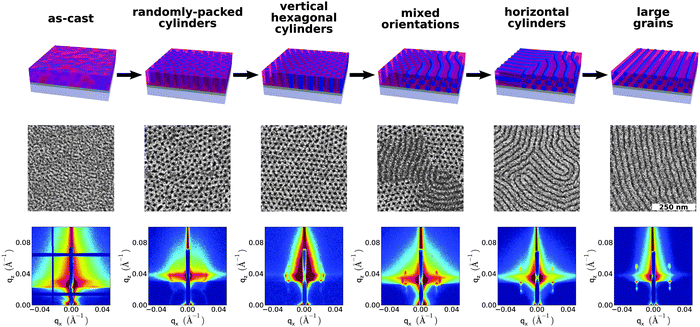
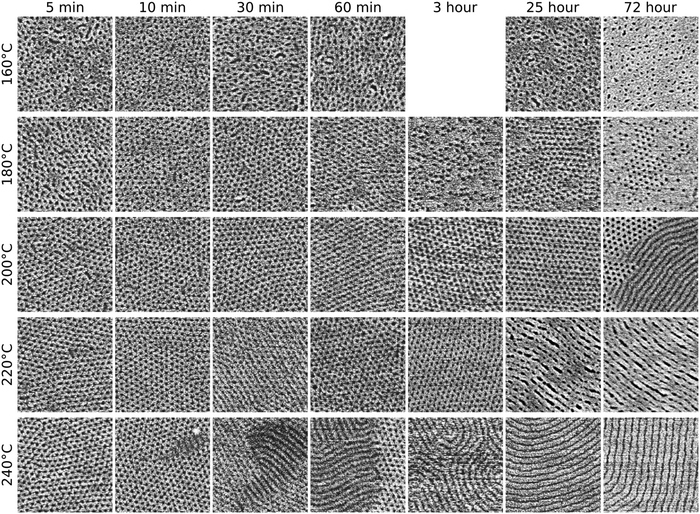
We examine the ordering history of cylinder-forming polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) diblock-copolymer thin films, cast onto weakly hydrophilic substrates (glass slides coated with a Ge layer, which exhibits a native oxide). After sufficient oven annealing, the 170 nm films form horizontal cylinder morphologies: i.e. the cylinder long-axis is parallel to the substrate plane (orthogonal to the film normal), and a majority-phase (PS) wetting layer is exposed at the free surface. However, for this BCP at this film thickness, several metastable intermediate states are observed along the way to this final morphology orientation (Fig. 1). The disordered as-cast film micro-phase separates into randomly-packed cylinders. This transient morphology reorders into a more well-defined hexagonally-packed vertical cylinder phase. As annealing proceeds, domains of horizontally-aligned cylinders nucleate, grow, and coalesce. This reordering transition thereby converts the film into an entirely horizontal state; i.e. the vertical cylinder state is also transient. In this paper, we study these reordering transitions to better understand the factors that govern the order seen in the final state.

Fig. 1 Ordering history of BCP cylinder phases. The upper row shows cartoons for various phases through the history of ordering, the center row shows typical experimental SEM images of these states (250 nm scale bar applies to all images), and the lower row shows representative GISAXS images of the same states. Once thermal annealing begins, the disordered as-cast state rapidly forms poorly-ordered cylinder. With time, the cylinders arrange hexagonally, and these grains coarsen. Eventually, grains of horizontal orientation nucleate, grow, and eventually dominate. The horizontal grains then coarsen with time.

Fig. 1 shows representative SEM and GISAXS data for the various stages of ordering discussed throughout this manuscript. While scanning electron microscopy (SEM) provides detailed realspace images of the sample surface, grazing-incidence small-angle X-ray scattering (GISAXS) provides complementary information about the ordering throughout the entire depth of the thin film. For the results described in this paper, the GISAXS data both above and below the film-vacuum critical angle were found to be consistent, which indicates that the ordering observed at the top surface is representative of the morphology throughout the film (ESI†, Fig. S1 to S5). As-cast films are essentially disordered, as confirmed by both SEM and reflection-mode X-ray scattering (GISAXS). The random structure observed in SEM, and the weak broad peak observed in GISAXS, indicate that the block-copolymer material is disordered: phase separation has barely begun, and the equilibrium morphology has not yet appeared. This as-cast semi-ordered state is metastable, but is ‘frozen in’ at room temperature, since the BCP cannot relax nor reorder while it is below the glass-transition temperature (T_g 110 °C). Upon thermal annealing, the disordered state rapidly micro-phase separates into cylinder domains, which appear as dots in the SEM images. The cylinders are disorganized (not forming a well-defined lattice). Corresponding GISAXS data show a scattering arc along q_x, consistent with vertical cylinder morphologies with a broad orientation distribution. Higher-order structural scattering peaks are absent, because of the lack of long-range lattice order. Further annealing leads to reorganization of the cylinders. The cylinders arrange into a locally hexagonal lattice. These vertical cylinders become more strictly vertically-aligned (as indicated by the straightened streak in GISAXS). Even at these early stages, a weak peak from a horizontal cylinder population can typically be observed. We note that GISAXS averages over macroscopic areas (regulated by the projected beam size), and is thus sensitive to this early formation of mixed orientations. Further annealing grows the fraction of horizontally-aligned material; eventually the film converts entirely to a horizontal cylinder morphology (as confirmed by the disappearance of the vertical cylinder scattering peak). Longer annealing time grows the grains, which leads to a sharpening of the GISAXS peaks. Fig. 2 shows SEM images of films across a range of annealing temperatures (T) and times (t). For sufficient time and temperature (e.g. 72 h at 200 °C, or 1 h at 240 °C), the BCP morphology reorients from the transient vertical orientation, to the ultimate horizontal orientation. We did not observe a transition to horizontal cylinders below 180 °C over the experimental timescale selected (72 h). However, it is possible that even at these temperatures, the material will ultimately reorient; the kinetics of reorientation are extremely slow at these low temperatures.

Fig. 2 SEM of oven-annealed BCP cylinder-phase thin films. SEM images (500 nm width) for a range of times and temperatures, during oven-annealing of PS-b-PMMA thin films (170 nm). Films form vertical cylinders (hexagonal dots) initially, which eventually transition to in-plane cylinders (line patterns). Higher temperatures lead to faster reordering and grain coarsening. Below 200 °C, reorientation to horizontal cylinders is not observed within the experimental time. The ‘broken lines’ in the images for 220 °C (25 and 72 h) result from imperfect etching during preparation of the sample for SEM imaging.

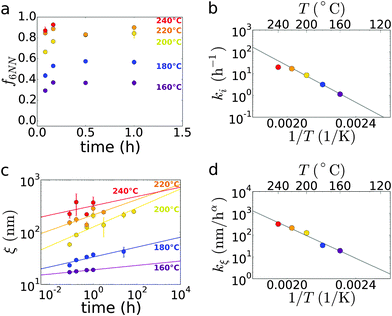
The reorganization of cylinders from random local packing into a hexagonal lattice can be thought of as a reordering transition. Using image analysis, we quantify the fraction of cylinders that have 6 nearest-neighbors (f_6NN), which provides a measure of how the film reorders from random-packing (f_6NN,i = 0.23, based on analysis of as-cast films) to hexagonal packing (f_6NN,f = 1.0). Fig. 3a shows the time scale of this reordering process. Not surprisingly, higher temperatures lead to faster rearrangement of cylinders into a hexagonal phase. We can estimate the kinetics of the initial rearrangement by fitting the early-time data (t < 0.5 h) to an exponential equation (see ESI,† Fig. S6a):

f_6NN = (f_6NN,f − f_6NN,i)[1 − e^−k_it] + f_6NN,i (1)

Fig. 3 Early stages of vertical cylinder ordering. (a) The fraction of dots that have 6 nearest neighbors (f_6NN) as a function of time, for various oven-annealing temperatures. The data are fit using exponential rise-to-max functions. (b) The rates of initial reorganization (k_i) of dots into hexagonal patterns follow a roughly Arrhenius trend. (c) The orientational correlation length (ξ) is used as a measure of the grain size of hexagonally-packed cylinder domains. The grains coarsen according to a power law. (d) The temperature-dependence of grain coarsening is roughly Arrhenius.

Fig. 3b shows that the initial kinetics (k_i) follow a roughly Arrhenius-like trend (k = Ae^−E_a/RT), suggesting that this reordering is thermally-activated, with an activation energy (based on slope of Arrhenius fit, Fig. 3b) of E_a = 81 ± 12 kJ mol⁻¹. This activation energy is of a similar magnitude to previous reports for defect annihilation in BCP systems.^36,55–59 Although reordering into hexagonal-packing should be strongly preferred, as this is the minimum-energy configuration for the BCP chains, the reordering evidently requires rearrangement and energy barriers of a similar scale to the defect annihilation events which govern grain coarsening. This is not surprising, since establishing hexagonal registry involves substantial displacement and deformations of the cylinders. The vertical orientation simplifies detection of the reordering transition; nevertheless, it is likely that a similar kind of reordering occurs in horizontal orientation films, where initially randomly-packed cylinders evolve into an in-plane hexagonal lattice.

The transient appearance of vertical cylinders occurs because of the selected film thickness. Indeed, previous studies have similarly observed transient vertical states for certain thicknesses, but persistently horizontal states for other thicknesses.³⁶ More generally, the average film thickness,^26,60–63 and the local thickness,^22,64,65 can influence the BCP morphology, orientation, and grain size.^11,21,31,66 Commensurability plays a key role. For precisely commensurate thicknesses (admitting an integer number of horizontal-cylinder layers), the defect-free horizontal state is lowest-energy and forms rapidly. For incommensurate thicknesses, the horizontal state may still be preferred due to preferential wetting at the substrate or surface interfaces. The incommensurate thickness cannot admit an integer number of cylinder layers without defects. The final compromise is for the surface to partition into locally-commensurate regions slightly thicker or thinner than the average thickness; i.e. one observes so-called ‘island and hole’ surface patterns.^67–69 This formation of additional surface area obviously involves an interfacial energy penalty. Experimentally, one observes an ‘incubation time’ for the nucleation and growth of these surface features;^69–71 during this incubation time, the BCP morphology must be distorted in some way (e.g. adopting a non-equilibrium repeat spacing) to accommodate the incommensurate thickness.⁷² For maximally-incommensurate thicknesses (midway between two commensurate conditions), the driving force to form surface structures is very large, and the incubation time is correspondingly short (tens of minutes). However, for ‘weakly incommensurate’ thicknesses, the incubation time during thermal annealing can be tens of hours.⁷³ Our selected film thickness is in this regime. As annealing proceeds, the film rearranges from a vertical to horizontal orientation. Initially, this horizontal state exhibits a smooth film surface. Yet, with sufficient annealing (e.g. >72 h at 240 °C), we observe the formation of a small number of surface islands. This incommensurate condition enables the early-stage formation of a vertical state. Various studies have shown that vertical orientations represent another possible configuration to relieve the stress inherent to an incommensurate film thickness.^65,74,75 Thus, our selected slightly-incommensurate film thickness represents a frustrated boundary condition. The BCP material initially accommodates this frustration by rapidly forming a vertical orientation. After sufficient annealing time, it is able to reorient (overcoming energy barriers, as will be discussed below). At still longer annealing times, the film nucleates a small number of surface islands to further relieve internal stresses.

We use image analysis to quantify the order in the hexagonally-packed vertical cylinder domains. The orientation map (see center column of Fig. 4 for false-color representations) allow grain boundaries to be easily discerned, and can be used to compute the in-plane orientational correlation length (ξ), which we use as a measure of grain size. Consistent with previous reports, the grain size coarsens following a power-law (Fig. 3c):

ξ = k_ξt^α (2)

where the exponent, α, describes the ordering mechanism, and is typically on the order of 0.2–0.3 for thin films,^28,31,49 while the prefactor, k_ξ, sets the scale of the coarsening kinetics. This power-law behavior is expected, owing to the mechanism of grain-growth in fully phase-separated BCP films: topological defects must diffuse and annihilate. Defect annihilation involves local rearrangement of the block-copolymer into high-energy intermediate states.^59,76,77 As grains grow, and defect densities decrease, the rate of defect annihilation, and thus grain-growth, continually decreases. In vertical cylinder phases (dot patterns), this growth becomes dominated by the defective grain boundaries, with smaller grains being consumed in favor of larger grains as the grain boundaries fluctuate.^50,78 For our system, an Arrhenius analysis (Fig. 3d) suggests an activation energy for this coarsening process of E_a = 69 ± 23 kJ mol⁻¹.

Fig. 4 Conversion of BCP from vertical to horizontal orientation. Using the raw SEM images (left column, 500 nm scale bar applies to all images), we compute an orientation map for the vertical cylinder (hexagonal dot) morphology (false-color image in center column). The rightmost images are Fourier filtered to emphasize the BCP morphology. The horizontal morphologies are highlighted in blue (automatically recognized using image analysis), and the vertical domain grain boundaries are denoted by yellow dashed lines. (a and b) Images during rapid thermal ramping (terminated LZA, v = 1.25 μm s⁻¹); after 413 s of ramping/annealing (time above T_g), and reaching local T = 288 °C. (c–f) Images of BCP films oven annealed at 200 °C for 72 h. Grains of horizontal orientation nucleate and grow at the boundaries between vertical grains.

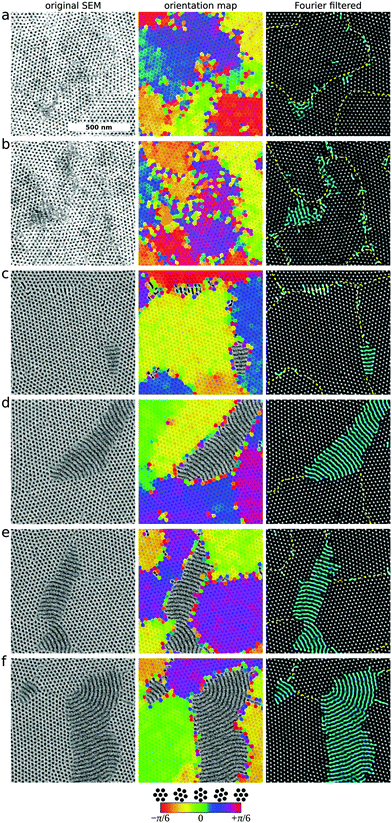
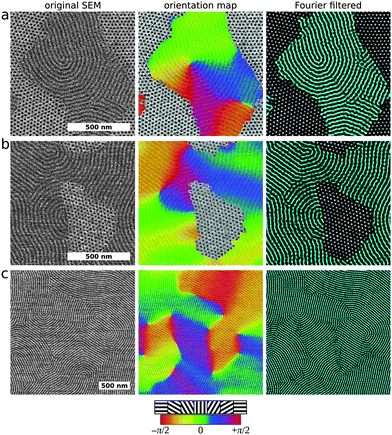
As can be seen in Fig. 2, the vertical cylinder morphology converts to horizontal cylinders after sufficient annealing time. This transition likely occurs at all temperatures, though the time scale for reordering of course increases dramatically as temperature is lowered.³⁸ We note that there is a relatively small difference in surface tensions between PS and PMMA, which facilitates the appearance of vertical cylinders; conversely this interfacial energy difference is partially responsible for driving the system towards the horizontal orientation. For PS-b-PMMA, it has been reported^6,8 that the surface energies become roughly equal near 230 °C. We observe the eventual reorientation to horizontal cylinders even at 240 °C, suggesting that substrate wetting is strongly selecting the equilibrium morphology. The lingering, yet ultimate transience, of the vertical state emphasizes the difficulty of analyzing self-assembly: even seemingly stable and ordered states may in fact be kinetically-trapped and ultimately subject to reordering. Fig. 4 investigates the origin of the reorientation transition, using SEM analysis of the early stages of the conversion. We compute an orientation map using local inter-particle vectors; the false-color orientation image (center column of Fig. 4) makes the location of grain boundaries evident. We use Fourier filtering to highlight the BCP morphology, and identify vertical and horizontal domains using image analysis (horizontal domains are highlighted in blue).

The horizontal orientation begins to form at the boundaries between vertical cylinder domains (Fig. 4a–c). This is not surprising, since grain boundaries represent defective, high-energy states. There is thus a lower energy penalty to nucleating small horizontal domains at these locations. The emerging horizontal grains moreover tend to grow along the grain boundaries (Fig. 4b–d). There is a clear epitaxial relationship between the rows of vertical hexagonal dots, and the lines of horizontal stripes. In some images, intermediate states can be seen, where nearby vertical cylinders in a row are fusing to become a single horizontal cylinder. This fusion of nearby vertical cylinders naturally minimizes the amount of rearrangement required to form a horizontal cylinder line. The newly-formed horizontal grains extend through the depth of the film (cf. GISAXS of mixed states in Fig. 1). The growing grains of horizontal morphology are generally anisotropic. In particular, the grains appear to grow more rapidly along the perpendicular direction (orthogonal to the cylinder long-axis) than the parallel direction (along the long-axis).

Fig. 5 explores the growth of the horizontal cylinders domains. As the grains grow, the horizontal domains begin to impinge on one another, creating horizontal-domain grain boundaries (abrupt changes in color in Fig. 5, center column). The PS-b-PMMA material also accommodates incompatible local grain orientations through regions of continuously curving morphology (gradual color changes in Fig. 5, center). As horizontal domains further coalesce and begin to dominate, the remaining vertical domains correspondingly shrink. These shrinking vertical regions typically have faceted boundaries, similar to that observed for hexagonal BCP grains growing from a disordered matrix.⁷⁹ We also note that the lingering vertical domains tend to be surrounded by horizontal domains oriented parallel (Fig. 5b), that is, the surrounding rows of cylinder lines have the cylinder long-axis pointing into the vertical domain. This is consistent with the preferred growth direction previously mentioned. Because the perpendicular direction of horizontal grains grows most rapidly, this direction is rapidly ‘consumed’. At later stages, only the slower-growing perpendicular boundaries persist. Even these slow-growth boundaries eventually expand and thereby consume all of the vertical-cylinder regions. It is interesting to note that the general shape of grains in the completely horizontal states (Fig. 5c and ESI,† Fig. S8) bear various telltale signatures of the reordering process. In particular, the anisotropic ‘fan-like’ and ‘wedge-like’ grain shapes observed in the final horizontal state arise from the preferred direction for conversion of vertical to horizontal cylinders.

Fig. 5 Growth and coalescence of horizontal domains. From the SEM data (left column), we compute the orientation of the horizontal cylinders (false-color images, center); the grain boundaries can be easily discerned as the regions where color changes abruptly. The right column shows Fourier filtered images (which highlight the structure of the BCP morphology), where the horizontal domains are colored blue. Representative images are shown for films after oven annealing at 240 °C for (a) 10 min., (b) 1 h, (c) 25 h.

The kinetics of the reorientation transition can be quantified by using image analysis to calculate the areal fraction of horizontal domains, f_H (Fig. 6). This conversion can be fit to an exponential function:

f_H = 1 − e^−k_Ht (3)

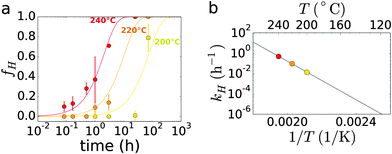Fig. 6 Kinetics of conversion from vertical to horizontal orientation. (a) The areal fraction of horizontal domains (growing in vertical hexagonal-cylinder phases) increases to 100% with time; solid lines are fits to eqn (3). (b) The associated rates as a function of temperature can be subjected to an Arrhenius analysis.

The temperature-dependence of the associate rate (k_H) can, again, be subjected to an Arrhenius analysis (Fig. 6b), from which we estimate E_a = 181 ± 59 kJ mol⁻¹ to be the energy-barrier for conversion of vertical cylinders into horizontal cylinders. We note that the relatively large error estimated for E_a is based on the spread of the data and the limited degrees-of-freedom. Nevertheless, even this may be an under-estimate, given the relatively poor fit quality of the time-dependent data (Fig. 6a). On the other hand, our principle aim in performing this Arrhenius analysis is to identify whether there is a temperature-dependence to the reorientation kinetics. The data of Fig. 6 make it clear that this reorientation is indeed thermally activated, with a corresponding energy barrier. The existence of this energy barrier confirms that the vertical state is meta-stable, existing only because of the timescale necessary to thermally overcome the barrier to reorientation. Once the system has converted entirely to a horizontal cylinder morphology, the grains coarsen in the usual manner: topological defects diffuse randomly,^55,80 defects experience a net attraction to one another,⁴⁹ and defect-pairs annihilate.^57,81,82 Overall, the density of defects decreases, and correspondingly grain sizes increase, following power-law coarsening.

As already described, we analyze the decay of the in-plane orientation correlation to compute an orientational correlation length (ξ), which we use as a measure of the average grain size. In order to compute grain anisotropy, we can similarly calculate orientational correlations along the parallel and perpendicular directions of the morphology. That is, ξ_per measures the correlation along the perpendicular direction (orthogonal to the cylinder long-axis), and ξ_par measures correlations in the parallel direction (along the long-axis). The ratio R_ξ = ξ_per/ξ_par provides a measure of grain anisotropy (i.e. R_ξ ≈ 1 indicates isotropic grains, R_ξ > 1 indicates grains larger along the perpendicular direction, and R_ξ < 1 indicates grains larger along the parallel direction). Applying this method to the SEM images of samples annealed at 240 °C, we compute R_ξ = 1.6 ± 0.2, with this value being essentially constant throughout the annealing process (ESI,† Fig. S9). That is, the same amount of grain anisotropy as observed in mixed phases (where horizontal grains are appearing in otherwise vertical morphologies) persists into the final fully-horizontal states. This thus provides a quantitative grounding for the anisotropic grain shapes that can be seen visually in the SEM images (Fig. 4 and 5).

To further explore the origin of this grain anisotropy, and the overall reorientation transition, we developed a simple Monte Carlo (MC) model for BCP cylinder phases. A triangular lattice is initially populated with a uniform grid of dots, representing a defect-free vertical cylinder morphology. On each MC step, a random connection between two dots is considered. Forming a connection represents the creation of a locally horizontal cylinder orientation. We assign different energies to local configurations of connections (where we define the initial dot-lattice to have zero energy, for reference). The candidate MC move is accepted or rejected according to a simulated annealing protocol. If the energy has decreased with the move, it is accepted, whereas if the move has increased energy, it is accepted with the probability:

P = e^−ΔE/T_MC (4)

where ΔE is the energy increase, and T_MC is the simulation temperature. This allows for thermal activation of higher-energy intermediate states, allowing the system to overcome energy barriers and ultimately evolve towards a lower-energy final state. The behavior of the MC model depends on the selected relative energies of various local configurations of the lattice. We describe here a set of energies selected to reproduce the experimentally-observed behavior (refer to ESI,† Fig. S10 to S16 for other possibilities that were considered). Most significantly, the energy of line-like states must be set to be lower than the energy of unconnected lattice sites. This captures the experimental observation of the horizontal cylinder state (line pattern) being lower energy than the vertical cylinder state (dot pattern). However, this alone is not sufficient to reproduce the experimental shape and configuration of grains, especially at intermediate times. The preferred growth along the perpendicular grain direction necessities the inclusion of an additional effect in the model. Specifically, the local energy is lowered when two lines are nearby and parallel.

Fig. 7 shows simulation results using relative energies selected so as to reproduce the experimentally-observed behavior. The grain anisotropy (longer along perpendicular direction) arises from the low-energy contribution from nearby parallel lines. This implies that isolated horizontal lines (in an otherwise vertical cylinder grain) are high-energy and disfavored. This is indeed consistent with experiment, where such states are only observed transiently. More generally, the simulation considers a variety of intermediate states as being high-energy. The boundaries of grains (which are have either terminal lines or lines without parallel neighbors), the bending of the lines has an energetic cost, and multiply-connected local morphologies (e.g. T-junctions) are all defective and high-energy. The MC simulation results suggest that grain anisotropy is ultimately related to the relative energy of the different defects which appear at grain boundaries of either parallel or perpendicular line-patterns.

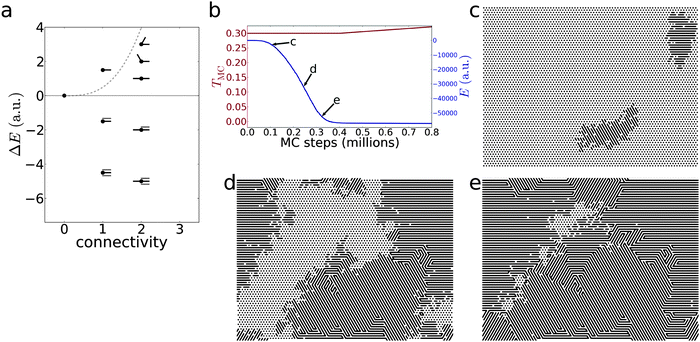Fig. 7 Monte Carlo simulation of conversion from vertical cylinder (hexagonal lattice of dots) to horizontal cylinder (line pattern) state. (a) Simulation behavior is regulated by the relative energy of different configurations for the lattice sites. Unconnected dots, which represent the vertical cylinder state, are given an energy of zero by definition. A variety of high-energy configurations are defined; these represent defective states that are disfavored but are necessary intermediate states as the system converts from vertical to horizontal. Multiply-connected lattice sites are given yet-higher energies (as implied by the dashed line; refer to ESI†). A negative energy adjustment is applied for lines with neighboring lines (grey). This establishes the experimentally-observed preference for horizontal orientation. (b) As a function of the simulation time, the system energy decreases, concomitant with the conversion to the lower-energy horizontal state. (c–e) Snapshots of the simulation area (at times noted in panel b) show the emergence, growth, and coalescence of the horizontal grains. The grain shapes and anisotropy are consistent with experimental results. This only occurs because of the appropriate selection of relative energies (refer to ESI† for exploration of other simulation conditions).

Literature reports similarly show anisotropic grains that are longer in the perpendicular direction for polystyrene-block-poly(methyl methacrylate),⁸³ polystyrene-block-poly(vinyl pyridine),^84–86 and polyisoprene copolymers.^87–93 On the other hand, there is some evidence in other systems of the opposite anisotropy (grains longer along the parallel direction): such as polystyrene-block-poly(dimethyl siloxane),^47,94,95 and blends of polystyrene and polystyrene-block-polyisoprene.⁹⁶ Chastek and Lodge studied in detail the shape and anisotropy of grains during ordering of polystyrene-block-polyisoprene,^97–99 where grain growth rate along the perpendicular direction was found to be larger (by a factor of ∼2). This was attributed to the relative energies of grain boundaries for different orientations of the BCP material. The parallel edges of a BCP cylinder grain expose the ends of cylinders, which of course incurs an energy penalty. However, the perpendicular edges of a grain involve an even larger energy penalty (and thus interfacial tension), because the entire length of a cylinder edge must be exposed in this case. In addition to these equilibrium arguments, ordering pathways may also be relevant. Hsieh et al. described results for solvent-annealed polystyrene-block-poly(dimethyl siloxane), where perpendicular anisotropic grains were observed (opposite anisotropy to other literature reports of similar BCP materials).¹⁰⁰ The authors convincingly demonstrate complex ordering pathways, involving metastable morphologies. Thus, grain anisotropy may be related both to equilibrium¹⁰¹ and kinetic aspects. It is interesting to note that this intrinsic anisotropy of BCP ordering has been exploited to yield anisotropic droplets of BCP material, within which the BCP morphology is aligned and anisotropic.^102–104

A limitation of our MC model is that it does not consider the lattice mismatch between the vertical and horizontal states. In particular, vertical hexagonal domains have cylinders organized into rows whose spacing is 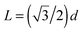, where d is the cylinder-to-cylinder distance. On the other hand, the horizontal cylinder lines (viewed from the top) are spaced by d. The mismatch between these two distances means that templated growth of the horizontal cylinders, from rows of vertical cylinders, must introduce defects. Indeed, this phenomenon can be observed in the SEM images, where the spacing of cylinder lines in the horizontal state (∼31 nm) is larger than the spacing between rows of dots (∼27 nm) in the vertical state. Correspondingly, the horizontal morphology includes meandering of orientation, and topological defects, which necessarily arise as it grows into the ordered vertical domains. This incommensurability may play a role in the relative energies of the parallel and perpendicular grain boundaries. In both cases, the expanding horizontal state must reorganize (occasionally introducing topological defects), in order to relax the stress induced by the lattice mismatch. However, the large number of cylinder ends which appear at parallel grain edges likely generates a greater amount of strain (i.e. distortion of the polymer chains).

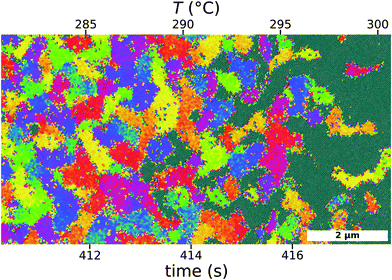
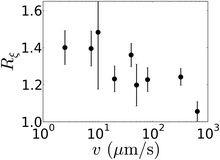
In our experimental and simulation results, we attribute the grain anisotropy to the different energies of parallel and perpendicular grain boundaries. Nevertheless, the appearance of grain anisotropy is a manifestly kinetic phenomenon. It arises due to the relative growth velocity of different grain directions, which in turn derives from relative energies of different morphological defects. The equilibrium state is instead to minimize energy by forming a large single domain of a particular orientation (which thereby eliminates grain boundaries), and to only have defects to the extent required by entropy at a given temperature. Experimentally, the grain sizes and shapes that are observed are instead a result of kinetic trapping and incomplete annealing. To study this kinetic influence systematically, we undertook a series of experiments that vary the heating rate during BCP annealing. In particular, we exploit our recent demonstration of laser zone annealing (LZA),^{38,46,105,106} a photothermal method that sweeps a narrow laser-line across the sample. Each sample position experiences heating, a thermal spike, and subsequent cooling. By focusing on the heating phase, we study how the initial stages of BCP self-assembly proceed. The heating rate can be conveniently adjusted simply by varying the laser sweep velocity (v). Moreover, we can investigate the entire history of annealing by abruptly terminating the laser exposure midway through the laser sweep; the temporal history of LZA annealing is then encoded as a function of position relative to the laser-line position at termination (Fig. 8). The stages and mechanisms of ordering during thermal ramping appear identical to oven annealing, though previous work indicates the in-plane thermal gradients are influencing the ordering kinetics.^36,38 As the BCP is heated through T_g, phase-separation into randomly-packed dots is observed. These reorder into hexagonal domains, which coarsen, and eventually convert into horizontal domains. The kinetics of all of these steps can be greatly influenced, however. For instance, at large heating rates, the vertical cylinder hexagonal grains are extremely small when conversion to horizontal orientations is initiated. This influences the ultimate grain size and grain anisotropy.

Fig. 8 Example SEM image from a terminated LZA heating/annealing experiment. Laser sweep velocity was 1.25 μm s⁻¹. The local temperatures in the sample (at the moment when laser-heating was terminated) are computed based on the LZA photothermal profile. The annealing times are measured from the moment the sample passes through the glass transition temperature. Terminated LZA experiments provide the full ordering history in a single sample, as a function of position. The image shows the conversion from vertical cylinders to horizontal cylinders. The vertical cylinder domains (dot patterns) are color-coded according to local grain orientation, making grain boundaries and defects evident. The horizontal domains (line patterns) are Fourier filtered and colored blue.

Grain anisotropy was found to be constant during any particular LZA experiment (ESI,† Fig. S17), consistent with oven annealing results. However, as shown in Fig. 9, grain anisotropy varies systematically with heating rate. For extremely rapid heating, the conversion from vertical to horizontal orientation is initiated when the vertical grains are very small. Many horizontal domains are nucleated throughout the sample. The numerous, small grains rapidly convert the entire sample to horizontal state. This process is thus dominated by nucleation, not growth, and so grains are roughly isotropic in shape. On the other hand, slow heating rates give rise to anisotropic grains. Horizontal domains are slowly nucleated at the boundaries between large vertical grains. These horizontal domains have ample time to grow, with a preferential growth direction, before finally impinging on another horizontal domain.

Fig. 9 Grain anisotropy as a function of LZA sweep velocity. The anisotropy of horizontal cylinder grains after LZA processing is plotted as a function of the LZA sweep velocity (v). Faster thermal ramping leads to nearly isotropic grains, whereas slow heating gives rise to anisotropic grains.

Finally, we emphasize that the reordering transitions described herein are intimately tied to the selected ordering pathway. Spin-casting is known to give rise to films that are kinetically-trapped. Starting from this highly disordered state, the BCP material encounters numerous energy-barriers as it progresses towards the ultimately-favored low-energy configuration.⁴⁶ One would not expect to encounter these meta-stable transient states under all ordering pathways. For instance, slow cooling of the film from above the order–disorder transition temperature (T_ODT) would instead nucleate ordered grains within a disorder matrix, with these grains growing and eventually dominating the film. Such a pathway would be expected to immediately nucleate the lowest-energy grain orientations. A deeper understanding of ordering pathways allows optimization of the annealing process to yield highly-ordered structures. On the other hand, it also provides the possibility of enforcing metastable configurations by carefully limiting the annealing protocol.

Conclusion

In summary, we have explored reordering transitions in block-copolymer cylinder phases in thin films; in particular, the reorganization of randomly-packed cylinders into hexagonally-packed vertical cylinders, as well as the reorientation transition from vertical to horizontal cylinders. We find these transitions to be thermally-activated, with activation energies similar to those reported for block-copolymer defect annihilation and grain coarsening. Thus, these transitions also involve local rearrangement of the BCP morphology, through transient high-energy configurations. We present a simple Monte Carlo model including such considerations, which reproduces the experimentally observed grain shapes. In particular, for the PS-b-PMMA materials studied herein, horizontal cylinder grains grow anisotropically, resulting in grains elongated along the perpendicular direction. The final grain anisotropy is kinetically-determined, and ultimately tied to the reordering transitions; for instance it is influenced by heating rate. The appearance of intermediate states, and their associated reordering transitions, highlights the pathway-dependent ordering of self-assembling films.

Methods

Polymer films

Glass slides (1 mm thick, BK-7 FisherFinest) were coated with 100 nm of germanium (Ar-plasma sputtered). Cylinder-forming polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) was obtained from Polymer Source, Inc., with total molecular weight 49.1 kg mol⁻¹ (31.6-b-17.5 kg mol⁻¹, PDI = 1.06, minority volume fraction f_PMMA = 0.33). This material exhibits a cylinder-to-cylinder repeat distance of 31 nm (and thus a hexagonal cylinder layering distance of 27 nm). Films were spin-cast from toluene solutions (typical conditions: solutions of ∼3% by weight, 1000 RPM) to a thickness of 170 nm (∼6 cylinder layers), onto freshly-cleaned (O₂ plasma) Ge-coated substrates. Films were dried under vacuum at 60 °C for 4 h to remove residual solvent.¹⁰⁷ Isotropic annealing was performed in a vacuum oven, with temperature stability ±3 °C (verified by independent thermocouple measurements).

Laser zone annealing

Laser zone annealing (LZA) was used to perform rapid annealing with controllable heating rate. The LZA setup has been previously described.^{38,46,105,106} To summarize: a green (532 nm) laser (3 W, Melles Griot 85 GHS 309) was focused into a sharp line at the sample position (20 μm FWHM × ∼20 mm breadth). The laser-light is absorbed by the Ge substrate coating, leading to local heating and large thermal gradients. Sample translation through the laser-line effectively exposes the BCP to a moving thermal zone. The thermal history is nontrivial; we characterize the annealing conditions using the half-height of the thermal spike. The thermal zone has a FWHM of ∼90 μm, a temperature (at half-maximum) of T_HM ≈ 270 °C, and induces thermal gradients of ∇T_HM ≈ 1500 °C mm⁻¹ (with ∇T > 3000 °C mm⁻¹ near the peak). The heating rate is directly related to the LZA sweep velocity (v). Samples that probe this heating history were prepared by abruptly terminating the laser illumination during an LZA sweep. These ‘frozen zone’³⁶ samples thus encode ordering history as function of position from the laser center-line at termination. The exact location of laser termination was recorded by translating the sample by a known amount, and using extreme laser exposure to generate a line of burned material, which then acts as a reference mark for positional measurements.

GISAXS

Synchrotron grazing-incidence small-angle X-ray scattering (GISAXS) experiments were performed at the X9 undulator beamline of the National Synchrotron Light Source at Brookhaven National Laboratory. Two-dimensional scattering images were collected using a fiber-taper charge-coupled device (MarCCD) or a hybrid pixel-array detector (Dectris Pilatus 1 M). Samples were measured under vacuum using an X-ray beam of 13.5 keV (λ = 0.0918 nm). GISAXS data were collected across a range of incidence angles (0.07° to 0.20°). The data presented in the manuscript are for 0.12° (the structures implied by GISAXS were not dependent on incident angle). The X-ray beam was focused using a KB mirror system to a spot 50 μm tall by 150 μm wide. Because of the grazing-incidence geometry, the beam height is projected to a stripe ∼20 mm in length, over-illuminating the sample length (∼12 mm). Thus the GISAXS data provide a statistically-robust average over the macroscopic area (∼2 mm²) illuminated by the X-ray beam. Silver behenate powder was used as a standard for data conversion to q-space.

SEM

Thin film surface morphology was characterized using a Hitachi S-4800 Scanning Electron Microscope (SEM). To highlight the underlying morphology, samples were UV-irradiated to crosslink the majority (PS) phase, followed by brief O₂ plasma treatment (Nordson CS-1701, 100 mT, 20 W), to remove the PS wetting layer, and partially etch the PMMA domains.

Image analysis

Image analysis is a popular and effective means of quantifying order in BCP phases.^31,35,49,108 In this work, SEM images were analyzed to extract a variety of quantitative measures of ordering, using custom-written Python code, and exploiting libraries for image manipulation (Python Image Library), numerical computation (numpy¹⁰⁹), and plotting (matplotlib¹¹⁰). We use the in-plane orientational correlation length as an estimate of the grain size, as previously reported.^35,36,38 For horizontal cylinders (which appear as line/stripe patterns), local spatial derivatives are used to compute an orientation map for the morphology. Average orientational correlation function is computed as a function of separation distance (r); this decaying function is fit to an exponential (e^−r/ξ), from which we extract the correlation length (ξ). For vertical cylinders (which appear as dot patterns), we use image thresholding to identify the cylinder cores. Nearest-neighbor cylinders are identified using a cutoff distance of 1.36 times the equilibrium cylinder–cylinder spacing. From this, we compute the fraction of cylinders that have six nearest-neighbors (f_6NN). The local orientation of hexagonally-packed cylinder is computed by averaging the angles from a given cylinder to its nearest-neighbors. In order to account for the circular symmetry inherent in averaging angles, we compute an average of the associated unit vectors, and modulo the angle of this average vector into the range −π/6 to +π/6. As before, the local orientation map can be used to compute an orientation correlation length (ξ).

For mixed morphologies, we use image analysis to identify the distinct horizontal (line) and vertical (dot) regions, and perform the corresponding orientation correlation analysis within the sub-domains. Morphology type is identified by using image thresholding and particle-counting to isolate image structures, and using a size-cutoff to differentiate between areas of small objects (dots) and large objects (lines).¹¹¹ From this, we directly compute the areal fraction of horizontal morphology (f_H). This method can also identify early stages of horizontal states (fused dots, small lines, etc.) in an otherwise hexagonal dot pattern.

We use Fourier-filtering to highlight the structure at the scale of the morphology. A two-dimensional fast Fourier transform (FFT) is computed. From the one-dimensional circular average of the FFT, we identify the peak corresponding to the BCP morphology (q ≈ 0.2 nm⁻¹). Information far from this peak in the FFT is suppressed, by multiplying the 2D FFT by an annular function centered on the BCP peak (annulus has a Gaussian spread of σ = 0.05 nm⁻¹ orthogonal to the arc). The modified FFT is then converted back into a realspace image using an inverse Fourier transform. The filtered images emphasize the BCP morphology by excluding high-frequency noise and low-frequency gradients in the original image.

Finally, we compute grain anisotropy by evaluating orientational correlation lengths along two orthogonal directions. That is, ξ_per is evaluated by generating an orientational correlation function where the average only considers the correlation to regions within a fan (±15°) pointed along the perpendicular direction to the morphology at each pixel position. The fan is two-sided, and thus captures (for each pixel position) all film regions along the perpendicular direction. Similarly, ξ_par is computed using a two-sided ±15° fan pointing along the parallel direction to the morphology (along the long-axis of the morphology, at any given position). We then compute the anisotropy as R_ξ = ξ_per/ξ_par. Thus, R_ξ ≈ 1 indicates roughly isotropic grains (similar size in both morphological directions), whereas R_ξ > 1 indicates anisotropic grains that are larger in the perpendicular direction (along the line-repeats) and R_ξ <1 indicates anisotropic grains in the parallel direction (along the cylinder long-axis).

Monte Carlo model

A simple Monte Carlo (MC) model for the conversion from vertical to horizontal cylinders was implemented in Python. The initial state is a triangular lattice where each lattice site is an unconnected ‘dot’; this represents a perfect vertical cylinder state. The 2D simulation region has periodic boundary conditions. Each MC step consists of randomly selecting a connection between dots to toggle (create or remove). If the candidate MC move lowers system energy (initial perfect lattice is defined as E = 0), it is accepted; if the move increases energy, it is accepted according to a probability exponential in simulation temperature (eqn (4)). The behavior of the simulation depends on the relative energies of various local states (number of connections, angle between connections, etc.). Refer to ESI† for exploration of a variety of possible conditions. The results presented in the manuscript are those physically-reasonable energy orderings which reproduce the experimentally-observed behavior.

Acknowledgements

Research carried out at the Center for Functional Nanomaterials, and National Synchrotron Light Source, Brookhaven National Laboratory, which are supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-SC0012704.

References

1. M. J. Fasolka and A. M. Mayes, Block Copolymer Thin Films: Physics and Applications, Annu. Rev. Mater. Res., 2001, 31, 323–355.
2. J. N. L. Albert and T. H. Epps, Self-Assembly of Block Copolymer Thin Films, Mater. Today, 2010, 13, 24–33.
3. F. S. Bates and G. H. Fredrickson, Block Copolymer Thermodynamics: Theory and Experiment, Annu. Rev. Phys. Chem., 1990, 41, 525–557.
4. H. Hu, M. Gopinadhan and C. O. Osuji, Directed Self-Assembly of Block Copolymers: A Tutorial Review of Strategies for Enabling Nanotechnology with Soft Matter, Soft Matter, 2014, 10, 3867–3889.
5. P. Mansky, T. P. Russell, C. J. Hawker, M. Pitsikalis and J. Mays, Ordered Diblock Copolymer Films on Random Copolymer Brushes, Macromolecules, 1997, 30, 6810–6813.
6. P. Mansky, T. P. Russell, C. J. Hawker, J. Mays, D. C. Cook and S. K. Satija, Interfacial Segregation in Disordered Block Copolymers: Effect of Tunable Surface Potentials, Phys. Rev. Lett., 1997, 79, 237.
7. E. Huang, L. Rockford, T. P. Russell and C. J. Hawker, Nanodomain Control in Copolymer Thin Films, Nature, 1998, 395, 757.
8. E. Han, K. O. Stuen, M. Leolukman, C.-C. Liu, P. F. Nealey and P. Gopalan, Perpendicular Orientation of Domains in Cylinder-Forming Block Copolymer Thick Films by Controlled Interfacial Interactions, Macromolecules, 2009, 42, 4896–4901.
9. G. E. Stein, N. Mahadevapuram and I. Mitra, Controlling Interfacial Interactions for Directed Self Assembly of Block Copolymers, J. Polym. Sci., Part B: Polym. Phys., 2014, 53, 96–102.
10. E. Sivaniah, Y. Hayashi, M. Iino, T. Hashimoto and K. Fukunaga, Observation of Perpendicular Orientation in Symmetric Diblock Copolymer Thin Films on Rough Substrates, Macromolecules, 2003, 36, 5894–5896.
11. E. Sivaniah, Y. Hayashi, S. Matsubara, S. Kiyono, T. Hashimoto, K. Kukunaga, E. J. Kramer and T. Mates, Symmetric Diblock Copolymer Thin Films on Rough Substrates. Kinetics and Structure Formation in Pure Block Copolymer Thin Films, Macromolecules, 2005, 38, 1837–1849.
12. Y. Tsori, E. Sivaniah, D. Andelman and T. Hashimoto, Orientational Transitions in Symmetric Diblock Copolymers on Rough Surfaces, Macromolecules, 2005, 38, 7193–7196.
13. K. G. Yager, B. C. Berry, K. Page, D. Patton, A. Karim and E. J. Amis, Disordered Nanoparticle Interfaces for Directed Self-Assembly, Soft Matter, 2009, 5, 622–628.
14. M. M. Kulkarni, K. G. Yager, A. Sharma and A. Karim, Combinatorial Block Copolymer Ordering on Tunable Rough Substrates, Macromolecules, 2012, 45, 4303–4314.
15. S. Kundu, R. Ganesan, N. Gaur, M. S. M. Saifullah, H. Hussain, H. Yang and C. S. Bhatia, Effect of Angstrom-Scale Surface Roughness on the Self-Assembly of Polystyrene-Polydimethylsiloxane Block Copolymer, Sci. Rep., 2012, 2, 617.
16. K. G. Yager, C. Forrey, G. Singh, S. K. Satija, K. A. Page, D. L. Patton, J. F. Douglas, R. L. Jones and A. Karim, Thermally-Induced Transition of Lamellae Orientation in Block-Copolymer Films on ‘Neutral’ Nanoparticle-Coated Substrates, Soft Matter, 2015, 11, 5154–5167.
17. I. Podariu and A. Chakrabarti, Block Copolymer Thin Films on Corrugated Substrates, J. Chem. Phys., 2000, 113, 6423.
18. Y. Tsori and D. Andelman, Parallel and Perpendicular Lamellae on Corrugated Surfaces, Macromolecules, 2003, 36, 8560–8566.
19. K. Ho-Cheol, T. R. Charles and S. Linnea, Fabrication of 20 nm Half-Pitch Gratings by Corrugation-Directed Self-Assembly, Nanotechnology, 2008, 19, 235301.
20. S. Park, D. H. Lee, J. Xu, B. Kim, S. W. Hong, U. Jeong, T. Xu and T. P. Russell, Macroscopic 10-Terabit-Per-Square-Inch Arrays from Block Copolymers with Lateral Order, Science, 2009, 323, 1030–1033.
21. S. M. Park, B. C. Berry, E. Dobisz and H. C. Kim, Observation of Surface Corrugation-Induced Alignment of Lamellar Microdomains in PS-b-PMMA Thin Films, Soft Matter, 2009, 5, 957–961.
22. X. Zhang, S. H. De Paoli Lacerda, K. G. Yager, B. C. Berry, J. F. Douglas, R. L. Jones and A. Karim, Target Patterns Induced by Fixed Nanoparticles in Block Copolymer Films, ACS Nano, 2009, 3, 2115–2120.
23. S. W. Hong, J. Huh, X. Gu, D. H. Lee, W. H. Jo, S. Park, T. Xu and T. P. Russell, Unidirectionally Aligned Line Patterns Driven by Entropic Effects on Faceted Surfaces, Proc. Natl. Acad. Sci. U. S. A., 2012.
24. D. G. Walton, G. J. Kellogg, A. M. Mayes, P. Lambooy and T. P. Russell, A Free Energy Model for Confined Diblock Copolymers, Macromolecules, 1994, 27, 6225–6228.
25. M. A. van Dijk and R. van den Berg, Ordering Phenomena in Thin Block Copolymer Films Studied Using Atomic Force Microscopy, Macromolecules, 1995, 28, 6773–6778.
26. T. L. Morkved and H. M. Jaeger, Thickness-Induced Morphology Changes in Lamellar Diblock Copolymer Ultrathin Films, Europhys. Lett., 1997, 40, 643.
27. C. Forrey, K. G. Yager and S. P. Broadaway, Molecular Dynamics Study of the Role of the Free Surface on Block Copolymer Thin Film Morphology and Alignment, ACS Nano, 2011, 5, 2895–2907.
28. C. T. Black and K. W. Guarini, Structural Evolution of Cylindrical-Phase Diblock Copolymer Thin Films, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 1970–1975.
29. X. Zhang, B. C. Berry, K. G. Yager, S. Kim, R. L. Jones, S. Satija, D. L. Pickel, J. F. Douglas and A. Karim, Surface Morphology Diagram for Cylinder-Forming Block Copolymer Thin Films, ACS Nano, 2008, 2, 2331–2341.
30. X. Zhang, K. G. Yager, N. J. Fredin, H. W. Ro, R. L. Jones, A. Karim and J. F. Douglas, Thermally Reversible Surface Morphology Transition in Thin Diblock Copolymer Films, ACS Nano, 2010, 4, 3653–3660.
31. S. Ji, C.-C. Liu, W. Liao, A. L. Fenske, G. S. W. Craig and P. F. Nealey, Domain Orientation and Grain Coarsening in Cylinder-Forming Poly(Styrene-b-Methyl Methacrylate) Films, Macromolecules, 2011, 44, 4291–4300.
32. X. Zhang, J. F. Douglas, S. Satija and A. Karim, Enhanced Vertical Ordering of Block Copolymer Films by Tuning Molecular Mass, RSC Adv., 2015, 5, 32307–32318.
33. T. Hashimoto, J. Bodycomb, Y. Funaki and K. Kimishima, The Effect of Temperature Gradient on the Microdomain Orientation of Diblock Copolymers Undergoing an Order-Disorder Transition, Macromolecules, 1999, 32, 952–954.
34. J. Bodycomb, Y. Funaki, K. Kimishima and T. Hashimoto, Single-Grain Lamellar Microdomain from a Diblock Copolymer, Macromolecules, 1999, 32, 2075–2077.
35. B. C. Berry, A. W. Bosse, J. F. Douglas, R. L. Jones and A. Karim, Orientational Order in Block Copolymer Films Zone Annealed Below the Order-Disorder Transition Temperature, Nano Lett., 2007, 7, 2789–2794.
36. K. G. Yager, N. J. Fredin, X. Zhang, B. C. Berry, A. Karim and R. L. Jones, Evolution of Block-Copolymer Order through a Moving Thermal Zone, Soft Matter, 2010, 6, 92–99.
37. G. Singh, K. G. Yager, D.-M. Smilgies, M. M. Kulkarni, D. G. Bucknall and A. Karim, Tuning Molecular Relaxation for Vertical Orientation in Cylindrical Block Copolymer Films Via Sharp Dynamic Zone Annealing, Macromolecules, 2012, 45, 7107–7117.
38. P. W. Majewski and K. G. Yager, Millisecond Ordering of Block Copolymer Films Via Photothermal Gradients, ACS Nano, 2015, 9, 3896–3906.
39. C. Park, C. De Rosa and E. L. Thomas, Large Area Orientation of Block Copolymer Microdomains in Thin Films Via Directional Crystallization of a Solvent, Macromolecules, 2001, 34, 2602–2606.
40. M. Kimura, M. J. Misner, T. Xu, S. H. Kim and T. P. Russell, Long-Range Ordering of Diblock Copolymers Induced by Droplet Pinning, Langmuir, 2003, 19, 9910–9913.
41. S. H. Kim, M. J. Misner and T. P. Russell, Solvent-Induced Ordering in Thin Film Diblock Copolymer/Homopolymer Mixtures, Adv. Mater., 2004, 16, 2119–2123.
42. J. E. Seppala, R. L. Lewis and T. H. Epps, Spatial and Orientation Control of Cylindrical Nanostructures in Aba Triblock Copolymer Thin Films by Raster Solvent Vapor Annealing, ACS Nano, 2012, 6, 9855–9862.
43. C. Sinturel, M. Vayer, M. Morris and M. A. Hillmyer, Solvent Vapor Annealing of Block Polymer Thin Films, Macromolecules, 2013, 46, 5399–5415.
44. H. Cui, Z. Chen, S. Zhong, K. L. Wooley and D. J. Pochan, Block Copolymer Assembly Via Kinetic Control, Science, 2007, 317, 647–650.
45. S. Mann, Self-Assembly and Transformation of Hybrid Nano-Objects and Nanostructures under Equilibrium and Non-Equilibrium Conditions, Nat. Mater., 2009, 8, 781–792.
46. P. W. Majewski and K. G. Yager, Latent Alignment in Pathway-Dependent Ordering of Block Copolymer Thin Films, Nano Lett., 2015, 15, 5221–5228.
47. Y. S. Jung and C. A. Ross, Orientation-Controlled Self-Assembled Nanolithography Using a Polystyrene-Polydimethylsiloxane Block Copolymer, Nano Lett., 2007, 7, 2046–2050.
48. H. J. Dai, N. P. Balsara, B. A. Garetz and M. C. Newstein, Grain Growth and Defect Annihilation in Block Copolymers, Phys. Rev. Lett., 1996, 77, 3677–3680.
49. C. Harrison, D. H. Adamson, Z. Cheng, J. M. Sebastian, S. Sethuraman, D. A. Huse, R. A. Register and P. M. Chaikin, Mechanisms of Ordering in Striped Patterns, Science, 2000, 290, 1558–1560.
50. C. Harrison, D. E. Angelescu, M. Trawick, C. Zhengdong, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Pattern Coarsening in a 2d Hexagonal System, Europhys. Lett., 2004, 67, 800.
51. D. A. Hajduk, S. M. Gruner, P. Rangarajan, R. A. Register, L. J. Fetters, C. Honeker, R. J. Albalak and E. L. Thomas, Observation of a Reversible Thermotropic Order–Order Transition in a Diblock Copolymer, Macromolecules, 1994, 27, 490–501.
52. N. Sakamoto, T. Hashimoto, C. D. Han, D. Kim and N. Y. Vaidya, Order–Order and Order–Disorder Transitions in a Polystyrene-Block-Polyisoprene-Block-Polystyrene Copolymer, Macromolecules, 1997, 30, 1621–1632.
53. K. Kimishima, T. Koga and T. Hashimoto, Order–Order Phase Transition between Spherical and Cylindrical Microdomain Structures of Block Copolymer. I. Mechanism of the Transition, Macromolecules, 2000, 33, 968–977.
54. I. Park, B. Lee, J. Ryu, K. Im, J. Yoon, M. Ree and T. Chang, Epitaxial Phase Transition of Polystyrene-b-Polyisoprene from Hexagonally Perforated Layer to Gyroid Phase in Thin Film, Macromolecules, 2005, 38, 10532–10536.
55. J. Hahm and S. J. Sibener, Time-Resolved Atomic Force Microscopy Imaging Studies of Asymmetric PS-b-PMMA Ultrathin Films: Dislocation and Disclination Transformations, Defect Mobility, and Evolution of Nanoscale Morphology, J. Chem. Phys., 2001, 114, 4730–4740.
56. M. R. Hammond, E. Cochran, G. H. Fredrickson and E. J. Kramer, Temperature Dependence of Order, Disorder, and Defects in Laterally Confined Diblock Copolymer Cylinder Monolayers, Macromolecules, 2005, 38, 6575–6585.
57. R. Ruiz, J. K. Bosworth and C. T. Black, Effect of Structural Anisotropy on the Coarsening Kinetics of Diblock Copolymer Striped Patterns, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 05420.
58. V. Mishra, G. H. Fredrickson and E. J. Kramer, Effect of Film Thickness and Domain Spacing on Defect Densities in Directed Self-Assembly of Cylindrical Morphology Block Copolymers, ACS Nano, 2012, 6, 2629–2641.
59. B. Kim, N. Laachi, K. T. Delaney, M. Carilli, E. J. Kramer and G. H. Fredrickson, Thermodynamic and Kinetic Aspects of Defectivity in Directed Self-Assembly of Cylinder-Forming Diblock Copolymers in Laterally Confining Thin Channels, J. Appl. Polym. Sci., 2014, 131, 40790.
60. G. E. Stein, E. J. Kramer, X. Li and J. Wang, Layering Transitions in Thin Films of Spherical-Domain Block Copolymers, Macromolecules, 2007, 40, 2453–2460.
61. G. E. Stein, W. B. Lee, G. H. Fredrickson, E. J. Kramer, X. Li and J. Wang, Thickness Dependent Ordering in Laterally Confined Monolayers of Spherical-Domain Block Copolymers, Macromolecules, 2007, 40, 5791–5800.
62. G. E. Stein, E. W. Cochran, K. Katsov, G. H. Fredrickson, E. J. Kramer, X. Li and J. Wang, Symmetry Breaking of in-Plane Order in Confined Copolymer Mesophases, Phys. Rev. Lett., 2007, 98, 158302.
63. M. J. Fasolka, P. Banerjee, A. M. Mayes, G. Pickett and A. C. Balazs, Morphology of Ultrathin Supported Diblock Copolymer Films: Theory and Experiment, Macromolecules, 2000, 33, 5702–5712.
64. K. S. Lyakhova, A. Horvat, A. V. Zvelindovsky and G. J. A. Sevink, Dynamics of Terrace Formation in a Nanostructured Thin Block Copolymer Film, Langmuir, 2006, 22, 5848–5855.
65. A. Knoll, A. Horvat, K. S. Lyakhova, G. Krausch, G. J. A. Sevink, A. V. Zvelindovsky and R. Magerle, Phase Behavior in Thin Films of Cylinder-Forming Block Copolymers, Phys. Rev. Lett., 2002, 89, 035501.
66. S.-W. Kim, E. Kim, H. Lee, B. C. Berry, H.-C. Kim and D. Y. Ryu, Thickness-Dependent Ordering of Perpendicularly Oriented Lamellae in PS-b-PMMA Thin Films, Polymer, 2015, 74, 63–69.
67. T. P. Russell, A. Menelle, S. H. Anastasiadis, S. K. Satija and C. F. Majkrzak, Unconventional Morphologies of Symmetric, Diblock Copolymers Due to Film Thickness Constraints, Macromolecules, 1991, 24, 6263–6269.
68. M. Maaloum, D. Ausserre, D. Chatenay and Y. Gallot, Spinodal Decomposition-Like Patterns Via Metastable State Relaxation, Phys. Rev. Lett., 1993, 70, 2577–2580.
69. S. Joly, D. Ausserré, G. Brotons and Y. Gallot, Hole Nucleation in Thin Diblock Copolymer Films, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 8, 355–363.
70. B. Collin, D. Chatenay, G. Coulon, D. Ausserre and Y. Gallot, Ordering of Copolymer Thin Films as Revealed by Atomic Force Microscopy, Macromolecules, 1992, 25, 1621–1622.
71. G. Vignaud, A. Gibaud, G. Grübel, S. Joly, D. Ausserré, J. F. Legrand and Y. Gallot, Ordering of Diblock PS-PBMA Thin Films: An X-Ray Reflectivity Study, Phys. B, 1998, 248, 250–257.
72. N. Koneripalli, N. Singh, R. Levicky, F. S. Bates, P. D. Gallagher and S. K. Satija, Confined Block Copolymer Thin Films, Macromolecules, 1995, 28, 2897–2904.
73. R. t. Peters and K. Dalnoki-Veress, Film Thickness Dependent Ordering Dynamics of Lamellar Forming Diblock Copolymer Thin Films, Eur. Phys. J. E: Soft Matter Biol. Phys., 2012, 35, 1–6.
74. H. C. Kim and T. P. Russell, Ordering in Thin Films of Asymmetric Diblock Copolymers, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 663–668.
75. S. Ham, C. Shin, E. Kim, D. Y. Ryu, U. Jeong, T. P. Russell and C. J. Hawker, Microdomain Orientation of PS-b-PMMA by Controlled Interfacial Interactions, Macromolecules, 2008, 41, 6431–6437.
76. H. Takahashi, N. Laachi, K. T. Delaney, S.-M. Hur, C. J. Weinheimer, D. Shykind and G. H. Fredrickson, Defectivity in Laterally Confined Lamella-Forming Diblock Copolymers: Thermodynamic and Kinetic Aspects, Macromolecules, 2012, 45, 6253–6265.
77. A. J. Peters, R. A. Lawson, B. D. Nation, P. J. Ludovice, C. L. Henderson, In Coarse-Grained Molecular Dynamics Modeling of the Kinetics of Lamellar Bcp Defect Annealing, 2015, p. 94231Y.
78. D. A. Vega, C. K. Harrison, D. E. Angelescu, M. L. Trawick, D. A. Huse, P. M. Chaikin and R. A. Register, Ordering Mechanisms in Two-Dimensional Sphere-Forming Block Copolymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 061803.
79. M. Komura, H. Komiyama, K. Nagai and T. Iyoda, Direct Observation of Faceted Grain Growth of Hexagonal Cylinder Domains in a Side Chain Liquid Crystalline Block Copolymer Matrix, Macromolecules, 2013, 46, 9013–9020.
80. Q. Tong and S. J. Sibener, Visualization of Individual Defect Mobility and Annihilation within Cylinder-Forming Diblock Copolymer Thin Films on Nanopatterned Substrates, Macromolecules, 2013, 46, 8538–8544.
81. J. Hahm, W. A. Lopes, H. M. Jaeger and S. J. Sibener, Defect Evolution in Ultrathin Films of Polystyrene-Block-Polymethylmethacrylate Diblock Copolymers Observed by Atomic Force Microscopy, J. Chem. Phys., 1998, 109, 10111–10114.
82. C. Harrison, Z. Cheng, S. Sethuraman, D. A. Huse, P. M. Chaikin, D. A. Vega, J. M. Sebastian, R. A. Register and D. H. Adamson, Dynamics of Pattern Coarsening in a Two-Dimensional Smectic System, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011706.
83. D. Borah, R. Senthamaraikannan, S. Rasappa, B. Kosmala, J. D. Holmes and M. A. Morris, Swift Nanopattern Formation of PS-b-PMMA and PS-b-PDMS Block Copolymer Films Using a Microwave Assisted Technique, ACS Nano, 2013, 7, 6583–6596.
84. J. Chai and J. M. Buriak, Using Cylindrical Domains of Block Copolymers to Self-Assemble and Align Metallic Nanowires, ACS Nano, 2008, 2, 489–501.
85. X. Zhang, K. D. Harris, N. L. Y. Wu, J. N. Murphy and J. M. Buriak, Fast Assembly of Ordered Block Copolymer Nanostructures through Microwave Annealing, ACS Nano, 2010, 4, 7021–7029.
86. C. Jin, J. N. Murphy, K. D. Harris and J. M. Buriak, Deconvoluting the Mechanism of Microwave Annealing of Block Copolymer Thin Films, ACS Nano, 2014, 8, 3979–3991.
87. B. L. Carvalho, R. L. Lescanec and E. L. Thomas, Grain Boundary Defects in Block Copolymer Systems: Bulk and Thin Film Results, Macromol. Symp., 1995, 98, 1131–1146.
88. T. Hashimoto and N. Sakamoto, Nucleation and Anisotropic Growth of Lamellar Microdomains in Block Copolymers, Macromolecules, 1995, 28, 4779–4781.
89. T. Hashimoto, N. Sakamoto and T. Koga, Nucleation and Growth of Anisotropic Grain in Block Copolymers near Order-Disorder Transition, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1996, 54, 5832–5835.
90. N. Sakamoto and T. Hashimoto, Ordering Dynamics of a Symmetric Polystyrene-Block-Polyisoprene. 1. Ordering Mechanism from the Disordered State, Macromolecules, 1998, 31, 3292–3302.
91. N. Sakamoto and T. Hashimoto, Ordering Dynamics of a Symmetric Polystyrene-Block-Polyisoprene. 2. Real-Space Analysis on the Formation of Lamellar Microdomain, Macromolecules, 1998, 31, 3815–3823.
92. S. Niu and R. F. Saraf, Stability of Order in Solvent-Annealed Block Copolymer Thin Films, Macromolecules, 2003, 36, 2428–2440.
93. H. J. Ryu, D. B. Fortner, S. Lee, R. Ferebee, M. De Graef, K. Misichronis, A. Avgeropoulos and M. R. Bockstaller, Role of Grain Boundary Defects During Grain Coarsening of Lamellar Block Copolymers, Macromolecules, 2013, 46, 204–215.
94. J. G. Son, K. W. Gotrik and C. A. Ross, High-Aspect-Ratio Perpendicular Orientation of PS-b-PDMS Thin Films under Solvent Annealing, ACS Macro Lett., 2012, 1, 1279–1284.
95. E. Kim, W. Kim, K. H. Lee, C. A. Ross and J. G. Son, A Top Coat with Solvent Annealing Enables Perpendicular Orientation of Sub-10 nm Microdomains in Si-Containing Block Copolymer Thin Films, Adv. Funct. Mater., 2014, 24, 6981–6988.
96. T. A. Mykhaylyk, S. Collins, I. W. Hamley, S. D. Evans and J. R. Henderson, Ordered Structures and Phase Transitions in Thin Films of Polystyrene/Polyisoprene Block Copolymer and Blends with the Corresponding Homopolymers, J. Mater. Sci., 2004, 39, 2249–2252.
97. T. Q. Chastek and T. P. Lodge, Grain Shapes and Growth Kinetics of the Cylinder Phase in a Block Copolymer Solution, Macromolecules, 2004, 37, 4891–4899.
98. T. Q. Chastek and T. P. Lodge, Twinning and Growth Kinetics of Lamellar Grains in a Diblock Copolymer Solution, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 405–412.
99. T. Q. Chastek and T. P. Lodge, Grain Shapes and Growth Kinetics During Self-Assembly of Block Copolymers, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 481–491.
100. I. F. Hsieh, H.-J. Sun, Q. Fu, B. Lotz, K. A. Cavicchi and S. Z. D. Cheng, Phase Structural Formation and Oscillation in Polystyrene-Block-Polydimethylsiloxane Thin Films, Soft Matter, 2012, 8, 7937–7944.
101. N. P. Balsara, C. M. Marques, B. A. Garetz, M. C. Newstein and S. P. Gido, Anisotropy of Lamellar Block Copolymer Grains, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 052802.
102. S.-J. Jeon, G.-R. Yi and S.-M. Yang, Cooperative Assembly of Block Copolymers with Deformable Interfaces: Toward Nanostructured Particles, Adv. Mater., 2008, 20, 4103–4108.
103. S. G. Jang, D. J. Audus, D. Klinger, D. V. Krogstad, B. J. Kim, A. Cameron, S.-W. Kim, K. T. Delaney, S.-M. Hur, K. L. Killops, G. H. Fredrickson, E. J. Kramer and C. J. Hawker, Striped, Ellipsoidal Particles by Controlled Assembly of Diblock Copolymers, J. Am. Chem. Soc., 2013, 135, 6649–6657.
104. S.-M. Hur, M. S. Onses, A. Ramírez-Hernández, P. F. Nealey, J. A. Rogers and J. J. de Pablo, Interplay of Surface Energy and Bulk Thermodynamic Forces in Ordered Block Copolymer Droplets, Macromolecules, 2015, 48, 4717–4723.
105. P. W. Majewski, A. Rahman, C. T. Black and K. G. Yager, Arbitrary Lattice Symmetries Via Block Copolymer Nanomeshes, Nat. Commun., 2015, 6, 7448.
106. P. W. Majewski and K. G. Yager, Block Copolymer Response to Photothermal Stress Fields, Macromolecules, 2015, 48, 4591–4598.
107. X. Zhang, K. G. Yager, S. Kang, N. J. Fredin, B. Akgun, S. Satija, J. F. Douglas, A. Karim and R. L. Jones, Solvent Retention in Thin Spin-Coated Polystyrene and Poly(Methyl Methacrylate) Homopolymer Films Studied by Neutron Reflectometry, Macromolecules, 2009, 43, 1117–1123.
108. J. N. Murphy, K. D. Harris and J. M. Buriak, Automated Defect and Correlation Length Analysis of Block Copolymer Thin Film Nanopatterns, PLoS One, 2015, 10, e0133088.
109. T. E. Oliphant, Python for Scientific Computing, Comput. Sci. Eng., 2007, 9, 10–20.
110. J. D. Hunter, Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 2007, 9, 90–95.
111. K. G. Yager, E. Lai and C. T. Black, Self-Assembled Phases of Block Copolymer Blend Thin Films, ACS Nano, 2014, 8, 10582–10588.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm02441b

---