Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion specific effects on the stability of layered double hydroxide colloids
Marko
Pavlovic
a,
Robin
Huber
a,
Monika
Adok-Sipiczki
a,
Corinne
Nardin
ab and
Istvan
Szilagyi
*a
aDepartment of Inorganic and Analytical Chemistry, University of Geneva, 30 Quai Ernest-Ansermet, CH-1205 Geneva, Switzerland. E-mail: istvan.szilagyi@unige.ch; Tel: +41 22 3796031
bInstitut des Sciences Analytiques et de Physicochimie pour l'Environnement et les Matériaux, Université de Pau et des Pays de l'Adour, 2 Avenue du Président Angot, F-64053 Pau, France
First published on 8th March 2016
Abstract
Positively charged layered double hydroxide particles composed of Mg2+ and Al3+ layer-forming cations and NO3− charge compensating anions (MgAl–NO3-LDH) were synthesized and the colloidal stability of their aqueous suspensions was investigated in the presence of inorganic anions of different charges. The formation of the layered structure was confirmed by X-ray diffraction, while the charging and aggregation properties were explored by electrophoresis and light scattering. The monovalent anions adsorb on the oppositely charged surface to a different extent according to their hydration state leading to the Cl− > NO3− > SCN− > HCO3− order in surface charge densities. The ions on the right side of the series induce the aggregation of MgAl–NO3-LDH particles at lower concentrations, whereas in the presence of the left ones, the suspensions are stable even at higher salt levels. The adsorption of multivalent anions gave rise to charge neutralization and charge reversal at appropriate concentrations. For some di, tri and tetravalent ions, charge reversal resulted in restabilization of the suspensions in the intermediate salt concentration regime. Stable samples were also observed at low salt levels. Particle aggregation was fast near the charge neutralization point and at high concentrations. These results, which evidence the colloidal stability of MgAl–NO3-LDH in the presence of various anions, are of prime fundamental interest. These are also critical for applications to develop stable suspensions of primary particles for water purification processes, with the aim of the removal of similar anions by ion exchange.
Introduction
Layered double hydroxides (LDHs) are anionic clays composed of mixed positively charged lamellar hydroxides of divalent (e.g., Mg2+, Zn2+ or Ca2+) and trivalent (e.g., Al3+, Fe3+ or Cr3+) metal ions with charge compensating anions between the layers.1 LDH particles and their composite materials are widely used in energy storage,2,3 medical treatments,4–6 coating,7 catalysis8–10 and the removal of water pollutants.11–13 For the latter application, their relatively high anion exchange capacity is utilized to capture various types of anions (e.g., NO3−, SO42−, SeO42−, PO43− and AsO43−) during water purification processes. Ion exchange can take place by intercalation between the layers and also by adsorption on the particle surface. To achieve high efficiencies of these procedures, stable LDH suspensions containing primary particles are required during the ion exchange process. In addition, the particles have to be aggregated at a later stage for their facile removal from the reaction mixture. The effect of anions on the colloidal stability thus needs to be comprehensively understood to control particle aggregation.The classical theory developed for aqueous suspensions of charged colloidal particles by Derjaguin, Landau, Verwey and Overbeek (DLVO) has proven to be suitable to predict colloidal stability in the presence of electrolytes.14,15 It states that the acting interparticle force is the superposition of the repulsive double layer and attractive van der Waals forces. The first one originates from the overlap of electrical double layers forming around the charged particles dispersed in a salt solution. Its magnitude decreases with an increase in the ionic strength due to the screening effect of the counterions on the surface charge. The attractive van der Waals forces are independent of the electrolyte concentration and only depend on the size and composition of the particles. Accordingly, aqueous colloids are stable at low ionic strength and unstable at higher electrolyte concentrations, while these stability regimes are separated by the critical coagulation concentration (CCC).16
The presence of simple salts of different compositions can lead to different CCCs. This ion specificity on particle aggregation usually follows the tendency described by the Hofmeister series17–19 for anions and cations as
| SO42− < HPO42− < HCO3− < Cl− < Br− < NO3− < I− < ClO4− < SCN− |
| N(CH3)4+ < NH4+ < Cs+ < Rb+ < K+ < Na+ < Li+ < Mg2+ < Ca2+ |
The effects of sodium salts of different anions (SCN−, Br−, Cl−, SO42−, HPO42− and CO32−) within the Hofmeister series on the aggregation of weakly charged LDHs have been also investigated.30 The reported CCC values showed good agreement with the tendency predicted by the indirect Hofmeister series for positively charged, hydrophobic particles. However, only a weak dependence on the type of salt was discovered for monovalent ions. The presence of multivalent anions decreased the CCCs significantly. This fact indicates the importance of the counterion valence on the colloidal stability of the particles, which has to be treated differently from the monovalent case.
Although the DLVO theory takes the valence of ions into account through the ionic strength, the type of salt (i.e., ion specificity) is not considered. Accordingly, electrical double layer forces decrease with the valence of counterions at the same salt concentrations and such a decrease leads to a dependence of the CCCs on the valence (z) as
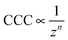 | (1) |
For LDH particles, interactions with multivalent anions (e.g., CO32−, SO42−, CrO42−, PO43− and AsO43−) have been extensively investigated to determine the adsorbed amount and to clarify the adsorption mechanism.45–51 In spite of the large number of such studies, no comprehensive investigation on the effect of anion adsorption on aggregation kinetics and related colloidal stability has been published yet.
In the present research, we aimed at investigating the surface charge properties and aggregation of LDH particles composed of Mg2+ and Al3+ metal ions and NO3− interlayer anions (denoted as MgAl–NO3-LDH) in the presence of the K+ salts of various mono- and multivalent anions. The NO3− intercalated LDHs are widely applied, since other anions can be easily intercalated between the layers by ion exchange. Electrophoretic and dynamic light scattering experiments were performed in aqueous suspensions to explore possible ion specific effects on the colloidal stability of the samples over a wide range of electrolyte concentrations. On the basis of the measured CCCs, we have clarified the Hofmeister series and the Schulze−Hardy rule for LDH particles.
Experimental section
Materials
Analytical grade KCl, KSCN, K2HPO4 (Acros Organics), KHCO3 (Alfa Aesar), KNO3, K2SO4, K2HAsO4, K3Fe(CN)6 and K4Fe(CN)6·3H2O (Sigma-Aldrich) were used. The salt solutions were prepared by dissolving the calculated amount of solid in ultrapure water (Millipore) and the pH was adjusted to 9 with 0.1 M KOH (Sigma-Aldrich) solution. This pH was also maintained in all stock suspensions and water was used for sample preparation throughout the experiments. The protonation constants (pK) of inorganic anions together with their actual charge at pH 9 are presented in Table 1. All stock solutions were filtered using a 0.1 μm pore-size filter (Millipore) prior to sample preparation and the measurements were carried out at 25 °C.| Anionsa | pK1b | pK2b | pK3b | Valence at pH 9c |
|---|---|---|---|---|
| a Chemical formula in the deprotonated form. b The pK values were obtained from the JESS (Joint Expert Speciation System) database75 at infinite dilution and 25 °C. c The valence was calculated on the basis of the protonation equilibria at pH 9 using the reported pK values. | ||||
| Cl− | −0.71 | — | — | 1.00 |
| NO3− | −1.40 | — | — | 1.00 |
| SCN− | −2.10 | — | — | 1.00 |
| CO32− | 10.33 | 6.35 | — | 1.04 |
| SO42− | 1.98 | −2.00 | — | 2.00 |
| AsO43− | 11.50 | 6.94 | 2.19 | 1.99 |
| PO43− | 12.35 | 7.21 | 2.14 | 1.98 |
| Fe(CN)63− | — | — | — | 3.00 |
| Fe(CN)64− | 4.20 | 2.00 | −1.00 | 4.00 |
The MgAl–NO3-LDH particles were prepared using the coprecipitation method.52–55 The solutions of Mg(NO3)2 and Al(NO3)3 (Sigma-Aldrich) were added dropwise under vigorous stirring to N2-blanketed 1.0 M NaOH (Acros Organics) until the final pH reached 10. The resulting suspension was subjected to hydrothermal treatment at 120 °C for 16 h in a teflon chamber embedded in a high-pressure steel reactor (Columbia International). The solid materials was rapidly filtered using a caustic resistant vacuum filter unit (Nalgene) equipped with a 0.45 μm membrane (Versapor) and washed thoroughly with ultrapure water. MgAl–NO3-LDH was then redispersed in pH 9 water resulting in a stock suspension of 10 g L−1, which was later diluted to reach the suitable particle concentration for the experiments. The X-ray diffraction (XRD) patterns, recorded on a STADI-P transmission powder diffractometer system (Stoe), unambiguously confirmed the LDH formation (Fig. 1). Accordingly, all patterns can be indexed to a 3R1 polytype where 3 is the number of layers stacked along the c-axis of the elementary cell, R refers to the rhombohedral symmetry and 1 indicates the trigonal prismatic assembly of the hydroxyl groups in the neighboring layers. This information was derived from the (012), (015) and (018) reflections. Such a polytype form is commonly used for the description of LDH structures.56 The lattice parameters were calculated from the observed peaks. An a dimension of 0.3 nm, which represents the shortest distance between two cations in the LDH layer, was calculated as twice the position of the (110) reflection.56 A c parameter of 2.4 nm was obtained from the (003) reflection and it represents the thickness of three layers plus the interlayer space between them. The average thickness of the particles (ν) was calculated using the Scherrer equation as
ν = Kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosθB cosθB | (2) |
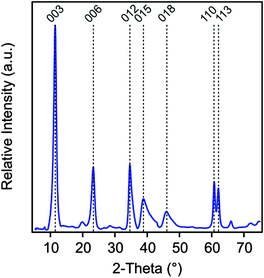 | ||
| Fig. 1 Powder XRD pattern of the MgAl–NO3-LDH particles synthesized by coprecipitation and subjected to hydrothermal treatment. | ||
Electrophoretic mobility and stability ratio measurements
Electrophoretic mobilities were measured using a ZetaNano ZS (Malvern) device. The experiments were performed in plastic capillary cells (Malvern). For sample preparation, the calculated amount of electrolyte stock solution was mixed with ultrapure water to obtain the desired salt concentration. In the last step, the particle stock suspension was added. The final volume (5 mL) and the MgAl–NO3-LDH concentration (5 mg L−1) were kept constant in the experiments. The suspensions were equilibrated overnight at room temperature and the electrophoretic mobilities were measured five times and the average values were reported. The standard deviation was always below 5%.Dynamic light scattering (DLS) measurements were performed using a compact goniometer system (ALV/CGS-3) at 90° scattering angle and borosilicate glass cuvettes (Kimble Chase). A hydrodynamic radius of 168 nm and a polydispersity index of 0.39 were obtained for the MgAl–NO3-LDH particles in stable aqueous suspensions. Time-resolved DLS experiments were carried out to explore particle aggregation. Fig. 2 shows some typical measurements, in which the hydrodynamic radius (Rh) was measured for 24 min under different experimental conditions. The initial increase in size was used to calculate the apparent aggregation rate (Δ) as
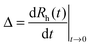 | (3) |
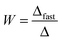 | (4) |
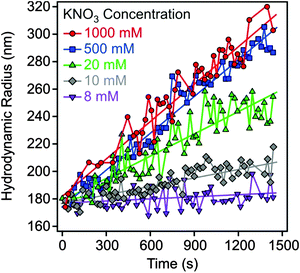 | ||
| Fig. 2 Hydrodynamic radius of MgAl–NO3-LDH particles (5 mg L−1) as a function of time of the experiment measured at different KNO3 concentrations. | ||
Results and discussion
The surface charge properties and aggregation of positively charged MgAl–NO3-LDH particles were studied by electrophoresis and DLS to investigate the suspension stability in the presence of simple inorganic electrolytes over a wide range of concentrations. The type and the charge of anions were systematically varied to explore ion specific effects on the colloidal stability of the samples. The anions are the counterions, whereas the K+ coion was used throughout all experiments. Monovalent anions within the Hofmeister series17 were investigated first, followed by di, tri and tetravalent ones to establish the validity of the Schulze−Hardy rule31 for anions interacting with the MgAl–NO3-LDH particles.Effect of monovalent anions
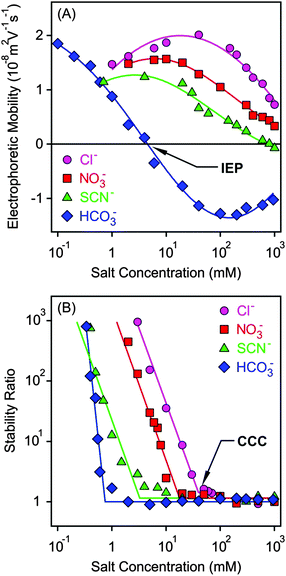
Electrophoretic mobilities of the MgAl–NO3-LDH particles were measured in the presence of K+ salts of different monovalent anions such as Cl−, NO3−, SCN− and HCO3− (Fig. 3A). The shape of the curves was similar for the first three anions. The mobilities were positive at low concentrations due to the structural charge of the particles and passed through a maximum, which can be predicted by the standard electrokinetic model.60 Upon further increasing the salt concentration, the electrophoretic mobilities decreased and were close to zero at high electrolyte levels due to the screening effect on the surface charge and the adsorption of the anions on the oppositely charged surface. The latter effect gave rise to slightly negative mobilities in the case of SCN− at high electrolyte levels. Such a charge reversal has already been observed with this anion and other colloidal particles.20,21 The electrophoretic mobilities also decreased at the same concentration in the Cl− > NO3− > SCN− order indicating specific adsorption of the ions. However, the surface charge properties of the particles are significantly different in the presence of the HCO3− anion. Its adsorption led to charge neutralization at the isoelectric point (IEP) and subsequent charge reversal at higher concentrations. The latter phenomenon was the most significant in this case among the monovalent anions due to the high affinity of HCO3− to the MgAl–NO3-LDH surface. The strong interaction between carbonate or carboxylate containing anions and LDH particles is well known and has also been reported in other systems.2,51,61 Finally, the mobilities start decreasing in magnitude at higher salt levels due to the screening effect of the K+ ions on the negative surface charge.Light scattering has been proved to be a suitable method to follow aggregation processes;62–66 therefore, DLS was used to determine stability ratios in the above systems under the same experimental conditions (Fig. 3B). In general, high stability ratios and stable suspensions were observed at low salt concentrations, whereas fast aggregation and unstable suspensions at high electrolyte levels were witnessed. These two regimes were separated by the CCC, which is the concentration at which the sharp transition between slow and fast aggregation occurs. The aggregation remains rapid after the CCC irrespectively of the types of anions used. The shape of the stability ratio versus salt concentration curves was very similar in the presence of Cl−, NO3− and SCN−, whereas the slope in the slow aggregation regime was higher for HCO3− due to its strong adsorption which modified the MgAl–NO3-LDH surface significantly.
The observed tendency is qualitatively in good agreement with the classical DLVO theory.14 Accordingly, the overlap of the electrical double layers surrounding the particles leads to repulsive forces at low salt concentrations, which transcend the attractive van der Waals forces giving rise to stable suspensions. The double layer forces weaken progressively with the increasing electrolyte level due to surface charge screening by the salts. In addition, anion adsorption on the positively charged MgAl–NO3-LDH surface leads to reduced surface charge density, and hence, to weaker double layer forces. Therefore, attractive van der Waals forces become predominant at high salt concentrations leading to aggregation of the particles and the formation of unstable samples.
The CCC values were determined from the stability plots and they decrease in the Cl− > NO3− > SCN− > HCO3− order (Fig. 4A and Table 2). The tendency for the first three ions agrees adequately with the indirect Hofmeister series for positively charged, hydrophobic particles.20 The poorly hydrated SCN− anions adsorb on the hydrophobic particles leading to lower surface charge, weaker repulsive forces and the lowest CCC. The well-hydrated Cl− anions prefer to stay in the bulk and hardly adsorb on MgAl–NO3-LDH giving rise to higher surface charge and the highest CCC within the anions investigated. A similar tendency was observed in other systems containing these anions and positively charged colloidal particles.18,20,21,27 The situation in the HCO3− case is more complicated. Considering the indirect Hofmeister series, one would expect the highest CCC in the presence of this anion. However, it is the opposite, the lowest CCC was measured. This is due to the specific affinity of the HCO3− ions to the MgAl–NO3-LDH surface of alkaline nature leading to strong adsorption on the oppositely charged particles. This adsorption induced a significant charge reversal as shown in the mobility curve (Fig. 3A). The strong interaction is due to electrostatic attraction and hydrogen bonding between the HCO3− anions and the hydroxyl groups of the surface.56
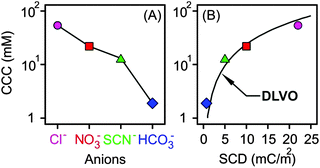 | ||
| Fig. 4 CCC values of positively charged MgAl–NO3-LDH particles in the presence of different monovalent anions (A) and as a function of the surface charge density (B). The solid line in (A) serves to guide the eyes, while in (B) it shows the DLVO prediction calculated by eqn (7). | ||
| Anionsb | First CCC (M) | Second CCC (M) | Third CCC (M) |
|---|---|---|---|
| a The CCCs were determined from the stability ratio versus salt concentration plots. The method has an error of about 10%. b Chemical formula in the deprotonated form. | |||
| Cl− | 5.4 × 10−2 | — | — |
| NO3− | 2.2 × 10−2 | — | — |
| SCN− | 1.3 × 10−2 | — | — |
| CO32− | 1.9 × 10−3 | — | — |
| SO42− | 3.2 × 10−5 | — | — |
| AsO43− | 4.0 × 10−5 | — | — |
| PO43− | 2.0 × 10−7 | 3.1 × 10−6 | 5.2 × 10−1 |
| Fe(CN)63− | 1.1 × 10−6 | 3.0 × 10−5 | 6.0 × 10−2 |
| Fe(CN)64− | 1.0 × 10−13 | 2.5 × 10−13 | 2.5 × 10−1 |
The anionic exchange capacity (AEC) of LDHs is typically in the range of 1–5 meq g−1.47,67,68 Given the low particle concentration (5 mg L−1) in our experiments, only a small fraction (always below 1.5%) of monovalent anions are involved in the ion exchange process. In addition, the AEC includes both intercalation and adsorption on the outer surface, but we are not able to distinguish these processes in our experiments. However, we believe that charging and aggregation of MgAl–NO3-LDH platelets are mostly sensitive to adsorption and the tendencies obtained are related to this process rather than to anion intercalation.
To further clarify the aggregation mechanism, surface charge densities of the MgAl–NO3-LDH particles were determined and their relation to the CCCs was examined. For this, electrophoretic mobility (u) was converted to the electrokinetic potential using the Smoluchowski equation as14
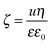 | (5) |
| σ = εε0κζ | (6) |
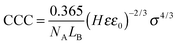 | (7) |
The calculated surface charge densities varied between +1 and +22 mC m−2 for different monovalent anions (Fig. 4B). This range is similar to that reported for LDHs of various compositions.61,69–72 The obtained sequence in the surface charge densities was Cl− > NO3− > SCN− > HCO3− which follows the indirect Hofmeister series with the exception of HCO3−. As discussed above, this anion has high affinity to the MgAl–NO3-LDH surface leading to significant adsorption and reduced surface charge.
Excellent agreement was found between the experimental CCCs and the calculated ones. This fact confirms that the predominating interparticle forces are of DLVO origin and ion specificity plays an important role in the adsorption mechanism. Accordingly, well-hydrated anions such as Cl− do not or only weakly adsorb on the MgAl–NO3-LDH particles and the surface charge density as well as the CCC is high in the presence of this anion. For poorly hydrated ions such as SCN−, stronger adsorption leads to low surface charge density and CCC. In the case of HCO3−, adsorption is further enhanced with specific interaction between the anion and the surface hydroxyl groups through mainly hydrogen bonds giving rise to the lowest CCC among the anions investigated. Although the adsorption processes resulted in different surface charge densities, the interparticle forces are still of DLVO origin as one can realize it from the excellent agreement between the experimental and calculated CCCs (Fig. 4B). A similar observation was also made on the basis of direct force and aggregation rate measurements for positively charged latex particles in the presence of similar anions.26
Effect of divalent anions
Charging and aggregation of the MgAl–NO3-LDH particles were also studied in the presence of divalent anions such as SO42−, HAsO42− and HPO42− with the K+ cation. Although LDHs of different compositions are widely used to capture these anions in water purification processes,12,13 their effect on colloidal stability has not been studied in detail to date.Electrophoretic mobilities were positive at low salt concentrations due to the positive structural charge of the particles (Fig. 5A). Upon increasing the dose of divalent anions, the mobilities decreased rapidly and reached the IEP in each case. Pronounced charge reversal occurred with all of the anions indicating their large affinity to the surface. Such a charge reversal has already been reported for other LDHs in the presence of divalent anions.30,47,51 However, the adsorption of HPO42− led to the most negative electrophoretic mobilities, while very similar values were measured for SO42− and HAsO42−. A previously reported competitive adsorption study also confirmed that HPO42− has greater affinity to the LDH surface than the HAsO42− ions.45 Upon further increasing the salt concentration, the mobilities increased due to the screening effect of the K+ cations on the surface charge. Note that K+ is the counterion of the negatively charged particles in this concentration regime.
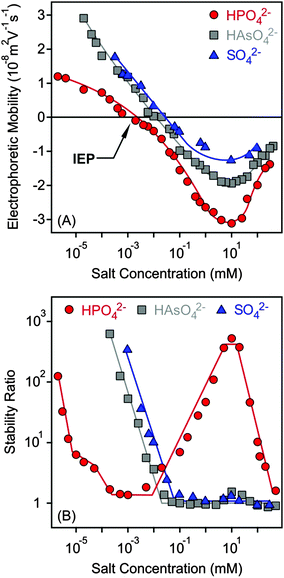 | ||
| Fig. 5 Electrophoretic mobility (A) and stability ratio (B) values of MgAl–NO3-LDH as a function of the salt concentration using K+ salts of divalent anions. The lines are just to guide the eyes. | ||
The tendency in the stability ratios was very similar to the monovalent case for SO42− and HAsO42− anions (Fig. 5B), which behaved alike in the aggregation experiments. Slow and fast aggregation regimes were separated by well-defined CCCs, which were lower compared to the monovalent anions (Table 2). This aggregation behaviour can be explained by the DLVO theory. Nevertheless, the stability curve was found to be very different for the HPO42− anions, as one would expect from the results of the electrophoretic mobility measurements performed with the same systems. Three CCC values were obtained. Accordingly, stable MgAl–NO3-LDH suspensions were observed at low salt concentrations and aggregation became fast at a higher HPO42− level (first CCC). The stability ratios increased (second CCC) in the intermediate regime and reached a plateau. At higher concentrations, the aggregation rates increased and fast aggregation occurred again (third CCC). Such a restabilization effect is typically induced by polyelectrolytes and multivalent ions in the presence of oppositely charged colloidal particles15,38,39,61,73 and can be explained as follows. The high stability at a low salt level is due to sufficiently strong repulsive double layer forces, which weaken with increasing salt concentration, since the adsorption of anions reduces the surface charge. The double layer forces vanish at the IEP and the particles rapidly aggregate after the first CCC due to the attractive van der Waals forces. The aggregation slows down after the second CCC where the charge reversal phenomenon occurs and the high negative charge induces the formation of electrical double layers, which leads to repulsive interparticle forces. Upon further increasing the salt concentration, the aggregation becomes faster and unstable suspensions can be observed after the third CCC due to the screening effect of the K+ ions on the negative surface charge. For the SO42− and HAsO42− anions, the charge reversal did not resulted in sufficiently high surface charge density (as one can see in Fig. 5A); therefore, restabilization did not occur.
Effect of multivalent anions
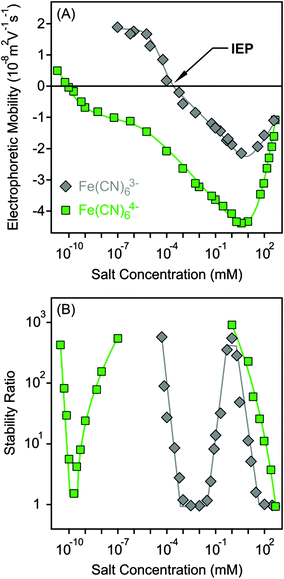
The surface charge and colloidal stability of the MgAl–NO3-LDH particles were studied in the presence of Fe(CN)63− and Fe(CN)64−, as tri- and tetravalent anions. The effect of these anions on the electrophoretic mobilities was similar to the divalent case. Accordingly, the particles were positively charged at low salt concentrations, while strong adsorption of the multivalent ions led to charge neutralization at the IEP and subsequent charge reversal at appropriately high electrolyte levels (Fig. 6A). The extremely low IEP and the large extent of charge reversal indicated higher affinity of Fe(CN)64− for the surface, while the behaviour of Fe(CN)63− was very similar to HPO42−. For tetravalent anions, the magnitude of electrophoretic mobilities was more than twice higher than for bare MgAl–NO3-LDH particles, similar to the case of adsorption of polyelectrolytes on oppositely charged surfaces.15,51,61 The mobilities started to increase after the minimum at higher concentrations due to the screening effect of counterions which are K+ for the negatively charged particles.Similar to HPO42−, three CCCs were observed for tri- and tetravalent ions (Fig. 6B and Table 2). The first CCC occurred due to charge neutralization, the second CCC originated from charge reversal induced restabilization, while the third CCC is the result of the screening effect on the negative surface charge by the K+ cations. The behaviour of Fe(CN)63− is so analogous to HPO42− in both electrophoretic and aggregation experiments that one could assume that the HPO42− anions deprotonate upon adsorption and show characteristic surface charge features for a trivalent anion. However, no unambiguous experimental evidence confirms this assumption. For the Fe(CN)64− anions, the particles were highly negative due to the overcharging process in the intermediate concentration regime, which resulted in highly stable samples, such that stability ratios could not be measured. Therefore, the stability ratios after the second CCC are not connected to the ones before the third CCC in Fig. 6B, since the expected maximum is above the detection limit of the experiment. Accordingly, Fe(CN)64− anions are powerful aggregating agents for LDHs and suspensions can be stabilized or destabilized by varying the salt concentration. The first CCC is much below the typical AEC value for LDHs; therefore, we assume that the adsorption of tetravalent anions on the outer particle surface plays the key role in the charging and aggregation processes of MgAl–NO3-LDH platelets, while intercalation between the layers can hardly take place due to short experiment time.
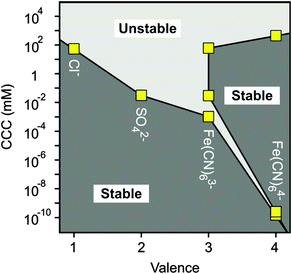
Let us now compare the CCCs in the presence of anions of different valences, such as Cl−, SO42−, Fe(CN)63− and Fe(CN)64− (Fig. 7). For the first two anions, only one CCC was observed since restabilization did not occur (Fig. 3B and 5B), while three CCCs were determined for the tri- and tetravalent ones. The first CCC decreases with the valence due to the increasing affinity and stronger adsorption on the MgAl–NO3-LDH surface. The second CCCs for Fe(CN)63− and Fe(CN)64− also decrease with valence. However, a higher third CCC was determined for the tetravalent ion than for the trivalent one. This behaviour can be correlated with the extent of charge reversal. The adsorption of Fe(CN)64− induced a much larger charge reversal and particles of highly negative charge were formed. Therefore, more K+ counterions are needed to screen the surface charge leading to a higher third CCC in the case of Fe(CN)64− than for the Fe(CN)63− anions. The stability map shows that the suspensions are stable in the low concentration region and unstable at high salt levels for all valences. The peninsula on the right side indicates another stable regime due to restabilization at intermediate concentrations induced by the strong adsorption of tri- and tetravalent ions. Similar stability maps were reported for charged latex particles in the presence of multivalent ions.38,39,73
As discussed above, multivalent ions are more powerful in the destabilization of MgAl–NO3-LDH suspensions. Fig. 8 shows the relative CCCs normalized for the Cl− case for all the anions investigated in the present study together with some data from the literature39,41,73,74 and with expected CCCs from the Schulze−Hardy rule.31,32 The CCC values from the present work are systematically lower than the ones predicted by z−6 dependence. The difference is the most significant for HPO42− and Fe(CN)64−, for which extremely low CCCs were observed indicating high affinity of these ions to the surface. Some of the literature data (e.g., for the hematite and latex particles) are also below the line predicted by the Schulze−Hardy rule. Such tendency is a bit surprising, since the z−6 dependence can be derived from the DLVO theory only for highly charged particles, whereas for surfaces of low surface charge density and surface potential (e.g., MgAl–NO3-LDH in our system), the DLVO theory predicts z−2 dependence.33–35 On the other hand, direct measurements of surface forces and aggregation rates with colloidal latex particles revealed that although some additional forces are also present, the DLVO theory can describe the interparticle forces relatively well, even in the case of multivalent ions.36,73 These facts indicate specific interaction between the anions and the particles surface, which enhances the adsorption and hence, decreases the surface charge density leading to lower CCCs. Therefore, the observed deviation from the expected dependence of the CCC on the valence is due to the high affinity of anions to MgAl–NO3-LDH, while the interparticle forces are still of DLVO origin. One of the reasons for the high affinity is the strong hydrogen bonding network between the anions and the hydroxyl groups of the surface, which can be different for ions of different abilities (e.g., electronegativity) to form hydrogen bonds. Besides, the hydration state of the anions plays also a crucial role. Poorly hydrated anions tend to more strongly adsorb on the hydrophobic surfaces leading to lower CCCs, whereas well-hydrated ones adsorb only weakly and remain in solution giving rise to higher CCCs. The knowledge generated by these results can be certainly applied wherever LDH particles are used as adsorbents for anion capture in aqueous samples, since the colloidal stability of suspensions can be predicted and tuned according to the desired goals.
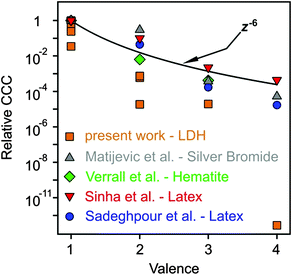 | ||
| Fig. 8 Relative CCCs, normalized to its value for Cl− ion in the present system and for the monovalent case in the others reported in the literature, as a function of the valence (actual charge under the experimental conditions applied). The solid line shows the dependence expected from the Schulze−Hardy rule (eqn (1)). Literature data include positively charged silver bromide,74 hematite41 and amidine functionalized polystyrene latex39,73 particles in the presence of various anions. | ||
Conclusions
Ion specific effects on charging and aggregation of positively charged MgAl–NO3-LDH particles were investigated. The types of monovalent anions significantly affects the surface charge density and also the CCCs, both of which decrease in the Cl− > NO3− > SCN− > HCO3− order. This tendency agrees with the indirect Hofmeister series only in part, since the HCO3− ion should be located on the left side. This deviation is due to the high affinity of HCO3− for the particle surface, which leads to strong adsorption and charge reversal at appropriately high salt concentrations. The extent of adsorption weakens towards the left side of the series due to the hydration level, which increases in this direction, and hence, well-hydrated ions such as Cl− adsorb only weakly and prefer to stay in the solution, giving rise to the highest CCC.Multivalent ions were found to be powerful destabilizing agents. Their adsorption led to charge neutralization and significant charge reversal in each case and restabilization of suspensions also occurred for HPO42−, Fe(CN)63− and Fe(CN)64− in the intermediate concentration regimes. The CCCs decreased with valence even more significantly than the ones predicted by the Schulze−Hardy rule. The present results indicate that multivalent inorganic anions show strong affinity for the MgAl–NO3-LDH surface through electrostatic attraction, hydrophobic interactions and hydrogen bonds forming between the anions and the hydroxyl groups of the surface. However, the predominant interparticle forces can be well described by the DLVO theory.
In conclusion, effective LDH-based adsorbent systems can be proposed for water treatment processes, considering that the colloidal stability of aqueous suspensions can be controlled with the valence (or actual charge under the pH applied) and the concentration of the ions.
Acknowledgements
This research was supported by the Swiss National Science Foundation (150162), Swiss Secretariat for Education, Research and Innovation (C15.0024) and COST Actions CM1303 and MP1106. The authors thank Professor Michal Borkovec for providing access to the light scattering instruments in his laboratory.References
- C. Forano, U. Costantino, V. Prevot and C. Taviot Gueho, in Handbook of Clay Science, ed. F. Bergayaand, G. Lagaly, Elsevier, Amsterdam, 2013, vol. 5A, pp. 745–782 Search PubMed.
- Z. Gu, J. J. Atherton and Z. P. Xu, Chem. Commun., 2015, 51, 3024–3036 RSC.
- Y. G. Li, M. Gong, Y. Y. Liang, J. Feng, J. E. Kim, H. L. Wang, G. S. Hong, B. Zhang and H. J. Dai, Nat. Commun., 2013, 4, 1805 CrossRef PubMed.
- A. Deak, L. Janovak, S. P. Tallosy, T. Bito, D. Sebok, N. Buzas, I. Palinko and I. Dekany, Langmuir, 2015, 31, 2019–2027 CrossRef CAS PubMed.
- K. Ladewig, Z. P. Xu and G. Q. Lu, Expert Opin. Drug Delivery, 2009, 6, 907–922 CrossRef CAS PubMed.
- G. Choi, O. J. Kwon, Y. Oh, C. O. Yun and J. H. Choy, Sci. Rep., 2014, 4, 4430 Search PubMed.
- A. L. Troutier-Thuilliez, H. Hintze-Bruening, C. Taviot-Gueho, V. Verney and F. Leroux, Soft Matter, 2011, 7, 4242–4251 RSC.
- S. Pausova, J. Krysa, J. Jirkovsky, C. Forano, G. Mailhot and V. Prevot, Appl. Catal., B, 2015, 170, 25–33 CrossRef.
- H. F. Liang, F. Meng, M. Caban-Acevedo, L. S. Li, A. Forticaux, L. C. Xiu, Z. C. Wang and S. Jin, Nano Lett., 2015, 15, 1421–1427 CrossRef CAS PubMed.
- S. Meszaros, J. Halasz, Z. Konya, P. Sipos and I. Palinko, Appl. Clay Sci., 2013, 80–81, 245–248 CrossRef CAS.
- S. L. Ma, L. Huang, L. J. Ma, Y. Shim, S. M. Islam, P. L. Wang, L. D. Zhao, S. C. Wang, G. B. Sun, X. J. Yang and M. G. Kanatzidis, J. Am. Chem. Soc., 2015, 137, 3670–3677 CrossRef CAS PubMed.
- F. L. Theiss, S. J. Couperthwaite, G. A. Ayoko and R. L. Frost, J. Colloid Interface Sci., 2014, 417, 356–368 CrossRef CAS PubMed.
- K. H. Goh, T. T. Lim and Z. Dong, Water Res., 2008, 42, 1343–1368 CrossRef CAS PubMed.
- D. F. Evans and H. Wennerstrom, The Colloidal Domain, John Wiley, New York, 1999 Search PubMed.
- I. Szilagyi, G. Trefalt, A. Tiraferri, P. Maroni and M. Borkovec, Soft Matter, 2014, 10, 2479–2502 RSC.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Particle Deposition and Aggregation: Measurement, Modeling, and Simulation, Butterworth-Heinemann Ltd, Oxford, 1995 Search PubMed.
- D. F. Parsons, M. Bostrom, P. Lo Nostro and B. W. Ninham, Phys. Chem. Chem. Phys., 2011, 13, 12352–12367 RSC.
- J. M. Peula-Garcia, J. L. Ortega-Vinuesa and D. Bastos-Gonzalez, J. Phys. Chem. C, 2010, 114, 11133–11139 CAS.
- N. Schwierz, D. Horinek and R. R. Netz, Langmuir, 2010, 26, 7370–7379 CrossRef CAS PubMed.
- T. Oncsik, G. Trefalt, M. Borkovec and I. Szilagyi, Langmuir, 2015, 31, 3799–3807 CrossRef CAS PubMed.
- T. Lopez-Leon, J. L. Ortega-Vinuesa and D. Bastos-Gonzalez, ChemPhysChem, 2012, 13, 2382–2391 CrossRef CAS PubMed.
- G. Lagaly and S. Ziesmer, Adv. Colloid Interface Sci., 2003, 100, 105–128 CrossRef.
- R. Tian, G. Yang, H. Li, X. D. Gao, X. M. Liu, H. L. Zhu and Y. Tang, Phys. Chem. Chem. Phys., 2014, 16, 8828–8836 RSC.
- B. H. Bijsterbosch and J. Lyklema, Adv. Colloid Interface Sci., 1978, 9, 147–251 CrossRef CAS.
- F. Dumont, J. Warlus and A. Watillon, J. Colloid Interface Sci., 1990, 138, 543–554 CrossRef CAS.
- F. J. M. Ruiz-Cabello, G. Trefalt, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2015, 119, 8184–8193 CrossRef PubMed.
- T. Lopez-Leon, J. M. Lopez-Lopez, G. Odriozola, D. Bastos-Gonzalez and J. L. Ortega-Vinuesa, Soft Matter, 2010, 6, 1114–1116 RSC.
- T. B. Schuster, D. D. Ouboter, E. Bordignon, G. Jeschke and W. Meier, Soft Matter, 2010, 6, 5596–5604 RSC.
- V. Merk, C. Rehbock, F. Becker, U. Hagemann, H. Nienhaus and S. Barcikowski, Langmuir, 2014, 30, 4213–4222 CrossRef CAS PubMed.
- G. Lagaly, O. Mecking and D. Penner, Colloid Polym. Sci., 2001, 279, 1090–1096 CAS.
- J. T. G. Overbeek, Pure Appl. Chem., 1980, 52, 1151–1161 CrossRef CAS.
- J. Lyklema, J. Colloid Interface Sci., 2013, 392, 102–104 CrossRef CAS PubMed.
- G. Trefalt, I. Szilagyi and M. Borkovec, J. Colloid Interface Sci., 2013, 406, 111–120 CrossRef CAS PubMed.
- G. Trefalt, F. J. Montes Ruiz-Cabello and M. Borkovec, J. Phys. Chem. B, 2014, 118, 6346–6355 CrossRef CAS PubMed.
- T. Oncsik, G. Trefalt, Z. Csendes, I. Szilagyi and M. Borkovec, Langmuir, 2014, 30, 733–741 CrossRef CAS PubMed.
- F. J. M. Ruiz-Cabello, G. Trefalt, Z. Csendes, P. Sinha, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2013, 117, 11853–11862 CrossRef CAS PubMed.
- C. Schneider, M. Hanisch, B. Wedel, A. Jusufi and M. Ballauff, J. Colloid Interface Sci., 2011, 358, 62–67 CrossRef CAS PubMed.
- I. Szilagyi, A. Polomska, D. Citherlet, A. Sadeghpour and M. Borkovec, J. Colloid Interface Sci., 2013, 392, 34–41 CrossRef CAS PubMed.
- A. Sadeghpour, I. Szilagyi and M. Borkovec, Z. Phys. Chem., 2012, 226, 597–612 CrossRef CAS.
- K. L. Chen, S. E. Mylon and M. Elimelech, Langmuir, 2007, 23, 5920–5928 CrossRef CAS PubMed.
- K. E. Verrall, P. Warwick and A. J. Fairhurst, Colloids Surf., A, 1999, 150, 261–273 CrossRef CAS.
- Y. Mori, K. Togashi and K. Nakamura, Adv. Powder Technol., 2001, 12, 45–59 CrossRef CAS.
- L. Wu, L. Liu, B. Gao, R. Munoz-Carpena, M. Zhang, H. Chen, Z. H. Zhou and H. Wang, Langmuir, 2013, 29, 15174–15181 CrossRef CAS PubMed.
- M. Sano, J. Okamura and S. Shinkai, Langmuir, 2001, 17, 7172–7173 CrossRef CAS.
- A. Violante, M. Pucci, V. Cozzolino, J. Zhu and M. Pigna, J. Colloid Interface Sci., 2009, 333, 63–70 CrossRef CAS PubMed.
- R. L. Frost, A. W. Musumeci, J. T. Kloprogge, M. O. Adebajo and W. N. Martens, J. Raman Spectrosc., 2006, 37, 733–741 CrossRef CAS.
- M. Jobbagy and A. E. Regazzoni, J. Colloid Interface Sci., 2013, 393, 314–318 CrossRef CAS PubMed.
- J. Hong, Z. L. Zhu, H. T. Lu and Y. L. Qiu, RSC Adv., 2014, 4, 5156–5164 RSC.
- T. Bujdoso, A. Patzko, Z. Galbacs and I. Dekany, Appl. Clay Sci., 2009, 44, 75–82 CrossRef CAS.
- K. Kuzawa, Y. J. Jung, Y. Kiso, T. Yamada, M. Nagai and T. G. Lee, Chemosphere, 2006, 62, 45–52 CrossRef CAS PubMed.
- Z. P. Xu, Y. G. Jin, S. M. Liu, Z. P. Hao and G. Q. Lu, J. Colloid Interface Sci., 2008, 326, 522–529 CrossRef CAS PubMed.
- J. He, M. Wei, B. Li, Y. Kang, D. G. Evans and X. Duan, in Layered Double Hydroxides, ed. X. Duanand and D. G. Evans, 2006, vol. 119, p. 89–119 Search PubMed.
- D. Sranko, A. Pallagi, E. Kuzmann, S. E. Canton, M. Walczak, A. Sapi, A. Kukovecz, Z. Konya, P. Sipos and I. Palinko, Appl. Clay Sci., 2010, 48, 214–217 CrossRef CAS.
- Q. Wang and D. O'Hare, Chem. Rev., 2012, 112, 4124–4155 CrossRef CAS PubMed.
- X. D. Sun and S. K. Dey, J. Colloid Interface Sci., 2015, 458, 160–168 CrossRef CAS PubMed.
- D. G. Evans and R. C. T. Slade, in Layered Double Hydroxides, ed. X. Duanand and D. G. Evans, 2006, vol. 119, p. 1–87 Search PubMed.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Langmuir, 1996, 12, 5541–5549 CrossRef CAS.
- M. Owczarz, A. C. Motta, M. Morbidelli and P. Arosio, Langmuir, 2015, 31, 7590–7600 CrossRef CAS PubMed.
- E. Tombacz and M. Szekeres, Appl. Clay Sci., 2004, 27, 75–94 CrossRef CAS.
- M. Borkovec, S. H. Behrens and M. Semmler, Langmuir, 2000, 16, 5209–5212 CrossRef CAS.
- M. Pavlovic, M. Adok-Sipiczki, C. Nardin, S. Pearson, E. Bourgeat-Lami, V. Prevot and I. Szilagyi, Langmuir, 2015, 31, 12609–12617 CrossRef CAS PubMed.
- K. K. Norrfors, M. Bouby, S. Heck, N. Finck, R. Marsac, T. Schafer, H. Geckeis and S. Wold, Appl. Clay Sci., 2015, 114, 179–189 CrossRef CAS.
- A. Zaccone, H. Wu, M. Lattuada and M. Morbidelli, J. Phys. Chem. B, 2008, 112, 1976–1986 CrossRef CAS PubMed.
- R. Ferretti, S. Stoll, J. W. Zhang and J. Buffle, J. Colloid Interface Sci., 2003, 266, 328–338 CrossRef CAS PubMed.
- A. Zaccone, J. J. Crassous, B. Beri and M. Ballauff, Phys. Rev. Lett., 2011, 107, 168303 CrossRef PubMed.
- E. Tombacz, C. Csanaky and E. Illes, Colloid Polym. Sci., 2001, 279, 484–492 CAS.
- J. H. Choy, M. Park and J. M. Oh, Curr. Nanosci., 2006, 2, 275–281 CrossRef CAS.
- S. Vial, V. Prevot, F. Leroux and C. Forano, Microporous Mesoporous Mater., 2008, 107, 190–201 CrossRef CAS.
- M. Pavlovic, L. Li, F. Dits, Z. Gu, M. Adok-Sipiczki and I. Szilagyi, RSC Adv., 2016, 6, 16159–16167 RSC.
- R. Rojas Delgado, M. Arandigoyen Vidaurre, C. P. De Pauli, M. A. Ulibarri and M. J. Avena, J. Colloid Interface Sci., 2004, 280, 431–441 CrossRef CAS PubMed.
- R. Rojas Delgado, C. P. De Pauli, C. B. Carrasco and M. J. Avena, Appl. Clay Sci., 2008, 40, 27–37 CrossRef CAS.
- R. B. Leggat, S. A. Taylor and S. R. Taylor, Colloids Surf., A, 2002, 210, 69–81 CrossRef CAS.
- P. Sinha, I. Szilagyi, F. J. M. Ruiz-Cabello, P. Maroni and M. Borkovec, J. Phys. Chem. Lett., 2013, 4, 648–652 CrossRef CAS PubMed.
- E. Matijevic and M. Kerker, J. Phys. Chem., 1958, 62, 1271–1276 CrossRef CAS.
- P. M. May, D. Rowland, E. Konigsberger and G. Hefter, Talanta, 2010, 81, 142–148 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |