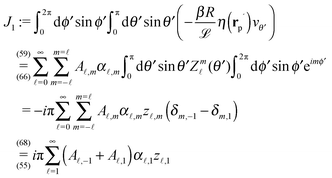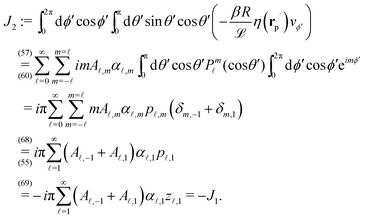DOI:
10.1039/C6SM00367B
(Paper)
Soft Matter, 2016,
12, 4007-4023
Active colloids at fluid interfaces
Received
12th February 2016
, Accepted 8th March 2016
First published on 9th March 2016
Abstract
If an active Janus particle is trapped at the interface between a liquid and a fluid, its self-propelled motion along the interface is affected by a net torque on the particle due to the viscosity contrast between the two adjacent fluid phases. For a simple model of an active, spherical Janus colloid we analyze the conditions under which translation occurs along the interface and we provide estimates of the corresponding persistence length. We show that under certain conditions the persistence length of such a particle is significantly larger than the corresponding one in the bulk liquid, which is in line with the trends observed in recent experimental studies.
1 Introduction
Micro- and nanometer scale particles capable of self-inducing motility within liquid environments1–5 are promising candidates for the development of novel lab-on-a-chip cell-sorting devices, chemical sensors,6 or targeted-drug-delivery systems,7 to cite just a few potential applications. One proposal, which has generated significant experimental and theoretical attention within the last decade (see, e.g., the recent reviews in ref. 1, 3 and 4), is to achieve self-motility by designing “active” particles capable of inducing chemical reactions within the surrounding liquid. One such system, which will be of particular interest for the present study, is represented by spherical beads partially covered over a spherical cap region by a catalyst which promotes, in the suspending solution, a chemical conversion of reactants (“fuel”) into product molecules.† Due to the partial coverage by the catalyst, the spherical symmetry of the system is broken in two ways. First, the material properties of the particle vary across the surface and an axis of symmetry, which passes through the center of the particle and the pole inside the catalyst covered cap, can be defined. Second, the chemical reaction takes place only on the catalytic part of the surface, and therefore the chemical composition of the surrounding solution is varying along the surface of the particle. The out-of-equilibrium chemical composition gradients along the surface, due to the chemical reaction, couple to the particle via the interactions of the molecules in solution with the surface of the particle. This interplay eventually leads to hydrodynamic flows and to the motion of the particle relative to the solution, analogous to classic phoresis.8,9 The active motion of such particles in the homogeneous bulk of the fluids has been the subject of numerous experimental (see, e.g., ref. 1, 3, 4, 10 and 11) and theoretical (see, e.g., ref. 9 and 12–15) studies.
However, in many cases such active Janus particles are suspended in a solution bound by a liquid–fluid interface, which raises several new issues. It is known that in thermal equilibrium, i.e., in the absence of such motility-promoting chemical reactions, owing to their amphiphilic nature Janus particles tend to accumulate at liquid–fluid interfaces. (This effect can be exploited, e.g., for the stabilization of binary emulsions.16–18) If the Janus particles are trapped at and confined to liquid–fluid interfaces their collective behavior, e.g., when externally driven or when relaxing towards equilibrium after a perturbation, can be strongly affected by this quasi two-dimensional (2D) confinement itself and by interface-promoted interactions, such as capillary interactions (see, e.g., ref. 19–21).
For an active Janus colloid, being trapped at the interface (i.e., being unable to move in the direction normal to the interface; see, e.g., ref. 22 for recent experimental results) can, on the one hand, affect the particle dynamics due to the effects discussed above. On the other hand, this trapping may induce novel self-propulsion mechanisms. For example, it has been recently predicted that if one of the reaction products exhibits a preference for the surface and thus tends to accumulate at the interface, the trapped Janus sphere will be set into motion along the interface by Marangoni flow, induced by the spatially non-uniform distribution of the reaction products.23,24 (A similar motility mechanism can originate from thermally induced Marangoni flows, e.g., if the Janus particle contains a metal cap which is heated by a laser beam;25 furthermore, as reported recently, induced Maragoni flows can drive the motion of active particles even if they are not trapped at but located nearby the interface.26)
If none of the reaction products exhibits a preference for the interface, the Marangoni type of propulsion is no longer in action. The question arises if for an active Janus particle, trapped at the interface, sustained motion along the interface can still occur due to the self-induced phoresis mechanism, which works in the bulk solution. For reasons of simplicity, in the following we focus solely on the case of planar interfaces. In thermal equilibrium (i.e., in the absence of diffusiophoresis), a Janus particle trapped at the interface typically exhibits a configuration in which the particle axis is not aligned with the normal of the interface (see Fig. 1). Therefore, at first it seems that, upon “turning on” the chemical reaction, motion along the interface may be achieved.‡ However, it is known that the motion at the interface between two fluids generally involves a coupling between translation and rotation.2,27,28 Thus the possibility arises that the translation along the interface may lead to a rotation of the axis of the particle towards alignment with the interface normal. Since self-phoresis of active particles is, in general, characterized by very small Reynolds (Re) numbers (i.e., inertia does not play a role),1,3,8,12 such a rotation of the axis of the particle leads to a motionless state once the axis is aligned with the normal, i.e., the motile state is just a transient. Therefore, predicting whether or not for a particular system sustained motion along the interface may occur via self-diffusiophoresis requires an understanding of the interplay between the equilibrium configuration of the Janus particle at the interface, the distribution of reactant and product molecules upon turning on the chemical reaction, and the induced hydrodynamic flows in the liquid and the fluid.
 |
| | Fig. 1 (a) Typical configurations of an active Janus particle, i.e., a spherical colloid (shown as a gray disk in sidewise projection onto the plane spanned by the symmetry axis of the particle and the interface normal n) with a spherical cap providing a catalytic region (red), trapped at the interface (solid black line) between two fluids. The leftmost configuration corresponds to the catalytic cap having a preference for the upper fluid and very strong, effective repulsive interactions between the interface and the catalytic cap. The configuration in the middle corresponds to the catalytic cap exhibiting a preference for the lower fluid and effective interactions between the interface and the catalytic cap, having a long-ranged attractive component and a dominant short-ranged repulsive one. The configuration on the right (“crossed out”) does not occur due to the assumed preference of the catalyst for contact with one of the two fluids. In all three configurations C denotes the center of the sphere. (b) The coordinate systems employed to describe the motion of such trapped active Janus colloids are shown at the right. In the spatially fixed unprimed coordinate system the interface normal n points into the y-direction, the x-direction is in the plane spanned by n and the symmetry axis of the particle, and the unit vector in the z-direction lies in the plane of the interface. The primed coordinate system is co-moving (translating and rotating) with the particle. The origin O′ of the primed coordinate system coincides with the center C of the sphere. The z′- and y′-directions lie in the plane spanned by n and the symmetry axis of the particle. The z′-axis passes through the center of the catalytic cap, and the unit vector in the x′-direction lies in the plane of the interface. The angle δ ∈ [δm,π − δm) ∪ [π + δm,2π − δm), where δm < π/2 denotes the value of δ (with the orientation of the cap in the upper fluid, as shown in the figure) at which the rim of the cap touches the interface, gives the orientation of the O′z′ direction with respect to Ox, where O is the origin of the fixed coordinate system. The unit vectors of the primed and unprimed coordinate systems are related viaex′ = ez, ez′ = cos(δ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex + sin(δ) ex + sin(δ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey, and ey′ = sin(δ) ey, and ey′ = sin(δ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex − cos(δ) ex − cos(δ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey. ey. | |
Here we study theoretically the issue of sustained self-diffusiophoresis along a liquid–fluid interface for a simple model of a spherical, chemically active Janus colloid trapped at a liquid–fluid interface. Nonetheless we expect this simple model to qualitatively capture some of the main physical features of the phenomenon. The chemical activity of the particle is modeled via the production of one species of solute molecules, with a uniform rate across the catalytic region. We determine the conditions under which this model system exhibits sustained motility. These conditions involve the interplay between the equilibrium configuration, the difference in viscosity between the two adjacent fluids, and the interactions between the particle and the product (solute) molecules. Finally, for particles trapped at the interface we analyze the persistence length and the stability of the motile state against thermal fluctuations and compare it with the corresponding motion in unbound fluids.
2 Model
In this section we discuss our model for a catalytically active, spherical Janus colloid9 trapped at a liquid–fluid interface (see Fig. 1(a)). The colloid (gray disk in Fig. 1(a)) of radius R has a spherical cap region (the red patch in Fig. 1(a)) decorated by a catalyst which promotes the conversion A → B of “fuel” molecules A into product (solute) molecules B. The particle is trapped at the interface (the horizontal black line in Fig. 1(a)) between the two fluids “1” and “2” (denoted also as fluid and liquid, respectively) with bulk viscosities η1 and η2, respectively. For simplicity we assume that the fuel (A) and the product (B) molecules diffuse freely in both fluids, that neither of the two species A and B exhibits a preference for either the interface or one of the two fluid phases, and that the concentration of A molecules in the two fluid phases is at a steady state. Furthermore, it is assumed that the fuel molecules A are present in abundance such that their number density is not affected by the reaction. (Under the latter assumption, the dynamics of the fuel molecules is irrelevant and their sole role is, similar to that of the catalyst, that of a “spectator” enabling the reaction due to which active motion emerges. Thus within this model the diffusion constants of the A particles in the two fluids do not enter the description.) Accordingly, we assume that the effects of the chemical reaction can be approximated by representing the catalyst area as an effective source of solute which releases molecules B (at a time independent rate per area of catalyst). We denote the diffusion constants of the solute molecules in the two fluids as D1 and D2, respectively.
For a Janus particle trapped at the interface several scenarios can emerge if the parameters controlling the effective particle–interface interactions, such as the coverage by the catalyst or the three-phase contact angle of the “bare” particle (i.e., without catalyst), are changed. Here we restrict the discussion to the case that the particle and the two fluid phases have densities and surface tensions for which the deformations of the interface due to buoyancy are negligible, and we assume that the catalytic cap is completely immersed in one of the two fluid phases. Thus the Janus particle forms the three-phase contact angle of the bare particle.16 Furthermore, we assume that the effective interaction between the particle and the interface is such that the catalytic cap cannot jut into the other fluid, i.e., the circular boundary between the catalytic cap and the bare regions gets pinned at the three-phase contact line (between fluid 1, fluid 2, and the particle surface) upon touching it. (Accordingly, if the symmetry axis of the particle, i.e., the axis passing through the center C of the particle and the center of the catalytic spherical cap, would rotate beyond this touching point, the interface would no longer be planar.) For simplicity, we further restrict our discussion to the case in which the three-phase contact angle of the bare particle is π/2, which implies that the catalytic cap has to be smaller than a hemisphere. Actually, the size of the catalytic cap should be sufficiently small so that thermal fluctuations of the orientation around the equilibrium one do not lead to the aforementioned touching, which causes pinning of the liquid–fluid interface. With these assumptions, the center of the Janus particle lies in the plane of the interface. (As it will be discussed in Section 3, this particular configuration significantly simplifies the technical details, and thus provides transparent and physically intuitive results.) The orientation of the symmetry axis is determined by the effective interactions between the catalytic cap and the interface. For net repulsive interactions16 we expect the equilibrium distribution of the symmetry axis of the particle to be peaked at the direction normal to the interface. If, on the other hand, the effective interaction between the catalytic cap and the interface includes a long-ranged attractive part and a dominant short-ranged repulsive part, the equilibrium distribution is expected to be peaked at a direction which is close to, but distinct from, an orientation parallel to the interface. (Since the catalytic material is assumed to be completely immersed in one of the fluids, a net attractive interaction between the catalytic cap and the interface would be incompatible with our model.)
Since the surface tension compensates any action of the active Janus particle in the direction of the interface normal (which implies that the particle is trapped at the interface), translation of the particle upon turning on the catalytic reaction is possible only within the planar interface. Thus a motile state can be reached only if the axis of the Janus particle is not oriented perpendicular to the interface. Due to the symmetry of the problem, all lateral directions of the particle translation are equivalent; in other words, at a given tilting angle of the symmetry axis with respect to the normal, upon rotating the symmetry axis around the normal a state of motion emerges which is identical to the one in the original configuration. This allows us to consider the particle motion in the plane spanned by the axis of the particle (in its orientation at the moment when the catalytic reaction is turned on) and the normal of the planar interface. Thus we neglect the effects of thermal fluctuations leading to a rotation of the axis of symmetry out of this plane. Under this assumption, and in accordance with Fig. 1(b), we choose the coordinate system with the y-axis along the interface normal, pointing towards the upper fluid, the x-axis as the intersection of the interface with the plane of motion, and the z-axis as the normal of the latter (see Fig. 1(b)). For future reference, we also introduce a system of coordinates – with the origin O′ at the center C of the particle and co-moving with the particle –, which is denoted by primed quantities. As shown in Fig. 1(b), in the plane spanned by the axis of symmetry and the normal to the interface passing through the center of the particle we choose the z′-axis to point through the center of the catalytic cap and the x′-axis to lie in the plane of the interface and to be parallel to the z-axis. (These choices for the primed and unprimed coordinates are taken as to facilitate more convenient calculations in Sections 3 and 4 below.)
A viscosity contrast between the two fluids forming the interface leads to the onset of net torques on particles translating along the interface. Therefore the orientation of the symmetry axis of the trapped Janus particle relative to the y-axis will change once the chemical reaction is turned on and the particle is set into translation. Depending on the viscosity contrast between the two fluids, a small fluctuation of the orientation of the symmetry axis can be either amplified by the induced torque, leading to a different, yet motile, state, or suppressed. In the former case the steady state orientation of the axis of the Janus particle is ultimately determined by the geometry of the particle including the shape of the catalytic patch and the details of the effective interactions between the catalytic cap and the interface, which is a complex problem. Here we shall assume that the motion is quasi-adiabatic, in the sense that the rotation of the particle is much slower than the time it takes for the distribution of solute molecules B and for the flow of the solution to reach a quasi-steady-state corresponding to the instantaneous orientation of the particle. Thus we focus solely on sustained motile states. The determination of the steady-state orientation of the symmetry axis of the particle (which, as noted above, ultimately involves the details of the effective interaction between the catalytic cap and the interface) is left to future research.
As discussed above, the rotations (spinning) of the particle around the symmetry axis are neither contributing to, nor being induced by, the motility along the interface, whereas the rotations of the symmetry axis around the interface normal have the sole effect of changing the direction of the in-plane translation. Therefore describing the motion of the particle at the interface requires only to account for one translational velocity component Ux and one angular velocity component Ωz corresponding to translation along the x-axis and rotation around the z-axis, respectively. These will be determined by assuming the motion of the fluids to be described by the Stokes equations and the translation and rotation of the particle to be quasi-adiabatic in the sense that the hydrodynamics obeys the (steady state) Stokes equations at the instantaneous state, i.e., the orientation and velocity, of the particle. Finally, we assume that the interface exerts no force on the particle when it is translating along the interface, that the torques exerted by the interface with respect to rotations of the particle around the z-axis are vanishingly small, and that the eventual, small deformations of the interface in the contact line region accompanying such a motion also have negligibly small effects.
The assumption of negligible torques deserves further consideration. In fact, if the catalytic cap leaves its equilibrium orientation, a torque will arise due to the effective interaction between the catalytic cap and the interface. Here we focus our attention on the case in which such contributions are negligible.§ Furthermore, the rotation around the x′-axis involves a moving contact line, which is a well-known conceptual issue in classical hydrodynamics.29,30 Here we do not attempt to provide a mechanism through which the associated contact line singularity (i.e., translation of the contact line while at the same time the fluids fulfill the no-slip boundary condition) is removed and motion occurs (see, e.g., ref. 31–33). Instead we assume that the region, where a microscopic description is necessary, is very small compared to the typical length scales in the system and that there the expected macroscopic velocity values provide a smooth interpolation.
3 Translational and angular velocities of Janus particles at liquid–fluid interfaces
In order to calculate the angular and translational velocity of Janus particles trapped at a liquid–fluid interface, we model the two immiscible fluids separated by a planar interface as having a continuous, but steeply varying, viscosity profile η(y) interpolating between η2 at y = −∞ and η1 at y = +∞ across the plane y = 0 (compare Fig. 1):| | 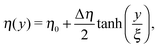 | (1) |
where η0 = (η1 + η2)/2 and Δη = η1 − η2 denote the mean viscosity η0 = η(0) and the viscosity contrast Δη, respectively, while ξ, which is of molecular size, characterizes the width of the interface. In the following we consider the case of a vanishingly thin interface, i.e., we take ξ → 0.
3.1 Reciprocal theorem for a particle at liquid–fluid interfaces
We exploit the reciprocal theorem,24,27,34 derived first by Lorentz35 (the English translation of the original paper is provided in ref. 36) for the case of a homogeneous fluid and later extended by Brenner27 to the case in which the viscosity of the fluid varies spatially.¶ The reciprocal theorem states that in the absence of volume forces any two incompressible flow fields u(r) and û(r), which are distinct solutions of the Stokes equations within the same domain ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , i.e., solutions subject to different boundary conditions but on the very same boundaries ∂
, i.e., solutions subject to different boundary conditions but on the very same boundaries ∂![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , obey the relation
, obey the relation| | 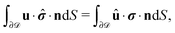 | (2) |
where σ and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) denote the stress tensors corresponding to the two flow fields.
denote the stress tensors corresponding to the two flow fields.
For our system, the assumption of immiscibility of the two fluids translates into the kinematic boundary condition that the velocity components of the flow fields above and below the interface along the direction of the normal to the interface must vanish at the interface. This effectively enforces the interface as a physical boundary across which, concerning the hydrodynamics, there is momentum transfer but no mass transfer. Therefore it is necessary that the hydrodynamic flow is obtained by solving the Stokes equations in the domains above (![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1) and below (
1) and below (![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2) the interface and by subsequently working out the problem by connecting the solutions corresponding to the upper and lower fluids via appropriate boundary conditions at the interface (see below).
2) the interface and by subsequently working out the problem by connecting the solutions corresponding to the upper and lower fluids via appropriate boundary conditions at the interface (see below). ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 is delimited by that part Σp1 of the particle surface Σp exposed to the upper fluid, the surface of the fluid at infinity in the half-plane y > 0, and the upper part, y = 0+, of the fluid interface Γ (note that this is the plane with y = 0 and less area occupied by the particle);
1 is delimited by that part Σp1 of the particle surface Σp exposed to the upper fluid, the surface of the fluid at infinity in the half-plane y > 0, and the upper part, y = 0+, of the fluid interface Γ (note that this is the plane with y = 0 and less area occupied by the particle); ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 is defined similarly.|| We note that the inner normals of the upper (n1) and lower (n2) parts of the interface Γ are n1 = ey = −n2.
2 is defined similarly.|| We note that the inner normals of the upper (n1) and lower (n2) parts of the interface Γ are n1 = ey = −n2.
We restrict the discussion to the case in which for both flow fields (i.e., the un-hatted and the hatted one, which are to be considered in the reciprocal theorem), there are no (e.g., externally imposed, or due to surface tension gradients) tangential stresses at the interface. For both the un-hatted and the hatted flow fields, the corresponding flow velocities and stress tensors within the upper and lower domains, which are connected via the boundary conditions they have to obey at the interface, are denoted by the indices “1” and “2”, respectively. By (i) applying the reciprocal theorem (eqn (2)) in each of the domains ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 (which can be done because Γ is a physical boundary at which the boundary conditions are formally prescribed by imposing the tangential velocity and the stress tensor to take the values given by the (yet unknown) velocity and stress tensor on the other side of the interface, respectively), (ii) adding the left and right hand sides of the two results of applying the reciprocal theorem in
2 (which can be done because Γ is a physical boundary at which the boundary conditions are formally prescribed by imposing the tangential velocity and the stress tensor to take the values given by the (yet unknown) velocity and stress tensor on the other side of the interface, respectively), (ii) adding the left and right hand sides of the two results of applying the reciprocal theorem in ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2, (iii) noting that for flow fields, which decay sufficiently fast with the distance from the particle (which typically is the case), the contribution from the integrals over the surfaces at infinity are vanishingly small, (iv) using the relation (see above) n1 = − n2 = ey between the interface normals, and (v) noting that the boundary conditions for the flow velocity at the interface Γ impose zero normal components, i.e., (u1·ey)|y=0 = 0, (u2·ey|)y=0 = 0 and continuous tangential components27 so that u1|y=0+ = u2|y=0− =: u∥e∥ (with similar relations for the hatted velocity field), where e∥·ey = 0, we arrive at
2, (iii) noting that for flow fields, which decay sufficiently fast with the distance from the particle (which typically is the case), the contribution from the integrals over the surfaces at infinity are vanishingly small, (iv) using the relation (see above) n1 = − n2 = ey between the interface normals, and (v) noting that the boundary conditions for the flow velocity at the interface Γ impose zero normal components, i.e., (u1·ey)|y=0 = 0, (u2·ey|)y=0 = 0 and continuous tangential components27 so that u1|y=0+ = u2|y=0− =: u∥e∥ (with similar relations for the hatted velocity field), where e∥·ey = 0, we arrive at
| | 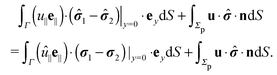 | (3) |
In the absence of tangential stresses at the interface the difference of normal stresses at the interface (
σ1 −
σ2)|
y=0·
ey is the force corresponding to the Laplace pressure,
27 and thus is a vector oriented along the normal
ey of the interface. Therefore the first integral on the left hand side of
eqn (3) vanishes due to
e∥⊥
ey. By a similar argument, the first integral on the right hand side of
eqn (3) vanishes, too. Thus for the present system the reciprocal theorem takes the simple form given in
eqn (2) but with
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
replaced by
Σp.
In order to determine the translational and the angular velocity of the Janus particle, we shall select an appropriate set of “dual problems” (the “hatted” quantities), typically associated with known solutions for spatially uniform translations or rotations (under the action of external forces or torques) of solid spheres with prescribed boundary conditions at their surfaces. To this end we consider a solid sphere of radius R with no-slip boundary conditions translating with velocity Û and rotating with angular velocity 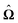 under the action of the external force
under the action of the external force ![[F with combining circumflex]](https://www.rsc.org/images/entities/b_char_0046_0302.gif) and the external torque
and the external torque ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) . At the surface of the particle, the flow û(rp), where rp denotes a point at the particle surface Σp, is given by
. At the surface of the particle, the flow û(rp), where rp denotes a point at the particle surface Σp, is given by
| | 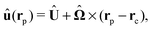 | (4) |
where
rC is the position of the center C of the sphere. (Both
rp and
rC are measured from a common, arbitrary origin, the location of which drops out from
rp −
rC.) Similarly, we consider a Janus particle, which translates with velocity
U =
Uxex and rotates with an angular velocity
Ω =
Ωzez around the axis, which is parallel to O
z and passes through the moving center C of the particle at its instantaneous position. If the particle exhibits boundary conditions given by a phoretic slip velocity
v(
rp), the flow
u(
rp) at its surface is given by
| | | u(rp) = U + Ω × (rp − rC) + v(rp). | (5) |
By using
eqn (4) and noting that
Û and
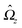
are spatially constant vectors, the right hand side (rhs) of
eqn (2) can be re-written as
| | 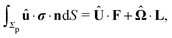 | (6) |
where
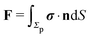
and
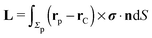
denote the force and the torque, respectively, experienced by the Janus particle. (In
eqn (6),
n denotes the normal of the surface
Σp of the particle, oriented into the fluid.) We note that while the active motion of Janus particles in the bulk is force- and torque-free, this is, in general, not the case if the motion occurs at the interface because the interface can exert forces and torques on the particle. However, because we have assumed that the interface does not exert a force in the case of translations of the Janus particle along the interface or a torque in the case of rotations around the
z-axis (in the sense of spinning around an axis parallel to the
z-axis, as discussed above), the components
Fx and
Lz vanish. Therefore, if the reciprocal problem involves only translations along the
x-axis and/or such rotations around the
z-axis, the rhs of
eqn (6), and, consequently, of
eqn (2) is zero. Restricting now the dual problem as discussed above to such a choice, and using
eqn (5) for the left hand side of
eqn (2), we arrive at
| | 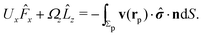 | (7) |
3.2 Calculation of the translational and angular velocities
We proceed by selecting two so-called dual problems, each involving only one of the two types of motions (translation or rotation only) for both of which eqn (7) holds. These will provide two relations allowing one to determine Ux and Ωz. The first one, denoted by the index “1”, is that of a sphere of radius R, the center of which lies in the plane of the flat, sharp (ξ → 0) liquid–fluid interface (see eqn (1)), translating without rotation with velocity Û = Ûxex along the interface. This problem has been solved analytically,28 and the result of interest here is| | 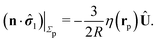 | (8) |
This leads to (see Appendix A for the details of the calculation)| | ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 1x = −6πRη0Ûx := α1Ûx 1x = −6πRη0Ûx := α1Ûx | (9a) |
and| | 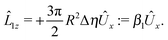 | (9b) |
After inserting eqn (8) and (9) into eqn (7) and canceling the common factor Ûx, we obtain| | 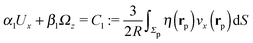 | (10) |
where vx(rp) is the x-component of the phoretic slip velocity at the point rp on the surface of the particle.
The second problem which we consider, denoted by the index “2”, is that of the driven rotation, without translation, with angular velocity 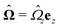 of a spherical particle of radius R, the center of which lies in the plane of the flat, sharp (ξ → 0) liquid–fluid interface. As noted before, this is a more involved problem due to the concomitant issue of contact line motion. For the case in which one of the two fluids has a vanishingly small viscosity, an exact solution was constructed in ref. 33 under the assumption that a slip boundary condition, with a spatially uniform slip length along the surface, applies across that surface region which is immersed in the fluid of non-vanishing viscosity, called liquid. The result of this calculation shows that for typical slip lengths l0, which are much smaller than the size of the particle,** at distances |y|/l0 ≫ 1 from the interface the hydrodynamic flow within the liquid is de facto identical to the one which would have occurred if the rotating sphere would have been completely immersed in the liquid and a no-slip boundary condition would have been applied. Thus in this context the only role played by the slip is to remove the contact line singularity, as discussed in Section 2. This can be interpreted in the sense that the same solution would emerge if one assumes that the fluid slips only in a narrow region localized close to the three-phase contact line, while the no-slip condition holds for the rest of the sphere. This view is confirmed by an alternative solution presented in ref. 38 for the same problem of the rotation of a sphere at the interface between a liquid and a fluid of vanishing viscosity.
of a spherical particle of radius R, the center of which lies in the plane of the flat, sharp (ξ → 0) liquid–fluid interface. As noted before, this is a more involved problem due to the concomitant issue of contact line motion. For the case in which one of the two fluids has a vanishingly small viscosity, an exact solution was constructed in ref. 33 under the assumption that a slip boundary condition, with a spatially uniform slip length along the surface, applies across that surface region which is immersed in the fluid of non-vanishing viscosity, called liquid. The result of this calculation shows that for typical slip lengths l0, which are much smaller than the size of the particle,** at distances |y|/l0 ≫ 1 from the interface the hydrodynamic flow within the liquid is de facto identical to the one which would have occurred if the rotating sphere would have been completely immersed in the liquid and a no-slip boundary condition would have been applied. Thus in this context the only role played by the slip is to remove the contact line singularity, as discussed in Section 2. This can be interpreted in the sense that the same solution would emerge if one assumes that the fluid slips only in a narrow region localized close to the three-phase contact line, while the no-slip condition holds for the rest of the sphere. This view is confirmed by an alternative solution presented in ref. 38 for the same problem of the rotation of a sphere at the interface between a liquid and a fluid of vanishing viscosity.
In the following we shall adopt the latter interpretation and make the ansatz that for our above problem “2” (in which the viscosities of both fluids are, in general, certain non-zero quantities) with a sharp interface (ξ → 0) the expression for the stress tensor at the surface of the particle is given by the one in ref. 33, i.e.,
| | 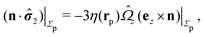 | (11) |
except for a small region localized close to the three-phase contact line. As noted, the expression above is expected to provide a reliable approximation if the viscosity contrast between the two fluids is large.
33 In the limiting case of the two fluids becoming identical, by construction
eqn (11) reduces to the exact result corresponding to a sphere rotating without slip in a spatially homogeneous fluid.
With the assumption that the small region near the three-phase contact line contributes negligibly to the integrals over the surface of the particle, eqn (11) implies that the corresponding components of the forces and torques required for the reciprocal theorem (eqn (7)) are given by (see Appendix A)
| | 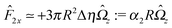 | (12a) |
and
| | 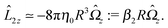 | (12b) |
After inserting
eqn (11) and (12) into
eqn (7) and canceling the common factor
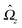
, we obtain
| | 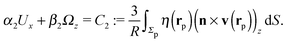 | (13) |
Once a particular model is given for the mechanism through which the chemical activity determines the phoretic slip v(rp), the quantities C1 and C2 can be computed and Ux and Ωz follow from eqn (10) and (13). This concludes the calculation of the translational (Ux) and angular (Ωz) velocities of the Janus particle trapped at the interface. We note that in the limit Δη → 0 eqn (10) and (13) reduce to the corresponding components for a Janus particle moving in a homogeneous fluid,34i.e., 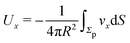 and
and 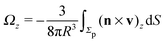 , respectively.
, respectively.
The latter result deserves further consideration. In the case of translation along the interface, in the limit Δη → 0 the recovery of the result corresponding to a particle moving in a homogeneous fluid is to be expected in the case of a particle having its center located at the interface. This is so, because the flow around the Janus particle translating at the interface converges, as the viscosity contrast approaches zero, towards the solution corresponding to the motion in a homogeneous fluid.†† On the other hand, this expectation does not hold in the case of rotation: the immiscibility of the fluids requires that the interface modifies the flow by “forcing” the fluid to flow along the interface. This different structure of the flow survives even if the viscosity contrast is vanishing. Therefore, recovering nonetheless the result for rotation in a homogeneous fluid simply means that the ansatz for the stress tensor at the surface of the particle (eqn (11)) renders the correct limiting behavior for vanishing viscosity contrast, irrespective of the corrections provided by the presence of the interface.
4 Results and discussion
Solving eqn (10) and (13) for Ux and Ωz leads to| | 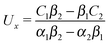 | (14a) |
and| | 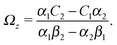 | (14b) |
For the discussion of these results we find it more convenient to employ the following alternative description of the orientation of the particle with respect to the interface. We define the director p of the Janus particle as being the unit vector corresponding to the axis of symmetry of the Janus particle oriented towards the catalytic cap. The acute angle between the director and the interface, in the plane (xOy), is denoted as χ (Fig. 2(a)). It is defined as a signed quantity, with the sign convention that χ is positive if p points towards the half-space y > 0 and negative otherwise; thus −π/2 ≤ χ ≤ π/2. (The angle χ is thus connected with δ (see Fig. 1(b)) via χ = min(δ,π − δ), if 0 < δ < π, and χ = −min(δ − π,2π − δ), if π < δ < 2π.) The states with χ = ±π/2 correspond to the director being parallel and antiparallel, respectively, to the interface normal ey, for which Ux vanishes. Therefore, in order for a state of motion along the surface, i.e., Ux ≠ 0, to be sustainable, any change in χ occurring as a result of motion along the interface should be such that |χ| decreases (i.e., the director rotates towards the interface).
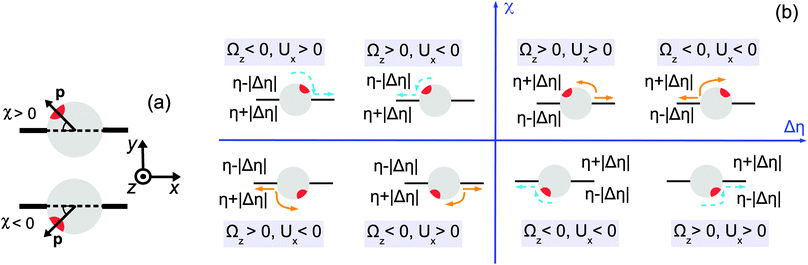 |
| | Fig. 2 (a) Definition of the director orientation with respect to the interface. (b) Schematic diagram indicating the configurations of sustained motility as a function of the viscosity contrast Δη = η1 − η2 and the position of the active cap (red) with respect to the interface (black) given by the acute angle χ between the director and the interface. The orange and blue colors of the arrows refer to repulsive and attractive interactions between the chemically generated solute and the particle, respectively. In each case we have illustrated both the situation in which the catalytic cap is tilted to the left and the situation in which it is tilted to the right of the interface normal ey, respectively. This change in the tilting of the cap amounts to all blue and orange arrows turning around and pointing into opposite directions but without changing colors because the stability criterion (sign(Ux/(RΩz))) is invariant with respect to this change. Therefore in each quadrant only either the repulsive or the attractive interaction case is associated with sustained motion. | |
4.1 Configurations of sustained motility
Referring now to Fig. 2(b) and considering as an example the situation shown in the upper part with the catalytic cap tilted slightly to the left of the normal ey, for which χ > 0, one infers that, upon turning on the chemical reaction, for repulsive (attractive) interactions between the solute (i.e., the reaction products) and the particle, the latter will tend to move towards the right (left), so that Ux > 0 (Ux < 0). If Δη > 0, i.e., the upper fluid is more viscous than the lower one, translation with Ux > 0 gives rise to a torque on the particle which induces a counterclockwise rotation, i.e., Ωz > 0. (The upper part of the particle experiences a stronger retarding friction than the lower part of the particle.) This corresponds to a decrease of χ towards zero and thus promotes motility. This situation is shown in the right upper quadrant of Fig. 2(b). On the other hand, translation with Ux < 0 (and still for χ > 0 as well as the cap tilted to the left of the interface normal; not shown in the right upper quadrant of Fig. 2(b)) gives rise to a clockwise rotation (i.e., Ωz < 0, for the same reason as above) and therefore to an increase of χ towards π/2, i.e., rotation opposes motility. If Δη < 0 (and still χ > 0 with the cap tilted to the left of the interface normal), the sign of those torques (which are described by the same color), and thus of the corresponding angular velocities, is reversed. In this case, the translation towards the left (Ux < 0) is accompanied by a rotation which decreases χ (i.e., Ωz > 0) and thus promotes motility (see the left upper quadrant of Fig. 2(b)), while translation towards the right (i.e., Ux > 0 and still χ > 0 with the cap tilted to the left of the interface normal; not shown in the left upper quadrant) is opposed by the rotation of the director. Following the above reasoning for the various possible configurations (i.e., catalytic cap above or below the interface, attractive or repulsive solute–particle interactions, and viscosity contrast positive or negative), in the plane (Δη,χ) one can identify the cases in which sustained motion would occur, depending on the repulsive or attractive character of the interactions between the solute and the particle. These configurations are summarized in Fig. 2(b), where the arrows indicate the corresponding directions of the translation and rotation. The colors blue and orange of the arrows refer to repulsive and attractive interactions, respectively.
From the discussion above (see also the schematic diagram in Fig. 2(b)) one infers that the states with sustained motion must satisfy Ux/(RΩz) > 0 for Δη > 0 or Ux/(RΩz) < 0 for Δη < 0. Therefore, for a given system these signs of Ux/(RΩz) as a function of the viscosity contrast Δη provide necessary conditions for the occurrence of such motile states. However, in order to explicitly calculate the sign of the ratio Ux/(ΩzR) one needs to provide an explicit form for vs(rp) which determines Ux and Ωz (eqn (10), (13) and (14)). In order to determine vs(rp) it is in principle necessary (i) to specify the geometrical properties of the catalytic cap responsible for the reaction within the fluids; (ii) to specify the reaction; (iii) to provide the diffusion constants of the reactant and product molecules in the two fluids (for example, they can either diffuse in both fluids but with different diffusion constants, or some of the reactants or products may effectively be confined to one of the two fluids), as well as any effective interaction between these molecules and the interface (e.g., whether or not they act as surfactants); (iv) to provide the interaction potentials of the various molecular species in the two solutions (i.e., the two fluids plus the reactants and the products) with the Janus particle as a whole as well as with its surface (for both the catalyst covered part and the inert part).
4.2 Motility of a model chemically active Janus colloid at fluid interfaces
Here we focus on the simple model of a chemically active Janus particle as introduced in Section 2, for which there is only a single reaction product (“solute”) diffusing in both fluids and for which the reactant molecules are present in abundance and diffusing very fast in both fluids, such that in both fluids the number density of reactant molecules is de facto time-independent and spatially uniform. The effective interaction of the solute with the colloidal particle is assumed to be of a range which is much smaller than the radius R of the colloid and to be similar for the catalyst-covered part and the inert part of the colloid. Furthermore, we assume a sharp interface (i.e., ξ → 0 so that η(rp) = η(y) with η(y) = η1 for y > 0, while η(y) = η2 for y < 0). The latter assumptions imply that, by adopting the classical theory of phoresis8,9,13 which has been developed for homogeneous (i.e., constant viscosity) fluids, one can express the phoretic slip as being proportional to the solute concentration gradient along the surface at all points of the surface of the particle except for a small region near the interface. Within the corresponding proportionality factor ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) /(βη) (the so-called “phoretic mobility”; see, cf., eqn (20)), where β = 1/(kBT), kB is the Boltzmann constant, and T denotes the absolute temperature, it is possible to identify the contribution
/(βη) (the so-called “phoretic mobility”; see, cf., eqn (20)), where β = 1/(kBT), kB is the Boltzmann constant, and T denotes the absolute temperature, it is possible to identify the contribution ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) of the solute–particle interaction (relative to the solvent–particle interaction).
(h) of the solute–particle interaction (relative to the solvent–particle interaction). ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) is encoded in
(h) is encoded in ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (which has the units of an area) according to8
(which has the units of an area) according to8| | 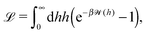 | (15) |
where h is the distance between the point-like solute and the particle surface. The potential ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) is assumed to be such that
(h) is assumed to be such that ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h → 0) = +∞, i.e., right at the particle surface the solvent is strongly preferred. The potential can be either repulsive at all distances, or it can become attractive beyond a certain distance h0 (and thus has to have an attractive minimum because at large distances it decays to zero); the latter case corresponds to the adsorption of the solute. Note that
(h → 0) = +∞, i.e., right at the particle surface the solvent is strongly preferred. The potential can be either repulsive at all distances, or it can become attractive beyond a certain distance h0 (and thus has to have an attractive minimum because at large distances it decays to zero); the latter case corresponds to the adsorption of the solute. Note that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) < 0 for purely repulsive interactions
< 0 for purely repulsive interactions ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h), while if
(h), while if ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) has an attractive part and h0 is sufficiently small, one has
(h) has an attractive part and h0 is sufficiently small, one has ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) > 0. In the following, the notion of “attractive interactions” will refer strictly to the latter case, i.e., potentials
> 0. In the following, the notion of “attractive interactions” will refer strictly to the latter case, i.e., potentials ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) which have attractive parts and satisfy
(h) which have attractive parts and satisfy ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) > 0. At this stage we do not yet particularize the cap to more than the assumed spherical cap shape and to being completely immersed into one of the two fluids.
> 0. At this stage we do not yet particularize the cap to more than the assumed spherical cap shape and to being completely immersed into one of the two fluids.
Under the above assumptions, the phoretic slip v(rp) follows from the solute distribution around the surface of the Janus particle. We further assume that the diffusivity D(r) of the solute molecules is sufficiently high such that the number density distribution ρ(r,t) of the solute is not affected by the convection of the fluids (i.e., we assume that the Péclet number Pe is small) and that a steady state distribution ρ(r) of solute is established at timescales which are much shorter than the characteristic translation time R/Ux of the colloid. With this, ρ(r) obeys the diffusion equation
subject to the boundary conditions
| | 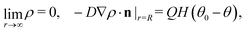 | (17) |
where
n is the outer normal of the particle,
Q denotes the number of solute molecules generated per area and per time at the location of the catalytic cap, and
H(
x) is the Heaviside step function (
H(
x > 0) = 1,
H(
x < 0) = 0). (In accordance with the assumptions of the model (see Section 2), in the above diffusion equation there are no terms to account for eventual interactions of the solute with the interface or with external fields.)
Since actually only the distribution of solute at the particle surface is required in order to calculate the phoretic slip, instead of seeking for the full solution ρ(r) of eqn (16), which is a difficult problem, we only focus on the solute distribution at the particle surface. In the co-moving (primed) coordinate system (see Fig. 1(b)), in which the phoretic slip velocity is most conveniently calculated, we introduce, in the usual manner, the common spherical coordinates (r′, θ′, ϕ′) defined via
x′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)cos(ϕ′) sin(θ′)cos(ϕ′) |
y′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)sin(ϕ′) sin(θ′)sin(ϕ′) |
| | z′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′). cos(θ′). | (18) |
Accordingly, the solute distribution at the particle surface
ρ(
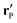
) =
ρ(
R,
θ′,
ϕ′) can be expressed as a series expansion in terms of the spherical harmonics
Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m
m(
θ′,
ϕ′):
39| | 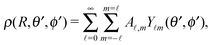 | (19) |
where the coefficients
A![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m
m are functions of the radius
R and of the other parameters (temperature, diffusion constants, viscosities, rate of solute production,
etc.) characterizing the system. In the co-moving system, the phoretic slip can be expressed in terms of the gradients of
ρ(
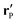
) along the surface of the particle
5,8,9,13 (except at the three-phase contact line):
| | 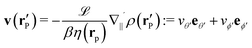 | (20) |
where
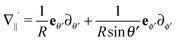
denotes the projection of the gradient operator along the surface of the particle.
In order to determine the x-component vx of the slip-velocity in the spatially fixed coordinate system, we use eqn (19) and (20) and employ the relationship between the unit vectors of the spatially fixed coordinate system and the co-moving one (see Fig. 1(b)). Knowledge of vx allows one to determine the quantities C1 and C2 introduced in eqn (10) and (13) (see Appendix B for details):
| | 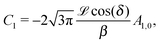 | (21) |
and
It is interesting to note that, apart from materials properties (
![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
) and temperature,
C1 depends solely on the projection (cos(
δ)) of the particle director onto the plane of the interface and on the real amplitude
A1,0 (see
eqn (19)) of
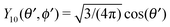
. This is that contribution to the angular dependence of
ρ along the particle surface which varies slowest between the poles at
θ′ = 0 (center of the cap) and
θ′ = π. This can be interpreted as an indication that for the model considered here the difference in the solute density between that at the catalytic pole and at the inert antipole is the dominant characteristics while the details of the variation of the density along the surface between these two values are basically irrelevant for the motion of the particle.
In the case that the two fluids have the same viscosity, i.e., Δη = 0, and the diffusion constant for the product molecules is the same in the two fluids (e.g., being related to the viscosity via the Stokes–Einstein relation), for the model considered here, according to which the reactant and product molecules can diffuse freely in both fluids and unhindered by the interface, the diffusion equation (eqn (16) and (17)) becomes identical to the one in a homogeneous bulk fluid which can be solved analytically.9,13 (Thus, in this limit there is no signature of the interface left in the diffusion problem.) The corresponding expansion into spherical harmonics of the solute density at the surface of the particle (for a bulk solvent without an interface) leads to the expression
| | 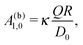 | (23) |
where
κ is a dimensionless factor determined by the geometry of the Janus sphere (
i.e., the extent of the catalyst covered area) and
D0 is the diffusion constant of the product molecules in the fluids of viscosities
η1 =
η2 =
η0. This leads to the ansatz
| | | A1,0 = ς(Δη/η0)A(b)1,0, | (24) |
for a system with an interface, where the dimensionless function
ς is expected to depend on the viscosities solely
via the dimensionless ratio
ε = Δ
η/
η0. Since in the limit
ε → 0, which renders the homogeneous bulk fluid case, one has
A1,0 →
A(b)1,0, the function
ς must obey the constraint
ς(
ε → 0) = 1.
By combining eqn (9), (12), (14) and (21)–(24), we obtain
| | 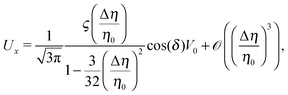 | (25a) |
| | 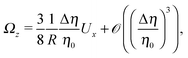 | (25b) |
where
| | 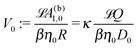 | (26) |
renders the characteristic translational and angular velocity scales |
V0| and
Ω0 = |
V0|/
R, respectively.
V0 is independent of the particle radius
R as well as of the value of the viscosity
η0 because, under the assumption of the Stokes–Einstein relation,
βη0D0 depends only on the radius
Rm of the product molecules. This implies that the translational velocity is independent of the radius
R of the particle while the angular velocity is proportional to 1/
R (up to eventual additional dependencies on
R arising from
ς).
Eqn (25) shows that both the translational and the angular velocity are proportional to cos(δ). Therefore both vanish for δ = π/2 which matches with the fact that in this case the particle is in fully upright orientation and thus cannot propel laterally. Moreover, both Ux and Ωz change sign when the director p (Fig. 2(a)) changes from pointing mainly to the right to pointing mainly to the left (Fig. 2(b)). On the other hand, the sign of the ratio Ux/Ωz, which, according to the discussion of Fig. 2(b) in the main text, decides on the sustainability of the motile state, is independent of δ but is determined by the sign of Δη. This is in agreement with the symmetry exhibited by the diagram shown in Fig. 2(b). In the limit of a vanishing viscosity contrast Δη/η0, Ux approaches the constant value 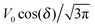 . (This corresponds to the motion in a homogeneous bulk fluid under the constraint of moving along a plane at an angle δ with respect to the orientation of the director position.) Thus, for small values of Δη, Ux(Δη) does not vary much, while, as expected, the angular velocity vanishes linearly ∝Δη/η0. In the limiting case Δη → 0 translation and rotation are decoupled and the particle translates without any rotation because there is no viscosity contrast. In such a case the net effect of the interface is to keep the particle center bound to the plane of the interface.
. (This corresponds to the motion in a homogeneous bulk fluid under the constraint of moving along a plane at an angle δ with respect to the orientation of the director position.) Thus, for small values of Δη, Ux(Δη) does not vary much, while, as expected, the angular velocity vanishes linearly ∝Δη/η0. In the limiting case Δη → 0 translation and rotation are decoupled and the particle translates without any rotation because there is no viscosity contrast. In such a case the net effect of the interface is to keep the particle center bound to the plane of the interface.
While the diagram in Fig. 2 is entirely determined by the ratio Ux/Ωz, which is independent of ς, the magnitudes of both Ux and Ωz do depend on it via the amplitude A1,0 (eqn (25) and (26)). Since determining the exact form of ς(ε) is clearly analytically intractable, one can try to analyze its behavior for ε ≪ 1. One option is to employ a perturbation series in terms of the small parameter ε in order to calculate the distribution of solute for ε ≪ 1, starting from the known solution ρ0(r) for ε = 0 (i.e., for a homogeneous bulk fluid without the interface), from which one can estimate A1,0 and implicitly ς(ε). (Note that ρ0(r) varies spatially due to the solute sources located at the surface of the particle and the solute sink at infinity.) We denote by ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (r) := ρ(r) − ρ0(r) and
(r) := ρ(r) − ρ0(r) and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (r) := D(r) − D0 the deviations (first order in ε) of the number density distribution and of the diffusion coefficient from their corresponding values ρ0(r) and D0 (spatially constant) in a homogeneous medium. (Note that by assuming the Stokes–Einstein relation between the diffusion coefficient and the viscosity
(r) := D(r) − D0 the deviations (first order in ε) of the number density distribution and of the diffusion coefficient from their corresponding values ρ0(r) and D0 (spatially constant) in a homogeneous medium. (Note that by assuming the Stokes–Einstein relation between the diffusion coefficient and the viscosity ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (r) is a known function determined by D0, ε, and the known variation of the viscosity across the interface (eqn (1)).) From eqn (16) and (17) one obtains that
(r) is a known function determined by D0, ε, and the known variation of the viscosity across the interface (eqn (1)).) From eqn (16) and (17) one obtains that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is the solution of the differential equation
is the solution of the differential equation
| | ∇·(![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ∇ρ0 + D0∇ ∇ρ0 + D0∇![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ) = 0, ) = 0, | (27) |
subject to the boundary conditions
| | 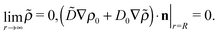 | (28) |
We have been unable to find an analytical solution of
eqn (27) and (28) for a general orientation of the (small) cap. Therefore we cannot make any further rigorous statements. Instead, we only formulate expectations concerning the behavior of
ς(
ε). For example, considering the case in which the catalytic cap is in the upper fluid region (
y > 0),
ε > 0 (
i.e., enhanced [reduced] viscosity in the upper [lower] fluid) leads to a reduction [increase] of the diffusion coefficient in the upper [lower] fluid. Compared with the homogeneous fluid (
ε = 0), intuitively this should lead to a relative accumulation of product molecules near the catalytic pole (located in the upper fluid) and to a relative depletion near the inert antipole (which is located in the lower fluid). For
ε < 0 the behavior is reversed. Since (as discussed after
eqn (22)) the coefficient
A1,0 can be viewed as a measure of the difference between the densities at the catalytic pole and at the antipole, the reasoning above suggests that, upon deviating from the homogeneous state (with
A(b)1,0),
A1,0 varies oppositely if the viscosity of fluid “1” relative to that of fluid “2” increases or decreases, respectively. Therefore, to first order in
ε the function
ζ(
ε) is expected to vary as
ζ(
ε → 0) = 1 + const·
ε +
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif)
(
ε2).
4.3 Persistence length and effective diffusion coefficient for a chemically active Janus colloid at fluid interfaces
The motion of active particles is characterized by distinct regimes occurring at different timescales. At short timescales the active motion amounts to a ballistic trajectory whereas at larger timescales the behavior is diffusive. A key parameter, which characterizes the motion of active particles, is the persistence length (which can be defined as below irrespective of whether the active particle is trapped at an interface or moving in a bulk fluid)| | λ = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) τ. τ. | (29) |
This is the typical distance a Janus particle, moving at an instantaneous velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , covers before thermal fluctuations will eventually change its direction. The time τ is determined by the rotational diffusion of the particle (see ref. 40). In the present case of the active particle being trapped at the interface there are two types of rotations. First, there are rotations of the catalytic cap orientation, i.e., of p around the interface normal, with a characteristic time τ∥. These rotations lead p out of the initial plane of motion spanned by p and the interface normal. This clearly changes the direction of motion. Second, there are fluctuations of p within the plane of motion with the normal of the plane of motion acting as the rotation axis. Small fluctuations of this kind do not change the direction of motion because p remains within the initial plane of motion. However, large fluctuations can rotate p, within the plane of motion, from a predominantly forward direction to a predominantly backward direction so that the particle runs backwards along the same straight line. This flipping of directions is associated with a timescale τ⊥. The minimum of these two timescales sets the rotational diffusion time τi = min(τ⊥,τ∥) for an active particle trapped at an interface.
, covers before thermal fluctuations will eventually change its direction. The time τ is determined by the rotational diffusion of the particle (see ref. 40). In the present case of the active particle being trapped at the interface there are two types of rotations. First, there are rotations of the catalytic cap orientation, i.e., of p around the interface normal, with a characteristic time τ∥. These rotations lead p out of the initial plane of motion spanned by p and the interface normal. This clearly changes the direction of motion. Second, there are fluctuations of p within the plane of motion with the normal of the plane of motion acting as the rotation axis. Small fluctuations of this kind do not change the direction of motion because p remains within the initial plane of motion. However, large fluctuations can rotate p, within the plane of motion, from a predominantly forward direction to a predominantly backward direction so that the particle runs backwards along the same straight line. This flipping of directions is associated with a timescale τ⊥. The minimum of these two timescales sets the rotational diffusion time τi = min(τ⊥,τ∥) for an active particle trapped at an interface.
In the absence of thermal fluctuations the distribution function of the orientation of the axis p of the particle is peaked at the steady state value. Thermal fluctuations promote a broadening of the distribution. Both cases of rotations translate into fluctuations of the value of the instantaneous velocity of the particle. Accordingly, the typical velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i of an active particle trapped at an interface is defined as the mean velocity of the Janus particle obtained as a weighted integral over all those possible configurations which give rise to a velocity with the same prescribed sign.‡‡ Before entering into further technical details concerning the definition of
i of an active particle trapped at an interface is defined as the mean velocity of the Janus particle obtained as a weighted integral over all those possible configurations which give rise to a velocity with the same prescribed sign.‡‡ Before entering into further technical details concerning the definition of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i, it is convenient to focus on one of the eight cases shown in Fig. 2(b), namely the case of a Janus particle characterized by V0 < 0 (see eqn (26) for repulsive solute–particle interactions so that
i, it is convenient to focus on one of the eight cases shown in Fig. 2(b), namely the case of a Janus particle characterized by V0 < 0 (see eqn (26) for repulsive solute–particle interactions so that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) < 0) and with the catalytic cap in the upper phase with δ < π/2 (so that χ = δ > 0). For Δη > 0, and within the linear regime ε ≪ 1, eqn (25) renders, in this case, Ux < 0 and Ωz < 0. This is the situation illustrated in the right part of the top right quadrant of Fig. 2(b). The other cases can be discussed along the same line. Accordingly, we define
< 0) and with the catalytic cap in the upper phase with δ < π/2 (so that χ = δ > 0). For Δη > 0, and within the linear regime ε ≪ 1, eqn (25) renders, in this case, Ux < 0 and Ωz < 0. This is the situation illustrated in the right part of the top right quadrant of Fig. 2(b). The other cases can be discussed along the same line. Accordingly, we define ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i as
i as
| | 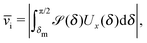 | (30) |
where
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
δ) is the steady state probability distribution to find a Janus particle with its axis forming an angle
δ ∈ (
δm,π/2) with the plane of the interface;
§§δm is the value of
δ for which the catalytic cap would touch the interface (see
Fig. 1(b)).
In thermal equilibrium, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) =
(δ) = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) depends only on the effective interactions between the catalytic cap and the interface. For example, in the absence of such interactions one has
eq(δ) depends only on the effective interactions between the catalytic cap and the interface. For example, in the absence of such interactions one has ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) = (π/2 − δm)−1. In contrast, in the presence of an effective attraction we expect that
eq(δ) = (π/2 − δm)−1. In contrast, in the presence of an effective attraction we expect that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) exhibits a peak closer to the interface (i.e., close to δ = 0) while the opposite holds in the case of an effective repulsion for which one expects
eq(δ) exhibits a peak closer to the interface (i.e., close to δ = 0) while the opposite holds in the case of an effective repulsion for which one expects ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) to be peaked at δ = π/2. When particles are active, an additional torque arises due to the catalytic activity, hence modifying the shape of
eq(δ) to be peaked at δ = π/2. When particles are active, an additional torque arises due to the catalytic activity, hence modifying the shape of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ). In order to estimate
(δ). In order to estimate ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) for active particles, we assume that
(δ) for active particles, we assume that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) factorizes as
(δ) factorizes as ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) =
(δ) = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ)
eq(δ)![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) into an equilibrium part
neq(δ) into an equilibrium part ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) (as discussed above) and a modulation
eq(δ) (as discussed above) and a modulation ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) due to the particle activity. As far as
neq(δ) due to the particle activity. As far as ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) is concerned, we assume that, although the system is out of thermal equilibrium, we can express it as a Boltzmann weight
neq(δ) is concerned, we assume that, although the system is out of thermal equilibrium, we can express it as a Boltzmann weight ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) ∝ e−βΦ(δ) of an effective potential Φ(δ) accounting for the torque arising due to the particle activity. (This assumption is based on the fact that
neq(δ) ∝ e−βΦ(δ) of an effective potential Φ(δ) accounting for the torque arising due to the particle activity. (This assumption is based on the fact that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) is the steady-state solution of a one-dimensional (with respect to δ) advection–diffusion equation with zero current. It is known that for such systems the steady-state solution has the form of a Boltzmann weight.41) Since within the present model there are no effective interactions with the interface,
neq(δ) is the steady-state solution of a one-dimensional (with respect to δ) advection–diffusion equation with zero current. It is known that for such systems the steady-state solution has the form of a Boltzmann weight.41) Since within the present model there are no effective interactions with the interface, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) is a constant which can be absorbed into the normalization:
eq(δ) is a constant which can be absorbed into the normalization:
| | 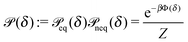 | (31) |
where
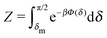
ensures that
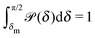
.
An estimate of the potential Φ can be obtained as follows. According to eqn (44), in our model a Janus particle, trapped at the interface and spinning with angular velocity Ωz around an axis which is contained in the plane of the interface and passes through the center of the particle, experiences a torque Lz = −8πη0R3Ωz. Therefore, in order to maintain the angular velocity Ωz(δ) of the particle an external torque equal to −Lz must be applied to the particle. Accordingly, for the Janus particle translating with Ux(δ) while simultaneously rotating with Ωz(δ), we introduce an effective torque
analogous to the external one which would have accounted for the same angular velocity, and define,
via L(
δ) = −d
Φ(
δ)/d
δ, the effective potential
Φ(
δ) as
| | 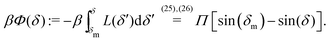 | (33) |
In this equation one has
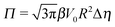
, the reference potential is set to
Φ(
δm) = 0, and we have accounted for the fact that here we discuss only the case in which
δm ≤
δ ≤ π/2 (each of the other three quadrants can be analyzed following the same line of reasoning).
The sign of Π is determined by the sign of V0 and Δη. As we noted above, here we focus on the case in which V0 < 0 (i.e., there is a repulsive interaction between the Janus particle and the product molecules of the catalysis) so that 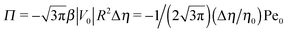 , where Pe0 = |V0|R/DP > 0 is the Péclet number of a Janus particle in a homogeneous fluid of viscosity η0 and DP = kBT/(6πη0R) is the diffusion constant of the Janus particle defined via the Stokes–Einstein relation. The above expression for Π shows that, for Δη > 0 and a Janus particle characterized by V0 < 0, Π is negative. In this case one has Φ(δ > δm) > 0 (eqn (33)) and thus Φ(δ) attains its minimum at δ = δm. This means that the action of the effective torque is consistent with Ωz < 0 (see eqn (25b)) which “drives” the particle towards its steady-state orientation δm, as discussed in Fig. 2(b) (right part of the top right quadrant). Accordingly, in the right part of the top right quadrant, corresponding to Δη > 0 and to the director pointing into the upper fluid, consistent with δm ≤ δ < π/2 and thus χ = min(δ,π − δ) > 0, repulsive interactions (orange arrows) ensure a sustained motility state by providing a torque which tilts the director towards the interface, i.e., which in the present case leads to a decrease of δ towards δm. As one can read off from eqn (33), the characteristics of the Janus particle (see eqn (26)) and of the fluid phases are all encoded in Π. Therefore the above conclusions can be extended directly to the case of attractive interactions between the Janus particle and the product molecules of the catalytic reaction by changing the sign of V0, and hence of Π. Therefore, in the case of attractive interactions (i.e., V0 > 0) and with the cap oriented such that δm ≤ δ < π/2 and χ = δ > 0, Π is negative for Δη < 0 and thus Φ(δ > δm) > 0 (in agreement with the situation illustrated in the left part of the top left quadrant of Fig. 2(b) for which Ux > 0 and Ωz < 0). Therefore, if particles have the catalytic cap in the upper phase, for which sin(δ) > 0, the states with small values of sin(δ), i.e., with the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π < 0. Similarly, if the catalytic cap of the particle is in the lower phase, where sin(δ) < 0, large values of sin(δ), i.e., the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π > 0.
, where Pe0 = |V0|R/DP > 0 is the Péclet number of a Janus particle in a homogeneous fluid of viscosity η0 and DP = kBT/(6πη0R) is the diffusion constant of the Janus particle defined via the Stokes–Einstein relation. The above expression for Π shows that, for Δη > 0 and a Janus particle characterized by V0 < 0, Π is negative. In this case one has Φ(δ > δm) > 0 (eqn (33)) and thus Φ(δ) attains its minimum at δ = δm. This means that the action of the effective torque is consistent with Ωz < 0 (see eqn (25b)) which “drives” the particle towards its steady-state orientation δm, as discussed in Fig. 2(b) (right part of the top right quadrant). Accordingly, in the right part of the top right quadrant, corresponding to Δη > 0 and to the director pointing into the upper fluid, consistent with δm ≤ δ < π/2 and thus χ = min(δ,π − δ) > 0, repulsive interactions (orange arrows) ensure a sustained motility state by providing a torque which tilts the director towards the interface, i.e., which in the present case leads to a decrease of δ towards δm. As one can read off from eqn (33), the characteristics of the Janus particle (see eqn (26)) and of the fluid phases are all encoded in Π. Therefore the above conclusions can be extended directly to the case of attractive interactions between the Janus particle and the product molecules of the catalytic reaction by changing the sign of V0, and hence of Π. Therefore, in the case of attractive interactions (i.e., V0 > 0) and with the cap oriented such that δm ≤ δ < π/2 and χ = δ > 0, Π is negative for Δη < 0 and thus Φ(δ > δm) > 0 (in agreement with the situation illustrated in the left part of the top left quadrant of Fig. 2(b) for which Ux > 0 and Ωz < 0). Therefore, if particles have the catalytic cap in the upper phase, for which sin(δ) > 0, the states with small values of sin(δ), i.e., with the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π < 0. Similarly, if the catalytic cap of the particle is in the lower phase, where sin(δ) < 0, large values of sin(δ), i.e., the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π > 0.
Concerning the persistence length λi = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) iτi of an active particle trapped at an interface (eqn (29) and (30)) one would like to understand its relation to the persistence length λb =
iτi of an active particle trapped at an interface (eqn (29) and (30)) one would like to understand its relation to the persistence length λb = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) bτb of a similar active particle moving freely in a homogeneous bulk fluid. To this end, we proceed by assuming that the characteristic time τi for the loss of orientation of a Janus particle, trapped at and moving along an interface between two fluids characterized by a (not too large) viscosity contrast Δη ≠ 0, is similar to the corresponding characteristic rotational diffusion time τb for the loss of orientation in a homogeneous bulk fluid of viscosity η0.¶¶ However, since one of the three possible independent rotations of a rigid body would affect the directionality for the particle trapped at the interface only if it is associated with a large fluctuation which would flip the director p with respect to the interface normal (see the discussion of τ⊥ after eqn (29)), it is a reasonable to expect that τi > τb. Furthermore, the argument concerning the weak influence of the rotations associated with τ⊥ suggests τi = ν0τb with ν0 ≃ 3/2 as a good ansatz for the relationship between the two characteristic timescales. Furthermore, we note that eqn (25b) has the form of a projection onto the x-axis (due to the factor cos(δ)) of a velocity (the factor multiplying cos(δ)) oriented along the director p. Thus in the limit Δη → 0 the latter factor can be identified with the velocity
bτb of a similar active particle moving freely in a homogeneous bulk fluid. To this end, we proceed by assuming that the characteristic time τi for the loss of orientation of a Janus particle, trapped at and moving along an interface between two fluids characterized by a (not too large) viscosity contrast Δη ≠ 0, is similar to the corresponding characteristic rotational diffusion time τb for the loss of orientation in a homogeneous bulk fluid of viscosity η0.¶¶ However, since one of the three possible independent rotations of a rigid body would affect the directionality for the particle trapped at the interface only if it is associated with a large fluctuation which would flip the director p with respect to the interface normal (see the discussion of τ⊥ after eqn (29)), it is a reasonable to expect that τi > τb. Furthermore, the argument concerning the weak influence of the rotations associated with τ⊥ suggests τi = ν0τb with ν0 ≃ 3/2 as a good ansatz for the relationship between the two characteristic timescales. Furthermore, we note that eqn (25b) has the form of a projection onto the x-axis (due to the factor cos(δ)) of a velocity (the factor multiplying cos(δ)) oriented along the director p. Thus in the limit Δη → 0 the latter factor can be identified with the velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) b of the active particle moving in a homogeneous bulk fluid of viscosity η0. With ς(ε → 0) = 1 this renders
b of the active particle moving in a homogeneous bulk fluid of viscosity η0. With ς(ε → 0) = 1 this renders 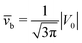 .
.
From eqn (30) and (31), after disregarding corrections to Ux of order 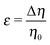 (eqn (25a)), one obtains
(eqn (25a)), one obtains
| | 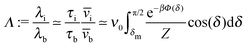 | (34) |
By inserting
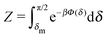
and
eqn (33) into
eqn (34), the dependencies of
Λ on
δm and on
Π can be calculated. For the choice
ν0 = 3/2 these are shown in
Fig. 3(a) and (b), respectively. (We recall that we have focused on the case of the catalytic cap exposed to the upper phase.) As shown in
Fig. 3, for sufficiently negative values of
Π the persistence length of a Janus particle moving at a liquid–fluid interface may be larger than the one in the corresponding bulk case,
i.e.,
Λ > 1. According to the discussion in the previous paragraphs, the case of
Π > 0 with the catalytic cap exposed to the upper phase corresponds to either Δ
η > 0 and repulsive interactions or Δ
η > 0 and attractive interactions,
i.e., the cases for which sustained motility emerges (see
Fig. 2(b)). On the other hand, we have noted that for a given type of interaction (
i.e., a given sign of
V0) and a given viscosity contrast Δ
η, the amplitude
Π of the potential
Φ changes sign if the catalytic cap is exposed to the lower phase,
i.e., for
δ > π, relative to the case of the catalytic cap being exposed to the upper phase. Therefore, these corresponding dependencies on
δm and on
Π are given by the curves in
Fig. 3(a) and (b) but with the opposite sign of
Π and with
δm → −
δm. Consequently, one infers that in this case one has
Λ > 1 for sufficiently large positive values of
Π. Thus also in the case that the cap is immersed in the lower phase the persistence length at the interface may be enhanced relative to the bulk one for those states in which sustained motility emerges. In summary, this implies that in all cases of sustained motility (
i.e., the system corresponds to any of the cases shown in
Fig. 2(b)) the particle trapped at the interface exhibits an enhanced persistence length for sufficiently large values of |
Π|.
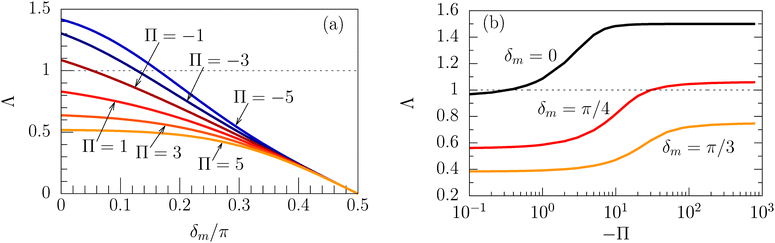 |
| | Fig. 3 (a) Approximate expression for the ratio Λ = λi/λb (eqn (34) with ν0 = 3/2) of the persistence length of a Janus particle at the interface (λi, catalytic cap in the upper phase) and in the bulk (λb) as a function of δm for various values of 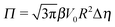 . The angle δm is the opening angle under which the catalytic cap is seen from the center of the particle when the cap touches the interface (Fig. 1(b)) and thus measures its size. (b) Approximate expression for Λ as a function of −Π > 0 for δm = 0, π/4, and π/3. Although the value δm = 0 is unphysical, because in this case the catalytic cap reduces to a point, the corresponding curve represents the limiting case for which Λ attains its maximal values. . The angle δm is the opening angle under which the catalytic cap is seen from the center of the particle when the cap touches the interface (Fig. 1(b)) and thus measures its size. (b) Approximate expression for Λ as a function of −Π > 0 for δm = 0, π/4, and π/3. Although the value δm = 0 is unphysical, because in this case the catalytic cap reduces to a point, the corresponding curve represents the limiting case for which Λ attains its maximal values. | |
Fig. 3(b) shows the dependency of Λ on Π for the case in which the catalytic cap is exposed to the upper phase. Interestingly, Λ saturates at negative values of Π with large |Π|. The saturation occurs at larger values of |Π| upon increasing δm. Concerning the magnitude of Π at which Λ starts to saturate, we recall that 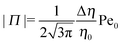 . Therefore, for
. Therefore, for 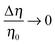 the onset of saturation at |Π| ≈ 5 requires, even for very small caps, i.e., δm → 0, Péclet numbers Pe0 ≃ 30 × (Δη/η0)−1 much larger than the typical values Pe0 ≃ 10 for Janus particles in a homogeneous bulk fluid. If, however, the viscosity contrast is high, the required corresponding Pe0 numbers are significantly smaller. For example, for the water–air interface the viscosity of air is negligible so that Δη = −2η0 which implies |Π| ≃ ⅓Pe0. In such a situation, as well as for other liquid–fluid interfaces characterized by high viscosity contrasts, large values of |Π| are encountered already for typical values of Pe0 and the persistence length at the interface may be enhanced relative to its bulk value, i.e., Λ > 1. As shown in Fig. 3, this effect is particularly pronounced for small catalytic caps (i.e., δm small).
the onset of saturation at |Π| ≈ 5 requires, even for very small caps, i.e., δm → 0, Péclet numbers Pe0 ≃ 30 × (Δη/η0)−1 much larger than the typical values Pe0 ≃ 10 for Janus particles in a homogeneous bulk fluid. If, however, the viscosity contrast is high, the required corresponding Pe0 numbers are significantly smaller. For example, for the water–air interface the viscosity of air is negligible so that Δη = −2η0 which implies |Π| ≃ ⅓Pe0. In such a situation, as well as for other liquid–fluid interfaces characterized by high viscosity contrasts, large values of |Π| are encountered already for typical values of Pe0 and the persistence length at the interface may be enhanced relative to its bulk value, i.e., Λ > 1. As shown in Fig. 3, this effect is particularly pronounced for small catalytic caps (i.e., δm small).
While the persistence length λ characterizes the active motion of a particle at timescales shorter than the characteristic rotational diffusion time τ, at timescales much larger than τ the motion of the particle crosses over to diffusion with an effective diffusion constant:40
| | 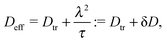 | (35) |
where
Dtr is the translational diffusion constant of the particle in the absence of activity and δ
D =
λ2/
τ is the activity-induced enhancement of the diffusion constant.
Eqn (35) allows us to compare the enhancement δ
D(i) for the Janus particle trapped at, and moving along, the interface to the one, δ
D(b), which holds for the same active Janus particle moving in a bulk fluid:
| | 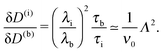 | (36) |
Therefore, according to the values of
Λ shown in
Fig. 3, for
ν0 = 3/2 the enhancement of the diffusion constant due to the activity of a Janus particle trapped at a liquid–fluid interface can be up to 1.5 times larger than the enhancement observed in a homogeneous bulk fluid. Finally, we note that for a particle trapped at the interface the activity induced contribution δ
D(i) can become much larger than the passive translational diffusion constant
DP in bulk fluid if (
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i2τi2
i2τi2)/(
τiDP) ≫ 1 (see the definition of δ
D(i) above and
eqn (29)). By using
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i
i =
Λ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) b
b/
ν0 (
eqn (34)),
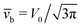
, Pe
0 = |
V0|
R/
DP, and
τi/
τb =
ν0, and by taking
τb = 1/
D(rot)P, where
D(rot)P = 4
DP/(3
R2) is the rotational diffusion constant of the particle in a homogeneous bulk fluid,
40 for
ν0 = 3/2 and by using
eqn (34)–(36) the condition δ
D(i)/
DP ≫ 1 translates into the condition Pe
0 ≫ 4.3/
Λ for the Péclet number of the particle.
5 Summary and conclusions
We have studied the behavior of a chemically active Janus particle trapped at a liquid–fluid interface, under the assumptions that the activity of the particle does not affect the surface tension of the interface and that the interface can be assumed to be flat. If particles are moving in such a set-up (Fig. 1), a coupling between rotation and translation arises due to the viscosity contrast Δη between the two adjacent fluids. Assuming that the particles are axisymmetric, and that both fluid phases are homogeneous and isotropic, the motile state of the particles is characterized by their linear velocity Ux in the plane of the interface and their angular velocity Ωz about an axis perpendicular to the plane of motion spanned by the interface normal and the velocity.
In Section 3 we have determined the linear and angular velocity Ux and Ωz, respectively, by using the Lorentz reciprocal theorem.35 Therein the stress-free interface is accounted for by imposing the corresponding boundary conditions on the fluid flow in both phases and the fluids are taken to be quiescent far away from the particle. The result in eqn (6) is valid for an arbitrary viscosity contrast Δη, including the limit of vanishing values of Δη as well as the case that one of the two phases has a vanishing viscosity.
Determining Ux and Ωzvia the reciprocal theorem requires to solve two independent auxiliary problems involving translation and rotation of a particle trapped at a liquid–fluid interface. In order to be able to obtain analytical solutions, we have considered neutrally buoyant particles exhibiting a contact angle of π/2 with the planar interface. Under these assumptions it is possible to exploit the available analytical solution for the stress exerted on the fluid by a particle which is translating without rotation.28 The case of a particle rotating at the interface is more challenging because it requires to determine the fluid flow close to the three-phase contact line formed as the intersection of the interface and the particle surface. In order to circumvent the issue of the motion of the three-phase contact line and in order to gain analytical insight into the problem, we have assumed that the fluid slips along the particle only in a small region close to the three-phase contact line. Accordingly, we can consider the fluid flow on each part of the surface of the particle to be de facto equal to the one which a particle experiences in a corresponding homogeneous bulk fluid under no-slip conditions on its surface (eqn (11)). The general expressions for Ux and Ωz (eqn (14a) and (b)) show that, for Δη ≠ 0, Ωz is nonzero. Therefore the motility of the particle along the interface is strongly affected by the change in the orientation of the axis of the particle relative to the interface normal. Accordingly, the velocity of the particle along the interface can be either enhanced or reduced.
In Section 4A we have established a diagram (Fig. 2) describing the situations for which Ωz promotes orientations of the Janus particle axis to be parallel to the interface, hence enforcing the motile state of the particle. In particular, for repulsive interactions between the particle and the self-generated solute (e.g., for catalytic platinum caps on polystyrene particles suspended in water–peroxide solutions||||) we have found that the motile state is fostered if the catalytic cap is immersed into the more viscous phase, while the opposite conclusion holds for an attractive interaction. Therefore, by tuning the viscosity contrast Δη, one can control the motility of Janus particles trapped at liquid–fluid interfaces.
In Section 4B these general considerations have been extended further by specifying model particles which allow one to analyze the density profiles of the reaction product. The expansion of these profiles in terms of spherical harmonics shows that only the amplitude A1,0 of the largest wavelength mode affects Ux and Ωz (see Appendix B). Accordingly, for the model considered here, different systems characterized by diverse physical properties (such as the viscosity contrast Δη, the catalytic reaction, or the interaction between the reaction product and the particle) but exhibiting the same value of A1,0 lead to the same values of Ux and Ωz (see eqn (25a) and (25b)). In particular we have found that both Ux and Ωz are proportional to the velocity scale V0 (eqn (26)) which depends linearly on the prefactor ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (see eqn (15)), the reaction rate Q per area, the inverse mean viscosity η0 and the inverse diffusivity D0 of the reaction product. The angular velocity experienced by the particle of radius R is proportional to V0/R and to the viscosity contrast Δη.
(see eqn (15)), the reaction rate Q per area, the inverse mean viscosity η0 and the inverse diffusivity D0 of the reaction product. The angular velocity experienced by the particle of radius R is proportional to V0/R and to the viscosity contrast Δη.
If the angular velocity promotes the alignment of the axis of the particle with the interface, the persistence length of the particle increases. In order to quantify this effect, in Section 4.3 we have proposed a factorization of the probability distribution (eqn (31)) for the orientation of the axis of the particle into an equilibrium and into a non-equilibrium distribution induced by the angular velocity and we have constructed an effective potential Φ (eqn (33)) describing the latter. The strength |Π| (eqn (33)) of this potential is proportional to the bulk Péclet number of the particle, which is of the order of 10, and therefore may lead to an increase of the persistence length of a trapped active particle relative to its value in the bulk fluid. Fig. 3(b) shows that this enhancement increases with |Π| as well as upon decreasing the size of the catalytic cap (which allows for smaller values of δm (see Fig. 1(b) and 3(a)). At long timescales the motion of active Janus particles is characterized by an effective diffusion coefficient (see eqn (35)). Concerning this regime our results predict that Δη as well as Π control the enhancement of the effective diffusion coefficient. In particular, by using eqn (36) and the data in Fig. 3, we have found that the presence of the interface can almost double the activity induced enhancement of the diffusion coefficient compared with the one in a homogeneous bulk fluid.
In sum we have obtained the following main results:
• Within a minimalistic model of active Janus particles trapped at a liquid–fluid interface, we have characterized their dynamics and have shown that their motility is strongly affected by the angular velocity induced on the particle due to the viscosity contrast Δη between the adjacent fluids.
• We have shown that the rotation–translation coupling induced by Δη can affect experimentally observable quantities such as the persistence length and the effective diffusion coefficient of active Janus particles trapped at liquid–fluid interfaces. In particular, the behavior described by our model is in agreement with recently reported, corresponding experimental observations of increased persistence lengths for chemically active Janus particles at water–air interfaces,22 and it sheds light on the proposition of an alternative explanation for the observed phenomenon.
• Since the viscosity contrast Δη can control the performance of active particles moving at liquid–fluid interfaces, we suggest that it can be relevant also for the onset of instabilities of thin films covered by active particles.42
Finally, we mention a few interesting extensions of the present study. Relaxing some of the simplifying assumptions employed here might shed light on alternative means to control active particle motility at liquid–fluid interfaces. In this respect we recall that we have assumed that the contact angle of the particle with the interface is π/2, and that pinning of the three-phase contact line is absent. Concerning the contact angle, we expect particles with a contact angle unequal π/2 to experience extra torques due to the offset of their center of mass from the plane of the interface. A similar scenario has been reported for particles which are pulled, without rotating, under the action of suitably distributed external forces and torques.28 On the other hand, pinning of the three-phase contact line might affect the effective rotational diffusion and, possibly, suppress it, as shown recently for an equilibrium system.43 Therefore we expect that for active Janus particles trapped at liquid–fluid interfaces the pinning of the three-phase contact line can enhance the persistence length, and therefore the effective diffusion, as argued in ref. 22, too.
Appendix
A Forces and torques
Here we present the steps of the derivations leading to eqn (9) and (12). In order to simplify the calculations, here it is convenient to translate the origin O of the unprimed coordinate system (fixed in space, see Fig. 1(b)) to the center C of the moving particle and to use spherical coordinates (r, θ, ϕ), which are defined as usual: x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)
sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), y = r
cos(ϕ), y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)
sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), and z = r
sin(ϕ), and z = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ). (Note that these are defined in the unprimed coordinate system which, although exhibiting here the same origin as the primed (co-moving) one, has different orientations of the axes as compared with the primed one. The unprimed coordinate system offers a less cumbersome parametrization of the location of the interface as compared with the primed coordinate system.) We start with deriving eqn (9).
cos(θ). (Note that these are defined in the unprimed coordinate system which, although exhibiting here the same origin as the primed (co-moving) one, has different orientations of the axes as compared with the primed one. The unprimed coordinate system offers a less cumbersome parametrization of the location of the interface as compared with the primed coordinate system.) We start with deriving eqn (9).
By using that for a translation (only) with velocity Û = Ûxex one has28
| | 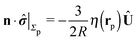 | (37) |
on the surface
Σp of the particle. By noting that
| | 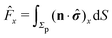 | (38) |
is the
x component of the integral over the surface of the normal pressure tensor as given by the above expression, using
eqn (1), and assuming a sharp interface (
ξ → 0 so that
η(
rp) =
η(
ϕ) with
η(
ϕ) =
η1 for 0 <
ϕ < π,
i.e.,
y > 0, while
η(
ϕ) =
η2 for π <
ϕ < 2π,
i.e.,
y < 0) one obtains
| | 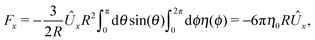 | (39) |
which agrees with
eqn (9a). The torque is defined as
| | 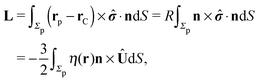 | (40) |
where we have used
rp −
rC =
Rn (see
Fig. 1). With the above choice of the coordinate system the torque is along the
z-direction. Since (
n ×
Û)
z =
nxÛy −
nyÛx and
Ûy = 0 (due to the choice of the dual problem “1”), with
ny = sin(
θ)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin(
ϕ) one obtains
| | 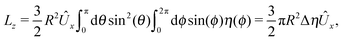 | (41) |
which agrees with
eqn (9b).
Concerning the derivation of eqn (12) we start from the relation (compare eqn (11) with 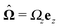 )
)
| | 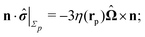 | (42) |
we note that
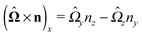
and recall that by definition of the dual problem “2” only the component
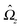
of the angular velocity is non-zero. Thus we obtain
| | 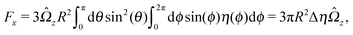 | (43) |
which agrees with
eqn (12a). For the torque one has, with
rp −
rC =
Rn,
| | 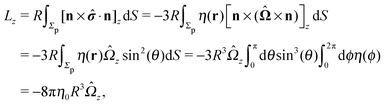 | (44) |
which agrees with
eqn (12b) and where the following relations have been used:
| | 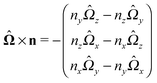 | (45) |
and
| | 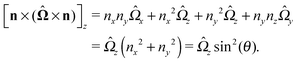 | (46) |
In
eqn (46) we have used, according to the definition of the dual problem “2”,
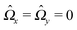
.
B Diffusiophoretic slip
We start the derivation of eqn (21) and (22) by employing spherical coordinates (r′, θ′, ϕ′):| | x′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′) sin(θ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ′), y′ = r′ cos(ϕ′), y′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′) sin(θ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ′), z′ = r′ sin(ϕ′), z′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′) cos(θ′) | (47) |
in the co-moving (primed) coordinate system (see Fig. 1(b)) with ρ(rp′) = ρ(R, θ′, ϕ′); in the following, for reasons of shorter notations we shall not indicate explicitly the dependence on R. The density can be expressed as a series expansion in terms of the spherical harmonics Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ′,ϕ′):
m(θ′,ϕ′):| | 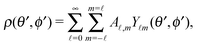 | (48) |
where39| | 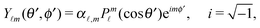 | (49) |
and| | 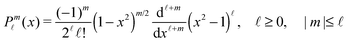 | (50) |
is the associated Legendre polynomial of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and order m with
and order m with| | 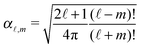 | (51) |
as a normalization constant.
Before proceeding, we list a few relations (obtained straightforwardly from the corresponding definitions) satisfied by Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m, Pm
m, Pm![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and α
, and α![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m, which will be needed below:
,m, which will be needed below:
| | 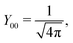 | (52) |
| |  | (53) |
| | 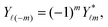 | (54) |
| | 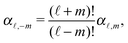 | (55) |
| | 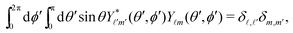 | (56) |
| | 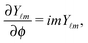 | (57) |
and
| | 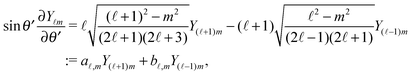 | (58) |
where * indicates the complex conjugate quantity.
From the definition of the phoretic slip v( ) (eqn (20)) one obtains
) (eqn (20)) one obtains
| | 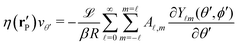 | (59) |
and
| | 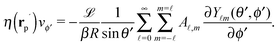 | (60) |
Noting that the unit vectors
er′,
eθ′, and
eϕ′ are given by
er′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + sin ex′ + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′ + cos ey′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ez′ ez′ |
eθ′ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + cos ex′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′ − sin ey′ − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ez′ ez′ |
| | eϕ′ = −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + cos ex′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′ ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′ ey′ | (61) |
and using geometry (see
Fig. 1(b)) one obtains
| | 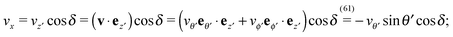 | (62) |
according to
eqn (20)vr′ = 0. Therefore
| | 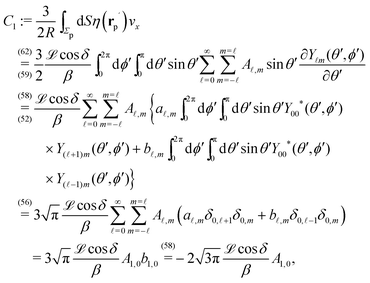 | (63) |
which agrees with
eqn (21).
We now proceed with the calculation of C2. First, we note that ez = ex′ (see Fig. 1(b)), and therefore (n × v)z := (n × v)·ez = (n × v)x′, where v = v(rp′). The latter but one expression is calculated as follows (note that in the primed coordinate system n = er′):
| | 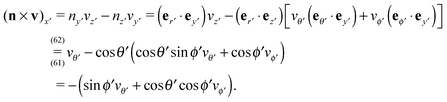 | (64) |
Therefore
C2 takes the form (
eqn (13))
| | 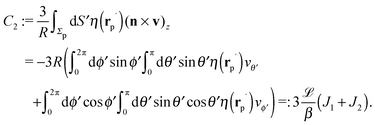 | (65) |
The integrals
J1 and
J2 are evaluated as follows. By introducing the notations
| |  | (66) |
and
| |  | (67) |
after observing that
| | 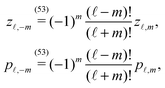 | (68) |
and with
| | 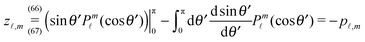 | (69) |
one arrives at
(note that
z0,1 = 0 due to |
m| ≤
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
) and
Therefore
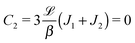
, which verifies
eqn (22).
Acknowledgements
P. M. thanks Dr Antonio Stocco for useful discussions and for providing the preprint version of ref. 22.
References
- S. J. Ebbens and J. R. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- E. Lauga and T. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- Y. Hong, D. Velegol, N. Chaturvedi and A. Sen, Phys. Chem. Chem. Phys., 2010, 12, 1423 RSC.
- S. Sánchez, L. Soler and J. Katuri, Angew. Chem., Int. Ed., 2015, 54, 1414 CrossRef PubMed.
-
W. C. K. Poon, Proceedings of the International School of Physics “Enrico Fermi”, Course CLXXXIV “Physics of Complex Colloids”, Amsterdam, 2013, p. 317 Search PubMed.
- J. El-Ali, P. K. Sorger and K. F. Jensen, Nature, 2006, 442, 403 CrossRef CAS PubMed.
- A. Z. Wang, R. Langer and O. C. Farokhzad, Annu. Rev. Med., 2012, 63, 185–198 CrossRef CAS PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61 CrossRef.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef PubMed.
- S. Ebbens, M.-H. Tu, J. R. Howse and R. Golestanian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 020401 CrossRef PubMed.
- T.-C. Lee, M. Alarcón-Correa, C. Miksch, K. Hahn, J. G. Gibbs and P. Fischer, Nano Lett., 2014, 14, 2407 CrossRef CAS PubMed.
- F. Jülicher and J. Prost, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 29, 27 CrossRef PubMed.
- M. Popescu, S. Dietrich and G. Oshanin, J. Chem. Phys., 2009, 130, 194702 CrossRef CAS PubMed.
- R. Kapral, J. Chem. Phys., 2013, 138, 202901 CrossRef PubMed.
- B. ten Hagen, S. van Teeffelen and H. Löwen, J. Phys.: Condens. Matter, 2011, 23, 194119 CrossRef CAS PubMed.
- R. Aveyard, Soft Matter, 2012, 23, 8 Search PubMed.
- B. J. Park and D. Lee, ACS Nano, 2012, 6, 782 CrossRef CAS PubMed.
- H. Rezvantalab and S. Shojaei-Zadeh, Soft Matter, 2013, 9, 3640 RSC.
- J. Bleibel, A. Domínguez, F. Günther, J. Harting and M. Oettel, Soft Matter, 2014, 10, 2945 RSC.
- J. Bleibel, A. Domínguez, M. Oettel and S. Dietrich, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 125 CrossRef CAS PubMed.
- M. Oettel, A. Domínguez and S. Dietrich, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051401 CrossRef CAS PubMed.
- X. Wang, M. In, C. Blanc, M. Nobili and A. Stocco, Soft Matter, 2015, 11, 7376 RSC.
- E. Lauga and A. M. J. Davis, J. Fluid Mech., 2011, 705, 120 CrossRef.
- H. Masoud and H. A. Stone, J. Fluid Mech., 2014, 741, R4 CrossRef CAS.
- A. Würger, J. Fluid Mech., 2014, 752, 589 CrossRef.
- A. Dominguez, P. Malgaretti, M. N. Popescu and S. Dietrich, Phys. Rev. Lett., 2016, 116, 078301 CrossRef PubMed.
-
J. Happel and H. Brenner, Low Reynolds Number Hydrodynamics, Prentice-Hall, Englewood Cliffs, NJ, 1965 Search PubMed.
- C. Pozrikidis, J. Fluid Mech., 2007, 575, 333 CrossRef.
- C. Huh and L. Scriven, J. Colloid Interface Sci., 1971, 35, 85 CrossRef CAS.
- E. Dusan V. and S. Davis, J. Fluid Mech., 1974, 65, 71 CrossRef.
- E. Dusan V., J. Fluid Mech., 1976, 77, 665 CrossRef.
- L. Hocking, J. Fluid Mech., 1976, 79, 209 CrossRef.
- M. E. O'Neill, K. B. Ranger and H. Brenner, Phys. Fluids, 1986, 29, 913 CrossRef.
- H. A. Stone and A. D. T. Samuel, Phys. Rev. Lett., 1996, 77, 4102 CrossRef CAS PubMed.
- H. A. Lorentz, Zittingsversl. Koninkl. Akad. van Wetensch. Amsterdam, 1896, 5, 168 Search PubMed.
- H. K. Kuiken, J. Eng. Math., 1996, 30, 19 CrossRef.
- P. Joseph and P. Taberling, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 035303 CrossRef PubMed.
- V. Sterr, R. Krauß, K. Morozov, I. Rehberg, A. Engel and R. Richter, New J. Phys., 2009, 10, 063029 CrossRef.
-
J. D. Jackson, Classical Electrodynamics, John Willey & Sons, New York, 1962 Search PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
-
H. Risken, The Fokker-Planck Equation, Springer-Verlag, Berlin, 1988 Search PubMed.
- A. Pototsky, U. Thiele and H. Stark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 030401 CrossRef PubMed.
- G. Boniello, C. Blanc, D. Fedorenko, M. Medfai, N. Ben Mbarek, M. In, M. Gross, A. Stocco and M. Nobili, Nat. Mater., 2015, 14, 908 CrossRef CAS PubMed.
Footnotes |
| † Such particles, which have distinct material properties across the two regions of their surface, are often called Janus particles; in the following we shall use this notation, too. |
| ‡ Even if the equilibrium configuration would correspond to the symmetry axis being aligned with the interface normal, as, e.g., in the case of strongly repulsive, effective interactions between the interface and the catalytic patch, fluctuations will perturb this state of alignment and the previous scenario is recovered. These fluctuations can be thermal fluctuations of the orientation of the axis around the equilibrium position, or non-equilibrium fluctuations of the rate of the catalytic reaction along the surface. |
| § Since the typical effective forces between the interface and the catalytic cap decay rapidly with the distance from the interface, the assumption remains valid as long as the catalytic cap is not very close to the interface. |
| ¶ A recent extension of this version of the reciprocal theorem to the case of a free interface, in which the viscosity exhibits an abrupt change across the liquid–air interface, can be found in ref. 24. |
|| Formally, the domains ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and 1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 as well as the interface Γ could be closed along the Ox direction by assuming periodic boundary conditions at |x| → ∞; alternatively, one may choose for the surface at infinity, which is closing the domains 2 as well as the interface Γ could be closed along the Ox direction by assuming periodic boundary conditions at |x| → ∞; alternatively, one may choose for the surface at infinity, which is closing the domains ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and 1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2, a spherical one, centered at C and with a radius R∞ → ∞. 2, a spherical one, centered at C and with a radius R∞ → ∞. |
| ** For example, for water on PDMS or on glass surfaces the estimated slip length l0 is well below 100 nm.37 |
| †† In the case of a homogeneous fluid the flow around the particle which translates is symmetric with respect to any plane containing the translation direction. Thus the flow is characterized by a vanishing velocity normal to such a symmetry plane and a continuous velocity tangential to that symmetry plane (which thus can be regarded as an “imaginary planar interface” where the kinematic boundary conditions of an actual interface between immiscible liquids are obeyed). |
| ‡‡ Since in the present case the system does not undergo any spontaneous symmetry breaking, the velocity obtained by averaging over all possible configurations, rather than only over those with a prescribed sign of the velocity, is zero. |
§§ The mean velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i for the same particle moving in the positive direction would be i for the same particle moving in the positive direction would be 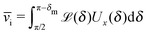 ; see the left part of the top right quadrant of Fig. 2(b). Here ; see the left part of the top right quadrant of Fig. 2(b). Here ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is the distribution of the angle δ ∈ (π/2,π − δm). is the distribution of the angle δ ∈ (π/2,π − δm). |
| ¶¶ It is particularly difficult to determine τi because it depends on the details of the effective interaction between the Janus particle and the interface and it involves the dynamics of the moving three-phase contact line. |
| |||| In this case the repulsive character of interaction is inferred from the experimentally observed motion away from the platinum cap and under the assumption that the mechanism of motion is self-diffusiophoresis and that only the oxygen production and the corresponding surface gradients of oxygen are relevant. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article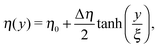
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , i.e., solutions subject to different boundary conditions but on the very same boundaries ∂
, i.e., solutions subject to different boundary conditions but on the very same boundaries ∂![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) , obey the relation
, obey the relation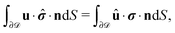
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/b_i_char_e111.gif) denote the stress tensors corresponding to the two flow fields.
denote the stress tensors corresponding to the two flow fields.
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1) and below (
1) and below (![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2) the interface and by subsequently working out the problem by connecting the solutions corresponding to the upper and lower fluids via appropriate boundary conditions at the interface (see below).
2) the interface and by subsequently working out the problem by connecting the solutions corresponding to the upper and lower fluids via appropriate boundary conditions at the interface (see below). ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 is delimited by that part Σp1 of the particle surface Σp exposed to the upper fluid, the surface of the fluid at infinity in the half-plane y > 0, and the upper part, y = 0+, of the fluid interface Γ (note that this is the plane with y = 0 and less area occupied by the particle);
1 is delimited by that part Σp1 of the particle surface Σp exposed to the upper fluid, the surface of the fluid at infinity in the half-plane y > 0, and the upper part, y = 0+, of the fluid interface Γ (note that this is the plane with y = 0 and less area occupied by the particle); ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 is defined similarly.|| We note that the inner normals of the upper (n1) and lower (n2) parts of the interface Γ are n1 = ey = −n2.
2 is defined similarly.|| We note that the inner normals of the upper (n1) and lower (n2) parts of the interface Γ are n1 = ey = −n2.![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 (which can be done because Γ is a physical boundary at which the boundary conditions are formally prescribed by imposing the tangential velocity and the stress tensor to take the values given by the (yet unknown) velocity and stress tensor on the other side of the interface, respectively), (ii) adding the left and right hand sides of the two results of applying the reciprocal theorem in
2 (which can be done because Γ is a physical boundary at which the boundary conditions are formally prescribed by imposing the tangential velocity and the stress tensor to take the values given by the (yet unknown) velocity and stress tensor on the other side of the interface, respectively), (ii) adding the left and right hand sides of the two results of applying the reciprocal theorem in ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2, (iii) noting that for flow fields, which decay sufficiently fast with the distance from the particle (which typically is the case), the contribution from the integrals over the surfaces at infinity are vanishingly small, (iv) using the relation (see above) n1 = − n2 = ey between the interface normals, and (v) noting that the boundary conditions for the flow velocity at the interface Γ impose zero normal components, i.e., (u1·ey)|y=0 = 0, (u2·ey|)y=0 = 0 and continuous tangential components27 so that u1|y=0+ = u2|y=0− =: u∥e∥ (with similar relations for the hatted velocity field), where e∥·ey = 0, we arrive at
2, (iii) noting that for flow fields, which decay sufficiently fast with the distance from the particle (which typically is the case), the contribution from the integrals over the surfaces at infinity are vanishingly small, (iv) using the relation (see above) n1 = − n2 = ey between the interface normals, and (v) noting that the boundary conditions for the flow velocity at the interface Γ impose zero normal components, i.e., (u1·ey)|y=0 = 0, (u2·ey|)y=0 = 0 and continuous tangential components27 so that u1|y=0+ = u2|y=0− =: u∥e∥ (with similar relations for the hatted velocity field), where e∥·ey = 0, we arrive at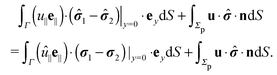
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) replaced by Σp.
replaced by Σp.
 under the action of the external force
under the action of the external force ![[F with combining circumflex]](https://www.rsc.org/images/entities/b_char_0046_0302.gif) and the external torque
and the external torque ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) . At the surface of the particle, the flow û(rp), where rp denotes a point at the particle surface Σp, is given by
. At the surface of the particle, the flow û(rp), where rp denotes a point at the particle surface Σp, is given by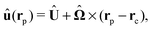
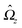 are spatially constant vectors, the right hand side (rhs) of eqn (2) can be re-written as
are spatially constant vectors, the right hand side (rhs) of eqn (2) can be re-written as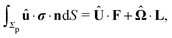
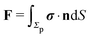 and
and 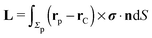 denote the force and the torque, respectively, experienced by the Janus particle. (In eqn (6), n denotes the normal of the surface Σp of the particle, oriented into the fluid.) We note that while the active motion of Janus particles in the bulk is force- and torque-free, this is, in general, not the case if the motion occurs at the interface because the interface can exert forces and torques on the particle. However, because we have assumed that the interface does not exert a force in the case of translations of the Janus particle along the interface or a torque in the case of rotations around the z-axis (in the sense of spinning around an axis parallel to the z-axis, as discussed above), the components Fx and Lz vanish. Therefore, if the reciprocal problem involves only translations along the x-axis and/or such rotations around the z-axis, the rhs of eqn (6), and, consequently, of eqn (2) is zero. Restricting now the dual problem as discussed above to such a choice, and using eqn (5) for the left hand side of eqn (2), we arrive at
denote the force and the torque, respectively, experienced by the Janus particle. (In eqn (6), n denotes the normal of the surface Σp of the particle, oriented into the fluid.) We note that while the active motion of Janus particles in the bulk is force- and torque-free, this is, in general, not the case if the motion occurs at the interface because the interface can exert forces and torques on the particle. However, because we have assumed that the interface does not exert a force in the case of translations of the Janus particle along the interface or a torque in the case of rotations around the z-axis (in the sense of spinning around an axis parallel to the z-axis, as discussed above), the components Fx and Lz vanish. Therefore, if the reciprocal problem involves only translations along the x-axis and/or such rotations around the z-axis, the rhs of eqn (6), and, consequently, of eqn (2) is zero. Restricting now the dual problem as discussed above to such a choice, and using eqn (5) for the left hand side of eqn (2), we arrive at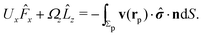
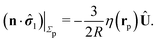
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) 1x = −6πRη0Ûx := α1Ûx
1x = −6πRη0Ûx := α1Ûx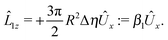
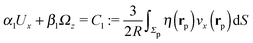
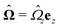 of a spherical particle of radius R, the center of which lies in the plane of the flat, sharp (ξ → 0) liquid–fluid interface. As noted before, this is a more involved problem due to the concomitant issue of contact line motion. For the case in which one of the two fluids has a vanishingly small viscosity, an exact solution was constructed in ref. 33 under the assumption that a slip boundary condition, with a spatially uniform slip length along the surface, applies across that surface region which is immersed in the fluid of non-vanishing viscosity, called liquid. The result of this calculation shows that for typical slip lengths l0, which are much smaller than the size of the particle,** at distances |y|/l0 ≫ 1 from the interface the hydrodynamic flow within the liquid is de facto identical to the one which would have occurred if the rotating sphere would have been completely immersed in the liquid and a no-slip boundary condition would have been applied. Thus in this context the only role played by the slip is to remove the contact line singularity, as discussed in Section 2. This can be interpreted in the sense that the same solution would emerge if one assumes that the fluid slips only in a narrow region localized close to the three-phase contact line, while the no-slip condition holds for the rest of the sphere. This view is confirmed by an alternative solution presented in ref. 38 for the same problem of the rotation of a sphere at the interface between a liquid and a fluid of vanishing viscosity.
of a spherical particle of radius R, the center of which lies in the plane of the flat, sharp (ξ → 0) liquid–fluid interface. As noted before, this is a more involved problem due to the concomitant issue of contact line motion. For the case in which one of the two fluids has a vanishingly small viscosity, an exact solution was constructed in ref. 33 under the assumption that a slip boundary condition, with a spatially uniform slip length along the surface, applies across that surface region which is immersed in the fluid of non-vanishing viscosity, called liquid. The result of this calculation shows that for typical slip lengths l0, which are much smaller than the size of the particle,** at distances |y|/l0 ≫ 1 from the interface the hydrodynamic flow within the liquid is de facto identical to the one which would have occurred if the rotating sphere would have been completely immersed in the liquid and a no-slip boundary condition would have been applied. Thus in this context the only role played by the slip is to remove the contact line singularity, as discussed in Section 2. This can be interpreted in the sense that the same solution would emerge if one assumes that the fluid slips only in a narrow region localized close to the three-phase contact line, while the no-slip condition holds for the rest of the sphere. This view is confirmed by an alternative solution presented in ref. 38 for the same problem of the rotation of a sphere at the interface between a liquid and a fluid of vanishing viscosity.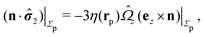
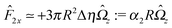
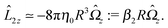
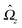 , we obtain
, we obtain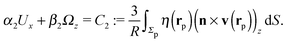
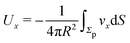 and
and 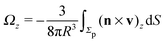 , respectively.
, respectively.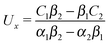
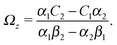
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) /(βη) (the so-called “phoretic mobility”; see, cf., eqn (20)), where β = 1/(kBT), kB is the Boltzmann constant, and T denotes the absolute temperature, it is possible to identify the contribution
/(βη) (the so-called “phoretic mobility”; see, cf., eqn (20)), where β = 1/(kBT), kB is the Boltzmann constant, and T denotes the absolute temperature, it is possible to identify the contribution ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) of the solute–particle interaction (relative to the solvent–particle interaction).
(h) of the solute–particle interaction (relative to the solvent–particle interaction). ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) is encoded in
(h) is encoded in ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (which has the units of an area) according to8
(which has the units of an area) according to8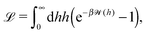
![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) is assumed to be such that
(h) is assumed to be such that ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h → 0) = +∞, i.e., right at the particle surface the solvent is strongly preferred. The potential can be either repulsive at all distances, or it can become attractive beyond a certain distance h0 (and thus has to have an attractive minimum because at large distances it decays to zero); the latter case corresponds to the adsorption of the solute. Note that
(h → 0) = +∞, i.e., right at the particle surface the solvent is strongly preferred. The potential can be either repulsive at all distances, or it can become attractive beyond a certain distance h0 (and thus has to have an attractive minimum because at large distances it decays to zero); the latter case corresponds to the adsorption of the solute. Note that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) < 0 for purely repulsive interactions
< 0 for purely repulsive interactions ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h), while if
(h), while if ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) has an attractive part and h0 is sufficiently small, one has
(h) has an attractive part and h0 is sufficiently small, one has ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) > 0. In the following, the notion of “attractive interactions” will refer strictly to the latter case, i.e., potentials
> 0. In the following, the notion of “attractive interactions” will refer strictly to the latter case, i.e., potentials ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) (h) which have attractive parts and satisfy
(h) which have attractive parts and satisfy ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) > 0. At this stage we do not yet particularize the cap to more than the assumed spherical cap shape and to being completely immersed into one of the two fluids.
> 0. At this stage we do not yet particularize the cap to more than the assumed spherical cap shape and to being completely immersed into one of the two fluids.
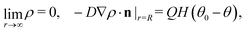
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)cos(ϕ′)
sin(θ′)cos(ϕ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)sin(ϕ′)
sin(θ′)sin(ϕ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′).
cos(θ′). ) = ρ(R,θ′,ϕ′) can be expressed as a series expansion in terms of the spherical harmonics Y
) = ρ(R,θ′,ϕ′) can be expressed as a series expansion in terms of the spherical harmonics Y![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ′,ϕ′):39
m(θ′,ϕ′):39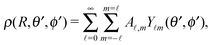
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m are functions of the radius R and of the other parameters (temperature, diffusion constants, viscosities, rate of solute production, etc.) characterizing the system. In the co-moving system, the phoretic slip can be expressed in terms of the gradients of ρ(
m are functions of the radius R and of the other parameters (temperature, diffusion constants, viscosities, rate of solute production, etc.) characterizing the system. In the co-moving system, the phoretic slip can be expressed in terms of the gradients of ρ( ) along the surface of the particle5,8,9,13 (except at the three-phase contact line):
) along the surface of the particle5,8,9,13 (except at the three-phase contact line):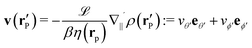
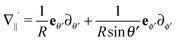 denotes the projection of the gradient operator along the surface of the particle.
denotes the projection of the gradient operator along the surface of the particle.
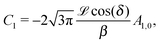
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ) and temperature, C1 depends solely on the projection (cos(δ)) of the particle director onto the plane of the interface and on the real amplitude A1,0 (see eqn (19)) of
) and temperature, C1 depends solely on the projection (cos(δ)) of the particle director onto the plane of the interface and on the real amplitude A1,0 (see eqn (19)) of 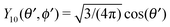 . This is that contribution to the angular dependence of ρ along the particle surface which varies slowest between the poles at θ′ = 0 (center of the cap) and θ′ = π. This can be interpreted as an indication that for the model considered here the difference in the solute density between that at the catalytic pole and at the inert antipole is the dominant characteristics while the details of the variation of the density along the surface between these two values are basically irrelevant for the motion of the particle.
. This is that contribution to the angular dependence of ρ along the particle surface which varies slowest between the poles at θ′ = 0 (center of the cap) and θ′ = π. This can be interpreted as an indication that for the model considered here the difference in the solute density between that at the catalytic pole and at the inert antipole is the dominant characteristics while the details of the variation of the density along the surface between these two values are basically irrelevant for the motion of the particle.
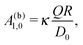
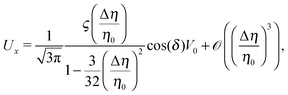
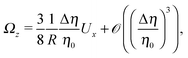
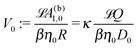
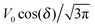 . (This corresponds to the motion in a homogeneous bulk fluid under the constraint of moving along a plane at an angle δ with respect to the orientation of the director position.) Thus, for small values of Δη, Ux(Δη) does not vary much, while, as expected, the angular velocity vanishes linearly ∝Δη/η0. In the limiting case Δη → 0 translation and rotation are decoupled and the particle translates without any rotation because there is no viscosity contrast. In such a case the net effect of the interface is to keep the particle center bound to the plane of the interface.
. (This corresponds to the motion in a homogeneous bulk fluid under the constraint of moving along a plane at an angle δ with respect to the orientation of the director position.) Thus, for small values of Δη, Ux(Δη) does not vary much, while, as expected, the angular velocity vanishes linearly ∝Δη/η0. In the limiting case Δη → 0 translation and rotation are decoupled and the particle translates without any rotation because there is no viscosity contrast. In such a case the net effect of the interface is to keep the particle center bound to the plane of the interface.![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (r) := ρ(r) − ρ0(r) and
(r) := ρ(r) − ρ0(r) and ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (r) := D(r) − D0 the deviations (first order in ε) of the number density distribution and of the diffusion coefficient from their corresponding values ρ0(r) and D0 (spatially constant) in a homogeneous medium. (Note that by assuming the Stokes–Einstein relation between the diffusion coefficient and the viscosity
(r) := D(r) − D0 the deviations (first order in ε) of the number density distribution and of the diffusion coefficient from their corresponding values ρ0(r) and D0 (spatially constant) in a homogeneous medium. (Note that by assuming the Stokes–Einstein relation between the diffusion coefficient and the viscosity ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) (r) is a known function determined by D0, ε, and the known variation of the viscosity across the interface (eqn (1)).) From eqn (16) and (17) one obtains that
(r) is a known function determined by D0, ε, and the known variation of the viscosity across the interface (eqn (1)).) From eqn (16) and (17) one obtains that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) is the solution of the differential equation
is the solution of the differential equation![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ∇ρ0 + D0∇
∇ρ0 + D0∇![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ) = 0,
) = 0,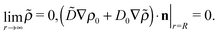
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ε2).
(ε2).
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) τ.
τ.![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , covers before thermal fluctuations will eventually change its direction. The time τ is determined by the rotational diffusion of the particle (see ref. 40). In the present case of the active particle being trapped at the interface there are two types of rotations. First, there are rotations of the catalytic cap orientation, i.e., of p around the interface normal, with a characteristic time τ∥. These rotations lead p out of the initial plane of motion spanned by p and the interface normal. This clearly changes the direction of motion. Second, there are fluctuations of p within the plane of motion with the normal of the plane of motion acting as the rotation axis. Small fluctuations of this kind do not change the direction of motion because p remains within the initial plane of motion. However, large fluctuations can rotate p, within the plane of motion, from a predominantly forward direction to a predominantly backward direction so that the particle runs backwards along the same straight line. This flipping of directions is associated with a timescale τ⊥. The minimum of these two timescales sets the rotational diffusion time τi = min(τ⊥,τ∥) for an active particle trapped at an interface.
, covers before thermal fluctuations will eventually change its direction. The time τ is determined by the rotational diffusion of the particle (see ref. 40). In the present case of the active particle being trapped at the interface there are two types of rotations. First, there are rotations of the catalytic cap orientation, i.e., of p around the interface normal, with a characteristic time τ∥. These rotations lead p out of the initial plane of motion spanned by p and the interface normal. This clearly changes the direction of motion. Second, there are fluctuations of p within the plane of motion with the normal of the plane of motion acting as the rotation axis. Small fluctuations of this kind do not change the direction of motion because p remains within the initial plane of motion. However, large fluctuations can rotate p, within the plane of motion, from a predominantly forward direction to a predominantly backward direction so that the particle runs backwards along the same straight line. This flipping of directions is associated with a timescale τ⊥. The minimum of these two timescales sets the rotational diffusion time τi = min(τ⊥,τ∥) for an active particle trapped at an interface.
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i of an active particle trapped at an interface is defined as the mean velocity of the Janus particle obtained as a weighted integral over all those possible configurations which give rise to a velocity with the same prescribed sign.‡‡ Before entering into further technical details concerning the definition of
i of an active particle trapped at an interface is defined as the mean velocity of the Janus particle obtained as a weighted integral over all those possible configurations which give rise to a velocity with the same prescribed sign.‡‡ Before entering into further technical details concerning the definition of ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i, it is convenient to focus on one of the eight cases shown in Fig. 2(b), namely the case of a Janus particle characterized by V0 < 0 (see eqn (26) for repulsive solute–particle interactions so that
i, it is convenient to focus on one of the eight cases shown in Fig. 2(b), namely the case of a Janus particle characterized by V0 < 0 (see eqn (26) for repulsive solute–particle interactions so that ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) < 0) and with the catalytic cap in the upper phase with δ < π/2 (so that χ = δ > 0). For Δη > 0, and within the linear regime ε ≪ 1, eqn (25) renders, in this case, Ux < 0 and Ωz < 0. This is the situation illustrated in the right part of the top right quadrant of Fig. 2(b). The other cases can be discussed along the same line. Accordingly, we define
< 0) and with the catalytic cap in the upper phase with δ < π/2 (so that χ = δ > 0). For Δη > 0, and within the linear regime ε ≪ 1, eqn (25) renders, in this case, Ux < 0 and Ωz < 0. This is the situation illustrated in the right part of the top right quadrant of Fig. 2(b). The other cases can be discussed along the same line. Accordingly, we define ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i as
i as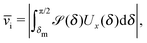
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) is the steady state probability distribution to find a Janus particle with its axis forming an angle δ ∈ (δm,π/2) with the plane of the interface;§§δm is the value of δ for which the catalytic cap would touch the interface (see Fig. 1(b)).
(δ) is the steady state probability distribution to find a Janus particle with its axis forming an angle δ ∈ (δm,π/2) with the plane of the interface;§§δm is the value of δ for which the catalytic cap would touch the interface (see Fig. 1(b)).
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) =
(δ) = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) depends only on the effective interactions between the catalytic cap and the interface. For example, in the absence of such interactions one has
eq(δ) depends only on the effective interactions between the catalytic cap and the interface. For example, in the absence of such interactions one has ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) = (π/2 − δm)−1. In contrast, in the presence of an effective attraction we expect that
eq(δ) = (π/2 − δm)−1. In contrast, in the presence of an effective attraction we expect that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) exhibits a peak closer to the interface (i.e., close to δ = 0) while the opposite holds in the case of an effective repulsion for which one expects
eq(δ) exhibits a peak closer to the interface (i.e., close to δ = 0) while the opposite holds in the case of an effective repulsion for which one expects ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) to be peaked at δ = π/2. When particles are active, an additional torque arises due to the catalytic activity, hence modifying the shape of
eq(δ) to be peaked at δ = π/2. When particles are active, an additional torque arises due to the catalytic activity, hence modifying the shape of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ). In order to estimate
(δ). In order to estimate ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) for active particles, we assume that
(δ) for active particles, we assume that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) factorizes as
(δ) factorizes as ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (δ) =
(δ) = ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ)
eq(δ)![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) into an equilibrium part
neq(δ) into an equilibrium part ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) (as discussed above) and a modulation
eq(δ) (as discussed above) and a modulation ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) due to the particle activity. As far as
neq(δ) due to the particle activity. As far as ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) is concerned, we assume that, although the system is out of thermal equilibrium, we can express it as a Boltzmann weight
neq(δ) is concerned, we assume that, although the system is out of thermal equilibrium, we can express it as a Boltzmann weight ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) ∝ e−βΦ(δ) of an effective potential Φ(δ) accounting for the torque arising due to the particle activity. (This assumption is based on the fact that
neq(δ) ∝ e−βΦ(δ) of an effective potential Φ(δ) accounting for the torque arising due to the particle activity. (This assumption is based on the fact that ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) neq(δ) is the steady-state solution of a one-dimensional (with respect to δ) advection–diffusion equation with zero current. It is known that for such systems the steady-state solution has the form of a Boltzmann weight.41) Since within the present model there are no effective interactions with the interface,
neq(δ) is the steady-state solution of a one-dimensional (with respect to δ) advection–diffusion equation with zero current. It is known that for such systems the steady-state solution has the form of a Boltzmann weight.41) Since within the present model there are no effective interactions with the interface, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) eq(δ) is a constant which can be absorbed into the normalization:
eq(δ) is a constant which can be absorbed into the normalization: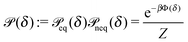
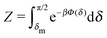 ensures that
ensures that 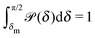 .
.
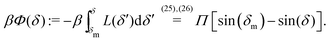
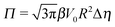 , the reference potential is set to Φ(δm) = 0, and we have accounted for the fact that here we discuss only the case in which δm ≤ δ ≤ π/2 (each of the other three quadrants can be analyzed following the same line of reasoning).
, the reference potential is set to Φ(δm) = 0, and we have accounted for the fact that here we discuss only the case in which δm ≤ δ ≤ π/2 (each of the other three quadrants can be analyzed following the same line of reasoning).
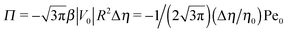 , where Pe0 = |V0|R/DP > 0 is the Péclet number of a Janus particle in a homogeneous fluid of viscosity η0 and DP = kBT/(6πη0R) is the diffusion constant of the Janus particle defined via the Stokes–Einstein relation. The above expression for Π shows that, for Δη > 0 and a Janus particle characterized by V0 < 0, Π is negative. In this case one has Φ(δ > δm) > 0 (eqn (33)) and thus Φ(δ) attains its minimum at δ = δm. This means that the action of the effective torque is consistent with Ωz < 0 (see eqn (25b)) which “drives” the particle towards its steady-state orientation δm, as discussed in Fig. 2(b) (right part of the top right quadrant). Accordingly, in the right part of the top right quadrant, corresponding to Δη > 0 and to the director pointing into the upper fluid, consistent with δm ≤ δ < π/2 and thus χ = min(δ,π − δ) > 0, repulsive interactions (orange arrows) ensure a sustained motility state by providing a torque which tilts the director towards the interface, i.e., which in the present case leads to a decrease of δ towards δm. As one can read off from eqn (33), the characteristics of the Janus particle (see eqn (26)) and of the fluid phases are all encoded in Π. Therefore the above conclusions can be extended directly to the case of attractive interactions between the Janus particle and the product molecules of the catalytic reaction by changing the sign of V0, and hence of Π. Therefore, in the case of attractive interactions (i.e., V0 > 0) and with the cap oriented such that δm ≤ δ < π/2 and χ = δ > 0, Π is negative for Δη < 0 and thus Φ(δ > δm) > 0 (in agreement with the situation illustrated in the left part of the top left quadrant of Fig. 2(b) for which Ux > 0 and Ωz < 0). Therefore, if particles have the catalytic cap in the upper phase, for which sin(δ) > 0, the states with small values of sin(δ), i.e., with the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π < 0. Similarly, if the catalytic cap of the particle is in the lower phase, where sin(δ) < 0, large values of sin(δ), i.e., the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π > 0.
, where Pe0 = |V0|R/DP > 0 is the Péclet number of a Janus particle in a homogeneous fluid of viscosity η0 and DP = kBT/(6πη0R) is the diffusion constant of the Janus particle defined via the Stokes–Einstein relation. The above expression for Π shows that, for Δη > 0 and a Janus particle characterized by V0 < 0, Π is negative. In this case one has Φ(δ > δm) > 0 (eqn (33)) and thus Φ(δ) attains its minimum at δ = δm. This means that the action of the effective torque is consistent with Ωz < 0 (see eqn (25b)) which “drives” the particle towards its steady-state orientation δm, as discussed in Fig. 2(b) (right part of the top right quadrant). Accordingly, in the right part of the top right quadrant, corresponding to Δη > 0 and to the director pointing into the upper fluid, consistent with δm ≤ δ < π/2 and thus χ = min(δ,π − δ) > 0, repulsive interactions (orange arrows) ensure a sustained motility state by providing a torque which tilts the director towards the interface, i.e., which in the present case leads to a decrease of δ towards δm. As one can read off from eqn (33), the characteristics of the Janus particle (see eqn (26)) and of the fluid phases are all encoded in Π. Therefore the above conclusions can be extended directly to the case of attractive interactions between the Janus particle and the product molecules of the catalytic reaction by changing the sign of V0, and hence of Π. Therefore, in the case of attractive interactions (i.e., V0 > 0) and with the cap oriented such that δm ≤ δ < π/2 and χ = δ > 0, Π is negative for Δη < 0 and thus Φ(δ > δm) > 0 (in agreement with the situation illustrated in the left part of the top left quadrant of Fig. 2(b) for which Ux > 0 and Ωz < 0). Therefore, if particles have the catalytic cap in the upper phase, for which sin(δ) > 0, the states with small values of sin(δ), i.e., with the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π < 0. Similarly, if the catalytic cap of the particle is in the lower phase, where sin(δ) < 0, large values of sin(δ), i.e., the catalytic patch being closer to the interface and thus promoting the motile state, are favored if Π > 0.![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) iτi of an active particle trapped at an interface (eqn (29) and (30)) one would like to understand its relation to the persistence length λb =
iτi of an active particle trapped at an interface (eqn (29) and (30)) one would like to understand its relation to the persistence length λb = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) bτb of a similar active particle moving freely in a homogeneous bulk fluid. To this end, we proceed by assuming that the characteristic time τi for the loss of orientation of a Janus particle, trapped at and moving along an interface between two fluids characterized by a (not too large) viscosity contrast Δη ≠ 0, is similar to the corresponding characteristic rotational diffusion time τb for the loss of orientation in a homogeneous bulk fluid of viscosity η0.¶¶ However, since one of the three possible independent rotations of a rigid body would affect the directionality for the particle trapped at the interface only if it is associated with a large fluctuation which would flip the director p with respect to the interface normal (see the discussion of τ⊥ after eqn (29)), it is a reasonable to expect that τi > τb. Furthermore, the argument concerning the weak influence of the rotations associated with τ⊥ suggests τi = ν0τb with ν0 ≃ 3/2 as a good ansatz for the relationship between the two characteristic timescales. Furthermore, we note that eqn (25b) has the form of a projection onto the x-axis (due to the factor cos(δ)) of a velocity (the factor multiplying cos(δ)) oriented along the director p. Thus in the limit Δη → 0 the latter factor can be identified with the velocity
bτb of a similar active particle moving freely in a homogeneous bulk fluid. To this end, we proceed by assuming that the characteristic time τi for the loss of orientation of a Janus particle, trapped at and moving along an interface between two fluids characterized by a (not too large) viscosity contrast Δη ≠ 0, is similar to the corresponding characteristic rotational diffusion time τb for the loss of orientation in a homogeneous bulk fluid of viscosity η0.¶¶ However, since one of the three possible independent rotations of a rigid body would affect the directionality for the particle trapped at the interface only if it is associated with a large fluctuation which would flip the director p with respect to the interface normal (see the discussion of τ⊥ after eqn (29)), it is a reasonable to expect that τi > τb. Furthermore, the argument concerning the weak influence of the rotations associated with τ⊥ suggests τi = ν0τb with ν0 ≃ 3/2 as a good ansatz for the relationship between the two characteristic timescales. Furthermore, we note that eqn (25b) has the form of a projection onto the x-axis (due to the factor cos(δ)) of a velocity (the factor multiplying cos(δ)) oriented along the director p. Thus in the limit Δη → 0 the latter factor can be identified with the velocity ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) b of the active particle moving in a homogeneous bulk fluid of viscosity η0. With ς(ε → 0) = 1 this renders
b of the active particle moving in a homogeneous bulk fluid of viscosity η0. With ς(ε → 0) = 1 this renders 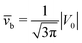 .
.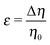 (eqn (25a)), one obtains
(eqn (25a)), one obtains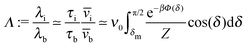
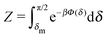 and eqn (33) into eqn (34), the dependencies of Λ on δm and on Π can be calculated. For the choice ν0 = 3/2 these are shown in Fig. 3(a) and (b), respectively. (We recall that we have focused on the case of the catalytic cap exposed to the upper phase.) As shown in Fig. 3, for sufficiently negative values of Π the persistence length of a Janus particle moving at a liquid–fluid interface may be larger than the one in the corresponding bulk case, i.e., Λ > 1. According to the discussion in the previous paragraphs, the case of Π > 0 with the catalytic cap exposed to the upper phase corresponds to either Δη > 0 and repulsive interactions or Δη > 0 and attractive interactions, i.e., the cases for which sustained motility emerges (see Fig. 2(b)). On the other hand, we have noted that for a given type of interaction (i.e., a given sign of V0) and a given viscosity contrast Δη, the amplitude Π of the potential Φ changes sign if the catalytic cap is exposed to the lower phase, i.e., for δ > π, relative to the case of the catalytic cap being exposed to the upper phase. Therefore, these corresponding dependencies on δm and on Π are given by the curves in Fig. 3(a) and (b) but with the opposite sign of Π and with δm → −δm. Consequently, one infers that in this case one has Λ > 1 for sufficiently large positive values of Π. Thus also in the case that the cap is immersed in the lower phase the persistence length at the interface may be enhanced relative to the bulk one for those states in which sustained motility emerges. In summary, this implies that in all cases of sustained motility (i.e., the system corresponds to any of the cases shown in Fig. 2(b)) the particle trapped at the interface exhibits an enhanced persistence length for sufficiently large values of |Π|.
and eqn (33) into eqn (34), the dependencies of Λ on δm and on Π can be calculated. For the choice ν0 = 3/2 these are shown in Fig. 3(a) and (b), respectively. (We recall that we have focused on the case of the catalytic cap exposed to the upper phase.) As shown in Fig. 3, for sufficiently negative values of Π the persistence length of a Janus particle moving at a liquid–fluid interface may be larger than the one in the corresponding bulk case, i.e., Λ > 1. According to the discussion in the previous paragraphs, the case of Π > 0 with the catalytic cap exposed to the upper phase corresponds to either Δη > 0 and repulsive interactions or Δη > 0 and attractive interactions, i.e., the cases for which sustained motility emerges (see Fig. 2(b)). On the other hand, we have noted that for a given type of interaction (i.e., a given sign of V0) and a given viscosity contrast Δη, the amplitude Π of the potential Φ changes sign if the catalytic cap is exposed to the lower phase, i.e., for δ > π, relative to the case of the catalytic cap being exposed to the upper phase. Therefore, these corresponding dependencies on δm and on Π are given by the curves in Fig. 3(a) and (b) but with the opposite sign of Π and with δm → −δm. Consequently, one infers that in this case one has Λ > 1 for sufficiently large positive values of Π. Thus also in the case that the cap is immersed in the lower phase the persistence length at the interface may be enhanced relative to the bulk one for those states in which sustained motility emerges. In summary, this implies that in all cases of sustained motility (i.e., the system corresponds to any of the cases shown in Fig. 2(b)) the particle trapped at the interface exhibits an enhanced persistence length for sufficiently large values of |Π|.

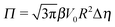 . The angle δm is the opening angle under which the catalytic cap is seen from the center of the particle when the cap touches the interface (Fig. 1(b)) and thus measures its size. (b) Approximate expression for Λ as a function of −Π > 0 for δm = 0, π/4, and π/3. Although the value δm = 0 is unphysical, because in this case the catalytic cap reduces to a point, the corresponding curve represents the limiting case for which Λ attains its maximal values.
. The angle δm is the opening angle under which the catalytic cap is seen from the center of the particle when the cap touches the interface (Fig. 1(b)) and thus measures its size. (b) Approximate expression for Λ as a function of −Π > 0 for δm = 0, π/4, and π/3. Although the value δm = 0 is unphysical, because in this case the catalytic cap reduces to a point, the corresponding curve represents the limiting case for which Λ attains its maximal values.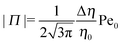 . Therefore, for
. Therefore, for 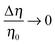 the onset of saturation at |Π| ≈ 5 requires, even for very small caps, i.e., δm → 0, Péclet numbers Pe0 ≃ 30 × (Δη/η0)−1 much larger than the typical values Pe0 ≃ 10 for Janus particles in a homogeneous bulk fluid. If, however, the viscosity contrast is high, the required corresponding Pe0 numbers are significantly smaller. For example, for the water–air interface the viscosity of air is negligible so that Δη = −2η0 which implies |Π| ≃ ⅓Pe0. In such a situation, as well as for other liquid–fluid interfaces characterized by high viscosity contrasts, large values of |Π| are encountered already for typical values of Pe0 and the persistence length at the interface may be enhanced relative to its bulk value, i.e., Λ > 1. As shown in Fig. 3, this effect is particularly pronounced for small catalytic caps (i.e., δm small).
the onset of saturation at |Π| ≈ 5 requires, even for very small caps, i.e., δm → 0, Péclet numbers Pe0 ≃ 30 × (Δη/η0)−1 much larger than the typical values Pe0 ≃ 10 for Janus particles in a homogeneous bulk fluid. If, however, the viscosity contrast is high, the required corresponding Pe0 numbers are significantly smaller. For example, for the water–air interface the viscosity of air is negligible so that Δη = −2η0 which implies |Π| ≃ ⅓Pe0. In such a situation, as well as for other liquid–fluid interfaces characterized by high viscosity contrasts, large values of |Π| are encountered already for typical values of Pe0 and the persistence length at the interface may be enhanced relative to its bulk value, i.e., Λ > 1. As shown in Fig. 3, this effect is particularly pronounced for small catalytic caps (i.e., δm small).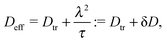
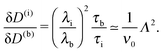
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i2τi2)/(τiDP) ≫ 1 (see the definition of δD(i) above and eqn (29)). By using
i2τi2)/(τiDP) ≫ 1 (see the definition of δD(i) above and eqn (29)). By using ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i = Λ
i = Λ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) b/ν0 (eqn (34)),
b/ν0 (eqn (34)), 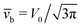 , Pe0 = |V0|R/DP, and τi/τb = ν0, and by taking τb = 1/D(rot)P, where D(rot)P = 4DP/(3R2) is the rotational diffusion constant of the particle in a homogeneous bulk fluid,40 for ν0 = 3/2 and by using eqn (34)–(36) the condition δD(i)/DP ≫ 1 translates into the condition Pe0 ≫ 4.3/Λ for the Péclet number of the particle.
, Pe0 = |V0|R/DP, and τi/τb = ν0, and by taking τb = 1/D(rot)P, where D(rot)P = 4DP/(3R2) is the rotational diffusion constant of the particle in a homogeneous bulk fluid,40 for ν0 = 3/2 and by using eqn (34)–(36) the condition δD(i)/DP ≫ 1 translates into the condition Pe0 ≫ 4.3/Λ for the Péclet number of the particle.
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (see eqn (15)), the reaction rate Q per area, the inverse mean viscosity η0 and the inverse diffusivity D0 of the reaction product. The angular velocity experienced by the particle of radius R is proportional to V0/R and to the viscosity contrast Δη.
(see eqn (15)), the reaction rate Q per area, the inverse mean viscosity η0 and the inverse diffusivity D0 of the reaction product. The angular velocity experienced by the particle of radius R is proportional to V0/R and to the viscosity contrast Δη.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)
sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ), y = r
cos(ϕ), y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ)
sin(θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ), and z = r
sin(ϕ), and z = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ). (Note that these are defined in the unprimed coordinate system which, although exhibiting here the same origin as the primed (co-moving) one, has different orientations of the axes as compared with the primed one. The unprimed coordinate system offers a less cumbersome parametrization of the location of the interface as compared with the primed coordinate system.) We start with deriving eqn (9).
cos(θ). (Note that these are defined in the unprimed coordinate system which, although exhibiting here the same origin as the primed (co-moving) one, has different orientations of the axes as compared with the primed one. The unprimed coordinate system offers a less cumbersome parametrization of the location of the interface as compared with the primed coordinate system.) We start with deriving eqn (9).
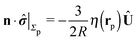
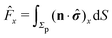
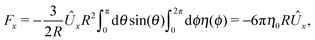
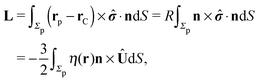
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ) one obtains
sin(ϕ) one obtains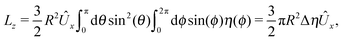
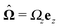 )
)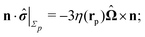
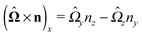 and recall that by definition of the dual problem “2” only the component
and recall that by definition of the dual problem “2” only the component 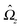 of the angular velocity is non-zero. Thus we obtain
of the angular velocity is non-zero. Thus we obtain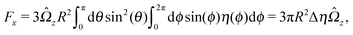
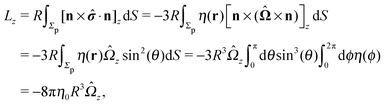
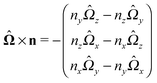
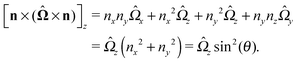
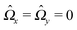 .
.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)
sin(θ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕ′), y′ = r′
cos(ϕ′), y′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(θ′)
sin(θ′)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ϕ′), z′ = r′
sin(ϕ′), z′ = r′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ′)
cos(θ′)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m(θ′,ϕ′):
m(θ′,ϕ′):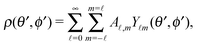
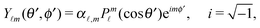
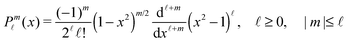
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and order m with
and order m with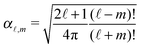
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) m, Pm
m, Pm![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , and α
, and α![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,m, which will be needed below:
,m, which will be needed below: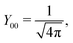

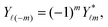
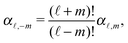
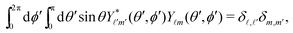
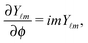
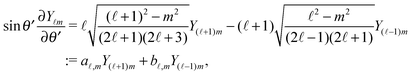
 ) (eqn (20)) one obtains
) (eqn (20)) one obtains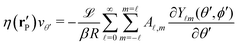
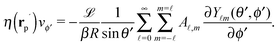
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + sin
ex′ + sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′ + cos
ey′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ez′
ez′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + cos
ex′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′ − sin
ey′ − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′
θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ez′
ez′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ex′ + cos
ex′ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ′
ϕ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ey′
ey′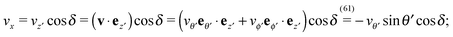
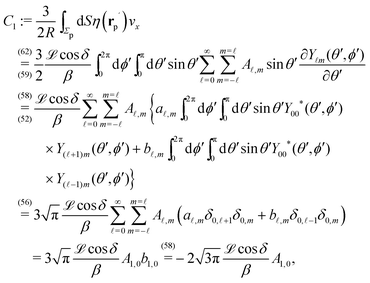
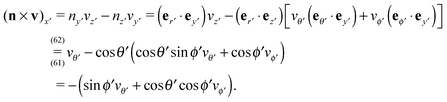
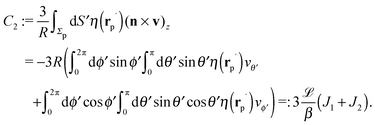
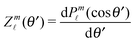
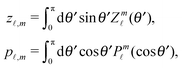
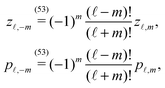
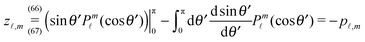
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) and
) and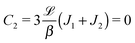 , which verifies eqn (22).
, which verifies eqn (22).
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2 as well as the interface Γ could be closed along the Ox direction by assuming periodic boundary conditions at |x| → ∞; alternatively, one may choose for the surface at infinity, which is closing the domains
2 as well as the interface Γ could be closed along the Ox direction by assuming periodic boundary conditions at |x| → ∞; alternatively, one may choose for the surface at infinity, which is closing the domains ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 1 and
1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) 2, a spherical one, centered at C and with a radius R∞ → ∞.
2, a spherical one, centered at C and with a radius R∞ → ∞.![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) i for the same particle moving in the positive direction would be
i for the same particle moving in the positive direction would be 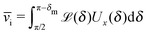 ; see the left part of the top right quadrant of Fig. 2(b). Here
; see the left part of the top right quadrant of Fig. 2(b). Here ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is the distribution of the angle δ ∈ (π/2,π − δm).
is the distribution of the angle δ ∈ (π/2,π − δm).