Hierarchically nanoporous nickel-based actuators with giant reversible strain and ultrahigh work density†
Qingguo
Bai
a,
Yan
Wang
b,
Jie
Zhang
a,
Yi
Ding
c,
Zhangquan
Peng
d and
Zhonghua
Zhang
*a
aKey Laboratory for Liquid–Solid Structural Evolution and Processing of Materials (Ministry of Education), School of Materials Science and Engineering, Shandong University, 17923 Jingshi Road, Jinan 250061, P. R. China. E-mail: zh_zhang@sdu.edu.cn
bSchool of Materials Science and Engineering, University of Jinan, 336 West Road of Nan Xinzhuang, Jinan 250022, P. R. China
cSchool of Materials Science and Engineering, Tianjin University of Technology, 391 Binshui Xidao, Xiqing District, Tianjin 300384, P. R. China
dState Key Laboratory of Electroanalytical Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Renmin Road 5625, Changchun 130022, P. R. China
First published on 27th November 2015
Abstract
Metallic actuators (metallic muscles) have attracted a great deal of interest because of their potential advantages over piezoelectric ceramics and conducting polymers. However, to develop high performance actuators using earth's abundant and inexpensive metallic elements is a formidable challenge so far. Here, we report the design and fabrication of nickel-based actuators with low material cost (<1/2000 of gold), which demonstrate an unprecedented performance including giant reversible strain (up to 2%), ultrahigh work density (11.76 MJ m−3, the highest among the known actuator materials), and long cycle life (70% strain retention after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles). This outstanding performance of the nickel-based actuators originates from their unique hierarchically nanoporous structure and the oxide-covered nature of the Ni surface.
000 cycles). This outstanding performance of the nickel-based actuators originates from their unique hierarchically nanoporous structure and the oxide-covered nature of the Ni surface.
Actuator materials can directly convert electrical or chemical energy into a mechanical response through changes in material dimensions, and are often called “artificial muscles” owing to their similarities to biological muscles. The best known piezoelectric and electrostrictive ceramics with high stiffness and strength have low hysteresis and a fast response, while their applications are restricted by high operating voltages, low strain amplitude of 0.1–0.2%, and low work density per cycle.1 Conducting polymers show extraordinarily large strain (up to 215%2), but function at only high voltages (tens to hundreds of MV m−1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) , ref. 2 and 3). Moreover, they have low stiffness and strength, and suffer from slow Faradaic processes associated with dopant diffusion and structural changes.4,5 Shape memory alloys (SMAs) generate high strain and mechanical force but are often correlated with large hysteresis and very slow speed.6 Furthermore, the actuation of SMAs is indirect and requires the conversion of electrical energy to thermal energy to cause actuation. Various carbon nanomaterials also show electrochemical actuation performance, including carbon nanotubes (CNTs),5,7 graphene8 and nanoporous carbon.9 However, CNTs and graphene arrays/films are poorly suitable for loading in compression, which limits their practical applications.
, ref. 2 and 3). Moreover, they have low stiffness and strength, and suffer from slow Faradaic processes associated with dopant diffusion and structural changes.4,5 Shape memory alloys (SMAs) generate high strain and mechanical force but are often correlated with large hysteresis and very slow speed.6 Furthermore, the actuation of SMAs is indirect and requires the conversion of electrical energy to thermal energy to cause actuation. Various carbon nanomaterials also show electrochemical actuation performance, including carbon nanotubes (CNTs),5,7 graphene8 and nanoporous carbon.9 However, CNTs and graphene arrays/films are poorly suitable for loading in compression, which limits their practical applications.
Recently, macroscopic and reversible strain effects have been observed for nanoporous (np-) metals/alloys with high surface-area-to-volume ratios in a chemical10 or electrochemical environment.11–21 These materials achieve their functionality as actuators by exploiting the variation of surface stress22 for inducing large compensating stress and strain in the bulk of their solid skeletons.23 Nanoporous metals/alloys are also called metallic muscles,24 and represent a kind of novel actuation materials with enhanced strain amplitude compared to piezoelectric ceramics.16 Moreover, nanoporous metallic actuators can function at low operating voltages (a few volts) and are much stiffer than conducting polymers. Nanoporous metals/alloys could be produced by dealloying.25,26 However, whether surface stress-driven actuation using nanoporous metals will develop into an economically viable technology strongly depends upon material cost, efficiency and long-term stability. To date, the fabrication of metallic actuators has been limited to noble metals, including Pt,11,15 Au,12–14,17,18 Au–Pt,16 Pd19 and Ag.20 From the viewpoint of load bearing, bulk materials with sufficient strength and stiffness are also crucial for applications of actuators. It is a great challenge to develop bulk nanoporous metallic actuators based upon earth-abundant elements like Ni, Co, Cu, and so forth. In addition, the long-term stability issue has never been achieved for metallic actuators.
Here, we devise a ‘localized dealloying’ strategy to dealloy a hybrid-phase alloy, which is composed of several phases with different activities, leading to the production of high-quality bulk nanoporous nickel (np-Ni) rods with variable lengths/diameters (up to the scale of centimeters). These np-Ni samples exhibit a hierarchically nanoporous structure composed of nested micron-sized and nano-sized channels. Most importantly, these np-Ni rods with quite low material cost show state-of-the-art figures of merit of metallic actuators (giant reversible strain of up to 2%, ultrahigh strain energy density of 11.76 MJ m−3 and excellent stability over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles) in alkaline media. And the outstanding actuation performance of np-Ni originates from its unique hierarchically nanoporous structure and the oxide-covered nature of the Ni surface.
000 cycles) in alkaline media. And the outstanding actuation performance of np-Ni originates from its unique hierarchically nanoporous structure and the oxide-covered nature of the Ni surface.
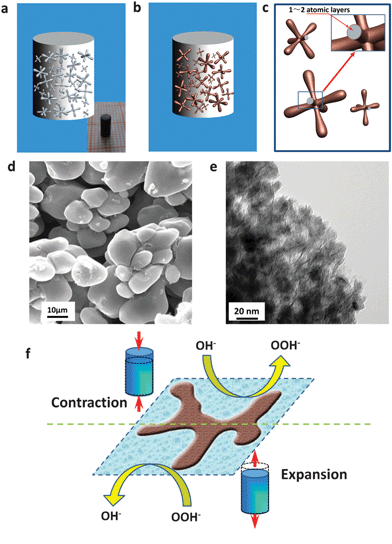
The design of hybrid-phase precursor alloys and the localized dealloying are schematically presented in Fig. S1 (ESI†). Different from homogeneous solid solution alloys (like Au–Ag), hybrid-phase alloys (here, Al–Ni) are comprised of two kinds of phases (less noble phase and more noble phase) with different activities. Moreover, the less noble phase (for example, α-Al) can be completely etched away in alkaline electrolytes leaving large-sized channels, which allow the rapid penetration of electrolytes into the inner part of the bulk samples and further make the dealloying be localized around these channels. Simultaneously, the more noble phase (for example, Al3Ni/Al3Ni2) can be dealloyed to form a nanoporous structure. Scanning electron microscopy (SEM), energy-dispersive X-ray analysis (EDX) and X-ray diffraction (XRD) confirm that the Al–Ni alloys with 20–31.5 at% Ni have this hybrid-phase microstructure (α-Al and Al3Ni2/Al3Ni) and are suitable for the proposed dealloying strategy, Fig. S2 (ESI†). As expected, high quality crack-free np-Ni rods with different diameters and lengths were fabricated through dealloying of the Al–Ni precursors in a 6 M KOH solution (inset of Fig. 1a, bottom-left inset of Fig. 2a, and Fig. S3, ESI†). The np-Ni rods look black due to their nanostructures, which differ from the bulk Ni. Furthermore, the size of these np-Ni rods can reach up to centimeters, indicating the advantage of the present localized dealloying strategy.
More importantly, the dealloying of such hybrid-phase Al–Ni alloys leads to the formation of np-Ni rods with a hierarchically porous structure (Fig. 1 and Fig. S4, ESI†). The low-magnification SEM images clearly show that the np-Ni rods are comprised of dendrite-like blocks with continuous large-sized channels (which originate from the etching of the less noble Al phase) in between, Fig. 1d and Fig. S4b (ESI†). The TEM observation verifies that the dendrite-like blocks are nanoporous and have nanopores of 10–20 nm, which come from the dealloying of the Al3Ni2/Al3Ni phases, Fig. 1e and Fig. S4c (ESI†). The electron diffraction (inset of Fig. S4c, ESI†) and XRD (Fig. S4d, ESI†) confirm that the np-Ni rods are composed of a single face centered cubic (fcc) Ni phase. In addition, the surface of the nanopores in these np-Ni rods could be covered with nickel oxide (NiO) of 1–2 atomic layers through further electrochemical treatment (Fig. 1b, c and Fig. S5, ESI†). These oxide-decorated np-Ni rods show OH− adsorption/desorption-induced reversible strain in alkaline media (Fig. 1f). As NiO is an electrode material for supercapacitors, the adsorption/desorption process of OH− ions corresponds to the Faradaic reaction on the surface of NiO according to the following equation: NiO + OH− ⇆ NiOOH + e−.21 The detail will be addressed in the following section.
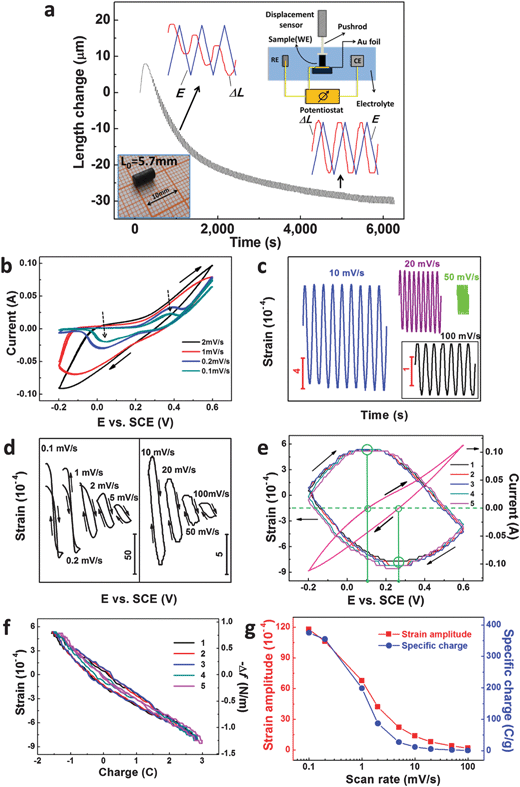
The electrochemical actuation properties of our np-Ni samples were measured in a 5 M NaOH aqueous solution through a displacement sensor in combination with a potentiostat, and the apparatus is schematically shown in the top-right inset of Fig. 2a. The as-prepared np-Ni rod was directly used as the working electrode (WE). Fig. 2a shows the length change (ΔL) of the np-Ni rod as a function of time during successive CV scans (−0.2–0.6 V vs. SCE). On the whole, the ΔL curve gradually decreases and finally levels off with increasing CV cycles (also see Fig. S5a, ESI†). This irreversible shrinkage may be associated with the creep deformation of the np-Ni samples.16 And this phenomenon was also observed in nanoporous Pt11 and Au–Pt alloys.16 After initial tens of CV scans, an obvious reversible strain (ΔL/L0) is superimposed to the irreversible change and is further enhanced by the potential cycles (Fig. 2a and Fig. S5a, ESI†). This process is accompanied by the formation of NiO on the ligament surface, which is documented by the evolution of cyclic voltammograms (CVs, Fig. S5b–d, ESI†). Moreover, the reversible strain amplitude tends towards stability after dozens of CV cycles. Meanwhile, the CVs also stabilize (Fig. S5d, ESI†). In addition, the reversible ΔL is not in phase with the potential (E) change (top-left and bottom-right insets of Fig. 2a), indicating the nature of the oxide-covered surface of ligaments in our np-Ni samples.14–16 For the oxide-covered np-Au,14 np-Pt15 and np-AuPt,16 all the reversible strain Δl/l is not in phase with the potential change, while the reversible strain of these samples with the clean surface is in phase with the potential change. The following shows the actuation data of our np-Ni samples after the stabilization treatment.
We firstly consider the effect of the potential scan rate, which has a significant influence on the profile of the CVs (Fig. 2b and Fig. S6, ESI†). For each scan rate, three successive CVs are presented and all almost overlap. At low scan rates (0.1 and 0.2 mV s−1), OH− adsorption (∼0.38 V vs. SCE) and desorption (∼0.03 V vs. SCE) peaks can be well distinguished (as marked by dotted arrows in Fig. 2b), corresponding to the reactions NiO + OH− → NiOOH + e− and NiOOH + e− → NiO + OH−, respectively. However, no obvious OH− adsorption/desorption peaks appear at high scan rates of above 1 mV s−1. At different scan rates, the corresponding strain–time plots are given in Fig. 2c and Fig. S7 (ESI†). The reversible strain curves show excellent stability with the potential cycles and almost no irreversible parts are observed, especially at high scan rates. Fig. 2d shows the reversible strain recorded simultaneously with the applied potentials. Clearly, there exists a negative correlation between the strain and the potential (also see Fig. S7a, ESI†), further verifying the nature of the oxide-covered surface of the np-Ni samples. Despite the non-noble nature of Ni, it is interesting to note that our results are in agreement with previous reports of noble metals/alloys (for example, np-Au and np-Au–Pt) with an oxygen-covered surface.14–16 Furthermore, there is obvious hysteresis at scan rates of ≥1 mV s−1, which is a typical feature of nanoporous metallic actuators.11,14–16 This is due to the fact that the nanopores in our np-Ni samples limit the diffusion kinetics of the involved species (for example, OH−). And the hysteresis is negligible at very low scan rates of 0.1 and 0.2 mV s−1 (Fig. 2d), because the time is long enough for the transfer of the involved species through these nanopores. We can clearly see the variation of the reversible strain of np-Ni with the potential scan, and the expansion–contraction (or contraction–expansion) converts at the zero-charge potential (Fig. 2e). The strain–charge (transferred charge, ΔQ) plots show an obvious negative correlation (Fig. 2f and Fig. S8, ESI†), which is different from nanoporous metals/alloys with a clean surface.11,14–16 And we can see an approximate linear relation between both quantities despite more or less hysteresis. Fig. 2g shows the scan rate dependence of the reversible strain. The lower the scan rate, the larger the reversible strain is. Similar phenomena were also observed for different potential windows (Fig. S9, ESI†), as well as the np-Ni rods with different lengths/diameters (Fig. S10, ESI†). It is noticeable that the strain amplitude exceeds 1% at the low scan rates. Additionally, the involved specific charge also shows a similar correlation with the scan rate. This suggests that the strain amplitude of our np-Ni samples is directly related to the involved specific charge during the CV processes, and the correlation between the strain amplitude and the specific charge will be discussed in the following section.
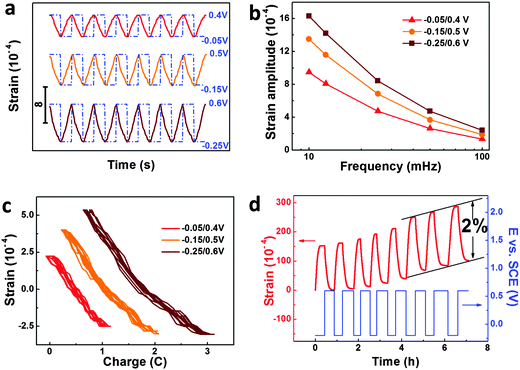
The response to the SWP (or potential jump) is an important indicator of actuators. Fig. 3a shows the reversible strain response of our np-Ni samples to the SWP stimuli with different windows (−0.05–0.4, −0.15–0.5 and −0.25–0.6 V vs. SCE) at the frequency of 25 mHz. For each potential window, the strain response exhibits excellent stability. Further, the strain amplitude increases with the enlarging of the potential window or the decrease of the frequency (Fig. 3b and Fig. S11, ESI†). Due to the response time limit of the displacement sensor, the actuation measurement of our np-Ni samples was confined to the high frequency of 100 mHz. Considering their bulk sizes and nanopores, the np-Ni rods perform well in response to the potential jump, which is even comparable to nanoporous carbon hybrid actuators.9 The reversible strain-charge curves give a good negative linear relationship, and almost no hysteresis could be observed (Fig. 3c). In addition, it is astonishing that the reversible strain amplitude of our np-Ni samples can be modulated up to 2% (Fig. 3d). This value is much higher than the state-of-the-art level (1.3% for np-Au–Pt alloy16) of nanoporous metallic actuators under similar test conditions. And the concomitant irreversible length change may be associated with the surface stress-induced plastic deformation which has been directly demonstrated by atomistic simulation study.27 More importantly, the strain stroke reaches 114.5 μm for the np-Ni rod with the length of 5.7 mm (Fig. S12, ESI†). Eventually, the giant strain strokes could be easily snapped by a digital microscope camera (Fig. S13 and Flash S1, ESI†).
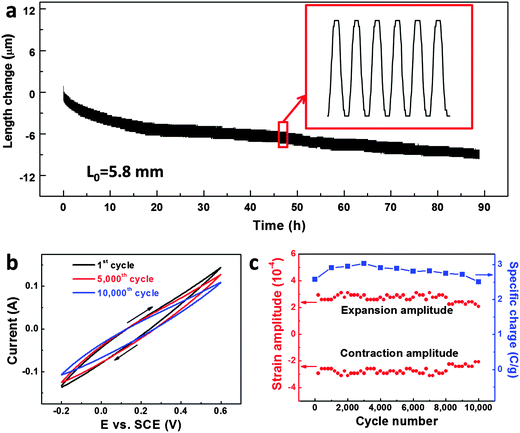
Stability is another important issue for practical applications of metallic actuators,10 but has received little attention in the past. For the first time, here we address this issue of our np-Ni actuator through CV coupled with strain measurements (Fig. 4 and Fig. S14, ESI†). Fig. 4a presents the length change of the np-Ni sample versus time during successive 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CV cycles in 5 M NaOH solution at a scan rate of 50 mV s−1. The sample periodically expanded and contracted together with the potential cycles. Although an irreversible length change could be observed, the superimposed reversible strain with comparable amplitude (highlighted by an enlarged panel) indicates the excellent long-term stability of our np-Ni samples. Fig. 4b illustrates the selected CVs (1st, 5000th and 10
000 CV cycles in 5 M NaOH solution at a scan rate of 50 mV s−1. The sample periodically expanded and contracted together with the potential cycles. Although an irreversible length change could be observed, the superimposed reversible strain with comparable amplitude (highlighted by an enlarged panel) indicates the excellent long-term stability of our np-Ni samples. Fig. 4b illustrates the selected CVs (1st, 5000th and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000th) with cycles of up to 10
000th) with cycles of up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The profile of the CVs changes a little and the involved specific charge slightly decreases from 2.58 C g−1 to 2.51 C g−1 (retention of over 97% after 10
000. The profile of the CVs changes a little and the involved specific charge slightly decreases from 2.58 C g−1 to 2.51 C g−1 (retention of over 97% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, Fig. 4c). By and large, the expansion/contraction amplitudes (absolute values) wave between 2.4 × 10−4 and 3.0 × 10−4 (Fig. 4c). Even if we consider the smallest value of 2.1 × 10−4, the reversible strain amplitude retains over 70% after 10
000 cycles, Fig. 4c). By and large, the expansion/contraction amplitudes (absolute values) wave between 2.4 × 10−4 and 3.0 × 10−4 (Fig. 4c). Even if we consider the smallest value of 2.1 × 10−4, the reversible strain amplitude retains over 70% after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles, indicating the excellent actuation stability of our np-Ni.
000 cycles, indicating the excellent actuation stability of our np-Ni.
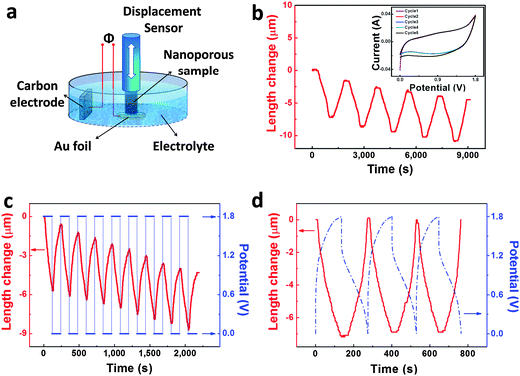
Normally, actuators give response to two-position input signals. Thus we constructed a model actuator with two positions (electrodes) using our np-Ni samples and Ni-foam supported carbon (Fig. 5a). The actuator reversibly contracts and expands with the potentials cycling between 0 and 1.8 V (Fig. 5b). The CVs almost overlap for five successive cycles (inset of Fig. 5b). The actuator also shows reversible length changes when the potential jumps to and fro between 1.8 and 0 V (Fig. 5c). In addition, the actuator could well respond to galvanostatic charge–discharge. The actuator correspondingly contracts when we charge it from 0 to 1.8 V, and then expands during the subsequent discharge process (Fig. 5d). Moreover, the reversible expansion/contraction variation of the actuator is out of phase with the charge–discharge process.
Generally, it is believed that the strain effect in nanoporous metals is caused by charge-induced changes in surface stress through injection of electronic charge in the space charge region at the metal/electrolyte interface.11–20 The strain of metallic actuators will increase with increasing charge per electrode weight because capacitance is the derivative of stored charge with respect to the applied potential.28 Thus it is crucial to obtain giant specific capacitance of electrode materials in order to achieve high strain of actuators at low voltages.11,24 The CVs of our np-Ni samples show a typical pseudo-capacitive behavior in the applied potential region (Fig. 2b), which is related to the reversible OH adsorption/desorption reaction: NiO + OH− ↔ NiOOH + e− (Fig. 1f).21,29 Considering the whole mass of the np-Ni samples, the calculated specific capacitance ranges from 0.75 F g−1 to 470 F g−1 for different scan rates (100–0.1 mV s−1). The specific capacitance is as high as 470 F g−1 for the scan rate of 0.1 mV s−1, which well explains the giant strain amplitude of our np-Ni actuator.
Then we discuss the stress-charge coefficients (ζ) of our np-Ni samples. It is known that the stress-charge coefficient could be related to the measured quantities, the macroscopic strain (ΔL/L0), the transferred charge (ΔQ) and the sample mass m via the equation:14,15
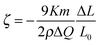 | (1) |
Furthermore, the charge-induced change in surface stress could be estimated through the equation 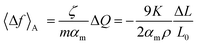 .15 Here, αm is the specific surface area of the actuator materials and 〈
.15 Here, αm is the specific surface area of the actuator materials and 〈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉A represents the areal average over the surfaces.11 For our np-Ni samples, the variation of surface stress versus charge shows an approximate linear relationship (Fig. 2f and Fig. S8, ESI†). The maximum variations in Δf and ΔQ are listed in Table S2 (ESI†) corresponding to different scan rates. At 1 mV s−1 the total transferred charge is as high as 26.3 C, and the stress change amplitude reaches up to 10.0 N m−1 which is about three times those (∼3 N m−1;11 3.35 N m−1, ref. 15) of np-Pt. Additionally, it is interesting to note that the maximum variations in surface stress show a good linear correlation with the total transferred charge (Fig. S15, ESI†). The lower the potential scan rate, the more the transferred charge (or specific capacitance), the larger reversible strain (stress) could be triggered in the np-Ni actuators. This further confirms that a higher maximum stress/strain of nanoporous metallic actuators can be achieved by exploiting the increased capacitance in the specific adsorption region.11
〉A represents the areal average over the surfaces.11 For our np-Ni samples, the variation of surface stress versus charge shows an approximate linear relationship (Fig. 2f and Fig. S8, ESI†). The maximum variations in Δf and ΔQ are listed in Table S2 (ESI†) corresponding to different scan rates. At 1 mV s−1 the total transferred charge is as high as 26.3 C, and the stress change amplitude reaches up to 10.0 N m−1 which is about three times those (∼3 N m−1;11 3.35 N m−1, ref. 15) of np-Pt. Additionally, it is interesting to note that the maximum variations in surface stress show a good linear correlation with the total transferred charge (Fig. S15, ESI†). The lower the potential scan rate, the more the transferred charge (or specific capacitance), the larger reversible strain (stress) could be triggered in the np-Ni actuators. This further confirms that a higher maximum stress/strain of nanoporous metallic actuators can be achieved by exploiting the increased capacitance in the specific adsorption region.11
As an important figure of merit for actuator materials, we now inspect the strain energy density (or work density, w) of our np-Ni samples. If we assume that the actuator behaves like a linear elastic solid, the work density of actuator materials is typically specified in terms of a volume-specific strain energy density which is given by wV = 1/2Yeffεmax2,11,16 where Yeff is the effective macroscopic Young's modulus and εmax is the maximum strain amplitude. And the mass-specific strain energy density is related to the mean mass density ρ of the porous material by wM = wV/ρ.11,16 Since the key parameters such as elastic constant or yield strength are still unavailable or controversial so far,30 we thus treat our np-Ni as an open-cell foam material and the effective Young's modulus can be evaluated by Yeff = Ys(ρnp/ρs)2,31 where Ys is the Young's modulus of solid nickel, and ρnp/ρs is the relative density (φ) of np-Ni. Taking Ys = 218 GPa32 and φ = 0.3 (see the ESI†), we calculated Yeff as 19.6 GPa for our np-Ni samples. Besides, the maximum volumetric strain amplitude of our np-Ni samples can reach up to 6% (ΔV/V0 = 3ΔL/L0) since the surface stress-driven macroscopic strain is isotropic in nanoporous metallic samples.11,16 The work density parameters wV and wM were thus determined to be 11.76 MJ m−3 (linear value: 3.92 MJ m−3) and 4404 J kg−1 (linear value: 1468 J kg−1) respectively (Table 1). We notice that the work density of our np-Ni samples is about 300 times that of skeletal muscles (∼40 kJ m−3).33
| Materials | Y (GPa) | ε max (10−4) | w V (MJ m−3) | w M (J kg−1) | U/V |
|---|---|---|---|---|---|
| Skeletal muscle33 | 0.01–0.06 | >4000 | 0.04 | 40 | — |
| Piezoceramic1,2 | 64 | 20 | 0.13 | 4.25 | 100 |
| Electrostrictor polymer3 | 1.1 | 450 | 1.1 | 500 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| Dielectric elastomer (VHB)2 | 0.001–0.003 | >30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3.4 | — | 1000 |
| Carbon nanotube actuator5,7 | 640 | 50 | 8 | — | ∼2 |
| Nanoporous carbon9 | 0.28 | 220 | — | 81 | 2 |
| np Au–Pt16 | 25 | 130 | 6 | 1200 | ∼1 |
| np Nickel (present work) | 19.6 | 200 | 11.76 | 4404 | ∼1 |
For practical applications of metallic actuators, several factors should be taken into consideration, including strain amplitude, work density, strain stroke, operating voltage, Young's modulus, and material cost. We summarize these parameters of the known nanoporous metal actuators in Table S3 (also in Fig. S16, ESI†). One can see that our np-Ni samples show the state-of-the-art figures of merit among all metallic actuators. Furthermore, the np-Ni samples exhibit excellent actuation stability and the reversible strain amplitude retains over 70% of its value even after 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles (Fig. 4). In addition, the cost is an important issue for the commercialization of metallic actuators. Previous studies on nanoporous metal actuators were mainly limited to expensive materials like Au, and Pt.11–18 In comparison, Ni is significantly cheaper and more abundant than Au/Pt. Biener et al.10 have argued that whether surface-chemistry-driven actuation will develop into an economically viable technology will strongly depend on material cost, efficiency and long-term stability. Thus the present np-Ni may grow into practical actuators.
000 cycles (Fig. 4). In addition, the cost is an important issue for the commercialization of metallic actuators. Previous studies on nanoporous metal actuators were mainly limited to expensive materials like Au, and Pt.11–18 In comparison, Ni is significantly cheaper and more abundant than Au/Pt. Biener et al.10 have argued that whether surface-chemistry-driven actuation will develop into an economically viable technology will strongly depend on material cost, efficiency and long-term stability. Thus the present np-Ni may grow into practical actuators.
We now compare our np-Ni with other actuator materials (Table 1 and Fig. S17, ESI†). Firstly, the modulus of np-Ni is on the same order of magnitude as piezoceramics, but much stiffer than electrostrictor polymers, dielectric elastomers (VHB) and skeletal muscles. Secondly, the np-Ni can perform with a reversible strain amplitude of 2% and a stroke of over 100 μm, which are much higher than those of piezoceramics and CNTs. Thirdly, our np-Ni actuators can be operated at an applied potential of ∼1 V, which is significantly smaller than the voltage (∼100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 V) needed for piezoceramics, electrostrictor polymers and dielectric elastomers (VHB). The last and most important indicator is the work density. The volume-specific strain energy density of our np-Ni reaches the highest value (11.76 MJ m−3) among all the known actuator materials (Table 1). Overall, our np-Ni actuators are quite promising considering their high stiffness, low operating voltage, large strain amplitude/stroke, ultrahigh work density, excellent stability and low material cost.
000 V) needed for piezoceramics, electrostrictor polymers and dielectric elastomers (VHB). The last and most important indicator is the work density. The volume-specific strain energy density of our np-Ni reaches the highest value (11.76 MJ m−3) among all the known actuator materials (Table 1). Overall, our np-Ni actuators are quite promising considering their high stiffness, low operating voltage, large strain amplitude/stroke, ultrahigh work density, excellent stability and low material cost.
In addition, it should be noted that the design of the hybrid-phase precursors and the localized dealloying strategy could be extended to fabricate other bulk nanoporous metals or alloys based upon earth-abundant elements such as copper, cobalt (Fig. S18, ESI†), iron, and so forth. We could further tune the relative density or porosity of np-Ni through the alloy design of precursors. For example, the np-Ni rod which was obtained by the dealloying of Al68.5Ni31.5 (at%), also shows good electrochemical actuation behavior (Fig. S19, ESI†). Besides, the bending experiment indicates that the np-Ni samples are quite brittle (see Fig. S3 and Movie S1, ESI†). Nevertheless, the surface charge induced reversible strain amplitude can reach 2% in our np-Ni samples. Using the volume strain (6%) and the bulk modulus (B = 190 GPa32) of Ni, the calculated strain-induced pressure variation (ΔP = B × ΔV/V) may be as large as 11.4 GPa in our np-Ni samples, which is much higher than that (∼1 GPa) in np-Pt.11 It is astonishing that so high reversible strain amplitude and stroke could be achieved in the brittle np-Ni rods. For the potential mechanism, some perspectives could be considered. The np-Ni rods are brittle when they are dry. The electrochemical actuation of np-Ni was measured in the alkaline electrolyte (aqueous solution). The existence of water (or the metal–water interaction) might have some effects on the mechanical behavior of nanoporous metals/alloys. The underlying mechanism needs to be further clarified.
Conclusions
In summary, high quality low-cost np-Ni rods (bulk samples with different lengths/diameters, free of cracks and with hierarchically porous structures) could be fabricated for electrochemical actuators by the design of hybrid-phase precursor alloys and a localized dealloying strategy. The np-Ni actuators exhibit giant reversible strain of up to 2% and ultrahigh work density of 11.76 MJ m−3, which is the highest among the known actuator materials (an enhanced factor of ∼300 compared with skeletal muscles). Moreover, these nickel actuators show excellent cycling stability and can perform over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles with strain preservation of over 70%. np-Ni also has a quite low material cost compared to gold, platinum and their alloys. Our findings could guide the design of metallic muscles based upon base metals like nickel, cobalt, copper etc., and will open the way to commercially viable nanoporous metal actuators. In addition, the bulk shape, flexible sizes and tunable porosity of our np-Ni samples are suitable for the study of the mechanical behaviors and physical properties of nanoporous metals/alloys as model materials. The np-Ni samples could also find applications in fields like supercapacitors, catalysis, sensing, and so forth.
000 cycles with strain preservation of over 70%. np-Ni also has a quite low material cost compared to gold, platinum and their alloys. Our findings could guide the design of metallic muscles based upon base metals like nickel, cobalt, copper etc., and will open the way to commercially viable nanoporous metal actuators. In addition, the bulk shape, flexible sizes and tunable porosity of our np-Ni samples are suitable for the study of the mechanical behaviors and physical properties of nanoporous metals/alloys as model materials. The np-Ni samples could also find applications in fields like supercapacitors, catalysis, sensing, and so forth.
Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China (51371106), the National Basic Program of China (973, 2012CB932800), the Specialized Research Fund for the Doctoral Program of Higher Education of China (20120131110017) and the Young Tip-top Talent Support Project (the Organization Department of the Central Committee of the CPC).References
- L. E. Cross, Mater. Chem. Phys., 1996, 43, 108–115 CrossRef CAS.
- R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839 CrossRef CAS PubMed.
- Q. M. Zhang, V. Bharti and X. Zhao, Science, 1998, 280, 2101–2104 CrossRef CAS PubMed.
- R. H. Baughman, Synth. Met., 1996, 78, 339–353 CrossRef CAS.
- R. H. Baughman, C. Cui, A. A. Zakhidov, Z. Iqbal, J. N. Barisci, G. M. Spinks, G. G. Wallace, A. Mazzoldi, D. De Rossi, A. G. Rinzler, O. Jaschinski, S. Roth and M. Kertesz, Science, 1999, 284, 1340–1344 CrossRef CAS PubMed.
- M. Kohl, Shape memory microactuators, Springer, Berlin, Germany, 2004 Search PubMed.
- M. Hughes and G. M. Spinks, Adv. Mater., 2005, 17, 443–446 CrossRef CAS.
- X. Xie, L. Qu, C. Zhou, Y. Li, J. Zhu, H. Bai, G. Shi and L. Dai, ACS Nano, 2010, 4, 6050–6054 CrossRef CAS PubMed.
- L.-H. Shao, J. Biener, H.-J. Jin, M. M. Biener, T. F. Baumann and J. Weissmüller, Adv. Funct. Mater., 2012, 22, 3029–3034 CrossRef CAS.
- J. Biener, A. Wittstock, L. A. Zepeda-Ruiz, M. M. Biener, V. Zielasek, D. Kramer, R. N. Viswanath, J. Weissmuller, M. Baumer and A. V. Hamza, Nat. Mater., 2009, 8, 47–51 CrossRef CAS PubMed.
- J. Weissmüller, R. N. Viswanath, D. Kramer, P. Zimmer, R. Würschum and H. Gleiter, Science, 2003, 300, 312–315 CrossRef PubMed.
- D. Kramer, R. N. Viswanath and J. Weissmüller, Nano Lett., 2004, 4, 793–796 CrossRef CAS.
- D. Kramer and J. Weissmüller, Surf. Sci., 2007, 601, 3042–3051 CrossRef CAS.
- H.-J. Jin, S. Parida, D. Kramer and J. Weissmüller, Surf. Sci., 2008, 602, 3588–3594 CrossRef CAS.
- R. N. Viswanath, D. Kramer and J. Weissmüller, Electrochim. Acta, 2008, 53, 2757–2767 CrossRef CAS.
- H.-J. Jin, X.-L. Wang, S. Parida, K. Wang, M. Seo and J. Weissmüller, Nano Lett., 2009, 10, 187–194 CrossRef PubMed.
- E. Detsi, S. Punzhin, J. Rao, P. R. Onck and J. T. M. De Hosson, ACS Nano, 2012, 6, 3734–3744 CrossRef CAS PubMed.
- E. Detsi, P. Onck and J. T. M. De Hosson, ACS Nano, 2013, 7, 4299–4306 CrossRef CAS PubMed.
- R. N. Viswanath and J. Weissmüller, Acta Mater., 2013, 61, 6301–6309 CrossRef CAS.
- E. Detsi, M. S. Sellès, P. R. Onck and J. T. M. De Hosson, Scr. Mater., 2013, 69, 195–198 CrossRef CAS.
- C. Cheng and A. H. W. Ngan, ACS Nano, 2015, 9, 3984–3995 CrossRef CAS PubMed.
- W. Haiss, Rep. Prog. Phys., 2001, 64, 591–648 CrossRef CAS.
- J. Weissmüller and J. W. Cahn, Acta Mater., 1997, 45, 1899–1906 CrossRef.
- R. H. Baughman, Science, 2003, 300, 268–269 CrossRef CAS PubMed.
- J. Erlebacher, M. J. Aziz, A. Karma, N. Dimitrov and K. Sieradzki, Nature, 2001, 410, 450–453 CrossRef CAS PubMed.
- J. Erlebacher, J. Electrochem. Soc., 2004, 151, C614–626 CrossRef CAS.
- D. A. Crowson, D. Farkas and S. G. Corcoran, Scr. Mater., 2009, 61, 497–499 CrossRef CAS.
- M. Hakamada, S. Matsumura and M. Mabuchi, Mater. Lett., 2012, 70, 132–134 CrossRef CAS.
- K. C. Liu and M. A. Anderson, J. Electrochem. Soc., 1996, 143, 124–130 CrossRef CAS.
- J. Weissmüller, R. C. Newman, H.-J. Jin, A. M. Hodge and J. W. Kysar, MRS Bull., 2009, 34, 577–586 CrossRef.
- J. Biener, A. M. Hodge, A. V. Hamza, L. M. Hsiung and J. H. Satcher, J. Appl. Phys., 2005, 97, 024301 CrossRef.
- H. M. Ledbetter and R. P. Reed, J. Phys. Chem. Ref. Data, 1973, 2, 531–618 CrossRef CAS.
- J. D. W. Madden, N. A. Vandesteeg, P. A. Anquetil, P. G. A. Madden, A. Takshi, R. Z. Pytel, S. R. Lafontaine, P. A. Wieringa and I. W. Hunter, IEEE J. Oceanic Eng., 2004, 29, 706–728 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental, calculation, supplementary figures (Fig. S1–S20) and tables (Tables S1–S3). See DOI: 10.1039/c5tc03048j |
| This journal is © The Royal Society of Chemistry 2016 |