Single parabolic band behavior of thermoelectric p-type CuGaTe2
Jiawen
Shen
,
Zhiwei
Chen
,
Siqi
lin
,
Linglang
Zheng
,
Wen
Li
and
Yanzhong
Pei
*
Key Laboratory of Advanced Civil Engineering Materials of Ministry of Education, School of Materials Science and Engineering, Tongji University, 4800 Caoan Rd., Shanghai 201804, China. E-mail: yanzhong@tongji.edu.cn
First published on 16th November 2015
Abstract
The existence of a noticeable discrepancy in thermoelectric properties reported in the literature motivates the current work on the transport properties of CuGaTe2. Taking Zn- and Mn-doping at the Ga site as an example, the hole concentration can be effectively tuned within 1018–1020 cm−3 that enables a reliable assessment of the transport properties. It is evident that both temperature and carrier concentration dependent transport properties follow well within the framework of a single parabolic band approximation with a dominant carrier scattering by acoustic phonons. This work helps distinguish the effects that contribute to the high thermoelectric figure of merit zT in CuGaTe2. The modeling further suggests that this compound can show a thermoelectric figure of merit of unity or higher, when further strategies are taken for reducing the lattice thermal conductivity and engineering the band structure.
1. Introduction
Thermoelectric materials enable a direct conversion between heat and electricity, leading to wide applications for both waste heat recovery and refrigeration.1 The characterization of the thermoelectric performance depends on the materials' dimensionless figure of merit, zT = S2T/ρ(κE + κL), where S, T, ρ, κE, and κL are the Seebeck coefficient, absolute temperature, electrical resistivity, and electronic and lattice thermal conductivity, respectively. Generally, S, ρ, and κE are coupled with each other strongly in a given material,2 leading to the difficulty of property manipulation.Since the lattice thermal conductivity, κL, is the only one independent property determining zT, it needs to be minimized. The majority of current efforts have been made to enhance the phonon scattering by various approaches such as alloying,3–5 lattice unharmonicity,6,7 liquid phonons8 and nanostructuring,9–12 to reduce the lattice thermal conductivity and therefore to improve the thermoelectric performance. Besides that, engineering the band structure13–15 or optimizing the carrier concentration16–18 to enhance the thermoelectric power factor has been proven to be effective as well.
The large family of semiconducting ternary I–III–VI2 chalcopyrite compounds (I = Cu, Ag; III = Al, Ga, In; VI = S, Se, Te) has been widely considered for photovoltaic solar cells and other optical applications, due to the appropriate band gaps.19 In the recent decade, I–III–VI2 chalcopyrite semiconductors have also been emphasized due to their potentially high thermoelectric performance.20–22 Therefore, these materials seem to be good candidates for thermoelectric-photovoltaic hybrid applications.23 Furthermore, the relatively high thermal conductivity20 and the highly tunable Seebeck coefficient suggest their great potential application as thermopower wave sources.24–28
Among all the members of semiconducting I–III–VI2 chalcopyrite compounds, CuGaTe2 exhibits a promising thermoelectric figure of merit zT,20 and therefore, attracts many theoretical and experimental studies on this compound and its alloys with high zT. For instance, CuGa1−xInxTe2,29 Cu1−xAgxGaTe230 and Cu1−xGaSbxTe231 solid solutions exhibited a great reduction in κL and therefore an increase in zT. A combination of solid solutions for lowering κL and carrier concentration optimization further leads to an enhancement in zT in Cu(In0.25Ga0.75)0.99Zn0.01Te2.32 Meanwhile, the band structure calculations33 suggested that the valence band had a very little contribution from Ga atoms, leading some researchers to try to optimize the thermoelectric performance via Ga-substitution.34,35
However, none of the work afterwards shows a zT as high as it is reported for the first time.20 This discrepancy mainly comes from its electronic performance, since the majority29,31,34,35 of the literature lattice thermal conductivity agrees with each other reasonably but is lower than that reported in ref. 20. In more detail, the reported Seebeck coefficient, resistivity and carrier mobility show a noticeable discrepancy at a given carrier concentration.29,31,34,35 Not only the detailed measurements on the carrier concentration dependent transport properties but also the underlying physics of this material seem to be important to guide the further improvement in the thermoelectric performance of this material.
Although this compound has been considered for a while as a thermoelectric material, detailed discussion on the fundamental parameters such as its scattering mechanism, effective mass and optimal doping level can be rarely seen. These parameters determine the thermoelectric transport properties, and therefore, help understand the physics of this material. For instance, it has been known than the optimal carrier concentration (nopt) is determined by the density of state effective mass (m*) and the working temperature (T) via nopt ∝ (m*T)1.5 when the charge scattering is dominated by acoustic phonons.18 Due to the different m*, nopt differs significantly from one material to another. For example, Bi2Te3/Sb2Te3 materials have a much lower nopt ∼ 1019cm−3 (ref. 36) than (1020–1021 cm−3) SiGe, CoSb3 and Zintl compounds.37
To approach a reliable estimation of the above fundamental parameters, a careful doping in this material is needed to discuss the carrier concentration dependent transport properties. In this study, various dopants have been used to tune the carrier concentration of CuGaTe2. These dopants include divalent Zn, Mn, Ba, Cd, Mg and Yb for p-type substitution at the Ga-site. It turns out that Zn, Mn, and Cd can tune carrier concentration effectively, ranging from 1018–1020 cm−3. This extends a detailed model prediction on the transport properties depending on not only the temperature but also the doping level. Focusing on the most effective doping by Zn and Mn, the thermoelectric properties can be well predicted by a single parabolic band model with acoustic scattering.38 This further allows a prediction on the maximal figure of merit assuming an amorphous limit for the lattice thermal conductivity, and the carrier concentration needed for realizing this maximum.
2. Experimental
Polycrystalline samples of CuGa1−xZnxTe2 (0 ≤ x ≤ 0.1) and CuGa1−xMnxTe2 (0 ≤ x ≤ 0.05) were synthesized by a melting, quenching and hot pressing technique. The stoichiometric amount of high purity elements (>99.99%) was melted at 1173 K for 10 hours, followed by quenching in cold water and annealing at 900 K for 3 days. The obtained ingots were hand ground into fine powder for consolidation at 873 K for 30 min under a uniaxial pressure of ∼90 MPa by an induction heating hot press system.39 The obtained dense pellet samples (>98% of the theoretical density) were ∼12 mm in diameter and ∼1.5 mm in thickness.The phase composition of the samples was examined by powder X-ray diffraction (XRD). The Seebeck coefficient was obtained from the slope of the thermopower vs. temperature gradients within 0–5 K;40 the resistivity and Hall coefficient were measured using the van der Pauw technique under a reversible magnetic field of 1.5 T. To reduce the measurement uncertainties resulting from the possible hysteresis and the sample dimension determinations, these transport properties were measured simultaneously in the temperature range of 300–850 K during both heating and cooling.
The thermal diffusivity (λ) was measured by a laser flash technique (Netzsch LFA457). A Dulong-Pettit limit of heat capacity (Cp) was used to determine the thermal conductivity via κ = dλCp, where d is the density estimated by a mass/volume method. The sound velocity was measured using an ultrasonic pulse-receiver (Olympus-NDT) equipped with an oscilloscope (Keysight). The uncertainty for the measurements of S, ρ and κ was 5% approximately.
3. Results and discussion
The hall carrier concentration (nH) dependent Seebeck coefficient and Hall mobility at room temperature for CuGaTe2 are shown in Fig. 1a and b, respectively. It can be seen that the available literature data20,29–31,34,35 are more scattered than the current work including not only Mn- but also Zn-doped materials. Most importantly, the results here can be very well described by a single parabolic band (SPB) behavior in a broad Hall carrier concentration range (1018–1020 cm−3), when a dominant charge scattering by acoustic phonons is assumed.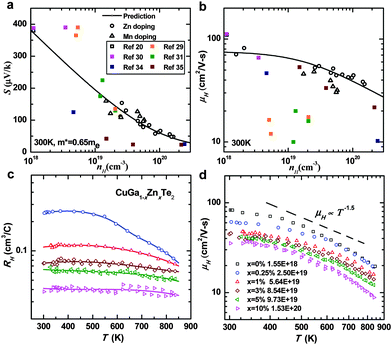 | ||
| Fig. 1 Carrier concentration dependent Seebeck coefficient (a) and Hall mobility (b) at room temperature for CuGaTe2 with various doping, with a detailed comparison to the available literature data.20,29–31,34,35 The experimental data here are much less scattered and follow well with the single parabolic band behavior. Temperature dependent Hall coefficient (c) and Hall mobility (d) for CuGa1−xZnxTe2 suggest a single band conduction behavior with a dominant scattering by acoustic phonons. | ||
In more detail, the nearly constant Hall coefficient (Fig. 1c) versus temperature in heavily doped samples indicates the single valence band transport behavior here, since mixed conduction (electrons and holes) or conduction by multiple bands usually leads to a much more complicated temperature dependence on the Hall coefficient.13,41 Furthermore, the wide band gap of 1.2 eV,19 which is much larger than that of conventional thermoelectric materials (0.2–0.5 eV for Bi2Te3, PbTe and CoSb3),36,41 suggests that the band can be approximated as parabolic due to the weak interaction between the valence and conduction band.41 As evidenced from the temperature dependent Hall mobility, the dominant mechanism of charge carrier scattering is by acoustic phonons. Therefore, one obtains the following equations according to the Boltzmann transport theory:36
The Seebeck coefficient,
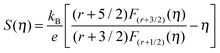 | (1) |
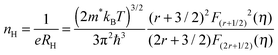 | (2) |
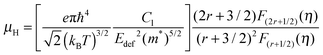 | (3) |
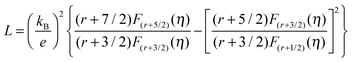 | (4) |
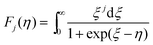 is the Fermi integral.
is the Fermi integral.
In the above equations, kB is the Boltzmann constant, ℏ is the reduced Planck constant, Cl is the elastic constant for longitudinal vibrations, Edef is the deformation potential coefficient characterizing the strength of carriers scattered by acoustic phonons,42m* is the density of state effective mass, and η is the reduced Fermi level. When charge carriers are scattered by acoustic phonons, r = −1/2.
Fig. 1a and b then suggest the possible discrepancy among the available literature studies, because many of the reported results show a large deviation from the SPB prediction. Providing good agreement between the experimental result (from different dopants) and the theoretical prediction by the SPB model, it is then reasonable to conclude that the transport properties should follow a single parabolic band behavior.
Based on this observation, one would then be able to evaluate the thermoelectric properties of this material theoretically, and to confirm them with the experimental measurements. It should be noted that similarly good agreement between the carrier concentration dependent Seebeck coefficient and mobility can be obtained at any other temperatures. This further suggests that either Mn- or Zn-doping at the Ga site does not change the valence band structure of this compound, which is consistent with the literature band calculation.33 All of these findings ensure CuGaTe2 as a suitable material system for thermoelectric transport property modeling.
Using the experimental Seebeck coefficient, the reduced Fermi level η can be obtained using eqn (1). Substituting the estimated η and the measured Hall carrier concentration and mobility into eqn (2) and (3), the effective mass and deformation potential coefficient can be calculated, respectively. Using the experimental longitudinal sound velocity (vl) of ∼3985 m s−1 and the density (d), the longitudinal elastic constant42 (Cl = vl2d) can be estimated for the following SPB model prediction. The modeling suggests a density of state mass (m*) of 0.65 me and a deformation potential coefficient (Edef) of ∼15 eV assuming a single valley conduction for CuGaTe2 at room temperature, where me is the mass of a free electron.
In more detail, the single band conducting behavior is evident from the temperature dependent Hall coefficient (RH) measurements as shown in Fig. 1c, where RH remains roughly constant in the entire temperature range in heavily doped samples. As for the lightly doped ones, RH decreases gradually with increasing temperature, suggesting an increase in the carrier concentration due to the thermal excitation of dopants or intrinsic defects.17 The temperature dependent Hall mobility (μH ∼ T−1.5) as shown in Fig. 1d nicely confirms the dominant charge carrier scattering mechanism of acoustic phonons, because any other scattering types such as by grain boundaries, optical phonons, ionized impurities, would predictably lead to a μH ∼ Tp with p ≥ −0.5.43,44 In this study, the room temperature hole concentration increases from ∼2 × 18 cm−3 for undoped CuGaTe2 to 1.5 × 20 cm−3 for doping with Zn. The observed p-type conduction and the significantly increased hole concentration suggest a successful substitution of the trivalent Ga by the divalent Zn and Mn.
However, Mn-doped materials show a slightly lower mobility as compared with Zn-Doped ones, which is presumably due to their additional carrier scattering by magnetic impurities.45,46 In order to evaluate the maximal thermoelectric performance in these material, the Zn-doped series are focused for the following discussion.
Following the same single parabolic band approximation discussed above for room temperature, the transport properties at high temperatures are found to agree with the theoretical prediction as well. This leads to a temperature dependent density of state effective mass (m*) and deformation potential coefficient (Edef), which are shown in Fig. 2. Both m* and Edef show a weak dependence on the carrier concentration, suggesting the rigid band behavior in this case.
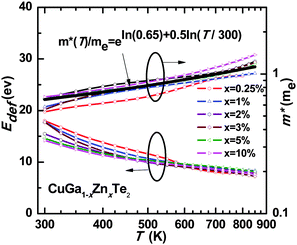 | ||
| Fig. 2 Temperature dependent density of state effective mass (m*) and the deformation potential coefficient for CuGa1−xZnxTe2. | ||
The strength of the carrier scattering by acoustic phonons is given by the deformation potential coefficient (Edef).42,47 Taking into account the above temperature dependent density of state effective mass (m*), the resulting deformation potential coefficient (Edef) decreases with increasing temperature and remains unchanged for different doping levels at any given temperature. With the above knowledge on the density of state effective mass and the scattering strength, the single parabolic band model actually enables a quantitative prediction on the resistivity and Seebeck coefficient at any given temperatures and carrier concentrations.
This is normally seen in IV–VI thermoelectric semiconductors,17,18,44,48–51 and can be ascribed to the increased band gap due to lattice expansion.41,52,53 This implies that the band gap may increase with increasing lattice parameter due to thermal expansion when temperature rises.
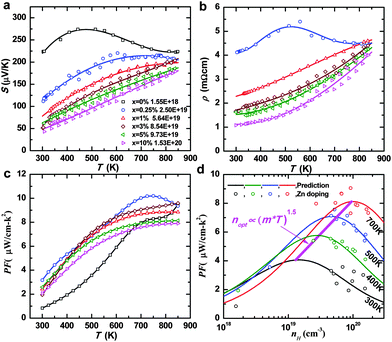
The measured Seebeck coefficient (S) and resistivity (ρ) for the CuGa1−xZnxTe2 samples, as a function of temperature up to 850 K, are shown in Fig. 3a and b, respectively. The majority (x ≥ 1%) of the samples obtained in this study show degenerate semiconducting behavior. Both the Seebeck coefficient and resistivity increase with increasing temperature.
For a material system with single parabolic band conduction including CuGaTe2 studied in this work, the Seebeck coefficient is determined by the reduced Fermi energy (η) and the scattering mechanism of the charge carriers as shown in eqn (1). According to the temperature dependent Hall mobility (Fig. 1d), Zn-doping does not change the scattering of the charge carriers. At a given temperature, the reduced Seebeck coefficient by Zn-doping corresponds to a reduced η, which is due to the increased hole concentration (Fig. 1c). When the sample is lightly doped or undoped, η remains to be small or negative, which means a Fermi level close to the conduction band edge. This leads to a significantly increased probability to have the thermally excited minority carriers (electrons in this case) contributing the conductivity at high temperatures, due to the thermal broadening of the Fermi distribution function. The opposite contributions to the Seebeck coefficient due to majority and minority carriers result in a strong compensation. All these effects eventually lead to a decrease in both the Seebeck coefficient (Fig. 3a) and resistivity (Fig. 3b) at high temperatures for the samples with low carrier concentrations.
The temperature dependent thermoelectric Power factor (PF = S2/ρ) is shown in Fig. 3c. Compared with the intrinsic CuGaTe2, the power factor for the doped ones is enhanced in the entire temperature range, due to the carrier concentration tuning. According to the above SPB model calculated m* and Edef at each temperature (Fig. 2), the carrier concentration dependent power factor is predicted at four exemplary temperatures, and is shown in Fig. 3d including a comparison to the experimental data. This model successfully predicts the power factor at any given temperatures and carrier concentrations. It is seen that not only the peak power factor but also the optimal carrier concentration (nopt, n required for peaking PF) increase significantly with increasing temperature. The increased peak PF largely comes from the decreased Edef at high temperatures. When the temperature rises, in addition to the resulting increase in the density of state effective mass (Fig. 2), the experimental optimal carrier concentration (nopt) agrees well with the relationship nopt ∝ (m*T)1.5 as predicted by the SPB model,17,18 which is shown in Fig. 3d.
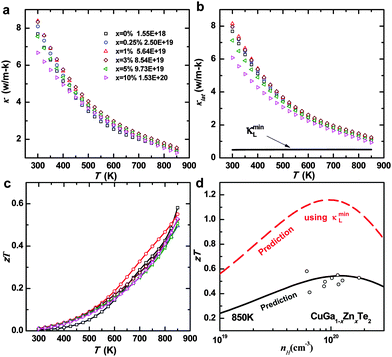
The temperature dependent total thermal conductivity and its lattice contribution for CuGa1−xZnxTe2 are shown in Fig. 4a and b, respectively. The lattice thermal conductivity is estimated by subtracting the electronic contribution, κe = LT/ρ via the Wiedemann–Franz law, from the total thermal conductivity, where the Lorenz factor is determined by the above SPB model. The room temperature total thermal conductivity of pure CuGaTe2 is ∼8 W m−1 K−1, which is consistent with the literature value.20
The lattice thermal conductivity decreases rapidly with increasing temperature with a rough T−1 relationship and shows a continuous decay, indicating a predominant Umklapp scattering for the phonons in these materials. Zn-doping in CuGaTe2 has little effect on lowering the lattice thermal conductivity due to the low concentration of impurity atoms. An observable reduction in κl is only achievable in the heaviest doped sample CuGa0.9Zn0.1Te2 near room temperature.
According to the Cahill model,54 one can estimate the minimal lattice thermal conductivity assuming a phonon mean free path of the average atomic distance. With the help of our sound velocity measurements, which lead to speeds of 2115 and 3985 m s−1 for transverse and longitudinal ultrasonic sound waves, respectively, the minimal lattice thermal conductivity (Fig. 4b) is determined to be ∼0.5 W m−1 K−1 at 300 K, which is consistent with the literature.20 Compared with the experimental κl of 1 W m−1 K−1, it is reasonably expected that there is still a big room for a further reduction by demonstrated strategies such as alloying3–5 and nanostructuring.9–12
The temperature dependent thermoelectric figure of merit zT for CuGa1−xZnxTe2 is given in Fig. 4c. Due to the nearly unchanged thermal conductivity, the main zT enhancement occurs at low temperature, which can be understood by the enhanced power factor particularly at low temperatures (Fig. 3c).
As discussed above, the SPB model enables a reasonable prediction on the Seebeck coefficient, resistivity and Lorenz factor; a prediction on zT becomes possible when the lattice thermal conductivity is known. As shown in Fig. 4d, utilizing the experimental lattice thermal conductivity, the SPB model successfully predicts zT for CuGa1−xZnxTe2 at different carrier concentrations. Upon further using the calculated minimum lattice thermal conductivity, one can evaluate the maximal available zT through a κl-reduction strategy. It is shown that a maximal zT of unity can be obtained when the minimal lattice thermal conductivity is achieved. On the other hand, appropriate band engineering approaches to improve the power factor are believed to enable a further advancement for thermoelectric p-type CuGaTe2.
4. Summary
In summary, Zn and Mn act as effective dopants at the Ga site for tuning the carrier concentration, which results in an enhancement of the power factor particularly at low temperatures. The single parabolic band model with acoustic scattering provides a reasonable prediction on the transport properties, enabling a detailed evaluation of this compound as a thermoelectric material. This work helps distinguishing the effects that contribute to the high zT in CuGaTe2. The principles used here could be equally applicable to other similar thermoelectrics. The remaining room for a further reduction in the lattice thermal conductivity and the applicability for the power factor increase by band engineering approaches suggest the great potential of CuGaTe2 as a high performance thermoelectric material.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 51422208, 11474219 and 51401147), the national Recruitment Program of Global Youth Experts (1000 Plan), the program for professor of special appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, the fundamental research funds for the central universities and the Bayer-Tongji Eco- Eco-Construction & Material Academy 90 (TB20140001).References
- L. E. Bell, Science, 2008, 321, 1457–1461 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- S. Li, J. Hinckley, J. Singh and P. Bhattacharya, Appl. Phys. Lett., 1993, 63, 1393–1395 CrossRef CAS.
- Y. Pei, A. D. LaLonde, N. A. Heinz and G. J. Snyder, Adv. Energy Mater., 2012, 2, 670–675 CrossRef CAS.
- H. Wang, A. Charoenphakdee, K. Kurosaki, S. Yamanaka and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 024303 CrossRef.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- D. T. Morelli, V. Jovovic and J. P. Heremans, Phys. Rev. Lett., 2008, 101, 035901 CrossRef CAS PubMed.
- H. Liu, X. Shi, F. Xu, L. Zhang and W. Zhang, Nat. Mater., 2012, 11, 422–425 CrossRef CAS PubMed.
- Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241–249 CrossRef CAS.
- K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Hogan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818–821 CrossRef CAS PubMed.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- B. Poudel, Q. Hao, Y. Ma, Y. C. Lan, A. Minnich, B. Yu, X. A. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634–638 CrossRef CAS PubMed.
- Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69 CrossRef CAS PubMed.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557 CrossRef CAS PubMed.
- Z. Jian, Z. Chen, W. Li, J. Yang, W. Zhang and Y. Pei, J. Mater. Chem. C, 2015 10.1039/C5TC03068D.
- J. Androulakis, I. Todorov, D. Y. Chung, S. Ballikaya, G. Y. Wang, C. Uher and M. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115209 CrossRef.
- Y. Pei, A. F. May and G. J. Snyder, Adv. Energy Mater., 2011, 1, 291–296 CrossRef CAS.
- Y. Pei, Z. M. Gibbs, B. Balke, W. G. Zeier and G. J. Snyder, Adv. Energy Mater., 2014, 4, 1400486 Search PubMed.
- J. L. Shay and J. H. Wernick, Ternary Chalcopyrite Semiconductors: Growth, Electronic Properties, and Applications: International Series of Monographs in The Science of The Solid State, Elsevier, 1974 Search PubMed.
- T. Plirdpring, K. Kurosaki, A. Kosuga, T. Day, S. Firdosy, V. Ravi, G. J. Snyder, A. Harnwunggmoung, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Adv. Mater., 2012, 24, 3622–3626 CrossRef CAS PubMed.
- R. Liu, L. Xi, H. Liu, X. Shi, W. Zhang and L. Chen, Chem. Commun., 2012, 48, 3818–3820 RSC.
- A. Yusufu, K. Kurosaki, A. Kosuga, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Appl. Phys. Lett., 2011, 99, 061902 CrossRef.
- N. Wang, L. Han, H. He, N.-H. Park and K. Koumoto, Energy Environ. Sci., 2011, 4, 3676 CAS.
- S. Walia, R. Weber, S. Sriram, M. Bhaskaran, K. Latham, S. Zhuiykov and K. Kalantar-zadeh, Energy Environ. Sci., 2011, 4, 3558 CAS.
- S. Walia, R. Weber, K. Latham, P. Petersen, J. T. Abrahamson, M. S. Strano and K. Kalantar-zadeh, Adv. Funct. Mater., 2011, 21, 2072–2079 CrossRef CAS.
- S. Walia, R. Weber, S. Balendhran, D. Yao, J. T. Abrahamson, S. Zhuiykov, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-zadeh, Chem. Commun., 2012, 48, 7462–7464 RSC.
- S. Walia, S. Balendhran, H. Nili, S. Zhuiykov, G. Rosengarten, Q. H. Wang, M. Bhaskaran, S. Sriram, M. S. Strano and K. Kalantar-zadeh, Prog. Mater. Sci., 2013, 58, 1443–1489 CrossRef CAS.
- S. Walia, S. Balendhran, P. Yi, D. Yao, S. Zhuiykov, M. Pannirselvam, R. Weber, M. S. Strano, M. Bhaskaran, S. Sriram and K. Kalantar-zadeh, J. Phys. Chem. C, 2013, 117, 9137–9142 CAS.
- Y. Li, Q. Meng, Y. Deng, H. Zhou, Y. Gao, Y. Li, J. Yang and J. Cui, Appl. Phys. Lett., 2012, 100, 231903 CrossRef.
- A. Yusufu, K. Kurosaki, Y. Ohishi, H. Muta and S. Yamanaka, Jpn. J. Appl. Phys., 2013, 52, 081801 CrossRef.
- J. Cui, Y. Li, Z. Du, Q. Meng and H. Zhou, J. Mater. Chem. A, 2013, 1, 677–683 CAS.
- W. D. Carr and D. T. Morelli, J. Alloys Compd., 2015, 630, 277–281 CrossRef CAS.
- D. Zou, S. Xie, Y. Liu, J. Lin and J. Li, J. Alloys Compd., 2013, 570, 150–155 CrossRef CAS.
- J. Zhang, X. Qin, D. Li, H. Xin, C. Song, L. Li, Z. Wang, G. Guo and L. Wang, J. Alloys Compd., 2014, 586, 285–288 CrossRef CAS.
- J. Zhang, X. Qin, D. Li, C. Song, X. Zhu, Y. Liu, H. Xin, L. Chen and T. Zou, Intermetallics, 2015, 60, 45–49 CrossRef CAS.
- H. J. Goldsmid, Introduction to Thermoelectricity, Springer, Heidelberg, 2009 Search PubMed.
- E. S. Toberer, A. F. May and G. J. Snyder, Chem. Mater., 2010, 22, 624–634 CrossRef CAS.
- N. Cheng, R. Liu, S. Bai, X. Shi and L. Chen, J. Appl. Phys., 2014, 115, 163705 CrossRef.
- A. D. LaLonde, T. Ikeda and G. J. Snyder, Rev. Sci. Instrum., 2011, 82, 025104 CrossRef PubMed.
- Z. H. Zhou and C. Uher, Rev. Sci. Instrum., 2005, 76, 023901 CrossRef.
- Y. I. Ravich, B. A. Efimova and I. A. Smirnov, Semiconducting Lead Chalcogenides, Plenum Press, New York, 1970 Search PubMed.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- A. May, E. Toberer, A. Saramat and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125205 CrossRef.
- Y. Pei, A. D. LaLonde, H. Wang and G. J. Snyder, Energy Environ. Sci., 2012, 5, 7963–7969 CAS.
- Y. Pei, H. Wang, Z. M. Gibbs, A. D. LaLonde and G. J. Snyder, NPG Asia Mater., 2012, 4, e28 CrossRef.
- W. Li, Z. Chen, S. Lin, Y. Chang, B. Ge, Y. Chen and Y. Pei, Journal of Materiomics, 2015 DOI:10.1016/j.jmat.2015.1009.1001.
- C. Erginsoy, Phys. Rev., 1950, 79, 1013 CrossRef CAS.
- M. K. Zhitinskaya, V. I. Kaidanov and I. A. Chernik, Sov. Phys. Solid State, 1966, 8, 246–247 Search PubMed.
- T. S. Stavitskaya, I. V. Prokofev, Y. I. Ravich and B. A. Efimova, Soviet Physics Semiconductors, 1968, 1, 952–956 Search PubMed.
- H. A. Lyden, Phys. Rev. A, 1964, 135, A514–A521 CrossRef.
- L. Rogers, J. Phys. D: Appl. Phys., 1971, 4, 1025 CAS.
- Y. I. Ravich, B. A. Efimova and V. I. Tamarche, Phys. Status Solidi B, 1971, 43, 11–33 CrossRef CAS.
- E. Kane, J. Phys. Chem. Solids, 1957, 1, 249–261 CrossRef.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |