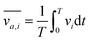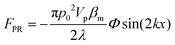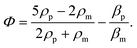DOI:
10.1039/C6AN01743F
(Paper)
Analyst, 2017,
142, 123-131
Acoustofluidic particle trapping, manipulation, and release using dynamic-mode cantilever sensors†
Received
2nd August 2016
, Accepted 14th November 2016
First published on 23rd November 2016
Abstract
We show here that dynamic-mode cantilever sensors enable acoustofluidic fluid mixing and trapping of suspended particles as well as the rapid manipulation and release of trapped micro-particles via mode switching in liquid. Resonant modes of piezoelectric cantilever sensors over the 0 to 8 MHz frequency range are investigated. Sensor impedance response, flow visualization studies using dye and micro-particle tracers (100 μm diameter), and finite element simulations of cantilever modal mechanics and acoustic streaming show fluid mixing and particle trapping configurations depend on the resonant mode shape. We found trapped particles could be: (1) rapidly manipulated on millimeter length scales, and (2) released from the cantilever surface after trapping by switching between low- and high-order resonant modes (less than 250 kHz and greater than 1 MHz, respectively). Such results suggest a potentially promising future for dynamic-mode cantilevers in separations, pumping and mixing applications as well as acoustofluidic-enhanced sensing applications.
1. Introduction
Dynamic-mode cantilevers have been used extensively in physical-, chemical-, and bio-sensing applications due to their sensitivity to detect fluid property changes and the selective binding of cellular and molecular targets.1,2 Although cantilever sensor size widely varies depending on the intended application,1–3 millimeter-scale cantilevers expressing high-order modes have shown promise in real-time sensing applications,4–16 as they exhibit minimal damping in liquid.14,17 Such a characteristic enables the continual monitoring of sensor properties throughout the measurement.1 Thus, millimeter-scale cantilevers have been widely investigated for sensitive biosensing applications using resonant modes ranging from 10 kHz–1 MHz in complex liquid matrices including source waters, body fluids, and food matrices.11,12,18,19 Importantly, recent work has shown dynamic-mode operation of cantilever-based11,13,20 and surface acoustic wave (SAW) devices21–23 during sensing measurements may contribute to reduced nonspecific binding. Likewise, it has been demonstrated that surface vibration reduces nonspecific binding, also called biofouling, in non-sensing applications.24–26 These studies suggest that dynamic-mode sensors and actuators may enable novel acoustofluidic applications and improve the fundamental understanding of device operation in liquid.
The study of cantilever sensor-based acoustofluidic phenomena also offers opportunities for advancing modern acoustofluidic platform design and applications. Modern applications include enhancement of heat and mass transfer rates27–32 as well as the separation33 and trapping33–37 of suspended particles. The vast majority of acoustofluidic devices and platforms are typically composed of an external transducer located near or adjacent to a fluid-containing chamber in which acoustofluidic phenomena, such as fluid mixing or particle trapping, occur. As a result, microfluidic-based platforms are common designs.38,39 Alternatively, devices and platforms based on transducers which are directly immersed in the fluid-containing chamber have been relatively less examined. The advantages of the latter design include: (1) high coupling between the transducer and the fluid, and (2) the ability to conduct sensing measurements in the fluid with the same transducer. Interestingly, dynamic-mode cantilevers are promising transducers for such designs as they operate in liquid and exhibit sensing capabilities.1,28,40 Thus, if dynamic-mode cantilever sensors generate acoustic phenomena in liquid, they could catalyze novel acoustofluidic separations and sensing applications.
In the current work, we show piezoelectric-excited millimeter-sized cantilever (PEMC) sensors generate a range of acoustofluidic phenomena in liquid via flow visualization studies using dye and micro-particle tracers (100 μm diameter). We found both low- and high-order resonant modes composed of out-of-plane and in-plane motion generate acoustic streaming and enable programmable particle trapping in cantilever-adjacent regions. Acoustic streaming profiles and particle trapping configurations are dependent on the mode shape. We demonstrate the manipulation of trapped particles in both axial and lateral directions as well as various trapped particle configurations via switching the resonant mode between low- and high-order modes. We also demonstrate the rapid release of trapped particles from the cantilever via switching to high-order resonant modes or noise waveforms. Such results suggest a promising future for dynamic-mode cantilevers in liquid-phase separations, pumping and mixing applications and acoustofluidic-enhanced sensing applications, as well as demonstrate the value of acoustofluidic coupling for mode shape visualization in liquid.
2. Theory
2.1 Cantilever motion
It is well established that the transverse mode shapes of a cantilever are given as:41| | 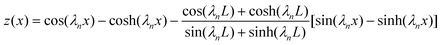 | (1) |
where x is the axial position in the x-direction, λn is the nth positive root of 1 + cos(λn)cosh(λn) = 0, and L is the cantilever length. Thus, the cantilever transverse velocity (vc) under a sinusoidal driving force is:| | vc(x, t) = Aω![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)z(x) cos(ωt)z(x) | (2) |
where A is the maximum vibration amplitude, ω = 2πf is the angular velocity, f is the driving frequency and t is the time.
2.2 Acoustic streaming
The governing equations for incompressible transient laminar flow of a Newtonian fluid are the equations of continuity:and linear momentum conservation:| | 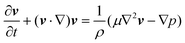 | (4) |
where v is the velocity field, p is the pressure field, ρ is the density and μ is the viscosity. It is well established that a vibrating boundary in contact with a fluid can establish standing acoustic waves and acoustic streaming (hereinafter referred to as streaming).42–45 Under the influence of a periodic disturbance (e.g. oscillating boundary), the velocity contains a harmonic (i.e. periodic) and a steady (i.e. ‘DC’) component. The acoustic streaming velocity (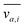 , i = x, y and z) is given as the time-averaged velocity:28
, i = x, y and z) is given as the time-averaged velocity:28| | 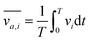 | (5) |
where T is the period of vibration. The method of successive approximations may also be applied to the nonlinear governing equations to obtain the governing equations for acoustic streaming as:44| | | F = −ρ0〈(v1·∇)v1 + v1(∇·v1)〉 | (7) |
where the brackets indicate the time-averaged value over a large number of cycles, v2 and p2 are the time-independent second-order velocity and pressure, respectively, ρ0 is the equilibrium density, F is the forcing term which captures the time-averaged vibration effect, and v1 is the oscillatory particle velocity.
3. Experimental
3.1 Reagents
Type-5A lead zirconate titanate (PZT-5A) with nickel electrode was purchased from PiezoSystems (Woburn, MA). Loctite Hysol 1D-LV epoxy was from McMaster Carr (Robbinsville, NJ). Polyurethane (MC, clear) was from Wassar Corporation (Auburn, WA). Parylene-c was from Specialty Coating Systems, Inc. (Indianapolis, IN). Trypan blue dye and phosphate buffered saline (PBS) were from Sigma-Aldrich (St Louis, MO). Caution: Trypan blue is a known carcinogen and should be handled with care. Neutrally-buoyant polyethylene micro-particles (100 μm diameter) were from Cospheric (Santa Barbara, CA). Tween-80 was from Fisher Scientific. De-ionized water was used in all preparations (DIW, Milli-Q, Millipore, Billerica, MA).
3.2 Piezoelectric-excited millimeter-sized cantilever (PEMC) sensor fabrication
A PZT sheet was first diced into 5 × 1 × 0.127 mm3 chips (American Dicing, Inc. Liverpool, NY) to provide the self-sensing and -exciting device layer. Electrical leads were then soldered to the nickel electrodes on the top and bottom faces near the chip's base to apply the exciting voltage across the cantilever thickness (127 μm) and monitor the sensor impedance response. The chip was then anchored asymmetrically via embedding into a 6 mm glass tube using epoxy. Subsequently, the device was insulated with polyurethane and parylene-c layers (10 μm) via spin-coating (30 s at 1500 rpm) and chemical vapor deposition following vendor-provided protocols (SCS Labcoter® 2), respectively. For sensing applications, a thin gold film may be deposited at the cantilever tip (Denton Desk IV, Denton Vacuum, Moorestown, NJ),7,11,12 although such was not the focus of the present study.
3.3 Dye preparation
Trypan blue dye was diluted by a factor of two in 10 mM PBS for establishing the density-driven flow of a dye tracer stream through quiescent DIW for flow visualization studies.
3.4 Neutrally-buoyant particle preparation
Particle suspensions were prepared at 10 and 100 mg beads per mL following vendor-provided protocols. Briefly, the bead suspensions were created by adding the beads to DIW which contained 0.05% Tween, heating the solution to 70 °C, and gently mixing the solution. The suspension was cooled to room temperature prior to use.
3.5 Device excitation
The PEMC sensor was actuated using a function generator (Agilent 33210A) which applied a sinusoidal excitation voltage across the PZT layer (0.1 to 10 V). A noise waveform (Gaussian; 7 MHz bandwidth) was also used as an alternative to the sine wave for release studies.
3.6 Electrical impedance analysis
The sensor's electrical impedance response was obtained using commercially available impedance analyzers (Agilent 4294A and HP 4192A). In all cases, the frequency response was measured under a driving voltage of 100 mV AC with zero DC bias across the two electrodes.
3.7 Finite element analysis
Finite element analysis (FEA) of two- and three-dimensional piezoelectric cantilever solid mechanics under the influence of the driving electric field was done using the structural mechanics module of commercially available FEA software (COMSOL Multiphysics, V.5.2). The mechanical boundary conditions involved a fixed boundary to simulate the cantilever anchor and the remainder of boundaries were unconstrained. The electrical boundary conditions involved application of a 100 mV driving voltage across the thickness of the piezoelectric layer; the remainder of boundaries were electrically insulated. Frequency response simulations were done using 374 elements and a frequency step size of 10 Hz. Damping was modeled as a loss factor (η = 0.05). Additional details are provided elsewhere.46 FEA of two-dimensional (2D) single-phase laminar acoustic streaming flow was done using the fluid flow module. The fluid behavior in the domain above the cantilever was modeled. The 2D fluid domain was 1 mm high and 3 mm wide. The input parameters of maximum vibration amplitude (A) and resonant frequency (fn) were obtained via eigenfrequency and frequency response simulations. The top boundary was modeled as a no-slip boundary condition. The bottom boundary which served as the cantilever–fluid interface was modeled as a moving wall. The wall transverse velocity (y-direction) was calculated viaeqn (1) and (2). The left and right boundaries were modeled as the inlet and outlet, respectively. The inlet and outlet were modeled as velocity field (v0 = [v0x, v0y] = [0, 0]) and pressure (p0 = 0 Pa) conditions, respectively. Transient simulations of fluid flow over 1000 cycles with a time step = 1/(10fn) (10 steps per period of vibration) were done using 2306 elements and took approximately three hours on a Dell Precision T7500 (2.66 GHz, 24 GB RAM, two Intel Xeon x5650 processors). The DC component of the flow, also known as the streaming flow, was obtained as the time-averaged velocity over all cycles viaeqn (5) by performing a time average evaluation in results post-processing which is consistent with previous studies.28 The mesh density was increased until an acceptable level of independence from the final solution was achieved (convergence within 5% of previous mesh). The time step per period of vibration, number of cycles, and number of elements are comparable to that used previously for CFD modeling of acoustic streaming caused by vibrating beams.28
3.8 Flow visualization
Imaging of fluid and particle motion was done via time-lapse photography and video recordings acquired under 10× magnification using a commercially available microscope camera (ScopeTek, DCM Series) and acquisition software (Scope Photo 3.0).
4. Results and discussion
4.1 Resonant modes of piezoelectric cantilever sensors
As shown schematically in Fig. 1A, PEMC sensors consist of an electrically-insulated, asymmetrically-anchored piezoelectric layer.46,47 Similar to the majority of cantilever sensors, sensing of target cells and molecules is achieved through the binding of targets to immobilized probes, for example, single-stranded DNA or antibodies immobilized on a gold surface. A representative photograph of a PEMC sensor is shown in Fig. 1B. The self-sensing and -exciting configuration enables frequency response analysis via electrical impedance spectroscopy. As shown in Fig. 1C, a typical PEMC sensor exhibits various impedance-coupled modes over the 0 to 8 MHz frequency range. Impedance-coupled modes are defined as mechanical resonant modes which cause net charge accumulation on the electrode faces during a period of vibration.46 As shown in Fig. 2A, PEMC sensors exhibited a fundamental bending mode (n = 1) at 12.2 kHz and a second-order bending mode (n = 2) at 66.9 kHz in air. The corresponding mode shapes obtained via FEA are shown as insets in Fig. 2A. The calculated resonant frequencies based on a vacuum environment of 11.2 and 69.1 kHz compare reasonably with the experimental results. As shown in Fig. 1C, high-order modes were also present at 0.2, 1.8, 4.6, and 6.6 MHz. Previous studies show high-order impedance-coupled modes are composed of out-of-plane and in-plane combination modes.46 Importantly, as shown in Fig. 1C and 2A, both the low- and high-order resonant modes persisted in water. The modes experience a slight decrease in resonant frequency and quality factor in liquid due to increased mass loading by the surrounding medium (see Fig. 1C and 2A). A detailed description of liquid immersion response has been described elsewhere.14,48
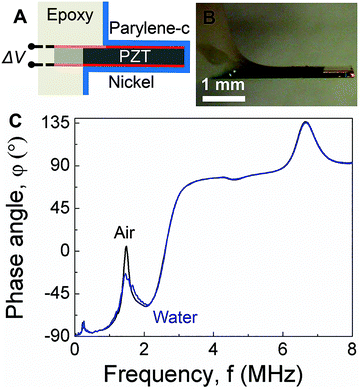 |
| | Fig. 1 (A) Schematic of a piezoelectric-excited millimeter-sized cantilever (PEMC) sensor. (B) Micrograph of a PEMC sensor. (C) Comparison of impedance spectra of the cantilever sensor in air and liquid over the 0–8 MHz frequency range showing the fundamental mode, second mode, 227 kHz mode, 1.8 MHz mode, 4.6 MHz mode and 6.6 MHz mode. | |
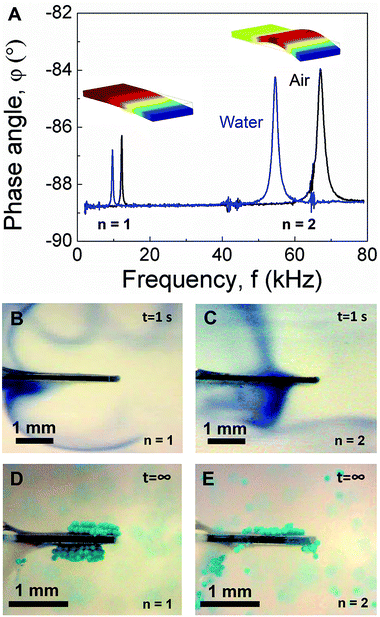 |
| | Fig. 2 (A) Comparison of cantilever sensor impedance spectra in air and liquid over the 0–80 kHz frequency range showing the fundamental and second mode. Insets show the corresponding mode shapes. Acoustic streaming profiles obtained in the fundamental (B) and second mode (C) using a dye tracer. Trapping configurations obtained in the fundamental (D) and second mode (E) using neutrally-buoyant micro-particle tracers (100 μm diameter). | |
4.2 Acoustic streaming in low-order resonant modes
Given the persistence of PEMC sensor resonance in liquid, it was of interest to determine the acoustofluidic coupling as such could lead to novel acoustofluidic and sensing applications as well as an improved fundamental understanding of dynamic-mode sensor operation in liquid. Thus, we conducted flow visualization studies using a dye tracer for the fundamental and second mode. For dye tracer flow visualization studies, dye was directly deposited onto the cantilever face using a syringe in the absence of cantilever vibration. Subsequently, the cantilever was excited at either the fundamental or second mode and the flow trajectory was monitored. Such a configuration was used in an earlier study for characterizing piezoelectric fans in air.32 As shown in Fig. 2B and C by the trajectory of the dye tracer, both the fundamental and second mode caused streaming. However, the resultant streaming profiles differed and showed strong correlation with the mode shape. Such a characteristic arises due to the dependence of the streaming force on wall displacement profile as indicated by eqn (6) and (7). Three critical observations arise from the data shown in Fig. 2B and C: (1) the displacement profiles of both modes were out-of-plane, (2) the transverse displacement profiles of the two modes differed, and (3) there was a nodal point in the second mode. Importantly, these observations agree with the FEA studies shown in Fig. 2A and cantilever deflection characteristics,48 suggesting dye tracer flow visualization studies enable imaging of cantilever mode shape in liquid. We note that previous mode shape analysis has been done via dynamic liquid submersion experiments,48 but in that case, the measurement principle required the cantilever to be in a partially submerged state.
4.3 Particle trapping in low-order resonant modes
Given the dynamic-mode cantilever caused streaming profiles which correlated with the mode shape, we next repeated the experiment using particle tracers (100 μm diameter; 10 mg mL−1) instead of dye. The data in Fig. 2D and E show dynamic-mode cantilevers not only cause streaming but also trap suspended particles adjacent to the cantilever top and bottom faces. Such is an important result as previous studies have shown that particle trapping occurred at the cantilever's sharp edges under flexural vibration.34 Importantly, we note that the distil tip of the top and bottom faces is typically the site of target binding in biosensing measurements. Videos of particle trapping in the fundamental and second mode are provided in ESI (see Movies S1 and S2,† respectively). Similar to the streaming profiles, the particle trapping zones exhibited a dependence on the mode shape. The trapping zones seeded at the regions of highest surface vibration amplitude. As shown in Fig. 2D, the two trapping zones for the fundamental mode were slightly asymmetric arising from the asymmetric anchor which provides electrically observable impedance-coupled modes.49 The trapping zone on the cantilever short side was slightly shifted towards the anchor. Movies S1 and S2† show particle trapping begins with a seeding region and extends from the cantilever surface with time, ultimately resulting in multiple layers of trapped particles at steady state. The amount of trapped particles and the size of the trapping region at steady state increased with the concentration of beads in the suspension (100 mg mL−1; data not shown). In contrast, as shown in Fig. 2E, the three trapping zones for the second mode were highly asymmetric. Interestingly, a trapping zone was observed near the cantilever anchor. We note that the particles remained trapped for the duration of excitation (examined over many hours). Importantly, as shown in Movies S1 and S2† no particle adsorption or trapping was observed in the absence of cantilever vibration (i.e. excitation voltage).
4.4 Acoustic streaming force and mode shape visualization
The streaming profiles and trapping configurations visualized in Fig. 2B–E suggest that the force exerted on the fluid by the dynamic-mode cantilever depends on the mode shape. Thus, a flow visualization experiment was designed to further image the mode shape and the positional dependence of the exerted force. As shown in Fig. 3A, a second dye visualization study was designed in which a density-driven tracer stream was established adjacent to a vertically-positioned cantilever. The tracer stream was thus surrounded by a quiescent water medium through which the streaming force penetrates. Such a configuration enabled control over dye rotation due to the continual density-driven axial flow. After allowing the dye stream to reach a steady state profile in the absence of cantilever vibration as shown in Fig. 3A, the cantilever was excited at either the fundamental or second mode and the flow trajectory was monitored. As shown in Fig. 3B, the presence of cantilever vibration in the fundamental mode led to a deflection of the dye stream. The deflection was largest near the tip and decreased along the cantilever length. The trajectory near the cantilever anchor was similar to the control stream shown in Fig. 3A obtained in the absence of cantilever vibration. Thus, as the fundamental mode shape contains no nodal points and exhibits maximum deflection at the tip (see Fig. 2A), the deflected dye stream trajectory provided imaging of the mode shape. Such is an interesting result as the cantilever was not in direct contact with the dye stream. In order to gain further confidence that the deflected dye stream trajectory provides imaging of the mode shape, experiments were repeated using the second mode. As shown in Fig. 3C, the deflection profile matched the mode shape which is characterized by a single nodal point at 0.78L. The observed dye stream deflection was larger for the fundamental mode than the second mode which is consistent with modal mechanics. In both cases, the dye stream deflection profile coincided with the mode shape indicating: (1) the cantilever-associated force on the surrounding fluid depends on vibration amplitude, and (2) dye stream tracers enable the imaging of dynamic-mode cantilever mode shape in liquid. These observations also align with previous modeling of streaming established by vibrating cantilevers40 and transversely oscillating walls50 in terms of: (1) the observation of vortices between nodal points and antinodes,28,50 (2) the dependence of the number of vortices on the number of nodes in the transverse oscillation profile,40 and (3) the presence of particle trapping in pressure nodes and antinodes of the established pressure field.34
 |
| | Fig. 3 Vibration-induced fluid body force visualization via a density-driven dye tracer stream through a quiescent water medium shown in the absence of vibration (A) and during excitation in the fundamental (B, n = 1) and second mode (C, n = 2). | |
4.5 Finite element analysis of acoustic streaming
In order to gain further confidence that cantilever vibration induces fluid motion by streaming, we modeled the vibration-induced flow established by the fundamental and second modes using FEA. As shown in Fig. 4, computational fluid dynamics (CFD) simulations showed contact between the vibrating cantilever and the fluid domain caused streaming in both modes, albeit with unique streaming profiles. As shown in Fig. 4A and B, the second mode produced more vortices in the fluid than the first mode which is expected as it contains more nodal points. The simulations also agree reasonably with the experimentally observed vortices and trapping zones (see Fig. 2 and 3), suggesting that the mechanism of dye mixing was dynamic-mode cantilever-driven acoustic streaming. The mechanism of particle motion and trapping is attributed to drag forces (FD) and primary radiation forces (FPR) exerted on the suspended particles given as:33,35,51| | 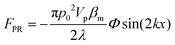 | (9) |
where Vp is the volume of the particle, vr is the flow velocity relative to the object, p0 is the pressure amplitude, λ is the ultrasonic wavelength, k is defined by 2π/λ, ci is the speed of sound in the ith material, βm is the compressibility of the medium = 1/ρmcm2, βp is the compressibility of the particle = 1/ρpcp2, ρm and ρp are the respective medium and particle densities, x is the distance from a pressure node, and the acoustic contrast factor (Φ) is given by the following relationship:| | 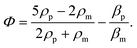 | (10) |
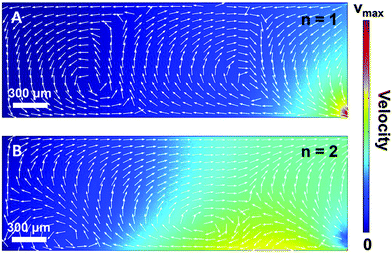 |
| | Fig. 4 (A) Finite element analysis of acoustic streaming in the fundamental (n = 1; A) and second (n = 2; B) mode. | |
4.6 Axial particle manipulation via switching between low-order modes
The streaming and particle trapping studies (Fig. 2 and 3) and simulation results (Fig. 4) demonstrate the streaming and trapping effects are governed by the characteristics of cantilever vibration, therein enabling mode shape visualization. However, the dependence of the trapping configuration on mode shape not only enables one to separate suspended particles from the surrounding medium, visualize mode shape, and confine particles to specific regions of the cantilever, but it also suggests that particles could be manipulated by switching between resonant modes after initially trapping. Therefore, we investigated if trapped particles could be manipulated by switching between resonant modes, hereinafter referred to as mode switching. As shown in Fig. 5A, the manipulation experiments began by first trapping particles in the fundamental mode. After the particles were trapped, the driving frequency was switched to the resonant frequency of the second mode. As shown in Fig. 5B, the initially trapped particles reorganized in seconds to a new configuration (see Movie S3 of ESI†). The configuration after switching showed a strong resemblance to the second mode trapping configuration shown in Fig. 2E which was obtained from trapping initially suspended particles. Having shown that trapped particles could be manipulated by mode switching from the fundamental to the second mode, we next examined if the already manipulated particles could be further manipulated into a new configuration by switching to a different resonant mode (fair = 227 kHz; fwater = 213 kHz) given previous research showed modes at this frequency are characterized by combination modes.46 As shown in Fig. 5C, mode switching from the second mode to the 227 kHz mode indeed resulted in a new trapping configuration. The new configuration was composed of three trapping zones, similar to the second mode configuration, but contained relatively more particles trapped at the tip and less particles trapped in the middle and base. Additionally, the particles trapped at the tip exhibited rotational motion (see Movie S4 of ESI†). The observation of rotational motion is an important feature as rotational manipulation of cells and organisms has significance across applications in medicine, biology, and chemistry.52 We also found switching the excitation frequency back to the fundamental mode caused the particles to return to the original configuration indicating that the particles could be reversibly manipulated (data not shown).
 |
| | Fig. 5 Particle manipulation via switching between low-order modes. (A) The initial trapping configuration obtained using the fundamental mode (n = 1). (B) The steady state trapping configuration obtained after switching from the fundamental to the second mode (n = 2). (C) The steady state trapping configuration obtained after switching from the second mode to a low-order mode at 227 kHz. | |
4.7 Lateral particle manipulation via switching between low- and high-order modes
Given the sensor impedance response in Fig. 1C shows high-order modes above 1 MHz, and previous research suggests they have complex mode shapes involving in-plane motion,46 we examined if trapped particles could be laterally manipulated in addition to the axial manipulation shown in Fig. 5. Thus, we repeated the manipulation experiments, but instead of switching to the second mode after initial trapping in the fundamental mode the frequency was switched to the high-order mode at 1.8 MHz. As shown in Fig. 6A and B, mode switching from the fundamental mode to the 1.8 MHz mode enabled lateral manipulation of trapped particles into a new trapping configuration. Two distinct trapping zones were identified which extended from the cantilever anchor to beyond the cantilever tip. As shown in Fig. 6C, mode switching to a different high-order mode at 4.6 MHz after the first manipulation resulted in a new trapping configuration which exhibited three laterally distributed trapping zones. Importantly, we note that the trapping zone at 1.8 MHz extended slightly beyond the cantilever tip. Similar to low-order mode switching, we also found the particles could be reversibly manipulated. Thus, we found particles may be manipulated in either axial or lateral directions by use of the appropriate resonant mode.
 |
| | Fig. 6 Particle manipulation via switching between low- and high-order modes. (A) The initially trapped particle configuration obtained in the fundamental mode (n = 1). (B) The steady state particle configuration obtained after switching from the fundamental mode to a high-order mode at 1.8 MHz. (C) The steady state particle configuration obtained after switching from the high-order mode at 1.8 MHz to a high-order mode at 4.6 MHz. | |
4.8 Release of trapped particles via mode switching
The ability for high-order modes to trap particles beyond the cantilever tip as shown in Fig. 6B suggests a potential opportunity to rapidly release trapped particles from the cantilever. Thus, we repeated the experiments shown in Fig. 5 and 6, but instead of switching to the second mode or the 1.8 MHz mode after initial trapping in the fundamental mode the driving waveform was switched to a noise signal which would simultaneously excite multiple high-order modes across the frequency spectrum. As shown in Fig. 7A–C, switching the waveform to a noise signal was effective for rapidly releasing trapped particles within ∼1 s (see Movie S5 of ESI†). We also found that switching to a single high-order mode at 6.6 MHz instead of the noise waveform was similarly effective for rapidly releasing trapped particles (data not shown). We note that the particles could be re-trapped after release by switching back to the low-order modes.
 |
| | Fig. 7 Release of particles trapped using the fundamental mode via switching the driving waveform to a noise signal showing the initial trapped particle configuration (A), the particle configuration ∼0.5 s after change to the noise signal (B), and the sensor post-release (C). | |
5. Conclusions
We have shown that dynamic-mode cantilevers exhibit significant acoustofluidic effects which enable acoustic streaming and trapping of suspended micro-particles adjacent to the traditional sensing locations. The vibration-induced streaming profiles and trapping configurations showed dependence on the mode shape and enabled mode shape visualization in liquid. We also showed that switching the resonant mode between low- and high-order modes enabled the deterministic manipulation of trapped particles in both axial and lateral directions. The trapped particles could be released from the vibrating cantilever by switching to a high-order mode or switching the waveform to a noise signal. This work suggests that dynamic-mode cantilever sensors may enable novel acoustofluidic applications and lead to an improved fundamental understanding of device operation in liquid.
Acknowledgements
The authors are grateful for the generous support of NSF Grant CBET-1159841 which provided the entire funding for the reported work.
References
- B. N. Johnson and R. Mutharasan, Biosens. Bioelectron., 2012, 32, 1–18 CrossRef CAS PubMed.
- C. Ziegler, Anal. Bioanal. Chem., 2004, 379, 946–959 CAS.
- N. V. Lavrik, M. J. Sepaniak and P. G. Datskos, Rev. Sci. Instrum., 2004, 75, 2229–2253 CrossRef CAS.
- G. A. Campbell and R. Mutharasan, Biosens. Bioelectron., 2006, 21, 1684–1692 CrossRef CAS PubMed.
- G. A. Campbell and R. Mutharasan, Biosens. Bioelectron., 2008, 23, 1039–1045 CrossRef CAS PubMed.
- Y. J. Ding and R. Mutharasan, Environ. Sci. Technol., 2011, 45, 1490–1496 CrossRef CAS PubMed.
- B. N. Johnson and R. Mutharasan, Analyst, 2013, 138, 6365–6371 RSC.
- D. Maraldo, F. U. Garcia and R. Mutharasan, Anal. Chem., 2007, 79, 7683–7690 CrossRef CAS PubMed.
- D. Maraldo and R. Mutharasan, Anal. Chem., 2007, 79, 7636–7643 CrossRef CAS PubMed.
- K. Rijal and R. Mutharasan, Anal. Chem., 2007, 79, 7392–7400 CrossRef CAS PubMed.
- B. N. Johnson and R. Mutharasan, Anal. Chem., 2012, 84, 10426–10436 CrossRef CAS PubMed.
- B. N. Johnson and R. Mutharasan, Environ. Sci. Technol., 2013, 47, 12333–12341 CrossRef CAS PubMed.
- B. N. Johnson and R. Mutharasan, Analyst, 2014, 139, 1112–1120 RSC.
- B. N. Johnson and R. Mutharasan, J. Appl. Phys., 2011, 109, 066105 CrossRef.
- L. Fadel, F. Lochon, I. Dufour and O. Francais, J. Micromech. Microeng., 2004, 14, S23–S30 CrossRef CAS.
- S. Q. Li, L. L. Fu, J. M. Barbaree and Z. Y. Cheng, Sens. Actuators, B, 2009, 137, 692–699 CrossRef CAS.
- C. A. Van Eysden and J. E. Sader, J. Appl. Phys., 2007, 101, 044908 CrossRef.
- G. A. Campbell and R. Mutharasan, Biosens. Bioelectron., 2005, 21, 597–607 CrossRef CAS PubMed.
- H. Sharma and R. Mutharasan, Biosens. Bioelectron., 2013, 45, 158–162 CrossRef CAS PubMed.
- S. Xu and R. Mutharasan, Sens. Actuators, B, 2013, 176, 1141–1146 CrossRef CAS.
- S. K. Sankaranarayanan, R. Singh and V. R. Bhethanabotla, J. Appl. Phys., 2010, 108, 104507 CrossRef.
- S. K. R. S. Sankaranarayanan, S. Cular, V. R. Bhethanabotla and B. Joseph, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 066308 CrossRef PubMed.
- R. Singh, S. Sankaranarayanan and V. R. Bhethanabotla, Appl. Phys. Lett., 2009, 94, 263503 CrossRef.
- C. H. Choi, A. J. Scardino, P. G. Dylejko, L. E. Fletcher and R. Juniper, Biofouling, 2013, 29, 195–202 CrossRef CAS PubMed.
-
P. Y. Yeh, J. Kizhakkedathu and M. Chiao, in Biomaterials for MEMS, Pan Stanford Publishing, 2011 Search PubMed.
- P.-Y. J. Yeh, J. N. Kizhakkedathu, J. D. Madden and M. Chiao, Colloids Surf., B, 2007, 59, 67–73 CrossRef CAS PubMed.
- H. K. Ma, B. R. Hou, H. Y. Wu, C. Y. Lin, J. J. Gao and M. C. Kou, Microsyst. Technol., 2008, 14, 1001–1007 CrossRef CAS.
- B.-G. Loh, S. Hyun, P. I. Ro and C. Kleinstreuer, J. Acoust. Soc. Am., 2002, 111, 875–883 CrossRef PubMed.
- Q. Wan, T. Wu, J. Chastain, W. Roberts, A. Kuznetsov and P. Ro, Flow, Turbul. Combust., 2005, 74, 195–206 CrossRef.
- H. Gomaa, A. M. Al Taweel and J. Landau, Chem. Eng. J., 2004, 97, 141–149 CrossRef CAS.
- T. Wu, P. I. Ro, A. I. Kingon and J. F. Mulling, Smart Mater. Struct., 2003, 12, 181 CrossRef CAS.
- S. M. Wait, S. Basak, S. V. Garimella and A. Raman, IEEE Trans. Compon. Packag. Technol., 2007, 30, 119–128 CrossRef.
- F. Petersson, L. Åberg, A.-M. Swärd-Nilsson and T. Laurell, Anal. Chem., 2007, 79, 5117–5123 CrossRef CAS PubMed.
- J. Hu, J. Yang and J. Xu, Appl. Phys. Lett., 2004, 85, 6042–6044 CrossRef CAS.
- B. Raeymaekers, C. Pantea and D. N. Sinha, J. Appl. Phys., 2011, 109, 014317 CrossRef.
- M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991 CrossRef CAS PubMed.
- H. Li, J. Friend and L. Yeo, Biomed. Microdevices, 2007, 9, 647–656 CrossRef PubMed.
- J. Friend and L. Y. Yeo, Rev. Mod. Phys., 2011, 83, 647–704 CrossRef.
- M. Wiklund, R. Green and M. Ohlin, Lab Chip, 2012, 12, 2438–2451 RSC.
- T. Açikalin, A. Raman and S. V. Garimella, J. Acoust. Soc. Am., 2003, 114, 1785–1795 CrossRef.
- H. T. Yu and X. X. Li, Appl. Phys. Lett., 2009, 94, 011901 CrossRef.
- S. J. Lighthill, J. Sound Vib., 1978, 61, 391–418 CrossRef.
- W. L. Nyborg, J. Acoust. Soc. Am., 1958, 30, 329–339 CrossRef.
- W. L. Nyborg, J. Acoust. Soc. Am., 1953, 25, 68–75 CrossRef.
- N. Riley, Theor. Comput. Fluid Dyn., 1998, 10, 349–356 CrossRef.
- B. N. Johnson and R. Mutharasan, Sens. Actuators, B, 2011, 155, 868–877 CrossRef CAS.
- B. N. Johnson, H. Sharma and R. Mutharasan, Anal. Chem., 2013, 85, 1760–1766 CrossRef CAS PubMed.
- B. N. Johnson and R. Mutharasan, J. Micromech. Microeng., 2011, 21, 065027 CrossRef.
- H. Sharma, R. S. Lakshmanan, B. N. Johnson and R. Mutharasan, Sens. Actuators, B, 2011, 153, 64–70 CrossRef CAS.
- F. Carlsson, M. Sen and L. Löfdahl, Phys. Fluids, 2004, 16, 1822–1825 CrossRef CAS.
- T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506 RSC.
- D. Ahmed, A. Ozcelik, N. Bojanala, N. Nama, A. Upadhyay, Y. Chen, W. Hanna-Rose and T. J. Huang, Nat. Commun., 2016, 7, 11085 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6an01743f |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article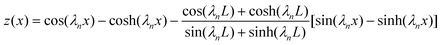
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt)z(x)
cos(ωt)z(x)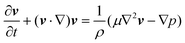
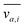 , i = x, y and z) is given as the time-averaged velocity:28
, i = x, y and z) is given as the time-averaged velocity:28