2D analysis of polydisperse core–shell nanoparticles using analytical ultracentrifugation†
Johannes
Walter
ab,
Gary
Gorbet
c,
Tugce
Akdas
ab,
Doris
Segets
ab,
Borries
Demeler
*c and
Wolfgang
Peukert
*ab
aInstitute of Particle Technology (LFG), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Cauerstr. 4, 91058 Erlangen, Germany. E-mail: wolfgang.peukert@fau.de; Tel: +49 9131 8529401
bInterdisciplinary Center for Functional Particle Systems (FPS), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Haberstr. 9a, 91058 Erlangen, Germany
cDepartment of Biochemistry, The University of Texas Health Science Center at San Antonio, 7703 Floyd Curl Drive, San Antonio, Texas 78229-3901, USA. E-mail: demeler@biochem.uthscsa.edu; Tel: +1 210 767 3332
First published on 28th November 2016
Abstract
Accurate knowledge of the size, density and composition of nanoparticles (NPs) is of major importance for their applications. In this work the hydrodynamic characterization of polydisperse core–shell NPs by means of analytical ultracentrifugation (AUC) is addressed. AUC is one of the most accurate techniques for the characterization of NPs in the liquid phase because it can resolve particle size distributions (PSDs) with unrivaled resolution and detail. Small NPs have to be considered as core–shell systems when dispersed in a liquid since a solvation layer and a stabilizer shell will significantly contribute to the particle's hydrodynamic diameter and effective density. AUC measures the sedimentation and diffusion transport of the analytes, which are affected by the core–shell compositional properties. This work demonstrates that polydisperse and thus widely distributed NPs pose significant challenges for current state-of-the-art data evaluation methods. The existing methods either have insufficient resolution or do not correctly reproduce the core–shell properties. First, we investigate the performance of different data evaluation models by means of simulated data. Then, we propose a new methodology to address the core–shell properties of NPs. This method is based on the parametrically constrained spectrum analysis and offers complete access to the size and effective density of polydisperse NPs. Our study is complemented using experimental data derived for ZnO and CuInS2 NPs, which do not have a monodisperse PSD. For the first time, the size and effective density of such structures could be resolved with high resolution by means of a two-dimensional AUC analysis approach.
1. Introduction
Nanoparticles (NPs) find a wide range of applications in nanotechnology and biomedicine.1–4 In order to guarantee a high performance in later applications, accurate characterization of NPs is required. Various techniques have been developed to characterize NPs being either directly synthesized in solution or deposited from solution on a solid substrate. Analytical ultracentrifugation (AUC) is one of the most accurate techniques for the characterization of NPs in the liquid phase because it can resolve particle size distributions (PSDs) with high resolution and detail also in the sub-nm range.5–8 Sizes ranging from less than one nanometer to a few micrometers can be analyzed depending on the particle's density.Small NPs must be considered as core–shell systems when dispersed in a liquid. The NP surface is functionalized by ligands or stabilizer molecules specifically binding to it and a solvation layer that further adds to the NP diameter. Therefore, the shell consists of two parts, the functionalization and the solvation layer. For the sake of simplicity, a core–shell model will be used in this work, incorporating contributions from both parts into the shell. The shell increases the hydrodynamic diameter of the NP and contributes to the partial specific volume, which is given here as the inverse of the density of the sedimenting NP, which also carries with it a solvation layer. To differentiate the observed density and partial specific volume from the anhydrous NP density and volume, we refer to it here as the “effective” density and “effective” partial specific volume. Since AUC measures the sedimentation and diffusion transport of the analytes, the effect of the shell composition on the size and effective partial specific volume directly translates into changes in sedimentation and diffusion properties.
The sedimentation and diffusion transport in AUC experiments is modelled by finite element solutions of the Lamm equation. High performance techniques such as the two-dimensional spectrum analysis (2DSA) and parametrically constrained spectrum analysis (PCSA) implemented in the UltraScan3 software or the c(s, D) analysis implemented in Sedfit offer the possibility to address polydispersity in more than one dimension.9–11 This allows for the simultaneous analysis of the size and shape anisotropy of macromolecules and NPs under the condition that the sedimentation and diffusion information is sufficiently represented in the data. Recent developments in data evaluation considerably widened the possibilities of NP analysis. Carney et al. showed for the first time that simultaneous characterization of NPs with respect to their size and effective density becomes possible by applying 2D analysis to sedimentation velocity (SV) data.12 Recently, it was shown by Demeler et al. that characterization of the size anisotropy and heterogeneity of the effective density of NPs can be determined by performing SV experiments using the Custom Grid 2DSA (CG).13 In both cases it has been demonstrated that these models work well for samples of fairly monodisperse NPs. This opens up a variety of new applications as the core–shell composition of NPs can now be measured in solution.
However, the majority of particle production methods, either performed as bottom up synthesis or top down comminution or emulsification, will yield polydisperse PSDs. As a consequence, most samples will contain a large number of different species, just slightly varying in size and effective density. However, this poses special challenges to high resolution algorithms because of the reduced experimental signal available from each individual species. Furthermore, a higher resolution grid that tries to represent the larger number of species also increases the degeneracy of the 2DSA solutions. In addition, simulating a large number of solutes makes the solution sensitive to systematic and random noise effects, which are present in any experimental data.
Mittal et al. compared the performance of different methods for the analysis of SV data with respect to NPs.14 However, the applicability of modern tools for the simultaneous analysis of the size and effective density was not addressed and thus only one-dimensional (1D) evaluations of the sedimentation coefficients were compared. Therefore, polydisperse and multimodal NPs have never been investigated by powerful multidimensional AUC analysis, even though these samples represent the majority of systems in nanotechnology.
In this work, we will place special emphasis on the analysis of NPs with different levels of polydispersity in their size and effective density. By simulating a variety of distributions containing up to 5000 solutes, the effects of random noise and rotor speeds on the evaluation results from high performance methods can be compared. Monomodal, fairly monodisperse (σ = 0.1) NPs, multimodal but fairly monodisperse (σ < 0.15) NPs as well as a multimodal polydisperse (σ < 1.0) distributions of NPs will be considered. Our results show that a newly developed parameterization for the PCSA for core–shell NPs achieves a more reliable model than any other technique developed so far. The PCSA method is designed to model systems where a systematic change in two hydrodynamic parameters can describe the heterogeneity in the system. Our new parameterization is especially designed for core–shell NPs and is capable of analyzing broad PSDs with high resolution and simultaneously providing the core–shell characteristics of these systems. Even shell thicknesses varying with the NP size can be addressed in principle by the proposed methodology. The simulated data will be complemented by AUC experiments with ZnO and CuInS2 quantum dots (QDs) representing typical examples of polydisperse core–shell NPs.
2. Theory
2.1 Core–shell nanoparticles
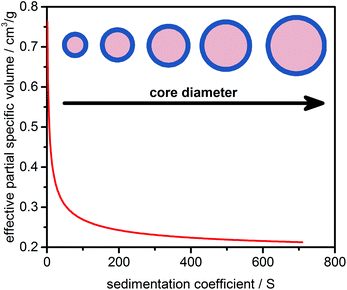
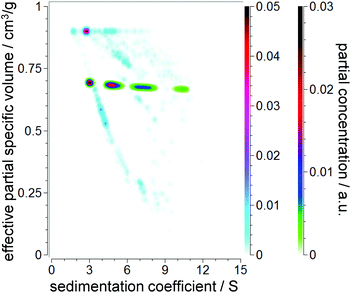
Strictly speaking, any NP dispersed in a liquid has to be treated as a core–shell system. Ligands, ions, and stabilizer and solvent molecules will form a thin layer on the NP surface. As a consequence, the effective density or effective partial specific volume of the sedimenting particle will be affected by the shell morphology (thickness, density). While the shell thickness can often be considered constant, the core diameter can vary due to NP growth and ripening. This leads to a decrease in the effective partial specific volume with the increasing core diameter and sedimentation coefficient as the effective density approaches the value of the particle core. A schematic representation of this dependency is illustrated in Fig. 1.2.2 Theory of sedimentation
The sedimentation of NPs has been described by Lamm, who considered the change in the concentration of an analyte in a gravitational field by sedimentation and diffusion in a sector shaped centrifuge cell:15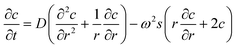 | (1) |
In this equation c denotes the concentration, r the radial distance from the axis of rotation and ω the angular velocity. The sedimentation coefficient s and diffusion coefficient D can be measured by AUC. Carney et al. were the first to show that these two quantities can be used to determine the hydrodynamic diameter and effective density of NPs provided that the shape anisotropy is known.12
D is linked to the hydrodynamic diameter dHvia Stokes–Einstein's equation:
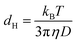 | (2) |
 | (3) |
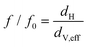 | (4) |
If the particle is spherical, f/f0 equals unity and the hydrodynamic diameter is equal to the volume equivalent as well as the effective diameter. This allows calculation of ρp,eff or the effective partial specific volume ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff:
p,eff:
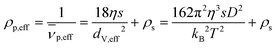 | (5) |
A detailed derivation of the equations discussed here is also given in the ESI, section 1.†
In summary, information on the hydrodynamic diameter and the effective density of the particle including all contributions from the shell can be derived from a single AUC experiment as long as s and D can be accurately measured and the shape of the particles is known. If detailed knowledge of the shape is not available, sedimentation and diffusion data derived by AUC could be misinterpreted. Potential shape induced errors for ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff and the calculated shell thicknesses are discussed in the ESI, section 2.†
p,eff and the calculated shell thicknesses are discussed in the ESI, section 2.†
2.3 Data evaluation strategies for core–shell nanoparticles
Owing to the nature of NP synthesis, a large number of different NP sizes can exist simultaneously in solution. To fully describe the core–shell properties of NPs, both parameters,![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff and s, have to be determined. As discussed in ref. 12 and 13 as well as the previous section, both parameters can be obtained in terms of the sedimentation and diffusion coefficients fitted to a SV experiment when additional prior knowledge, such as particle anisotropy or molar mass, is available. In the special cases considered here, particle anisotropy is assumed to be constant for all particles. Then, these parameters can be further interpreted in terms of hydrodynamic diameter and effective density. Assuming that the density of the solvent in the solvation layer is the same as the bulk density or that the solvation layer does not add to the hydrodynamic diameter, the shell thickness can also be estimated based on a mass conservation approach.12,16,17
p,eff and s, have to be determined. As discussed in ref. 12 and 13 as well as the previous section, both parameters can be obtained in terms of the sedimentation and diffusion coefficients fitted to a SV experiment when additional prior knowledge, such as particle anisotropy or molar mass, is available. In the special cases considered here, particle anisotropy is assumed to be constant for all particles. Then, these parameters can be further interpreted in terms of hydrodynamic diameter and effective density. Assuming that the density of the solvent in the solvation layer is the same as the bulk density or that the solvation layer does not add to the hydrodynamic diameter, the shell thickness can also be estimated based on a mass conservation approach.12,16,17
Recent studies have revealed that AUC is a highly accurate technique for the simultaneous investigation of core–shell properties of NPs in solution. Being sensitive to the mass as well as the hydrodynamic diameter, it provides multidimensional access to these properties. New generations of direct boundary models offer new insights into AUC data because two-dimensional (2D) analysis in combination with noise fitting is possible. Earlier methods like c(s) required assumption of a fixed shape (f/f0) and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff to perform a direct boundary analysis.
p,eff to perform a direct boundary analysis.
The c(s, D) analysis in Sedfit and the 2DSA in UltraScan3 allow for the independent determination of s and D. In addition, UltraScan3 offers the possibility to generate custom grids, which allows variation of two selected parameters such as s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff in the 2D space. High performance computing can further be performed using UltraScan3, which permits the use of higher resolution grids and greatly enhances the throughput. This is critical for the analysis of multiwavelength (MWL) data.18
p,eff in the 2D space. High performance computing can further be performed using UltraScan3, which permits the use of higher resolution grids and greatly enhances the throughput. This is critical for the analysis of multiwavelength (MWL) data.18
Unlike CG allowing for multiple combinations of hydrodynamic parameters, the PCSA implementation in UltraScan versions prior to release version 1977 provided access to variations of f/f0 as a function of s. This makes sense for systems with constant ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff and predictable anisotropy changes as a function of mass, such as rods of increasing length. However, as discussed above, spherical core–shell NPs can be perfectly fitted by the PCSA reparameterized in terms of the sedimentation coefficient and effective partial specific volume because of their unique correspondence as shown in Fig. 1. This is of greater interest to us than the constant shape anisotropy of many NPs which tend to remain spherical regardless of size. However, parameterization via a straight or horizontal line or an increasing or decreasing sigmoidal function is not suitable to mathematically reproduce the change of s versus
p,eff and predictable anisotropy changes as a function of mass, such as rods of increasing length. However, as discussed above, spherical core–shell NPs can be perfectly fitted by the PCSA reparameterized in terms of the sedimentation coefficient and effective partial specific volume because of their unique correspondence as shown in Fig. 1. This is of greater interest to us than the constant shape anisotropy of many NPs which tend to remain spherical regardless of size. However, parameterization via a straight or horizontal line or an increasing or decreasing sigmoidal function is not suitable to mathematically reproduce the change of s versus ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff for most NP systems.
p,eff for most NP systems.
In this work, we expanded the PCSA in such a way that it can handle any variation of parameters. Here the variation of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,effversus s is of interest. Moreover, we sought of a parameterization correctly representing core–shell systems. Previous parameterizations relied on only one (horizontal line) or two (straight line, sigmoidal) variables. An empirical 2nd order power law with three variables was found to fit the curve of s versus
p,effversus s is of interest. Moreover, we sought of a parameterization correctly representing core–shell systems. Previous parameterizations relied on only one (horizontal line) or two (straight line, sigmoidal) variables. An empirical 2nd order power law with three variables was found to fit the curve of s versus ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff developed for a core–shell system (see Fig. 1) very well (R2 > 0.99):
p,eff developed for a core–shell system (see Fig. 1) very well (R2 > 0.99):
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff = asb + c p,eff = asb + c | (6) |
During the parameterization of the 2D space the parameters a, b and c are varied based on the minimum and maximum x- and y-ranges. Here, a has units of [s−1![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff] = cm3 gS−1, c has units of [
p,eff] = cm3 gS−1, c has units of [![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff] = cm3 g−1 and b is dimensionless. It is important to note that s and
p,eff] = cm3 g−1 and b is dimensionless. It is important to note that s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff are used for the parameterization, while s and D are fitted. The transformation of s and
p,eff are used for the parameterization, while s and D are fitted. The transformation of s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff to the fitted s and D combinations is based on eqn (5) and entirely rigorous. It only requires the assumption of a known shape anisotropy. No assumption on the functionalization or solvation properties is made up to this point. More information about the equations for the calculations of those variables can be found online in the open source wiki of UltraScan3, which provides access to the source code: http://wiki.bcf2.uthscsa.edu/ultrascan3/.
p,eff to the fitted s and D combinations is based on eqn (5) and entirely rigorous. It only requires the assumption of a known shape anisotropy. No assumption on the functionalization or solvation properties is made up to this point. More information about the equations for the calculations of those variables can be found online in the open source wiki of UltraScan3, which provides access to the source code: http://wiki.bcf2.uthscsa.edu/ultrascan3/.
Moreover, data retrieved from the analysis can always be plotted and interpreted in terms of s and D. Options for parameterization of other valid combinations of parameters exist. In the present work ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff and s were chosen for parameterization because of the aforementioned reasons.
p,eff and s were chosen for parameterization because of the aforementioned reasons.
An example set of parametric curves based on the 2nd order power law is shown in Fig. 2. The density of curves can be easily increased by choosing a higher variation count. The variation count K gives the number of variations per variable. For the 2nd order power law this results in K3 combinations. For a detailed description of the PCSA algorithm the reader is referred to the work of Gorbet et al.11 Briefly, the PCSA discretizes s and D along the parametric curves and fits the amplitudes of individual terms in the linear combinations of the corresponding Lamm equation solutions to the experimental data. The parametric curve giving rise to the lowest root mean square deviation (RMSD) will then represent the best parameterization for the underlying distribution.
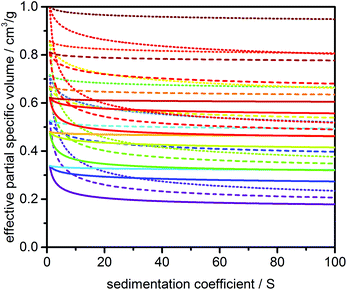 | ||
| Fig. 2 Representative set of model lines used for the PCSA generated with the 2nd order power law parameterization and a variation count K of 3. | ||
As discussed above, when s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff are varied in the PCSA, the assumption is made that f/f0 is known and constant for all analytes in the mixture. For core–shell NPs with variable
p,eff are varied in the PCSA, the assumption is made that f/f0 is known and constant for all analytes in the mixture. For core–shell NPs with variable ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff, a constant f/f0 has to be verified by other techniques, e.g. transmission electron microscopy (TEM). Fortunately, in a first approximation many particulate systems can be treated as spherical. However, in the case of rods or sheets with variable anisotropies or mixtures of different shapes, a unique solution is not available. Thus, knowledge of the particle shape is at the core of this methodology and therefore immediately constrains the approach to selected systems in nanotechnology.
p,eff, a constant f/f0 has to be verified by other techniques, e.g. transmission electron microscopy (TEM). Fortunately, in a first approximation many particulate systems can be treated as spherical. However, in the case of rods or sheets with variable anisotropies or mixtures of different shapes, a unique solution is not available. Thus, knowledge of the particle shape is at the core of this methodology and therefore immediately constrains the approach to selected systems in nanotechnology.
3. Methods and materials
3.1 Materials and sample preparation
3.2 Simulation of synthetic data
All NP simulations were calculated with a Lamm equation solution based on the finite-element method (FEM) proposed by Claverie et al. with a constant time grid and a regular radial grid containing 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 radial points.24 UltraScan3 (release version 1977) was used to carry out the simulations. The simulated solution was interpolated onto a radial grid with 10 μm spacing. The same solution was used before as a reference solution for determining the accuracy of the adaptive space-time FEM (ASTFEM) solution.25 Each experiment was simulated with 200–300 equally spaced scans depending on the rotor speed and width of the distributions, such that the moving boundary spanned the entire solution column. The meniscus position was fixed at 5.8 cm and the bottom of the cell position was held constant at 7.2 cm for all simulations. Rotor acceleration was simulated during the finite-element calculation for each dataset.
000 radial points.24 UltraScan3 (release version 1977) was used to carry out the simulations. The simulated solution was interpolated onto a radial grid with 10 μm spacing. The same solution was used before as a reference solution for determining the accuracy of the adaptive space-time FEM (ASTFEM) solution.25 Each experiment was simulated with 200–300 equally spaced scans depending on the rotor speed and width of the distributions, such that the moving boundary spanned the entire solution column. The meniscus position was fixed at 5.8 cm and the bottom of the cell position was held constant at 7.2 cm for all simulations. Rotor acceleration was simulated during the finite-element calculation for each dataset.
Three different types of distributions with increasing complexity were simulated using up to four normally distributed (Gaussian) probability functions: model #1 (narrow monomodal PSD), model #2 (narrow multimodal PSD) and model #3 (multimodal polydisperse PSD). For these PSDs, the core diameter of the ZnO NPs was varied, while keeping the thickness of the shell constant (0.235 nm).
In practice, the number of ligands bound per particle surface can vary due to changes of the surface chemistry. To reflect such changes, a fourth model based on model #3 was simulated with identical distribution parameters but a shell of decreasing thickness. The thickness of the shell was varied linearly between 0.5 nm for a core diameter of 0 nm and 0.2 nm for a core diameter of 15 nm (−0.02 nm nm−1), see Fig. S8† for a graphical representation. The expected values, standard deviations and relative concentrations for all models can be found in Table 1.
| Model # | 1 | 2 | 3 | 4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Species # | 1 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Core diameter dcore/nm | 4.00 | 2.00 | 3.00 | 4.50 | 6.50 | 2.00 | 3.00 | 4.25 | 8.00 | 2.00 | 3.00 | 4.25 | 8.00 |
| Standard deviation σ/– | 0.10 | 0.05 | 0.15 | 0.10 | 0.15 | 0.40 | 0.45 | 0.40 | 1.00 | 0.40 | 0.45 | 0.40 | 1.00 |
| Shell thickness dshell/nm | 0.235 | 0.235 | 0.235 | 0.235 | 0.235 | 0.235 | 0.235 | 0.235 | 0.235 | 0.50 nm–0.02 × dcore | |||
| Relative concentration crel/% | 100 | 10 | 40 | 30 | 20 | 20 | 40 | 30 | 10 | 20 | 40 | 30 | 10 |
For all simulations, the density and viscosity of the solution was assumed to be that of water at 20 °C (0.9982 g cm−3, 1.0019 cp). The ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) of the core was assumed to be 0.1783 cm3 g−1 (pure ZnO) and the
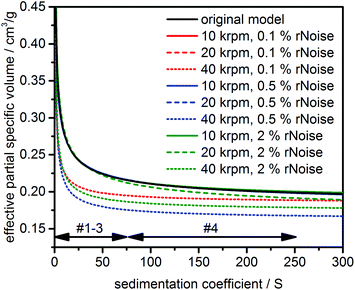
of the core was assumed to be 0.1783 cm3 g−1 (pure ZnO) and the ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) of the shell was set at 0.9524 cm3 g−1 (pure acetic acid). The effect of solvation on the shell thickness and density was not considered for the simulations for the sake of simplicity. For models #1–#3 we further compared different levels of random noise proportional to the loading concentration of 1.0 OD (0.1%, 0.5%, 2.0%) as a “worst-case” scenario (see chapter 12 in the ESI† for more discussion) as well as rotor speeds (10 krpm, 20 krpm, 40 krpm) to assess their influence on the performance of the analysis and the obtained distributions. Model #4 was simulated at a rotor speed of 20 krpm and a random noise level of 0.05%, which is a typical value achieved in an AUC experiment. Time and radially invariant noise with levels of 0.1% each were simulated for all datasets to mimic imperfections being present in any experiment. However, it should be noted that such a type of noise can be effectively removed mathematically as it has been described in ref. 26 and, as implemented in UltraScan3, in ref. 27.
of the shell was set at 0.9524 cm3 g−1 (pure acetic acid). The effect of solvation on the shell thickness and density was not considered for the simulations for the sake of simplicity. For models #1–#3 we further compared different levels of random noise proportional to the loading concentration of 1.0 OD (0.1%, 0.5%, 2.0%) as a “worst-case” scenario (see chapter 12 in the ESI† for more discussion) as well as rotor speeds (10 krpm, 20 krpm, 40 krpm) to assess their influence on the performance of the analysis and the obtained distributions. Model #4 was simulated at a rotor speed of 20 krpm and a random noise level of 0.05%, which is a typical value achieved in an AUC experiment. Time and radially invariant noise with levels of 0.1% each were simulated for all datasets to mimic imperfections being present in any experiment. However, it should be noted that such a type of noise can be effectively removed mathematically as it has been described in ref. 26 and, as implemented in UltraScan3, in ref. 27.
The simulated SV profiles are shown in Fig. S4–S7 in the ESI† for all models and simulation parameters.
3.3 Methods and measurements
UltraScan3 (Version 3.3, Revisions: 1977–2059) was used for performing the 2DSA, CG and PCSA. The resolution (in s × D) was varied between 80 × 80 and 120 × 100 grid points for the 2DSA and CG as well as 150 and 400 points in s for the final PCSA depending on the data analyzed. A lower resolution of 75 grid points was used to find the best parameterization in the PCSA. For the 2DSA/CG, Monte Carlo (MC) analyses with 100 iterations were performed. The final model of the PCSA was further smoothed using the Tikhonov regularization (TR). MC analysis was also tested but TR was chosen due to the prior knowledge of the smooth distributions.
4. Results and discussion
4.1 Synthetic data
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff and f/f0.8,14,30,31 For narrow PSDs, the c(s) analysis performs well if the correct
p,eff and f/f0.8,14,30,31 For narrow PSDs, the c(s) analysis performs well if the correct ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff is provided. The detailed results are given in the ESI, Fig. S9.† However, broad PSDs such as the case for models #2 and #3 will result in a wide range of
p,eff is provided. The detailed results are given in the ESI, Fig. S9.† However, broad PSDs such as the case for models #2 and #3 will result in a wide range of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff values which invalidates the direct boundary analysis by c(s) since inappropriate diffusion information is used for the solution of the Lamm equation. This resulted in false positives and reduced resolution as can be seen in Fig. 3 for model #3 (further discussed in ref. 11). The results for models #1 and #2 are shown in Fig. S9.†
p,eff values which invalidates the direct boundary analysis by c(s) since inappropriate diffusion information is used for the solution of the Lamm equation. This resulted in false positives and reduced resolution as can be seen in Fig. 3 for model #3 (further discussed in ref. 11). The results for models #1 and #2 are shown in Fig. S9.†
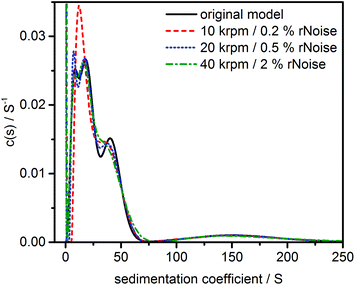 | ||
| Fig. 3 Sedimentation coefficient distribution as obtained by the c(s) analysis for a multimodal polydisperse PSD (model #3) simulated at different noise levels and rotor speeds. For other models see Fig. S9.† | ||
In addition, information about ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff is also not available. Despite the popularity of the c(s) method, it is unsuitable for the analysis of broad PSDs of small NPs which display a prominent change in
p,eff is also not available. Despite the popularity of the c(s) method, it is unsuitable for the analysis of broad PSDs of small NPs which display a prominent change in ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff with s, or in cases where the core–shell properties need to be investigated.
p,eff with s, or in cases where the core–shell properties need to be investigated.
The c(s, D) algorithm as implemented in Sedfit is an extension of the c(s) analysis and allows for covering a grid of about 30 × 30 sedimentation and diffusion coefficient pairs. The best result is further regularized to stabilize the solution against random noise and thus provides a smooth sedimentation 2D distribution appearance depending on the degree of regularization applied. Our investigations revealed that it performs well for monomodal or multiple discrete species comparable to the results presented previously by Carney et al.12 The individual species were nicely separated, even though the distributions clearly broadened for higher noise levels and rotor speeds due to the regularization (see Fig. S10–S15† for further results). However, when considering polydisperse distributions, such as those present in model #3, c(s, D) failed to resolve the populations due to insufficient resolution and the regularization applied. This makes c(s, D) unsuitable for most core–shell systems where the dependency of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff on the particle size is of interest. Only global values for the hydrodynamic diameter and effective particle density can be obtained. In addition, slow calculations and the lack of parallelization capabilities in Sedfit make this method impractical for the analysis of MWL data available from the new generation of AUC.8,18,32,33
p,eff on the particle size is of interest. Only global values for the hydrodynamic diameter and effective particle density can be obtained. In addition, slow calculations and the lack of parallelization capabilities in Sedfit make this method impractical for the analysis of MWL data available from the new generation of AUC.8,18,32,33
The results of c(s, D) were compared to the 2DSA-MC analyses which were performed next. Our studies revealed that a much higher resolution could be obtained compared to the c(s, D) analysis and that it works well for fairly monodisperse PSDs. 2DSA-MC also provided superior resolution compared to the c(s, D) analyses for the more polydisperse models #2 and #3 even though significant peak broadening occurred at higher levels of random noise and increased rotor speed. Peak broadening can be reduced by a global analysis where all rotor speeds are fitted simultaneously. Here, the analysis benefited from the fact that lower rotor speeds enhance the diffusion signal of larger particles, while higher rotor speeds help with the resolution of smaller species. However, the resolution was too small to have an accurate representation of the size and density dependent sedimentation coefficient and the size dependent diffusion coefficient. Figures for all 2DSA-MC analyses can be found in the ESI, Fig. S10–S16.†
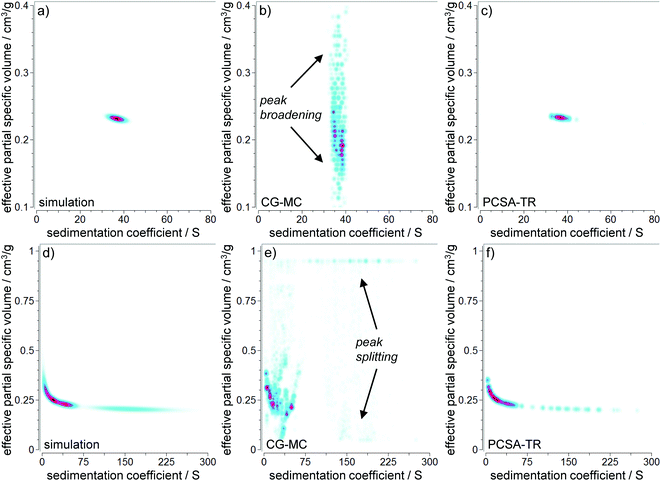
We used 2DSA in combination with custom grids in the next step to allow for a more detailed picture of the capabilities of 2DSA to analyze polydisperse core–shell NPs. Demeler et al. have recently shown that the high performance analysis, 2DSA, can be used to resolve the core–shell morphology of NPs when applying custom grids.13 We compared the performance of the CG-MC for the monodisperse model #1 at a very high level of random noise (2%) and the highly polydisperse model #3 at a moderate level of random noise (0.5%). Even though CG-MC performs well at very low levels of random noise (0.1%) and moderate rotor speeds, peak broadening occurs for ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff at larger noise levels and higher rotor speeds as can be seen in Fig. 4 (indicated by arrows). Global speed analyses again provided increased resolution. These results are consistent with the results obtained by 2DSA-MC analysis, which is based on the same mathematical principles. For model #3, peak splitting occurred in addition to peak broadening. Evaluations at different noise levels and rotor speeds can also be found in the ESI, Fig. S17–S25.†
p,eff at larger noise levels and higher rotor speeds as can be seen in Fig. 4 (indicated by arrows). Global speed analyses again provided increased resolution. These results are consistent with the results obtained by 2DSA-MC analysis, which is based on the same mathematical principles. For model #3, peak splitting occurred in addition to peak broadening. Evaluations at different noise levels and rotor speeds can also be found in the ESI, Fig. S17–S25.†
In the following section the reasons for peak broadening and peak splitting in the 2DSA-MC and CG-MC will be discussed. Since many more species are contained within the sedimentation data than can ever be resolved by AUC, a high resolution model covering the entire parameter space introduces significant degeneracy in the solution. This problem is accentuated further by higher noise levels. One approach to address this challenge is to stabilize the solution by TR, which smoothens distributions by damping large fluctuations in the amplitudes of the identified solutes. Nevertheless, in cases where broad distributions are expected, regularization is a valid approach to improve the analysis interpretation. The price to be paid for regularization is a reduction in resolution (see the results of the c(s, D), Fig. S10–S15†). The proper balance between regularization and resolution is given by the L-curve criterion, available in the PCSA implementation of UltraScan.11
In summary, we found that the 2DSA-(CG)-MC performs well for discrete species or narrow distributions. However, without regularization it is not the ideal method for broad PSDs where degeneracy of the solution space fails to reliably recover the information of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff heterogeneity, especially in noisy data. For example, regularization was applied during the c(s, D) analyses. However, it was shown that regularization reduced the resolution to a level where it was too low to analyze polydisperse PSDs in a meaningful way (Fig. S13–S15†).
p,eff heterogeneity, especially in noisy data. For example, regularization was applied during the c(s, D) analyses. However, it was shown that regularization reduced the resolution to a level where it was too low to analyze polydisperse PSDs in a meaningful way (Fig. S13–S15†).
Introduction to PCSA. Since c(s, D) lacked resolution and accuracy, and 2DSA-MC/CG-MC proved to be particularly sensitive to stochastic noise contained in the data due to degeneracy issues when analyzing polydisperse core–shell systems, a new core–shell parameterization for the PCSA was tested next. The idea behind this approach is to restrict any combination of s and
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff to a parametric curve in the parameter space when fitting linear combinations of Lamm equation solutions. For core–shell NPs this is a valid assumption since every
p,eff to a parametric curve in the parameter space when fitting linear combinations of Lamm equation solutions. For core–shell NPs this is a valid assumption since every ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff can be exclusively assigned to a single s (see Fig. 1), and a smooth variation of
p,eff can be exclusively assigned to a single s (see Fig. 1), and a smooth variation of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff as a function of s is a reasonable expectation. This significantly reduces the degeneracy encountered in the 2DSA-MC and CG-MC, by reducing the number of possible s–
p,eff as a function of s is a reasonable expectation. This significantly reduces the degeneracy encountered in the 2DSA-MC and CG-MC, by reducing the number of possible s–![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff combinations by a factor of 100 (assuming a 100 × 100 grid for 2DSA and 100 grid points for PCSA). In turn, this automatically constrains the analysis to well determined s–
p,eff combinations by a factor of 100 (assuming a 100 × 100 grid for 2DSA and 100 grid points for PCSA). In turn, this automatically constrains the analysis to well determined s–![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff pairs without the necessity of performing regularization in the 2D-space. Of course, regularization can still be used to regularize the distribution in the reduced 2D space where a fixed correlation of s and
p,eff pairs without the necessity of performing regularization in the 2D-space. Of course, regularization can still be used to regularize the distribution in the reduced 2D space where a fixed correlation of s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff exists. Alternatively, MC analysis can be applied, which guarantees statistical detail without unnecessarily broadening the distribution through regularization.
p,eff exists. Alternatively, MC analysis can be applied, which guarantees statistical detail without unnecessarily broadening the distribution through regularization.
The best regularization parameters of the 2nd order power law are chosen by the lowest RMSD curve obtained by parameter variation in the 2D space. An optional nonlinear least squares fit by Levenberg Marquardt can further be applied to optimize the curve parameters. Importantly, also non-constant shell thicknesses are covered by this procedure as long as it can be described by a 2nd order power law parameterization (e.g., continuously increasing or decreasing shell thickness with increasing core diameter). A theoretical example for such a case is given later in this manuscript.
PCSA-TR results for models #1–#3. The results of the PCSA-TR performed on the same datasets as CG-MC can be found in Fig. 4c and d (see Fig. S17–S25† for further results). An excellent agreement for s and
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff could be found. The non-continuous properties of the distribution in the pseudo 3D plot are caused by the finite number of solutes in the grid used in the analysis. As shown in Fig. 4, the s and
p,eff could be found. The non-continuous properties of the distribution in the pseudo 3D plot are caused by the finite number of solutes in the grid used in the analysis. As shown in Fig. 4, the s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff found by the PCSA-TR fit were in excellent agreement with the simulated data despite the simulated noise in the experimental data and a suboptimal rotor speed. Table 2 summarizes the s and
p,eff found by the PCSA-TR fit were in excellent agreement with the simulated data despite the simulated noise in the experimental data and a suboptimal rotor speed. Table 2 summarizes the s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff for the individual species obtained for models #1–#3 by the PCSA-TR. For model #1, the correct s and
p,eff for the individual species obtained for models #1–#3 by the PCSA-TR. For model #1, the correct s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff could be retrieved for all rotor speeds and levels of random noise. The maximum error for s was 0.08% and the maximum error for
p,eff could be retrieved for all rotor speeds and levels of random noise. The maximum error for s was 0.08% and the maximum error for ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff was 0.62%. For model #2, the influence of the rotor speed and noise became more decisive due to the broad PSD. For the lowest rotor speed, the s of the smallest species showed more deviation. The maximum error was 50.85% (species #1, lowest rotor speed and highest level of random noise). The same holds true for
p,eff was 0.62%. For model #2, the influence of the rotor speed and noise became more decisive due to the broad PSD. For the lowest rotor speed, the s of the smallest species showed more deviation. The maximum error was 50.85% (species #1, lowest rotor speed and highest level of random noise). The same holds true for ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff, whose determination was compromised at the highest rotor speed and largest level of random noise. The maximum error was 15.54% (species #2, highest rotor speed and level of random noise). Here the spread of the sedimentation boundary could no longer be attributed exclusively to the particle size, nor could the effect of diffusion be resolved. The effect of random noise and the rotor speed on the accuracy of the PCSA-TR was further examined for model #3. Fig. 5 illustrates the best fit parameterizations as found by PCSA-TR. The parameterizations are in very good agreement with the original simulation, with the only exceptions being found at the highest rotor speed (maximum error for
p,eff, whose determination was compromised at the highest rotor speed and largest level of random noise. The maximum error was 15.54% (species #2, highest rotor speed and level of random noise). Here the spread of the sedimentation boundary could no longer be attributed exclusively to the particle size, nor could the effect of diffusion be resolved. The effect of random noise and the rotor speed on the accuracy of the PCSA-TR was further examined for model #3. Fig. 5 illustrates the best fit parameterizations as found by PCSA-TR. The parameterizations are in very good agreement with the original simulation, with the only exceptions being found at the highest rotor speed (maximum error for ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff was 21.61%). This is to be expected as insufficient diffusion information was available at the highest rotor speed. Hence, the same behaviour was obtained as for model #2.
p,eff was 21.61%). This is to be expected as insufficient diffusion information was available at the highest rotor speed. Hence, the same behaviour was obtained as for model #2.
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff obtained by the PCSA-TR for models #1–#3 at different levels of random noise and rotor speeds.
p,eff obtained by the PCSA-TR for models #1–#3 at different levels of random noise and rotor speeds. ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff values are shown in parentheses. Values displayed in bold were found to have a deviation larger than 2% compared to the original simulations
p,eff values are shown in parentheses. Values displayed in bold were found to have a deviation larger than 2% compared to the original simulations
| Model # | 1 | 2 | 3a | |||
|---|---|---|---|---|---|---|
| Species # | 1 | 1 | 2 | 3 | 4 | 1 |
| Simulated | 36.80 (0.232) | 8.37 (0.288) | 20.08 (0.250) | 47.10 (0.226) | 101.08 (0.211) | 38.31 (0.249) |
a Due to the continuous shape of the PSD, only weight averaged values for s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff are reported. p,eff are reported.
|
||||||
| 10 krpm/0.1% | 36.80 (0.231) | 9.11 (0.285) | 20.28 (0.252) | 47.10 (0.227) | 101.06 (0.210) | 38.51 (0.248) |
| 20 krpm/0.1% | 36.79 (0.232) | 8.42 (0.288) | 20.11 (0.252) | 47.10 (0.227) | 101.07 (0.210) | 38.31 (0.248) |
| 40 krpm/0.1% | 36.80 (0.231) | 8.36 (0.320) | 20.09 (0.278) | 47.10 (0.249) | 101.07 (0.229) | 38.40 (0.211) |
| 10 krpm/0.5% | 36.79 (0.232) | 9.23 (0.284) | 20.30 (0.252) | 47.13 (0.227) | 100.96 (0.210) | 39.73 (0.245) |
| 20 krpm/0.5% | 36.77 (0.231) | 8.41 (0.288) | 20.11 (0.252) | 47.11 (0.227) | 101.06 (0.210) | 38.29 (0.248) |
| 40 krpm/0.5% | 36.80 (0.232) | 8.35 (0.320) | 20.12 (0.278) | 47.11 (0.249) | 101.07 (0.229) | 38.53 (0.195) |
| 10 krpm/2% | 36.80 (0.231) | 4.11 (0.318) | 19.48 (0.243) | 47.19 (0.216) | 101.72 (0.199) | 39.56 (0.245) |
| 20 krpm/2% | 36.80 (0.232) | 8.32 (0.298) | 20.06 (0.256) | 47.09 (0.226) | 101.12 (0.207) | 38.80 (0.249) |
| 40 krpm/2% | 36.80 (0.233) | 8.31 (0.332) | 20.12 (0.289) | 47.09 (0.260) | 100.92 (0.240) | 38.30 (0.206) |
PCSA-TR results for models of varying shell thicknesses. Finally, model #4 was analyzed which is similar to model #3 but contains a shell of varying thickness. For the investigation of varying shell thicknesses it is crucial that the actual s–
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff dependency can be covered with sufficient accuracy by the 2nd order power law. Otherwise, any deviations in the parameterization due to improper fits will be misinterpreted as variations in shell thicknesses. Therefore, we first confirmed that the provided s–
p,eff dependency can be covered with sufficient accuracy by the 2nd order power law. Otherwise, any deviations in the parameterization due to improper fits will be misinterpreted as variations in shell thicknesses. Therefore, we first confirmed that the provided s–![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff dependency can be sufficiently described by the parameterization. The size dependent shell thickness obtained from the PCSA is shown in Fig. 6.
p,eff dependency can be sufficiently described by the parameterization. The size dependent shell thickness obtained from the PCSA is shown in Fig. 6.
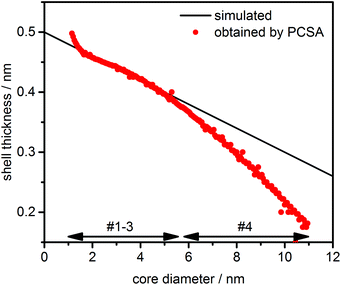 | ||
| Fig. 6 Size dependent shell thickness obtained by PCSA for model #4 compared to the original variation as provided in the simulated data. The core diameter range of species is indicated by arrows. | ||
A good agreement with the simulated data was obtained for species #1–#3, demonstrating that the PCSA-TR together with a 2nd order power law is in principle also well suited for the analysis of varying shell thicknesses. The negligible increase of the shell thickness at a core diameter of about 1 nm can be attributed to the slight imperfection of the parameterization. For the largest species in the distribution (#4), the deviation from the original simulations became larger as the shell thickness was underestimated. This can be explained by the fact that insufficient diffusion information was available from the larger species at the given rotor speed of 20 krpm. Hence, an incorrect parameterization was chosen during the PCSA, resulting in underestimated shell thicknesses.
In summary, continuous variation of the shell thickness is in principle accessible by PCSA. However, the experimental design must assure that the diffusion signal from all NPs is well-represented. In the given example, this was not the case for species #4. Especially for heterogeneous mixtures this can be most readily achieved by performing multiple experiments at different rotor speeds with subsequent global analysis. In such experiments the size separation is emphasized by high rotor speed experiments, while the diffusion signal is optimized in experiments with a lower rotor speed.
Summary of PCSA. In summary, these results, together with the additional figures for the PCSA-TR shown in S12–S20,† revealed that the PCSA-TR with the 2nd order power law parameterization excels at a wide range of noise levels and rotor speeds where currently existing analyses fail to produce satisfactory results. Nevertheless, the level of random noise should not be too high (<2%) and the applied rotor speed should be reasonable for the investigated PSD to obtain accurate results for s and
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff. These requirements fall well within the capabilities of AUC instruments available today.
p,eff. These requirements fall well within the capabilities of AUC instruments available today.
It must be pointed out that the parameters determined by the 2nd order power law parameterization found by the PCSA-TR are only meaningful in the range where analytes have been found. As an example, numerous functions can be found for a monodisperse species. In turn, the broader the s- and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff-range, the higher the confidence in the parameterization function will be. For broad distributions the diffusion information will have the strongest signal for smaller species. Since the slope of the parameterization function is highest in the lower s-range, any variations of the parameters in the 2nd order power law will also be much more sensitive here. In contrast, higher s will have only little effect on the best function found via the PCSA. The most important value here is the intercept of the function, assuming that a sufficient diffusion signal is available from the data. Hence, for broad PSDs, s and
p,eff-range, the higher the confidence in the parameterization function will be. For broad distributions the diffusion information will have the strongest signal for smaller species. Since the slope of the parameterization function is highest in the lower s-range, any variations of the parameters in the 2nd order power law will also be much more sensitive here. In contrast, higher s will have only little effect on the best function found via the PCSA. The most important value here is the intercept of the function, assuming that a sufficient diffusion signal is available from the data. Hence, for broad PSDs, s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff for large NPs will also fit much better compared to CG-MC as peak splitting is prevented during the PCSA-TR. In contrast, the large species will follow the parameterization curve obtained for the majority of smaller NPs. For systems with constant shell thicknesses this will provide much more reliable information on the large structures in mixtures than with other methods like c(s, D) or 2DSA-MC and CG-MC.
p,eff for large NPs will also fit much better compared to CG-MC as peak splitting is prevented during the PCSA-TR. In contrast, the large species will follow the parameterization curve obtained for the majority of smaller NPs. For systems with constant shell thicknesses this will provide much more reliable information on the large structures in mixtures than with other methods like c(s, D) or 2DSA-MC and CG-MC.
For systems where such assumptions on the shell-morphology cannot be asserted or where insufficient diffusion information is available in the data, global analysis at different rotor speeds is recommended. This is available in the supercomputer implementation and is a subject of ongoing research for the PCSA. Moreover, a logarithmic scaling of s will also improve the resolution in the lower s-range and could be implemented in future versions of the PCSA-TR. Another possibility could be a discretization schema that matches grid spacings adaptively to the information content of different grid regions.
So far, we have shown that the PCSA-TR, in combination with a 2nd order power law, provides excellent results for simulated sedimentation data of spherical core–shell systems. It is a very robust approach, which was found to work for a very broad range of noise levels and rotor speeds. The exact limitations strongly depend on the sample itself as well as the experimental parameters and can therefore only be specified in general terms. However, the RMSDs of the individual parameterizations offer a good indication for the validity of an analysis. Therefore, the RMSD of the best fit model should be sufficiently different from RMSDs of the other parameterizations to ensure a well-defined parameterization. However, what “sufficient” actually means will depend to a large extent on the signal-to-noise ratio of the data.
A summary of the capabilities of the different algorithms with respect to the analysis of the simulated data is provided in Table 3. In conclusion, PCSA-TR in combination with a 2nd order power law is far superior to the c(s) and c(s, D) analysis or 2DSA-MC/CG-MC in the case of polydisperse core–shell NPs because it provides high resolution as well as the correct hydrodynamic parameters.
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff
p,eff
| Model # | c(s)a | c(s, D) | CG-MC | PCSA |
|---|---|---|---|---|
a No information on ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff provided but s correctly reproduced for narrow PSDs or high rotor speeds.
b Resolution severely limited dependent upon the noise level and rotor speed.
c Significant peak broadening and splitting occurring for higher RMSDs and rotor speeds only allows to derive mean parameters for single species.
d Larger deviations for large random noise levels and rotor speeds.
e Varying shell thicknesses accessible under certain restrictions. p,eff provided but s correctly reproduced for narrow PSDs or high rotor speeds.
b Resolution severely limited dependent upon the noise level and rotor speed.
c Significant peak broadening and splitting occurring for higher RMSDs and rotor speeds only allows to derive mean parameters for single species.
d Larger deviations for large random noise levels and rotor speeds.
e Varying shell thicknesses accessible under certain restrictions.
|
||||
| 1 | ✗ | ✓ | ✓ | ✓ |
| 2 | ✗ | ✓/✗b | ✓ | ✓d |
| 3 | ✗ | ✗ | ✓/✗c | ✓d |
| 4 | ✗ | ✗ | ✗ | ✓e |
4.2 ZnO NPs
In the next step, experimental datasets of ZnO QDs ripened for 3 h and 4 h were investigated. The spherical shape was carefully proven by image analysis in the TEM prior to this study.34 Moreover, small-angle X-ray (SAXS) and small-angle neutron scattering (SANS) studies conducted in cooperation with the Chair for Crystallography and Structural Physics at FAU also showed that scattering data for ZnO colloids can only be reasonably fitted when assuming polydisperse spherical NPs.17,35 In contrast, data could not be fitted accurately and consistently with TEM data when using models for shape anisotropic NPs.The ZnO NPs contain an organic acetate shell and have ethanol molecules attached to the ZnO core. This results in a size dependency of ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff. The
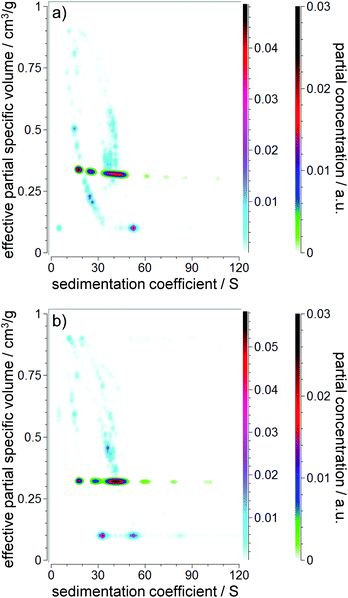
p,eff. The ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff value is expected to range between the values of the pure core (0.1783 cm3 g−1) and shell (1.2533 cm3 g−1 and 0.9524 cm3 g−1 for pure ethanol and pure acetic acid, respectively). First, a CG-MC was performed to remove the time and radially invariant noise from the data and to fit the actual meniscus position. The results of the evaluations including MC analyses can be found in Fig. 7. As expected, heavy peak broadening and splitting were present due to the polydisperse nature of the PSDs. However, the random noise levels were excellent (0.00261 OD and 0.00282 OD for the 3 h and 4 h samples, respectively). While reliable information on s can be obtained, information on
p,eff value is expected to range between the values of the pure core (0.1783 cm3 g−1) and shell (1.2533 cm3 g−1 and 0.9524 cm3 g−1 for pure ethanol and pure acetic acid, respectively). First, a CG-MC was performed to remove the time and radially invariant noise from the data and to fit the actual meniscus position. The results of the evaluations including MC analyses can be found in Fig. 7. As expected, heavy peak broadening and splitting were present due to the polydisperse nature of the PSDs. However, the random noise levels were excellent (0.00261 OD and 0.00282 OD for the 3 h and 4 h samples, respectively). While reliable information on s can be obtained, information on ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff is not useful due to the observed peak splitting. Therefore, a PCSA-TR with the new parameterization was performed in the next step.
p,eff is not useful due to the observed peak splitting. Therefore, a PCSA-TR with the new parameterization was performed in the next step.
The PCSA-TR using the 2nd order power law parameterization (eqn (6)) has been found to have almost identical RMSD values (0.00260 OD and 0.00289 OD for the 3 h and 4 h samples, respectively) compared to the CG-MC. The PCSA-TR provided a constrained correlation for s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff as shown in Fig. 7. This is very near the weight average of the observed signals from the CG-MC, and eliminated the peak splitting. Based on the derived s and
p,eff as shown in Fig. 7. This is very near the weight average of the observed signals from the CG-MC, and eliminated the peak splitting. Based on the derived s and ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff values, the shell thicknesses were calculated according to the procedure presented previously (see Table 4 for further information).17 The simulation in model #4 showed that a size-dependent shell thickness is difficult to extract from single speed experiments. Therefore, we restrict our analyses to the calculation of the weight average thickness. The experimental determination of varying shell thickness will be pursued in future work. Such work would require further developments in data evaluation in combination with strong orthogonal techniques for comparison.
p,eff values, the shell thicknesses were calculated according to the procedure presented previously (see Table 4 for further information).17 The simulation in model #4 showed that a size-dependent shell thickness is difficult to extract from single speed experiments. Therefore, we restrict our analyses to the calculation of the weight average thickness. The experimental determination of varying shell thickness will be pursued in future work. Such work would require further developments in data evaluation in combination with strong orthogonal techniques for comparison.
| Sample | s 20,w/S |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff/cm3 g−1
p,eff/cm3 g−1 |
ρ p,eff/g cm−3 | d shell/nm |
|---|---|---|---|---|
| a Calculated assuming a density of pure ethanol for the shell. b Calculated assuming a density of pure acetic acid (representing acetate) for the shell. | ||||
| ZnO 3 h | 35.34 | 0.323 | 3.10 | 0.60a/0.65b |
| ZnO 4 h | 39.88 | 0.320 | 3.13 | 0.62a/0.67b |
| CuInS2 | 5.83 | 0.680 | 1.47 | 1.08 |
The shell thickness was found to vary between 0.60 nm and 0.67 nm, depending on the sample and the assumed shell density. It is expected that the true shell thickness is in between these two values as it will consist of ethanol and acetate molecules. However, the variation of less than 1 Å confirms the excellent reproducibility and robustness of the PCSA-TR. These results on the shell morphology are further in good agreement with the known length of an acetate molecule bound to a ZnO QD (0.49 nm).36 A slightly larger hydrodynamic diameter is to be expected due to an ethanol solvation layer formed around the NP surface. A combined SAXS/SANS study revealed slightly larger shell thicknesses reaching from 0.7 nm to 1.3 nm.35 In contrast to AUC, the shell thickness provided by SAXS/SANS is not derived from the hydrodynamic properties of the NP but it describes the native stabilizing layer of the NPs and how far it extends into the dispersion medium. Thus, also acetate molecules exceeding the shear plane of the NP are considered by SAXS/SANS, which is the reason why slightly larger values in the case of scattering methods are clearly expected.
4.3 CuInS2 NPs
CuInS2 NPs prepared via batch synthesis were used to obtain additional experimental evidence to test the capabilities of the new methodology. The spherical shape of these NPs was previously demonstrated by image analysis using TEM.22,23 In contrast to ZnO, these NPs have a thicker organic shell of about 1 nm.22 In our previous work, resolution with respect to the simultaneous determination of the size and effective density was severely limited because the c(s, D) analysis was employed.22 c(s) analysis was further used to determine the PSD but this approach incurred drawbacks due to the assumption of a constant effective NP density. Herein we performed a PCSA-TR using the 2nd order power law parameterization to further investigate the structure of those semiconductor NPs. The results are shown in Fig. 8 and Table 4.As can be seen in Fig. 8, the s distribution covered a range from about 3 S to 12 S, while ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) p,eff deviated significantly from the value expected for the pure core material (0.211 cm3 g−1). This suggests a significant contribution from a thick shell as was previously confirmed by TGA results.23 Next, the shell thickness was calculated using the
p,eff deviated significantly from the value expected for the pure core material (0.211 cm3 g−1). This suggests a significant contribution from a thick shell as was previously confirmed by TGA results.23 Next, the shell thickness was calculated using the ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) of the organic ligand (1.186 cm3 g−1), which was almost identical to the
of the organic ligand (1.186 cm3 g−1), which was almost identical to the ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) of the solvent (1.160 cm3 g−1). A value of 1.08 nm was obtained. The value for the shell thickness is in very good agreement with our previous c(s, D) analysis of such NPs prepared in batch synthesis (deviation is less than 1 Å).22 However, in contrast to recent analyses, a high resolution sedimentation coefficient distribution is available together with information about the shell thickness. Moreover, MWL analysis is in principle now also accessible for such core–shell NPs.
of the solvent (1.160 cm3 g−1). A value of 1.08 nm was obtained. The value for the shell thickness is in very good agreement with our previous c(s, D) analysis of such NPs prepared in batch synthesis (deviation is less than 1 Å).22 However, in contrast to recent analyses, a high resolution sedimentation coefficient distribution is available together with information about the shell thickness. Moreover, MWL analysis is in principle now also accessible for such core–shell NPs.
5 Conclusions
In this work, the capabilities of modern algorithms for the evaluation of sedimentation data from polydisperse PSDs were investigated. Previous work clearly revealed that the analysis of most NPs having a comparably broad PSD and consisting of a core–shell structure has not been sufficiently addressed so far. For example, 1D analysis fails to provide information on the core–shell properties of NPs. Moreover, this type of analysis can result in false positives routinely found by the c(s) analysis because frictional heterogeneity cannot be addressed by c(s). A comparison of current 2D analysis revealed that the c(s, D) analysis is more robust against random noise and high rotor speeds, but the resolution is very low due to excessive smoothening of the distributions by regularization. Hence, only weight averaged information is provided in the case of broad PSDs. Moreover, the possibility of high performance computing is not available, which makes Sedfit unsuitable for large datasets produced by the recently described MWL detector.The 2DSA-MC and CG-MC provide unrivaled resolution and accuracy but fail to analyze broad PSDs because peak broadening and splitting can occur in the 2nd dimension. This compromises the determination of effective partial specific volumes and hence core–shell parameters. Thus, present analysis methods show either a lack of information on the hybrid composition or the resolution is too low to determine the core–shell composition.
In contrast, PCSA in combination with a 2nd order power law parameterization developed in this work provides high resolution and unrivaled information on the core–shell properties of NPs in polydisperse PSDs. Our simulations showed that it performs well for a wide range of stochastic noise levels, rotor speeds and different PSDs. After validating our method with simulated data, we applied it to experimental systems of ZnO and CuInS2 NPs. For the first time, the core–shell properties of polydisperse QDs could be addressed with high resolution and reliability by means of 2D-AUC.
We believe that these developments will significantly expand the application of AUC because 2D analysis is no longer limited to narrow PSDs. Recently, it was demonstrated that MWL-AUC in combination with 2DSA can be used to determine the spectral properties and sizes of multiple but discrete QD species.37 Further studies shall be focused on MWL analysis to derive the size dependent extinction spectra for all species in polydisperse PSDs. AUC together with PCSA will then permit the study of the quantum size effect for continuous distributions of semiconductor NPs.
The 2nd order power law parameterization in PCSA is available for free download in UltraScan3 viahttp://www.ultrascan3.uthscsa.edu/.
Acknowledgements
The DFG is thanked by J. W., D. S., T. A. and W. P. for financial support through project PE 427/28-2 and the Cluster of Excellence “Engineering of Advanced Materials”. J. Born is thanked for her help during data evaluation. The authors gratefully acknowledge the computing time granted (HER21) by the John von Neumann Institute for Computing (NIC) and provided on the supercomputers Juropa and Jureca at Jülich Supercomputing Centre (JSC). B. D. acknowledges support from the National Science Foundation (ACI-1339649), XSEDE (MCB-070039) and the National Institutes of Health (RO1-GM120600).Notes and references
- M. De, P. S. Ghosh and V. M. Rotello, Adv. Mater., 2008, 20, 4225–4241 CrossRef CAS.
- K. Saha, S. S. Agasti, C. Kim, X. Li and V. M. Rotello, Chem. Rev., 2012, 112, 2739–2779 CrossRef CAS PubMed.
- O. Salata, J. Nanobiotechnol., 2004, 2, 3 CrossRef PubMed.
- Z. Zhang, J. Zhang, N. Chen and L. Qu, Energy Environ. Sci., 2012, 5, 8869–8890 CAS.
- H. Cölfen and T. Pauck, Colloid Polym. Sci., 1997, 275, 175–180 Search PubMed.
- W. Mächtle and L. Börger, Analytical Ultracentrifugation of Polymers and Nanoparticles, Springer-Verlag, Berlin, Heidelberg, 2006 Search PubMed.
- V. Strauss, J. T. Margraf, C. Dolle, B. Butz, T. J. Nacken, J. Walter, W. Bauer, W. Peukert, E. Spiecker, T. Clark and D. M. Guldi, J. Am. Chem. Soc., 2014, 136, 17308–17316 CrossRef CAS PubMed.
- J. Walter, K. Löhr, E. Karabudak, W. Reis, J. Mikhael, W. Peukert, W. Wohlleben and H. Cölfen, ACS Nano, 2014, 8, 8871–8886 CrossRef CAS PubMed.
- E. Brookes, W. Cao and B. Demeler, Eur. Biophys. J., 2010, 39, 405–414 CrossRef PubMed.
- P. H. Brown and P. Schuck, Biophys. J., 2006, 90, 4651–4661 CrossRef CAS PubMed.
- G. Gorbet, T. Devlin, B. I. Hernandez Uribe, A. K. Demeler, Z. L. Lindsey, S. Ganji, S. Breton, L. Weise-Cross, E. M. Lafer, E. H. Brookes and B. Demeler, Biophys. J., 2014, 106, 1741–1750 CrossRef CAS PubMed.
- R. P. Carney, J. Y. Kim, H. Qian, R. Jin, H. Mehenni, F. Stellacci and O. M. Bakr, Nat. Commun., 2011, 2, 335 CrossRef PubMed.
- B. Demeler, T.-L. Nguyen, G. E. Gorbet, V. Schirf, E. H. Brookes, P. Mulvaney, A. a. O. El-Ballouli, J. Pan, O. M. Bakr, A. K. Demeler, B. I. Hernandez Uribe, N. Bhattarai and R. L. Whetten, Anal. Chem., 2014, 86, 7688–7695 CrossRef CAS PubMed.
- V. Mittal, A. Völkel and H. Cölfen, Macromol. Biosci., 2010, 10, 754–762 CrossRef CAS PubMed.
- O. Lamm, Ark. Mat. Astron. Fys., 1929, 21B, 1–4 Search PubMed.
- E. E. Lees, M. J. Gunzburg, T.-L. Nguyen, G. J. Howlett, J. Rothacker, E. C. Nice, A. H. A. Clayton and P. Mulvaney, Nano Lett., 2008, 8, 2883–2890 CrossRef CAS PubMed.
- T. Schindler, J. Walter, W. Peukert, D. Segets and T. Unruh, J. Phys. Chem. B, 2015, 119, 15370–15380 CrossRef CAS PubMed.
- G. E. Gorbet, J. Z. Pearson, A. K. Demeler, H. Cölfen and B. Demeler, in Methods Enzymol, ed. L. C. James, Academic Press, 2015, vol. 562, pp. 27–47 Search PubMed.
- E. A. Meulenkamp, J. Phys. Chem. B, 1998, 102, 5566–5572 CrossRef CAS.
- L. Spanhel and M. A. Anderson, J. Am. Chem. Soc., 1991, 113, 2826–2833 CrossRef CAS.
- H. Zhong, Y. Zhou, M. Ye, Y. He, J. Ye, C. He, C. Yang and Y. Li, Chem. Mater., 2008, 20, 6434–6443 CrossRef CAS.
- T. Akdas, J. Walter, D. Segets, M. Distaso, B. Winter, B. Birajdar, E. Spiecker and W. Peukert, Nanoscale, 2015, 7, 18105–18118 RSC.
- T. Akdas, M. Distaso, S. Kuhri, B. Winter, B. Birajdar, E. Spiecker, D. M. Guldi and W. Peukert, J. Colloid Interface Sci., 2015, 445, 337–347 CrossRef CAS PubMed.
- J.-M. Claverie, H. Dreux and R. Cohen, Biopolymers, 1975, 14, 1685–1700 CrossRef CAS PubMed.
- W. Cao and B. Demeler, Biophys. J., 2005, 89, 1589–1602 CrossRef CAS PubMed.
- P. Schuck and B. Demeler, Biophys. J., 1999, 76, 2288–2296 CrossRef CAS PubMed.
- B. Demeler, in Current Protocols in Protein Science, John Wiley & Sons, Inc., 2001 Search PubMed.
- S. K. Bhattacharyya, P. Maciejewska, L. Börger, M. Stadler, A. M. Gülsün, H. B. Cicek and H. Cölfen, in Analytical Ultracentrifugation VIII, ed. C. Wandrey and H. Cölfen, Springer-Verlag, Berlin, Heidelberg, 2006, vol. 131, pp. 9–22 Search PubMed.
- P. Schuck, Biophys. J., 2000, 78, 1606–1619 CrossRef CAS PubMed.
- J. A. Fagan, M. Zheng, V. Rastogi, J. R. Simpson, C. Y. Khripin, C. A. Silvera Batista and A. R. Hight Walker, ACS Nano, 2013, 7, 3373–3387 CrossRef CAS PubMed.
- K. Nontapot, V. Rastogi, J. A. Fagan and V. Reipa, Nanotechnology, 2013, 24, 0957–4484 CrossRef PubMed.
- J. Z. Pearson, F. Krause, D. Haffke, B. Demeler, K. Schilling and H. Cölfen, in Methods Enzymol, ed. L. C. James, Academic Press, 2015, vol. 562, pp. 1–26 Search PubMed.
- J. Walter, P. J. Sherwood, W. Lin, D. Segets, W. F. Stafford and W. Peukert, Anal. Chem., 2015, 87, 3396–3403 CrossRef CAS PubMed.
- D. Segets, L. Martinez Tomalino, J. Gradl and W. Peukert, J. Phys. Chem. C, 2009, 113, 11995–12001 CAS.
- T. Schindler, M. Schmiele, T. Schmutzler, T. Kassar, D. Segets, W. Peukert, A. Radulescu, A. Kriele, R. Gilles and T. Unruh, Langmuir, 2015, 31, 10130–10136 CrossRef CAS PubMed.
- R. Marczak, D. Segets, M. Voigt and W. Peukert, Adv. Powder Technol., 2010, 21, 41–49 CrossRef CAS.
- E. Karabudak, E. Brookes, V. Lesnyak, N. Gaponik, A. Eychmüller, J. Walter, D. Segets, W. Peukert, W. Wohlleben, B. Demeler and H. Cölfen, Angew. Chem., Int. Ed., 2016, 55, 11770–11774 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Model #4, results of the c(s), c(s, D), 2DSA-MC, 2DSA-GL-MC, CG-MC, CG-GL-MC and PCSA-TR for various simulation parameters. See DOI: 10.1039/c6an02236g |
| This journal is © The Royal Society of Chemistry 2017 |