Characteristics of chemical bonding of pentavalent uranium in La-doped UO2
Sergei M.
Butorin
*a,
Kristina O.
Kvashnina
bc,
Damien
Prieur
d,
Murielle
Rivenet
e and
Philippe M.
Martin
f
aMolecular and Condensed Matter Physics, Department of Physics and Astronomy, Uppsala University, P.O. Box 516, SE-751 20 Uppsala, Sweden. E-mail: sergei.butorin@physics.uu.se
bThe European Synchrotron, CS40220, 38043 Grenoble Cedex 9, France
cHelmholtz Zentrum Dresden-Rossendorf (HZDR), Institute of Resource Ecology, P.O. Box 510119, 01314, Dresden, Germany
dEuropean Commission, Joint Research Centre, Institute for Transuranium Elements, P.O. Box 2340, D-76125 Karlsruhe, Germany
eUniversité Lille, CNRS, Centrale Lille, ENSCL, Université Artois, UMR 8181, UCCS, Unité de Catalyse et Chimie du Solide, F-59000 Lille, France
fCEA Marcoule, CEA, DEN, DTEC/SECA/LCC, F-30207 Bagnols-sur-Cèze Cedex, France
First published on 15th November 2016
Abstract
The effect of La doping on the electronic structure of U in UO2 was studied using an advanced technique, namely, X-ray absorption spectroscopy (XAS) in the high-energy-resolution fluorescence-detection (HERFD) mode, at the U 3d3/2 (M4) edge. Thanks to a significant reduction of the core–hole lifetime broadening and distinct chemical shifts of the HERFD-XAS lines, the U(V) formation as a result of La doping was identified. The isolated contribution of U(V) in the M4 HERFD-XAS spectrum reveals the so-called charge-transfer satellites due to the U 5f–O 2p hybridization. The analysis of the experimental data within the framework of the Anderson impurity model (AIM) indicates a significant change in the characteristics and degree of covalency for the chemical bonding in the U(V) subsystem of UO2 as compared to undoped UO2, which is a Mott–Hubbard system. The results are also supported by AIM calculations of X-ray photoelectron and optical absorption data.
The change of charge on uranium atoms, the dopant position within the crystal lattice, and the possible crystallographic re-arrangement of the oxygen sublattice are fundamental questions (see e.g.ref. 1 and 2) accompanying the doping of UO2 that help to better understand the observed properties of resulting compounds. These questions are also important for the nuclear industry since UO2 is used as a nuclear fuel. Some of the created fission products are dissolved in the UO2 matrix and thereby affect the structural, thermomechanical, thermodynamic and other properties of the nuclear fuel. In the case of UO2 doped with trivalent rare-earths (REs), it is generally expected that there will be an appearance of the U(V) fraction or/and formation of O vacancies as charge-compensation mechanisms.3 However, the situation appears to be more complex since both O vacancies and oxygen excess are found in U1−xRExO2±δ for the range of the RE doping4 and the phase separation between U1−xRExO2−δ and U1−xRExO2 is also suggested for doped systems.5,6
The charge compensation mechanism due to the change of the oxidation state of U atoms in UO2 upon RE insertion also presents an open question. Besides the U(V) appearance in such a case of doping, the U(VI) contribution has been also found from the analysis of the magnetic susceptibility2 and X-ray photoelectron spectroscopy (XPS) data.7–10 However, the results obtained by different research groups do not agree with each other. Herrero et al.8 have found dominant U(V) with a small U(VI) admixture in hyperstoichiometric U1−xLaxO2+δ for the 0.3 < x < 0.5 range and have only detected the existence of the U(IV) + U(VI) combination with a dominant U(VI) contribution in hypostoichiometric U1−xLaxO2−δ for x > 0.5. On the other hand, the U(V) content has been reported by Venkata Krishnan et al.9 to be significantly larger than that of U(VI) in hypostoichiometric U1−xLaxO2−δ.
The consequences of the U(V) appearance in the RE-doped UO2 lattice in terms of the local symmetry and local structure changes are also not clear. While, in Am(III)-doped UO2, which is claimed11 to behave more like trivalent lanthanide-doped UO2 (once the Am/(U + Am) ratio is ≥40%), the U(V) appearance is accompanied by a formation of the U6O12 cuboctahedral-type clusters as detected by extended X-ray absorption fine structure and Raman spectroscopies;11 the Raman measurements on Nd-doped6 and Gd, Dy-doped10 UO2 have not confirmed that. Another important consequence is a change in the chemical bonding that affects the physical and chemical properties of the doped compound. While it has been shown that stoichiometric UO2 is a Mott–Hubbard system12 with a high degree of 5f localization, for which even the description of relatively delocalized U 6d13 and O 2p14 states requires taking into account the 5f–5f Coulomb interaction, there are no spectroscopic data available for RE-doped UO2 that would help to assess the situation.
Recently, an advanced technique, namely X-ray absorption spectroscopy (XAS) in the high energy resolution fluorescence detection (HERFD) mode, which improves the experimental resolution due to a significant reduction in the core–hole lifetime broadening of the recorded spectra, has been extensively used in the study of molecular systems and solids.15–17 For actinides in particular, it has been shown18 that HERFD-XAS at the actinide 3d3/2 edge can easily distinguish between U(IV), U(V) and U(VI) oxidation states. Furthermore, this advanced technique has allowed us to resolve both the crystal-field splitting of the 5f shell and the so-called charge-transfer satellites in the HERFD-XAS spectra of Th (ref. 19) and U (ref. 20) compounds. Analysis of these satellites provides information about the characteristics of the chemical bonding and the degree of hybridization of the actinide states with the ligand states.
In this communication, we employ the advanced HERFD-XAS technique to study the effect of La doping on UO2. By isolating the U(V) contribution in the spectra and by analyzing this contribution in the framework of the Anderson impurity model21 (AIM), we find a significant change in the characteristics of the chemical bonding in the U(V) subsystem of UO2, which must affect the physical and chemical properties of the compound.
U1−xLaxO2±δ (x = 0.06, 0.11, 0.22, and 0.40) samples have been prepared via gel-supported precipitation, also referred to as sol–gel external gelation.22 Uranyl nitrate and 139La nitrate solutions were mixed to achieve a molar stoichiometry of x = La/(U + La), as defined above. An organic thickener (Methocel, Dow Chemicals) was added to increase the viscosity of the solutions. These were then dropped into an ammonia bath where the droplet to particle conversion took place due to hydroxide precipitation of the metals inside the polymer backbone of the droplet. The resulting beads were washed, dried, and then calcined at 873 K in air (2 h) to remove organics and then at 973 K in Ar/H2 (2 h) to ensure uranium reduction. The samples were then enriched at about 30% in 17O by heating in 17O enriched gas at 1073 K (24 h) and then sintered for 4 hours at 1923 K under Ar/H2. The resulting samples represented solid solutions with the single-(FCC)-phase fluorite structure as confirmed by X-ray diffraction analysis. The β-UO3 sample was obtained by calcining uranyl nitrate in air at 723–773 K over several weeks as described in ref. 23.
The measurements in the energy range of the U 3d X-ray absorption edge were performed at beamline ID2624 of the European Synchrotron in Grenoble. The incident energies were selected using the 〈111〉 reflection from a double Si-crystal monochromator. The XAS data were measured in the HERFD mode using an X-ray emission spectrometer.17 The U HERFD spectra at the M4 (3d3/2 → 5f5/2,7p transitions) edge were obtained by recording the outgoing photons with an energy of ∼3337 eV as a function of the incident energy. This emission energy which corresponds to the maximum of the U Mβ (4f5/2 → 3d3/2 transitions) X-ray emission line was selected using the 〈220〉 reflection of five spherically bent Si crystal analyzers (with 1 m bending radius) aligned at 75° Bragg angle. The directions of the incident and emitted photons were 45° to the surface of the sample. The spectral intensity was normalized to the incident flux. A combined (incident convoluted with emitted) energy resolution of 0.4 eV was obtained as determined by measuring the full width at half maximum (FWHM) of the elastic peak.
The Anderson impurity model21 was used for the calculations which included the 5f and core (3d or 4f) states on a single actinide ion and a filled ligand 2p band. The calculations were performed in a manner described in ref. 25 and 26.
The XAS and core-level X-ray photoelectron spectroscopy (XPS) data were calculated using the following equations:
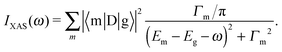 | (1) |
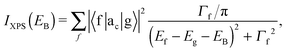 | (2) |
The required Slater integrals Fk, Gk and Rk (ref. 27), spin–orbit coupling constants ζ and matrix elements were obtained using the TT-MULTIPLETS package which combines Cowan's atomic multiplet program28 (based on the Hartree–Fock method with relativistic corrections) and Butler's point-group program,29 which were modified by Thole,30 as well as the charge-transfer program written by Thole and Ogasawara.
We used the AIM approach for the calculations of the spectra because the ab-initio methods based on density functional theory, which are successful in many cases,15–17 still have difficulties in the proper description of the transitions involving the 5f electrons31 when the on-site 5f–5f Coulomb interaction is strong.
The U M4 HERFD-XAS spectra of UO2, U1−xLaxO2 (x = 0.06, 0.11, 0.22, and 0.4) and β-UO3 are displayed in Fig. 1. The spectra are normalized to the maximum. A significant chemical shift between the U M4 lines of UO2 and UO3 is observed since they contain nominal U(IV) and U(VI), respectively. Similar chemical shifts between the M4 HERFD-XAS spectra of the U(IV) and U(VI) species have been reported earlier.18,20,31–33 Upon La doping, the shoulder on the high-energy side of the U M4 main line of UO2 starts to grow and evolves into a dominant peak at ∼3726.4 eV for U0.6La0.4O2. The energy of this peak falls in between those of the M4 main lines of U(IV) and U(VI) substances. As in the case of U4O918 and NaUO3,20 this is an indication of U(V) formation. It is clear from Fig. 1 that the U(V) content increases with x in U1−xLaxO2.
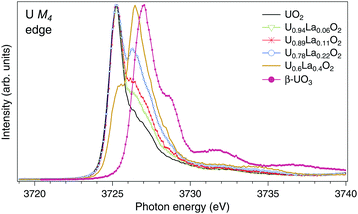 | ||
| Fig. 1 High-resolution XAS spectra at the U M4 edge of UO2,32 U1−xLaxO2 and β-UO3. The spectra are normalized to the maximum. | ||
To analyze the newly appeared ∼3726.4 eV structure, we subtracted the U(IV) contribution from the U M4 HERFD-XAS spectrum of U0.6La0.4O2 using the U M4 HERFD-XAS spectrum of undoped UO2 from Fig. 1. Based on the charge-compensation considerations for the stoichiometric O content, the U(IV) contribution was taken as one-third of the total U M4 spectral weight. The resulting spectrum is shown in Fig. 2. It looks similar to the U M4 HERFD-XAS spectrum of NaUO3 (ref. 20), thus supporting its own U(V) origin. However, the U cation in NaUO3 is six-fold coordinated while the eight-fold coordination is expected for the U(V) atoms in the UO2 lattice. To compare with experimental data, we calculated the M4 XAS spectrum of U(V) in the UO2 lattice using the AIM and eqn (1). Earlier we have shown20 that there is no significant difference between calculated conventional XAS (with artificially reduced broadening) and HERFD-XAS spectra of U(V), therefore we limit the calculations to the conventional XAS spectrum to simplify the computational framework.
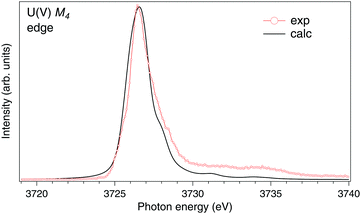 | ||
| Fig. 2 High-resolution U M4 XAS spectrum of U0.6La0.4O2 after subtraction of the U(IV) contribution compared to the calculated XAS spectrum at the M4 edge of U(V) in the UO2 lattice. | ||
In the AIM calculations, the ground (final) state of the system was described using a linear combination of the 5f1 and 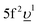 (3d95f2 and
(3d95f2 and 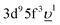 ) configurations, where
) configurations, where 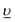 stands for an electronic hole in the O 2p band. The Slater integrals were reduced to 70% of their Hartree–Fock values to account for the configuration interaction effect.34 To describe the crystal-field interaction for the U(V) atom with the eight-fold coordination, the values of Wybourne's crystal-field parameters35 for the 5f shell in the cubic (Oh) symmetry were set to B04 = −0.93 eV and B06 = 0.35 eV, which are similar to those derived from the inelastic neutron scattering measurements36 on UO2.
stands for an electronic hole in the O 2p band. The Slater integrals were reduced to 70% of their Hartree–Fock values to account for the configuration interaction effect.34 To describe the crystal-field interaction for the U(V) atom with the eight-fold coordination, the values of Wybourne's crystal-field parameters35 for the 5f shell in the cubic (Oh) symmetry were set to B04 = −0.93 eV and B06 = 0.35 eV, which are similar to those derived from the inelastic neutron scattering measurements36 on UO2.
In the limit of the U 5f–O 2p hybridization term V → 0, the difference between the configuration averaged energies for the ground state can be written as 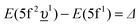 (where Δ ≡ εf − εn, with εn corresponding to the center of the O 2p band) which is the so-called charge-transfer energy (εf and εn are one-electron energies of the U 5f and O 2p levels). For the final state, this difference is
(where Δ ≡ εf − εn, with εn corresponding to the center of the O 2p band) which is the so-called charge-transfer energy (εf and εn are one-electron energies of the U 5f and O 2p levels). For the final state, this difference is 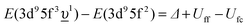 , where Uff denotes the 5f–5f Coulomb interaction and Ufc is the 3d core–hole potential acting on the 5f electron. Treated as parameters, the Δ, Uff and Ufc values were taken to be 3.5, 3.5, and 6.0 eV, respectively. The hybridization term (hopping matrix element) between 5f1 and
, where Uff denotes the 5f–5f Coulomb interaction and Ufc is the 3d core–hole potential acting on the 5f electron. Treated as parameters, the Δ, Uff and Ufc values were taken to be 3.5, 3.5, and 6.0 eV, respectively. The hybridization term (hopping matrix element) between 5f1 and 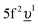 configurations in the ground state was taken to be Vg = 1.2 eV. To account for the electronic-configuration dependence of V, this value was scaled down to 75% (0.75Vg = Vm) to describe the mixing between 3d95f2 and
configurations in the ground state was taken to be Vg = 1.2 eV. To account for the electronic-configuration dependence of V, this value was scaled down to 75% (0.75Vg = Vm) to describe the mixing between 3d95f2 and 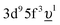 configurations in the final state.25,37 The 3d3/2 core–hole-lifetime Lorentzian broadening (Γm) was taken to be 0.3 eV with an additional Gaussian convolution to account for the instrumental resolution.
configurations in the final state.25,37 The 3d3/2 core–hole-lifetime Lorentzian broadening (Γm) was taken to be 0.3 eV with an additional Gaussian convolution to account for the instrumental resolution.
Furthermore, the (super)-exchange interaction38 and the linear polarization of the incident X-ray beam were taken into account in the calculations of the U(V) M4 spectrum; this spectrum was calculated at room temperature.
The results of the calculations are shown in Fig. 2, together with the U M4 spectrum of U0.6La0.4O2 after subtraction of the U(IV) contribution. The experimental and calculated spectra are in rather good agreement, thus indicating that most of the U(V) atoms are in the cubic-symmetry fluorite-type environment and coordinated by eight O atoms. The structure at ∼8 eV above the main line in the experimental spectrum is assigned by the calculations to the U 5f → O 2p charge-transfer satellite as a result of the U 5f–O 2p hybridization. This satellite depends on both V and Δ values.
Our estimations of the AIM parameters for the U(V) subsystem from the analysis of the HERFD-XAS data at the U 3d edge are also supported by the calculations of the U 4f XPS spectrum (Fig. 3) of La-doped UO2 that contains 100% U(V) as found in ref. 9. The U0.4La0.6O2−δ sample also had the single-(FCC)-phase fluorite crystal structure. Despite that the sample was hypostoichiometric, the U(V) cations are eight-fold coordinated because the O vacancies are expected to be located around the La sites.
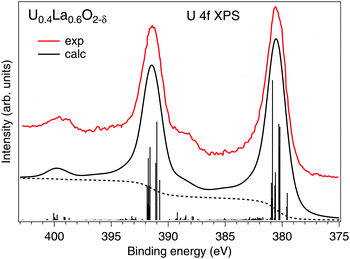 | ||
| Fig. 3 Calculated U 4f XPS spectrum of U(V) in the UO2 lattice using the Anderson impurity model. The spectrum is compared with the experimental data from ref. 9. The dashed curves represent the photoelectron background. | ||
The experimental data were well reproduced (Fig. 3) using the same set of AIM parameters apart from that for Ufc which is expected to be smaller for the 4f level. In this case, the Ufc value was set to 5.0 eV, which is similar to that used in the AIM calculations in ref. 39. In our calculations of the U(V) 4f XPS spectrum, the final state configurations with the 4f core hole had the same number of 5f electrons as the corresponding ground state configurations due to an excited electron leaving the system. The calculated spectrum reproduces the experimental data in terms of the energy separation (∼8 eV) and relative intensity of the charge-transfer satellites at binding energies of ∼388.4 and ∼399.4 eV for the main U 4f7/2 and 4f5/2 lines, respectively.
Table 1 compares the lowest excited states of the U(V) 5f multiplet obtained in the AIM calculations with those measured using diffuse reflectance spectroscopy (DRS), which is an analogue of optical absorption spectroscopy.8,40 The DRS spectra of La-doped UO2 with a dominant U(V) contribution show an intense peak at ∼6400 cm−1 and a broad structure at ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, which are associated with the electronic transitions within the U(V) 5f shell (also see the DRS spectrum of U(V) in stabilized ZrO2 [ref. 41]). Since the DRS spectra were measured in the 4000–40
000 cm−1, which are associated with the electronic transitions within the U(V) 5f shell (also see the DRS spectrum of U(V) in stabilized ZrO2 [ref. 41]). Since the DRS spectra were measured in the 4000–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 range, the first calculated transition (Γ8 → Γ7) in Table 1 is out of the measured range. Our calculations suggest that the ∼6400 cm−1 peak consists of two transitions Γ8 → Γ8′ and Γ8 → Γ6, thus explaining why this peak is so intense. The broad structure at ∼12
000 cm−1 range, the first calculated transition (Γ8 → Γ7) in Table 1 is out of the measured range. Our calculations suggest that the ∼6400 cm−1 peak consists of two transitions Γ8 → Γ8′ and Γ8 → Γ6, thus explaining why this peak is so intense. The broad structure at ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 can be assigned to the Γ8 → Γ7′ transition.
000 cm−1 can be assigned to the Γ8 → Γ7′ transition.
| State | Experiment | Calculations |
|---|---|---|
| Γ 8 | 0 | |
| Γ 7 | 175 | |
| Γ 8′ | 794 | 954 |
| Γ 6 | 794 | 958 |
| Γ 7′ | ∼1488 | 1378 |
As a whole, the results of our calculations indicate a very significant change in the nature of the chemical bonding in the formed U(V) subsystem upon RE-doping of UO2 as compared to undoped UO2. Based on the ratio between Δ and Uff (ref. 42), the locally formed U(V) environment is characterized as a charge-transfer subsystem in contrast to the Mott–Hubbard system of UO2. The contributions of the 5f1 and 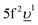 configurations in the ground state of the U(V) subsystem were estimated to be 65% and 35%, respectively, thus resulting in the 5f occupancy of nf = 1.35 electrons. In comparison with nominal nf = 1 for U(V), extra nf arises from the U 5f–O 2p hybridization. This extra nf amounts to 0.35 electrons and is higher than that in undoped UO2 (0.24 electrons) estimated from similar AIM calculations.39,43
configurations in the ground state of the U(V) subsystem were estimated to be 65% and 35%, respectively, thus resulting in the 5f occupancy of nf = 1.35 electrons. In comparison with nominal nf = 1 for U(V), extra nf arises from the U 5f–O 2p hybridization. This extra nf amounts to 0.35 electrons and is higher than that in undoped UO2 (0.24 electrons) estimated from similar AIM calculations.39,43
References
- (a) G. C. Allen, P. A. Tempest and J. W. Tyler, Nature, 1982, 295, 48–49 CrossRef CAS; (b) S. D. Conradson, S. M. Gilbertson, S. L. Daifuku, J. A. Kehl, T. Durakiewicz, D. A. Andersson, A. R. Bishop, D. D. Byler, P. Maldonado, P. M. Oppeneer, J. A. Valdez, M. L. Neidig and G. Rodriguez, Sci. Rep., 2015, 5, 15278 CrossRef CAS PubMed.
- Y. Hinatsu, J. Alloys Compd., 1993, 201, 139–144 CrossRef CAS.
- (a) C. R. A. Catlow, J. Chem. Soc., Faraday Trans. 2, 1987, 83, 1065–1072 RSC; (b) J. M. Solomon, V. Alexandrov, B. Sadigh, A. Navrotsky and M. Asta, Acta Mater., 2014, 78, 282–289 CrossRef CAS.
- (a) T. B. Lindemer and J. Brynestad, J. Am. Ceram. Soc., 1986, 69, 867–876 CrossRef CAS; (b) K. Park and D. R. Olander, J. Nucl. Mater., 1992, 187, 89–96 CrossRef CAS.
- T. Fujino, K. Ouchi, Y. Mozumi, R. Ueda and H. Tagawa, J. Nucl. Mater., 1990, 174, 92–101 CrossRef CAS.
- L. Desgranges, Y. Pontillon, P. Matheron, M. Marcet, P. Simon, G. Guimbretiere and F. Porcher, Inorg. Chem., 2012, 51, 9147–9149 CrossRef CAS PubMed.
- C. Keller and C. K. Jørgensen, Chem. Phys. Lett., 1975, 32, 397–400 CrossRef CAS.
- P. Herrero, P. Garcia-Chain and R. M. Rojas, J. Solid State Chem., 1990, 87, 331–343 CrossRef CAS.
- R. Venkata Krishnan, V. K. Mittal and R. Babu, J. Alloys Compd., 2011, 509, 3229–3237 CrossRef CAS.
- M. Razdan and D. W. Shoesmith, J. Electrochem. Soc., 2014, 161, H105–H113 CrossRef CAS.
- F. Lebreton, D. Horlait, R. Caraballo, P. M. Martin, A. C. Scheinost, A. Rossberg, C. Jégou and T. Delahaye, Inorg. Chem., 2015, 54, 9749–9760 CrossRef CAS PubMed.
- (a) S. L. Dudarev, D. Nguyen Manh and A. P. Sutton, Philos. Mag. B, 1997, 75, 613–628 CrossRef CAS; (b) Y. Baer and J. Schoenes, Solid State Commun., 1980, 33, 885–888 CrossRef CAS.
- K. O. Kvashnina, Y. O. Kvashnin, J. R. Vegelius, A. Bosak, M. Martin and S. M. Butorin, Anal. Chem., 2015, 87, 8772–8780 CrossRef CAS PubMed.
- A. Modin, M.-T. Suzuki, J. Vegelius, Y. Yun, D. K. Shuh, L. Werme, J. Nordgren, P. M. Oppeneer and S. M. Butorin, J. Phys.: Condens. Matter, 2015, 27, 315503 CrossRef CAS PubMed.
- (a) A. J. Atkins, M. Bauer and C. R. Jacob, Phys. Chem. Chem. Phys., 2015, 17, 13937–13948 RSC; (b) A. J. Atkins, M. Bauer and C. R. Jacob, Phys. Chem. Chem. Phys., 2013, 15, 8095–8105 RSC.
- J. C. Swarbrick, Y. Kvashnin, K. Schulte, K. Seenivasan, C. Lamberti and P. Glatzel, Inorg. Chem., 2010, 49, 8323–8332 CrossRef CAS PubMed.
- P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95 CrossRef CAS.
- K. O. Kvashnina, S. M. Butorin, P. Martin and P. Glatzel, Phys. Rev. Lett., 2013, 111, 253002 CrossRef CAS PubMed.
- S. M. Butorin, K. O. Kvashnina, J. R. Vegelius, D. Meyer and D. K. Shuh, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8093–8097 CrossRef CAS PubMed.
- S. M. Butorin, K. O. Kvashnina, A. L. Smith, K. Popa and P. M. Martin, Chem. – Eur. J., 2016, 22, 9693–9698 CrossRef CAS PubMed.
- P. W. Anderson, Phys. Rev. [Sect.] B, 1961, 124, 41 CrossRef CAS.
- (a) U. Carvajal-Nunez, D. Prieur, T. Vitova and J. Somers, Inorg. Chem., 2012, 51, 11762–11768 CrossRef CAS PubMed; (b) L. Martel, J.-F. Vigier, D. Prieur, S. Nourry, A. Guiot, K. Dardenne, J. Boshoven and J. Somers, J. Phys. Chem. C, 2014, 118, 27640 CrossRef CAS.
- P. C. Debets, Acta Crystallogr., 1966, 21, 589–593 CrossRef CAS.
- C. Gauthier, V. A. Sole, R. Signorato, J. Goulon and E. Moguiline, J. Synchrotron Radiat., 1999, 6, 164–166 CrossRef CAS PubMed.
- S. M. Butorin, D. C. Mancini, J.-H. Guo, N. Wassdahl, J. Nordgren, M. Nakazawa, S. Tanaka, T. Uozumi, A. Kotani, Y. Ma, K. E. Myano, B. A. Karlin and D. K. Shuh, Phys. Rev. Lett., 1996, 77, 574–577 CrossRef CAS PubMed.
- M. Nakazawa, H. Ogasawara and A. Kotani, Surf. Rev. Lett., 2002, 9, 1149–1153 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1929, 34, 1293–1322 CrossRef CAS.
- R. D. Cowan, Theory of Atomic Structure and Spectra, University of California Press, Berkeley, 1981 Search PubMed.
- P. H. Butler, Point Group Symmetry Applications: Methods and Tables, Plenum Press, New York, 1981 Search PubMed.
- B. T. Thole, G. van der Laan and P. H. Butler, Chem. Phys. Lett., 1988, 149, 295–299 CrossRef CAS.
- K. O. Kvashnina, Y. O. Kvashnin and S. M. Butorin, J. Electron Spectrosc. Relat. Phenom., 2014, 194, 27–36 CrossRef CAS.
- A. L. Smith, P. E. Raison, L. Martel, D. Prieur, T. Charpentier, G. Wallez, E. Suard, A. C. Scheinost, C. Hennig, P. Martin, K. O. Kvashnina, A. K. Cheetham and R. J. M. Konings, Inorg. Chem., 2015, 54, 3552–3561 CrossRef CAS PubMed.
- R. Bès, M. Rivenet, P.-L. Solari, K. O. Kvashnina, A. C. Scheinost and P. M. Martin, Inorg. Chem., 2016, 55, 4260–4270 CrossRef PubMed.
- J. Sugar, Phys. Rev. B: Solid State, 1972, 5, 1785–1792 CrossRef.
- B. G. Wybourne, Spectroscopic Properties of Rare Earths, Wiley, New York, 1963 Search PubMed.
- H. Nakotte, R. Rajaram, S. Kern, R. J. McQueeney, G. H. Lander and R. A. Robinson, J. Phys.: Conf. Ser., 2010, 251, 012002 CrossRef CAS.
- O. Gunnarsson and O. Jepsen, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3568–3571 CrossRef CAS.
- C. Miyake, O. Kawasaki, K. Gotoh and A. Nakatani, J. Alloys Compd., 1993, 200, 187–190 CrossRef CAS.
- T. Yamazaki and A. Kotani, J. Phys. Soc. Jpn., 1991, 60, 49–52 CrossRef CAS.
- S. Kemmler-Sack, Z. Anorg. Allg. Chem., 1968, 363, 295–304 CrossRef CAS.
- E. R. Vance, Y. Zhan and and Z. Zhang, J. Nucl. Mater., 2010, 400, 8–14 CrossRef CAS.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1985, 55, 418–421 CrossRef CAS PubMed.
- S. M. Butorin, A. Modin, J. R. Vegelius, K. O. Kvashnina and D. K. Shuh, J. Phys. Chem. C Search PubMed , submitted.
| This journal is © The Royal Society of Chemistry 2017 |
