Planar pentacoordinate carbon atoms embedded in a metallocene framework

Abstract

Viable planar pentacoordinate carbon (ppC) systems with a ppC bonded to a transition metal and embedded in a metallocene framework are reported. Our detailed global minima search shows that CAl₄MX₂ (M = Zr and Hf; X = F–I and C₅H₅) clusters with ppCs are appropriate candidates for experimental realization in the gas phase. The fulfillment of the 18 electron rule and electron delocalization is found to be crucial for the stabilization of these ppC arrangements.

---

Forty-six years ago, Hoffmann et al. introduced some rules to stabilize a tetracoordinate carbon atom in a planar fashion instead of a regular tetrahedron, transcending one of the firmest paradigms in organic chemistry.¹ Since then the number of planar tetracoordinate carbon (ptC) systems (proposed on paper, detected in the gas phase, or synthesized) has increased considerably.^2–6 In 1991, Schleyer and Boldyrev suggested a class of structures with unusual planar tetracoordinate central atoms (OAl₄, NAl₄⁻, NAl₃Si, cis-CAl₂Si₂, trans-CAl₂Si₂, and BAlSi₃).⁷ A common characteristic of these clusters is that they all have 18 valence electrons. Boldyrev and Simons rationalized the preference of the planar structure over the tetrahedral one by a molecular orbital analysis. They suggested that the presence of 18 valence electrons is the optimal case for planar structures, since three σ- and one π-bond occur as well as one ligand–ligand bond.⁸ This intriguing 18 electron rule has been used by other theoreticians to design new ptC compounds and gratifyingly some of them have been detected experimentally.^9,10

In 2008, Pei et al. extrapolated this 18 electron rule to stabilize planar pentacoordinate carbon (ppC) centers.¹¹ They explored the potential energy surface (PES) of CAl₅⁺ and found that the global minimum is a perfect aluminum pentagon with a carbon atom at the center. Several groups, including ours, have suggested a series of ppC clusters based on the substitution of aluminum centers in CAl₅⁺ by other atoms.^12–14

Despite the theoretical predictions of stable ptC systems in various bonding motifs, most of the synthesized ptC molecules have been encountered with at least one transition metal (M) atom linked directly to the ptC atom.^4,5 The question that we consider here is this: is it possible to locate a ppC in which the carbon site is surrounded by at least one M atom? Even better, is it possible to stabilize a ppC embedded in a metallocene framework? Of course, we are thinking about global minimum energy structures. So, in this article we explore the possibility of stabilizing a ppC by substituting one aluminum center in the CAl₅⁺ framework by one M atom or fragments comprising an M center. Our computations show that the lowest lying form of the clusters with the formula CAl₄MX₂ (M = Zr and Hf; X = F, Cl, Br, and I) contains an Al₄M pentagon with a carbon atom at the ring center. Interestingly, the substitution of the halogen atom by a cyclopentadienyl (Cp) ring leads to a global minimum without altering the ppC skeleton as well. So, an organometallic ppC in a metallocene framework may actually be achievable, suggesting the possibility of the experimental realization of such ppC systems.

The initial search was done using the PBE0¹⁵ functional in conjunction with a LANL2DZ^16–18 basis set on both the singlet and triplet state PESs. The located structures were reminimized and characterized at the PBE0/def2-TZVP¹⁹ level, including dispersion via Grimme’s DFT-D3 approximation.²⁰ To get better energetics, single point energies are computed at the CCSD(T)/def2-TZVP//PBE0-D3/def2-TZVP level for the seven lowest energy isomers of CAl₄MX₂ (X = F–I) clusters. In the cases of CAl₄MCp₂ (M = Ti, Zr and Hf; Cp = cyclopentadienyl) compounds, the search was restricted to those forms obtained from the interaction among two C₅H₅ rings and the rest of the atoms in overall singlet and triplet spin multiplicities. So, in strictly speaking, we explored only a region of the PES for such aggregates. Atomic charges (q) and Wiberg bond indices (WBIs) were computed by using the natural bonding orbital (NBO) partitioning scheme.^21–23 All these computations were done using Gaussian 09.²⁴ Additionally, we performed a chemical bonding analysis using the adaptive natural density partitioning (AdNDP) method developed by Zubarev and Boldyrev.²⁵

Let us first substitute one Al atom of the Al₅ ring in CAl₅⁺ by an M atom. Since the charge and multiplicity of the clusters can be decisive for the stability, the dianionic, neutral, and dicationic forms of the cluster in both the singlet and triplet states are investigated. The results of our systematic exploration of the CAl₄M (M = Ti, Zr, and Hf) PESs are summarized in the ESI (see Fig. S1–S3, ESI†). In order to satisfy the 18 valence electron rule, which seems to be operative for the stability of these ppCs as they are for the ptCs, the charge of the CAl₄M cluster should be +2. However, all the charged ppC species (dications and dianions) bear at least one imaginary frequency irrespective of their spin states. Among the neutral clusters, the ppC arrangements of CAl₄Zr and CAl₄Hf are just local minima with 10.4 and 13.8 kcal mol⁻¹ higher in energy than that of the corresponding global minimum, at the PBE0-D3/def2-TZVP level. In the case of CAl₄Ti, a ppC structure in the triplet state is found to be the global minimum, whereas the same in the singlet state is 6.7 kcal mol⁻¹ higher in energy than the former one.

The second strategy that we followed was to start with CAl₄M²⁺ systems, which satisfy the 18 valence electron rule, and to balance the positive charges with simple and practical anions. In particular, we considered the halide ions. The resulting compounds have the formula CAl₄MX₂ (M = Ti, Zr, and Hf; X = F–I). In the case of M = Ti, the corresponding ppC structure is not the global minimum, except for CAl₄TiF₂ (see Fig. 1 and Fig. S4–S7, ESI†). Although the global minima for those Ti clusters are triplet three-dimensional arrangements with low symmetry, the ppC structures of CAl₄TiX₂ (X = Cl–I) are very close to the energy of the corresponding global minimum (0.2 for Cl, 0.6 for Br, and 1.8 kcal mol⁻¹ for I at the CCSD(T)/def2-TZVP//PBE0-D3/def2-TZVP level). Therefore, in an experimental situation the ppC arrangements might also be expected.

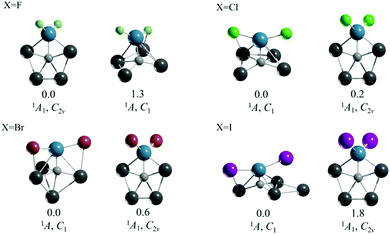Fig. 1 CCSD(T)/def2-TZVP//PBE0-D3/def2-TZVP global minimum and the second lowest energy isomer of CAl₄TiX₂ (X = F–I). Relative energy values are in kcal mol⁻¹.

Gratifyingly, the global minima of the CAl₄ZrX₂ and CAl₄HfX₂ clusters (Fig. 2) adopt a C_2v symmetry with a ppC atom. Fifteen low-lying energy isomers for these systems found within the range of 0–20 kcal mol⁻¹ with respect to the planar pentacoordinate global minimum are summarized in Fig. S8–S15 (ESI†). For the Zr clusters, two significant trends are observed in going from X = F to X = I: (i) the second lowest lying isomer comes closer in energy to the global minimum (8.1 (F), 6.7 (Cl), 5.1 (Br), and 2.8 (I) kcal mol⁻¹ at the CCSD(T)/def2-TZVP//PBE0-D3/def2-TZVP level), as X gets larger and (ii) the number of halogen bridged structures increases. Similar tendencies are found for the CAl₄HfX₂ clusters as well, but in these cases the energy differences between the global minimum and the nearest energy isomers are larger by 1.8–5.0 kcal mol⁻¹ at the CCSD(T) level with respect to their Zr analogues.

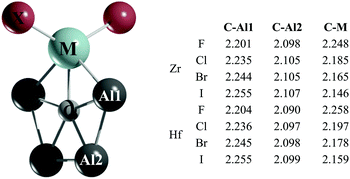Fig. 2 PBE0-D3/def2-TZVP lowest energy isomer of CAl₄MX₂. The C–Al1, C–Al2 and C–M bond lengths are given in Å.

Let us focus on the global minimum energy structures for the Zr and Hf systems as shown in Fig. 2. The important geometrical parameters for all of these systems are also summarized therein. Notice that the C–Al bond lengths in the title systems are longer than the computed C–Al bond lengths in CAl₅⁺ at the PBE0-D3/def2-TZVP level (2.089 Å) and they further increase in moving from F to I. In contrast, the C–M bond lengths shorten as X gets larger. So, it is apparent that the electronegativity and the size of X have an impact on the C–Al and C–M bonds, and these effects are reflected in the variation of the relative stabilities of the global minima with ppC sites and the second lowest energy isomers.

Natural population analysis (NPA) charges provide important insight into the bonding in these molecules. The charge on carbon (q(C)) in the set of systems with ppCs (−2.21 to −2.37 |e|) indicates a substantial electron transfer from the peripheral atoms to carbon and the corresponding q(C) gradually reduces with the decrease in the electronegativity of X in the molecule. These charges in the Zr and Hf systems are slightly smaller than the natural charge on carbon computed for CAl₅⁺ (−2.68 |e|), but this can be explained perhaps by the presence of the electronegative X atoms in the systems, even if the Zr and Hf are slightly less electronegative than Al.

In the ppC systems, the carbon atom acts as a σ-acceptor and this charge acceptance is accompanied by a donation of the C 2p_z electrons to the π-system of the molecule (see Table S1, ESI†), satisfying a condition for the stabilization suggested by Hoffmann et al. for ptC systems.¹ Note that the 2p_z orbital occupations (∼1.4 |e|) are slightly less than those of the 2p_x and 2p_y orbitals (∼1.6 |e|), indicating a degree of back-donation. The 2p_z orbitals of the title ppCs are 0.1 |e| more occupied than that in the CAl₅⁺ cluster. So, even though the σ-bonding is apparently weaker in the title compounds compared to CAl₅⁺, the π-interactions are at least similar. The electronegativity of X has a notable effect on the bonds around the ppC; while the WBI_C–Al values for the C–Al contacts range from 0.34 to 0.53 (see Table S1, ESI†), the WBI_C–M values for the C–M bonds are more dependent on the identity of X than those in C–Al bonds. Particularly, the WBI_C–M value is 0.75 for CAl₄ZrF₂, but 1.05 for CAl₄ZrI₂. With the decrease in electronegativity of X, more electrons of M participate in the covalent bonding with X and C centers, as reflected from the gradual increase in WBI values in moving from F to I. This is in turn responsible for the steady reduction of negative charge on C centers along the same line. Notice that an increase in the WBI_C–M values involves a decrease in the WBI_C–Al ones, but the total bond index for the central carbon atom is approximately 2.6. So, although no single C–Al bond is close to the nominal bond order of 1.0, the fractional contributions from the individual C–Al and C–M interactions work together to stabilize the hypercoordinate structure without violating the octet rule.

The lowest vibrational frequencies computed at the PBE0-D3/def2-TZVP level range from 29 to 46 cm⁻¹, and all of them correspond to an out-of-plane twisting mode leading to the formation of the so-called boat-like conformation in the Al₄M moiety. The vibrational frequencies associated with the out-of-plane displacement of ppC are found to be quite high ranging from 204 to 293 cm⁻¹. Born–Oppenheimer molecular dynamics (BO-MD) simulations at the PW91/DZVP-GGA level support the thermal stability of the Zr species at 700 K.^26,27 Equilibrium geometries were used for all of the simulations with the assignment of random velocities to the atoms. The analysis of the structural evolution along the recorded trajectories of the simulations shows that the ppC structures remain intact up to 30 ps (see the movies in the ESI†).

Is it possible to stabilize a ppC in a metallocene framework? The computational evidence suggests that it is. We have found that the replacement of the halide ions by the far more elaborate cyclopentadienyl (Cp) anions yields species with the formula CAl₄MCp₂ (M = Ti, Zr, and Hf). While in the computed global minimum of CAl₄TiCp₂, the Ti atom in triplet three-dimensional arrangements of CAl₄Ti interacts with two Cp rings (Fig. S16, ESI†), and the lowest lying energy forms of the Zr and Hf analogues adopt a singlet structure with a ppC (see Fig. 3 and Fig. S17, S18, ESI†).²⁸ In the Ti analogue, the second and third lowest energy isomers, which are 4.9 and 6.6 kcal mol⁻¹ higher in energy than the global minimum, contain a ptC and a ppC, respectively. On the other hand, the second lowest energy isomers of both the CAl₄ZrCp₂ and CAl₄HfCp₂ complexes (at 2.6 and 2.3 kcal mol⁻¹, respectively) possess ptC centers instead. Perhaps, the most substantial structural change in these ppC metallocene complexes is the elongation of the C–M bonds with respect to the halogen congeners (approximately 0.2 Å).

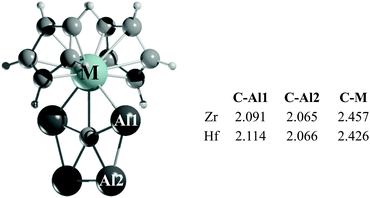Fig. 3 PBE0-D3/def2-TZVP lowest energy isomer of CAl₄MCp₂. The C–Al1, C–Al2 and C–M bond lengths are given in Å.

In the lowest lying isomers of Cp complexes, the NPA charges on the ppC (−2.30 |e|) are close to those of their fluorine analogues (see Table S1, ESI†). However, the charges on Zr and Hf in the former complexes are significantly smaller than those of the latter ones, being +0.53 and +0.65 |e|, respectively, which is due to the electron-donation from the Cp rings to the M centers. The charges of the Al₄ fragment, +2.36 |e| (Zr) and +2.27 |e| (Hf), indicate a greater net charge transfer from the Al atoms to the ppC in comparison to their halogen analogues discussed in preceding sections.

Let us focus our attention on Zr analogues to analyze the electron delocalization therein. The results of AdNDP analysis describing bonding only within the CAl₄Zr moiety are shown in Fig. 4. In both CAl₄ZrX₂ (X = F–I) and CAl₄ZrCp₂ clusters, there are six localized 2c–2e σ-bonds among which five are involved within the Al₄Zr ring and one in between Zr and ppC. In the delocalized σ-bonding framework, while in CAl₄ZrX₂ there are one delocalized 3c–2e σ-bond involving a ppC and two Al centers, and one fully delocalized 6c–2e σ-bond within the CAl₄Zr moiety, CAl₄ZrCp₂ possesses two 3c–2e σ-bonds, formed among the Al centers and ppC. Most importantly, both the systems have one totally delocalized 6c–2e π-bond over the CAl₄Zr moiety, satisfying the Hückel's aromaticity criterion. Therefore, the title clusters are π-aromatic systems.

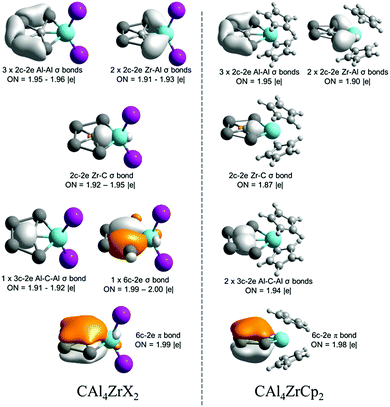Fig. 4 AdNDP results for the bonding involved in the CAl₄M moiety of CAl₄ZrX₂ (X = F–I) and CAl₄ZrCp₂ systems.

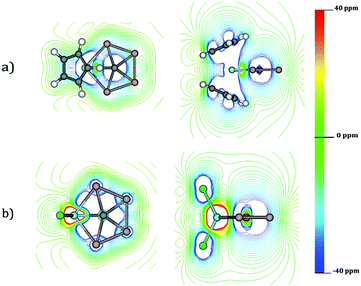
An alternative option to understand the delocalization in a molecular system is to analyze its magnetic response. The isolines of the z-component of B^ind (B^ind_z) for CAl₄ZrCl₂ and CAl₄ZrCp₂ are provided in Fig. 5. For both the systems, the Al₄ moiety shows a strong diatropic response (−20 to −40 ppm) upon the application of an external field perpendicular to the molecular plane.

Fig. 5 Isolines of B^ind_z in CAl₄ZrCp₂ (a) and CAl₄ZrCl₂ (b) systems.

So, in principle the electron density in the CAl₄M fragment is fully delocalized. However, there are some small differences between both systems. While both Zr and C are located at a paratropic region in CAl₄ZrCl₂, in CAl₄ZrCp₂ both atoms are placed at one diatropic region. This is a consequence of the long-range diatropic response of the Cp rings. In other words, an increase in the diatropic response in the CAl₄M fragment does not really mean a higher aromaticity of CAl₄ZrCp₂ than its Cl analogue, rather it is simply a consequence of the long-range response of the Cp units.

In summary, we have answered two important questions, required for the advancement of ppC systems: (1) is it possible to predict viable transition metal supported ppC, akin to the ptC systems? (2) Would it be achievable a ppC, embedded in a metallocene framework? Our systematic study indicates that both might be possible but an appropriate choice of M along with the satisfaction of the 18 electron rule are required. Herein, a set of compounds with the general formula CAl₄MX₂ (M = Zr and Hf; X = F–I and Cp) with a ppC is proposed to be viable candidates for the experimental realization.

The work in Mexico was supported by Conacyt (Grant CB-2015-252356). The CGSTIC (Xiuhcoalt) and ABACUS at Cinvestav are gratefully acknowledged for generous allocation of computational resources. The work in China was funded by the National Natural Science Foundation of China (No. 21273093, 21473069, and 21503088).

Notes and references

1. R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992–4993.
2. K. Sorger and P. v. R. Schleyer, J. Mol. Struct., 1995, 338, 317–346.
3. L. Radom and D. R. Rasmussen, Pure Appl. Chem., 1998, 70, 1977–1984.
4. W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371.
5. R. Keese, Chem. Rev., 2006, 106, 4787–4808.
6. G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372.
7. P. v. R. Schleyer and A. I. Boldyrev, J. Chem. Soc., Chem. Commun., 1991, 1536–1538.
8. A. I. Boldyrev and J. Simons, J. Am. Chem. Soc., 1998, 120, 7967–7972.
9. X. Li, H. F. Zhang, L. S. Wang, G. D. Geske and A. I. Boldyrev, Angew. Chem., Int. Ed., 2000, 39, 3630–3633.
10. L. S. Wang, A. I. Boldyrev, X. Li and J. Simons, J. Am. Chem. Soc., 2000, 122, 7681–7687.
11. Y. Pei, W. An, K. Ito, P. v. R. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400.
12. Z. H. Cui, J. J. Sui and Y. H. Ding, Phys. Chem. Chem. Phys., 2015, 17, 32016–32022.
13. J. O. C. Jimenez-Halla, Y. B. Wu, Z. X. Wang, R. Islas, T. Heine and G. Merino, Chem. Commun., 2010, 46, 8776–8778.
14. Y. B. Wu, Y. Duan, H. G. Lu and S. D. Li, J. Phys. Chem. A, 2012, 116, 3290–3294.
15. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
16. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270.
17. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
18. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284.
19. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
20. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
21. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
22. E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593–609.
23. A. E. Reed, R. B. Weinsk and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
24. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, USA 2009.
25. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. Real-temperature simulations on realistic time scales are computationally impossible for quantum-mechanical systems to date. An alternative way is to increase the temperature, so that the systems would get enough kinetic energy to undergo any geometrical transformation within a small time frame (30 ps in this case). This is reason we employed 700 K.
28. Our searches for potential energy surfaces include the possibility of the cleavage of C–H bond in Cp unit and with the formation of new M–H or Al–H bonds. For example, we have noted an isomer for CAl₄TiCp₂ with a cleaved C–H bond of Cp unit and formation of new C–H bond with the C of the CAl₄Ti unit. However, this is 10.9 kcal mol⁻¹ higher in energy than the lowest energy form. Similarly, the isomers with cleaved Cp C–H bonds and new M–H and/or Al–H bonds are found to be very higher energy isomers and lie beyond our selected energy window in this manuscript.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary figures and Cartesian coordinates of all isomers, and the BO-MD movies. See DOI: 10.1039/c6cc08273d

---