Observing non-classical crystallisation processes in gypsum via infrared attenuated total reflectance spectroscopy

Abstract

The nature of crystallisation processes is of major interest, as they are among the most frequently occurring reactions associated with a variety of relevant processes in chemistry, biochemistry, and geochemistry. In this study, an innovative approach towards fundamentally understanding crystallisation pathways in a seemingly simple system – gypsum – has been developed via infrared spectroscopic techniques. Specifically, infrared attenuated total reflection spectroscopy (IR-ATR) was instrumental in revealing detailed information on inter- and intramolecular interactions during gypsum crystallization via subtle changes in the vibrational spectra of the involved reactants. When applying D₂O as an isotope marker, it was shown that isotopically labelled water may serve as a viable spectroscopic probe during mid-infrared (3–15 μm) studies providing unique insight into the crystallization process at molecular-level detail. In addition, it was revealed that H₂O and D₂O give rise to distinctly different reaction kinetics during the crystallization process.

---

Gypsum is a well-studied molecule with its crystal structure investigated via a variety of different methods.^1–3 In addition, the intra- and intermolecular interactions between water molecules and gypsum have been investigated.^4,5 Compared to other non-soluble sulfates such as barite, water indeed plays a crucial role during the crystallisation process, as reported by Jones et al.⁶ Consequently, in the present study D₂O was applied as an isotope marker for tracing the pathways of crystallisation in molecular detail. While it is anticipated that its molecular behaviour is similar to water, D₂O has a distinct infrared signature facilitating its spectral differentiation from H₂O even in mixtures.⁷ To date, the influence of D₂O on the reaction kinetics was only reported for bio-minerals though.⁸ While the influence of deuterium, and especially of HOD on the crystal structure of CaSO₄ was the subject of earlier studies, to the best of our knowledge the process of gypsum crystallisation in heavy water has been not examined in satisfactory detail.⁹

Even more so, in view of the recently emerging non-classical nucleation theory (non-CNT), the investigated system is of substantial interest, as the reaction proceeds sufficiently slow for monitoring the associated kinetics and nucleation pathways. Non-CNT mechanisms were observed during the nucleation of a variety of different systems including proteins, organic crystals, and crystals derived from bio-minerals.^8,10,11 Derived from previous reports,^6,12 it was anticipated that gypsum should likewise follow a non-CNT pathway. Recently, Stawski et al. proposed a four step mechanism including the formation of 3 nm anhydrite particles determined via SAXS/WAXS.¹³ Alternatively and complimentarily, IR-ATR spectroscopy – as an in situ technique – provides chemical information on the occurring processes without the immediate need of synchrotron radiation. Consequently, the aim of the present studies was to gain in depth understanding on the crystallization processes of CaSO₄ in various media for unequivocally determining non-classical pathways in this system.

The crystallisation process towards CaSO₄·2H₂O and CaSO₄·2D₂O was monitored as a function of time via infrared attenuated total reflection (IR-ATR) spectroscopy using a single-bounce diamond ATR crystal (detailed experimental procedure see ESI†). To prevent evaporation and exchange processes with the ambient environment, a fluidic sample cell was designed and 3D printed (see ESI† Fig. S1), which may be sealed in a controlled nitrogen atmosphere.

During the crystallisation of gypsum in ultrapure water, significant changes of the H₂O bending mode (1640 cm⁻¹), and of the SO₄²⁻ vibrations at 1000 cm⁻¹ (ν₁), 1105 cm⁻¹ (ν₃), and 645 cm⁻¹ (ν₄) were observed.^14,15 The SO₄²⁻ν₃ mode minutely increases until it reaches a plateau. Hence, it is concluded that this initial crystallisation reaction eventually (Fig. 1) stops, and eventually saturation is reached as anticipated for a batch system assuming that precursors for later crystalline nuclei formation are established.

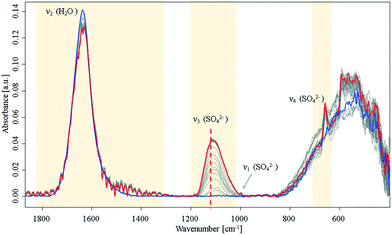Fig. 1 Infrared spectra of an aqueous Ca²⁺ and SO₄²⁻ solution during crystallisation. Spectra were collected over a period of 16 h in the closed sample cell under nitrogen atmosphere. Blue: start at t₀; red: end at t = 16 h. For a detailed view of the ν₃ band, see ESI† Fig. S2. The dashed line highlights a shift of the SO₄²⁻ν₃ mode at 1105 cm⁻¹ to higher wavenumbers.

During the entire observed period (16 h) the sulfate ν₃ band intensity revealed an exponential approximation towards a plateau along with a shift to higher wavenumbers. After approx. 10 h, the ν₁ and ν₄ bands appeared in the spectrum. This observation is indicative of a transition of sulfate from a T_d to a C_2v or C_3v symmetry, as the ν₁ band is in fact IR-inactive in the T_d symmetry.^16,17 Additionally, an increase of the ν₄ vibration located at 645 cm⁻¹ was evident during the crystallisation process, which has been reported in literature.^6,9,14,15 Resulting from group theory, the ν₄ vibration of the calcium sulfate molecule was expected to be observed as a triplet – especially regarding recent studies on formation of anhydrite during the process.^16–18 However, the remaining two peaks were not observed during these experiments; instead, the signal at 645 cm⁻¹ leads to the assumption that an amorphous phase has formed rather than a final crystalline phase, which would reveal all characteristic signals of the crystal lattice. Likewise, the characteristic splitting of the gypsum water band (1685 cm⁻¹ and 1623 cm⁻¹)⁹ was not observed. The onset of a signal at 1480 cm⁻¹ combined with the minute decrease of the water bending band indicates that a new population of H₂O–Ca²⁺–SO₄²⁻ related modes is present. Direct precipitation of the gypsum monocline structure with C⁶_2h symmetry¹⁹ may be precluded though, as the ν₄ doublet is absent.^15,20

After reaching equilibrium the system remained stable for at least 16 hours until a perturbation was applied (approx. 10 hours after the spectral behaviour was equilibrated), e.g., via forced evaporation. Then, later stages of crystallisation were observed via additional spectral changes indicative of the final formation of the crystal lattice. This behaviour matches with a process of forming disordered solids from stable pre-nucleation clusters as the initial step towards a final lattice.^10,21 The suggested hypothesis of solution clusters is consistent with a recently proposed pathway describing crystallization via an amorphous precursor phase by Y. W. Wang et al.¹² and Stawski et al.¹³

Following previous reports on crystallization of biomolecules⁸ and preliminary experiments during the present study, it was expected that crystallisation occurs more rapidly in D₂O vs. H₂O. For example, it was reported that D₂O enhances the aggregation speed of lysozyme. Turbidity experiments and kinetic calculations suggested that different kinetic routes for H₂O and D₂O are evident, and thus, different crystallisation mechanisms prevail.⁸ The associated IR spectra recorded during the crystallization process in neat D₂O clearly evidenced distinct differences in crystallization behaviour, as shown in Fig. 2.

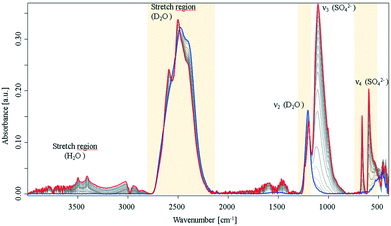Fig. 2 IR-ATR spectra of a CaSO₄ solution in D₂O during crystallisation collected over a period of 16 h under nitrogen atmosphere. Evolution of the D₂O stretching vibrations and of the sulfate ν₃ mode, see ESI† Fig. S3.

In comparison to the same processes in H₂O, the spectra in deuterated water show progressively distinct spectral changes over the observation period, and a more rapid crystallisation process. The sulfate ν₃ vibration rises rapidly with an exponential behaviour (see, ESI† Fig. S3), and approaches maximum intensity after approx. 350 min. Furthermore, the signal intensity is 10-times stronger compared to the same signal in H₂O. The early (i.e., at approx. 60 min) emergence of the sulfate ν₁ and ν₄ vibrations again evidence a change in symmetry. In the spectral region of the D₂O stretching mode, a peak-shift towards higher wavenumbers was observed combined with a peak splitting. Fig. S3 (ESI†) illustrates the progress of the peak splitting. The green curve indicates the increase of a new band at 2590 cm⁻¹, which occurs during a simultaneous decrease and shift of the 2500 cm⁻¹ band. Likewise, the D₂O bending vibration splits into two separate peaks. It is hypothesized that this splitting behaviour is similar to the characteristic water splitting observed in CaSO₄·2H₂O IR spectra, and provides strong evidence that D₂O is incorporated into the crystal lattice instead of H₂O. It should be noted that during these experiments bands of H₂O (i.e., stretching vibrations) were also observed resulting from the usage of hydrated initial constituents. However, minute amounts of remaining water apparently did not interfere with the observed processes. In addition, two bands were arising at 665 cm⁻¹ and 597 cm⁻¹, where in fact a triplet from the ν₄ mode was expected due to the C_2v symmetry of calcium sulfate molecules; however, the spectral behaviour indicates direct precipitation of crystalline species with C⁶_2h symmetry. This is in distinct contrast to the process in H₂O, which only formed a crystalline product when evaporation was allowed. After the crystallisation process appeared complete, the samples were extensively dried under a nitrogen atmosphere, which resulted in crystalline CaSO₄·2H₂O and CaSO₄·2D₂O (see, ESI† Fig. S4). Interestingly, the deuterated gypsum samples revealed excellent stability against H-D exchange with ambient water, which diffuses into the solid over a period of ten days. Likewise, treatment with small amounts of water did not lead to a measurable exchange of hydrogen and deuterium. Hence, it may be assumed that D₂O forms very stable deuterium bonds within the crystal lattice. In the IR-ATR spectra of the dried samples (ESI† Fig. S4), the features, which appeared during the crystallisation process appear well resolved, and the generated gypsum spectra compare well with the spectrum of natural gypsum. As expected, the water bending and stretching vibrations split into two vibrational modes, and additionally, a well-resolved SO₄²⁻ν₄ triplet is apparent (see, ESI† Fig. S4, blue spectrum), as reported elsewhere as a shoulder for natural gypsum samples.²² This indicates that the precipitate does not provide perfect C⁶_2h symmetry in contrast to the samples grown in D₂O.

The D₂O stretching and bending modes clearly show splitting as well (red spectrum). In comparison to CaSO₄·2H₂O, the bands within the H₂O stretching region of CaSO₄·2D₂O are shifted to smaller wavenumbers. This implies that this band is resulting from HDO integration into the crystal lattice due to H-D exchange with residual water. Furthermore, a strong sulfate vibration is evident. Interestingly, the v₄ mode of D₂O-grown gypsum still appears as a pronounced doublet (red spectrum). This indicates that the structural arrangements of both crystalline species do not reveal the same symmetry. The apparent doublet leads to the assumption that sulfate in CaSO₄·2D₂O, which was crystallized in heavy water established a perfect C⁶_2h symmetry. Although the CaSO·2H₂O spectrum reveals a v₄ triplet, the vibrational pattern of the spectrum – as reported elsewhere – provides no direct evidence for the presence of anhydrite or basanite.^15,23 However, the lifetime of these species is too short to be observable at the timescales of the present studies. SEM images of CaSO₄·2D₂O (ESI† Fig. S4) reveal distinct monocline crystals, as commonly reported for gypsum, which aligns well with the obtained characteristic IR spectra and a C⁶_2h symmetry.²⁰ In comparison, gypsum samples grown in H₂O have a tendency to crystallise in large plates with only a small proportion of monocline structures. Combined with observations derived from the spectral data, it may be assumed that D₂O promotes nucleation and growth during the crystallisation process by following different kinetic routes explained as follows.

According to non-classical nucleation theory, two energy barriers are proposed for the reaction from ion pairs to ordered crystalline nuclei. First, the reactants have to overcome an energy barrier to form stable solution clusters. This barrier can be insignificant in some systems, for example calcium carbonate (see the work of Gebauer and Cölfen).^10,24 From this stable state, the system needs to overcome a second energy barrier for establishing ordered crystalline nuclei from the initially disordered yet stable state.^10,11 In pure D₂O, proof for solution clusters – as evident in the H₂O experiments – could not be observed. For the case of D₂O, if a non-CNT mechanism is operative, the transition of the pre-nucleation clusters into crystalline solids is kinetically faster than the collection of the spectrum. Thus, either the crystallisation process is via a classical pathway or in the presence of D₂O there is a very fast pre-nucleation clusters to amorphous solids to crystalline solids transition. Clearly, the presence of D₂O also increases the overall rate of crystallisation (a crystalline product is formed after 60 min). Nonetheless, the reactants precipitated as perfect monocline crystals and a perfect C⁶_2h symmetry. The obtained IR-ATR spectra provide evidence for the occurrence of crystalline species, which are different in symmetry compared to the same reaction in water. Solubility effects may be neglected, since the solubility in both solvents only differs by 12.86% ± 1.6% measured via total reflection X-ray fluorescence (TXRF), see ESI.†

In pure H₂O, Stawski et al.,¹³ proposed a four step process that includes the formation of pre-nucleation clusters and nano-sized particles prior to formation of gypsum particles. These solids were proposed based on calculated electron densities, which involved some assumptions, while the work presented here is based only on the infrared signatures of the system as it evolves temporally.

Additional experiments, were performed by spiking D₂O into an aqueous CaSO₄ system at deliberately selected intervals. The first spike was injected after approx. 30 min, i.e., sufficient time was provided to facilitate the presence of solution clusters and amorphous solids; the associated spectra are shown in Fig. 3 (experimental details are given in the ESI†).

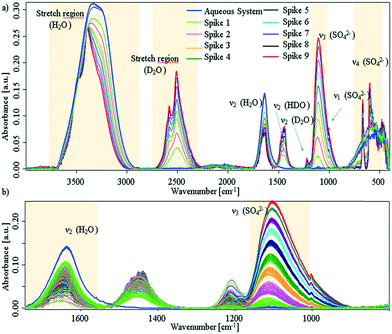Fig. 3 a) IR-ATR spectra of aqueous CaSO₄ solution, which was spiked with D₂O in intervals of 30 min. Blue spectra: prior to spiking; red spectrum: last D₂O spike. b) Zoom onto the sulfate ν₃ band and water bending region. The spectral behaviour as a function of time is given in Fig. S5 within the ESI.†

It is clearly evident that each D₂O spike induces a crystallisation event. After each injection of D₂O, the sulfate band increases with an exponential behaviour until D₂O is consumed by the system. In turn, this indicates if the freely available D₂O concentration drops below a certain limit, precipitation stops and the system resides in a stable equilibrium state (see, ESI† Fig. S5). After nine spikes, the entire ATR crystal surface is covered, and no further changes may be observed. Effects due to different solubility may safely be neglected, as the injected amount of D₂O is too small (i.e., 5% for each spike) to change the overall solubility of gypsum within the system.

Due to the behaviour of the water bending mode, it is suggested that D₂O is consumed by both H-D exchange and crystal growth. Regarding Fig. 3a), all bands of deuterated water show distinct band splitting. Likewise, bands in the H₂O/HDO stretching region shift to higher wavenumbers, get more pronounced, and start to split. Thus, apparently both species are incorporated into the crystal lattice. In lieu of the ν₄ triplet of gypsum seen, a doublet is apparent, which compares well to the D₂O-grown crystals shown in ESI† Fig. S4. It can therefore be assumed that a crystalline structure with C⁶_2h symmetry is directly established and precipitates. The missing triplet and well resolved splits in the D₂O stretching regime proves that deuterium oxide not only initiates the reaction, but is intimately involved in the crystallisation process within that mixture.

The IR-ATR spectra obtained in the present study clearly supports a non-classical crystallization mechanism for the water-gypsum system, and reveals a substantial impact of D₂O on the crystallisation kinetics. Compared to SAXS/WAXS requiring a synchrotron light source, IR-ATR spectroscopy provides in-depth in situ information on the nature and chemistry of such nucleation processes with fewer assumptions being necessary. Evidence for the formation of anhydrite or basanite during the nucleation process, as reported elsewhere¹³ could not be observed, which is probably related to the lifetime of these species.²³ In any case, the obtained results are consistent with previously suggested amorphous precursor phases.^6,12,13

Due to the impact of D₂O on the crystallisation process, transformation from solution clusters to crystalline solids – may be induced via D₂O spikes. Each D₂O injection into the H₂O system, which is initially in an equilibrium state, instantly triggers precipitation into perfect monocline crystals.

Thus, it is suggested that molecular restructuring from solution clusters to ordered crystalline nuclei is a critical rate-determining step for the formation of gypsum solids. From the perspective of the two step nucleation theory, this indicates that the energy barrier between those states is lower in D₂O vs. H₂O, which explains the accelerated crystal formation. This data also shows, very importantly, that the kinetic barriers are critical in determining whether the system crystallises through a classical or non-classical pathway.

Acknowledgements

RS thanks D. Rommel at the team of Prof. K. Leopold (IABC, Ulm Univ.) for assistance with TXRF measurements.

Notes and references

1. G. A. Lager, T. Armbruster, F. J. Rotella, J. D. Jorgensen and D. G. Hinks, Am. Mineral., 1984, 69, 910–918.
2. H. Takahashi, I. Maehara and N. Kaneko, Spectrochim. Acta, Part A, 1983, 39, 449–455.
3. W. F. Cole and C. J. Lancucki, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 921–929.
4. R. Kling, J. Chem. Phys., 1971, 54, 5331.
5. K. Iishi, Phys. Chem. Miner., 1979, 4, 341–359.
6. F. Jones, CrystEngComm, 2012, 14, 8374–8381.
7. D. Neubauer, J. Korbmacher, M. Frick, J. Kiss, M. Timmler, P. Dietl, O. H. Wittekindt and B. Mizaikoff, Anal. Chem., 2013, 85, 4247–4250.
8. L. Xin Qi and S. Yoh, J. Protein Chem., 1998, 17, 9–14.
9. M. Hass and G. B. B. M. Sutherland, Proc. R. Soc. London, Ser. A, 1956, 236, 427–445.
10. D. Gebauer and H. Cölfen, Nano Today, 2011, 6, 564–584.
11. D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629.
12. Y.-W. Wang, Y.-Y. Kim, H. K. Christenson and F. C. Meldrum, Chem. Commun., 2012, 48, 504.
13. T. M. Stawski, A. E. S. van Driessche, M. Ossorio, J. Diego Rodriguez-Blanco, R. Besselink and L. G. Benning, Nat. Commun., 2016, 7, 11177.
14. I. R. Moraes, M. C. P. M. Da Cunha and F. C. Nart, J. Braz. Chem. Soc., 1996, 7, 453–460.
15. J. L. Bishop, M. D. Lane, M. D. Dyar, S. J. King, A. J. Brown and G. A. Swayze, Am. Mineral., 2014, 99, 2105–2115.
16. F. A. Cotton, Chemical applications of group theory, Wiley, Cambridge, 3rd edn, 1991, vol. 249.
17. J. J. Wylde, C. A. Geoffrey and I. R. Collins, Appl. Spectrosc., 2001, 55, 1155–1160.
18. G. Renaudin, R. Segni, F. Leroux and C. Taviot-Gueho, 12th Int. Congr. Chem. Cem., 2007.
19. J. F. Ferraro, Low-Frequenzy Vibrations of Inorganic and Coordination Compounds, Plenum Press, New York, 1st edn, 1971.
20. W. A. Deer, R. A. Howie and J. Zussman, An introduction to the Rock- Forming Minerals, Pearson Education Limited, Edinburgh, 2nd edn, 1992.
21. A. S. Myerson, Faraday Discuss., 2011, 179, 11–14.
22. M. D. Lane, Am. Mineral., 2007, 92, 1–18.
23. U. Tritschler, A. E. S. Van Driessche, A. Kempter, M. Kellermeier and H. Cölfen, Angew. Chem., Int. Ed., 2015, 54, 4083–4086.
24. D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43, 2348–2371.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ce01787h

---