Stacking interactions between hydrogen-bridged and aromatic rings: study of crystal structures and quantum chemical calculations†
Jelena P.
Blagojević
a,
Dušan Ž.
Veljković
a and
Snežana D.
Zarić
*ab
aDepartment of Chemistry, University of Belgrade, Studentski trg 12-16, Belgrade, Serbia. E-mail: szaric@chem.bg.ac.rs
bDepartment of Chemistry, Texas A&M University at Qatar, P. O. Box 23874, Doha, Qatar
First published on 25th October 2016
Abstract
Geometric analysis of data from Cambridge Structural Database (CSD) reveals that contacts between planar hydrogen-bridged rings and C6-aromatic rings are mostly parallel stacked geometries. High-level quantum chemical calculations show that their interaction energies are comparable with interactions between two hydrogen-bridged rings. Namely, the interaction energy, at the CCSD(T)/CBS level, of the most stable geometry is −4.38 kcal mol−1, which is comparable with that of interaction between two hydrogen-bridged rings (−4.89 kcal mol−1) and significantly stronger than that of stacking between two benzene rings (−2.73 kcal mol−1).
Introduction
Although stacking (parallel) interactions have been considered to be typical for aromatic rings and studied extensively on model systems with aromatic rings, evidence of parallel interactions of other planar molecules and fragments has been reported.1–14It has been discovered that the monomer aromaticity can even hinder stacking interactions in some cases. By analysing stacking energies calculated for a wide range of π-stacking systems, it has been concluded that stacking interactions involving non-aromatic polyenes are as favourable as, if not more favourable than, interactions among equivalent aromatic species.15,16
Cyclohexane and benzene dimers have similar interaction energies, but the energy differences are dependent on the functional and basis set used. The electrostatic component is the largest contributor to the observed differences.17 When the number of condensed rings becomes larger, aromatic rings begin to exhibit distinct behaviour from their aliphatic analogues. Thus, the calculated stacking interaction of tetracene is 5–7 kcal mol−1 more stable than stacking of octadecahydrotetracene, depending on the method used.18 This additional effect, called the π–π stacking effect, is a special nonlocal electron correlation between π-electrons in the two fragments and it is not pronounced in small stacked systems.
Some recent studies reveal that aromatic interactions in amyloid formation are not as important as previously postulated, since aliphatic peptides show similar self-assembly, justifying the use of aliphatic ultrasmall peptides as a simplified model-system to study amyloidosis.19 Theoretical investigation of the nonintercalative binding of an aliphatic and an aromatic bisguanylhydrazone (BGH) to the minor groove of double-stranded (dA–dT)n oligomers shows that the binding energy is larger with the aliphatic BGH than with the aromatic one. Interactions with water are also larger with the aliphatic BGH than with the aromatic BGH. Dehydration energy is what makes the energy balance more favourable for the interaction of the aromatic than of the aliphatic BGH with the polynucleotide.20
Rings containing metals or hydrogen bonds can also form stacking interactions.3,4,6,11–14,21 Thus, planar metal chelates with delocalized π-bonds can stack with aromatic species and with other metal chelate rings, exhibiting large interaction energies.3,4,6,11 Quasi-rings, formed by resonance-assisted hydrogen bonding,12,21 can form π-stacking interactions. Moreover, hydrogen-bridged rings (HBR) with only single bonds in the ring form stacking interactions much stronger than stacking of two benzene molecules.13,14 Saturated hydrogen-bridged rings in the crystal phase are mostly antiparallel with normal distances typical for stacking (3.0–4.0 Å). High-level ab initio calculations of interaction energies of dimers showed that energies can be much higher than those of stacking in benzene dimers. The stacking energy of the 2-methylidenehydrazinecarbothioamide dimer, by far the most common saturated hydrogen-bridged species found in the CSD, is −4.89 kcal mol−1 at the CCSD(T)/CBS level,13 while stacking between two benzene molecules is much weaker, having an energy of −2.73 kcal mol−1 (ref. 22) calculated at the same level of theory.
Studying interactions between hydrogen-bridged and aromatic rings is important for understanding supramolecular systems. For example, small angle neutron scattering (SANS) and molecular dynamics (MD) simulations were used to characterize hydrophobic clusters of isopropanol and pyridine in aqueous solutions, which serve as highly soluble analogues of the nonpolar aliphatic and aromatic side chains of proteins, respectively. Addition of guanidinium chloride reduced the aggregation of pyridine molecules, but had no effect on isopropanol aggregation, which indicates the denaturant activity of guanidinium chloride in proteins involving aromatic amino acid side chains.23 The guanidinium cation is among the most frequent hydrogen-bridged species found in the Cambridge Structural Database (CSD).14
In this work, we studied stacking between aromatic and hydrogen-bridged rings, by inspecting their mutual contacts in the CSD and by calculating the interaction energies at high quantum mechanical level.
Methodology
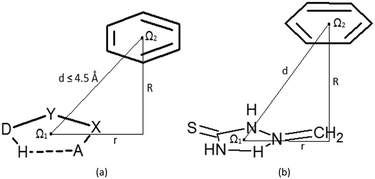
Contacts between hydrogen-bridged rings, having only single bonds, which are all parts of acyclic systems, and C6-aromatic groups are studied in this work. A CSD search (CSD version 5.36 and updates-February 2015) is performed by using ConQuest 1.17. Constraints applied in the search were: (1) distances between donor (D) and acceptor (A) atoms within the hydrogen-bridged ring less than 4.0 Å; (2) angles between donor (D), hydrogen, and acceptor (A) atoms within the ring from 90° to 180°; (3) absolute torsions AXYD and XYDH (Fig. 1a) from 0 to 10°; (4) donor (D) and acceptor (A) atoms include N, O, Cl, S and F atoms, due to their considerable electronegativities; (5) all covalent bonds within the hydrogen-bridged ring are set to be single acyclic; (6) all atoms in the hydrogen-bridged ring are planar (rings with nonplanar atoms; tetrahedral nitrogen, oxygen or carbon atoms and polyvalent sulphur or metal atoms were excluded); (7) intermolecular contacts having distances between two centroids of 4.5 Å or less (Fig. 1a) are considered as contacts between rings. Criterion (6), for planar atoms in the ring, was set in order to avoid side interactions or steric hindrances coming from atoms or groups which are situated in the region between the rings. The crystallographic R factor is set to be less than 10%, disordered structures are excluded, and coordinates are error-free; according to the criteria used in the CSD, the H-atom positions were normalized using the CSD default X–H bond lengths (O–H = 0.983 Å, C–H = 1.083 Å and N–H = 1.009 Å), and no polymer and powder structures were included.Molecules of benzene and 2-methylidenehydrazinecarbothioamide (Fig. 1b) were chosen for the estimation of stacking energies among hydrogen-bridged and aromatic molecules. Results from our previous work,13 where stacking between two 2-methylidenehydrazinecarbothioamide molecules is calculated, could be useful for comparison. Optimizations of monomers were performed at the MP2/cc-pVTZ level. Stacking interaction energies between two rings at certain mutual positions were calculated at the CCSD(T)/CBS level, while potential curves were obtained by methods that are in good agreement with CCSD(T)/CBS (ESI†). Single-point interaction energy was determined as a difference of the dimer energy and the sum of energies of monomers, having included correction of basis set superposition error (BSSE).24 All calculations were carried out by using Gaussian09 series of programs.25
Energy decomposition analysis was conducted using the perturbation method SAPT.26 In the SAPT approach, the calculated interaction energies can be decomposed into four components: electrostatic, exchange, induction and dispersion energies. High-order SAPT2+3 computations with a density-fitting approximation and aug-cc-PVDZ basis set were performed using the PSI4 program.27,28
Results and discussion
Interactions in crystal structures from the CSD
The number of structures with both planar hydrogen-bridged rings, with only single bonds in the ring (satisfying constraints 1–6 from the Methodology section), and C6-aromatic rings, was 1985. The number of rings (only constraints 1–6) was 1053. It was considered that an interaction between hydrogen-bridged and aromatic rings exists if the distance between the centers of the rings is 4.5 Å or less (Fig. 1a). In this way, we found 493 contacts (47% of the 1053 rings found). A somewhat smaller fraction of hydrogen-bridged rings in the CSD forms interactions between two hydrogen-bridged rings (31%).13Fig. 2 shows the interplanar angle distribution which indicates that contacts between hydrogen-bridged and aromatic rings are mostly parallel, namely 221 contacts (44.8%), which have interplanar angles smaller than 10°. A similar number of parallel contacts between hydrogen-bridged rings are found, namely 264 contacts.13
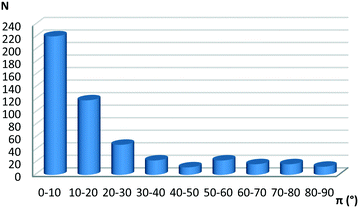 | ||
| Fig. 2 Interplanar angle (π) distribution of contacts between planar hydrogen-bridged rings and aromatic rings. | ||
The typical normal distances of parallel contacts (with interplanar angle π smaller than 10°) found in the CSD are common for stacking interactions,3,11–14,29,30 since most of them are between 3.0 Å and 4.0 Å. The normal distance dependence on offset values is given in Fig. 3.
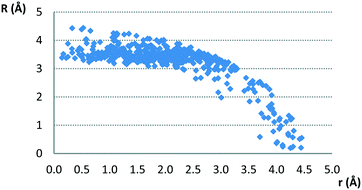 | ||
| Fig. 3 Normal distance dependence on offset values for parallel contacts between planar hydrogen-bridged rings and aromatic rings. | ||
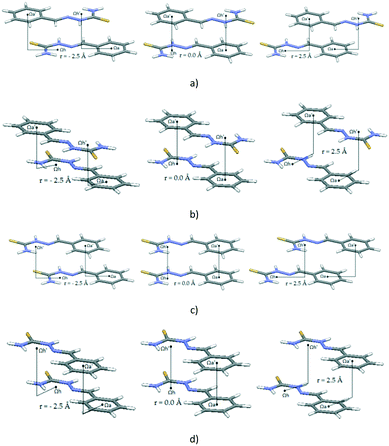
It is noticed by visual inspection that most of the obtained contacts are between molecules that contain both C6-aromatic and hydrogen-bridged rings. Some structural motifs are particularly frequent. The most frequent is the structural motif presented in Fig. 4a. It was found in 129 intermolecular parallel interactions (58% of 221 parallel contacts). In this structural motif, a C6-aromatic group is attached to the acceptor atom by a linker consisting of one planar carbon atom. The structure presented in Fig. 4b, where a C6-aromatic group is directly attached to the donor atom, is less numerous (21 contacts, 9.5%).
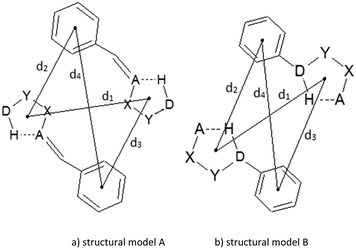 | ||
| Fig. 4 Some of the most common structural motifs observed in the CSD with the distances between centers of the rings. | ||
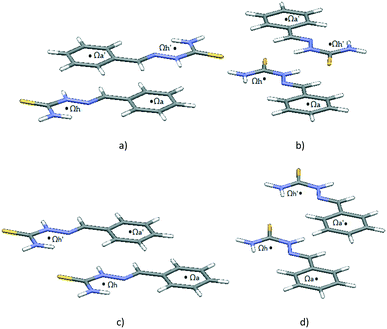
Interactions between two molecules with structural motif A were inspected more closely. The number of motifs A found in the CSD and the number of contacts between particular rings are shown in Table 1. Contacts between hydrogen-bridged and aromatic rings are roughly three times as frequent as contacts between two hydrogen-bridged or two aromatic rings, which are approximately equally frequent. The prevalence of hydrogen-bridged/aromatic contacts is probably a consequence of the possibility for the existence of two simultaneous HBR/aromatic interactions between two molecules (Fig. 5). Results from Table 2 support this conclusion, since two simultaneous hydrogen-bridged/aromatic interactions are present in most cases (80 contacts, which are 62% of the total 129 HBR/aromatic contacts).
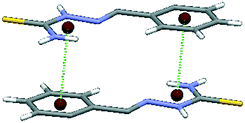 | ||
| Fig. 5 One of the possible structural fragments found in the CSD illustrating the typical orientation of the interacting rings with two simultaneous hydrogen-bridged/aromatic interactions. | ||
Quantum chemical calculations on interactions
In order to evaluate the energies of parallel interactions between hydrogen-bridged and aromatic rings, we performed quantum chemical calculations. Estimation of the best method for calculating stacking energies is based on good agreement with CCSD(T)/CBS energies.31 Potential surfaces are calculated at the MP2/cc-pVTZ level, since the energies are very similar to the CCSD(T)/CBS limit for all five orientations (Table S1†). The model system used for calculations is presented in Fig. 7.Potential surfaces were calculated by varying offset values in the Ω1-C direction and in the orthogonal direction in steps of 0.5 Å, while normal distances were examined for every particular offset value in order to obtain the strongest energy. The potential curves, showing the strongest energy for a given offset value, are given in Fig. 6. The corresponding normal distance dependencies on offset values are shown in Fig. S5.†
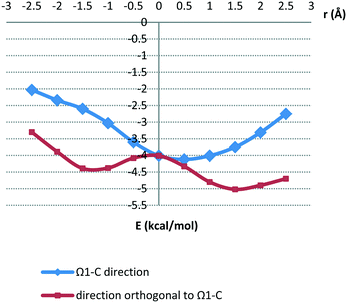 | ||
| Fig. 6 Potential curves calculated at the MP2/cc-pVTZ level. The strongest energy for a given offset value is shown. | ||
The potential curves in Fig. 6 show that minima occur at parallel-displaced positions, similar to benzene,22 pyridine30 and hydrogen-bridged ring stacking dimers.13 Interaction energies in the Ω1-C direction are less strong than those in the orthogonal direction (Fig. 6). The strongest interaction is in the direction orthogonal to Ω1-C (Fig. 6 and 7a); the interaction energy at the −1.5 Å minimum on the curve is −4.38 kcal mol−1 at the CCSD(T)/CBS level (Table 3). This energy is comparable to the stacking energy in the hydrogen-bridged ring dimer, −4.89 kcal mol−1, for the same hydrogen-bridged ring (2-methylidenehydrazinecarbothioamide)13 (Table 3). The result is somewhat surprising because the benzene molecule does not possess dipole moment.
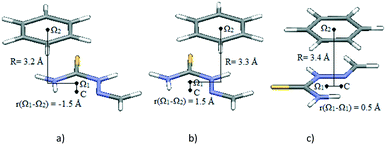 | ||
| Fig. 7 Geometries of potential curve minima (Fig. 6, Table 3): a) minimum at −1.5 Å, along the direction orthogonal to Ω1-C, corresponding to stacking interaction of the two rings; b) minimum at 1.5 Å, along the direction orthogonal to Ω1-C, corresponding to interaction of a benzene ring with a doubly bonded methylidene group; c) minimum at 0.5 Å, along the Ω1-C direction, corresponding to stacking interactions of the two rings. | ||
| 2-Methylidenehydrazinecarbothioamide/benzene | |||
|---|---|---|---|
| ΔE (kcal mol−1) | r (Å) | R (Å) | |
| Along the Ω–Ω′ direction | −4.04 | 0.5 | 3.4 |
| Orthogonal to the Ω–Ω′ direction | −4.38 | −1.5 | 3.2 |
The other minimum at the positive offset of 1.5 Å, on the same curve, does not correspond to interaction between hydrogen-bridged and aromatic rings; it is a consequence of side interactions with the doubly bonded methylidene group (Fig. 7b). The energy corresponding to the Ω1-C curve minimum (Fig. 6 and 7c), calculated at the CCSD(T)/CBS level, is −4.04 kcal mol−1 (Table 3). Energies at both minima on potential curves for stacking between the hydrogen-bridged ring and benzene are significantly stronger than those of stacking of two benzene molecules (−2.73 kcal mol−1).22
Since the data from crystal structures showed that most of the stacking interactions are between molecules that contain both C6-aromatic and hydrogen-bridged rings (Fig. 6), we performed calculations on E-benzylidenehydrazinecarbothioamide dimers. This molecule was chosen as an example of structural motif A (Fig. 4a). Quite strong energies were calculated for stacking dimers of E-benzylidenehydrazinecarbothioamide (Fig. 8b). The potential curve is obtained by calculations using the MP2/cc-pVTZ method, since it was shown that this method is good for interaction energy calculations of 2-methylidenehydrazinecarbothioamide/benzene dimers in different mutual positions (ESI†).
Two E-benzylidenehydrazinecarbothioamide molecules in antiparallel and parallel alignment are moved in the Ωh–Ωa direction and in orthogonal direction in steps of 0.5 Å, while normal distances were varied for every particular offset value in order to obtain the most stable interaction for each offset value.
Potential curves are given in Fig. 9, while geometries corresponding to the minima are given in Fig. 10. For the antiparallel orientation, energies at the minima for both curves (at the offset of 1.5 Å in both cases and normal distances of 3.2 Å and 3.3 Å, for the Ωh–Ωa direction and orthogonal direction, respectively) are quite strong, −12.26 kcal mol−1 and −12.21 kcal mol−1, for the Ωh–Ωa direction and orthogonal direction, respectively. In the geometries at the minima, there are two simultaneous stacking interactions between hydrogen-bridged and aromatic rings (Fig. 10a and b). In the geometries at the curve minima, the two molecules are slipped (Fig. 10a and b).
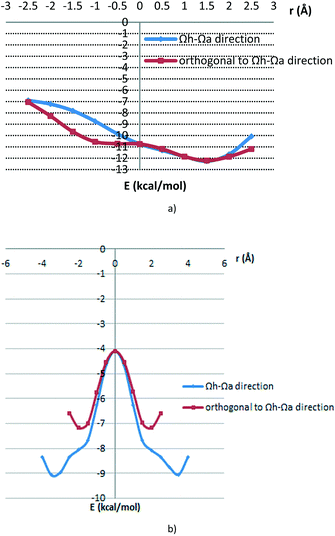 | ||
| Fig. 9 Potential curves for the dimer interaction of E-benzylidenehydrazinecarbothioamide in a) antiparallel alignment and b) parallel alignment; model systems are shown in Fig. 8. | ||
Potential curves corresponding to parallel orientations (Fig. 9b) are symmetric since dimer geometries at positive and negative offsets are the same (Fig. 8c and d). Compared to the minima in antiparallel positions (Fig. 9, Table 4), interaction energies are less strong (−9.07 kcal mol−1 and −7.18 kcal mol−1, Ωh–Ωa and orthogonal directions, respectively) and offset values at the curve minima are larger (−3.0 Å and −2.0 Å in Ωh–Ωa and orthogonal directions, respectively) (Table 4).
| Antiparallel alignment | |||
|---|---|---|---|
| ΔE (kcal mol−1) | r (Å) | R (Å) | |
| Ωh–Ωa direction | −12.26 | 1.5 | 3.2 |
| Orthogonal to the Ωh–Ωa direction | −12.21 | 1.5 | 3.3 |
| Parallel alignment | |||
|---|---|---|---|
| ΔE (kcal mol−1) | r (Å) | R (Å) | |
| Ωh–Ωa direction | −9.07 | ±3.5 | 3.3 |
| Orthogonal to the Ωh–Ωa direction | −7.18 | ±2.0 | 3.3 |
The strong calculated energies of stacking interactions for the antiparallel orientation explain data from the CSD search (Tables 1 and 2 and Fig. S3†), i.e. structures with two simultaneous interactions between hydrogen-bridged and aromatic rings (and consequently antiparallel) are significantly more prevalent than structures with single contacts (HBR/HBR, aromatic/aromatic or HBR/aromatic) or two simultaneous interactions in parallel orientation.
SAPT decomposition
In order to better understand the nature of stacking between aromatic and hydrogen-bridged rings, SAPT decomposition analysis was applied using the aug-cc-pVDZ basis set of Dunning. The SAPT calculations were performed on two minima presented in Fig. 7 and Table 3, the minimum along the Ω–Ω′ direction and the minimum orthogonal to the Ω–Ω′ direction.The results given in Table 5 show that terms for both studied minima are similar. In both systems, electrostatic, induction and dispersion energies are attractive, while the strongest attractive contribution is dispersion; it is more than two times larger than the electrostatic term. Exchange is repulsive in both systems. The calculated total SAPT energies (−3.94 and −4.44 kcal mol−1, Table 5) are in very good agreement with the CCSD(T)/CBS values (−4.04 and −4.38 kcal mol−1, Table 3). The stronger interaction energy for the minimum orthogonal to the Ω–Ω′ direction is a consequence of stronger electrostatic, induction and dispersion energies, although the repulsive exchange term is also larger for this minimum (Table 5).
| Energy term | Minimum along the Ω–Ω′ direction | Minimum orthogonal to the Ω–Ω′ direction |
|---|---|---|
| Electrostatic | −3.20 | −4.29 |
| Exchange | 8.48 | 9.49 |
| Induction | −0.86 | −1.04 |
| Dispersion | −8.36 | −8.59 |
| Total SAPT2+3 | −3.94 | −4.44 |
Comparison with SAPT decomposition for stacked benzene dimers32 shows that electrostatic and dispersion terms are more attractive in benzene/hydrogen-bridged rings, while repulsive exchange terms are similar. This results in significantly more stable stacking in benzene/hydrogen-bridged rings in comparison to benzene.
Conclusions
In summary, contacts between planar hydrogen-bridged rings and aromatic C6-rings, found in the CSD, are mostly parallel-displaced, with normal distances typical for stacking. In the crystal structures, very often these interactions are between two molecules that possess both hydrogen-bridged and aromatic rings.Interaction energies are calculated on the model system composed of a hydrogen-bridged ring (2-methylidenehydrazinecarbothioamide) and a benzene molecule. The most stable orientation is parallel-displaced, in accordance with data in the crystal structures, with an interaction energy of −4.38 kcal mol−1 at the CCSD(T)/CBS level. SAPT decomposition of interaction energies shows that the main contribution to attraction is dispersion energy, although attractive electrostatic energy is also significant.
The data show that interaction energy between hydrogen-bridged and benzene rings is comparable with that of interaction between two hydrogen-bridged rings (2-methylidenehydrazinecarbothioamide), −4.89 kcal mol−1, while it is significantly stronger than that of stacking between two benzene rings, −2.73 kcal mol−1.
Acknowledgements
This work was supported by the Serbian Ministry of Education, Science and Technological Development [grant number 172065] and an NPRP grant from the Qatar National Research Fund (a member of the Qatar Foundation) [grant number NPRP8-425-1-087]. The HPC resources and services used in this work were partially provided by the IT Research Computing group in Texas A&M University at Qatar. IT Research Computing is funded by the Qatar Foundation for Education, Science and Community Development (http://www.qf.org.qa).Notes and references
- E. Craven, C. Zhang, C. Janiak, G. Rheinwald and H. Lang, Z. Anorg. Allg. Chem., 2003, 629, 2282 CrossRef CAS.
- G. V. Janjić, D. Ž. Veljković and S. D. Zarić, Cryst. Growth Des., 2011, 11, 2680 Search PubMed.
- D. N. Sredojević, G. A. Bogdanović, Z. D. Tomić and S. D. Zarić, CrystEngComm, 2007, 9, 793 RSC; D. N. Sredojević, Z. D. Tomić and S. D. Zarić, Cryst. Growth Des., 2010, 10, 3901 Search PubMed; Z. D. Tomić, V. M. Leovac, S. V. Pokorni, D. Zobel and S. D. Zarić, Eur. J. Inorg. Chem., 2003, 1222 CrossRef; Z. D. Tomić, D. N. Sredojević and S. D. Zarić, Cryst. Growth Des., 2006, 6, 29 Search PubMed.
- X.-J. Wang, H.-X. Jian, Z.-P. Liu, Q.-L. Ni, L.-C. Gui and L.-H. Tang, Polyhedron, 2008, 27, 2634 CrossRef CAS; P. P. Chakrabarty, D. Biswas, S. Garcia-Granda, A. D. Jana and S. Saha, Polyhedron, 2012, 35, 108 CrossRef; D. Biswas, P. P. Chakrabarty, S. Saha, A. D. Jana, D. Schollmeyer and S. García-Granda, Inorg. Chim. Acta, 2013, 408, 172 CrossRef; S. Jana, S. Khan, A. Bauzá, A. Frontera and S. Chattopadhyay, J. Mol. Struct., 2017, 1127, 355 CrossRef; S. Bhattacharya, S. Roy, K. Harms, A. Bauza, A. Frontera and S. Chattopadhyay, Inorg. Chim. Acta, 2016, 442, 16 CrossRef; G. Mahmoudi, A. Castiñeiras, P. Garczarek, A. Bauzá, A. L. Rheingold, V. Kinzhybalo and A. Frontera, CrystEngComm, 2016, 18, 1009 RSC.
- J. Granifo, M. Vargas, M. T. Garland, A. Ibanez, R. Gavino and R. Baggio, Inorg. Chem. Commun., 2008, 11, 1388 CrossRef CAS.
- X.-J. Wang, L.-C. Gui, Q.-L. Ni, Y.-F. Liao, X.-F. Jiang, L.-H. Tang, Z. Zhang and Q. Wu, CrystEngComm, 2008, 10, 1003 RSC; Q.-L. Ni, X.-F. Jiang, L.-C. Gui, X.-J. Wang, K.-G. Yang and X.-S. Bi, New J. Chem., 2011, 35, 2471 RSC; T. S. Basu Baul, S. Kundu, H. Höpfl, E. R. T. Tiekink and A. Linden, J. Coord. Chem., 2014, 6, 1061 CrossRef CAS; A. P. McKay, W. K. C. Lo, D. Preston, G. I. Giles, J. D. Crowley, J. E. Barnsley, K. C. Gordon and D. A. McMorran, Inorg. Chim. Acta, 2016, 446, 41 CrossRef; S. Basu Baul, S. Kundu, S. Weng Ng, N. Guchhait and E. R. T. Tiekink, J. Coord. Chem., 2014, 1, 96 CrossRef; T. S. Basu Baul, S. Kundu, H. Höpfl, E. R. T. Tiekink and A. Linden, Polyhedron, 2013, 55, 270 CrossRef.
- K. F. Konidaris, C. N. Morrison, J. G. Servetas, M. Haukka, Y. Lan, A. K. Powell, J. C. Plakatouras and G. E. Kostakis, CrystEngComm, 2012, 14, 1842 RSC; K. F. Konidaris, A. K. Powell and G. E. Kostakis, CrystEngComm, 2011, 13, 5872 RSC.
- E. R. T. Tiekink, Chem. Commun., 2014, 50, 11079 RSC; T. S. BasuBaul, S. Kundu, S. Mitra, H. Höpfl, E. R. T. Tiekink and A. Linden, Dalton Trans., 2013, 42, 1905 RSC; H. R. Khavasi and B. Mir Mohammad Sadegh, Dalton Trans., 2015, 44, 5488 RSC; H. Hosseini-Monfared, E. Pousaneh, S. Sadighian, S. Weng Ng and E. R. T. Tiekink, Z. Anorg. Allg. Chem., 2013, 639, 435 CrossRef CAS; N. Qing-Ling, J. Xuan-Feng, G. Liu-Cheng, W. Xiu-Jian, Y. Kun-Guo and B. Xian-Shu, New J. Chem., 2011, 35, 2471 RSC; K. Molčanov, M. Jurić and B. Kojić-Prodić, Dalton Trans., 2013, 42, 15756 RSC.
- E. Melnic, E. B. Coropceanu, O. V. Kulikova, A. V. Siminel, D. Anderson, H. J. Rivera-Jacquez, A. E. Masunov, M. S. Fonari and V. Ch. Kravtsov, J. Phys. Chem. C, 2014, 118, 30087 CAS.
- Y. Zhao, X.-H. Chang, G.-Z. Liu, L.-F. Ma and L.-Y. Wang, Cryst. Growth Des., 2015, 15, 966 CAS.
- D. P. Malenov, D. B. Ninković, D. N. Sredojević and S. D. Zarić, ChemPhysChem, 2014, 15, 2458 CrossRef CAS PubMed; D. P. Malenov, D. B. Ninković and S. D. Zarić, ChemPhysChem, 2015, 16, 761 CrossRef PubMed.
- H. Karabiyik, H. Karabiyik and N. OcakIskeleli, Acta Crystallogr., Sect. B: Struct. Sci., 2012, 68, 71 CAS.
- J. P. Blagojević and S. D. Zarić, Chem. Commun., 2015, 51, 12989 RSC.
- J. P. Blagojević, G. V. Janjić and S. D. Zarić, Crystals, 2016, 6, 34 CrossRef.
- J. W. G. Bloom and S. E. Wheeler, Angew. Chem., Int. Ed., 2011, 50, 7847 CrossRef CAS PubMed.
- C. Corminboeuf, P. von Ragué Schleyer and P. Warner, Org. Lett., 2007, 9, 3263 CrossRef CAS PubMed.
- K. S. Kim, S. Karthikeyan and N. J. Singh, J. Chem. Theory Comput., 2011, 7, 3471 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430 CrossRef CAS PubMed.
- A. Lakshmanan, D. W. Cheong, A. Accardo, E. Di Fabrizio, C. Riekel and C. A. E. Hauser, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 519 CrossRef CAS PubMed.
- N. Gresh and B. Pullman, Theor. Chim. Acta, 1984, 64, 383 CrossRef CAS.
- L. Sobczyk, S. J. Grabowski and T. M. Krygowski, Chem. Rev., 2005, 105, 3513 CrossRef CAS PubMed; K. A. Lyssenko and M. Y. Antipin, Russ. Chem. Bull., 2006, 55, 1 CrossRef; P. Sanz, O. Mó, M. Yañez and J. Elguero, J. Chem. Phys., 2007, 111, 3585 CrossRef PubMed.
- (a) J. Rezač, K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2011, 7, 2427 CrossRef PubMed; (b) D. B. Ninković, G. V. Janjić, D. Ž. Veljković, D. N. Sredojević and S. D. Zarić, ChemPhysChem, 2011, 12, 3511 CrossRef PubMed.
- P. E. Mason, C. E. Dempsey, G. W. Neilson, S. R. Kline and J. W. Brady, J. Am. Chem. Soc., 2009, 131, 16689 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
- B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Chem. Phys., 2010, 133, 014101 CrossRef PubMed.
- J. M. Turney, A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill and T. D. Crawford, Psi4: An open-source ab initio electronic structure program, WIREs Comput. Mol. Sci., 2012, 2, 556 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656 CrossRef CAS PubMed; R. Podeszwa, R. Bukowski and K. Szalewicz, J. Phys. Chem. A, 2006, 110, 10345 CrossRef PubMed; M. Pitonak, P. Neogrady, J. Rezac, P. Jurecka, M. Urban and P. Hobza, J. Chem. Theory Comput., 2008, 4, 1829 CrossRef PubMed; D. B. Ninković, J. M. Andrić and S. D. Zarić, ChemPhysChem, 2013, 14, 237 CrossRef PubMed.
- D. B. Ninković, G. V. Janjić and S. D. Zarić, Cryst. Growth Des., 2012, 12, 1060 Search PubMed.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- E. G. Hohenstein and C. D. Sherrill, J. Phys. Chem. A, 2009, 113, 878 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ce02045c |
| This journal is © The Royal Society of Chemistry 2017 |