Adsorption and diffusion of lithium in a graphene/blue-phosphorus heterostructure and the effect of an external electric field

Abstract

The adsorption and diffusion behaviors of lithium (Li) in a graphene/blue-phosphorus (G/BP) heterostructure have been investigated using a first principles method based on density functional theory (DFT). The effect of an external electric field on the adsorption and diffusion behaviors has also been investigated. The results show that the adsorption energy of Li on the graphene side of the G/BP heterostructure is higher than that on monolayer graphene, and Li adsorption on the BP side of the G/BP/Li system is slightly stronger than that on monolayer BP (BP/Li). The adsorption energy of Li reaches 2.47 eV, however, the energy barriers of Li diffusion decrease in the interlayer of the G/BP heterostructure. The results mentioned above suggest that the rate performance of the G/BP heterostructure is better than that of monolayer graphene. Furthermore, the adsorption energies of Li atoms in the three different most stable sites, i.e., H_G, T_P and H₁ sites, increase by about 0.49 eV, 0.26 eV, and 0.13 eV, respectively, as the electric field intensity reaches 0.6 V Å⁻¹. The diffusion energy barrier is significantly decreased by an external electric field. It is demonstrated that the external electric field can not only enhance the adsorption but can also modulate the diffusion barriers of Li atoms in the G/BP heterostructure.

---

1. Introduction

Nowadays, the booming development of the intelligent electronics market and the ever-increasing demand for advanced battery systems have led to significant research efforts for high-performance electrode materials.^1–4 As one of the secondary batteries, lithium ion batteries (LIBs) are regarded as the most promising energy storage and conversion battery system owing to their high energy density, flexible and lightweight design, longer lifespan,^5,6 high reversible capacity,⁷ and environmental friendliness,⁸ and they are widely used in portable electronic devices, communication facilities, stationary energy storage systems and ever-enlarging markets for electric vehicles.⁹

The electrochemical performance of LIBs strongly depends on the physical and chemical properties of anode and cathode materials.^9,10 Typically, graphite has been used as the anode material in conventional LIBs due to its high abundance, outstanding kinetics, high energy stability, cycling stability and low cost.^11,12 The graphite anode has a theoretical capacity of 372 mA h g⁻¹,^13,14 which limits its further demand for high power density or long term applications.

As a representative two-dimensional (2D) thin material, graphene has been widely investigated and utilized as an electrode material and obtained great success.^15–17 Monolayer graphene has a theoretical Li ion storage capacity of 744 mA h g^−1 18 and a high specific surface area of 2965 m² g⁻¹.¹⁹ However, the volumetric energy density of graphene limits its implementation in commercial applications. The design of graphene-based composite materials is one of the feasible strategies to improve the rate capability, energy density, and power density of electrode materials.¹⁸ The design of novel composite materials is performed easily more and more with the progress of nanotechnology.

High-performance LIBs critically depend on excellent electrode materials with high rate capability, capacity, fast Li ion mobility, cheap price, good thermal stability, etc.^20–23 In recent years, graphene-based composite materials, such as graphene/MoS₂,²⁴ graphene/MnO₂,²⁵ graphene/phosphorene²⁶ and boron nitride/phosphorene,²⁷ have attracted much attention due to their extraordinary mechanical, electronic and electrochemical properties.

Recently, blue phosphorus (P) nanosheets proposed by Zhu and Tománek have been reported to be equally stable as 2D black P, which should be exfoliated to form a quasi-2D material for potential electronic applications.^28,29 In spite of blue P still not being fabricated by experiment, it has also attracted sufficient attention due to its interesting electrochemical properties with a graphene type structure.^28–32

Both blue and black P nanosheets exhibit excellent adsorption capability to Li, Na, and Mg atoms, and the adsorption energies of the adatoms on blue and black P are stronger than that on the BN, SiC, and MoS₂ sheets.^30,33 Different from black P, blue P has a wider band gap.²⁸ Li et al.³² have reported that Li diffusion on the surfaces of black and blue P has a relatively low energy, and the blue P nanosheet has high charge capacities. The nanocomposite structure is an effective way to integrate the properties of the isolated components.²⁶ Reports from experimental research showed that phosphorus–carbon nanocomposites have high capacities (1700 mA h g⁻¹),³⁴ and the phosphorus/graphene nanosheet hybrid structure displays extraordinarily high cycling stability as an anode material in LIBs.³⁵ Recently, a study on the silicon/carbon nanotube/BaTiO₃ nanocomposite indicated, as an anode of the LIBs, that this composite can improve the cycle performance and discharge capacity.³⁶

Detailed work on the graphene/blue-phosphorus (G/BP) heterostructure is lacking. In the present work, we have provided significant insights into the Li atom adsorption and diffusion behaviors and investigated the effect of an external electric field on adsorption and diffusion in the G/BP heterostructure.

2. Theoretical methods

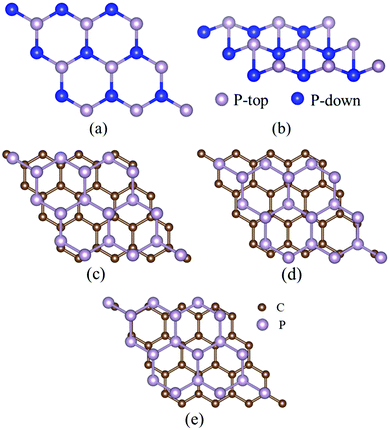
A first-principles method based on DFT has been used in the present work, and the Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) code³⁷ has been employed using the GGA (generalized gradient approximation)³⁸ with the PBE (Perdew–Burke–Ernzerhof) functional³⁹ in our calculations. 3 × 3 × 1 and 5 × 5 × 1 Brillouin zone k-point sampling and the Monkhorst–Pack (MP) mesh are used for testing. The results show that the adsorption energies of Li on graphene more or less depend on the k-point sampling, but the order of the adsorption energies is almost unacted on k-points. For computational efficiency, 3 × 3 × 1 Brillouin zone k-point sampling and the Monkhorst–Pack (MP) mesh are used in our calculations. Valence electron wave functions were expanded using the double-ζ basis set³⁷ with a plane wave energy cutoff of 150 Ry. The convergence of the total energy with respect to the plane wave energy cutoff has been tested. The total energies of the graphene unit cell and blue P unit cell convergence at an energy cutoff of 150 Ry with the total energy change of 0.0005 and 0.007 eV, respectively, have been evaluated. A large vacuum of 30 Å has been added to avoid the interaction of layers due to periodic repeats.

Firstly, the geometry optimizations of 3 × 3 × 1 blue P and 4 × 4 × 1 graphene supercells with a full relaxation of the atomic positions, the shape and the size of the supercell have been performed. The norm-conserving Troullier–Martins pseudopotentials⁴⁰ from the SIESTA databases have been employed, which have been proved to well describe the properties of graphene and carbon nanotubes,⁴¹ the Si–P system,⁴² and Li adsorption in the MoS₂ monolayer.⁴³ The calculated bond-lengths of C–C in graphene and P–P in blue P are 1.42 Å and 2.30 Å agreeing well with the experimental value of 1.42 Å⁴⁴ and the other theoretical value of 2.27 Å,²⁸ respectively. The relaxed stable structure of blue P is shown in Fig. 1(a) and (b).

Fig. 1 Relaxed lattice structures: (a) top view for blue P, (b) side view for blue P, (c) S1 for the G/BP heterostructure, (d) S2 for the G/BP heterostructure, and (e) S3 for the G/BP heterostructure.

In order to test the effect of supercell size on the calculated results, 5 × 5 × 1 supercells with 50 atoms for graphene and blue P have been used to calculate the adsorption energies of Li, and the results show that adsorption energies depend slightly on the supercell size, which agrees with the reported calculations.³² Therefore, the G-(4 × 4 × 1)/BP-(3 × 3 × 1) supercell has been mainly employed in the present calculations.

The stacking patterns of the G/BP heterostructure have been tested in our calculations. Three different stacking patterns have been investigated as shown in Fig. 1(c)–(e). Fig. 1(c) shows that the bridge of blue P (BP) appears to be directly over the hexagons of graphene, called the S1 structure. One top-layer P atom (P-top) of BP overlaps the center of the hexagons of graphene, denoted as S2, see Fig. 1(d). Fig. 1(e) shows that one down-layer P atom (P-down) of BP overlaps the center of the hexagons of graphene denoted as S3. The results show that all the three structures are stable configurations, and the S1 structure is more stable with a slightly larger binding energy of about 11 meV than the S2 and S3 configurations. The bond lengths of C–C and P–P are 1.44 Å and 2.30 Å in the relaxed G/BP structure being preserved well compared to the pristine graphene (1.42 Å) and BP (2.30 Å), respectively, which demonstrates the structure stability of the present stacking structure pattern. To assess the role of van der Waals (vdW) interactions in the G/BP heterostructure, the calculations on the stacking structures of G/BP with the vdW correction (vdW-DF)⁴⁵ have been performed. Our calculations show that S1, S2 and S3 structures also are all stable configurations with nearly equal binding energy, and the bond lengths of C–C and P–P are 1.43 Å and 2.31 Å in G/BP with vdW-DF, which indicates that the PBE exchange–correlation functional (PBE) can correctly describe the G/BP heterostructure. On the basis of the above calculations from PBE and vdW-DF, we mainly consider the S1 structure to investigate the properties of adsorption and diffusion for Li in the G/BP heterostructure.

3. Results and discussion

3.1. Adsorption and diffusion

The adsorption energies of Li in the monolayer graphene, monolayer BP and G/BP heterostructure have been determined. The adsorption energy is defined by

E_ad. = E_G/BP + ε_Li − E_G/BP+Li, (1)

where E_G/BP+Li and E_G/BP are the total energies of the G/BP heterostructure with and without Li adsorption, respectively. ε_Li is the total energy of an isolated Li atom. A large box of 15 × 15 × 15 ų with one Li atom located at the center has been relaxed to obtain the total energy of an isolated Li atom, which is determined to be −13.180 eV. The adsorption energy is important for understanding the Li adsorption ability. By the definition shown in eqn (1), the positive adsorption energy indicates that the Li atom is combined tightly with the G/BP heterostructure, i.e., larger adsorption energy corresponds to a more stable Li adsorption.

These Li adsorption sites in the Li/G/BP, G/BP/Li and G/Li/BP systems are illustrated in Fig. 2. H_G, B_G, and T_G represent Li on the graphene side (Li/G/BP), and H_P, B_P, and T_P represent Li on the blue P side (BP side, i.e., G/BP/Li), as shown in Fig. 2(a) and (b), respectively. Four Li adsorption sites (H₁, H₂, H₃ and H₄) in the interlayer of the G/BP heterostructure (G/Li/BP) have been considered. As shown in Fig. 2(b), H₁, H₂, H₃ and H₄ sites represent that Li atoms locate in the hollow site (H site) of the graphene in the G/BP heterostructure. Our calculations show that the H₄ site is not a stable adsorption position for the Li atom; the Li atom markedly deviates from the hollow site (H site) of the graphene due to the P-top atom of BP.

Fig. 2 Top and side views of Li adsorption sites in (a) Li/G/BP, (b) G/BP/Li and G/Li/BP.

As shown in Table 1, Li adsorption in hollow (H), bridge (B) and top (T) sites on the monolayer graphene and BP has been considered. The configurations of Li adsorption on the monolayer graphene and BP are the same as in ref. 46 and ref. 32, respectively, and can also be referred to those in Fig. 2. It is worth mentioning here that the T site is one Li atom on the top of the P-down atom in the monolayer BP. We have also investigated that the adsorption site is one Li atom on the top of the P-top atom, which shows that it is not a stable Li adsorption position.

Table 1 Adsorption energies (in eV) of Li in graphene, BP and the G/BP heterostructure

		Li site	E ad.		Li site	E ad.
PBE	G/Li	H	1.17	BP/Li	H	1.96
PBE		B	0.83		B	1.90
PBE		T	0.82		T	2.05
PBE	Li/G/BP	HG	1.37	G/BP/Li	HP	1.98
vdW-DF		HG	1.29		HP	1.86
PBE		BG	1.02		BP	1.92
vdW-DF		BG	1.03		BP	1.81
PBE		TG	1.01		TP	2.07
vdW-DF		TG	1.02		TP	1.92
PBE	G/Li/BP	H1	2.47
vdW-DF		H1	2.20
PBE		H2	2.41
vdW-DF		H2	2.16
PBE		H3	2.39
vdW-DF		H3	2.12

---

The vdW interactions may affect the results of binding energies of Li in the G/BP heterostructure. Therefore, the adsorption energies of Li in the Li/G/BP, G/BP/Li and G/Li/BP systems with the vdW correction (vdW-DF) have been investigated. As shown in Table 1, the adsorption energies with the vdW correction slightly decrease compared to those resulting from PBE without vdW-DF. Nevertheless, for the Li/G/BP, G/BP/Li and G/Li/BP systems, respectively, the order of the adsorption energies of Li is independent of the vdW corrections. Therefore, PBE without vdW corrections has been used in the following calculations.

Table 1 shows that the most stable adsorption site of Li is the H site for the monolayer graphene (G/Li). The adsorption energy of the B site is 0.01 eV higher than the value of the T site, which is in good agreement with the previous studies.^46,47 The Li adsorption on the graphene side of the Li/G/BP system is stronger than that on monolayer graphene. For the monolayer BP, the Li atom prefers to occupy the T site with an adsorption energy of 2.05 eV, which agrees well with the previous calculations (2.02 eV).³² The adsorption energies of Li on the BP side of the G/BP/Li system is slightly higher than that on monolayer BP (BP/Li). It is evident that the adsorption energies of Li in the G/Li/BP system are 2.47, 2.41 and 2.39 eV, 1.18, 1.12 and 1.10 eV higher than the value of the H site on the monolayer graphene, respectively. The H₁ site is almost the most stable site on both monolayer graphene and BP (see Fig. 2(b)). Table 1 shows that, in G/Li/BP, H₁ is the most stable Li adsorption site, followed by H₂ and H₃, which indicates that the stability of the Li adsorption on G/Li/BP depends on both graphene and BP.

To further understand the interaction between Li and the G/BP heterostructure, we have investigated the densities of state (DOS) of Li, C and P atoms in G/BP, Li/G/BP and G/Li/BP systems. The present calculations indicate that the major electron contribution is mainly attributed to the s state of Li and the p state of C and P atoms, so, the DOS of Li-2s for Li and C-2p and P-3p for the nearest neighbor C and P atoms of the Li atom are plotted in Fig. 3.

Fig. 3 DOS of (a) C and P atoms in the G/BP heterostructure without the Li atom (G/BP), (b) for H_G site Li atom and its nearest neighbor C and P atoms in Li/G/BP, and (c) H₁ site Li atom and its nearest neighbor C and P atoms in G/Li/BP. The Fermi level is set to 0 eV.

Fig. 3(a) shows the DOS of C and P atoms in G/BP without Li adsorption. It can be seen that there is no hybridization between the C-2p and P-3p states due to the physical adsorption nature of graphene on BP with a binding energy of 0.06 eV per C atom between graphene and BP. As seen from Fig. 3(b) and (c), the DOS of C-2p and P-3p shift to lower energies, i.e., Li adsorption shifts the Fermi level into the conduction band, which indicates that charge transfers to graphene and BP as well as the titanium-graphene system.^46,48,49 The prominent peaks of the Li-2s and C-2p states at about 1.0 eV appear as shown in Fig. 3(b), which demonstrates the strong hybridization interaction between the two states. Fig. 3(c) shows that the DOS of P-3p is strongly altered due to the presence of the Li atom compared to that in G/BP and in Li/G/BP systems. One can see from Fig. 3(c) that, as Li intercalates into the interlayer of G/Li/BP, the peaks of Li-2s, C-2p and P-3p almost appear at the same position, which indicates the hybridization interaction between Li-2s and C-2p (P-3p) states, which is similar to that of Li intercalation in graphene/black P.²⁶ Strong hybridization results in the strong bonding between the Li and C (P) atoms, which may account for the higher adsorption energy of H₁ in G/Li/BP compared to that of H_G in Li/G/BP.

For graphene, the disadvantage of zero-gap restricts the applications in electronic and optoelectronic devices.^24,50 The band structures of the G/BP and G/Li/BP systems have been investigated, as shown in Fig. 4. Fig. 4(a) shows the band structure of G/BP without Li adsorption. The band structure of G/Li/BP with a Li intercalating interlayer is plotted in Fig. 4(b). It is found that the Dirac point shifts to the valence band due to the presence of Li atoms, which may be attributed to the electron interaction between Li and the G/BP heterostructure as shown in Fig. 3(c), and a similar phenomenon has also been observed in potassium–graphene⁴⁶ and graphene/Li/MoS₂²⁴ systems. With Li atom intercalating into the G/BP heterostructure, as well as the case of Li in graphene/MoS₂,²⁴ the band gap has been found to be 0.05 eV as shown in Fig. 4(b). The relatively small gap opening is advantageous for the electrode conductivity.⁵¹

Fig. 4 Band structures of (a) the G/BP heterostructure without Li and (b) G/Li/BP with a Li intercalating interlayer.

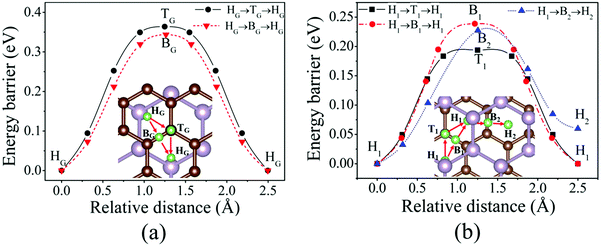
The diffusion properties have been investigated due to the importance of the Li-ion mobility in an electrode material. As the NEB method has not been implemented in the newest siesta 4.0 code, the energy barriers of Li diffusion are calculated by using a constrained method in this work, in which Li ions are constrained in the direction along the diffusion path, whereas the relaxation in the directions perpendicular to the diffusion path is allowed.⁵² The calculations on Li diffusion are carried out at a fixed volume,⁵² but a full relaxation of the atomic positions (Li atoms are constrained to relax in the directions perpendicular to the diffusion path) has been performed. We assume that Li moves between two adjacent favored sites via a high-symmetry site. We mainly focus on the change mechanism of the diffusion barrier. Therefore, the energy difference between one favored site and the high-symmetry site is referred to as the diffusion barrier.⁴⁶Fig. 5(a) shows two different possible paths and the corresponding energy barriers of Li diffusion on the graphene side (Li/G/BP). The first path on the graphene side is that one Li atom moves from the H_G site to the adjacent H_G site across the B_G site and the second path is that one Li atom moves from the H_G site to the adjacent H_G site passing over the T_G site. Fig. 5(b) illustrates three possible paths and the corresponding energy barriers of Li diffusion in G/Li/BP. Similar to that on the graphene side, the H₁ → B₁ → H₁ path is the Li diffusion between two H₁ sites across the B₁ site, and the H₁ → T₁ → H₁ path is the diffusion between two H₁ sites across the T₁ site. We have also investigated the third possible path that one Li atom moves from the H₁ site to the adjacent metastable adsorption site (H₂ site) across B₂ (H₁ → B₂ → H₂) as shown in Fig. 5(b).

Fig. 5 Diffusion path and energy barriers: (a) two possible paths and energy barriers of Li diffusion on the graphene side of the Li/G/BP system, (b) three possible paths and energy barriers of Li diffusion in the G/Li/BP system.

The diffusion barrier calculated in the present work is 0.34 eV for Li diffusion on the monolayer graphene, which agrees with the values of 0.30 eV²⁶ and 0.32 eV⁵³ reported previously. As shown in Fig. 5(a), the Li atom prefers to move along H_G → B_G → H_G with an energy barrier of 0.34 eV on the graphene side. However, Fig. 5(b) shows that the energy barriers decrease as Li atoms diffuse in the interlayer of the G/BP heterostructure. One Li atom moves between two H₁ sites via H₁ → B₁ → H₁ and H₁ → B₂ → H₂ paths by overcoming 0.23 and 0.22 eV energy barriers, respectively, which clearly decrease compared to that on the monolayer graphene and on the graphene side of the Li/G/BP system. The energy barrier of Li diffusion along the H₁ → T₁ → H₁ path decreases about 0.16 eV. At the same time, the mobility of Li on the BP side of the G/BP heterostructure is preserved with an almost equal energy barrier of 0.09 eV to the monolayer BP, which is similar to that of Li on graphene/black P.²⁶ The above results suggest that the rate performance of the G/BP heterostructure is better than that of monolayer graphene.

3.2. Effect of an external electric field

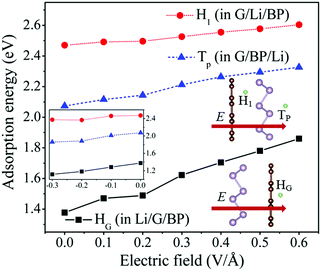
Recently, Shi et al.⁴³ have proposed an effective method to improve the charging rate by applying an external electric field. In this work, the effect of the external electric field on the adsorption behavior and diffusion properties of Li atoms has also been investigated. The effect of the electric field direction on the results has been tested, which shows that the electric field perpendicular to the G/BP surface can bring about a more significant effect on the adsorption energies and diffusion barriers of Li than the other directions. As proposed by Ortiz-Medina et al.,⁵⁴ the electric field applied for all the systems is a static and homogeneous external potential. The electric field is perpendicular to the G/BP surface, and its positive direction is shown in the inset of Fig. 6.

Fig. 6 The adsorption energies of H_G, T_P and H₁ sites in the Li/G/BP, G/BP/Li and G/Li/BP applied electric field. The positive direction of E is shown by arrows, and the case of reverse electric field applied is shown as inset.

In Fig. 6, we have plotted the adsorption energies of H_G, T_P and H₁ sites in Li/G/BP, G/BP/Li and G/Li/BP, respectively. The adsorption energies of the H_G, T_P and H₁ adsorption sites increase from 1.37 to 1.86, from 2.07 to 2.33 and from 2.47 to 2.60 eV with the electric field intensities (E), ranging from 0 to 0.6 V Å⁻¹, respectively. The adsorption energies almost show a linear increase with increasing E. We have also investigated the case of the applied reverse electric field. As shown in the inset of Fig. 6, the adsorption energies decrease with E, ranging from 0 to −0.3 V Å⁻¹, at H_G, T_P and H₁ sites, respectively. In other words, the adsorption energies of Li in the G/BP heterostructure decrease when the reverse E increases. That is to say, as well as the case of the gas molecule on the hexagonal boron nitride sheet,⁵⁵ the external electric field can significantly enhance the adsorption of Li on the G/BP heterostructure, but this enhancement of Li adsorption depends on the direction of E.

To investigate the effect of the external electric field on the diffusion properties, the diffusion of Li atoms on the graphene side of the Li/G/BP system is chosen as the representative case. Fig. 7 illustrates the schematic of Li diffusion along the H_G → B_G → H_G path for 6 values of E ranging from 0.1 to 0.6 V Å⁻¹, and the positive direction of E is shown in the inset of Fig. 6. It is found clearly that the energy barrier for the H_G → B_G → H_G path decreases with increasing E. The energy barrier decreases about 0.13 eV as E reaches 0.6 V Å⁻¹. The diffusion behavior is sensitive to the external electric field.

Fig. 7 The diffusion of Li on the graphene side of the Li/G/BP system with E ranging from 0.0 to 0.6 V Å⁻¹.

To investigate the effect of the external electric field on the interaction between Li and G/BP, the Bader charge analysis has been performed to explore the charge transfer from Li to G/BP in H_G and B_G sites of the Li/G/BP system. As shown in Fig. 8, N_e represents the amount of charge transferred from Li to G/BP in H_G and B_G sites with E ranging from 0.0 to 0.6 V Å⁻¹.

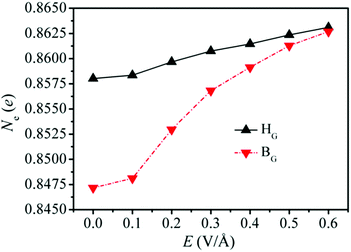Fig. 8 The charge transferred from Li to G/BP for H_G and B_G sites in the Li/G/BP system with an external electric field.

It is found that the amounts of charge transferred from Li increase due to the presence of an external electric field. The larger charge transfer from Li to G/BP leads to the stronger electron interaction between Li and the G/BP heterostructure, which may be responsible for the increase of adsorption energies of Li in H_G sites for the Li/G/BP system when the electric field is applied (see Fig. 6). One can also see that the charge transferred from Li in the H_G site almost increases linearly with increasing E, which corresponds to the increase in the mechanism for the adsorption energies of the H_G site induced by the electric field in the Li/G/BP system (see Fig. 6). Fig. 8 shows that the charge transferred from Li increases in H_G and B_G sites with E ranging from 0.0 to 0.6 V Å⁻¹, respectively. When E = 0.0 V Å⁻¹, i.e., without the external electric field, the amount of charge transferred from Li in the H_G site is larger than that in the B_G site, which can be used to explain the fact that the adsorption energy of Li in the H_G site is higher than the value in the B_G site, as shown in Table 1.

It is of interest that charge transfer caused by the external electric field in the B_G site increases more sharply than that in the H_G site. Therefore, the difference in the charge transferred from Li between B_G and H_G becomes smaller and smaller with increasing E as shown in Fig. 8. For example, the difference between B_G and H_G is about 0.0004 e when E reaches 0.6 V Å⁻¹, which is much smaller than the value of 0.0109 e without the external electric field, which indicates that the charge transfer of Li in the B_G site is more sensitive to the increase of E compared with that in the H_G site when E ranges from 0.1 to 0.6 V Å⁻¹. The analysis above may account for the fact that the diffusion energy barrier decreases with increasing E, as shown in Fig. 7.

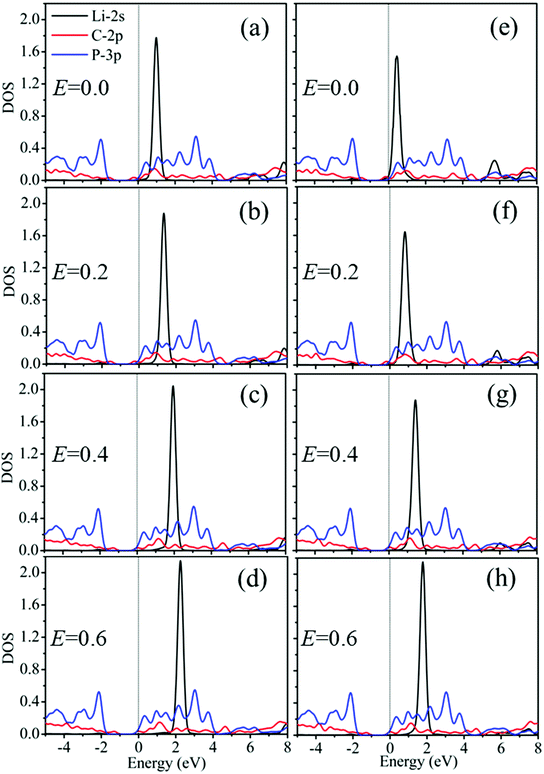
To further explore the interaction between Li and G/BP, we have calculated the DOS of the Li atom and its nearest neighbor C and P atoms in the Li/G/BP system with E of 0.0, 0.2, 0.4 and 0.6 V Å⁻¹, as the representative case studied above. The results on DOS are shown in Fig. 9.

Fig. 9 DOS for the adsorption sites of the Li atom and its nearest neighbor C and P atoms on the graphene side of the Li/G/BP system with E of 0.0, 0.2, 0.4 and 0.6 V Å⁻¹, (a)–(d) H_G site and (e)–(h) B_G site. The Fermi level is set to 0 eV.

It is shown that since the Li-2s of H_G and B_G sites is above the Fermi level, Li atoms donate electrons to G/BP, which is in accordance with the conclusion inferred from our Bader charge analysis and similar to Li adsorption in graphene/MoS₂.²⁴ It is evident that the DOS of Li-2s shift to the deep conduction band with increasing E, which also supports the conclusion of a large charge transfer inferred from the Bader charge analysis between the Li and G/BP.^24,56–58 The above results may account for the stronger interaction between the Li atoms and G/BP. Therefore, the external electric field can enhance the adsorption of Li on the G/BP heterostructure. When E = 0.0 V Å⁻¹, Fig. 9(e) shows that the Li adsorption on the B_G site introduces a lower DOS peak of the Li-2s and C-2p states at ∼0.7 eV, which may be attributed to the lighter hybridization between the two states, so, the adsorption energy of Li in the B_G site is smaller than that in the H_G site, as shown in Table 1. More importantly, the evident difference in the DOS peaks of Li-2s between H_G and B_G sites is observed when E = 0.0 V Å⁻¹, i.e., without the external electric field. However, the difference in the DOS peaks mentioned above decreases with increasing E, which can also be used to explain the decrease of the diffusion barrier.

The adsorption and diffusion behavior of Li is vital for the electrochemical performance in anode materials for LIBs. The experimental study indicates that the safety and reversibility of LIBs depend on the adsorption behavior.⁵⁹ The lower diffusion energy barrier improves the mobility of Li in anode materials for LIBs, and the high mobility is beneficial for rapid charging.⁶⁰ Guo et al.²⁶ have studied the graphene/black-phosphorus heterostructure; they found that the graphene/black-phosphorus heterostructure can greatly improve the binding energy, meanwhile, the high mobility of Li in the graphene/black-phosphorus heterostructure has been maintained in anode materials. Our work shows that the adsorption energy of Li reaches 2.47 eV; however, the energy barriers of Li diffusion decrease in the interlayer of the G/BP heterostructure, which indicates, as well as the graphene/black-phosphorus heterostructure, that the G/BP heterostructure should be regarded as a good electrode material in LIBs. The present investigation on the G/BP heterostructure combined with Li adsorption in the graphene/MoS₂,²⁴ graphene/MnO₂,²⁵ and graphene/phosphorene²⁶ is beneficial to systematically understand the graphene-based nanosheets. Furthermore, our calculations indicate that the adsorption and diffusion behavior of Li can be modulated by an external electric field.

4. Conclusions

We have investigated the adsorption and diffusion behaviors of Li in the G/BP heterostructure. The effect of an electric field on the adsorption and diffusion behaviors has also been investigated. All of the present calculations are performed using the first principles method based on DFT. The results show that adsorption energies of Li on the graphene side of the G/BP heterostructure are higher than that on monolayer graphene, and Li adsorption on the BP side of the G/BP/Li system is slightly stronger than that on the monolayer BP.

The energy barriers of Li diffusion decrease about 0.16 eV, 0.13 eV and 0.12 eV for the three diffusion paths considered in the interlayer of the G/BP heterostructure, respectively, compared to that on the monolayer graphene. At the same time, the mobility of Li on the BP side of the G/BP heterostructure is preserved. The above results suggest that the rate performance of G/BP is significantly better than that of monolayer graphene.

Furthermore, the adsorption energies of Li atoms in the three different most stable sites, i.e., H_G, T_P and H₁ sites, increase about 0.49 eV, 0.26 eV, and 0.13 eV, respectively, as E reaches 0.6 V Å⁻¹. The diffusion energy barrier is significantly decreased by the external electric field. The Bader charge analysis and the DOS calculations indicate that the external electric field is able to urge the charge transfer from Li to G/BP, and can promote strong electronic interaction between Li and G/BP, which demonstrates that the external electric field can not only enhance the adsorption but can also modulate the diffusion barriers of Li in the G/BP heterostructure.

Acknowledgements

This work was financially supported by the Scientific Research Fund of Sichuan Provincial Education Department (No. 14ZB0308, 16ZA0355) and the Scientific Research Fund of Sichuan University of Arts and Science (No. 2014YY001).

References

1. C. Zhao, X. Wang, J. Kong, J. M. Ang, P. S. Lee, Z. Liu and X. Lu, ACS Appl. Mater. Interfaces, 2016, 8, 2372–2379.
2. J. Shi, Z. Wang and Y. Q. Fu, Electrochim. Acta, 2015, 186, 71–75.
3. X. Sun, Z. Wang and Y. Q. Fu, Sci. Rep., 2015, 5, 18712.
4. Z. Wang, X. Niu, J. Xiao, C. Wang, J. Liu and F. Gao, RSC Adv., 2013, 3, 16775–16780.
5. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
6. M. S. Balogun, Y. Luo, W. Qiu, P. Liu and Y. Tong, Carbon, 2015, 98, 162–178.
7. E. Yoo, J. Kim, E. Hosono, H. S. Zhou, T. Kudo and I. Honma, Nano Lett., 2008, 8, 2277–2282.
8. T. M. Bandhauer, S. Garimella and T. F. Fuller, J. Electrochem. Soc., 2011, 158, R1–R25.
9. G. N. Zhu, Y. G. Wang and Y. Y. Xia, Energy Environ. Sci., 2012, 5, 6652–6667.
10. K. Chang and W. Chen, Chem. Commun., 2011, 47, 4252–4254.
11. S. Yang, X. Feng, L. Zhi, Q. Cao, J. Maier and K. Müllen, Adv. Mater., 2010, 22, 838–842.
12. M. Yoshio, H. Wang and K. Fukuda, Angew. Chem., 2003, 115, 4335–4338.
13. J. Zhu, R. Duan, S. Zhang, N. Jiang, Y. Zhang and J. Zhu, SpringerPlus, 2014, 3, 1–8.
14. R. Raccichini, A. Varzi, S. Passerini and B. Scrosati, Nat. Mater., 2015, 14, 271–279.
15. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
16. M. S. Park, J. S. Yu, K. J. Kim, G. Jeong, J. H. Kim, Y. N. Jo, U. Hwang, S. Kang, T. Woo and Y. J. Kim, Phys. Chem. Chem. Phys., 2012, 14, 6796–6804.
17. H. Wang, Y. Yang, Y. Liang, J. T. Robinson, Y. Li, A. Jackson, Y. Cui and H. Dai, Nano Lett., 2011, 11, 2644–2647.
18. K. Chen, S. Song, F. Liu and D. Xue, Chem. Soc. Rev., 2015, 44, 6230–6257.
19. H. K. Chae, D. Y. Siberio-Pérez, J. Kim, Y. Go, M. Eddaoudi, A. J. Matzger, M. O'Keeffe and O. M. Yaghi, Nature, 2004, 427, 523–527.
20. T. Doi, M. Zhou, L. Zhao, S. Okada and J. I. Yamaki, Electrochem. Commun., 2009, 11, 1405–1408.
21. W. Li, Y. Yang, G. Zhang and Y. W. Zhang, Nano Lett., 2015, 15, 1691–1697.
22. Z. Wang, Q. Su, H. Deng and Y. Q. Fu, ChemElectroChem, 2015, 2, 1182–1186.
23. Z. Wang, Q. Su, H. Deng, W. He, J. Lin and Y. Q. Fu, J. Mater. Chem. A, 2014, 2, 13976–13982.
24. X. Shao, K. Wang, R. Pang and X. Shi, J. Phys. Chem. C, 2015, 119, 25860–25867.
25. G. Yu, L. Hu, N. Liu, H. Wang, M. Vosgueritchian, Y. Yang, Y. Cui and Z. Bao, Nano Lett., 2011, 11, 4438–4442.
26. G. C. Guo, D. Wang, X. L. Wei, Q. Zhang, H. Liu, W. M. Lau and L. M. Liu, J. Phys. Chem. Lett., 2015, 6, 5002–5008.
27. Y. Cai, G. Zhang and Y.-W. Zhang, J. Phys. Chem. C, 2015, 119, 13929–13936.
28. Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802.
29. J. Guan, Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 113, 046804.
30. Y. Ding and Y. Wang, J. Phys. Chem. C, 2015, 119, 10610–10622.
31. Y. Li and X. Chen, 2D Mater., 2014, 1, 031002.
32. Q. F. Li, C. G. Duan, X. G. Wan and J. L. Kuo, J. Phys. Chem. C, 2015, 119, 8662–8670.
33. W. Jin, Z. Wang and Y. Q. Fu, J. Mater. Sci., 2016, 51, 7355–7360.
34. T. Ramireddy, T. Xing, M. Rahman, Y. Chen, Q. Dutercq, D. Gunzelmann and A. Glushenkov, J. Mater. Chem. A, 2015, 3, 5572–5584.
35. Z. Yu, J. Song, M. L. Gordin, R. Yi, D. Tang and D. Wang, Adv. Sci., 2015, 2, 1400020.
36. B. S. Lee, J. Yoon, C. Jung, K. Y. Kim, S. Y. Jeon, K. H. Kim, J. H. Park, H. Park, K. H. Lee, Y. S. Kang, J. H. Park, H. Jung, W. R. Yu and S. G. Doo, ACS Nano, 2016, 10, 2617–2627.
37. J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2799.
38. J. A. White and D. M. Bird, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 4954–4957.
39. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
40. N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
41. M. Hammouri, S. K. Jha and I. Vasiliev, J. Phys. Chem. C, 2015, 119, 18719–18728.
42. D. W. Drumm, A. Budi, M. C. Per, S. P. Russo and L. C. L. Hollenberg, Nanoscale Res. Lett., 2012, 8, 1–11.
43. W. Shi, Z. Wang, Z. Li and Y. Q. Fu, Mater. Chem. Phys., 2016, 183, 392–397.
44. N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Butterworth-Heinemann Ltd, Oxford, 2nd edn, 1997, vol. 15.
45. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406.
46. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
47. Y. Li, X. Wang, W. Shi and Z. Yan, J. Appl. Phys., 2014, 116, 084308.
48. V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 992–1000.
49. V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 13921–13928.
50. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
51. J. Sun, H. W. Lee, M. Pasta, H. Yuan, G. Zheng, Y. Sun, Y. Li and Y. Cui, Nat. Nanotechnol., 2015, 10, 980–985.
52. C.-C. Fu, F. Willaime and P. Ordejón, Phys. Rev. Lett., 2004, 92, 175503.
53. J. Zheng, Z. Ren, P. Guo, L. Fang and J. Fan, Appl. Surf. Sci., 2011, 258, 1651–1655.
54. J. Ortiz-Medina, F. López-Urías, H. Terrones, F. J. Rodríguez-Macías, M. Endo and M. Terrones, J. Phys. Chem. C, 2015, 119, 13972–13978.
55. H. Guo, W. Zhang, N. Lu, Z. Zhuo, X. C. Zeng, X. Wu and J. Yang, J. Phys. Chem. C, 2015, 119, 6912–6917.
56. Q. Yue, Z. Shao, S. Chang and J. Li, Nanoscale Res. Lett., 2013, 8, 425.
57. S. Meng and S. Gao, J. Chem. Phys., 2006, 125, 014708.
58. F. Valencia, A. H. Romero, F. Ancilotto and P. L. Silvestrelli, J. Phys. Chem. B, 2006, 110, 14832–14841.
59. C. M. Park and H. J. Sohn, Adv. Mater., 2007, 19, 2465–2468.
60. D. Datta, J. Li, N. Koratkar and V. B. Shenoy, Carbon, 2014, 80, 305–310.

---